22.3(1)特殊的平行四边形(矩形和菱形)性质
- 格式:ppt
- 大小:152.50 KB
- 文档页数:6

第一章特殊的平行四边形考点回顾:1、矩形的性质和判定性质:(1)矩形具有平行四边形的所有性质;(2)矩形的四个角都是直角;(3)矩形的对角线相等;(4)矩形既是轴对称图形,也是中心对称图形.判定:(2)有一个是直角的平行四边形叫矩形;对角线相等的平行四边形是矩形;有三个角是直角的四边形是矩形.2、菱形的性质与判定性质:(1)菱形具有平行四边形的所有性质;(2)菱形的四条边都相等;(3)菱形的对角线互相垂直,且每一条对角线平分一组对角;(4)菱形是轴对称图形,也是中心对称图形.判定:(1)一组邻边相等的平行四边形叫菱形;(2)对角线互相垂直平分的四边形是菱形;(3)四边相等的四边形是菱形.3、正方形有一组邻边相等的矩形是正方形,或有一个角为直角的菱形是正方形.考点精讲精练:例1、如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE.(1)求证:DA⊥AE;(2)试判断AB和DE是否相等?并证明你的结论.证明:(1)∵AE、AD分别平分∠BAF,∠BAC,,∴AD⊥AE.(2)答:AB=DE.∵AB=AC,AD平分∠BAC,∴AD⊥BC.∠BDA=90°.又∵∠BEA、∠DAE都为直角,∴四边形ADBE为矩形.∴AB=DE.变式练习1、如图,将□ABCD的边DC延长到点E,使CE=DC,连AE,交BC于F.(1)求证:△ABF≌△ECF;(2)若∠AFC=2∠D,连AC,BE,求证:四边形ABEC为矩形.证明:(1)∵四边形ABCD为平行四边形,∴AB CD.又∵CE=CD,∴AB EC,∴四边形ABEC为平行四边形,∴ AF=EF,BF=CF,又∠AFB=∠EFC,∴△ABF≌△ECF.(2)在□ABCD中,∠ABC=∠D.∵∠AFC=2∠D=2∠ABC=∠ABC+∠BAF,∴∠ABF=∠BAF,∴FA=FB,∵FA=FE,FB=FC,∴FA=FB=FE=FC.∴BC=EA,∴四边形ABEC为矩形.例2、在菱形ABCD中,对角线AC与BD交于点O,AB=5,AC=6,过D点作DE∥AC,交BC的延长线于点E,如图所示.(1)求△BDE的周长;(2)点P为线段BC上的点,连PO并延长交AD于点Q,求证:BP=DQ.解:(1)在菱形ABCD中,AC⊥BD,且OB=OD.∵AB=5,AC=6,∴OA=3..∴BD=8.∵AD∥BC,∴AD∥CE,∴四边形ACED为平行四边形.∴DE=AC=6.BE=2BC=2AB=10.∴△BDE的周长为8+6+10=24.(2)证明:在菱形ABCD中,DA∥BC,∴∠ODQ=∠OBP,∠OQD=∠OPB.又OD=OB,∴△BPO≌△DQO.∴BP=DQ.变式练习2、如图,DE为□ABCD的∠ADC的平分线,EF∥AD交DC于F.(1)求证:四边形AEFD为菱形;(2)若∠A=60°,AD=5,求菱形AEFD的面积.证明:(1)∵DF∥AE,AD∥EF,∴四边形AEFD为平行四边形.∴∠FDE=∠AED.∵DE为∠ADC的平分线,∴∠ADE=∠FDE,∴∠ADE=∠AED,∴□ABCD为菱形.(2)∠A=60°,AD=AE,∴△ADE为等边三角形.例3、如图,在△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明结论;(3)在(2)的条件下,△ABC满足什么条件时,四边形AECF为正方形?证明你的结论.解:(1)∵EF∥BC,∴∠OEC=∠ECB,∵CE平分∠ACB,∴∠OCE=∠BCE,∴∠OEC=∠OCE,∴OE=OC,同理OF=OC,∴OE=OF.(2)当点O为AC的中点时,四边形AECF为矩形.∵OA=OC=OE=OF,∴四边形AECF为矩形.(3)当∠ACB=90°时,为正方形.∵当∠ACB=90°时,∵MN∥BC,∴∠AOE=90°,∴AC⊥EF.∴矩形AECF的对角线互相垂直,∴四边形AECF为正方形.变式练习3、已知,如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(1)求证:BE=DF;(2)连AC交EF于点O,延长OC至点M,使OM=OA,连EM,FM,判断四边形AEMF是什么特殊四边形?证明你的结论.证明:(1)∵ AB=AD,∠B=∠D=90°,AE=AF,∴Rt△ABE≌Rt△ADF,∴BE=DE.(2)四边形AEMF为菱形,∵四边形ABCD为正方形,∴∠BCA=∠DCA=45°,BC=DC.∵BE=DF,∴BC-BE=DC-DF.即CE=CF,∴OE=OF.∵OM=OA,∴四边形AEMF为平行四边形.∵AE=AF,∴□AEMF为菱形.备考模拟一、填空题1、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3=__________.2、如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF 的面积为__________cm2.3、如图,四边形ABCD为矩形,点E在线段CB的延长线上,连DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为__________.4、如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以为__________.5、如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC =60°,则四边形ABCD的面积等于__________cm2.6、①如图,在四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD边上的中点,则四边形EFGH 为__________.②若ABCD为平行四边形,则EFGH为__________.③若ABCD为矩形,则EFGH为__________.④若ABCD为菱形,则EFGH为__________.答案:1、135°2、3、4、15°;或165°5、6、①平行四边形;②平行四边形;③菱形;④矩形二、选择题7、如图,四边形ABCD是菱形,△AEF为正三角形,点E、F分别在边BC,CD上,且AB=AE,则∠B=().A.60°B.80°C.100°D.120°8、如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折叠为EF,若∠EFC′=125°,则∠ABE的度数为().A.15°B.20°C.25°D.30°9、如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别为边AB,BC的中点,点P在AC 上运动,在运动过程中,存在PE+PF的最小值,则这个最小值为().A.3 B.4 C.5 D.610、如图,菱形ABCD的周长为20cm,DE⊥AB于E,,则下列结论中正确的个数有().①DE=3cm;②BE=1cm;③菱形的面积为15cm2;④.A.1个B.2个C.3个D.4个11、如图,矩形ABCD中,AB=3,BC=5,过对角线交点O作OE⊥AC交AD于E,则AE的长为().A.1.6 B.2.5 C.3 D.3.47-11 BBCCD三、综合题12、如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并证明理由.(2)若AB=6,BC=8,求S四边形OCED.解:(1)∵DE∥AC,CE∥BD,∴四边形OCED为平行四边形.又∵矩形ABCD中,OC=OD,∴四边形OCED为菱形.(2)连OE.则四边形BCEO为平行四边形,∴OE=BC=8..13、如图,边长为4的正方形ABCD中,点P在AB上从A向B运动,连DP交AC于点Q.(1)试证明:无论P运动到AB上何处时,都有△ADQ≌△ABQ;(2)当点P在AB上运动到什么位置时,△ADQ的面积为正方形ABCD面积的?解:(1)∵AD=AB,∠DAQ=∠BAQ,AQ=AQ,∴△ADQ≌△ABQ.(2)△ADQ的面积恰好为正方形ABCD面积的时,过点Q作QE⊥AD于E,QF⊥AB 于F,则QE=QF,.由△DEQ∽△DAP得,解得AP=2.∴当AP=2时,△ADQ的面积是正方形ABCD面积的.14、如图,在Rt△ABC中,∠B=90°,,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点随之停止运动,设点D、E运动的时间为t秒,过点D作DF⊥BC于点F,连DE、EF.(1)求证:AE=DF;(2)四边形AEFD能成为菱形吗?若能,求出相应的t值;若不能,说明理由.解:(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF=t.又∵AE=t,∴AE=DF.(2)能.理由如下:∵AB⊥BC,DF⊥BC,∴AE∥DF.又∵AE=DF,∴四边形AEFD为平行四边形.∴AC=2AB=10.∴AD=AC-DC=10-2t.若使□AEFD为菱形,则需AE=AD=10-2t,即. 即当时,四边形AEFD为菱形.。

特殊平行四边形知识点01 菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2. 性质:菱形除具有平行四边形的一切性质外,还有一些特殊性质:(1) 菱形的四条边都相等;(2) 菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.注意:(1)菱形是特殊的平行四边形,是中心对称图形,过中心的任意直线可将菱形分成完全全等的两部分;(2) 菱形也是轴对称图形,有两条对称轴(对角线所在的直线),对称轴的交点就是对称中心;(3) 菱形的面积有两种计算方法:一种是平行四边形的面积公式:底×高;另一种是两条对角线乘积的一半(即四个小直角三角形面积之和).实际上,任何一个对角线互相垂直的四边形的面积都是两条对角线乘积的一半.3. 判定:定义判定:邻边相等的平行四边形是菱形菱形的判定定理1:四条边都相等的四边形是菱形菱形的判定定理2:对角线互相垂直的平行四边形是菱形【例1】菱形具有而平行四边形不一定具有的性质是()A.两组对边分别平行B.两组对角分别相等C.对角线互相平分D.对角线互相垂直【例2】如图,菱形ABCD中,E,F分别是AD,BD的中点,若4EF ,则菱形ABCD的周长为( )知识精讲A .8B .16C .24D .32【例3】如图,在ABC 中,90,6,8B AB BC ∠=︒==,将ABC 沿DE 折叠,使点C 落在边AB 上的点C '处,并且//C D BC ',则CD 的长是( )A .409B .509C .154D .254【例4】如图,在ABC 中,作以A ∠为内角,四个顶点都在ABC 边上的菱形时,如下的作图步骤是打乱的.①分别以点A ,G 为圆心,大于12AG 的长为半径在AG 的两侧作弧,两弧相交于点M ,N ;②作直线MN 分别交AB ,AC 于点P ,Q ,连接PG ,GQ ;③分别以点D ,E 为圆心,大于12DE 的长为半径作弧,两弧相交于ABC 内一点F ,连接AF 并延长交边BC 于点G ;④以点A 为圆心,小于AC 长为半径作弧,分别交AB ,AC 于点D ,E .则正确的作图步骤是( )A .②④①③B .④③②①C .②④③①D .④③①②【例5】一个菱形的边长为5,两条对角线的长度之和为14,则此菱形的面积为___________.【例6】如图,在四边形ABCD 中,AB =AD ,CB =CD ,点F 是AC 上一点,连接BF 、DF .(1)证明:△ABF ≌△ADF ;(2)若AB //CD ,试证明四边形ABCD 是菱形.知识点02矩形1. 定义:有一个内角是直角的平行四边形叫做矩形.注意:矩形的定义既是矩形的基本性质,也是判定矩形的基本方法.2. 性质:矩形除具有平行四边形的一切性质外,还有一些特殊性质.(1) 矩形的四个角都是直角;(2) 矩形的两条对角线相等.注意:(1) 矩形是特殊的平行四边形,因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.(2) 矩形也是轴对称图形,有两条对称轴(分别是通过对边中点的直线).对称轴的交点就是对角线的交点 (即对称中心).3. 判定:定义:有一个内角是直角的平行四边形是矩形矩形的判定定理1:有三个角是直角的四边形是矩形.矩形的判定定理2:对角线相等的平行四边形是矩形.【例1】直角三角形的斜边长为10,则斜边上的中线长为( ).A .2B .3C .4D .5【例2】如图,矩形ABCD 绕点A 逆时针旋转()090αα︒<<︒得到矩形AB C D ''',此时点B '恰好在DC 边上,若15B BC '∠=︒,则α的大小为( )A .15︒B .25︒C .30D .45︒【例3】如图,在矩形ABCD 中,AD =3,M 是CD 上的一点,将△ADM 沿直线AM 对折得到△ANM ,若AN 平分∠MAB ,则折痕AM 的长为_____.【例4】 如图,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,且2AB =,3BC =,那么图中阴影部分的面积为__________.【例5】如图,在ABC ∆中,AB AC =,BAC ∠的平分线AD 交BC 于点D ,E 为AB 的中点,若12BC =,8AD =,则DE 的长为_____.【例6】已知:在矩形ABCD 中,点E 在BC 边上,连接DE ,且DE BC =,过点A 作AF DE ⊥于点F .求证:AB AF =;【例7】如图,矩形纸片ABCD 中,AB =CD =4,AD =BC =8,∠BAD =∠B =∠C =∠D =90°,将纸片沿EF 折叠,使点C 与点A 重合,使点G 与点D 重合.(1)求证:AE =AF ;(2)求GF 的长.【例8】如图,在菱形ABCD中,AC,BD相交于点O,过B,C两点分别作AC,BD的平行线,相交于点E.(1)求证:四边形BOCE是矩形;(2)连接EO交BC于点F,连接AF,若∠ABC=60°,AB=2,求AF的长.知识点03 正方形1. 定义:有一组邻边相等并且有一个内角是直角的平行四边形叫做正方形.2. 正方形与矩形、菱形的关系矩形邻边相等正方形菱形一个角是直角正方形3. 性质定理正方形即是矩形又是菱形,因而它具备两者所有的性质.性质定理1:正方形的四个角都是直角;正方形的四条边都相等.性质定理2:正方形的两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角.4. 判定定理:定义:有一组邻边相等并且有一个内角是直角的平行四边形是正方形判定定理1:有一组邻边相等的矩形是正方形.判定定理2:有一个内角是直角的菱形是正方形.【例1】设M表示平行四边形,N表示矩形,P表示菱形,Q表示正方形,则它们之间的关系用图形来表示正确的是()A.B.C.D.【例2】下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的平行四边形是正方形C.对角线平分一组对角的平行四边形是菱形D.对角线互相垂直的四边形是正方形【例3】有一正方形卡纸,如图①,沿虚线向上翻折,得到图②,再沿虚线向右翻折得到图③,沿虚线将一角剪掉后展开,得到的图形是( )A.B.C.D.【例4】如图,四边形ABCD为矩形,E、F、G、H为AB、BC、CD、DA的中点,则四边形EFGH的形状是()A.平行四边形B.矩形C.菱形D.正方形【例5】如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点C 折叠纸片,使点C 落在MN 上的点F 处,折痕为BE .若AB 的长为1,则FM 的长为( )A .1B .2C .2D .12【例6】已知点P 是正方形ABCD 内部一点,且PAB △是正三角形,则∠CPD =______度.【例7】边长分别为a 和2a 的两个正方形按如图的样式摆放,则图中阴影部分的面积为_____.【例8】如图,直线l 过正方形ABCD 的顶点A ,点B 、D 到直线l 的距离分别为1、3,则正方形的边长为_______.【例9】如图,在等边ABE △下方作一个正方形BCDE ,连接AC ,AD .(1)求证:ABC ≌AED ;(2)求CAD 的度数.【例10】.如图,已知平行四边形ABCD ,若M ,N 是BD 上两点,且BM =DN ,AC =2OM ,(1)求证:四边形 AMCN 是矩形;(2)△ABC 满足什么条件,四边形AMCN 是正方形,请说明理由.1.如图,在平行四边形ABCD 中,AE 、BF 分别是∠DAB 、∠CBA 的角平分线,AE 、BF 交于O 点,与DC 分别交于E 、F 两点。

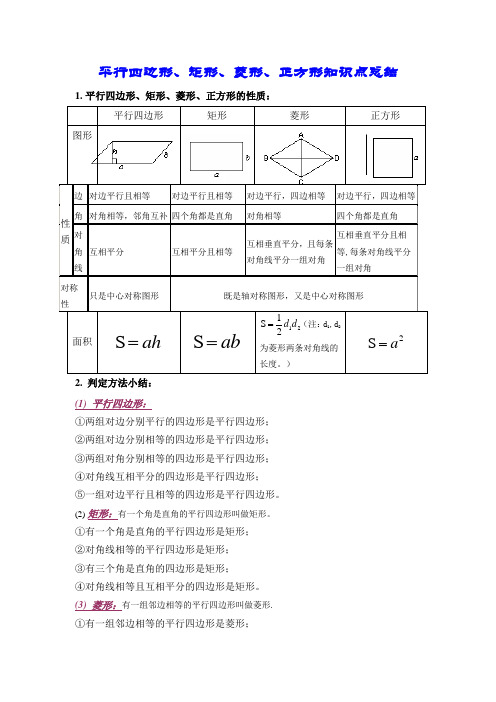
平行四边形、矩形、菱形、正方形知识点总结1.平行四边形、矩形、菱形、正方形的性质:
图形
2. 判定方法小结:
(1) 平行四边形:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形。
(2)矩形:有一个角是直角的平行四边形叫做矩形。
①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形;
④对角线相等且互相平分的四边形是矩形。
(3) 菱形:有一组邻边相等的平行四边形叫做菱形.
①有一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四边都相等的四边形是菱形;
④对角线互相垂直平分的四边形是菱形。
(4) 正方形:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
①有一组邻边相等且有一个角是直角的平行四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③有一组邻边相等的矩形是正方形;
④对角线互相垂直的矩形是正方形;
⑤有一个角是直角的菱形是正方形;
⑥对角线相等的菱形是正方形;
⑦对角线互相垂直平分且相等的四边形是正方形。

一、平行四边形的性质:
1. 平行四边形是中心对称图形,对称中心是两条对角线的交点;
2. 平行四边形对边平行且相等;
3. 平行四边形的对角相等,邻角互补;
4. 平行四边形两条对角线互相平分;
二、平行四边形的判定:
1. 两组对边分别平行的四边形是平行四边形;
2. 两组对边分别相等的四边形是平行四边形;
3. 一组对边平行且相等的四边形是平行四边形
4. 对角线互相平分的四边形是平行四边形;
三、矩形的性质:
1. 矩形具备平行四边形的一切性质;
2. 矩形对角线相等;
3. 矩形的四个内角都是90°;
4. 矩形是轴对称图形
四、矩形的判定:
1. 有一个角是直角的平行四边形是矩形;
2. 有三个角是直角的四边形是矩形;
3. 对角线相等的平行四边形是矩形;
五、菱形的性质:
1. 菱形具备平行四边形的一切性质;
2. 对角线互相垂直;
3. 四条边都相等;
4. 菱形是轴对称图形,对称轴是两条对角线所在的直线。
六、菱形的判定:
1. 一组邻边相等的平行四边形是菱形;
2. 四条边都相等的四边形是菱形;
3. 对角线互相垂直的平行四边形是菱形;
七、正方形的性质:
1.正方形具有平行四边形、菱形、矩形的一切性质。
八、正方形的判定:
1. 有一组邻边相等的矩形是正方形;
2. 对角线互相垂直的矩形是正方形;
3. 有一个角是直角的菱形是正方形;
4. 对角线相等的菱形是正方形;。

菱形,矩形,正方形复习新知详解1、菱形的定义:有一组邻边相等的平行四边形叫做菱形。
2、菱形也是特殊的平行四边形,故菱形具备平行四边形的多有性质。
除此之外,菱形的性质还有:菱形的性质一:边菱形的四条边相等。
菱形的性质二:对角线菱形的对角线互相垂直,并且每一条对角线平分一组对角。
菱形的性质三:对称性菱形是轴对称图形,对角线所在的直线是对称轴,菱形有2条对称轴。
例1:已知,如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F。
(1)求证:AM=DM;(2)若DF=2,求菱形ABCD的周长。
练习1:如图所示,菱形的周长为20cm,两邻角的比为1:2.求:(1)较短对角线的长;(2)一组对边的距离。
例2:如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,PB+PE的最小值是3,求AB的值.练习2:如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,求△AEF 的周长。
第21题图A BCDEFMFADEBC例3:如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.求:(1)∠ABC的度数;(2)菱形ABCD的面积.练习3:已知菱形ABCD中,AC与BD相交O点,若∠BDC=030,菱形的周长为20厘米,求菱形的面积.小结:S菱形ABCD =AB× DE或S菱形ABCD = S△ABD+S△BCD = AC×BD (菱形的面积=底×高=对角线乘积的一半)菱形判定定理2:对角线互相垂直的平行四边形是菱形例2:如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.菱形判定定理3:四条边都相等的四边形是菱形例3:如图所示,四边形ABCD、DEBF都是矩形,AB=BF,AD、BE相交于M,BC、DF交于N,求证:四边形BMDN是菱形.ABCDO练习1:如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD。
【初中数学】初中数学知识点总结:特殊的平行四边形(1)平行四边形的所有性质矩形、菱形、正方形都具有,但矩形、菱形、正方形具有的性质平行四边形不一定具有,这点易出现混淆;(2)矩形、菱形具有的性质正方形都具有,而正方形具有的性质,矩形不一定具有,菱形也不一定具有,这点也易出现混淆;(3)不能正确的理解和运用判定定理进行证明,(如在证明菱形时,把四条边相等的四边形是菱形误解成两组邻边相等的四边形是菱形);(3)再利用对角线长度求菱形的面积时,忘记乘;(3)判定一个四边形是特殊的平行四边形的条件不充分。
【典型例题】(2021天门、潜江、仙桃)正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;(2)当点P在线段DB上 (不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由初三;(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.【解析】(1)AP=EF,AP⊥EF,理由如下:连接AC,则AC必过点O,延长FO交AB于M;∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,∴四边形OECF是正方形,∴OM=O F=OE=AM,∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,∴△AMO≌△FOE,∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,故AP=EF,且AP⊥EF.(2)题(1)的结论仍然成立,理由如下:延长AP交BC于N,延长FP交AB于M;∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,∴四边形MBEP是正方形,∴MP=PE,∠AMP=∠FPE=90°;又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,∴AM=PF,∴△AMP≌△FPE,∴AP=EF,∠APM=∠FPN=∠PEF∵∠PEF+∠PFE=90°,∠FPN=∠PEF,∴∠FPN+∠PFE=90°,即AP⊥EF,故AP=EF,且AP⊥EF.(3)题(1)(2)的结论仍然成立;如右图,延长AB交PF于H,证法与(2)完全相同感谢您的阅读,祝您生活愉快。
平行四边形、矩形、菱形、正方形知识点
总结
本文介绍了平行四边形、矩形、菱形、正方形的性质和判定方法。
首先,平行四边形、矩形、菱形、正方形都是特殊的四边形。
它们的边和角有不同的性质。
平行四边形的边对边平行且相等,角对角相等,邻角互补;矩形的对边平行且相等,四个角都是直角;菱形的对边平行,四边相等,对角线互相垂直平分;正方形的对边平行且相等,四个角都是直角,对角线相等且互相垂直。
其次,本文总结了判定这些特殊四边形的方法。
对于平行四边形,可以根据两组对边分别平行、相等或对角线互相平分等条件来判断。
对于矩形,可以根据有一个角是直角、对角线相等或有三个角是直角等条件来判断。
对于菱形,可以根据有一组邻边相等、对角线互相垂直或四边都相等等条件来判断。
对于正方形,可以根据有一组邻边相等且有一个角是直角、对角线互相垂直且相等或有一个角是直角的菱形等条件来判断。
最后,需要注意的是,本文中的公式中,d1和d2分别表示菱形的两条对角线的长度。
同时,文章中存在格式错误和明显有问题的段落,需要删除。