2018年四年级暑期奥数班测试卷

四年级奥数综合测试题班级考号姓名总分一、填空题（每题10分，共60分）１、计算：⑴454+999×999+545⑵999+998+997+996+1000+1004+1003+1002+10012、数一数下面的图形.（）条线段（）个长方形3、要使上下两排的小猫一样多，应该怎样移？4、按下面图形的排列情况，算出第24个图形是什么？（1）○○△□○○△□○○△□……第24个图形是（）（2）☆◇◇△△☆◇◇△△☆◇◇△△……第24个图形是（）5、用火柴棍拼成的数字和符号如下图所示，那么用火柴棍拼成一个减法等式最少要用_______根火柴6、有学生若干人参加植树活动，如果每组12人，就多11人，如果每组14人，就少9人。

问分成______组，共有______人。

二、填空题（每题10分，共90分）1、村姑卖鸡蛋，第一次卖出一篮的一半又二个；第二次卖出余下的一半又二个；第三次卖出再剩下的一半又二个，这时篮里只剩下二个蛋，问这篮鸡蛋有多少个?2、一个文具店中橡皮的售价为每块5角，圆珠笔的售价为每支1元，签字笔的售价为每支2元5角。

小明要在该店花5元5角购买其中两种文具，他有___________种不同的选择。

3、一个书架上有数学、语文、英语、历史4种书共27本，且每种书的数量互不相同。

其中数学书和英语书共有12本，语文书和英语书共有13本。

有一种书恰好有7本，是_________书。

4、下面两个算式中，相同的字母代表相同的数字，不同的字母代表不同的数字，那么A＋B＋C＋D＋E＋F＋G=_____________。

5、芳芳和明明两人集邮，芳芳给明明4张邮票后，芳芳还比明明多2张.芳芳原来比明明多几张邮票?6、做一道加法题时，小虎把个位上的6看作9，把十位上的3看作5，结果和是86，问正确答案应是多少?附：参考答案一、填空题：1、999000 90002、10 183、从三排移三个小猫到下排。

4、□△5、12根（2-1＝1）6、10组131人二、应用题：1、44个鸡蛋2、8种（一个2.5+6个0.5 二个2.5+一个0.5 一个2.5+3个1 5个1+1个0.5 4个1+3个0.5 3个1+5个0.5 2个1+7个0.5 1个1+9个0.5）3、是英语书，用假设法去推理。

2018 年小学四年级奥数竞赛试卷一、计数问题1.甲乙丙3 个小朋友站成一排照相，共有种不同的排列方法．2.用1 元，2 元和5 元的纸币，有种不同的方法凑出6 元钱．3.数一数，图中有个三角形．4.如图所示，在2×2 方格中，画一条直线最多穿过3 个方格；在3×3 方格中，画一条直线最多穿过5 个方可知；那么在5×5 方格中，画一条直线，最多穿过个方格．5.六一儿童节，四位小朋友各做了一个小礼物准备相互赠送，但要求自己不得留下自己做的礼物，他们收到礼物的不同方式有种．二、几何图形问题6.将一张长方形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形一定是．（填“三角形”、“长方形”、“梯形”或“菱形”）7.图是3×3 的正方形方格，∠1 与∠2 相比，较大的是．8.各图中，阴影部分的面积与整个图形面积的比值最大的是图．9.将图中所示的三角形ABC 分成面积相等的四个部分，请给出三种不同的分法．要求：在下面所给的三个图中作答．10.将一个三角形的三条边同时扩大相同的倍数，如图，得到的新三角形的面积变为原三角形面积的9 倍，则新三角形的周长是原三角形的周长的倍．11.下列图形经过折叠不能围成正方体的是．12.把2、4、6、8、10、12 这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图，最左边的正方形上的数字是12，则最右边的正方形上的数字是．13.将若干个边长为1 的正六边形（即单位六边形）拼接起来，得到一个拼接图形，如图：那么，要拼接成周长等于18 的拼接图形，需要多少个单位六边形？画出对应的一种图形．三、找规律14．3+12、6+10、12+8、24+6、48+4、…是按一定规律排列的一串算式，其中第六个算式的计算结果是．15.按规律填数：①2，4，7，11，16，②12，19，33，61，117，16.找一找规律，再在横线里填上适当的数．3、4、5、8、7、16、9、32、、四、其他问题17.请你任意写出5 个真分数．18.光明小学参加课外活动小组的人数统计如图所示，则该校参加课外活动小组的共有人．19．2005 年4 月lO 日是星期日，则2005 年6 月1 日是星期．20．一个活动性较强的细菌每经过10 秒就分裂为一个活动性较强的与一个活动性较弱的细菌，而一个活动性较弱的细菌每经过20 秒就分裂为两个活动性较弱的细菌．问：一个活动性较强的细菌，经过60 秒可繁殖多少个细菌？21．赛马比赛前，五位观众给A、B、C、D、E 五匹赛马预测名次．甲说：“B 第三名，C 第五名．”乙说：“E 第四名，D 第五名．”丙说：“A 第一名，E 第四名．”丁说：“A 第二名，B 第一．”戊说：“A 第三名，D 第四名．”结果每人都只预测对了一半．“请问：这五匹马的名次是怎样排列的？”22.作家A、B、C、D、E 依次坐成一排为同学们签名售书，已知每位同学恰好找座位相邻的三位作家签名，已知一共有22 个同学同时找到B 和D 签名，并且C 一共签名38 次，A 比E 多签名6 次，那么B 一共签名次．23.如图，ABCD 是一个梯形，已知三角形ABD 的面积是12 平方厘米，三角形AOD 的面积比三角形BOC 的面积少12 平方厘米，那么，梯形ABCD 的面积是平方厘米．24．2006 年学校1 月20 日开始放寒假，3 月1 日上学，学校放了天寒假．25.假设某餐厅备有肉4 种，鱼3 种，蔬菜5 种，有位客人预计肉、鱼和蔬菜各点一种，他有种点菜的方法．26.将自然数按下面的形式排列，试问：第20 行最左边的数是，第20 行所有数的和是．27.芳芳说：“我13 岁，比惠惠小3 岁，比萍萍大一岁”；惠惠说：“我不是年龄最小的，萍萍和我差4 岁，萍萍是11 岁”；萍萍说：“我比芳芳年龄小，芳芳10 岁，惠惠比芳芳大2 岁，”以上每人所说的三句话中，都有一句是错误的，则芳芳多少岁？惠惠多少岁，萍萍多少岁？2018 年小学四年级奥数竞赛试卷参考答案与试题解析一、计数问题【分析】最左边的位置有3 个小朋友可以选，中间位置还有2 个小朋友可以选，最后一个位置只有1 个小朋友可以选；各个位置上可以选的方法的积就是总的次数．【解答】解：3×2×1=6（种）；答：有6 种不同的排列方法．故答案为：6．【点评】本题也可以采取给三人编号，然后写出全部排列的方法求解．【分析】分类计数，分只有一种，只有两种逐个列举即可．【解答】解答：5+1=62+2+2=62+2+1+1=62+1+1+1+1=61+1+1+1+1+1=6共有5 种方法．故答案为：5．【点评】本题考查了筛选与枚举问题，关键是确定分类的办法和凑数的范围，要注意按顺序列举．【分析】单个的小三角形有12 个，由三个小三角形组成的三角形有6 个，由九个小三角形组成的三角形有2 个，则可以求出三角形的总个数．【解答】解：图中有三角形：12+6+2=20（个）．故答案为：20．【点评】此题关键是将三角形进行分类再计数．【分析】如下图所示，那么在5×5 方格中，画一条直线，最多穿过9 个方格．【解答】解：在2×2 方格中，画一条直线最多穿过3 个方格，2+1；在3×3 方格中，画一条直线最多穿过5 个方可知，3+2；以此类推，那么在5×5 方格中，画一条直线，最多穿过5+4=9 个方格．答：那么在5×5 方格中，画一条直线，最多穿过9 个方格．故答案为：9．【点评】此题考查了数与形结合的规律，以上两种方法都可得解．【分析】结合题目的要求，我们不妨先设出四个小朋友，然后具体分析（过程见解答）即可得出答案．【解答】解答：设这四个小朋友分别是a，b，c，d，则收到a 送的礼物有b、c、d 三种可能，下面不妨以其中的一种可能为例分析：①以给 b 为例：b 收到a 送的礼物那么b 送的礼物如果给a，那么必然是 c 和 d 交换礼物，这是一种b 送的礼物如果给了c，那么c 不能给a 只能给d，所以d 要给a，这也是一种同理b 的礼物给了d 又是一种则总共有1+1+1=3 种即 a 送给 b 有3 种；②同样，若给c 和d 也是各有3 种；因此共计3+3+3=9 种．故：此空为9．【点评】解答此题关键是理解题意，按要求进行分析即可得出答案．二、几何图形问题【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有 4 条边，并且这4 条边还相等，从而可以进行从题后的答案中选择．【解答】解：由题意知，对折实际上就是对称，对折2 次的话，剪下应有4 条边，并且这4 条边还相等，只有菱形满足这一条件，故答案为：菱形．【点评】此题考查了利用对称设计图案．【分析】借助正方形和线段构成的角来比较角的大小．：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【解答】解：∠1=180°﹣（∠3+∠4），∠2=180°﹣（∠4+∠5）=180°﹣2∠4．很明显∠3＜∠4，所以180°﹣（∠3+∠4）＞180°﹣2∠4．即∠1＞∠2．【点评】利用正方形来确定角的度数．【分析】先写出分个图形阴影部分的面积与整个图形面积的比，然后比较这几个比值的大小，从而得出答案．【解答】解：由题意知：A、把圆平均分在了6 份，阴影部分的面积与整个图形面积的比值是：，B、把正方形平均分成了8 份，阴影部分的面积与整个图形面积的比值是：，C、把正方形平均分成了8 份，阴影部分的面积与整个图形面积的比值是：，D、通过割补法可知，阴影部分的面积与整个图形面积的比值是：，通过比较可知最大的为，故答案为：B．【点评】此题考查了分数的意义和大小比较．【分析】根据等底等高的三角形面积相等划分即可．【解答】解：（答案不唯一）【点评】本题考查了等底等高的三角形面积相等的灵活应用．【分析】根据题干分析可得，原三角形与新三角形相似三角形，相似比是1：3．根据相似三角形的性质可得：相似三角形的面积的比等于相似比的平方，相似三角形的周长的比等于相似比．由此即可得出答案．【解答】解：根据题干可得原三角形与新三角形相似，相似比是1：3，由相似三角形的性质可得：周长的比等于相似比，即：原三角形周长：新三角形周长=1：3答：新三角形的周长是原三角形的周长的 3倍．故答案为：3．【点评】此题考查了相似三角形的相似比与它们周长的比以及面积的比的性质．【分析】根据正方体展开图的常见形式作答即可．【解答】解：由展开图可知：A、B 能围成正方体；C 围成几何体时，有两个面重合，故不能围成正方体．故选C．【点评】展开图能折叠成正方体的基本类型有：“一，四，一”“三，三”“二，二，二”“一，三，二”．【分析】根据正方体的特征和展开图的形状可知，2 在正面，4 在背面；6 和8 在侧面；10 和12 在上下面；由此解答．【解答】解：通过上面的分析得：最右边的正方形上的数字是4．故答案为：4．【点评】此题主要考查正方体的特征及展开图的形状．【分析】先从变化中观察，寻找规律．细心观察四个图形，可以发现：在拼接图形时，每增加一个单位六边形，拼接图形的周长要么不增加，要么增加2 或4，据此分析解答即可．【解答】解：因为两个单位六边形拼接的图形的周长只能是10，18﹣10=8，8=4+4=4+2+2=2+2+2+2，所以当拼接图形的周长等于18 时，所拼接的单位六边形有 4 个、5 个、6 个或7 个，如下图：【点评】本题考查图形的规律．三、找规律【分析】观察算式可以发现，式子中有两个加数，第一个加数3、6、12、24、48、…依次扩大2 倍，第二个加数12、10、8、6、4…依次减少2，据此规律，第六个算式是96+2=98．【解答】解：第一个加数3、6、12、24、48、…依次扩大2 倍，第二个加数12、10、8、6、4…依次减少2，第六个算式为：48×2+（4﹣2）=96+2=98．故答案为：98．【点评】观察式子，找出式子的变化规律，然后运用总结的规律解决问题．【分析】①后一个数是前一个数依次增加2，3，4，…所得．②19﹣12=7，33﹣19=14，61﹣33=28，117﹣61=56，依次增加7 的1、2、4、8、16 倍即可．【解答】解：①16+6=22②117+7×16=229故答案为：22，229．【点评】通过观察数字的特点，找出相邻两个数之间的倍数关系或者差之间的关系，再由此求解即可．【分析】奇数项是它前面的奇数项加2 所得，偶数项是它前面的偶数项乘2 所得，由此得出答案．【解答】解：9+2=11，32×2=64；故答案为：11，64．【点评】数列中的规律：关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律，然后再利用这个变化规律再回到问题中去解决问题．四、其他问题【分析】根据真分数的定义解答即可．【解答】解：由题意知，分子小于分母的分数叫真分数，所以任意写出的 5 个真分数可为：、、、、；故答案为：、、、、；【点评】此题考查了真分数的定义．【分析】由于条形统计图的高度代表了数量的多少，所以要求参加课外活动小组的共有多少人，只要把所有小组的人数加起来即可．【解答】解：6+9+15+20+25+30，=105（人）；故答案为：105．【点评】此题考查了学生根据条形统计图回答问题的能力．【分析】先求出从4 月10 日到6 月1 日经过了多少天，再求这些天里有几个星期，还余几天，根据余数判断6 月1 日是星期几．【解答】解：4 月10 日到4 月30 日经过了20 天，5 月有31 天，再到6 月1 日又经过1 天；共经过：20+31+1=52（天），52÷7=7（周）…3（天）；即6 月1 日是星期三．故答案为：三．【点评】本题先求出经过的天数，再求这些天里有几周，还余几天，然后根据余数推算．【分析】每一个活动性较强的细菌都会分解，经过60 秒仍然是1 个一个活动性较强的细菌；根据一个活动性较弱的细菌每经过20 秒就分裂为两个活动性较弱的细菌，而每10 秒又会分裂出 1 个活动性较弱的细菌，列举出60 秒内它们的数量．【解答】解：一个活动性较强的细菌最后只剩下 1 个；活动性较弱的细菌分裂过程如下：第10 秒：1 个，第20 秒：1+1=2（个），第30 秒：2+1+1=4（个），第40 秒：2+2+1+1=6（个），第50 秒：4+2+2+1+1=10（个），第60 秒：4+4+2+2+1+1=14（个），14+1=15（个）；答：一个活动性较强的细菌经过60 秒可繁殖15 个细菌．【点评】根据两种不同的细菌分裂方式分别求出60 秒时它们各有的数量，再相加即可．【分析】根据丙说：“A 第一名，E 第四名．”假设E 不是第四名，则A 是第一名就正确，那么丁说：“A第二名，B 第一．”都错误，这与每人都只预测对了一半相矛盾；所以E 是第四名是正确，据此进一步解答即可．【解答】解：根据丙说：“A 第一名，E 第四名．”假设A 是第一名，则E 不是第四名，那么丁说：“A 第二名，B 第一．”都错误，这与每人都只预测对了一半相矛盾；所以E 是第四名是正确，则，根据戊的表述可得 A 是第三名，再根据甲的表述可得 C 是第五名，因为A 是第三名，再根据丁的表述可得B 是第一名，则剩下的D 就是第二名，综合上述可得，B 是第一名，D 是第二名，A 是第三名，E 是第四名，C 是第五名．【点评】条件分析﹣﹣﹣假设法：假设可能情况中的一种成立，然后按照这个假设去判断，如果有与题设条件矛盾的情况，说明该假设情况是不成立的，那么与他的相反情况是成立的．【分析】同时找到 B 和 D 签名的肯定找了C 签名，因为 C 一共签了38 次，这样就可以确定找A 和E 签名的次数之和是38﹣22=16 次，再由A 比E 多签名6 次可以求出A 签的次数，因为找A 签名的人肯定找B 签名，所以可以推算出B 签名的次数．【解答】解：38﹣22=16（次）（16+6）÷2=11（次）11+22=33（次）故填33．【点评】此题的关键是分析38﹣22=16 次所代表的含义是什么．【分析】根据等量加等量差不变，可知三角形ABD 和三角形ABC 的面积的差也是12 平方厘米，由此可以求出三角形ABC 的面积，据此分析解答即可．【解答】解：S△AOD+S△AOB=S△ABD，S△BOC+S△AOB=S△ABC，则三角形ABD 的面积比三角形ABC 的面积少12 平方厘=12+12=24（平方厘米）米．S△ABCS 梯形ABCD=24+12=36（平方厘米）故填：36．【点评】本题考查的是三角形和梯形的面积计算．【分析】2006 年的 1 月份有31 天，2 月份有28 天，据此解答即可．【解答】解：31﹣20+1+28=40（天）故填：40【点评】本题考查的是周期问题．【分析】根据题意可得，肉有4 种选择，鱼有3 种选择，蔬菜有5 种选择，根据乘法原理可得，共有4×3×5=60 种选择；据此解答即可．【解答】解：4×3×5=60（种）故答案为：60．【点评】本题考查了乘法原理：做一件事，完成它需要分成n 个步骤，做第一步有m1 种不同的方法，做第二步有m2种不同的方法，…，做第n 步有m n种不同的方法，那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法．【分析】观察数阵可得规律，每行数据的个数是奇数列，先求出第19 行有多少个数，即1+2×（19﹣1）=37 个，再求出19 行的总个数1+3+5+…+37=361，再进一步解答即可．【解答】解：1+2×（19﹣1）=37（个）1+3+5+…+37=19×19=361（个）1+2×（20﹣1）=39（个）所以，第20 行最左边的数是361+1=362；第20 行最后一个数是：361+39=400第20 行所有数的和是：（362+400）×39÷2=762×39÷2=14859故答案为：562；14859．【点评】一般地说，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．【分析】根据题意可知：芳芳说的“我13 岁”和萍萍说的“芳芳10 岁”这两句话中肯定有一句是对的，有一句是错的，据此分析解答即可．【解答】解：假设芳芳13 岁是对的，则芳芳10 岁就是错的，此时惠惠比芳芳大 2 岁，则惠惠是15 岁，芳芳比萍萍大1 岁，则萍萍是12 岁，这样惠惠和萍萍就相差3 岁，和惠惠说的“萍萍和我相差4 岁”相矛盾，不符合题意．所以芳芳是10 岁，此时惠惠13 岁，萍萍9岁．答：芳芳10 岁，惠惠13 岁，萍萍9 岁．【点评】本题考查的是逻辑推理．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

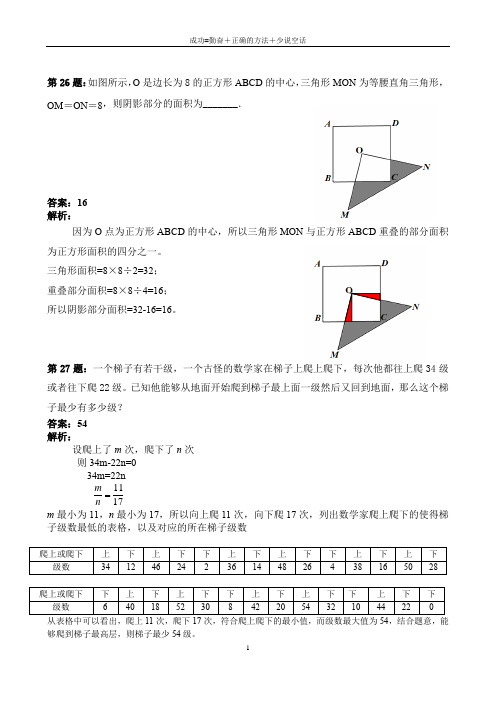
第26题：如图所示，O 是边长为8的正方形ABCD 的中心，三角形MON 为等腰直角三角形，OM ＝ON ＝8，则阴影部分的面积为_______．答案：16 解析：因为O 点为正方形ABCD 的中心，所以三角形MON 与正方形ABCD 重叠的部分面积为正方形面积的四分之一。

三角形面积=8×8÷2=32； 重叠部分面积=8×8÷4=16； 所以阴影部分面积=32-16=16。

第27题：一个梯子有若干级，一个古怪的数学家在梯子上爬上爬下，每次他都往上爬34级或者往下爬22级。

已知他能够从地面开始爬到梯子最上面一级然后又回到地面，那么这个梯子最少有多少级？答案：54 解析：设爬上了m 次，爬下了n 次 则34m-22n=0 34m=22n1711 n m m 最小为11，n 最小为17，所以向上爬11次，向下爬17次，列出数学家爬上爬下的使得梯子级数最低的表格，以及对应的所在梯子级数从表格中可以看出，爬上11次，爬下17次，符合爬上爬下的最小值，而级数最大值为54，结合题意，能够爬到梯子最高层，则梯子最少54级。

第28题：从下图的中心点出发，沿着格线移动至相邻点。

问这样的操作重复了10次后回到中心点的方法有几种？（途中可以通过中心点）答案：16384种解析：方法1：使用标数法第一次第二次第三次第四次第五次第六次第七次第八次第九次第十次所以重复了10次后回到中心点的方法有16384种。

方法2：如下图，从白点开始移动一次到达黑点，从黑点移动一次到达白点。

于是从中心的黑点开始移动的奇数次到达的是4个白点中的1个。

由此可知，无论最后一次怎样移动，9次移动后到达的点为白点，第10次移动后到达中心点的方法只有一种。

再考虑从白点移动2次的方法，首先向中心点移动的话有4种方法，向四角上的点移动的话有2种方法，故共有4＋2×2=8种。

又最初一次移动有4种方法。

所求值为484⨯=16384种。

四年级暑期班期末测试（满分：100分出卷人：君君老师）一．填空题（共8题，每题5分）1.在三角形ABC 中，∠A=20°，∠ C=80°，则∠ B= _________°.2.四年级一班要从18 名男生和17 名女生中选出一名学生当班长，有__________ 种选法.3.文文在做一道加法题时，把其中一个加数十位上的6看成了2，得到的结果为125，那么正确的结果是______。

4.（1）甲乙两辆车分别从A、B两地同时出发，相向而行，经过3小时相遇，甲每小时行45千米，乙每小时行55千米，则A、B两地间的距离是_________千米。

（2）A、B两地相距600米，艾迪和薇儿分别从A、B两地同时出发，薇儿在前，艾迪在后，同向而行，艾迪每秒钟行5米，薇儿每秒钟行3米，则艾迪需要_________秒才能追上薇儿。

5.已知平行四边形ABCD的面积为20，AE是垂直CD，AE=4，CE=3，阴影三角形ADE的面积为________。

6.8支队伍参加排球比赛，若采用淘汰赛赛制，一共要进行________场比赛。

若采用单循环赛赛制，一共要进行________场比赛。

7.在下列加法竖式中，相同字母代表相同数字，不同字母代表不同数字，那么A+B+C=________。

AA B+ A B C7 1 58.如图：每行的左边和每列的上边所标数字代表该行、列连续黑色方块的数量。

那么，在这个5×5的方格中，第3行第4列的方块颜色为________。

二．解答题（共6题，每题10分）9.计算：（1）3.74+1.26 - 21÷5 （2）4.5×3 - 1.0110.用2,0,1,7,8,6这六个数字，可以组成多少个无重复数字的三位数？11.如图，两个正方形并排放在一起，正方形ABCD 边长为8厘米，正方形CEFG 边长为6厘米，求三角形ABE 的面积是多少？12.君君老师计划买一批教具，已知三角尺1 元一个，圆规2 元一个，已知计划买圆规和三角尺共100 个，且买圆规的总花费比三角尺的总花费多20 元，请问君君老师为买这批教具需要花费多少钱？13.红星小学早晨去操场做早操，第一排1 人，第二排3 人，第三排5 人，每一排都比上一排多2 人，按此规律站了20 排，则第二十排有多少人？操场上总共多少人？14.某果园工人带一筐梨去慰问住院病人，已知梨的个数是苹果的3 倍，每次取出5个梨和2 个苹果分给一个病人，最后还剩11 个梨，苹果正好分完。

小学四年级奥数题：统筹规划1、烧水沏茶时，洗水壶要用1分钟，烧开水要用10分钟，洗茶壶要用2分钟，洗茶杯用2分钟，拿茶叶要用1分钟，如何安排才能尽早喝上茶。

2、有137吨货物要从甲地运往乙地，大卡车的载重量是5吨，小卡车的载重量是2吨，大卡车与小卡车每车次的耗油量分别是10公升和5公升，问如何选派车辆才能使运输耗油量最少？这时共需耗油多少升？3、用一只平底锅烙饼，锅上只能放两个饼，烙熟饼的一面需要2分钟，两面共需4分钟，现在需要烙熟三个饼，最少需要几分钟？4、甲、乙、丙、丁四人同时到一个小水龙头处用水，甲洗拖布需要3分钟，乙洗抹布需要2分钟，丙用桶接水需要1分钟，丁洗衣服需要10分钟，怎样安排四人的用水顺序，才能使他们所花的总时间最少，并求出这个总时间。

5、甲、乙、丙、丁四个人过桥，分别需要1分钟，2分钟，5分钟，10分钟。

因为天黑，必须借助于手电筒过桥，可是他们总共只有一个手电筒，并且桥的载重能力有限，最多只能承受两个人的重量，也就是说，每次最多过两个人。

现在希望可以用最短的时间过桥，怎样才能做到最短呢？你来帮他们安排一下吧。

最短时间是多少分钟呢？6、小明骑在牛背上赶牛过河，共有甲乙丙丁四头牛，甲牛过河需1分钟，乙牛需2分钟，丙牛需5分钟，丁牛需6分钟，每次只能骑一头牛，赶一头牛过河。

要过河时间最少？是多少？四年级奥数题：速算与巧算（一）1.【试题】计算9＋99＋999＋9999＋999992【试题】计算199999＋19999＋1999＋199＋193【试题】计算(2+4+6+…+996+998+1000)－－(1+3+5+…+995+997+999)4【试题】计算9999×2222＋3333×33345.【试题】56×3+56×27+56×96-56×57+566.【试题】计算98766×98768－98765×98769四年级奥数题：年龄问题1、父亲45岁，儿子23岁。

成功＝勤奋＋正确的方法＋少说空话第76题：将下图的竖式谜补充完整。

答案：此题答案不唯一，填出一种就算对。

（本题还有其它答案，不一一列举）第77题：如果一个数字不是 11 的倍数，但是移除一个任意位上的数字后，它就变成了 11 的倍数，（例如 111，无论移除其个位、十位或百位上的数字，都变成 11 的倍数），这样的四位数共有多少个？答案：共有0个 解析：假设这个四位数为abcd ————，则任意移除其中一位之后 移除千位，为bcd ————，能被11整除，则：cd b -+|11； 移除百位，为acd ————，能被11整除，则：cd a -+|11 移除十位，为abd ————，能被11整除，则：bd a -+|11 移除个位，为abc ————，能被11整除，则：bc a -+|11结合以上四个算式可得出：a|11，d|11而a 与d 均为一位数字，则0==d a因为首位数字为0，所以这样的四位数不存在，个数为0。

第78题：将 6 个不同的正整数从小到大排成一排为 a 、b 、c 、d 、e 、f ，任意两个相邻数中，后面数都是前面数的倍数，已知 a +b + c + d + e + f =79 ,求：f 的值是多少？ 答案：48 解析：b ，c ，d ，e ，f 都是a 的倍数，且79=+++++f e d c b a,当a ＞1时，结果超过79，所以1=a ，从而推出39278⨯==++++f e d c b 。

同理，fe d c b ++++是b 的倍数，所以78|b，考虑到1＜b ＜c ＜d ＜e ＜f ，所以取2=b，带入78=++++f e d c b，则19476⨯==+++f e d c。

同理，fe d c +++是c 的倍数，所以76|c ，考虑到2＜c ＜d ＜e ＜f ，所以取4=c ，代入76=+++f e d c ，则233272⨯==++f e d。

同理，fe d++是d 的倍数，所以72|d ，由于de 2≥、de f 42≥≥，所以 dd d d fe d 742=++≥++，从而推出df e d 772≥++=，则10≤d。

小学四年级奥数竞赛试卷2018.6班级姓名得分一、填空：（36分）1、妈妈买来一些青枣，小明第一次吃了一半少2 个，第二次吃了剩下的一半多2 个，还剩下3 个，妈妈买了（）个青枣。

2、3个千万、5个十万、60个十和2个一组成的数是（），这个数读作（）。

3、已知A×B=380，若A乘3，则积是（），若B除以5，则积是（）4、用1—6 这六个数字分别组成两个三位数，使这两个三位数的乘积最小，这两个数分别是（）和（）。

5、过平行四边形的一个顶点画高，最多能画（）条。

6、如果一个三角形中最小的角大于45°，那么这个三角形是（）三角形。

7、某年的四月20 日是星期四，当年的九月1 日是星期（）。

8、一个等腰三角形，顶角是88度，一个底角是（）度。

9、找规律填数（1） 2、3、5、（）、（）17、23（2 ）1、8、9、17、26、（）、69二、计算（28分）（1）选择合适的方法计算299＋99×99 =132―27＋68―73 = 3333×6666 =78 ×4＋5×78＋78 = 25×401= 1＋2＋3＋4…29＋30=（2）把1—10 这10 个数填在圆圈里，使两个大圆圈上六个数的和都等于29三、解决问题（36分）1、一个平行四边的周长是120厘米，相邻的两条边中，一条边的长度是另一条边的长度的3倍，这个平行四边形相邻的两条边的长度分别是多少厘米？2、一个鱼塘长45米，如果长增加10米，面积就增加180平方米，如果宽也增加10米，面积一共增加多少平方米？3、妈妈买来一些青枣，小明第一次吃了一半少2 个，第二次吃了剩下的一半多2 个，还剩下3 个，妈妈买了多少个青枣。

4、养鸡场的母鸡只数是公鸡只数的6倍，后来公鸡和母鸡各增加60只，结果母鸡的只数就是公鸡只数的4倍。

养鸡场原来一共养了多少只鸡？5、今年，妈妈的年龄是卡尔的8倍，再过3年，妈妈的年龄就是卡尔年龄的5倍，妈妈今年多少岁？6、兄妹二人同时离家去上学。

四年级奥数暑期测试题一．填空。

(每空2分，共26分) 1）2，5，8，（ ），14，17，（ ） 2）4，6，8，（ ）12，14，（ ） 3）4，5，7，10，（ ），194）3，2，5，2，7，2，（ ），（ ）11，2 5）1，2，3，5，8，（ ），21 6）（3，10），（1，12），（9，4），（5，□）7）8）用平底锅烙饼，锅上同时只能放两张饼，烙熟一面要3分钟，烙熟3 个饼，最少( )分钟。

9）数出图中有几条线段。

( )条 10）数出图中有多少个锐角。

( )个二、计算。

(共39分)1、利用规律计算。

(每题3分，共9分)1) 75－57=(□－□)×9=□ 2) 95-59=(□－□)×9=□3) 53－35=(□－□)×9=□2、用格子乘法计算。

(3分)54×37=3、根据下面两个算式，求○和□各代表多少？(4分)○＋○＋○=15 ○＋□=8○= □=4、在下面算式中填上合适的数。

(8分)7 6 □ 6 式 谜 巧= ＋ □ 4 7 填 式 谜 填= □ 2 1 □ ＋ 巧 填 式 谜 式= 1 9 9 5 谜= 5、计算下面各题(运用求和公式计算)每题3分，共6分。

1) 6＋7＋8＋9＋10＋11 2)1＋2＋3＋……＋49＋506、① 把1、2、3、4、5、6这6个数字， 分别填在图中，使每条边三个数的和 都等于9。

(4分)② 把1-9九个数填在图中的九个方格 使每一横行，每一纵行和两条对角线 上三个数之和相等。

(5分)三、应用题。

(每题5分，共35分)1、一盒果冻的重量等于两盒水果糖的重量，6盒奶糖的重量等于一盒果冻的重量，一盒水果糖的重量等于几盒奶糖的重量？A B C DABCD E3 7………………………………密……………………………………………………………………封………………………………………………………线……………………………………校 区：__________________ 姓 名：__________________ 分 数：______________2、小红从家到学校有2条路可走，从学校到新华书店有4条路可走，那么小红从家经过学校到新华书店共有几种不同的走法？3、光明路小学在一条大路一边从头到尾栽了树31棵，每隔5米栽一棵，这条路长多少米。