下载文档原格式
【实验目的】学习利用光杠杆测量金属棒的线胀系数。
【实验仪器】金属线胀系数测量仪光杠杆金属测量棒【实验原理】金属固体的长度一般随温度的升高而增长，其长度L和温度t之间的关系为L=L0（1+t+t+…）(1)式中L0为温度t=0℃时的长度，、、…是和被测物质有关的常数，都是很小的数值。
而以下各系数和相比甚小，所以在常温下可以忽略，则（1）式可写成L=L0（1+t）（2）此处就是通常所称的线胀系数，单位℃-1。
设物体在温度t1（单位℃）时的长度为L，温度升到t2（单位℃）时，其长度增加，根据（2）式，可得L=L0（1+t1）L+=L0（1+t2）由此二式相比消去L0，整理后得出= —————————L（t2- t1）-t1由于和L相比甚小，L（t2- t1）＞＞t1，所以上式可近似写成= —————————（3）L（t2- t1）由上式可知，测量线胀系数的主要问题是怎样测准温度变化引起长度的微小变化量。
本实验是利用光杠杆测量微小长度的变化。
如图所示，实验时，将待测金属棒直立在线胀系数测定仪的金属加热筒中，将光杠杆的后足尖置于金属棒上端，二前足置于固定的台上。
设在温度为t1时通过望远镜和光杠杆的平面镜，看见直尺上的刻度a1刚好在望远镜中叉丝横线（或交点）处。
当温度升至t2时，直尺上刻度a2移至叉丝横线上，根据光杠杆原理，有（a2- a1）d1= ————————————（4）2 d2式中d2为光杠杆镜面至直尺的距离，d1为光杠杆后足尖到二前足尖连线的垂直距离。
将（4）式代入（3），则（a2- a1）d1= —————————（5）2 d2 L（t2- t1）【实验内容和步骤】1、用米尺测量金属棒长度L之后，将其插入线胀系数测定仪的加热筒中，棒的下端要和基座紧密相接，上端露在筒外。
2、安装温度计。
插温度计时要小心，切勿碰撞，以防损坏。
3、将光杠杆放在仪器平台上，其后足尖放在金属棒的顶湍上。
二前足放在平台的凹槽里。
金属线胀系数的测定实验报告一、实验目的1、学会使用千分表测量微小长度的变化。
2、掌握用光杠杆法测量金属棒的线胀系数。
3、观察金属受热膨胀的现象，加深对热膨胀规律的理解。
二、实验原理固体受热时会发生长度的伸长，这种现象称为线膨胀。
设固体在温度为$t_1$时的长度为$L_1$，温度升高到$t_2$时的长度为$L_2$，则固体在温度区间$（t_2 t_1)＄内的平均线胀系数$＼alpha$定义为：＼＼alpha ＝＼frac{L_2 L_1}｛L_1(t_2 t_1)｝＼由于长度的变化量$＼Delta L ＝ L_2 L_1$通常很小，难以直接测量，本实验采用光杠杆法将微小的长度变化量放大进行测量。
光杠杆是一个带有可旋转的平面镜的支架，其结构如图 1 所示。
平面镜固定在一个三脚支架的一端，三脚支架的另两个脚与一个等腰直角三角形的底边重合，而三角形的直角顶点处装有一个能沿金属棒长度方向自由移动的尖头，尖头与金属棒接触。
当金属棒受热伸长时，带动光杠杆的尖头移动，使光杠杆绕其前两脚尖的连线转动一微小角度$＼theta$，从而使反射光线转过$2\theta$的角度。
设开始时望远镜中叉丝横线对准的刻度为$n_1$，当光杠杆转动$＼theta$角后，叉丝横线对准的刻度为$n_2$，则望远镜中标尺读数的变化量为$＼Delta n ＝ n_2 n_1$。
根据几何关系可得：＼＼tan 2\theta ＼approx 2\theta ＝＼frac{＼Delta n}｛D}＼其中，＄D$为望远镜到光杠杆平面镜的距离。
又因为$＼theta$很小，所以有：＼＼tan ＼theta ＼approx ＼theta ＝＼frac{＼Delta L}｛b}＼其中，＄b$为光杠杆后脚尖到两前脚尖连线的垂直距离。
联立以上两式可得：＼＼Delta L ＝＼frac{b}｛2D}＼Delta n＼将上式代入线胀系数的定义式中，可得：＼＼alpha ＝＼frac{1}｛L_1(t_2 t_1)｝＼cdot ＼frac{b}｛2D}＼Delta n＼三、实验仪器1、线胀系数测定仪：包括加热装置、金属棒、光杠杆、望远镜和标尺。
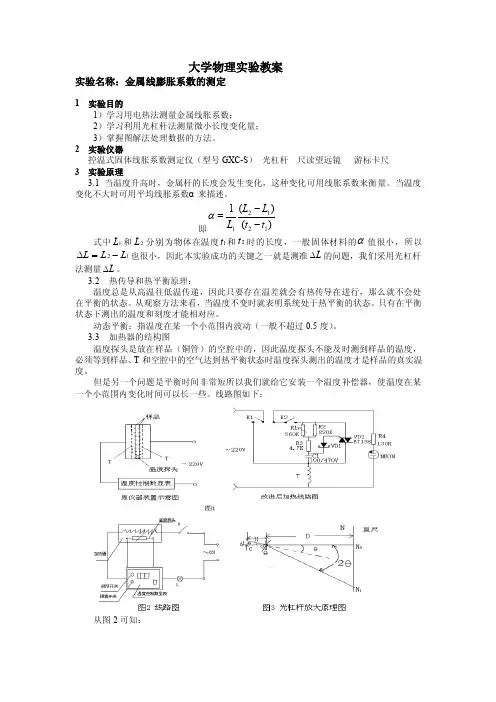
大学物理实验教案实验名称：金属线膨胀系数的测定1 实验目的1）学习用电热法测量金属线胀系数；2）学习利用光杠杆法测量微小长度变化量；3）掌握图解法处理数据的方法。
2 实验仪器控温式固体线胀系数测定仪（型号GXC-S ） 光杠杆 尺读望远镜 游标卡尺 3 实验原理3.1 当温度升高时，金属杆的长度会发生变化，这种变化可用线胀系数来衡量。
当温度变化不大时可用平均线胀系数α来描述。
即)()(112121t t L L L --=α式中1L 和2L 分别为物体在温度1t 和2t 时的长度，一般固体材料的α值很小，所以12L L L -=∆也很小，因此本实验成功的关键之一就是测准L ∆的问题，我们采用光杠杆法测量L ∆。
3.2 热传导和热平衡原理：温度总是从高温往低温传递，因此只要存在温差就会有热传导在进行，那么就不会处在平衡的状态。
从观察方法来看，当温度不变时就表明系统处于热平衡的状态。
只有在平衡状态下测出的温度和刻度才能相对应。
动态平衡：指温度在某一个小范围内波动（一般不超过0.5度）。
3.3 加热器的结构图温度探头是放在样品（铜管）的空腔中的，因此温度探头不能及时测到样品的温度，必须等到样品、T 和空腔中的空气达到热平衡状态时温度探头测出的温度才是样品的真实温度。
但是另一个问题是平衡时间非常短所以我们就给它安装一个温度补偿器，使温度在某一个小范围内变化时间可以长一些。
线路图如下：从图2可知：()D NH D H L 2201∆=N -N =∆所以可得：()1221t t D L -H ∆N =α=t LD ∆H∆N 2 4 教学内容1）用卷尺测量金属杆的长度L2）光杠杆放在仪器平台上，其后足尖放在金属杆顶端的金属套上，光杠杆的镜面在铅直方向。
在光杠杆前1.5~2.0m 处放置望远镜及直尺（尺在铅直方向）。
调节镜尺组让望远镜与直尺相对镜面成对称关系，调节望远镜的目镜使叉丝清晰，如图2，再调节望远镜使直尺的象进入望远镜中。
金属线胀系数的测量一、实验目的学习利用光杠杆法测量金属杆的线胀系数二、实验仪器控温式固体线胀系数测定仪（型号GXC-S ） 光杠杆 尺读望远镜 卷尺 游标卡尺三、实验原理1）当温度升高时，一般固体中原子的热运动随固体温度的升高而加剧，把这种由于温度升高而引起固体中原子间平均距离增大，进而引起固体体积增大的现象称为固体的热膨胀。
固体的热膨胀又可分为体膨胀和线膨胀，本实验主要研究线膨胀。
设L t 表示温度t 时物体的长度，dL 表示温度变化dt 时物体长度的变化，定义 dtdL L t t 1=α…………………………………………（1） t α为物体在温度时的线胀系数，其物理意义是固体的温度每升高1ºC 时的相对升长量。
它不仅与物体的材料有关，还与温度有关。
但是除了在物体熔点附近有很大的突变外，在其他温度范围内变化不大。
因此，在远离固体熔点，而且温度变化范围不大时，可以引进一个平均线胀系数的概念，即)()(112121t t L L L --=α ……………………………………….（2） 式中1L 和2L 分别为物体在温度1t 和2t 时的长度，α是一个很小的量。
当温度变化较大时，精密的测量表明α和t 有关，经验公式为=αa+b t +c t 2+...... .. (3)式中a 、b 、c 、……是常量。
一般固体材料的α值很小，所以12L L L -=∆也很小，因此本实验成功的关键之一就是测准L ∆的问题，我们采用光杠杆法测量L ∆。
图1在距光杠杆前约1—2米处放置望远镜R 及标尺N 。
调节好望远镜后，可通过望远镜看到光杠杆的镜面内标尺的象。
设望远镜中水平叉丝（或叉丝交点）对准标尺上的刻度为N 0,如图1,当金属杆受热膨胀而伸长△L 时，光杠杆后足随金属杆C 向上移动。
这时光杠杆的两个前足固定，于是平面镜绕前两足的水平轴线而转动θ角（实线为光杠杆原来的位置，虚线为转动后的位置），如图1所示。
金属线胀系数的测定实验报告一、实验目的1、学习用光杠杆法测量金属的线胀系数。
2、掌握千分表的使用方法。
3、学会对实验数据进行处理和误差分析。
二、实验原理固体受热时会发生膨胀，其长度的增加量与温度的升高量成正比。
设固体在温度为 t1 时的长度为 L1，温度升高到 t2 时的长度为 L2，线胀系数为α，则有：ΔL ＝ L2 L1 ＝αL1Δtα ＝（L2 L1) ／（L1Δt)式中，Δt ＝ t2 t1 为温度的变化量。
本实验采用光杠杆法测量微小长度的变化。
光杠杆是一个带有三个尖足的平面镜，前两尖足放在一个固定的平台上，后尖足置于被测微小长度变化的物体上。
当被测物体长度发生微小变化时，光杠杆将绕前两尖足的连线转动一个微小角度θ，反射光线将在远处的标尺上移动一段距离 n。
根据几何关系，可以得到：tanθ ≈ θ ＝ n ／ D又因为θ很小，所以有：ΔL ／ b ＝θ联立可得：ΔL ＝ n b ／ D将其代入线胀系数的表达式，可得：α ＝ n b ／（L1 Δt D)三、实验仪器1、线胀系数测定仪：由加热装置、待测金属棒、温度计等组成。
2、光杠杆及望远镜尺组：包括光杠杆、望远镜、标尺等。
3、千分表。
4、游标卡尺。
5、米尺。
四、实验步骤1、用米尺测量金属棒的长度 L1，在不同位置测量多次，取平均值。
2、用游标卡尺测量金属棒的直径 d，在不同位置测量多次，取平均值。
3、将光杠杆的前脚放在平台的凹槽中，后脚放在金属棒的顶端，使光杠杆平面镜与平台垂直。
4、调节望远镜，使其与光杠杆平面镜等高，并能看到平面镜反射的标尺像。
5、记录望远镜中标尺的初始读数 n1 。
6、打开加热装置，缓慢升温，每隔一定温度（如 10℃）记录一次温度t 和望远镜中标尺的读数n ，直到温度升高到一定值（如80℃）。
7、关闭加热装置，待金属棒冷却后，再次测量金属棒的长度L2 。
五、实验数据记录与处理1、金属棒长度的测量｜测量次数|1|2|3|4|5|平均值|｜｜｜｜｜｜｜｜｜L1（cm）｜＿____|＿____|＿____|＿____|＿____|＿____|2、金属棒直径的测量｜测量次数|1|2|3|4|5|平均值|｜｜｜｜｜｜｜｜｜d（cm）｜＿____|＿____|＿____|＿____|＿____|＿____|3、温度和标尺读数的记录｜温度 t（℃）｜10|20|30|40|50|60|70|80|｜｜｜｜｜｜｜｜｜｜｜标尺读数 n（cm）｜＿____|＿____|＿____|＿____|＿____|＿____|＿____|＿____|4、数据处理（1）计算金属棒的平均直径 d ＝（d1 ＋ d2 ＋ d3 ＋ d4 ＋ d5）／5 。
实验四 金属线胀系数的测定【实验目的】学习用光杠杆法测量金属棒的线胀系数。
【实验仪器】GXZ 型金属系数测定仪，光杠杆，尺度望远镜，钢卷尺，游标卡尺，蒸汽发生器，待测金属棒。
【实验原理】固体的长度通常随着温度的升高而增加，其长度l 和温度t 之间的关系为)1(20 +++=t t l l βα (4-1)式中0l 为温度C t 00=的长度，α、β是和被测物体有关的常数，都为很小的数值，而β以下各系数与α相比更小，常温下可以忽略，则(13-1)可写成)1(0t l l α+= (4-2)式子中α即为通常所称的线胀系数，单位是10-C 。
设物体在温度为C t 01时的长度为l ，温度升高到C t 02时，其长度增加δ，根据式(13-2)，可得)1(10t l l α+=)1(20t l l αδ+=+由此二式消去0l ，整理后得出)34()(112---=t t t l δδα因l 与δ相比很小，112)(t t t l δ>>-，所以式(13-3)可近似写成)44()(12--=t t l δα线胀系数α测量中，最重要的工作是如何准确测量出当温度变化时引起的金属长度产生的微小变化δ。
实际测量中常常使用的方法有：（1）光杠杆法测量微小长度变化法实验时将待测金属棒直立在金属线胀系数测定仪的金属筒中(图13-1)，将光杠杆的后足尖置于金属棒的上端，二前足置于固定台上。
设在温度C t 01时，通过望远镜和光杠杆平面镜，看见直尺上的刻度1a 刚好在望远镜中叉丝横线(或交点)处，当温度升高至C t 02时，直尺上刻度2a 移至叉丝横线上，根据光杠杆原理(光杠杆的使用方法参见本书实验九中的仪器原理介绍)可得)54(2)(12--=Dda a δ式中d 为光杠杆后足尖到二前足尖连线的垂直距离，D 为光杠杆镜面到直尺的距离。
将式(13-5)代入式(13-4)中，则)64()(2)(1212---=t t Dl da a α(2)利用螺旋测微器原理测量金属微小长度 如图13-2所示。
实验六 金属线膨胀系数测定实验物质内部的分子都处于不停地运动且强弱不同，造成绝大多数材料都表现出热胀冷缩的特性。
人们在工程结构设计时，例如在房屋、铁路、桥梁、机械和仪器制造、材料的焊接等行业中一定要考虑到这一因素，如果忽略这一特性，将造成工程结构稳定性差，严重的可造成损毁，使仪表失灵以及在材料焊接中引起缺陷等。
线膨胀系数的测定在工程技术中是非常重要的，本实验的目的主要是利用GXZ －2型金属线膨胀系数测定仪测定不同金属的线膨胀系数。
实验目的：1．掌握GXZ －2型金属线膨胀系数测定仪的原理和使用方法。
2．测量铁和铜两种金属材料的线膨胀系数。
3．学会使用最小二乘法。
实验仪器：GXZ －2型金属线膨胀系数测定仪，望远镜，标尺照明器， PID 恒温控制器，温度传感器，直尺注：（测温的范围：室温～100°C ，加热电压：95～220V 可调。
） 实验原理本实验采用GXZ －2型金属线膨胀系数测定仪利用电热法及光杠杆原理测定金属线膨胀系数，其优点是结构紧凑，性能稳定克服了汽热法温度场不均匀、误差大等缺点。
用此仪器测量管材的线膨胀系数，其误差不超过3％。
1．材料的线膨胀系数各种材料热胀冷缩的强弱是不同的，为了定量区分它们，人们找到了表征这种热胀冷缩特性的物理量，线膨胀系数和体膨胀系数。
本实验只测量线膨胀系数。
线膨胀是材料在受热膨胀时，在一维方向上的伸长。
在一定的范围内，固体受热后，其长度都会增加，设物体原长为L ，由初温t 1°C 加热到末温t 2°C ，物体伸长了ΔL ，则有ΔL ＝αL （t 2－t 1） （1） α＝)(12t t L L -∆ （2） 上式表明，物体受热后生长量与温度的增长量成正比，和原长也成正比。
比例系数α称为固体的线膨胀系数。
2．线膨胀系数的测量线膨胀系数是选用材料时的一项重要指标。
实验表明，不同材料的线膨胀系数是不同的，塑料的线膨胀系数最大，其次是金属、殷钢，熔凝石英的线膨胀系数很小。
