线膨胀系数测量的讲义

材料线膨胀系数测量材料的线膨胀系数是一个重要的物性参数，用来描述材料在温度变化时的膨胀行为。

了解材料的线膨胀系数可以帮助工程师在设计中考虑到温度变化对结构的影响。

材料的线膨胀系数定义为单位温度变化引起的长度变化与原始长度的比值。

线膨胀系数通常用符号α来表示，单位为1/°C或1/°F。

线膨胀系数与材料的内部结构相关，在材料的晶格结构和原子排列方式不同的情况下，线膨胀系数也会不同。

要测量材料的线膨胀系数，可以使用不同的方法和设备。

下面介绍几种常用的线膨胀系数测量方法：1.膨胀试验器法：这是一种常用的测量线膨胀系数的方法。

这种方法通过将材料制成试样，在恒定温度条件下测量试样长度的变化，从而计算出线膨胀系数。

2.热膨胀计法：这种方法利用了热膨胀计的原理，通过测量试样的长度变化或形变来计算出线膨胀系数。

热膨胀计可以使用不同的原理，如电阻、光学或机械等。

3.拉伸测量法：这种方法使用拉伸试样，并在温度变化时测量试样的长度变化。

通过测量试样的变形和应力，可以计算出线膨胀系数。

4.表面形貌法：这种方法通过观察材料表面形貌的变化来推测材料的线膨胀系数。

这种方法不需要具体的测量设备，但是相对准确度较低。

无论使用哪种方法1.选择合适的试样形状和尺寸。

试样的尺寸和形状应保证能够准确测量长度变化，并具有代表性。

2.控制好温度变化的方式和范围。

要保证温度变化均匀并且在一定范围内，以充分测量材料的膨胀行为。

同时，要避免过大的温度变化引起材料的热失控或损坏。

3.测量仪器的准确性和稳定性。

仪器的精度和稳定性对于测量结果的准确性至关重要。

应保证仪器的校准和维护，并进行合理的测量数据处理和分析。

总之，材料的线膨胀系数测量是一个复杂而重要的过程。

准确测量材料的线膨胀系数可以为工程设计提供重要的参考数据，帮助工程师考虑到温度变化对结构的影响，避免材料的膨胀引起的不必要问题。

不同的测量方法和设备可以根据实际需要选择，但要确保测量过程的准确性和可靠性。

固体线膨胀系数的测定大多数固体材料内部分子热运动的剧烈程度与物体的温度有关，故而都遵从热胀冷缩的规律。

固体的体积随温度升高而增大的现象称为热膨胀。

固体热膨胀时，它在各个线度上（如长、宽、高、直径等）都要膨胀，我们把物体线度的增长称为线膨胀；将体积的增大称为体膨胀。

若固体在各方向上热膨胀规律相同时，可以用固体在一个方向上的线膨胀规律来表征它的体膨胀，所以线膨胀系数是很多工程技术中选材料的重要技术指标。

在道路、桥梁、建筑等工程设计、精密仪器仪表设计、材料的焊接、加工等领域都必须考虑该参数的影响。

线膨胀系数的测量方法有很多种，包括：光杠杆法、千分表法、读书显微镜法、光学干涉法、组合法等，本实验采用千分表法测金属线膨胀系数，用FD-LEB 线膨胀系数测定仪进行测量。

一、实验目的1.学习测量固体线膨胀系数的方法；2.掌握用千分表测量微小长度变化的方法；3.练习作图法处理实验数据的方法；4.分析影响测量精度的因素。

二、实验原理固体受热后的长度L 和温度t 之间的关系为：)1(20 +++=t t L L βα (1)式中L 0为温度t=0℃时的长度， βα、是和被测物质有关的数值很小的常数，而β以后的各系数和α相比甚小，所以常温下可以忽略，则上式可写成：)1(0t L L α+= (2)式中α就是固体的线膨胀系数，其物理意义为温度每升高一度时物体的伸长量与它在零度时的长度比，单位是摄氏度分之一。

如果在温度t 1和t 2时，金属杆的长度分别为L 1和L 2，则有：)1(101t L L α+= (3) )1(202t L L α+= (4) 联立(3)、(4)式可得：)(1122112t L L t L L L --=α。

由于L 2与L 1相差微小，1/12≈L L 所以上式可近似写为tL L ∆∆=1α。

式中12L L L -=∆是固体当温度变化12t t t -=∆时相对应的伸长量。

该式通常可简单表示为：t L L ∆∆=α。

材料线膨胀系数测定杆膨胀测量法是最常用的一种测量方法。

其原理是通过测量金属杆在温度变化下的长度变化来求得杆材料的线膨胀系数。

测量时首先将杆材料固定在装置上，将装置放在恒温槽中，然后通过温度变化使杆材料发生膨胀或收缩，通过对杆材料的长度变化进行测量，再将测量到的长度变化数据与温度变化数据进行对比，就可以求得杆材料的线膨胀系数。

光栅测量法是近年来发展起来的一种新型测量方法。

其原理是通过光栅的干涉原理实现对材料线膨胀系数的测量。

测量时首先将材料制成薄片，将之固定在测量台上。

测量台上放置一组光栅，将光栅分成两个部分。

当材料发生膨胀或收缩时，光栅之间的相位差会发生变化，通过测量光栅之间的相位差的变化，就可以求得材料的线膨胀系数。

电容测量法也是一种常用的测量方法。

其原理是通过在材料上开设两个电容，当材料发生膨胀或收缩时，电容之间的距离会发生变化，从而使得电容的电容值发生变化。

通过测量电容值的变化，就可以求得材料的线膨胀系数。

在进行材料线膨胀系数测定时，需要注意以下几点：1.温度控制：在测量过程中，必须严格控制温度的稳定性，以确保测量结果的准确性。

2.实验设备：需要选择合适的实验设备，包括温度控制装置、测量仪器等。

3.样品制备：样品制备过程中要保证材料的均匀性和准确性，避免造成误差。

4.测量精度：在测量过程中，需要注意仪器的精确度与测量精度，以确保测量结果的准确性。

总之，材料线膨胀系数的测定是材料研究和工程应用中的一个重要参数。

通过选择合适的测量方法和仪器设备，严格控制实验条件，可以获得准确可靠的线膨胀系数数据，为材料设计和应用提供参考依据。

实验十五材料线膨胀系数的测定——示差法概述物体的体积或长度随温度的升高而增大的现象称为热膨胀。

热膨胀系数是材料的主要物理性质之一，它是衡量材料的热稳定性好坏的一个重要指标。

在实际应用中，当两种不同的材料彼此焊接或熔接时，选择材料的热膨胀系数显得尤为重要，如玻璃仪器、陶瓷制品的焊接加工，都要求二种材料具备相近的膨胀系数。

在电真空工业和仪器制造工业中广泛地将非金属材料(玻璃、陶瓷)与各种金属焊接，也要求两者有相适应的热膨胀系数；如果选择材料的膨胀系数相差比较大，焊接时由于膨胀的速度不同，在焊接处产生应力，降低了材料的机械强度和气密性，严重时会导致焊接处脱落、炸裂、漏气或漏油。

如果层状物由两种材料迭置连接而成，则温度变化时，由于两种材料膨胀值不同，若仍连接在一起，体系中要采用一中间膨胀值，从而使一种材料中产生压应力而另一种材料中产生大小相等的张应力，恰当地利用这个特性，可以增加制品的强度。

因此，测定材料的热膨胀系数具有重要的意义。

目前，测定材料线膨胀系数的方法很多，有示差法(或称“石英膨胀计法”)、双线法、光干涉法、重量温度计法等。

在所有这些方法中，以示差法具有广泛的实用意义。

国内外示差法所采用的测试仪器很多，有分立式膨胀仪(如weiss立式膨胀仪)和卧式膨胀仪(如HTV型、UBD型、RPZ―1型晶体管式自动热膨胀仪)两种。

有工厂的定型产品，也有自制的石英膨胀计。

些外，双线法在生产中也是—种快速测量法。

本实验采用示差法。

一、实验目的1．了解测定材料的膨胀曲线对生产的指导意义；2．掌握示差法测定热膨胀系数的原理和方法，以及测试要点；3．利用材料的热膨胀曲线，确定玻璃材料的特征温度。

二、实验原理一般的普通材料，通常所说膨胀系数是指线膨胀系数，其意义是温度升高1℃时单位长度上所增加的长度，单位为厘米╱厘米·度。

假设物体原来的长度为L，温度升高后长度的增加量为∆L，它们之间存在如下关系：∆L╱L＝α1∆t （1）式中，α1称为线膨胀系数，也就是温度每升高1℃时，物体的相对伸长。

金属线膨胀系数的测量实验原理引言：金属材料在受热或受冷时会发生热膨胀或热收缩现象，这是由于金属的晶格结构发生变化引起的。

金属线膨胀系数是描述金属材料在温度变化时膨胀程度的物理量，它是研究热膨胀现象的重要参数之一。

本文将介绍金属线膨胀系数的测量实验原理。

一、实验目的本实验旨在通过测量金属材料在不同温度下的长度变化，计算出其线膨胀系数。

二、实验器材1. 金属材料样品：选取一定长度的金属线作为实验样品，通常选择线性膨胀系数较大的金属材料，如铁、铜等；2. 温度计：用于测量温度变化；3. 定尺尺子：用于测量金属线的初始长度和变化后的长度；4. 实验台：提供支撑和固定实验样品的平台。

三、实验步骤1. 准备工作：将金属线样品固定在实验台上，保证其自由伸展；2. 测量初始长度：使用定尺尺子测量金属线样品的初始长度，并记录下来；3. 升温实验：将金属线样品置于恒温环境中，使用温度计测量环境温度，并记录下来；随着温度的升高，观察金属线的长度变化，并在每个温度点上测量并记录其长度；4. 降温实验：将金属线样品置于恒温环境中，使用温度计测量环境温度，并记录下来；随着温度的降低，观察金属线的长度变化，并在每个温度点上测量并记录其长度；5. 数据处理：根据测得的金属线长度和温度数据，计算金属线的线膨胀系数。

四、实验原理解析金属线膨胀系数是指金属材料在单位温度变化下的长度变化率。

一般来说，金属材料的线膨胀系数与其晶格结构、原子间距离等因素有关。

在实验中，我们可以通过测量金属线样品在不同温度下的长度变化来计算其膨胀系数。

根据热膨胀原理，金属材料的线膨胀量与其初始长度、温度变化量以及线膨胀系数之间存在如下关系：ΔL = α * L * ΔT其中，ΔL为线膨胀量，α为线膨胀系数，L为初始长度，ΔT为温度变化量。

通过实验测量金属线样品在不同温度下的长度变化，可以得到线膨胀量ΔL和温度变化量ΔT的数据。

将这些数据代入上述公式，可以解得金属线的线膨胀系数α。

固体线胀系数的测定绝大多数物体都具有 “热胀冷缩” 的特性， 这是由于构成物体的微观粒子热运动随温度的升、 降而加剧或减弱造成的。

固体材料的线胀系数是反映固体材料受热膨胀时， 在一维方向上伸长性质的重要参数。

线胀 系数是选用材料的一项重要指标， 是材料工程、 热力工程和自动控制技术中的一个重要技术参数， 在工程设计（如桥梁和过江电缆工程） 、精密仪表设计，材料的焊接和加工中都必须加以考虑。

、实验目的1． 学会一种测定金属线胀系数的方法。

2． 掌握光杠杆法测量长度微小变化量的原理和方法。

3． 学会用最小二乘法处理数据。

、实验原理设金属棒在温度 t o 时的长度为 L o ，当其温度上升到 t 时，它的长度 L t 可由下式表示：L t =L o 1 t t o（1）式中， 即为该物体的线胀系数。

可将式（ 1）改写成：L t L o L L o t t oL o t t o由此可见，线胀系数 的物理意义是温度每升高 1 o C 时物体的伸长量 L 与原长之比。

般 随温度有微小的变化，但在温度变化不太大时，可把它当作常量。

由式（ 2）可以看出，测量线胀系数的关键是准确测量长度的微小变化量估算一下 L 的大小。

若 L o 500mm ，温度变化 t t o 100 C ，金属线胀系数 的数量级 为10 5 C 1 ，则可估算出 L 0.50mm 。

对于这么微小的长度变化量，用普通量具如钢尺 和游标卡尺无法进行精确测量，一般采用千分表法（分度值为0.001mm ），光杠杆法，光学干涉本实验采用光杠杆法， 整套实验装置由固体线胀系数测定仪， 光杠杆和尺读望远镜等几部分 组成，如图 1 所示。

2）L 。

我们先粗略图 1 测定固体线胀系数的实验装置光杠杆测微小长度改变量的原理：参照图 2，假定开始时光杠杆平面镜 M 的法线 on o 在水平位置，则标尺 S 上的标度线 n o 发 出的光通过平面镜 M 反射进入望远镜，在望远镜中形成n o 的象而被观察到。

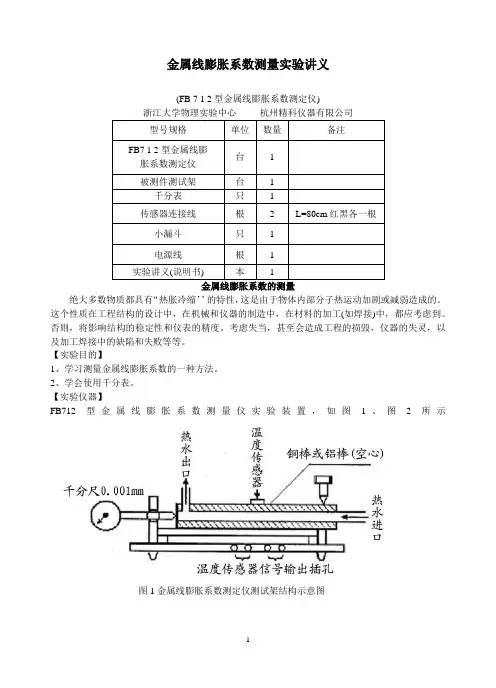
金属线膨胀系数测量实验讲义(FB 7 1 2型金属线膨胀系数测定仪)浙江大学物理实验中心杭州精科仪器有限公司金属线膨胀系数的测量绝大多数物质都具有“热胀冷缩’’的特性，这是由于物体内部分子热运动加剧或减弱造成的。

这个性质在工程结构的设计中，在机械和仪器的制造中，在材料的加工(如焊接)中，都应考虑到。

否则，将影响结构的稳定性和仪表的精度。

考虑失当，甚至会造成工程的损毁，仪器的失灵，以及加工焊接中的缺陷和失败等等。

【实验目的】1、学习测量金属线膨胀系数的一种方法。

2、学会使用千分表。

【实验仪器】FB712型金属线膨胀系数测量仪实验装置，如图1、图2所示图1金属线膨胀系数测定仪测试架结构示意图图2 FB7 12型金属线膨胀系数测定仪面板【实验原理】材料的线膨胀是材料受热膨胀时，在一维方向的伸长。

线胀系数是选用材料的一项重要指标。

特别是研制新材料，少不了要对材料线胀系数做测定。

固体受热后其长度的增加称为线膨胀。

经验表明，在一定的温度范围内，原长为L 的物体，受热后其伸长量△L 与其温度的增加量△t 近似成正比，与原长L 亦成正比，即：△L=α· L ·△t (1)式中的比例系数α称为固体的线膨胀系数(简称线胀系数)。

大量实验表明，不同材料的线胀系数不同，塑料的线胀系数最大，金属次之，殷钢、熔融石英的线胀系数很小。

殷钢和石英的这一特性在精密测量仪器中有较多的应用。

几种材料的线胀系数生变化的温度附近，同时会出现线胀量的突变。

另外还发现线膨胀系数与材料纯度有关，某些材料掺杂后，线膨胀系数变化很大。

因此测定线胀系数也是了解材料特性的一种手段。

但是，在温度变化不大的范围内，线胀系数仍可认为是一常量。

为测量线胀系数，我们将材料做成条状或杆状。

由(1)式可知，测量初始杆长L 、受热后温度从t1升高到t2时的伸长量△t 和受热前后的温度升高量△t (△t =t 2－t1)，则该材料在(t1，t2)温度区域的线胀系数为： tL L ∆*∆=α （2）其物理意义是固体材料在（t1，t2)温度区域内，温度每升高1℃时材料的相对伸长量，其单位为（℃）－1测量线胀系数的主要问题是如何测伸长量△L 。

材料线膨胀系数测量材料的线膨胀系数是指材料在温度变化时单位温度变化引起的单位长度变化。

它是一个反映材料热膨胀性能的重要参数，对于材料的设计和应用非常关键。

本文将介绍材料线膨胀系数的测量方法及其应用。

测量方法：材料线膨胀系数的测量通常会采用热膨胀仪或光栅测量系统。

其中，热膨胀仪主要通过测量材料在不同温度下的长度来计算线膨胀系数。

而光栅测量系统则是利用光栅的原理，通过测量材料表面的位移来计算材料的线膨胀系数。

热膨胀仪的测量步骤如下：1.准备样品：选取需要测量线膨胀系数的材料样品，并进行表面处理，确保材料表面光滑和平行度要求。

2.搭建测量系统：将样品固定在测量装置上，并将热电偶连接到材料的制样区域以测量温度变化。

3.温度控制：设置初始温度，并根据实验需要进行温度逐渐升高或下降。

4.记录长度变化：在温度变化过程中，通过位移传感器或测微仪测量样品的长度变化。

5.计算线膨胀系数：根据样品的长度变化和温度变化，利用公式计算出材料的线膨胀系数。

光栅测量系统的测量步骤如下：1.准备样品：与热膨胀仪的测量步骤相同。

2.接入光栅系统：将光栅传感器固定在样品的一侧，并保持光栅的相对位置不变。

3.记录位移变化：在温度变化过程中，通过光栅传感器测量样品表面的位移变化。

4.计算线膨胀系数：根据位移变化和温度变化，利用光栅原理计算出材料的线膨胀系数。

应用：1.材料选型：在设计产品时，需要考虑材料的热膨胀性能，以避免因温度变化导致的变形和破裂。

2.结构设计：材料线膨胀系数的测量结果可以用于预测结构在温度变化时的变形，从而对结构进行合理设计。

3.工程测量：在工程测量中，能够准确测量材料的线膨胀系数有助于工程测量中的温度校正。

综上所述，材料线膨胀系数的测量是一个重要的过程，通过热膨胀仪或光栅测量系统可以准确测量材料在温度变化下的长度变化，并计算出材料的线膨胀系数。

这一参数对于材料设计和应用都具有重要的意义。

金属线膨胀系数的测定实验原理金属线膨胀系数的测定实验原理：小伙伴们，今天我们来聊聊一个非常有趣的话题——金属线膨胀系数的测定实验原理。

你们知道吗？金属线膨胀系数可是关系到我们日常生活中很多重要物品的质量哦！那么，这个实验到底是怎么进行的呢？别着急，让我来给大家一一道来。

我们要了解一下什么是金属线膨胀系数。

金属线膨胀系数，顾名思义，就是金属线在不同温度下体积变化的比值。

简单来说，就是金属线受热后，长度会变长，而宽度和厚度不会发生变化。

这个比值越大，说明金属线受热后膨胀得越厉害。

所以，测量金属线的膨胀系数，对于了解金属线的性能和质量非常重要。

那么，我们如何进行金属线膨胀系数的测定实验呢？这里，我给大家分成了三个步骤来进行讲解。

第一步，准备实验器材。

我们需要准备的器材有：金属线、千分尺、温度计、水槽等。

这些器材都是我们在日常生活中非常常见的，相信大家都能轻松找到。

当然啦，还有一个非常重要的工具——量热器。

量热器是用来测量金属线受热后的温度变化的，所以一定要准备好哦！第二步，测量金属线的初始长度。

我们需要用千分尺来测量金属线的初始长度，并记录下来。

这样，在实验过程中，我们就可以比较金属线受热前后的长度变化，从而计算出金属线的膨胀系数。

第三步，进行加热实验。

这一步可是非常关键的哦！我们需要将金属线放入水槽中，然后用温度计测量水温。

等到水温达到我们设定的目标温度时，就可以让金属线开始受热了。

在金属线受热的过程中，我们要时刻观察金属线的长度变化。

当金属线受热到一定程度时，我们可以停止加热，让金属线自然冷却。

这样，我们就可以得到金属线的最终长度。

接下来，我们就要开始计算金属线的膨胀系数了。

根据金属线受热前后的长度变化，我们可以得出金属线的体积变化。

而根据金属线的体积变化和初始体积，我们可以计算出金属线受热后的体积。

我们可以用金属线受热后的体积除以初始体积，再乘以1000(因为膨胀系数的单位是千帕斯卡),就可以得到金属线的膨胀系数了。

实验十 干涉法测量金属的线膨胀系数固体的线膨胀是指固体受热时在某一方向上的伸长。

这种特性是工程结构设计、机械和仪表制造、材料加工中要考虑的重要 因素。

在相同条件下，不同材料的固体线膨胀的程度不同。

各种材料膨胀特性用线膨胀系数（简称线胀系数）来描述。

线胀系数是选用材料的一项重要指标，实际中经常要对材料线胀系数做测定。

对于金属材料，温度变化引起长度的微小变化比较微小,一般采用光杠杆、光的衍射法等进行精确测量。

本实验中利用干涉法测量金属棒的热膨胀系数。

一、实验目的1．观察物体线膨胀现象，学会测量金属的线胀系数. 2．掌握应用迈氏干涉仪测量物体长度微小变化的方法. 二、实验仪器SGR —1型热膨胀实验装置、游标卡尺、铜棒、铝棒. 三、工作原理在不太大的温度变化范围内，原长为l 0的物体，受热后其伸长量l ∆与其原长l 0、温度的增加量t ∆近似成正比，即0l l t α∆=⋅⋅∆ （1）式中的比例系数α 即称为线胀系数，它表示当温度升高1℃时固体的相对伸长量。

由上式可得l l tα∆=⋅∆ （2）不同材料的线胀系数不同，塑料的线胀系数最大，金属次之，石英玻璃线胀系数很小。

线胀系数是选用材料的一项重要指标。

附表中列出几种物质的线胀系数值，对应有一个温度范围。

表1 几种材料的线胀系数实验指出，同一材料在不同的温度区段，其线胀系数是不同的，但在温度变化不大的范围内，线膨胀系数近似是一个常量。

线膨胀系数的测定是人们了解材料特性的一种重要手段。

在本实验中我们用SGR-1型热膨胀实验装置测量金属棒在20℃～50℃范围内的线膨胀系数，其工作原理是基于光干涉法来进行微小长度量的测量，其光路图见图1所示。

从He-Ne 激光器出射的激光束经过分束器（半反镜）后分成两束，分别由两个反射镜：定镜和动镜反射回来，由于分束器的作用两束反射光在观察屏上会相遇并形成明暗相间的同心环状干涉条纹。

长度为l 0的待测固体试件被电热炉加热，当温度从t 0上升至t 时，试件因受热膨胀，从l 0伸长到l ，同时推动迈克耳孙干涉仪的动镜，使干涉条纹发生N 个环的变化，则l - l 0 = Δl = N2λ（3）数显温控仪扩束器观察屏分束器定镜 M 1石英垫转向镜 M 2测温探头电热炉石英管动镜试样He-Ne 激光器图1而线膨胀系数00()ll t t α∆=- （4）所以只要测出某一温度范围的固体试件的伸长量和加热前的长度，就可以测出该固体材料的线膨胀系数。

固体线热膨胀系数的测定物体因温度改变而发生的膨胀现象叫“热膨胀”。

通常是指外压强不变的情况下，大多数物质在温度升高时，其体积增大，温度降低时体积缩小。

也有少数物质在一定的温度范围内，温度升高时，其体积反而减小。

在相同条件下，固体的膨胀比气体和液体小得多，直接测定固体的体积膨胀比较困难。

但根据固体在温度升高时形状不变可以推知，一般而言，固体在各方向上膨胀规律相同。

因此可以用固体在一个方向上的线膨胀规律来表征它的体膨胀。

测量固体线热膨胀系数的方法和实验仪器有很多种，本实验只是其中的一种。

一、实验目的⒈ 了解DH4608A 金属热膨胀系数实验仪的基本结构和工作原理。

⒉ 掌握千分表和温度控制仪的使用方法。

⒊ 掌握测量金属线热膨胀系数的基本原理。

4．测量不锈钢管、紫铜管的线膨胀系数。

5、学会用热电偶测量温度。

二、实验原理在一定温度范围内，原长为0L （在0t ＝0℃时的长度）的物体受热温度升高，一般固体会由于原子的热运动加剧而发生膨胀，在t （单位℃）温度时，伸长量△L ，它与温度的增加量△t （△t=t-0t ）近似成正比，与原长0L 也成正比，即：△L=α×0L ×△t （1）此时的总长是：t L ＝0L +△L （2） 式中α为固体的线膨胀系数，它是固体材料的热学性质之一。

在温度变化不大时，α是一个常数，可由式（1）和（2）得tL L t L L L t 1000∙∆=-=α （3） 由上式可见，α的物理意义：当温度每升高1℃时，物体的伸长量△L 与它在0℃时的长度之比。

当温度变化较大时，α可用t 的多项式来描叙：α＝A+Bt+C 2t +……式中A ，B ，C 为常数。

在实际的测量当中，通常测得的是固体材料在室温1t 下的长度1L 及其在温度1t 至2t 之间的伸长量，就可以得到热膨胀系数，这样得到的热膨胀系数是平均热膨胀系数α：()()1212112112t t L L t t L L L -∆=--≈α （4）式中1L 和2L 分别为物体在1t 和2t 下的长度，△21L ＝2L -1L 是长度为1L 的物体在温度从1t 升至2t 的伸长量。