《理论力学》第七章点的合成运动习题解
- 格式:docx
- 大小:1.23 MB
- 文档页数:25

习 题7-1 如图7-26所示,光点M 沿y 轴作谐振动,其运动方程为:x = 0,)cos(θω+=t A y ,式中,A 、ω、θ均为常数。
如将点M 投影到感光记录纸上,此纸以等速v e 向左运动,试求点在记录纸上的轨迹。
图7-26t v x e =')cos()cos(eθωθω+'=+=='x v A t A y y7-2 用车刀切削工件的端面,车刀刀尖M 的运动方程为 t b x ωsin =,其中b 、ω为常数,工件以等角速度ω逆时针方向转动,如图7-27所示。
试求车刀在工件端面上切出的痕迹。
图7-27t b t y t x x ωωωsin sin cos ='-'= 0cos sin ='+'=t y t x y ωω 解得)2sin(2cos sin sin tan cos sin t b t t b t t t t b x ωωωωωωω==+=' ]1)2[cos(2sin tan 2-=-='-='t bt b t x y ωωω4)2()(222b b y x =+'+'7-3 河的两岸相互平行,如图7-28所示。
设各处河水流速均匀且不随时间改变。
一船由点A 朝与岸垂直的方向等速驶出,经过10 min 到达对岸,这时船到达点B 的下游120 m 处的点C 。
为使船A 能垂直到达对岸的点B ,船应逆流并保持与直线AB 成某一角度的方向航行。
在此情况下,船经12.5 min 到达对岸。
试求河宽L 、船相对于水的相对速度v r 和水的流速v 的大小。
图7-28m/s 2.0600120==v 600r L v =船A 能垂直到达对岸的点B750a L v = 2a22r v v v += 2222.0)750()600(+=L L m 200)7501()6001(2.022=-=L m/s 31r =v7-4 半径R = 60mm 的半圆管BC 绕定轴OO 1按规律)5(t t -=ϕ转动,点在管内运动,相对于管子的运动方程为2π10t BM =(弧长的单位为mm),如图7-29所示。




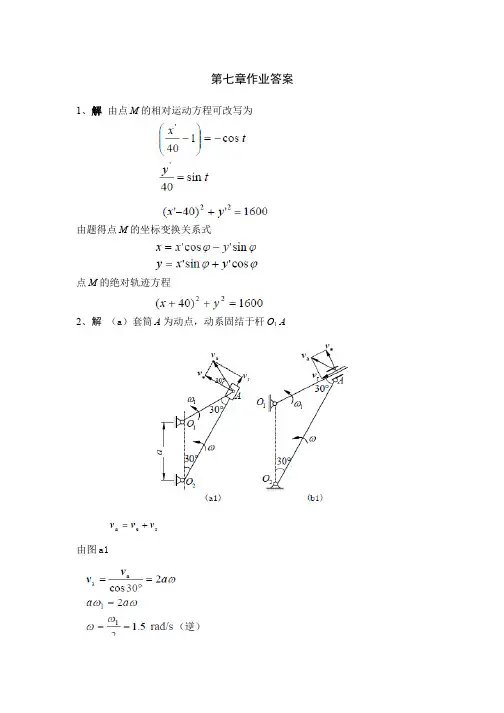
第七章作业答案1、解 由点M 的相对运动方程可改写为
由题得点M 的坐标变换关系式
点M 的绝对轨迹方程
2、解 (a)套筒A 为动点,动系固结于杆O1 A
由图a1
(b)套筒A 为动点,动系固结于杆O2 A,速度分析如图b1 所示。
3、解 ① 活动销子M 为动点,动系固结于轮O
② 活动销子M 为动点,动系固结于杆OA
速度分析如图b 所示
4、解 速度分析,如图b所示
加速度分析,如图c所示
5、解 点A 为动点,动系固结于小车,加速度分析如图b 所示。
由题意得t = 1 s时,各量为
分别向轴x , y 方向投影得
6、解 小环M 为动点,动系固结于曲杆OBC,速度分析如图b 所示。
加速度分析如图c 所示。




第7章 点的合成运动一、是非题(正确的在括号内打“√”、错误的打“×”)1.点的速度和加速度合成定理建立了两个不同物体上两点之间的速度和加速度之间的 关系。
( √ ) 2.根据速度合成定理,动点的绝对速度一定大于其相对速度。
( × )3.应用速度合成定理,在选取动点和动系时,若动点是某刚体上的一点,则动系不可以固结在这个刚体上。
( √ )4.从地球上观察到的太阳轨迹与同时在月球上观察到的轨迹相同。
( × ) 5.在合成运动中,当牵连运动为转动时,科氏加速度一定不为零。
( × ) 6.科氏加速度是由于牵连运动改变了相对速度的方向而产生的加速度。
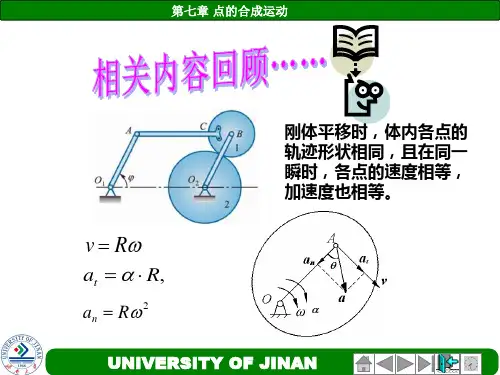
( √ ) 7.在图中,动点M 以常速度r v 相对圆盘在圆盘直径上运动,圆盘以匀角速度ω绕定轴O 转动,则无论动点运动到圆盘上的什么位置,其科氏加速度都相等。
( √ )二、填空题1.已知r 234=++v i j k ,e 63=-ωi k ,则k =a 18 i + -60 j + 36 k 。
2.在图中,两个机构的斜杆绕O 2的角速度均为2ω,O 1O 2的距离为l ,斜杆与竖直方向的夹角为θ,则图(a)中直杆的角速度=1ωθθωcos sin 2,图(b)中直杆的角速度=1ω2ω。
图 图3.科氏加速度为零的条件有:动参考系作平动、0=r v 和r e v ω//。
4.绝对运动和相对运动是指动点分别相对于定系和动系的运动,而牵连运动是指牵连点相对于定系的运动。
牵连点是指某瞬时动系上和动点相重合的点,相应的牵连速度和加速度是指牵连点相对于定系的速度和加速度。
5.如图所示的系统,以''Ax y 为动参考系,Ax'总在水平轴上运动,AB l =。
则点B 的相对轨迹是圆周,若kt ϕ= (k 为常量),点B 的相对速度为lk ,相对加速度为2lk 。
图6.当点的绝对运动轨迹和相对运动轨迹都是曲线时,牵连运动是直线平动时的加速度合成定理表达式是a e r =+a a a ;牵连运动是曲线平动时的加速度合成定理表达式是 a e r =+a a a ;牵连运动是转动时的加速度合成定理表达式是a e r k =++a a a a 。
第7章点的合成运动习题1.是非题(对画√,错画×)7-1.绝对运动是动点相对于定系的运动。
()7-2.相对运动是动点相对于动系的运动。
()7-3.牵连运动是动点相对于动系的运动。
()7-4.动点的绝对运动看成动点的相对运动和牵连运动的合成。
()7-5.动点相对速度对时间的导数等于动点的相对加速度。
()7-6.在一般情况下,某瞬时动点的绝对加速度等于动点的相对加速度和牵连加速度矢量和。
()2.填空题(把正确的答案写在横线上)7-7.在研究点的合成运动中,应确定、、。
7-8.图示机构设A 滑块为动点,BC 为动系,则A 滑块的绝对运动为;A 滑块的相对运动为;A 滑块的牵连运动为;科氏加速度的方向。
7-9.上题中若AD=l ,AD 以ω作匀角速度转动,且三角形ABD 构成等边直角三角形,则A 滑块的绝对速度a v = ;相对速度r v = ;牵连速度e v = ;绝对加速度τaa = 、n r a = ;相对加速度r a = ;牵连速度τe a = 、nea = ;科氏加速度c a = 。
ABCωD3.简答题7-10.定系一定是不动的吗?动系是动的吗?7-11.牵连速度的导数等于牵连加速度吗?相对速度的导数等于相对加速度吗?为什么?7-12.为什么动点和动系不能选择在同一物体上?7-13.如何正确理解牵连点的概念?在不同瞬时牵连运动表示动系上同一点的运动吗?7-14.科氏加速度是怎样产生的?当动系作平移时,科氏加速度等于多少?科氏加速度是怎样产生的?当动系作平移时,科氏加速度等于多少? 7-15.速度合成定理对牵连运动为平移或转动都成立,但加速度合成定理r e a a a a +=对牵连运动为转动却不成立?为什么?牵连运动为转动却不成立?为什么?7-16.如图所示曲柄滑块机构,若取B 为动点,动系固结于曲柄OA 上,动点B 的牵连速度如何?如何画出速度的平行四边形?速度如何?如何画出速度的平行四边形?OABCω7-17.如图所示的四连杆机构,曲柄OA 与BC 平行AB=BC=r ,问销钉B 相对于曲柄OA 的速度为多少?的速度为多少?4.计算题7-18.如图所示,点M 在平面y x O ¢¢中运动,运动方程为中运动,运动方程为)t cos (x -=¢140 t s i ny 40=¢ t 以s 计,x ¢、y ¢以mm 计,平面y x O ¢¢绕O 轴转动,其转动方程为t =j (rad ),试求点M 的相对运动轨迹和绝对运动轨迹。
第七章点的合成运动一、是非题1、牵连速度是动参考系相对于固定参考系的速度。
×2、不论牵连运动的何种运动,点的速度合成定理 v a =v e +v r 皆成立。
( 答案:√3、在点的合成运动中, 动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
( 答案:×4、当牵连运动为平动时,相对加速度等于相对速度对时间的一阶导数。
( 答案:√5、用合成运动的方法分析点的运动时,若牵连角速度ωe ≠ 0,相对速度υr ≠ 0,则一定有不为零的科氏加速度。
( 答案:×6、若将动坐标取在作定轴转动的刚体上,则刚体内沿平行于转动轴的直线运动的动点,其加速度一定等于牵连加速度和相对加速度的矢量和。
( 答案:√7、刚体作定轴转动,动点 M 在刚体内沿平行于转动轴的直线运动,若取刚体为动坐标系, 则任一瞬时动点的牵连加速度都是相等的。
( 答案:×8、当牵连运动定轴转动时一定有科氏加速度。
( 答案:×9、如果考虑地球自转,则在地球上的任何地方运动的物体(视为质点 ,都有科氏加速度。
(答案:×二、选择题1. 在点的合成运动问题中,当牵连运动为平动时 ------。
①一定会有科氏加速度②不一定会有科氏加速度③一定没有科氏加速度答案:③2. 平行四边形机构, 在图示瞬时, 杆以角速度转动。
滑块 M 相对 AB 杆运动若取 M 为动点, AB 为动坐标,则该瞬时动点的牵连速度与杆 AB 间的夹角为 ------。
①②③④答案:②3、长 L 的直杆 OA ,以角速度ω绕 O 轴转动,杆的 A 端铰接一个半径为 r 的圆盘, 圆盘相对于直杆以角速度ωr 绕 A 轴转动。
今以圆盘边缘上的一点 M 为动点, OA 为动坐标,当 AM 垂直 OA时,点 M 的相对速度为。
A υr =Lωr ,方向沿 AM ;B υr =r(ωr -ω ,方向垂直 AM ,指向左下方;C υr =r(L 2+r2 1/2ωr ,方向垂直 OM ,指向右下方;D υr =rωr ,方向垂直 AM ,指向在左下方。
习 题7-1 如图7-26所示,光点M 沿y 轴作谐振动,其运动方程为:x = 0,)cos(θω+=t A y ,式中,A 、ω、θ均为常数。
如将点M 投影到感光记录纸上,此纸以等速v e 向左运动,试求点在记录纸上的轨迹。
图7-26t v x e =')cos()cos(eθωθω+'=+=='x v A t A y y7-2 用车刀切削工件的端面,车刀刀尖M 的运动方程为 t b x ωsin =,其中b 、ω为常数,工件以等角速度ω逆时针方向转动,如图7-27所示。
试求车刀在工件端面上切出的痕迹。
图7-27t b t y t x x ωωωsin sin cos ='-'=0cos sin ='+'=t y t x y ωω解得)2sin(2cos sin sin tan cos sin t b t t b t t t t b x ωωωωωωω==+=' ]1)2[cos(2sin tan 2-=-='-='t b t b t x y ωωω 4)2()(222b b y x =+'+'7-3 河的两岸相互平行,如图7-28所示。
设各处河水流速均匀且不随时间改变。
一船由点A 朝与岸垂直的方向等速驶出,经过10 min 到达对岸,这时船到达点B 的下游120 m 处的点C 。
为使船A 能垂直到达对岸的点B ,船应逆流并保持与直线AB 成某一角度的方向航行。
在此情况下,船经12.5 min 到达对岸。
试求河宽L 、船相对于水的相对速度v r 和水的流速v 的大小。
图7-28m/s 2.0600120==v 600r L v = 船A 能垂直到达对岸的点B750a L v = 2a 22r v v v += 2222.0)750()600(+=L L m 200)7501()6001(2.022=-=L m/s 31r =v 7-4 半径R = 60mm 的半圆管BC 绕定轴OO 1按规律)5(t t -=ϕ转动,点在管内运动,相对于管子的运动方程为2π10t BM =(弧长的单位为mm),如图7-29所示。
第七章 点的合成运动一、是非题7.1.1动点的相对运动为直线运动,牵连运动为直线平动时,动点的绝对运动必为直线运动。
( × ) 7.1.2无论牵连运动为何种运动,点的速度合成定理r e av v v +=都成立。
( ∨ ) 7.1.3某瞬时动点的绝对速度为零,则动点的相对速度和牵连速度也一定为零。
( × ) 7.1.4当牵连运动为平动时,牵连加速度等于牵连速度关于时间的一阶导数。
( ∨ ) 7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。
( × ) 7.1.6不论牵连运动为何种运动,关系式a a +a a r e =都成立。
(× ) 7.1.7只要动点的相对运动轨迹是曲线,就一定存在相对切向加速度。
( × ) 7.1.8在点的合成运动中,判断下述说法是否正确:(1)若r v 为常量,则必有r a =0。
( × ) (2)若e ω为常量,则必有e a =0.( × )(3)若e r ωv //则必有0=C a 。
( ∨ ) 7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
( × ) 7.1.10当牵连运动为定轴转动时一定有科氏加速度。
( × )二、 填空题7.2.1 牵连点是某瞬时 动系 上与 动点 重合的那一点。
7.2.2e a v v =大小为,在一般情况下,若已知v e 、v r ,应按a 的大小。
三、选择题:7.3.1 动点的牵连速度是指某瞬时牵连点的速度,它相对的坐标系是( A )。
A 、 定参考系B 、 动参考系C 、 任意参考系 7.3.2 在图示机构中,已知t b a s ωsin +=, 且t ωϕ=(其中a 、b 、ω均为常数),杆长为L ,若取小球A 为动点,动系固结于物块B ,定系固结于地面,则小球的牵连速度v e 的大小为( B )。
2v v e =1v v =ABr v v =045045v r =N第七章 点的合成运动习题解析[习题7-1] 汽车A 以h km v /401=沿直线道路行驶,汽车B 以h km v /2402=沿另一叉道行驶。
求在B 车上观察到的A车的速度。
解: 动点:A 车。
动系:固连于B 车的坐标系。
静系:固连地面的坐标系。
绝对运动:动点A 相对于地面的运动。
相对运动:动点A 相对于B 车的运动。
牵连运动:在动系中,动点与动系的重合点, 即牵连点相对于静系(地面)的运动。
当A、 B两车相遇时,即它们之间的距离趋近于0时, A、B相重合,B车相对于地面的速度就是 牵连速度。
2v v e =。
由速度合成定理得:→→→+=r e v v v 。
用作图法求得:h km v v AB r /40== (↑)故,B车上的人观察到A车的速度为h km v v AB r /40==,方向如图所示。
[习题7-2] 由西向东流的河,宽1000m ,流速为0.5m/s ,小船自南岸某点出发渡至北岸,设小船相对于水流的划速为1m/s 。
问:(1)若划速保持与河岸垂直,船在北岸的何处靠岸?渡河时间需多久?(2)若欲使船在北岸上正对出发点处靠岸,划船时应取什么方向?渡河时间需多久? 解:(1) 动点:船。
动系:固连在流水上。
静系:固连在岸上。
绝对运动:岸上的人看到的船的运动。
相对运动:船上的有看到的船的运动。
牵连运动:与船相重合的水体的运动。
绝对速度:未知待求,如图所示的v 。
相对速度:s m v r /1=,方向如图所示。
牵连速度:s m v e /5.0=,方向如图所示。
由速度合成定理得:→→→+=r e v v vv r1=N1v sm /2sm v e /1=v)/(118.115.02222s m v v v r e =+=+=0435.635.01arctan arctan===e r v v θ )(50021000tan 1000m AC ===θ,即,船将在北岸下流500m 处靠岸。
如图所示,A为出发点,B为靠岸点。
渡河所花的时间:秒分4016)(1000/110001===s sm mt(2)03015.0arcsin arcsin ===r e v v α)/(866.05.012222s m v v v e r =+=-=即船头对准方向为北偏西030 渡河所花的时间:秒分1519)(1155/866.010002===s sm mt[习题7-3] 播种机以匀速率s m v /11=直线前进。
种子脱离输种管时具有相对于输种管的速度s m v /22=。
求此时种子相对于地面的速度,及落至地面上的位置与离开输种管时的位置之间水平距离。
解: 动点:种子。
动系:固连于输种管的坐标系。
静系:固连于地面的坐标系。
绝对速度:种子相对于地面的速度,未知待求。
相对速度:s m v v r /22== 牵连速度:s m v v e /11==→→→+=r e v v v)/(65.2120cos 21221022s m v =⨯⨯-+=0120sin 65.2)60sin(1=-θ0007.1965.2120sin arcsin 60==-θ093.40=θ即→v 与→1v 之间的夹角为093.40=θ。
种子走过的水平距离为:t v t v s x ⋅==θcos221gt t v h y += 221sin gt t v h +=θ 208.95.093.40sin 65.225.0t t ⨯+= 025.0736.19.42=-+t t⎩⎨⎧-=±-=⨯-⨯⨯-±-=不合舍去))((464.0)(11.08.9813.2736.19.42)25.0(9.44736.1736.12s s t )(22.011.093.40cos 65.20m s =⨯⨯=[习题7-4] 砂石料从传送带A落到另一传送带B的绝对速度为s m v /41=,其方向与铅直线成030角。
设传送带B与水平面成015角,其速度为s m v /22=,求此时砂石料对于传送带B的相对速度。
又当传送带B的速度多大时,砂石料的相对速度才能与B 带垂直。
解:动点:砂石料。
动系:固连于传送带B的坐标系。
静系:固连于地面的坐标系。
绝对速度:砂石料相对于地面的速度,s m v v /41==。
相对速度:砂石料相对于传送带B的速度,待求。
牵连速度:传送带B相对于地面的速度:s m v v e /22==→→→+=r e a v v v)/(98.375cos 42242022s m v r =⨯⨯-+=e Aa v v =vev当B r v v ⊥时,传送带B的速度为:)/(04.115sin 415sin 00s m v v a B ===[习题7-5] 三角形凸轮沿水平方向运动,其斜边与水平线成α角。
杆AB的A端搁置在斜面上,另一端B在气缸内滑动,如某瞬时凸轮以速度v 向右运动,求活塞B的速度。
解: 动点:A。
动系:固连于凸轮上的坐标系。
静系:固连于地面的坐标系。
绝对速度:A相对于地面的速度,待求。
相对速度:A相对于凸轮的速度。
牵连速度:凸轮相对于地面的速度。
→→→+=r e a v v vαtan v v A =因为杆AB作上下平动,故活塞B的速度为:αtan v v v A B ==[习题7-6] 图示一曲柄滑道机构,长r OA =的曲柄,以匀角速度ω绕O轴转动。
装在水平杆CB上的滑槽DE与水平线成060角。
求当曲柄与水平线的夹角ϕ分别为00、030、060时,杆BC的速度。
解: 动点:A。
a90BCOaevC动系:固连于CBDE上的坐标系。
动系平动,BCCBDEAvvv==静系:固连于地面的坐标系。
绝对速度:A相对于地面的速度。
相对速度:A相对于DE的速度。
牵连速度:CBDE相对于地面的速度。
→→→+=reavvvωrva=0120sin)90120180sin(aBCvv=+--ϕ0120sin)30sin(ϕϕrvBC=-ωϕrvBC⋅-=120sin)30sin(ωωωϕrrrvBC332321120sin)30sin(|-=-=⋅-==负号表示此时速度方向与图示方向相反,即向左。
120sin)3030sin(|300=-==ϕBCv,此时往复运动改变方向。
ωωωϕrrrvBC332321120sin)3060sin(|600==⋅-==,向右。
[习题7-7] 摇杆OC带动齿条AB上下移动,齿条又带动直径为100mm的齿轮绕O1轴摆动。
在图所示瞬时,OC之角速度ω0=0.5rad/s,求这时齿轮的角速度。
解:动点:C。
动系:固连于OC杆上的坐标系。
静系:固连于地面的坐标系。
av ev rv A30090绝对速度:C相对于地面的速度。
相对速度:C相对于OC杆的速度。
牵连速度:OC杆相对于地面的速度。
)/(231.05.030cos 4.00s m OC v e =⨯=⋅=ω→→→+=r e a v v v)/(267.030cos 2.030cos 020s m v v e a ===75.0/2.01===ωr v v AB a)/(33.505.075.0/2.0/267.011s rad r ===ω即齿轮的角速度为s rad /33.51=ω[习题7-8] 摇杆滑道机构的曲柄OA长l ,以匀角速度ω0绕O轴转动。
已知在图所示位置 OA⊥OO1,l AB 2=,求该瞬时BC杆的速度。
解: 动点:A。
动系:固连于D O 1杆上的坐标系。
静系:固连于地面的坐标系。
绝对速度:A相对于地面的速度,0ωl v a =。
相对速度:A相对于D O 1杆的速度。
牵连速度:D O 1杆相对于地面的速度。
→→→+=r e a v v v002130sin ωl v v a e == 01211ωωl A O v D O e =⋅= 02121ωωl l D O =⋅ 0411ωω=D O动点:B。
avrBeav rvaa n动系:固连于D O 1杆上的坐标系。
静系:固连于地面的坐标系。
绝对速度:B相对于地面的速度。
相对速度:B相对于D O 1杆的速度。
牵连速度:D O 1杆相对于地面的速度。
→→→+=r e a v v v0014141ωωωl l B O v D O e =⨯=⋅=000155.1866.030cos ωωl l v v e a ===BC 作平动,故0155.1ωl v v a BC ==[习题7-9] 一外形为半圆弧的凸轮A,半径r=300mm,沿水平方向向右作匀加速运动,其加速度aA=800mm/s2。
凸轮推动直杆BC沿铅直导槽上下运动。
设在图所示瞬时,vA=600mm/s,求杆BC的速度及加速度。
解:动点:B。
动系:固连于凸轮A上的坐标系。
静系:固连于地面的坐标系。
绝对速度:B相对于地面的速度。
相对速度:B相对于凸轮的速度。
牵连速度:B相对于凸轮的速度。
→→→+=r e a v v v凸轮在水平面上作平动,BC在铅垂方向上作平动。
A e v v =)/(23.1039360030cot 30cot 00s mm v v v v v A e a B BC ====== )/(12006002230sin 0s mm v v v e er =⨯===→→→→→→++=+=τr n re r e a a a a a a aeCv rv ra aa ea上式在x 轴上的投影为:n r e a a a a -=0030cos 60cosrv a a a a r e n re a 22323⋅-=-=)/(4.8214300)1200(2800732.122s mm a a -=⨯-⨯=,负号表示方向向下。
[习题7-10] 铰接四边形机构中的O1A=O2B=100mm,O1O2=AB,杆O1A以等角速度ω=2rad/s绕O1轴转动。
AB杆上有一套筒C,此筒与CD杆相铰接,机构各部件都在同一铅直面内。
求当φ=60°时CD杆的速度和加速度。
解:动点:C。
动系:固连于AB杆上的坐标系。
静系:固连于地面的坐标系。
绝对速度:C相对于地面的速度。
相对速度:C相对于AB杆的速度。
牵连速度:AB杆相对于地面的速度。
→→→+=r e a v v v)/(20021001s mm A O v v v A C e =⨯=⋅===ω )/(1005.020060cos 0s mm v v e a =⨯==)/(100s mm v v v a C CD ===→→→+=r e a a a aA e a a = 0=τe a)/(4002100222112s mm A O AO v a a n ee =⨯=⋅===ω)/(4.346866.040060sin 20s mm a a e a =⨯==)/(4.346s mm a a a a C CD ===[习题7-11] 具有圆弧形滑道的曲柄滑道机构,用来使滑道CD获得间歇往复运动。