同济材料力学 顾志荣 第十章 - 应力状态理论的基础
- 格式:ppt
- 大小:5.21 MB
- 文档页数:116






第十章强度理论同济大学航空航天与力学学院顾志荣一、教学目标掌握强度理论的概念。
了解材料的两种破坏形式(按破坏现象区分)。
了解常用的四个强度理论的观点、破坏条件、强度条件。
掌握常用的四个强度理论的相当应力。
了解莫尔强度理论的基本观点。
会用强度理论对一些简单的杆件结构进行强度计算。
二、教学内容讲解强度理论的概念及材料的两种破坏形式。
讲解常用的四个强度理论的基本观点,并推导其破坏条件从而建立强度计算方法。
介绍几种强度理论的应用范围和各自的优缺点。
简单介绍莫尔强度理论。
三、重点难点重点:强度理论的概念、常用的四个强度理论的观点、强度条件及其强度计算。
难点:常用四个强度理论的理解;危险点的确定及其强度计算。
四、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
五、计划学时 2学时 六、实施学时 七、讲课提纲(一)为什么需要强度理论及强度理论的概念?1、为什么需要强度理论(回顾基本变形下强度条件的建立)2、复杂应力状态下的强度条件是什么?怎样建立?3、强度理论的概念4、四个强度理论及其相当应力 (二)四个强度理论第一强度理论——最大拉应力理论 第二强度理论——最大拉应变理论 第三强度理论——最大剪应力理论第四强度理论——⎪⎩⎪⎨⎧形状改变比能理论均方根剪应力理论 (三)相当应力11σσ=r-=12σσr μ)(32σσ+ 313σσσ-=r2132322214)()()(21σσσσσσσ-+-+-=r (四)复杂应力状态下强度条件的表达式 σr ≤[σ](一)为什么需要强度理论?强度理论的概念1、回顾构件处于简单变形下的强度条件的建立 [拉、压] (单向)图10-1强度条件:[]nA F o N σσσ=≤=,b S oσσσ由试验得[扭转](双向)图10-2强度条件:[]nW M on n τττ=≤=max ,b S o τττ由试验得[弯曲](二向)强度条件(上下边缘点):[]σσ≤=zW M maxmax 中性层处:[]ττ≤⋅=bI S F Z z Q *maxmax max ([]σ、[]τ由试验得)为什么可以这样来建立强度条件? 因为:⑴构件内的应力状态比较简单;⑵用接近这类构件受力情况的试验装置测定极限应力值比较容易实现。


第四章扭转同济大学航空航天与力学学院顾志荣一、教学目标与教学内容1、教学目标(1)掌握扭转的概念;(2)熟练掌握扭转杆件的内力(扭矩)计算和画扭矩图;(3)了解切应力互等定理及其应用,剪切胡克定律与剪切弹性模量;(4) 熟练掌握扭转杆件横截面上的切应力计算方法和扭转强度计算方法;(5) 熟练掌握扭转杆件变形(扭转角)计算方法和扭转刚度计算方法;(6)了解低碳钢和铸铁的扭转破坏现象并进行分析。
(7)了解矩形截面杆和薄壁杆扭转计算方法。
2、教学内容(1) 扭转的概念和工程实例;(2) 扭转杆件的内力(扭矩)计算,扭矩图;(3) 切应力互等定理, 剪切胡克定律;(4) 扭转杆件横截面上的切应力, 扭转强度条件;(5) 扭转杆件变形(扭转角)计算,刚度条件;(6) 圆轴受扭破坏分析;(7) 矩形截面杆的只有扭转;(8) 薄壁杆件的自由扭转。
二、重点和难点1、重点:教学内容中(1)~(6)。
2、难点:切应力互等定理,横截面上切应力公式的推导,扭转变形与剪切变形的区别,扭转切应力连接件中切应力的区别。
通过讲解,多媒体的动画演示扭转与剪切的变形和破坏情况,以及讲解例题来解决。
三、教学方式通过工程实例建立扭转概念,利用动画演示和实物演示表示扭转时的变形,采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时6学时五、实施学时六、讲课提纲工程实例:图4-1**扭转和扭转变形1、何谓扭转?如果杆件受力偶作用,而力偶是作用在垂直于杆件轴线的平面内,则这杆件就承受了扭转。
换言之,受扭杆件的受力特点是:所受到的外力是一些力偶矩,作用在垂直于杆轴的平面内。
2、何谓扭转变形?在外力偶的作用下,杆件的任意两个横截面都绕轴线发生相对转动。
杆件的这种变化形式称为扭转变形。
换言之,受扭转杆件的变形特点是:杆件的任意两个横截面都绕轴线发生相对转动。
I 圆轴扭转时的应力和强度计算 一、外力偶矩、扭矩和扭矩图 1、外力偶矩(T )的计算nP T p⨯=02.7 KN ·m (7-1) P p 指轴所传递的功率(马力) n 指轴的转速(转/分、r/min )nP T kW⨯=55.9 KN ·m (7-2)P kW 指轴所传递的功率(千瓦、Kw ) n 指轴的转速(转/分、r/min )2、扭矩(M n )的确定及其符号规定 (1)M n 的确定 截面法图4-30=∑x M0=-A n T M 左 A n T M =左0=∑x M0=+-B n T M 右 B n T M =右(2)M n 的符号规定 右手螺旋法则图4-43、扭矩图扭矩随轴线横截面位置改变而变化的规律图,称为扭矩图。
土体应力计算补充一、力学基础知识材料力学研究物体受力后的内在表现,即变形规律和破坏特征。
一、材料力学的研究对象材料力学以“梁、杆”为主要研究对象。
二、材料力学的任务材料力学的任务:在满足强度、刚度、稳定性的要求下,以最经济的代价,为构件确定合理的形状和尺寸,选择适宜的材料,而提供必要的理论基础和计算方法。
强度:杆件在外载作用下,抵抗断裂或过量塑性变形的能力。
刚度:杆件在外载作用下,抵抗弹性变形的能力。
稳定性:杆件在压力外载作用下,保持其原有平衡状态的能力。
如:自行车结构也有强度、刚度和稳定问题;大型桥梁的强度、刚度、稳定问题强度、刚度、稳定性三、基本假设1、连续性假设:物质密实地充满物体所在空间,毫无空隙。
(可用微积分数学工具)2、均匀性假设:物体内,各处的力学性质完全相同。
3、各向同性假设:组成物体的材料沿各方向的力学性质完全相同。
(这样的材料称为各项同性材料;沿各方向的力学性质不同的材料称为各项异性材料。
)4、小变形假设:材料力学所研究的构件在载荷作用下的变形与原始尺寸相比甚小,故对构件进行受力分析时可忽略其变形。
假设四、杆件变形的基本形式五、内力?截面法?轴力1、内力指由外力作用所引起的、物体内相邻部分之间分布内力系的合成(附加内力)。
2、截面法内力的计算是分析构件强度、刚度、稳定性等问题的基础。
求内力的一般方法是截面法。
(1)截面法的基本步骤:①截开:在所求内力的截面处,假想地用截面将杆件一分为二。
②代替:任取一部分,其弃去部分对留下部分的作用,用作用在截开面上相应的内力(力或力偶)代替。
③平衡:对留下的部分建立平衡方程,根据其上的已知外力来计算杆在截开面上的未知内力(此时截开面上的内力对所留部分而言是外力)截面法例如:截面法求N截开:代替:平衡:3、轴力轴向拉压杆的内力,用N 表示。
轴力的正负规定:N与外法线同向,为正轴力(拉力)N与外法线反向,为负轴力(压力)六、截面上应力1、应力的概念定义:由外力引起的内力集度。
第九章应力状态理论基础同济大学航空航天与力学学院顾志荣一、教学目标通过本章学习,掌握应力状态的概念及其研究方法;会从受力杆件中截取单元体并标明单元体上的应力情况;会计算平面应力状态下斜截面上的应力;掌握平面应力状态和特殊空间应力状态下的主应力、主方向的计算,并会排列主应力的顺序;掌握广义胡克定律;了解复杂应力状态比能的概念;了解主应力迹线的概念。
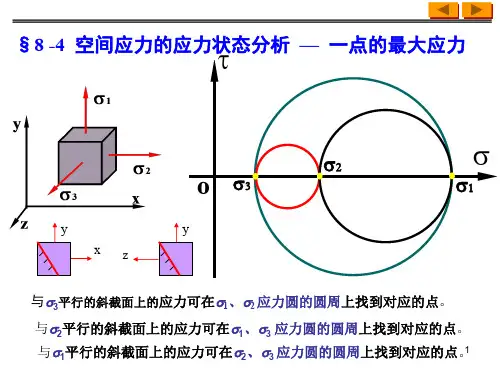
二、教学内容1、应力状态的概念;2、平面应力状态分析--数解法3、平面应力状态分析—图解法4、三向应力状态下的最大应力;5、广义胡克定律•体应变;6、复杂应力状态的比能;7、梁的主应力•主应力迹线的概念。
三、重点难点重点:1、平面应力状态下斜截面上的应力计算,主应力及主方向的计算,最大剪应力的计算。
2、广义胡克定律及其应用。
难点:1、应力状态的概念,从具体受力杆件中截面单元体并标明单元体上的应力情况。
2、斜截面上的应力计算公式中关于正负符号的约定。
3、应力主平面、主应力的概念,主应力的大小、方向的确定。
4、广义胡克定律及其应用。
四、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
五、计划学时6学时六、实施学时七、讲课提纲本章与前几章在研究对象上的不同之处。
回顾:内力图:N F 、n M 、Q F 、M --一根(杆、轴、梁)强度计算⎪⎩⎪⎨⎧一面(危险截面)一段—、—、max max max max M F M F Q n N 本章:应力状态— 一点。
(一)应力状态的概念一、为什么要研究一点的应力状态?简单回顾:拉压:图9-1强度条件:[]⎪⎩⎪⎨⎧=≤=nn A F bs N σσσσ 扭转:图9-2 强度条件:[]⎪⎩⎪⎨⎧=≤=nn W M bs n n ττττmax弯曲:图11-3强度条件:[][]⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧=≤⋅=⎪⎩⎪⎨⎧=≤=*n n b I S F n n W M b s z z x ma Q x ma bs z x ma ττττσσσσmax 但,到目前为止尚不能对如第4点的应力情况进行校核,因此:1、为了对某些复杂受力构件中既存在σ又存在τ的点建立强度条件提供依据。