通过类比联想引申拓展研究典型题目

南昌县2023-2024学年度第一学期期中考试九年级数学试题一、选择题（共6小题，满分18分，每小题3分）1．下列图案中不是中心对称图形的是（ ）A ．B ．C ．D ．2．一元二次方程的一次项系数是（ ）A ．3xB ．C ．3D ．3．抛物线的顶点坐标是（ ）．A ．B ．C ．D ．4．已知三角形两边长分别为5和9，第三边长是方程的根，第三边长（）A ．1B ．6C ．8D ．95．若a ，b 是方程的两个实数根，则的值是（ ）．A ．2021B ．2022C ．2023D ．20246．如图，一段抛物线，记为抛物线，它与x 轴交于点O ，；将抛物线绕点旋转得抛物线，交x 轴于点；将抛物线绕点旋转得抛物线，交x 轴于点．…如此进行下去，得到一条“波浪线”，若点在此“波浪线”上，则m 的值为（ ）．A ．B ．3C ．D ．4二、填空题（共6小题，满分18分，每小题3分）7．若点与点关于原点对称，则__________．8．如果将抛物线向左平移1个单位，再向下平移1个单位，那么所得到的新抛物线的表达式是__________．9．已知点，在抛物线上，且，则__________．（填“”或22350x x -+=3x -3-22(3)4y x =++()3,4()3,4-()3,4-()3,4--2980x x -+=2220230x x +-=23a a b ++24(04)y x x x =-+≤≤1C 1A 1C 1A 180︒2C 2A 2C 2A 180︒3C 3A (2023,)M m 3-4-(1,2)A (,2)B m -m =22y x =+11(,)A x y 22(,)B x y 23y x =-120x x <<1y 2y <“”或“”）10．一个人患了流感，经过两轮传染后共有144人患了流感，每轮传染中平均一个人传染了__________人．11．若二次函数的图象与x 轴只有一个公共点，则__________．12．如图，在平面直角坐标系中，O 为坐标原点，四边形是矩形，点A ，C 的坐标分别为，，点D 以2个单位长度/s 的速度从A 出发沿A 至O 方向向终点O 运动，点P 以1个单位长度/s 的速度从C 出发沿C 至B 方向向终点B 运动，当是以为一腰的等腰三角形时，点P 的坐标为__________．三、解答题（共5小题，满分30分，每小题6分）13．解下列方程：（1）；（2）．14．如图，是二次函数图象的一部分，其对称轴为直线，若其与x 轴一交点为，则由图象直接回答：（1）方程的解是__________；（2）当x__________时，y 随x 的增大而减小；（3）当x 满足________时，函数值大于0．15．如图，在正方形中，点M 是边上任意一点，请你仅用无刻度直尺、用连线的方法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）（1）在图（1）中，在边上求作一点N ，连接，使；（2）在图（2）中，在边上求作一点Q ，连接，使．16．《九章算术》被称为人类科学史上应用数学的“算经之首”．书中记载：“今有户不知高、广，竿不知长短．横之不出四尺，从之不出二尺，邪之适出．问户高、广、邪各几何？”译文：今有门，不知其高宽；有竿，不知其长短，横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、门宽、对角线的长各是多少（如图）？>=22y x x k =-+k =OABC (9,0)A (0,3)C ODP △OP 230x x -=28150x x ++=2y ax bx c =++1x =(3,0)A 20ax bx c ++=ABCD BC AB CN CN AM =AD CQ CQ AM∥17．如图所示，点D 是等边内一点，，，，将绕点A 逆时针旋转到的位置，求的周长．四、解答题（共3小题，满分24分，每小题8分）18．某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量y （件）与销售单价x （元）之间存在一次函数关系，如图所示．（1）求y 与x 之间的函数关系式；（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？19．已知：的两边，的长是关于x 的方程的两个实数根．（1）当m 为何值时，四边形是菱形？求出这时菱形的边长；（2）若的长为2，那么的周长是多少？20．将两个全等的和按图1方式摆放，其中，点E 落在上，所在直线交直线于点F ．（1）求证：；（2）若将图1中绕点B 按顺时针方向旋转到图2位置，其他条件不变（如图2），请写出此时、与之间的数量关系，并加以证明．ABC △13DA =19DB =21DC =ABD △ACE △DEC △ABCD AB AD 21024m x mx -+-=ABCD AB ABCD Rt ABC △Rt DBE △90ACB DEB ∠=∠=︒AB DE AC CF EF =DBE △AF EF DE五、解答题（共2小题，满分18分，每小题9分）21．如图，四边形是证明勾股定理时用到的一个图形，a ，b ，c 是和边长，易知，这时我们把关于x 的形如的一元二次方程称为“勾系一元二次方程”．请解决下列问题：（1）写出一个“勾系一元二次方程”；（2）求证：关于x 的“勾系一元二次方程”必有实数根；（3）若是“勾系一元二次方程”的一个根，且四边形的周长是，求面积．22．通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．原题：如图①，点E ，F 分别在正方形的边，上，，连接，试猜想，，之间的数量关系．（1）【思路梳理】把绕点A 逆时针旋转至，可使与重合，由，得，即点F ，D ，G 共线，易证__________，故，，之间的数量关系为__________．（2）【类比引申】如图②，点E ，F 分别在正方形的边，的延长线上，．连接，试猜想，，之间的数量关系，并证明．ACDE Rt ABC △Rt BED△AE=20ax b +=20ax b +=1x =-20ax b ++=ACDE ABC △ABCD BC CD 45EAF ∠=︒EF EF BE DF ABE △90︒ADG △AB AD 90ADG B ∠=∠=︒180FDG ∠=︒AFG ≌△EF BE DF ABCD CB DC 45EAF ∠=︒EF EF BE DF六、解答题（共1小题，满分12分，每小题12分）23．如图，抛物线与x 轴交于、两点，与y 轴交于点C ．点P 是第一象限内抛物线上的一个动点，过点P 作直线轴于点D ，交直线于点E ．（1）求抛物线的解析式；（2）求线段的最大值；（3）当时，求点P 的坐标．南昌县2023-2024学年度第一学期期中考试九年级数学试题参考答案及评分标准说明：1．除本参考答案外，其它正确解法可根据评分标准相应给分。

通过类比联想引申拓展研究典型题目摘要：一、引言：类比联想的意义和价值二、研究典型题目的方法论1.分析题目背景和条件2.寻找类比对象和关系3.运用类比联想进行拓展思考4.总结解题经验和技巧三、类比联想在典型题目中的应用实例1.数学题目的类比联想2.科学实验的类比联想3.语文题目的类比联想4.社会问题的类比联想四、类比联想引申拓展的注意事项1.确保类比关系的合理性2.防止过度引申和偏离主题3.保持逻辑性和条理性五、总结：类比联想在解决问题中的重要作用正文：一、引言类比联想，作为一种思维方式，在我们的生活和工作中具有广泛的应用。

它可以帮助我们从一个已知的问题或现象中提炼出规律，进而解决新的、相似的问题。

在研究典型题目的过程中，类比联想发挥着至关重要的作用。

本文将从类比联想的意义和价值出发，探讨如何利用类比联想研究典型题目，以及类比联想在典型题目中的应用实例和注意事项。

二、研究典型题目的方法论1.分析题目背景和条件：在解决典型题目时，我们首先要对题目的背景和条件进行全面、深入的分析。

这有助于我们了解题目的本质，从而找到解决问题的切入点。

2.寻找类比对象和关系：在分析题目背景和条件的基础上，我们要寻找与之相似的已知问题或现象，进而建立类比关系。

类比对象可以是现实生活中的实例、历史事件、其他学科的知识等。

3.运用类比联想进行拓展思考：在建立类比关系后，我们要运用类比联想进行拓展思考。

这一过程需要我们充分发挥想象力和创造力，从已知问题中提炼出规律，并尝试将其应用于新问题。

4.总结解题经验和技巧：在完成类比联想后，我们要对新问题进行总结，提炼出解题经验和技巧。

这些经验和技巧可以为我们今后解决类似问题提供指导。

三、类比联想在典型题目中的应用实例1.数学题目的类比联想：在数学领域，许多题目都可以通过类比联想找到解题思路。

例如，线性方程组的求解可以类比为图形在平面内的运动，从而利用向量运算求解。

2.科学实验的类比联想：在科学实验中，类比联想可以帮助我们发现新的实验方法和思路。

类比、拓展探究题类比、拓展探究题是近两年中考热门考题，题型的模式基本分为三步：初步尝试、类比发现、深入探究，考查的知识点有：三角形旋转、平行四边形性质、相似、全等、矩形折叠、勾股定理等．此类问题解答往往是层层深入，从特殊到一般，然后是拓展运用．在解题时需要牢牢把握特殊情况、特殊位置下的结论，然后探寻一般情况下是否也成立，最后是类比应用．类比模仿是解决此类问题的重要手段．例1数学活动课上，某学习小组对有一内角为120°的平行四边形ABCD (∠BAD ＝120°)进行探究：将一块含60°的直角三角板如图放置在平行四边形ABCD 所在平面内旋转，且60°角的顶点始终与点C 重合，较短的直角边和斜边所在的两直线分别交线段AB ，AD 于点E ，F (不包括线段的端点)．(1)初步尝试如图①，若AD ＝AB ，求证：①△BCE ≌△ACF ，②AE ＋AF ＝AC ； (2)类比发现如图②，若AD ＝2AB ，过点C 作CH ⊥AD 于点H ，求证：AE ＝2FH ； (3)深入探究如图③，若AD ＝3AB ，探究得AE ＋3AFAC的值为常数t ，则t ＝________．例题分层分析(1)①先证明△ABC ，△ACD 都是________三角形，再证明∠BCE ＝________，即可解决问题． ②根据①的结论得到________，由此可证明．(2)设DH ＝x ，由题意，可得CD ＝________，CH ＝________(用含x 的代数式表示)，由△ACE ∽△HCF ，得AE FH ＝AC CH，由此即可证明．(3)如图③，过点C 作CN ⊥AD 于N ，CM ⊥BA ，交BA 的延长线于点M ，CM 与AD 交于点H .先证明△CFN ∽△CEM ，得CN CM ＝FN EM ，由AB ·CM ＝AD ·CN ，AD ＝3AB ，推出CM ＝3CN ，所以CN CM ＝FN EM ＝13，设CN ＝a ，FN＝b ，则CM ＝3a ，EM ＝3b ，想办法求出AC ，AE ＋3AF 即可解决问题．对应练习：我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．(1)概念理解请你根据上述定义举一个等邻角四边形的例子； (2)问题探究如图①，在等邻角四边形ABCD 中，∠DAB ＝∠ABC ，AD ，BC 的中垂线恰好交于AB 边上一点P ，连结AC ，BD ，试探究AC 与BD 的数量关系，并说明理由；(3)应用拓展如图②，在Rt △ABC 与Rt △ABD 中，∠C ＝∠D ＝90°，BC ＝BD ＝3，AB ＝5，将Rt △ABD 绕着点A 顺时针旋转角α(0°＜∠α＜∠BAC )得到Rt △AB ′D ′(如图③)，当凸四边形AD ′BC 为等邻角四边形时，求出它的面积．解题方法点析(1)矩形或正方形邻角相等，满足“等邻角四边形”的条件；(2)连结PD，PC，根据PE，PF分别为AD，BC的垂直平分线，可得到PA＝________，PB＝________，∠DAP＝________＝∠ABC＝________，从而可得∠APC＝∠DPB，利用SAS可证得△APC≌△DPB，即可得到AC＝BD.(3)分两种情况考虑：(i)当∠AD′B＝∠D′BC时，延长AD′，CB交于点E，由S四边形ACBD′＝S△ACE－S△BED′，求出四边形ACBD′的面积；(ii)当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC于点E，由S四边形ACBD′＝S△AED′＋S矩形ECBD′，求出四边形ACBD′的面积即可．课后练习：1．【操作发现】如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．(1)请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连结BB′；(2)在(1)所画图形中，∠AB′B＝________．【问题解决】如图，在等边三角形ABC中，AC＝7，点P在△ABC内，且∠APC＝90°，∠BPC＝120°，求△APC的面积．小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连结PP′，寻找PA，PB，PC三条线段之间的数量关系；想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连结PP′，寻找PA，PB，PC三条线段之间的数量关系．……请参考小明同学的想法，完成该问题的解答过程．(―种方法即可)【灵活运用】如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB(k为常数)，求BD的长(用含k的式子表示)．2．问题呈现：如图①，点E，F，G，H分别在矩形ABCD的边AB，BC，CD，DA上，AE＝DG.求证：2S四边形EFGH＝S矩形ABCD.(S表示面积)实验探究：某数学实验小组发现：若图①中AH≠BF，点G在CD上移动时，上述结论会发生变化．分别过点E，G 作BC边的平行线，再分别过点F，H作AB边的平行线，四条平行线分别相交于点A1，B1，C1，D1，得到矩形A1B1C1D1.如图②，当AH＞BF时，若将点G向点C靠近(DG>AE)，经过探索，发现：2S四边形EFGH＝S矩形ABCD＋S矩形A1B1C1D1.如图③，当AH＞BF时，若将点G向点D靠近(DG<AE)，请探索S四边形EFGH、S矩形ABCD与S矩形A1B1C1D1之间的数量关系，并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题．(1)如图，点E，F，G，H分别是面积为25的正方形ABCD各边上的点，已知AH>BF，AE>DG，S四边形EFGH ＝11，HF＝29，求EG的长．(2)如图，在矩形ABCD中，AB＝3，AD＝5，点E，H分别在边AB，AD上，BE＝1，DH＝2，点F，G分别是边BC，CD上的动点，且FG＝10，连结EF，HG，请直接写出四边形EFGH面积的最大值．3.【探索发现】如图①是一张直角三角形纸片，∠B＝90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE，EF剪下时，所得的矩形的面积最大．随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为________．【拓展应用】如图②，在△ABC中，BC＝a，BC边上的高AD＝h，矩形PQMN的顶点P，N分别在边AB，AC上，顶点Q，M在边BC上，则矩形PQMN面积的最大值为________．(用含a，h的代数式表示) 【灵活应用】如图③，有一块“缺角矩形”ABCDE，AB＝32，BC＝40，AE＝20，CD＝16，小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角)，求该矩形的面积．【实际应用】如图，现有一块四边形的木板余料ABCD，经测量AB＝50 cm，BC＝108 cm，CD＝60 cm，且tan B＝tan C＝43，木匠徐师傅从这块余料中裁出了顶点M，N在边BC上且面积最大的矩形PQMN，求该矩形的面积．答案与解析【例1】【解答】解：（1）AE+AF＝AC；理由如下：∵四边形ABCD是平行四边形，∠BAD＝120°，∴∠D＝∠B＝60°，∵四边形ABCD是菱形，∴AD＝AB，∴△ABC，△ACD都是等边三角形，∴∠B＝∠CAD＝60°，∠ACB＝60°，BC＝AC，∵∠ECF＝60°，∴∠BCE+∠ACE＝∠ACF+∠ACE＝60°，∴∠BCE＝∠ACF，在△BCE和△ACF中，，∴△BCE≌△ACF（ASA）．∴BE＝AF，∴AE+AF＝AE+BE＝AB＝AC；故答案为：AE+AF＝AC；（2）设DH＝x，由由题意，CD＝2x，CH＝，∴AD＝2AB＝4x，∴AH＝AD﹣DH＝3x，∵CH⊥AD，∴AC＝＝，∴AC2+CD2＝AD2，∴∠ACD＝90°，∴∠BAC＝∠ACD＝90°，∴∠CAD＝30°，∴∠ACH＝60°，∵∠ECF＝60°，∴∠HCF＝∠ACE，∴△ACE∽△HCF，∴，（3），理由如下：如图3中，作CN⊥AD于N，CM⊥BA于M，CM与AD交于点H．∵∠ECF+∠EAF＝180°，∴∠AEC+∠AFC＝180°，∵∠AFC+∠CFN＝180°，∴∠CFN＝∠AEC，∵∠M＝∠CNF＝90°，∴△CFN∽△CEM，∴，∵AB•CM＝AD•CN，AD＝4AB，∴CM＝4CN，∴，设CN＝a，FN＝b，则CM＝4a，EM＝4b，∵∠MAH＝60°，∠M＝90°，∴∠AHM＝∠CHN＝30°，∴HC＝2a，HM＝2a，HN＝a，∴AM＝，AH＝，∴AC＝＝，AE+4AF＝（EM﹣AM）+4（AH+HN﹣FN）＝EM﹣AM+4AH+4HN﹣4FN＝4AH+4HN﹣AM＝，∴．∴t＝，故答案为：．【对应练习】【解答】解：（1）矩形或正方形；（2）AC＝BD，理由为：连接PD，PC，如图1所示：∵PE是AD的垂直平分线，PF是BC的垂直平分线，∴P A＝PD，PC＝PB，∴∠P AD＝∠PDA，∠PBC＝∠PCB，∴∠DPB＝2∠P AD，∠APC＝2∠PBC，即∠P AD＝∠PBC，∴∠APC＝∠DPB，∴△APC≌△DPB（SAS），∴AC＝BD；（3）分两种情况考虑：（i）当∠AD′B＝∠D′BC时，延长AD′，CB交于点E，如图3（i）所示，∴∠ED′B＝∠EBD′，∴EB＝ED′，设EB＝ED′＝x，由勾股定理得：42+（3+x）2＝（4+x）2，解得：x＝4.5，过点D′作D′F⊥CE于F，∴D′F∥AC，∴△ED′F∽△EAC，∴＝，即＝，解得：D′F＝，∴S△ACE＝AC×EC＝×4×（3+4.5）＝15；S△BED′＝BE×D′F＝×4.5×＝，则S四边形ACBD′＝S△ACE﹣S△BED′＝15﹣＝10；（ii）当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC于点E，如图3（ii）所示，∴四边形ECBD′是矩形，∴ED′＝BC＝3，在Rt△AED′中，根据勾股定理得：AE＝＝，∴S△AED′＝AE×ED′＝××3＝，S矩形ECBD′＝CE×CB＝（4﹣）×3＝12﹣3，则S四边形ACBD′＝S△AED′+S矩形ECBD′＝+12﹣3＝12﹣．【课后练习】1.【解答】解：【操作发现】（1）如图所示，△AB′C′即为所求；（2）连接BB′，将△ABC绕点A按顺时针方向旋转90°，∴AB＝AB′，∠B′AB＝90°，∴∠AB′B＝45°，故答案为：45°；【问题解决】如图②，∵将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，∴△APP′是等边三角形，∠AP′C＝∠APB＝360°﹣90°﹣120°＝150°，∴PP′＝AP，∠AP′P＝∠APP′＝60°，∴∠PP′C＝90°，∠P′PC＝30°，∴PP′＝PC，即AP＝PC，∵∠APC＝90°，∴AP2+PC2＝AC2，即（PC）2+PC2＝72，∴PC＝2，∴AP＝，∴S△APC＝AP•PC＝7；【灵活运用】如图③中，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝4k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG＝＝．∴BD＝CG＝．2.【解答】问题呈现：证明：如图1中，∵四边形ABCD是矩形，∴AB∥CD，∠A＝90°，∵AE＝DG，∴四边形AEGD是矩形，∴S△HGE＝S矩形AEGD，同理S△EGF＝S矩形BEGC，∴S四边形EFGH＝S△HGE+S△EFG＝S矩形ABCD．实验探究：结论：2S 四边形EFGH＝S矩形ABCD﹣．理由：∵＝，＝，＝，＝，∴S 四边形EFGH＝+++﹣，∴2S 四边形EFGH＝2+2+2+2﹣2，∴2S 四边形EFGH＝S矩形ABCD﹣．迁移应用：解：（1）如图4中，∵2S四边形EFGH＝S矩形ABCD﹣．∴＝25﹣2×11＝3＝A1B1•A1D1，∵正方形的面积为25，∴边长为5，∵A1D12＝HF2﹣52＝29﹣25＝4，∴A1D1＝2，A1B1＝，∴EG2＝A1B12+52＝，∴EG＝．（2）∵2S 四边形EFGH＝S矩形ABCD+．∴四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．①如图5﹣1中，当G与C重合时，四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．此时矩形A1B1C1D1面积＝1•（﹣2）＝，∴2S 四边形EFGH＝S矩形ABCD+＝15+（﹣2）＝13+，∴S四边形EFGH＝②如图5﹣2中，当G与D重合时，四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．此时矩形A1B1C1D1面积＝2•1＝2，∴2S 四边形EFGH＝S矩形ABCD+＝15+2＝17，∴S四边形EFGH＝8.5∵8.5＞，∴四边形EFGH的面积最大值8.5．3.【解答】解：【探索发现】设EF＝x，ED＝y，∵EF、ED为△ABC中位线，∴ED∥AB，EF∥BC，EF＝BC，ED＝AB，∴AB＝2ED＝2y，BC＝2EF＝2x，又∠B＝90°，∴四边形FEDB是矩形，则＝＝＝，故答案为：；【拓展应用】设PN＝b，∵PN∥BC，∴△APN∽△ABC，∴，∵BC＝a，BC边上的高AD＝h，∴，PQ＝，∴S＝b•PQ＝＝﹣+bh，∴S的最大值为：＝；则矩形PQMN面积的最大值为；故答案为：；【灵活应用】如图1，延长BA、DE交于点F，延长BC、ED交于点G，延长AE、CD交于点H，取BF中点I，FG 的中点K，由题意知四边形ABCH是矩形，∵AB＝32，BC＝40，AE＝20，CD＝16，∴EH＝20、DH＝16，∴AE＝EH、CD＝DH，在△AEF和△HED中，∵，∴△AEF≌△HED（ASA），∴AF＝DH＝16，同理△CDG≌△HDE，∴CG＝HE＝20，∴BI＝＝24，∵BI＝24＜32，∴中位线IK的两端点在线段AB和DE上，过点K作KL⊥BC于点L，由【探索发现】知矩形的最大面积为×BG•BF＝×（40+20）×（32+16）＝720，答：该矩形的面积为720；【实际应用】如图2，延长BA、CD交于点E，过点E作EH⊥BC于点H，∵tan B＝，设EH＝4x，BH＝3x，∵tan C＝2＝，∴CH＝2x，∵BC＝BH+CH＝105＝3x+2x，x＝21，∴BH＝63，CH＝42，EH＝84，由勾股定理得：BE＝＝＝105，CE＝＝＝42，∵AB＝60，∴AE＝45，∴BE的中点Q在线段AB上，∵CD＝70，∴CE的中点P在线段CD上，∴中位线PQ的两端点在线段AB、CD上，由【拓展应用】知，矩形PQMN的最大面积为BC•EH＝＝2205cm2，答：该矩形的面积为2205cm2．。

达州市2013年高中阶段教育学校招生统一考试数 学本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷1至2页，第II 卷3至10页。

考试时间120分钟，满分120分。

第I 卷（选择题，共30分） 温馨提示：1、答第I 卷前，请考生务必将姓名、准考证号、考试科目等按要求填涂在机读卡上。

2、每小题选出正确答案后，请用2B 铅笔把机读卡上对应题号的答案标号涂黑。

3、考试结束后，请将本试卷和机读卡一并交回。

一．选择题：（本题10个小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1．－2013的绝对值是（ ）A ．2013B ．-2013C ．±2013D ．12013-答案：A解析：负数的绝对值是它的相反数，故选A 。

2．某中学在芦山地震捐款活动中，共捐款二十一万三千元。

这一数据用科学记数法表示为（ ）A ．321310⨯元 B ．42.1310⨯元 C ．52.1310⨯元 D ．60.21310⨯元 答案：C解析：科学记数法写成：10n a ⨯形式，其中110a ≤<，二十一万三千元＝213000＝52.1310⨯元3．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）答案：D解析：A 、C 只是轴对称图形，不是中心对称图形；B 是中心对称图形，不是轴对称轴图形，只有D 符合。

4．甲、乙、丙三家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%；乙超市连续两次降价15%；丙超市一次降价30%。

那么顾客到哪家超市购买这种商品更合算（ ）A ．甲B ．乙C ．丙D ．一样 答案：C解析：设原价a 元，则降价后，甲为：a （1－20%）（1－10%）＝0.72a 元，乙为：（1－15%）2a ＝0.7225a 元，丙为：（1－30%）a ＝0.7a 元，所以，丙最便宜。

5．下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序正确的是（ ）A ．（3）（1）（4）（2）B ．（3）（2）（1）（4）C ．（3）（4）（1）（2）D ．（2）（4）（1）（3） 答案：C解析：因为太阳从东边出来，右边是东，所以，早上的投影在左边，（3）最先，下午的投影在右边，（2）最后，选C 。

山东省济南市章丘区2024-2025学年上学期第一次质量检测九年级数学试卷一、单选题1．下列方程是关于x 的一元二次方程的是（ ）A ．20ax bx c ++=B ．2112x x +=C ．2221x x x +=-D ．23(1)2(1)x x +=+ 2．柜子里有2双鞋，随机取出两只刚好配成一双鞋的概率是（ ）A ．12B ．16C ．14 D ．133．用配方法解一元二次方程2870x x ++=，则方程可化为（ ）A ．2(4)9x -=B ．2(4)9x +=C ．2(8)23x +=D ．2(8)9x -= 4．如图，一条处处等宽的丝带部分重叠，则丝带重叠的部分一定是（ ）A ．正方形B ．矩形C ．菱形D ．都有可能 5．一个等腰三角形的两条边长分别是方程x 2﹣9x +18＝0的两根，则该等腰三角形的周长是（ ）A ．12B ．9C ．15D ．12或15 6．关于x 的一元二次方程2420kx x +-=有实数根，则k 的取值范围是（ ） A ．2k ≥- B ．2k >-且0k ≠ C ．2k ≥-且0k ≠ D ．2k ≤- 7．如图，在菱形ABCD 中，∠A=60°，AD=4，点P 是AB 边上的一个动点，点E 、F 分别是DP 、BP 的中点，则线段EF 的长为( )A ．2B ．4C ．D ．8．手卷是国画装裱中横幅的一种体式，以能握在手中顺序展开阅览得名，它主要由“引首”、“画心”、“拖尾”三部分组成（这三部分都是矩形形状），分隔这三部分的其余部分统称为“隔水”．如图，墨涵同学装裱了一幅《雀华秋色图》的手卷，手卷长1000厘米，宽40厘米．引首和拖尾完全相同，其宽度都为100厘米，若隔水的宽度为x 厘米，画心的面积为15200厘米2，根据题意，可列方程是（ ）A ．()()1000440215200x x --=B ．()()10002100240415200x x -⨯--=C ．()()10002100240215200x x -⨯--=D ．()()10002100440215200x x -⨯--=9．如图，下列四组条件中，能判定ABCD Y 是正方形的有( )①AB =BC ，∠A =90°；②AC ⊥BD ，AC =BD ；③OA =OD ，BC =CD ；④∠BOC =90°，∠ABD =∠DCAA ．1个B ．2个C ．3个D ．4个10．对于两个实数a ，b ，用()max ,a b 表示其中较大的数，则方程()max ,21x x x x ⨯-=+的解是（ ）A ．1，1B ．1，1C ．1-，1D ．1-，1二、填空题11．在某次试验数据整理过程中，某个事件发生的频率情况如表所示．估计这个事件发生的概率是（精确到0.01）．12．已知方程2560x x +-=的两个根分别为12,x x ，则1212x x x x ++的值为．13．直角三角形斜边的中线长是4cm ，则它的两条直角边中点的连线长为cm ．14．如图，菱形ABCD 的周长为26，对角线AC BD 、交于点O ，过A 作AE BC ⊥交CB 延长线于点E ，连接OE BD ，的长为5，则OE =．15．如图，E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE ＝DF ，AE 、BF 相交于点O ，下列结论：①AE ＝BF ；②AE ⊥BF ；③S △AOB ＝S 四边形DEOF ；④AO ＝OE ；⑤∠AFB ＋∠AEC ＝180°，其中正确的有（填写序号）．三、解答题16．解方程：(1)225x x -=；(2)215204x -+=；(3)()()2454x x +=+；(4)27120x x -+=17．如图，在菱形ABCD 中，点E F 、分别在BC CD 、边上，AEB AFD ∠=∠，求证：BE DF =．18．已知关于x 的方程220x ax a ++-=（1）当该方程的一个根为1时，求a 的值及该方程的另一根；（2）求证：不论a 取何实数，该方程都有两个不相等的实数根．19．如图，在ABC V 中，90BAC ∠=︒，AD 是中线，E 是AD 的中点，过点A 作AF ∥BC 交BE 的延长线于F ，连接CF ．(1)求证：BD AF =；(2)试判断四边形ADCF 的形状，并证明你的结论．20．端午节期间，某食品店平均每天可卖出300只粽子，卖出1只粽子的利润是1元，经调查发现，零售单价每降0.1元，每天可多卖出100只粽子，为了使每天获利的利润更多，该店决定把零售单价下降()01m m <<元．(1)零售单价下降m 元后，该店平均每天可卖出___________只粽子，利润为__________元．(2)不在考虑其他因素的条件下，当m 定为多少时，才能使该店每天获取的利润是420元并且卖出的粽子更多？21．有四张正面分别标有数字2，1，﹣3，﹣4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从四张卡片中随机地摸取一张不放回，将该卡片上的数字记为m ，再随机地摸取一张，将卡片上的数字记为n ．(1)请画出树状图并写出（m ，n ）所有可能的结果；(2)求所选出的m ，n 能使一次函数y =mx +n 的图象经过第二、三、四象限的概率． 22．如图，学校在教学楼后面搭建了两个简易的矩形自行车车棚，一边利用教学楼的后墙（可利用墙长为60m），其他的边用总长70m的不锈钢栅栏围成，左右两侧各开一个1m的出口后，不锈钢栅栏状如“山”字形．（备注信息：距院墙7米处，规划有机动车停车位）x，则车棚长度BC为_______m；(1)若设车棚宽度AB为m(2)若车棚面积为2285m，试求出自行车车棚的长和宽．(3)若学校拟利用现有栅栏对车棚进行扩建，请问能围成面积为2450m的自行车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由．23．在矩形ABCD中，已知5cm6cm，，点P从点A开始沿边AB向终点B以1cm/sAB BC==的速度运动；同时，点Q从点B开始沿边BC向终点C以2cm/s的速度运动．当点Q运动到点C时，两点停止运动．设运动时间为t秒．(1)分别用含t的代数式表示PB与BQ；(2)当t为何值时，PQ的长度等于5cm？(3)是否存在t的值，使得五边形APQCD的面积等于226cm？若存在，请求出此时t的值；若不存在，请说明理由．DE BE．24．如图1，四边形ABCD为正方形，E为对角线AC上一点，且不与点,A C重合，连接,(1)求证：BE DE=．D EE F为邻边作矩形DEFG，连接CG．(2)如图2，过点E作EF DE⊥，交边BC于点F，以,①求证：矩形DEFG是正方形；②若正方形ABCD 的边长为9,CG =DEFG 的边长．25．通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．原题：如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，试猜想EF 、BE 、DF 之间的数量关系．(1)思路梳理把ABE V 绕点A 逆时针旋转90°至ADG △，可使AB 与AD 重合，由90ADG B ∠=∠=︒，得180FDG ∠=︒，即点F 、D 、G 共线，易证AFG ≅△______，故EF 、BE 、DF 之间的数量关系为______．（要求写出必要的推理过程）(2)类比引申如图2，点E 、F 分别在正方形ABCD 的边CB 、DC 的延长线上，45EAF ∠=︒，连接EF ，试猜想EF 、BE 、DF 之间的数量关系为______，并给出证明．(3)联想拓展如图3，在ABC V 中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45BAD EAC ∠+∠=︒，若3BD =，6EC =，求DE 的长．。

一、选择题1．如图，根据ABC 的已知条件，按如下步骤作图：（1）以A 圆心，AB 长为半径画弧；（2）以C 为圆心，CB 长为半径画弧，两弧相交于点P ；（3）连接BP ，与AC 交于点O ，连接AP 、CP ．以下结论：①BP 垂直平分AC ；②AC 平分BAP ∠；③四边形ABCP 是轴对称图形也是中心对称图形；④ABC APC ≌△△，请你分析一下，其中正确的是（ ） A ．①④ B ．②③ C ．①③ D ．②④ 2．下列图形中既是轴对称图形，又是中心对称图形的是（ ）A ．B ．C ．D ．3．如图，在△ABC 中，AB=3，BC=5.2，∠B=60°，将△ABC 绕点A 逆时针旋转△ADE ，若点B 的对应点D 恰好落在BC 边上时，则CD 的长为( )A ．0.8B ．2C ．2.2D ．2.84．如图，将ABC 绕点C 逆时针旋转得到DEC ，若点D 刚好落在边AB 上，CB 与DE 交于点F ，120,20ACB E ∠=︒∠=︒，则ADC ∠的度数为（ ）A．40︒B．50︒C．55︒D．60︒5．下列图形是我国国产汽车的标识，在这四个汽车标识中，是中心对称图形的是（）A．B．C．D．6．下列图形中，是中心对称图形的有（）A．1个B．2个C．3个D．4个7．如图，点D是等腰直角三角形ABC内一点，AB=AC，若将△ABD绕点A逆时针旋转到△ACE的位置，则∠AED的度数为（）A．25°B．30°C．40°D．45°8．如图，把△ABC绕着点C顺时针旋转m°，得到△EDC，若点A、D、E在一条直线上，∠ACB=n°，则∠ADC的度数是（）A．190-2m n⎛⎫+︒⎪⎝⎭B．()m n-︒C．190-2n m⎛⎫+︒⎪⎝⎭D．()180n m--︒9．如图，已知ABC 和A B C '''关于点O 成中心对称，则下列结论错误的是（ ）．A ．ABC ABC '''∠=∠B ．AOB A OB ''∠=∠C ．AB A B ''=D ．OA OB '=10．下列图形中，是中心对称图形，但不是轴对称图形的是（ ）A ．B ．C ．D ． 11．将ABC ∆沿BC 方向平移3个单位得DEF ∆，若ABC ∆的周长等于20，则四边形ABFD 的周长为（ ）A ．28B ．26C ．24D ．20 12．在平面直角坐标系中，点(2,3)P -先向左平移3个单位，再向下平移2个单位，得到的（ ）A ．(4,1)-B ．()4,5-C ．(5,1)-D ．(1,1)二、填空题13．如图，在平面直角坐标系xOy 中，将四边形ABCD 先向下平移，再向右平移，得到四边形1111D C B A ，已知点()3,5A -，点()4,3B -，点()13,3A ，则点1B 的坐标为___．14．如图，在平面直角坐标系中，点A ，B ，C 的坐标分别为()0,1，()1,0，()1,0-，一个电动玩具从坐标原点O 出发，第一次跳跃到点1P ，使得点1P 与点O 关于点A 成中心对称；第二次跳跃到点2P ，使得点1P 与点2P 关于点B 成中心对称；第三次跳跃到点3P ，使得点3P 与点2P 关于点C 成中心对称，第四次跳跃到点4P ，使得点4P 与点3P 关于点A 成中心对称；第五次跳跃到点5P ，使得点5P 与点4P 关于点B 成中心对称……照此规律重复下去，则点2021P 的坐标为_________．15．如图，在△ABC 中，∠BAC ＝105°，将△ABC 绕点A 逆时针旋转得到△AB ′C ′．若点B 恰好落在BC 边上，且AB ′＝CB ′，则∠C ′的度数为_____°．16．如图，在△ABC 中，AB ＝4，BC ＝6，∠B ＝60°，将△ABC 沿射线BC 的方向平移2个单位后，得到A B C '''，连接A C '，则A B C ''的周长为________．17．如图，将直角三角形ABC 沿斜边AC 的方向平移到三角形DEF 的位置，DE 交BC 于点G ，BG ＝4，EF ＝12，△BEG 的面积为4，下列结论：①DE ⊥BC ；②△ABC 平移的距离是4；③AD ＝CF ；④四边形GCFE 的面积为20，其中正确的结论有________（只填写序号）．18．如图，将△ABC 沿BC 方向平移到△DEF ，若A 、D 间的距离为1，CE ＝2，则BF ＝_____．19．如图1，在ABC ∆中，AB=AC=4， 90,,BAC D E ︒∠=分别是边AB ，AC 的中点，保持ADE ∆不动，将ABC ∆从图1位置开始绕点A 顺时针旋转90度，旋转角小于90度，连接BD ，CE从下面A ，B 两题中任选一题作答，我选择____________题A ．如图2，当DB//AE 时，线段CE 的长为__________________；B ．如图3，当点B 在线段ED 的延长线上时，线段CE 的长为__________________；20．在 ABC 内的任意一点 ()P a b ， 经过平移后的对应点为 ()1P cd ，，已知 ()32A ， 在经过此次平移后对应点 1A 的坐标为 ()51-，，则 c d a b +-- 的值为________________．三、解答题21．通过类比联想、引申拓展研究典型题目，可以达到解一题知一类题的目的，下面是一个案例，请补充完整．原题；如图①，点E F 、分别在正方形ABCD 的边BC CD 、上，45EAF ∠=︒，连接EF ，则EF BE DF =+，试说明理由，（1）（思路梳理）∵AB AD =，∴把ABE △绕点A 逆时针旋转90︒至ADG ，可使AB 与AD 重合，∵90ADG B ∠=∠=︒，∴180FDG ∠=︒，即：点F D G 、、共线，根据“SAS ”，易证AFG ≌△_______，得EF FG BE DF ==+； （2）（类比引申）如图②，四边形ABCD 中，,90AB AD BAD =∠=︒，点E F 、分别在BC CD 、上，45EAF ∠=︒，若,B D ∠∠都不是直角，则当B 与D ∠满足等量关系__________时，仍有EF BE DF =+；（3）（联想拓展）如图③，在ABC 中，90,BAC AB AC ∠=︒=，点D E 、均在边BC 上，且45DAE ∠=︒，猜想,,BD DE EC 应满足的等量关系，并写出推理过程．22．如图，ABC 是等边三角形，点D 在AC 边上，将BCD △绕点C 旋转得到ACE △，连接DE ．（1）求证：//DE BC ．（2）若8AB =，7BD =，求ADE 的周长．23．如图，在平面直角坐标系中，ABC 三个顶点的坐标分别是A （2，4），B （1，2），C （5，3）．（1）作出ABC 关于点O 对称的图形111A B C △；（2）以点O 为旋转中心，将ABC 顺时针旋转90°，得到222A B C △，在坐标系中画出222A B C △．24．如图，在边长为8的等边ABC 中，点D 是AB 的中点，点E 是平面上一点，且线段2DE =，将线段EB 绕点E 顺时针旋转60°得到线段EF ，连接AF ．（1）如图1，当2BE =时，求线段AF 的长；（2）将线段BE 绕点B 旋转得到图2，求证：AF CE =．25．已知：点A 、B 在平面直角坐标系中的位置如图所示，则：（1）写出这两点坐标：A_______，B________；（2）点A 平移到点（0，-1），请说出是怎样平移的，并写出点B 平移后的坐标． （3）求△AOB 的面积．26．如图，Rt ABC △中，90C ∠=︒，AC BC =，ABC 绕点A 逆时针旋转45°得到ADE （B ，D 两点为对应点）．（1）画出旋转后的图形；（2）连接BD ，求BDE ∠的度数．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】由题意得：AB=AP ，CB=CP ，从而可判断①；根据等腰三角形的性质，可判断②；根据轴对称和中心对称图形的定义，可判断③；根据SSS ，可判断④．【详解】由题意得：AB=AP ，CB=CP ，∴点A 、C 在BP 的垂直平分线上，即：AC 垂直平分BP ，故①错误；∵AB=AP ，AC ⊥BP ，∴AC 平分BAP ∠，故②正确；∵AC 垂直平分BP ，∴点B 、P 关于直线AC 对称，即：四边形ABCP 是轴对称图形，但不是中心对称图形，故③错误；∵AB=AP ，CB=CP ，AC=AC ，∴ABC APC ≌△△，故④正确；故选D ．【点睛】本题主要考查垂直平分线的判定定理。

专题03 半角模型半角模型：是指有公共顶点，锐角等于较大的角的一半，且较大的角的两边相等(不等)，通过旋转，可将角进行等量转化，构造全等（相似）的三角形的几何模型。

主要解法：一、经典之旋转法。

二、创新之翻折法。

三、常规之补短法。

熟练掌握：正方形的10个结论。

学会变通：矩形通过截或补变成正方形。

含60°角的菱形除旋转外，还可以借助对角线，构成等边三角形，利用三边相等，构造全等。

模型总讲:如图，已知在正方形ABCD 中，∠EAF =45°，连接BD 与AM ，AN 分别交于E 、F 两点。

1. BE+DF=EF ；2. △CEF 的周长等于正方形的边长的2倍。

3. S △ABE +S △ADF =S △AEF4. 点A 到MN 的距离等于正方形的边长；即AH=AD5. MN 2=MB 2+DN 2；6. 点A,M,F,D 四点共圆。

点A,B,E,N 四点共圆. 点M,E,F,N四点共圆。

点N,F,C,E,M 五点共圆。

7. 证明△AFM 和△AEN 为等腰直角三角形。

8.MN EF=√229. S △AMF =2S △AEF 10. 5组相似△HMN ∼△DFN(图9) △HMN ∼△BME(图10) △AMN ∼△BNA(图11) △AMN ∼△DMA(图12) △ AMN∽△ AFE证明如下: 结论1(图1)将△ABE 逆时针旋转90°，与△ADE'重合. 则AE=AE', ∠BAE=∠DAE’,易得 ∠EAF=∠E'AF=45° 又∵ AF=AF∴△EAF ≌ △E'AF （SAS ）(图2) ∴EF=E'F=DE'+DF ∴BE+DF=EF(结论1成立) 结论2 由结论1可得:AO HN M EBCD FAE'OEBCD F图1C △CEF =CE+CF+EF= CE+CF+BE+DF=BC+CD=2BC即△CEF 的周长等于正方形的边长的2倍。

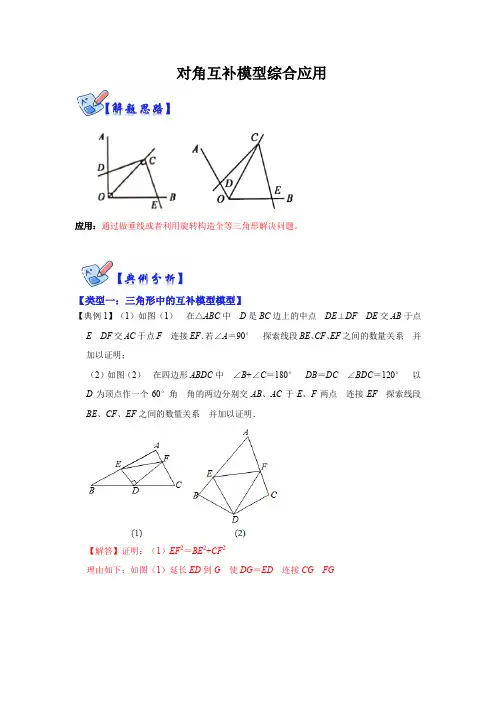
对角互补模型综合应用应用：通过做垂线或者利用旋转构造全等三角形解决问题。

【类型一：三角形中的互补模型模型】【典例1】（1）如图（1）在△ABC中D是BC边上的中点DE⊥DF DE交AB于点E DF交AC于点F连接EF．若∠A＝90°探索线段BE、CF、EF之间的数量关系并加以证明；（2）如图（2）在四边形ABDC中∠B+∠C＝180°DB＝DC∠BDC＝120°以D为顶点作一个60°角角的两边分别交AB、AC于E、F两点连接EF探索线段BE、CF、EF之间的数量关系并加以证明．【解答】证明：（1）EF2＝BE2+CF2理由如下：如图（1）延长ED到G使DG＝ED连接CG FG在△DCG与△DBE中∴△DCG≌△DBE（SAS）∴DG＝DE CG＝BE∠B＝∠DCG又∵DE⊥DF∴FD垂直平分线段EG∴FG＝FE∵∠A＝90°∴∠B+∠ACB＝90°∴∠FCG＝90°在△CFG中CG2+CF2＝FG2∴EF2＝BE2+CF2（2）如图（2）结论：EF＝EB+FC理由如下：延长AB到M使BM＝CF∵∠ABD+∠C＝180°又∠ABD+∠MBD＝180°∴∠MBD＝∠C在△BDM和△CDF中∴△BDM≌△CDF（SAS）∴DM＝DF∠BDM＝∠CDF∴∠EDM＝∠EDB+∠BDM＝∠EDB+∠CDF＝∠CDB﹣∠EDF＝120°﹣60°＝60°＝∠EDF在△DEM和△DEF中∴△DEM≌△DEF（SAS）∴EF＝EM∴EF＝EM＝BE+BM＝EB+CF．【变式1】（1）阅读理解：如图①在△ABC中若AB＝5 AC＝3 求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE＝AD再连接BE这样就把AB AC2AD集中在△ABE中利用三角形三边的关系可判断线段AE的取值范围是；则中线AD的取值范围是；（2）问题解决：如图②在△ABC中D是BC边的中点DE⊥DF于点D DE交AB于点E DF交AC于点F连接EF此时：BE+CF EF（填“＞”或“＝”或“＜”）；（3）问题拓展：如图③在四边形ABCD中∠B+∠D＝180 CB＝CD∠BCD＝140°以C为顶点作∠ECF＝70°边CE CF分别交AB AD于E F两点连接EF此时：BE+DF EF（填“＞”或“＝”或“＜“）；（4）若在图③的四边形ABCD中∠ECF＝α（0°＜α＜90°）∠B+∠D＝180 CB ＝CD且（3）中的结论仍然成立则∠BCD＝（用含α的代数式表示）.【解答】解：（1）在△ADC与△EDB中∴△ADC≌△EDB（SAS）∴BE＝AC＝3在△ABE中AB﹣BE＜AE＜AB+BE即2＜AE＜8∴2＜2AD＜8∴1＜AD＜4故答案为：2＜AE＜8；1＜AD＜4；（2）如图延长FD至点G使DG＝DF连接BG EG∵点D是BC的中点∴DB＝DC∵∠BDG＝∠CDF DG＝DF∴△BDG≌△CDF（SAS）∴BG＝CF∵ED⊥FD FD＝GD∴EF＝EG在△BEG中BE+BG＞EG∴BE+CF＞EF故答案为：＞；（3）BE+DF＝EF如图延长AB至点G使BG＝DF连接CG∵∠ABC+∠D＝180°∠ABC+∠CBG＝180°∴∠CBG＝∠D又∵CB＝CD BG＝DF∴△CBG≌△CDF（SAS）∴CG＝CF∠BCG＝∠DCF∵∠BCD＝140°∠ECF＝70°∴∠DCF+∠BCE＝70°∴∠BCE+∠BCG＝70°∴∠ECG＝∠ECF＝70°又∵CE＝CE CG＝CF∴△ECG≌△ECF（SAS）∴EG＝EF∵BE+BG＝EG∴BE+DF＝EF故答案为：＝；（4）由（3）同理可得△CBG≌△CDF∴CG＝CF∠BCG＝∠DCF若BE+DF＝EF则EG＝EF∴△ECF≌△ECG（SSS）∴∠ECG＝∠ECF∴∠BCD＝2∠ECF＝2α故答案为：2α．【类型二：四边形中的互补模型】【典例2】（1）如图1 四边形ABCD是边长为5 cm的正方形E F分别在AD CD边上∠EBF＝45°．为了求出△DEF的周长．小南同学的探究方法是：如图2 延长EA到H使AH＝CF连接BH先证△ABH≌△CBF再证△EBH≌△EBF得EF＝EH从而得到△DEF的周长＝cm；（2）如图3 在四边形ABCD中AB＝AD∠BAD＝100°∠B＝∠ADC＝90°．E F 分别是线段BC CD上的点．且∠EAF＝50°．探究图中线段EF BE FD之间的数量关系；（3）如图4 若在四边形ABCD中AB＝AD∠B+∠D＝180°E F分别是线段BC CD上的点且2∠EAF＝∠BAD（2）中的结论是否仍然成立若成立请证明若不成立请说明理由；（4）若在四边形ABCD中AB＝AD∠B+∠D＝180°点E、F分别在CB、DC的延长线上且2∠EAF＝∠BAD请画出图形并直接写出线段EF、BE、FD之间的数量关系．【解答】解：（1）如图1 延长EA到H使AH＝CF连接BH∵四边形ABCD是正方形∴AB＝BC＝AD＝CD＝5cm∠BAD＝∠BCD＝90°∴∠BAH＝∠BCF＝90°又∵AH＝CF AB＝BC∴△ABH≌△CBF（SAS）∴BH＝BF∠ABH＝∠CBF∵∠EBF＝45°∴∠CBF+∠ABE＝45°＝∠HBA+∠ABE＝∠EBF∴∠EBH＝∠EBF又∵BH＝BF BE＝BE∴△EBH≌△EBF（SAS）∴EF＝EH∴EF＝EH＝AE+CF∴△DEF的周长＝DE+DF+EF＝DE+DF+AE+CF＝AD+CD＝10（cm）．故答案为：10．（2）EF＝BE+DF．证明：如图2所示延长FD到点G．使DG＝BE．连接AG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠BAD＝100°∠EAF＝50°∴∠BAE+∠F AD＝∠DAG+∠F AD＝50°∴∠EAF＝∠F AG＝50°在△EAF和△GAF中∴△EAF≌△GAF（SAS）∴EF＝FG＝DF+DG∴EF＝BE+DF；（3）成立．证明：如图3 延长EB到G使BG＝DF连接AG．∵∠ABC+∠D＝180°∠ABG+∠ABC＝180°∴∠ABG＝∠D∵在△ABG与△ADF中∴△ABG≌△ADF（SAS）∴AG＝AF∠BAG＝∠DAF∵2∠EAF＝∠BAD∴∠DAF+∠BAE＝∠BAG+∠BAE＝∠BAD＝∠EAF ∴∠GAE＝∠EAF又AE＝AE∴△AEG≌△AEF（SAS）∴EG＝EF∵EG＝BE+BG∴EF＝BE+FD；（4）EF＝DF﹣BE理由如下：在DF上截取DH使DH＝BE∵∠ABC+∠ADC＝180°∠ABC+∠ABE＝180°∴∠ABE＝∠ADH且AB＝AD DH＝BE∴△ABE≌△ADH（SAS）∴∠BAE＝∠DAH AH＝AE∵∠EAF＝∠BAD∴∠DAH+∠BAF＝∠BAD∴∠HAF＝∠BAD＝∠EAF且AF＝AF AE＝AH∴△F AH≌△F AE（SAS）∴HF＝EF∴EF＝HF＝DF﹣DH＝DF﹣BE【变式2-1】如图在四边形ABCD中AB＝AD∠B+∠D＝180°E F分别是边BC CD上的点且∠EAF＝∠BAD求证：EF＝BE+FD．【解答】证明：延长CB至M使BM＝FD连接AM如图所示：∵∠ABC+∠D＝180°∠ABM+∠ABC＝180°∴∠ABM＝∠D在△ABM与△ADF中∴△ABM≌△ADF（SAS）∴AF＝AM∠BAM＝∠DAF∵∠EAF＝∠BAD∴∠DAF+∠BAE＝∠BAD＝∠F AE∴∠BAM+∠BAE＝∠EAF即∠MAE＝∠EAF在△AME与△AFE中∴△AME≌△AFE（SAS）∴EF＝ME∵ME＝BE+BM∴EF＝BE+FD．【变式2-2】“截长补短法”证明线段的和差问题：先阅读背景材料猜想结论并填空然后做问题探究．背景材料：（1）如图1：在四边形ABCD中AB＝AD∠BAD＝120°∠B＝∠ADC＝90°E F 分别是BC CD上的点且∠EAF＝60°．探究图中线段BE EF FD之间的数量关系．探究的方法是延长FD到点G．使DG＝BE连接AG先证明△ABE≌△ADG再证明△AEF≌△AGF可得出的结论是．探索问题：（2）如图2 若四边形ABCD中AB＝AD∠B+∠D＝180°E F分别是BC CD 上的点且∠EAF＝∠BAD上述结论是否仍然成立？成立的话请写出推理过程．【解答】证明：（1）在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠EAF＝∠BAD∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF∴∠EAF＝∠GAF在△AEF和△GAF中∴△AEF≌△AGF（SAS）∴EF＝FG∵FG＝DG+DF＝BE+DF∴EF＝BE+DF；故答案为：EF＝BE+DF．（2）解：结论EF＝BE+DF仍然成立；理由：延长FD到点G．使DG＝BE．连接AG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠EAF＝∠BAD∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF ∴∠EAF＝∠GAF在△AEF和△GAF中∴△AEF≌△AGF（SAS）∴EF＝FG∵FG＝DG+DF＝BE+DF∴EF＝BE+DF．1．阅读理解：课外兴趣小组活动时老师提出了如下问题：如图1 △ABC中若AB＝5 AC＝3 求BC边上的中线AD的取值范围．小明在组内经过合作交流得到了如下的解决方法：延长AD到E使得DE＝AD再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD）把AB、AC、2AD集中在△ABE中利用三角形的三边关系可得2＜AE＜8 则1＜AD＜4．感悟：解题时条件中若出现“中点”“中线”字样可以考虑构造以中点为对称中心的中心对称图形把分散的已知条件和所求证的结论集中到同一个三角形中．（1）问题解决：受到（1）的启发请你证明下面命题：如图2 在△ABC中D是BC边上的中点DE ⊥DF DE交AB于点E DF交AC于点F连接EF．①求证：BE+CF＞EF；②若∠A＝90°探索线段BE、CF、EF之间的等量关系并加以证明；（2）问题拓展：如图3 在四边形ABDC中∠B+∠C＝180°DB＝DC∠BDC＝120°以D为顶点作一个60°角角的两边分别交AB、AC于E、F两点连接EF探索线段BE、CF、EF之间的数量关系并加以证明．【解答】解：①延长FD到G使得DG＝DF连接BG、EG．（或把△CFD绕点D逆时针旋转180°得到△BGD）∴CF＝BG DF＝DG∵DE⊥DF∴EF＝EG．在△BEG中BE+BG＞EG即BE+CF＞EF．（4分）②若∠A＝90°则∠EBC+∠FCB＝90°由①知∠FCD＝∠DBG EF＝EG∴∠EBC+∠DBG＝90°即∠EBG＝90°∴在Rt△EBG中BE2+BG2＝EG2∴BE2+CF2＝EF2；（3分）（2）将△DCF绕点D逆时针旋转120°得到△DBG．∵∠C+∠ABD＝180°∠4＝∠C∴∠4+∠ABD＝180°∴点E、B、G在同一直线上．∵∠3＝∠1 ∠BDC＝120°∠EDF＝60°∴∠1+∠2＝60°故∠2+∠3＝60°即∠EDG＝60°∴∠EDF＝∠EDG＝60°∵DE＝DE DF＝DG∴△DEG≌△DEF∴EF＝EG＝BE+BG即EF＝BE+CF．（4分）2．如图△ABC中AB＝AC点D为△ABC内一点其中AD平分∠BAC且∠CBD＝30°点E为AC中点EF⊥AC交BD延长线于点F连接AF、CF．（1）求∠ADF的大小；（2）求证：△ACF是等边三角形；（3）猜想AD、BD、DF的数量关系并说明理由．【解答】解：（1）延长AD交BC于点M∵AB＝AC AD平分∠BAC∴AM⊥BC∵∠CBD＝30°∴∠BDM＝90°﹣∠CBD＝60°∴∠ADF＝∠BDM＝60°；（2）由（1）知∠ADC＝∠BDC＝120°∵∠ADF＝60°∴∠CDF＝60°过点F作FG⊥AD于点G FH⊥DC于点H∴FG＝FH∵EF⊥AC E为AC的中点∴AF＝CF在Rt△AGF和Rt△CHF中∴Rt△AGF≌Rt△CHF（HL）∴∠AFG＝∠CFH∵∠DGF＝∠H＝90°∠DGF+∠H+∠GDH+∠GFH＝360°∴∠GDH+∠GFH＝180°∵∠GDH＝120°∴∠GFH＝60°∴∠AFC＝∠AFG+∠GFC＝∠CFH+∠GFC＝60°又∵AF＝CF∴△ACF为等边三角形；（3）DF＝AD+BD．理由：在BF上截取PF＝BD连接AP∵△ACF为等边三角形∴AF＝AC又∵AF＝AC∴AB＝AF∴∠ABD＝∠AFP∴△ABD≌△AFP（SAS）∴AD＝AP又∵∠ADP＝60°∴△ADP为等边三角形∴AD＝DP∴DF＝DP+PF＝AD+BD．3．（1）问题背景．如图1 在四边形ABCD中AB＝AD∠B+∠D＝180°E、F分别是线段BC、线段CD上的点．若∠BAD＝2∠EAF试探究线段BE、EF、FD之间的数量关系．小明同学探究此问题的方法是延长FD到点G．使DG＝BE．连接AG先证明△ABE ≌△ADG．再证明△AEF≌△AGF可得出结论他的结论应是．（2）猜想论证．如图2 在四边形ABCD中AB＝AD∠B+∠ADC＝180°E在线段BC上、F在线段CD延长线上．若∠BAD＝2∠EAF上述结论是否依然成立？若成立说明理由；若不成立试写出相应的结论并给出你的证明．【解答】解：延长FD到点G．使DG＝BE连接AG∵∠B+∠ADF＝180°∠ADF+∠ADG＝180°∴∠ADG＝∠B在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠BAD＝2∠EAF∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF∴∠EAF＝∠GAF在△AEF和△AGF中∴△AEF≌△AGF（SAS）∴EF＝FG∵FG＝DG+DF＝BE+DF∴EF＝BE+DF；故答案为：EF＝BE+DF．（2）结论EF＝BE+FD不成立结论：EF＝BE﹣FD．理由如下：证明：如图2中在BE上截取BG使BG＝DF连接AG．∵∠B+∠ADC＝180°∠ADF+∠ADC＝180°∴∠B＝∠ADF．∵在△ABG与△ADF中∴△ABG≌△ADF（SAS）．∴∠BAG＝∠DAF AG＝AF．∴∠BAD＝∠BAG+∠GAD＝∠DAF+∠GAD＝∠GAF．∵∠BAD＝2∠EAF∴∠GAF＝2∠EAF∴∠GAE＝∠EAF．∵AE＝AE∴△AEG≌△AEF（SAS）．∴EG＝EF∵EG＝BE﹣BG∴EF＝BE﹣FD4．通过类比联想引申拓展研究典型题目可达到解一题知一类的目的下面是一个案例请补充完整．原题：如图1 点E、F分别在正方形ABCD的边DC、BC上∠EAF＝45°连接EF试猜想EF、BF、DE之间的数量关系．（1）思路梳理把△ADE绕点A顺时针旋转90°至△ABG可使AD与AB重合由∠ABG＝∠D＝90°得∠FBG＝180°即点F、B、G共线易证△AFG≌故EF、BF、DE之间的数量关系为．（2）类比引申如图②在四边形ABCD中AB＝AD∠ABC＝∠ADC＝90°．E、F分别是DC、BC 上的点．且∠EAF＝∠BAD．猜想图中线段BF、EF、DE之间的数量关系．（3）拓展提高如图③若在四边形ABCD中AB＝AD∠B+∠D＝180°．E、F分别是BC、CD上的点且∠EAF＝∠BAD探究上述结论是否仍然成立？说明理由．【解答】解：（1）思路梳理：如图①把△ADE绕点A顺时针旋转90°至△ABG可使AD与AB重合即AB＝AD 由旋转得：∠ABG＝∠D＝90°DE＝BG∠1＝∠2 AE＝AG∴∠FBG＝∠ABF+∠ABG＝90°+90°＝180°即点F、B、G共线∵四边形ABCD为正方形∴∠BAD＝90°∵∠EAF＝45°∴∠DAE+∠B＝∠F AG＝45°∴∠EAF＝∠F AG＝45°在△AFE和△AFG中∴△AFE≌△AFG（SAS）∴EF＝FG∴EF＝BF+BG＝BF+DE；故答案为：△AFE EF＝BF+DE；（2）类比引申如图②把△ADE绕点A顺时针旋转90°至△ABG可使AD与AB重合即AB＝AD 由旋转得：∠ABG＝∠D＝90°DE＝BG∠GAB＝∠DAE AE＝AG∴∠FBG＝∠ABF+∠ABG＝90°+90°＝180°即点F、B、G共线∵∠EAF＝∠BAD∴∠DAE+∠BAF＝BAD∴∠GAF＝∠EAF在△AFE和△AFG中∴△AFE≌△AFG（SAS）∴EF＝FG∴EF＝BF+BG＝BF+DE；（3）拓展提高结论DE+BF＝EF仍然成立理由如下：如图③将△ADE绕点A顺时针旋转90°得到△ABH由旋转可得AH＝AE BH＝DE∠1＝∠2∵∠EAF＝∠DAB∴∠HAF＝∠1+∠3＝∠2+∠3＝∠BAD∴∠HAF＝∠EAF∵∠ABH+∠ABF＝∠D+∠ABF＝180°∴点H、B、F三点共线在△AEF和△AHF中∴△AEF≌△AHF（SAS）∴EF＝HF∵HF＝BH+BF∴EF＝DE+BF．5．如图1 在四边形ABCD中AB＝AD∠BAD＝120°∠B＝∠ADC＝90°EF分别是BC CD上的点且∠EAF＝60°探究图中线段BE EF FD之间的数量关系．（1）提示：探究此问题的方法是延长FD到点G使DG＝BE连接AG先证明△ABE ≌△ADG再证明△AEF≌△AGF．请根据提示按照提示的方法完成探究求解过程．（2）探索延伸：如图2 若在四边形ABCD中AB＝AD∠B+∠D＝180°E F分别是BC CD上的点且∠EAF＝∠BAD上述结论是否仍然成立？（成立或不成立）（3）实际应用：如图3 在某次军事演习中舰艇甲在指挥中心（O处）北偏西30°的A处舰艇乙在指挥中心南偏东70°的B处并且两舰艇到指挥中心的距离相等．接到行动指令后舰艇甲向正东方向以60海里/小时的速度前进舰艇乙沿北偏东50°的方向以80海里/小时的速度前进 1.5小时后指挥中心观测到甲、乙两舰艇分别到达E F处且两舰艇之间夹角为70°试求此时两舰艇之间的距离．【解答】解：（1）EF＝BE+DF．理由如下：如图1 延长FD到G使DG＝BE连接AG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠EAF＝∠BAD∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF∴∠EAF＝∠GAF在△AEF和△GAF中∴△AEF≌△GAF（SAS）∴EF＝FG∵FG＝DG+DF＝BE+DF∴EF＝BE+DF；（2）EF＝BE+DF仍然成立．证明：如图2 延长FD到G使DG＝BE连接AG∵∠B+∠ADC＝180°∠ADC+∠ADG＝180°∴∠B＝∠ADG在△ABE和△ADG中∴△ABE≌△ADG（SAS）∴AE＝AG∠BAE＝∠DAG∵∠EAF＝∠BAD∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF ∴∠EAF＝∠GAF在△AEF和△GAF中∴△AEF≌△GAF（SAS）∴EF＝FG∵FG＝DG+DF＝BE+DF∴EF＝BE+DF；故答案是：成立；（3）如图3 连接EF延长AE、BF相交于点C∵∠AOB＝30°+90°+（90°﹣70°）＝140°∠EOF＝70°∴∠EOF＝∠AOB又∵OA＝OB∠OAC+∠OBC＝（90°﹣30°）+（70°+50°）＝180°∴符合探索延伸中的条件∴结论EF＝AE+BF成立即EF＝1.5×（60+80）＝210（海里）．答：此时两舰艇之间的距离是210海里．6．在四边形ABCD中AB＝AD∠B＝∠D＝90°∠BCD＝120°现将一个30°角的顶点落在点A处．（1）如图①当该角的两边分别与BC、CD边相交于E、F时．求证：EF＝BE+DF；（2）现在将该角绕点A进行旋转其两边分别与BC、CD边的延长线相交于点F那么（1）中的结论是否仍然成立？若成立说明理由；若不成立试探究线段BE与DF之间的等量关系并加以证明．（利用图②进行探索）【解答】解：（1）如图①延长CB到H点使BH＝DF连接AH∵∠B＝∠D＝90°∠BCD＝120°∴∠D+∠B＝180°∵∠ABE+∠ABH＝180°∴∠ABH＝∠D∵AD＝AB BH＝DF∴在△ABH和△ADF中∴△ABH≌△ADF（SAS）∴AH＝AF∠HAB＝∠F AD∵∠DAB＝60°∠F AE＝30°∴∠F AD+∠BAE＝30°∴∠BAE+∠HAB＝30°即∠HAE＝30°在△HAE和△EAF中∴△HAE≌△F AE（SAS）∴HE＝EF∵HE＝HB+BE＝DF+BE∴EF＝BE+DF；（2）（1）中的结论不成立如图②在BC上截取BH＝DF在△ABH与△ADF中∴△ABH≌△ADF∴∠BAH＝∠DAF AH＝AF∴∠EAF＝30°∴∠BAH+∠EAD＝30°∵∠B＝∠D＝90°∠BCD＝120°∴∠BAD＝60°∴∠HAE＝30°在△HAE与△F AE中∴△HAE≌△F AE∴HE＝EF∵BE＝BH+HE∴BE＝DF+EF．7．【初步探索】（1）如图1：在四边形ABCD中AB＝AD∠B＝∠ADC＝90°E、F分别是BC、CD 上的点且EF＝BE+FD探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G使DG＝BE．连接AG先证明△ABE ≌△ADG再证明△AEF≌△AGF可得出结论他的结论应是；【灵活运用】（2）如图2 若在四边形ABCD中AB＝AD∠B+∠D＝180°．E、F分别是BC、CD 上的点且EF＝BE+FD上述结论是否仍然成立并说明理由；【拓展延伸】（3）如图3 已知在四边形ABCD中∠ABC+∠ADC＝180°AB＝AD若点E在CB 的延长线上点F在CD的延长线上如图3所示仍然满足EF＝BE+FD请写出∠EAF与∠DAB的数量关系并给出证明过程．【解答】解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1 延长FD到点G使DG＝BE连接AG根据SAS可判定△ABE≌△ADG进而得出∠BAE＝∠DAG AE＝AG再根据SSS可判定△AEF≌△AGF可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立理由：如图2 延长FD到点G使DG＝BE连接AG∵∠B+∠ADF＝180°∠ADG+∠ADF＝180°∴∠B＝∠ADG又∵AB＝AD∴△ABE≌△ADG（SAS）∴∠BAE＝∠DAG AE＝AG∵EF＝BE+FD＝DG+FD＝GF AF＝AF∴△AEF≌△AGF（SSS）∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3 在DC延长线上取一点G使得DG＝BE连接AG ∵∠ABC+∠ADC＝180°∠ABC+∠ABE＝180°∴∠ADC＝∠ABE又∵AB＝AD∴△ADG≌△ABE（SAS）∴AG＝AE∠DAG＝∠BAE∵EF＝BE+FD＝DG+FD＝GF AF＝AF∴△AEF≌△AGF（SSS）∴∠F AE＝∠F AG∵∠F AE+∠F AG+∠GAE＝360°∴2∠F AE+（∠GAB+∠BAE）＝360°∴2∠F AE+（∠GAB+∠DAG）＝360°即2∠F AE+∠DAB＝360°∴∠EAF＝180°﹣∠DAB．。

yBE AFNx关于二次函数的压轴题一、抛物线关于三角形面积问题例题 二次函数 y = (x + m )2 + k 的图象，其顶点坐标为 M(1， -4 ).（1） 求出图象与 x 轴的交点 A ，B 的坐标；（2） 在二次函数的图象上是否存在点 P ，使S请说明理由；∆PAB= 5 S4∆MAB ,若存在，求出 P 点的坐标；若不存在， （3） 将二次函数的图象在 x 轴下方的部分沿 x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线 y = x + b (b < 1) 与此图象有两个公共点时， b 的取值范围.练习： 1.如图．平面直角坐标系 xOy 中，点 A 的坐标为（－2，2），点 B 的坐标为（6，6），抛物线经过 A 、O 、B 三点，线段 AB 交 y 轴与点 E ．（1） 求点 E 的坐标； （2） 求抛物线的函数解析式；（3） 点 F 为线段 OB 上的一个动点（不与 O 、B 重合），直线 EF 与抛物线交与 M 、N 两点（点N 在 y 轴右侧），连结 ON 、BN ，当点 F 在线段 OB 上运动时，求∆ BON 的面积的最大值，并求出此时点 N 的坐标；xAOEQ P F y B2. 如图，已知抛物线 y = - 1x 2 + x + 4 交 x 轴的正半轴于点 A ，交 y 轴于点 B ．2（1） 求 A 、B 两点的坐标，并求直线 AB 的解析式；（2） 设 P (x , y ) （ x > 0 ）是直线 y = x 上的一点，Q 是 OP 的中点（O 是原点），以 PQ 为对角线作正方形 PEQF ．若正方形 PEQF 与直线 AB 有公共点，求 x 的取值范围；（3） 在（2）的条件下，记正方形 PEQF 与△OAB 公共部分的面积为 S ，求 S 关于 x 的函数解析式，并探究 S 的最大值．二、抛物线中线段长度最小问题例题如图，对称轴为直线 x ＝－1 的抛物线 y ＝ax 2＋bx ＋c (a ≠0)与 x 轴相交于 A 、B 两点，其中点 A 的坐标为（－3，0）．（1） 求点 B 的坐标；（2） 已知 a =1，C 为抛物线与 y 轴的交点．①若点 P 在抛物线上，且 S △POC ＝4S △BOC ，求点 P 的坐标；②设点 Q 是线段 AC 上的动点，作 QD ⊥x 轴，QD 交抛物线于点 D ，求线段 QD 长度的最大值．yBCN MAODEx练习：1. 如图， Rt △ABO 的两直角边 OA 、OB 分别在 x 轴的负半轴和 y 轴的正半轴上，O 为坐标原点， A 、B 两点的坐标分别为（ -3 ，0）、（0，4），抛物线 y = 2x 2 + bx + c 经过 B 点，且顶点在直线3 x =5 上．2（1） 求抛物线对应的函数关系式；（2） 若△DCE 是由△ABO 沿 x 轴向右平移得到的，当四边形 ABCD 是菱形时，试判断点 C 和点D 是否在该抛物线上，并说明理由；（3） 若 M 点是 CD 所在直线下方该抛物线上的一个动点，过点 M 作 MN 平行于 y 轴交 CD 于点N ．设点 M 的横坐标为 t ，MN 的长度为 l ．求 l 与 t 之间的函数关系式，并求 l 取最大值时，点 M 的坐标．三、抛物线与线段和最小的问题例题 如图，已知抛物线 y = 1(x - 2)(x + a )(a > 0)与 x 轴交于点 B 、C ，与 y 轴交于点 E ，且点 Ba在点 C 的左侧．（1） 若抛物线过点 M （﹣2，﹣2），求实数 a 的值； （2） 在（1）的条件下，解答下列问题；①求出△BCE 的面积；②在抛物线的对称轴上找一点 H ，使 CH+EH 的值最小，直接写出点 H 的坐标．练习：1.如图，已知二次函数y =ax2- 4x +c 的图象与坐标轴交于点A（-1，0）和点B（0，-5）．（1）求该二次函数的解析式；（2）已知该函数图象的对称轴上存在一点P，使得△ABP 的周长最小．请求出点P 的坐标．2.如图，抛物线y = ax2 + bx + 4 与x 轴的两个交点分别为A（－4，0）、B（2，0），与y 轴交于点C，顶点为D．E（1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F、G．（1）求抛物线的函数解析式，并写出顶点D 的坐标；（2）在直线EF 上求一点H，使△CDH 的周长最小，并求出H 的坐标；（3）若点K 在x 轴上方的抛物线上运动，当K 运动到什么位置时，△EFK 的面积最大？并求出最大面积．四、抛物线与等腰三角形例题：已知抛物线y＝ax2＋bx＋c 经过A(－1，0)、B(3，0)、C(0，3)三点，直线l 是抛物线的对称轴．(1)求抛物线的函数关系式；(2)设点P 是直线l 上的一个动点，当△PAC 的周长最小时，求点P 的坐标；(3)在直线l 上是否存在点M，使△MAC 为等腰三角形？若存在，直接写出所有符合条件的点M 的坐标；若不存在，请说明理由．练习：1..如图，抛物线与x 轴交于A、B 两点，与y 轴交C 点，点A 的坐标为（2，0），点C 的坐标为1（0，3）它的对称轴是直线x =-2（1）求抛物线的解析式；（2）M 是线段AB 上的任意一点，当△MBC 为等腰三角形时，求M 点的坐标．2.如图，在平面直角坐标系中，点A 的坐标为（m，m），点B 的坐标为（n，﹣n），抛物线经过A、O、B 三点，连接OA、OB、AB，线段AB 交y 轴于点C．已知实数m、n（m＜n）分别是方程x2﹣2x﹣3=0 的两根．（1）求抛物线的解析式；（2）若点P 为线段OB 上的一个动点（不与点O、B 重合），直线PC 与抛物线交于D、E 两点（点D 在y 轴右侧），连接OD、BD．①当△OPC 为等腰三角形时，求点P 的坐标；②求△BOD 面积的最大值，并写出此时点D 的坐标．3.如图1，在直角坐标系中，已知△AOC 的两个顶点坐标分别为A（2，0），C（0，2）．（1）请你以AC 的中点为对称中心，画出△AOC 的中心对称图形△ABC，此图与原图组成的四边形OABC 的形状是，请说明理由；（2）如图2，已知D（ 1，0），过A，C，D 的抛物线与（1）所得的四边形OABC 的边BC 交2于点E，求抛物线的解析式及点 E 的坐标；（3）在问题（2）的图形中，一动点P 由抛物线上的点A 开始，沿四边形OABC 的边从A﹣B ﹣C 向终点C 运动，连接OP 交AC 于N，若P 运动所经过的路程为x，试问：当x 为何值时，△AON 为等腰三角形（只写出判断的条件与对应的结果）？4.如图，已知抛物线于x 轴交于A（－1，0）、B（3，0）两点，与y 轴交于点C（0，3）.（1）求抛物线的解析式；（2）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC 是等腰三角形，若存在，求出符合条件的点P 的坐标；若不存在，请说明理由：（3）若点M 是抛物线上一点，以B、C、D、M 为顶点的四边形是直角梯形，试求出点M 的坐标。

通过类比联想引申拓展研究典型题目通过类比联想引申拓展研究典型题目1. 引言在学术研究和日常生活中，我们经常会遇到各种典型题目，它们的特点是具有一定的代表性和研究价值。

而要深入理解和深度挖掘典型题目，类比联想引申是一种非常有效的方法。

本文将就如何通过类比联想引申拓展研究典型题目进行探讨。

2. 类比联想引申的概念和意义在研究过程中，类比联想引申是指通过对已有知识、经验或现象的类比和联想，来拓展新的研究领域和深度。

这种方法的意义在于可以利用已有的知识和经验，在对新的典型题目进行研究时找到更为深入的视角和解决途径。

3. 类比联想引申的具体运用那么，类比联想引申在研究典型题目时究竟如何具体运用呢？以“人工智能在医疗领域的应用”为例，我们可以通过以下步骤展开类比联想引申的研究过程：3.1 类比：我们可以类比传统医疗领域的临床诊断和治疗经验，来对比人工智能在医疗领域的优势和不足之处，从而对其应用进行更深入的思考。

3.2 联想：我们可以联想人工智能在其他行业的应用，如智能交通、智能制造等领域的成功经验，来启发医疗领域的人工智能应用的新思路和可能性。

3.3 引申：通过类比和联想的过程，我们可以引申出人工智能在医疗领域的研究方向和未来发展趋势，为相关领域的研究提供更加全面和深入的视角。

4. 总结与回顾通过以上的探讨，可以看出类比联想引申在研究典型题目时的重要性和价值所在。

通过类比联想引申，我们可以更好地理解和挖掘典型题目的研究意义，为研究工作提供新的视角和思路。

5. 个人观点和理解在我看来，类比联想引申是一种非常富有创造性和深度的研究方法。

它可以使我们在研究过程中充分利用已有的知识和经验，同时又能够开拓新的研究领域和深度，为学术研究和实践应用提供更为丰富和有力的支持。

6. 结语通过以上的阐述，相信读者已经对如何通过类比联想引申拓展研究典型题目有了一定的理解。

在今后的研究工作中，希望大家能够灵活运用类比联想引申的方法，深入挖掘典型题目的研究意义和应用潜力，为学术和实践工作贡献自己的思考和力量。

1.如图，正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转，给出下列结论:①BE=DG；②BE_LDG；®DE2+BG2=2a2+2b2,其中正确结论有（）A.0个B.1个C.2个D.3个2.如图，正方形ABCD的边长为4,E为BC上的一点，BE=1,F为AB的中点，P为AC上一个动点,3.如图，四边形ABCD是边长为6的正方形，点E在边上，BE=4,过点E作EF//BC,分别交CD 于G,F两点.若N分别是OG,CE的中点，则"的长为（）4.如图，正方形ABCD的边长为3,点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，己知BE=1,则EF的长为（）359A.2B.2C.4D.35.如图，正方形ABCD中，AB=6,点E在边CD上，且CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论：©AABG^AAFG；②BG=GC；③ZEAG=45°；④AG〃CF；⑤S aecg：S a aeg=2：5,其中正确结论的个数A.2B.3C.4D.56.如图，正方形ABCD中，AB=1,M,N分别是AD,BC边的中点，沿BQ将△BCQ折叠，若点C恰好落在MN上的点P处，则PQ的长为（）1^1A.2B.3C.3D.B7.如图，在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG±AE 于点G,交AD于点H,则下列结论错误的是（）A.AH=DFB.S四边形EFHG=S a DC f+S a aghC.ZAEF=45°D.△ABH^ADCF8.如图，正方形ABCD和正方形CEFG中，点。

在CG上，BC=L,CE=3,H是AF的中点，那么CH的长是（）.9.如图，在A AB C中，ZC=90°,AC=BC=4,Q是AB的中点，点E、F分别在AC、BC边上运动（点、E 不与点A、。

x
图象有两个交点,则t>2,由对称性可知t<-2也符合.)
2.(2018河南,22,10分)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
① A C 的值为
;
BD
②∠AMB的度数为
.
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线
以先求出BD的两个值,根据 A C = ,再3 求出AC的两个值.
BD
3.(2017四川成都,27,10分)问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点
D,则D为BC的中点,∠BAD= 1 ∠BAC=60°,于是 B C = 2 B =D ; 3
2
AB AB
,n=
;
x
…
-3
-2
-1
- 1 - 1 1 1 1
2
3
4
…
2
3
3
2
y
… - 1 0 - 5 -2
- 5 - 1 0 m
5 2
5 n
1 7
…
3
2
2
3
224Fra bibliotek(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出 该函数的图象; (4)结合函数的图象,请完成:
思路分析 (1)由分母不为零可得x的取值范围.(2)由代入法计算即可.(3)根据描出的点画出图 象即可.(4)①由代入法计算即可.②答案不唯一,从对称性、单调性等方面思考.③利用数形结

2024-2025学年第一学期期中质量检测卷九年级数学（考试时间为120分钟，满分为120分）一、选择题（本大题共6小题，每小题3分，共18分）1.《国家宝藏》节目立足于中华文化宝库资源，通过对文物的梳理与总结，演绎文物背后的故事与历史，让更多的观众走进博物馆，让一个个馆藏文物鲜活起来，下面四幅图是我国一些博物馆的标志，其中是中心对称图形的是（ ）A. B. C. D.2.若关于x 的一元二次方程有一个根为0，则a 的值为（ ）A. B.1C. D.03.用配方法解一元二次方程，下列变形正确的是（ ）A. B. C. D.4.如图，将绕着点O 逆时针旋转至，使点B 恰好落在线段上，若，则的度数为（ ）A. B. C. D.5.关于二次函数；下列叙述正确的是（ ）A.函数的图象开口向下 B.对称轴是y 轴C.当时，y 有最大值D.当时，y 随x 的增大而增大6.生物学研究表明、在一定的温度范围内，酶的活性会随温度的升高逐渐增强，在最适宜温度时，酶的活性最强，超过一定温度范围时，酶的活性又随温度的升高逐渐减弱，甚至会失去活性.现已知某种酶的活性值y （单位：IU ）与温度t （单位：℃）的关系可以近似用二次函数来表示.则当温度为最适宜时，该种酶的活性值为（ ）A.14B.C.240D.4423510x x a +++=1±1-22150x x +-=2(1)16x +=-2(1)14x -=-2(1)14x +=-2(1)16x +=OAB △OA B ''△A B ''32AOA ︒'∠=B '∠58︒64︒74︒78︒228y x =-0x =8-0x <21141422y t t =-++72二、填空题（本大题共6小题，每小题3分，共18分）7.抛物线与y 轴交于点P ，则点P 的坐标为________.8.若点与点关于原点对称，则的值为________.9.将方程化为一元二次方程的一般式为________.10.如表为二次函数自变量x 与函数值y 之间满足的数量关系，则时，________.x …0123…y…2125…11.如图，已知拋物线和线段MN ，点M 和点N 的坐标分别为，，将抛物线向上平移个单位长度后，抛物线的顶点恰好在线段MN 上，则k 的值为_________.12.如图，在中，，，将AB 绕点A 逆时针旋转角得到AP ，连接PC ，PD .当为等腰三角形时，旋转角的度数为_________.三、解答题（本大题共5小题，每小题6分，共计30分）13.解下列方程：（1）；（用配方法求解）（2）.14.如图，一块等腰直角的三角板ABC，在水平桌面上绕点C 按顺时针方向旋转到的位置，A ，B 的对应点分别为E ，D ，且A ，C ，D 三点在同一直线上，连接AE ，求的度数.15.已知抛物线的顶点A 在直线上，求抛物线的顶点坐标.246y x x =++(,5)A m (2,)B n -2m n +235(2)x x =+2(0)y ax bx c a =++≠1x =-y =242y x x =-+-(0,4)(5,4)(0)k k >ABCD Y 60B ∠=︒2BC AB =()0360αα︒<<︒PCD △α22240x x --=23230x x +-=CDE △DEA ∠24y x x h =-+41y x =--16.若点关于原点对称的点是第一象限的点，求a 的取值范围.17.图1、图2均为的正方形网格，每个小正方形的顶点称为格点，的顶点和点D 均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求作图、并保留作图痕迹.图1图2（1）在图1中，画出将绕点D 顺时针旋转得到的；（2）在图2中，画出，使与关于点D 成中心对称.四、解答题（本大题共3小题，每小题8分，共24分）18.如图是一张长12dm ，宽6dm 的长方形纸板，将纸板四个角各剪去一个同样的边长为x dm 的正方形，然后将四周突出部分折起，可制成一个无盖长方体纸盒.（1）无盖方盒盒底的长为_________dm ，宽为_________dm （用含x 的式子表示）.（2）若要制作一个底面积是的一个无盖长方体纸盒，求剪去的正方形边长x .19.若二次函数的x 与y 的部分对应值如表：x …01…y…343…（1）求此二次函数的解析式；（2）画出此函数图象.20.已知关于x 的一元二次方程.（1）求证：该方程总有两个实数根；(32,24)P a a ---55⨯ABC △ABC △90︒111A B C △222A B C △222A B C △ABC △240dm 2y ax bx c =++4-3-2-1-5-2(4)40x k x k -++=（2）若该方程有一个根小于2，求k 的取值范围.五、解答题（本大题共2小题，每小题9分，共计18分）21.阅读与思考下面是小文撰写的数学小论文，请仔细阅读并完成相应任务.任务：（1）已知p ，q 是两个常数，一元二次方程的两个实数根为，，则二次三项式分解因式的结果是________.（2）因式分解：的结果是________.（3）请用阅读内容中的方法，因式分解：.22.我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形，不妨简称为“锅线”，锅口直径为6dm ，锅深3dm ，锅盖高1dm （锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为，把锅盖纵断面的抛物线记为.20x px q ++=15x =-22x =2x px q ++212x x --246x x +-1C 2C实物图图①（1）求和的解析式；（2）如果炒菜时锅的水位高度是1dm ，求此时水面的直径；（3）如果将一个底面直径为3dm ，高度为3.2dm 的圆柱形器皿放入炒菜锅内蒸食物，锅盖能否正常盖上？请说明理由.六、解答题（本大题共12分）23.通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整.原题：如图1，点E 、F 分别在正方形ABCD 的边BC ，CD 上，，连接EF ，试猜想EF ，BE ，DF 之间的数量关系.图1图2图3（1）思路梳理：把绕点A 逆时针旋转至，可使AB 与AD 重合，由，得，即点F ，D ，G 共线，易证_________，故EF ，BE ，DF 之间的数量关系为________.（2）类比引申：如图2，点E ，F 分别在正方形ABCD 的边CB ，DC 的延长线上，.连接EF ，试猜想EF ，BE ，DF 之间的数量关系为__________，并给出证明.（3）联想拓展：如图3，在中，已知，垂足于点D ，且，.求AD 的长.1C 2C 45EAF ∠=︒ABE △90︒ADG △90ADG B ︒∠=∠=180FDG ︒∠=AFG △≌45EAF ∠=︒ABC △45BAC ∠=︒AD BC ⊥6BD =4CD =。

2023-2024学年吉林省吉林市九年级上学期期中数学质量检测模拟试题注意事项：1答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题上答题无效．一、选择题（本大题共6小题，每小题2分，共12分）1．一元二次方程24610x x -+=的二次项系数、一次项系数、常数项分别是（）A ．4，6，1B ．4，6，1-C ．4，6-，1D ．4，6-，1-2．中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量．下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）A ．B ．C ．D ．3．若关于x 的一元二次方程230x x m -+=有两个相等的实数根，则实数m 的值为（）A ．.9-.B ．94-C ．94D ．94．已知二次函数()2323y x =---，下列说法正确的是（）A ．对称轴为2x =-B ．顶点坐标为()2,3C ．函数的最大值是3-D ．函数的最小值是3-5．如图，在ABC △中，90C ∠=︒，70BAC ∠=︒，将ABC △绕点A 顺时针旋转70︒，B ，C 旋转后的对应点分别是B '和C '，连接BB '，则BB C ''∠的度数是（）A ．35︒B ．40︒C ．45︒D ．50︒6．如图，抛物线2y ax c =+经过正方形OABC 的三个顶点A ，B ，C ，点B 在y 轴上，则ac 的值为（）A ．1-B ．2-C ．3-D ．4-二、填空题（本大题共8小题，每小题3分，共24分）7．已知关于x 的方程2200x mx +-=的一个根是4-，则它的另一个根是________．8．已知一元二次方程2310x x -+=有两个实数根1x ，2x ，则1212x x x x +-的值等于________．9．将抛物线()23y x =+向下平移1个单位长度，再向右平移________个单位长度后，得到的新抛物线经过原点．10．如图，一名学生推铅球，铅球行进高度y （单位：m ）与水平距离x （单位：m ）之间的关系是()()110412y x x =--+，则铅球推出的距离OA =________m ．11．在方格纸上建立如图所示的平面直角坐标系，将ABO △绕点O 按顺时针方向旋转90︒，得A B O ''△，则点A 的对应点A '的坐标为________．12．我们古代数学家研究过一元二次方程．下面是我国南宋数学家杨辉在1275年提出的一个问题：“直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步．”意思是一块田是矩形，矩形面积为2864m ，长比宽多12m ，如果设宽为m x ，则列出的方程为________．13．如图，将面积为7的正方形OABC 和面积为9的正方形ODEF 分别绕原点O 顺时针旋转，使OA ，OD 落在数轴上，点A ，D 在数轴上对应的数字分别为a ，b ，则b a -=________．14．如图，二次函数()20y ax bx c a =++≠图像的一部分与x 轴的一个交点坐标为()3,0，对称轴为直线1x =，结合图像给出下列结论：①0abc >；②2b a =；③30a c +=；④关于x 的一元二次方程()2200axbx c k a +++=≠有两个不相等的实数根；⑤若点()1,m y ，()22,m y -+均在该二次函数图像上，则12y y =．其中正确结论的序号为________．三、解答题（每小题5分，共20分）15．解方程：2320x x -+=．16．在平面直角坐标系xOy 中，抛物线2y xbx c =-++经过点()2,3，对称轴为直线1x =，求抛物线的表达式．17．如图所示，在ABC △中，40B ∠=︒，将ABC △绕点A 逆时针旋转至ADE △处，使点B 落在BC 延长线上的D 点处，求BDE ∠的度数．18．为增强学生身体素质，某校开展篮球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应安排多少个球队参赛．四、解答题（每小题7分，共28分）19．如图，在建立平面直角坐标系的网格纸中，每个小方格都是边长为1个单位长度的小正方形，ABC △的顶点均在格点上，点P 的坐标为()1,0-．（1）把ABC △绕点P 旋转180︒得到B C A '''△，作出B C A '''△；（2）把ABC △向右平移7个单位长度得到A B C ''''''△，作出A B C ''''''△；（3）B C A '''△与A B C ''''''△是否成中心对称？若是，则找出对称中心P '，并写出其坐标；若不是，请说明理由．20．已知关于x 的一元二次方程()22210x m x m m -+++=．（1）求证：无论m 取何值时，方程都有两个不相等的实数根；（2）设该方程的两个实数根为a 、b ，若()()2220a b a b ++=，求m 的值．21．如图，点O 是等边三角形ABC 内的一点，150BOC ∠=︒，将BOC △绕点C 按顺时针旋转得到ADC △，连接OD ，OA ．（1）求ODC ∠的度数；（2）若4OB =，5OC =，求AO 的长．22．超市的某种牛奶平均每天可销售20箱，每箱盈利30元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，若每箱降价1元，每天可多售5箱，若设每箱降价x 元．（1）根据题意，填表：每箱利润（元）销售量（箱）利润（元）降价前3020600降价后①________②________（2）若每天盈利1200元，则每箱应降价多少元？五、解答题（每小题8分，共16分）23．在杭州举行的亚运会比赛中，一名运动员在10m 高的跳台进行跳水，身体（看成一点）在空中的运动轨迹是一条抛物线，运动员离水面OB 的高度()m y 与离起跳点A 的水平距离()m x 之间的函数关系如图所示，运动员离起跳点A 的水平距离为1m 时达到最高点，当运动员离起跳点A 的水平距离为3m 时离水面的距离为7m ．（1）求y 关于x 的函数表达式；（2）求运动员从起跳点到入水点的水平距离OB 的长．24．阅读材料：解方程()()22215140x x ---+=，我们可以将()21x -视为一个整体，然后设()21x y -=，则()2221x y -=，原方程化为2540y y -+=，解得11y =，24y =．当1y =时，211x -=，22x ∴=，x ∴=±当4y =时，214x -=，25x ∴=，x ∴∴原方程的解为1x =，2x =3x =4x =根据上面的解答，解决下面的问题：（1）填空：在由原方程得到方程①的过程中，利用________法达到降次的目的，体现了________的数学思想；（2）解方程42120x x --=．六、解答题（每小题10分，共20分）25．我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．原题：如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，则EF BE DF =+，试说明理由．图1图2图3（1）思路梳理AB AD = ，∴把ABE △绕点A 逆时针旋转90︒至ADG △，可使AB 与AD 重合．90ADC B ∠=∠=︒ ，FDG ∴∠=________︒，点F 、D 、G 共线．根据________，易证AFE △≌________，得EFBE DF =+．（2）类比引申如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E 、F 分别在边BC 、CD 上，45EAF ∠=︒，若B ∠、D ∠都不是直角，则当B ∠与D ∠满足等量关系________时，仍有EF BE DF =+．（3）联想拓展如图3，在ABC △中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45DAE ∠=︒．猜想BD 、DE 、EC 应满足的等量关系，并写出推理过程．26．根据以下素材，探索完成任务．如何设计拱桥景观灯的悬挂方案？素材1图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽20m ，拱顶离水面5m ．据调查，该河段水位在此基础上再涨1.8m 达到最高．图1图2素材2为迎佳节，拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼，如图3．为了安全，灯笼底部距离水面不小于1m ；为了实效，相邻两盏灯笼悬挂点的水平间距均为1.6m ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．图3问题解决任务1确定桥拱形状在图2中建立合适的直角坐标系，求抛物线的函数表达式．在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐任务2探究悬挂范围标的最小值和横坐标的取值范围．给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标任务3拟定设计方案（填空即可）系，求出最左边一盏灯笼悬挂点的横坐标．参考答案及评分标准一、选择题（每小题2分，共12分）1.C2.C6.B 2.C3.C4.C5.A6.B二、填空题（每小题3分，共24分）7.5；8.2；9.2或410.1011.（2，3）；12.x （x +12）=864；13.3；14.①③⑤三、解答题（每小题5分，共20分）15.解：2320x x -+=∴(1)(2)0x x --=………2分∴10x -=或20x -=………4分∴11x =，x 2=2．………5分其它正确做法正常给分.16.解：（1）∵抛物线y =﹣x 2+bx +c 经过点（2，3），对称轴为直线x =1，∴42312b c b -++=⎧⎪⎨=⎪⎩，………2分解得23b c =⎧⎨=⎩，………4分∴抛物线的表达式为y =﹣x 2+2x +3…5分17.解：∵将△ABC 绕点A 逆时针旋转至△ADE 处，∠B =40°，∴∠B =∠ADE =40°，………2分∵AB =AD ，则∠BDE =∠BDA +∠ADE =40°+40°=80°．.......................5分18.解：设应安排x 个球队参赛，依题意得：()1121212x x -=，………2分整理得：x 2﹣x ﹣42＝0，………3分解得：x 1＝7，x 2＝﹣6（不符合题意，舍去），………4分∴应安排7个球队参赛．……5分四、解答题（每小题7分，共28分）19.解：（1）如图，△A 'B 'C '即为所求；………3分（2）如图，A ''B ''C ''即为所求；………6分（3）如图，P '（2.5，0）． (7)20.（1）证明：∵()()22Δ21410m m m ⎡⎤=-+-⨯+=>⎣⎦，………2分∴无论m 取何值，方程都有两个不相等的实数根．………3分（2）解：∵()22210x m x m m -+++=的两个实数根为,a b ，∴221,a b m ab m m +=+=+．………4分∵()()2220a b a b ++=，∴2224220a ab b ab +++=，22()20a b ab ++=．………5分∴222(21)20m m m +++=．即220m m +-=．………6分解得1m =或2m =-．∴m 的值为1或2-．………7分21.解：（1）由旋转的性质得，CD =CO ，∠ACD =∠BCO ，……1分∵∠ACB =∠ACO +∠OCB =60°，∴∠DCO =∠ACO +∠ACD =∠ACO +∠OCB =60°.……2分∴△OCD 为等边三角形.∴∠ODC =60°.……3分（2）由旋转的性质得，AD =OB =4.∵△OCD 为等边三角形，∴OD =OC =5.……4分∵∠BOC =150°，∠ODC =60°，∴∠ADO =90°.………5分在Rt △AOD 中，由勾股定理得AO =41542222=+=+OD AD ……7分22.解：（1）①30﹣x ②20+5x ………2分（2）根据题意得：（30﹣x ）（20+5x ）＝1200………4分整理得：（x ﹣6）（x ﹣20）＝0，………5分解得：1220,6x x ==（不合题意，舍去）答：每箱应降价20元.……7分五、解答题（每小题8分，共16分）23.（1）解：由题意得抛物线的对称轴为1x =，经过点()010，，()37，，设抛物线的表达式为2y ax bx c =++，………1分∴1210937b a c a b c ⎧-=⎪⎪=⎨⎪++=⎪⎩，………2分解得1210a b c =-⎧⎪=⎨⎪=⎩，………3分∴y 关于x 的函数表达式为2210y x x =-++；………4分（2）解：令0y =，则22100x x -++=，………6分解得1x =±………7分（负值舍去），∴运动员从起跳点到入水点的水平距离O B的长为(1m +．………8分24.解：（1）换元………1分转化………2分（2）令x 2=a ，原方程化为a 2-a -12=0，………4分解得a 1=-3，a 2=4………6分当a =-3时，x 2=-3，∴该方程无解；………7分当a =4时，x 2=4∴x =±2综上，该方程的解为x 1=2x 2=-2………8分六、解答题（每小题10分，共20分）25.解：（1）180；SAS ；△AFG ；………3分（2）∠B +∠D =180°.………5分（3）猜想：DE 2=BD 2+EC 2.………6分证明如下：把△AEC 绕点A 顺时针旋转90°得到△ABE ′，连接DE ′，∴△AEC ≌△ABE ′.∴BE ′=EC ，AE ′=AE ，∠C =∠ABE ′，∠EAC =∠E ′AB .……………………7分在Rt △ABC 中，∵AB =AC ，∴∠ABC =∠ACB =45°.∴∠ABC +∠ABE ′=90°.即∠E ′BD =90°.∴E ′B 2+BD 2=E ′D 2.………………………8分又∵∠DAE =45°，∴∠BAD +∠EAC =45°.∴∠E ′AB +∠BAD =45°.即∠E ′AD =45°.在△AE ′D 和△AED 中，AE AE E AD EAD AD AD '=⎧⎪'∠=∠⎨⎪=⎩，∴△AE ′D ≌△AED （SAS ）.…………………………9分∴DE =DE ′.∴DE 2=BD 2+EC 2． (10)分26.解：任务1：以拱顶为原点，建立如图1所示的直角坐标系， (1)分则顶点为（0，0），且过点B （10，﹣5），………2分设抛物线的解析式为：y ＝ax 2，把点B （10，﹣5）代入得：100a ＝﹣5，120a ∴=-，………3分∴抛物线的函数表达式为：2120y x =-………4分任务2：∵该河段水位再涨1.8m 达到最高，灯笼底部距离水面不小于1m ，灯笼长0.4m ，∴当悬挂点的纵坐标y ≥﹣5+1.8+1+0.4＝﹣1.8，即悬挂点的纵坐标的最小值是﹣1.8m ，………6分任务3：由（2）可得悬挂点的横坐标的取值范围是：﹣6≤x ≤6；方案一：如图2（坐标轴的横轴），从顶点处开始悬挂灯笼，∵﹣6≤x ≤6，相邻两盏灯笼悬挂点的水平间距均为1.6m ，∴若顶点一侧悬挂4盏灯笼时，1.6×4＞6，若顶点一侧悬挂3盏灯笼时，1.6×3＜6，∴顶点一侧最多悬挂3盏灯笼，∵灯笼挂满后成轴对称分布，∴共可挂7盏灯笼，…..7分∴最左边一盏灯笼的横坐标为：﹣1.6×3＝﹣4.8；………..8分方案二：如图3，∵若顶点一侧悬挂5盏灯笼时，0.8+1.6×（5﹣1）＞6，若顶点一侧悬挂4盏灯笼时，0.8+1.6×（4﹣1）＜6，∴顶点一侧最多悬挂4盏灯笼，∵灯笼挂满后成轴对称分布，∴共可挂8盏灯笼，………..9分∴最左边一盏灯笼的横坐标为：﹣0.8﹣1.6×3＝﹣5.6………..10分此答案仅供参考，若有其它正确做法正常给分！。

数学全全等三角形截长补短知识点-+典型题及答案一、全等三角形截长补短1．通过类比联想、引申拓展典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．（解决问题）如图，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，则EF BE DF =+，试说明理由．证明：延长CD 到G ，使DG BE =，在ABE △与ADG 中，90AB AD B ADG BE DG =⎧⎪∠=∠=︒⎨⎪=⎩∴ABE ADG ≌理由：（SAS ）进而证出：AFE △≌___________，理由：（__________）进而得EF BE DF =+．（变式探究）如图，四边形ABCD 中，AB AD =，90BAD ∠=︒点E 、F 分别在边BC 、CD 上，45EAF ∠=︒．若B 、D ∠都不是直角，则当B 与D ∠满足等量关系________________时，仍有EF BE DF =+．请证明你的猜想．（拓展延伸）如图，若AB AD =，90≠︒∠BAD ，45EAF ∠≠︒，但12EAF BAD ∠=∠，90B D ∠=∠=︒，连接EF ，请直接写出EF 、BE 、DF 之间的数量关系．2．在四边形ABDE 中，C 是BD 边的中点．（1）如图（1），若AC 平分BAE ∠，90ACE ∠=︒，则线段AE 、AB 、DE 的长度满足的数量关系为______；（直接写出答案）（2）如图（2），AC 平分BAE ∠，EC 平分AED ∠，若120ACE ∠=︒，则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系？写出结论并证明．3．如图，△ABC 中，AB=AC ，∠EAF=12∠BAC ，BF ⊥AE 于E 交AF 于点F ，连结 CF ．（1）如图 1 所示，当∠EAF 在∠BAC 内部时，求证：EF ＝BE +CF ．（2）如图 2 所示，当∠EAF 的边 AE 、AF 分别在∠BAC 外部、内部时，求证：CF ＝BF +2BE ．4．阅读材料并完成习题：在数学中，我们会用“截长补短”的方法来构造全等三角形解决问题．请看这个例题：如图1，在四边形ABCD 中，∠BAD=∠BCD=90°，AB=AD ，若AC=2cm ，求四边形ABCD 的面积． 解：延长线段CB 到E ，使得BE=CD ，连接AE ，我们可以证明△BAE ≌△DAC ，根据全等三角形的性质得AE=AC=2， ∠EAB=∠CAD ，则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°，得S 四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ，这样，四边形ABCD 的面积就转化为等腰直角三角形EAC 面积．（1）根据上面的思路，我们可以求得四边形ABCD 的面积为 cm 2．（2）请你用上面学到的方法完成下面的习题．如图2，已知FG=FN=HM=GH+MN=2cm ，∠G=∠N=90°，求五边形FGHMN 的面积． 5．如图，在菱形ABCD 中，∠A ＝60°，E 为菱形ABCD 内对角线BD 左侧一点，连接BE 、CE 、DE ．（1）若AB ＝6，求菱形ABCD 的面积；（2）若∠BED ＝2∠A ，求证：CE ＝BE+DE ．6．如图，ABC 是边长为2的等边三角形，BDC 是顶角为120°的等腰三角形，以点D 为顶点作60MDN ∠=︒，点M 、N 分别在AB 、AC 上． （1）如图①，当//MN BC 时，则AMN 的周长为______；（2）如图②，求证：BM NC MN +=．7．如图，在四边形ABCD 中，AB =AD ，∠B =∠D =90°，E 、F 分别是边BC 、CD 上的点，且∠EAF =12∠BAD ．求证：EF =BE +FD ．8．已知，在ABCD 中，AB BD AB BD E ⊥=，，为射线BC 上一点，连接AE 交BD 于点F .（1）如图1，若E 点与点C 重合，且25AF =，求AD 的长；（2）如图2，当点E 在BC 边上时，过点D 作DG AE ⊥于G ，延长DG 交BC 于H ，连接FH .求证：AF DH FH =+．（3）如图3，当点E 在射线BC 上运动时，过点D 作DG AE ⊥于G M ，为AG 的中点，点N 在BC 边上且1BN =，已知42AB =MN 的最小值．9．在数学活动课上，数学老师出示了如下题目：如图①，在四边形ABCD 中，E 是边CD 的中点，AE 是BAD ∠的平分线，AD BC ∥．求证：AB AD BC =+．小聪同学发现以下两种方法：方法1：如图②，延长AE 、BC 交于点F ．方法2：如图③，在AB 上取一点G ，使AG AD =，连接EG 、CG ．（1）请你任选一种方法写出这道题的完整的证明过程；（2）如图④，在四边形ABCD 中，AE 是BAD ∠的平分线，E 是边CD 的中点，60BAD ∠=︒，11802D BCD ∠+∠=︒，求证：CB CE =．10．阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图，四边形ABCD，AD∥BC，AB=AD，E为对角线AC上一点，∠BEC=∠BAD=2∠DEC，探究AB与BC的数量关系．某学习小组的同学经过思考，交流了自己的想法：小柏：“通过观察和度量，发现∠ACB=∠ABE”；小源：“通过观察和度量，AE和BE存在一定的数量关系”；小亮：“通过构造三角形全等，再经过进一步推理，就可以得到线段AB与BC的数量关系”．……老师：“保留原题条件，如图2， AC上存在点F，使DF=CF=k AE，连接DF并延长交BC于点G，求ABFG的值”．（1）求证：∠ACB=∠ABE；（2）探究线段AB与BC的数量关系，并证明；（3）若DF=CF=k AE，求ABFG的值（用含k的代数式表示）．【参考答案】***试卷处理标记，请不要删除一、全等三角形截长补短1．（1）AFE AFG △≌△，理由：SAS ；（2）180B D ∠+∠=︒，证明见解析；（3）BE+DF=EF ．【分析】（1）在前面已证的基础上，得出结论AE AG =，进而证明AFE AFG △≌△，从而得出结论；（2）利用“解决问题”中的思路，同样去构造AFE AFG △≌△即可；（3）利用前面两步的思路，证明全等得出结论即可．【详解】（1）ABE ADG ≌，,,AE AG BAE DAG BE DG ∴=∠=∠=，则BAE FAD FAD ADG FAG ∠+∠=∠+∠=∠，45EAF ∠=︒，45FAG ∴∠=︒，在AFG 与AFE △中，AE AG EAF GAF AF AF =⎧⎪=⎨⎪=⎩∠∠ AFE AFG ∴△≌△，理由：（SAS ）EF FG FD DG FD BE ∴==+=+；（2）满足180B D ∠+∠=︒即可，证明如下：如图，延长FD 至G ，使BE DG =，180B ADF ∠+∠=︒，180ADF ADG ∠+∠=︒，B ADG ∴∠=∠，在ABE △与ADG 中，AB AD B ADG BE DG =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴≌，,,AE AG BAE DAG BE DG ∴=∠=∠=，则BAE FAD FAD ADG FAG ∠+∠=∠+∠=∠，45EAF ∠=︒，45FAG ∴∠=︒，在AFG 与AFE △中，AE AG EAF GAF AF AF =⎧⎪=⎨⎪=⎩∠∠ AFE AFG ∴△≌△，理由：（SAS ）EF FG FD DG FD BE ∴==+=+；（3）BE+DF=EF ．证明如下：如图，延长FD 至G ，使BE DG =，在ABE △与ADG 中，90AB AD B ADG BE DG =⎧⎪∠=∠=︒⎨⎪=⎩()ABE ADG SAS ∴≌，,AE AG BAE DAG ∴=∠=∠，则BAE FAD FAD ADG FAG ∠+∠=∠+∠=∠， 12EAF BAD ∠=∠，12FAG EAD FAE ∴∠=∠=∠， 在AFG 与AFE △中，AE AG EAF GAF AF AF =⎧⎪=⎨⎪=⎩∠∠ AFE AFG ∴△≌△，理由：（SAS ）EF FG FD DG FD BE ∴==+=+；．【点睛】本题考查了截长补短的方法构造全等三角形，能够理解前面介绍的方法并继续探究是解决问题的关键．2．（1）AE ＝AB ＋DE ；（2）AE ＝AB ＋DE ＋12BD ，证明见解析． 【分析】 （1）在AE 上取一点F ，使AF ＝AB ，由三角形全等的判定可证得△ACB ≌△ACF ，根据全等三角形的性质可得BC ＝FC ，∠ACB ＝∠ACF ，根据三角形全等的判定证得△CEF ≌△CED ，得到EF ＝ED ，再由线段的和差可以得出结论；（2）在AE 上取点F ，使AF ＝AB ，连结CF ，在AE 上取点G ，使EG ＝ED ，连结CG ，根据全等三角形的判定证得△ACB ≌△ACF 和△ECD ≌△ECG ，由全等三角形的性质证得CF ＝CG ，进而证得△CFG 是等边三角形，就有FG ＝CG ＝12BD ，从而可证得结论． 【详解】解：（1）如图（1），在AE 上取一点F ，使AF ＝AB ．∵AC 平分∠BAE ，∴∠BAC ＝∠FAC ．在△ACB 和△ACF 中，AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△ACB ≌△ACF （SAS ）．∴BC ＝FC ，∠ACB ＝∠ACF ．∵C 是BD 边的中点，∴BC ＝CD ．∴CF ＝CD ．∵∠ACE ＝90°，∴∠ACB ＋∠DCE ＝90°，∠ACF ＋∠ECF ＝90°．∴∠ECF ＝∠ECD ．在△CEF 和△CED 中，CF CD ECF ECD CE CE ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△CEF ≌△CED （SAS ）．∴EF ＝ED ．∵AE ＝AF ＋EF ，∴AE ＝AB ＋DE ．故答案为：AE ＝AB ＋DE ；（2）AE ＝AB ＋DE ＋12BD ． 证明：如图（2），在AE 上取点F ，使AF ＝AB ，连结CF ，在AE 上取点G ，使EG ＝ED ，连结CG ．∵C 是BD 边的中点，∴CB ＝CD ＝12BD ． ∵AC 平分∠BAE ，∴∠BAC ＝∠FAC ．在△ACB 和△ACF 中，AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△ACB ≌△ACF （SAS ）．∴CF ＝CB ，∠BCA ＝∠FCA ．同理可证：△ECD ≌△ECG∴CD ＝CG ，∠DCE ＝∠GCE ．∵CB ＝CD ，∴CG ＝CF ．∵∠ACE ＝120°，∴∠BCA ＋∠DCE ＝180°−120°＝60°．∴∠FCA ＋∠GCE ＝60°．∴∠FCG ＝60°．∴△FGC 是等边三角形．∴FG ＝FC ＝12BD ． ∵AE ＝AF ＋EG ＋FG ，∴AE ＝AB ＋DE ＋12BD ． 【点睛】 本题主要考查了全等三角形的判定与性质的运用，能熟练应用三角形全等的判定和性质是解决问题的关键．3．（1）见解析；（2）见解析【分析】（1）在EF 上截取EH BE =，由“SAS ”可证ACF AHF ∆≅∆，可得CF HF =，可得结论；（2）在BE 的延长线上截取EN BE =，连接AN ，由“SAS ”可证ACF ANF ∆≅∆，可得CF NF =，可得结论．【详解】解：证明：（1）如图，在EF 上截取EH BE =，连接AH ，EB EH =，AE BF ⊥，AB AH ∴=，AB AH =，AE BH ⊥，BAE EAH ∴∠=∠，AB AC =，AC AH ∴=，12EAF BAC ∠==∠ BAE CAF EAF ∴∠+∠=∠，BAE CAF EAH FAH ∴∠+∠=∠+∠，CAF HAF ∴∠=∠，在ACF ∆和AHF ∆中，AC AH CAF HAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()ACF AHF SAS ∴∆≅∆，CF HF ∴=，EF EH HF BE CF ∴=+=+；（2）如图，在BE 的延长线上截取EN BE =，连接AN ，AE BF ⊥，BE EN =，AB AC =，AN AB AC ∴==，AN AB =，AE BN ⊥，BAE NAE ∴∠=∠，12EAF BAC ∠==∠ 1(2)2EAF NAE BAC NAE ∴∠+∠=∠+∠ 12FAN CAN ∴∠=∠， FAN CAF ∴∠=∠，在ACF ∆和ANF ∆中，AC AN CAF NAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()ACF ANF SAS ∴∆≅∆，CF NF ∴=，2CF BF BE ∴=+．【点睛】本题考查了全等三角形的判定和性质，添加恰当辅助线构造全等三角形是本题的关键． 4．（1）2；（2）4【分析】（1）根据题意可直接求等腰直角三角形EAC 的面积即可；（2）延长MN 到K ，使NK=GH ，连接FK 、FH 、FM ，由（1）易证FGH FNK ≌，则有FK=FH ，因为HM=GH+MN 易证FMK FMH ≌，故可求解． 【详解】（1）由题意知21=22ABC ADC ABC ABE AEC ABCD AC S SS S S S =+=+==四边形， 故答案为2；（2）延长MN到K，使NK=GH，连接FK、FH、FM，如图所示：FG=FN=HM=GH+MN=2cm，∠G=∠N=90°，∴∠FNK=∠FGH=90°，∴FGH FNK≌，∴FH=FK，又FM=FM，HM=KM=MN+GH=MN+NK，∴FMK FMH≌，∴MK=FN=2cm，∴12=242FGH HFM MFN FMKFGHMNS S S S S MK FN=++=⨯⋅=五边形．【点睛】本题主要考查全等三角形的性质与判定，关键是根据截长补短法及割补法求面积的运用．5．（1）183；（2）见解析【分析】（1）过点B作BH⊥AD于H，由直角三角形的性质可求BH的长，由菱形的面积公式可求解；（2）延长DE至M，使ME＝BE，连接MB，由题意可证△ABD是等边三角形，△BCD是等边三角形，△BEM是等边三角形，可得∠CBD＝∠ABD＝60°＝∠MBE，AB＝BD＝BC，BM ＝BE，由“SAS”可证∴△MBD≌△EBC，可得MD＝EC，即可得结论．【详解】解：（1）如图，过点B作BH⊥AD于H，∵四边形ABCD是菱形，∴AB＝AD＝6，∵∠A＝60°，BH⊥AD，∴∠ABH＝30°，∴AH＝12AB＝3，BH3AH＝3∴菱形ABCD 的面积＝AD×BH ＝6×33＝183；（2）如图，延长DE 至M ，ME ＝BE ，连接MB ，∵四边形ABCD 是菱形，∴AB ＝AD ＝CD ＝BC ，∠A ＝60°＝∠BCD ，∴△ABD 是等边三角形，△BCD 是等边三角形，∴∠CBD ＝∠ABD ＝60°，AB ＝BD ＝BC ，∵∠BED ＝2∠A ＝120°，∴∠BEM ＝60°，又∵BE ＝ME ，∴△BEM 是等边三角形，∴BM ＝BE ，∠MBE ＝∠DBC ＝60°，∴∠MBD ＝∠EBC ，∴△MBD ≌△EBC （SAS ），∴MD ＝EC ，∴CE ＝BE+DE ．【点睛】本题主要考查了菱形的性质应用，结合等边三角形的性质是解题的关键．6．（1）4；（2）见解析【分析】（1）首先证明△BDM ≌△CDN ，进而得出△DMN 是等边三角形，∠BDM=∠CDN=30°，NC=BM=12DM=12MN ，即可解决问题； （2）延长AC 至点E ，使得CE BM =，连接DE ，首先证明BDM CDE △≌△，再证明MDN EDN △≌△，得出MN NE =，进而得出结果即可．【详解】解：（1）∵ABC 是等边三角形，//MN BC ，60AMN ABC ∴∠=∠=︒，60ANM ACB ∠=∠=︒∴AMN 是等边三角形，AM AN ∴=，则BM NC =，∵BDC 是顶角120BDC ∠=︒的等腰三角形，30DBC DCB ∴∠=∠=︒，90DBM DCN ∴∠=∠=︒，在BDM 和CDN △中，,,,BM CN MBD DCN BD CD =⎧⎪∠=∠⎨⎪=⎩()BDM CDN SAS ∴△≌△，DM DN ∴=，BDM CDN ∠=∠，∵60MDN ∠=︒，∴DMN 是等边三角形，30BDM CDN ∠=∠=︒，1122NC BM DM MN ∴===，MN MB NC ∴=+， ∴AMN 的周长4AB AC =+=．（2）如图，延长AC 至点E ，使得CE BM =，连接DE ，∵ABC 是等边三角形，BDC 是顶角120BDC ∠=︒的等腰三角形，60ABC ACB ∴∠=∠=︒，30DBC DCB ∠=∠=︒，90ABD ACD ∠∴∠==︒，90DCE ∴∠=︒，在BDM 和CDE △中，,,,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩()BDM CDE SAS ∴△≌△，MD ED ∴=，MDB EDC ∠=∠，120120MDE MDB EDC ∴∠=︒-∠+∠=︒，∵60MDN ∠=︒，60NDE ∴∠=︒，在MDN △和EDN △中，,60,,MD ED MDN NDE DN DN =⎧⎪∠=∠=︒⎨⎪=⎩()MDN EDN SAS ∴△≌△．MN NE ∴=，又∵NE NC CE NC BM =+=+，BM NC MN ∴+=．【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质，掌握全等三角形的性质与判定，等边三角形及等腰三角形的性质是解题的关键．7．证明见解析．【分析】延长EB 到G ，使BG =DF ，连接AG ．先说明△ABG ≌△ADF ，然后利用全等三角形的性质和已知条件证得△AEG ≌△AEF ，最后再运用全等三角形的性质和线段的和差即可解答．【详解】延长EB 到G ，使BG =DF ，连接AG ．∵∠ABG =∠ABC =∠D =90°，AB =AD ，∴△ABG ≌△ADF ．∴AG =AF ，∠1=∠2．∴∠1+∠3=∠2+∠3=∠EAF =12∠BAD ． ∴∠GAE =∠EAF ．又∵AE =AE ，∴△AEG ≌△AEF ．∴EG =EF ．∵EG =BE +BG ．∴EF =BE +FD【点睛】本题考查了全等三角形的判定与性质，做出辅助线构造全等三角形是解答本题的关键． 8．（1）42AD =2）见解析；（3）MN 的最小值为3．【分析】（1）如图1中，利用等腰三角形的性质可得90ABD ∠=︒，利用平行四边形的性质可得F 为BD 中点，在Rt ABF ∆中，由勾股定理可求得BF ，则可求得AB ，在Rt ABD ∆中，再利用勾股定理可求得AD ；（2）如图2中，在AF 上截取AK HD =，连接BK ，可先证明ABK DBH ∆≅∆，再证明BFK BFH ∆≅∆，可证得结论；（3）连接AN 并延长到Q ，使NQ AN =，连接GQ ，取AD 的中点O ，连接OG ，得到90AGD ∠=︒，于是得到点G 的轨迹是以O 为圆心，以OG 为半径的弧，且4OG =，求得GQ 最小值为6，根据三角形的中位线定理即可得到结论．【详解】（1）45AB BD BAD =∠=︒,，45BDA BAD ∴∠=∠=︒90 ABD ∴∠=︒，四边形ABCD 是平行四边形，∴当点E 与点C 重合时，1122BF BD AB == 在Rt ABF 中，222AF AB BF =+()()222252BF BF ∴=+ 24BF AB ∴==,Rt ABD ∴中，42AD =.（2）证明：如图2中，在AF 上截取AK HD =，连接BK ，23AFD ABF FGD ∠=∠+∠=∠+∠，90ABF FGD ∠=∠=︒，23∴∠=∠，在ABK 和DBH ∆中，23AB BD AK HD =⎧⎪∠=∠⎨⎪=⎩， ABK DBH ∴∆≅∆，BK BH ∴=，61∠=∠，AK DH =，四边形ABCD 是平行四边形，//AD BC ∴，41645∴∠=∠=∠=︒，5645ABD ∴∠=∠-∠=︒，51∴∠=∠，在FBK ∆和FBH ∆中，51BF BF BK BH =⎧⎪∠=∠⎨⎪=⎩， FBK FBH ∴∆≅∆，KF FH ∴=，AF AK KF =+，AF DH FH ∴=+；()3解：连接AN 并延长到Q ，使NQ AN =，连接GQ ，取AD 的中点O ，连接OG ，作AK ⊥BC ，交BC 延长线于点K ，作QP ⊥AD ，交AD 延长线于点P ．90AGD ∠=︒，∴点G 的轨迹是以O 为圆心，以OG 为半径的弧，且4OG =，根据△ABD 为等腰直角三角形，可得AD 228AB BD +=, ∴AO=142AD =， 根据△ABK 为等腰直角三角形，可得AK =BK =4，可得QE =PE =4，∴PQ =8，∵BK=4,BN =1，∴KN =5，∴KE=AP =10，∴OP =6，10OQ ∴=，4OG =，GQ ∴最小值为6， MN 是AGQ ∆的中位线，MN ∴的最小值为3．【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、中位线定理，解题的关键是学会添加常用辅助线，构造全等三角形．9．（1）方法1：证明见解析；方法2：证明见解析；（2）证明见解析．【分析】（1）方法1：先根据角平分线的定义、平行线的性质得出BAF DAE F ∠=∠=∠，再根据等腰三角形的性质可得AB BF =，根据三角形全等的判定定理与性质得出AD FC =，然后根据线段的和差即可得证；方法2：先根据角平分线的定义得出DAE GAE ∠=∠，再根据三角形全等的判定定理与性质可得,DE GE D AGE =∠=∠，然后根据线段中点的定义、等腰三角形的性质可得ECG EGC ∠=∠，最后根据平行线的性质、平角的定义可得BCG BGC ∠=∠，由等腰三角形的定义可得BG BC =，由此根据线段的和差即可得证；（2）如图（见解析），参照方法1构造辅助线，先根据等腰三角形的性质得出EF 平分AFG ∠，从而有12EFC AFG ∠=∠，再根据平行线的性质、角的和差得出60EFC BFC ∠=∠=︒，ECF BCF ∠=∠，然后根据三角形全等的判定定理与性质即可得证．【详解】（1）方法1：如图②，延长AE 、BC 交于点FAE ∵是BAD ∠的平分线BAF DAE ∴∠=∠//AD BCDAE F ∴∠=∠BAF F ∴∠=∠AB BF FC BC ∴==+E 是边CD 的中点DE CE ∴=在ADE 和FCE △中，DAE F AED FEC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADE FCE AAS ∴≅AD FC ∴=AB FC BC AD BC ∴=+=+；方法2：如图③，在AB 上取一点G ，使AG AD =，连接EG 、CGAE ∵是BAD ∠的平分线DAE GAE ∴∠=∠在ADE 和AGE 中，AD AG DAE GAE AE AE =⎧⎪∠=∠⎨⎪=⎩()ADE AGE SAS ∴≅,DE GE D AGE ∴=∠=∠E 是边CD 的中点DE CE ∴=CE GE ∴=ECG EGC ∴∠=∠//AD BC180D BCD ︒∴∠+∠=，即180D ECG BCG ∠+∠+∠=︒180AGE EGC BCG ∴∠+∠+∠=︒，即180AGC BCG ∠+∠=︒又180AGC BGC ∠+∠=︒BCG BGC ∴∠=∠BG BC ∴=AB AG BG AD BC ∴=+=+；（2）如图，过点C 作//CG AD ，交AE 延长线于点G ，延长GC 交AB 于点F ，连接EF 由方法1可知：,AF GF AE GE ==AFG ∴是等腰三角形EF ∴平分AFG ∠12EFC AFG ∴∠=∠ //CG AD ，60BAD ∠=︒60,180120BFC BAD AFG BAD ∴∠=∠=︒∠=︒-∠=︒60EFC ∴∠=︒//CG AD180D ECF ∴∠+∠=︒11802D BCD ︒∠+∠=，即1()1802D ECF BCF ∠+∠+∠=︒ 1()2ECF ECF BCF ∴∠=∠+∠ ECF BCF ∴∠=∠在ECF △和BCF △中，60EFC BFC CF CF ECF BCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()ECF BCF ASA ∴≅ CB CE ∴=．【点睛】本题考查了角平分线的定义、平行线的性质、三角形全等的判定定理与性质等知识点，较难的是题（2），参照方法1，通过作辅助线，构造全等三角形是解题关键． 10．（1）见解析；（2）CB=2AB ；（3）3AB k FG k = 【分析】（1）利用平行线的性质以及角的等量代换求证即可；（2）在BE 边上取点H ，使BH=AE ，可证明△ABH ≌△DAE ，△ABE ∽△ACB ，利用相似三角形的性质从而得出结论；（3）连接BD 交AC 于点Q ，过点A 作AK ⊥BD 于点K ，得出12AD DK CB DB ==，通过证明△ADK ∽△DBC 得出∠BDC=∠AKD=90°，再证DF=FQ ，设AD=a ，因此有DF=FC=QF=ka ，再利用相似三角形的性质得出AC=3ka ，3AB ka =，1122FG DF ka ==，从而得出答案．【详解】解：（1）∵∠BAD=∠BEC∠BAD=∠BAE+∠EAD∠BEC=∠ABE+BAE∴∠EAD=∠ABE∵AD ∥BC∴∠EAD=∠ACB∴∠ACB=∠ABE（2）在BE 边上取点H ，使BH=AE∵AB=AD∴△ABH ≌△DAE∴∠AHB=∠AED∵∠AHB+∠AHE=180°∠AED+∠DEC=180°∴∠AHE=∠DEC∵∠BEC=2∠DEC∠BEC=∠HAE+∠AHE∴∠AHE=∠HAE∴AE=EH∴BE=2AE∵∠ABE=∠ACB∠BAE=∠CAB∴△ABE ∽△ACB ∴EB AE CB AB= ∴CB=2AB ； （3）连接BD 交AC 于点Q ，过点A 作AK ⊥BD 于点K∵AD=AB∴12DK BD =∠AKD=90°∵12AB AD BC == ∴12AD DK CB DB == ∵AD ∥BC∴∠ADK=∠DBC∴△ADK ∽△DBC∴∠BDC=∠AKD=90°∵DF=FC∴∠FDC=∠DFC∵∠BDC=90°∴∠FDC+∠QDF=90°∠DQF+∠DCF=90°∴DF=FQ设AD=a∴DF=FC=QF=ka∵AD ∥BC∴∠DAQ=∠QCB∠ADQ=∠QBC∴△AQD ∽△CQB ∴12AD QA BC CQ== ∴AQ=ka=QF=CF∴AC=3ka∵△ABE ∽△ACB ∴AE AB AB AC= ∴AB =同理△AFD ∽△CFG12DF AF FG FC == ∴1122FG DF ka ==AB FG = 【点睛】本题是一道关于相似的综合题目，难度较大，根据题目作出合适的辅助线是解此题的关键，解决此题还需要较强的数形结合的能力以及较强的计算能力．。

旋转1 今年，6月12日为端午节。

在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况。

请根据小丽提供的信息，解答小华和小明提出的问题。

2已知整数k＜5，若△ABC的边长均满足关于x的方程2380-+=，则△ABC的周长x k x是。

3如果三角形的两边长分别是方程x2﹣8x+15=0的两个根，那么连接这个三角形三边的中点，得到的三角形的周长可能是（）A．5.5 B．5C．4.5 D．44通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。

下面是一个案例，请补充完整。

FF原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。

（1）思路梳理∵AB=CD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。

∵∠ADC=∠B=90°，∴∠FDG=180°，点F、D、G共线。

根据__SAS__________，易证△AFG ≌_△AFE_______，得EF=BE+DF 。

（2）类比引申如图2，四边形ABCD 中，AB=AD ，∠BAD=90°点E 、F 分别在边BC 、CD 上，∠EAF=45°。

若∠B 、∠D 都不是直角，则当∠B 与∠D 满足等量关系_互补___时，仍有EF=BE+DF 。

（3）联想拓展如图3，在△ABC 中，∠BAC=90°，AB=AC ，点D 、E 均在边BC 上，且∠DAE=45°。

猜想BD 、DE 、EC 应满足的等量关系，并写出推理过程。

解：BD 2+EC 2=DE 2解析：(1)SAS ………………………(1分）△AFE ………………………(2分）(2)∠B+∠D=180°………………………(4分）(3)解：BD 2+EC 2=DE 2.………………………(5分） ∵AB=AC ，∴把△ABD 绕A 点逆时针旋转90°至△AC G ，可使AB 与AC 重合.∵△ABC 中，∠BAC=90°.∴∠ACB+∠ACG=∠ACB+∠B=90°,即∠ECG=90°.∴EC 2+CG 2=EG 2.………………………(7分） 在△AEG 与△AED 中,∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD, 又∵AD=AG ，AE=AE ， ∴△AEG ≌△AED. ∴DE=EG.又∵CG=BD,∴BD 2+EC 2=DE 2.………………………(9分）5如图，在11×11的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC （即三角形的顶点都在格点上）。

正方形-旋转问题L如图，已知正方形ABCD,E是AB延长线上一点，F是DC延长线上一点，且满足BF=EF,将线段EF绕点F顺时针旋转90。

得FG,过点B作FG的平行线，交DA的延长线于点N,连接NG.⑴求证:BE=2CF；(2)试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明.2.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转，角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.(1)如图1,当乙EAF被对角线AC平分时，求a、b的值；(2)当AAEF是直角三角形时，求a、b的值.A n图i3.如图①，已知AABC是等腰直角三角形，/BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG、DE上，连接AE、BG.(1)试猜想线段BG和AE的数量关系，请直接写出你得到的结论；(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°，小于或等于360°)，如图②，(1)中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．4.如图①，将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE'F'D',旋转角为a.(1)当点D’恰好落在EF边上时，求旋转角a的值；(2)如图②，G为BC中点，且0°<a<90°,求证：GD‘二E'D；⑶小长方形CEFD绕点C顺时针旋转一周的过程中，ADCD'与ACBD'能否全等？若能，直接写出旋转角a的值；若不能，说明理由.图①图②5.在综合实践课上，老师让同学们“以三角形的旋转”为主题进行数学活动，如图（1）,在三角形纸片ABC中，AB=AC,ZB=ZC=a.图（1）圄（2）图（3）（1）创新小组将图（1）中的AABC以点B为旋转中心，逆时针旋转角度］，得到ADBE,再将AABC以点A为旋转中心，顺时针旋转角度a,得到AAFG,连接DF，得到图（2），则四边形AFDE的形状是.⑵实践小组将图⑴中的AABC以点B为旋转中心，逆时针逆转90°,得到△DBE,再将AABC以点A为旋转中心，顺时针旋转90°,得到AAFG,连接DF、DG、AE,得到图⑶，发现四边形AFDB为正方形，请你证明这个结论.（3）请你在实践小组操作的基础上,再写出图（3）中的一个特殊四边形,并证明你的结论．6.通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．原题：如图①，点E,F分别在正方形ABCD的边BC,CD上，/EAF=45°连接EF，则EF=BE+DF，试说明理由．（1）思路梳理因为AB=AD,所以把A ABE绕点A逆时针旋转90°至A ADG,可使AB与AD重合.因为乙ADC=Z B=90°,所以4FDG=180°,点F,D,G共线.根据，易证A AFG三，得EF=BE+DF.请证明.（2）类比引申如图②，四边形8CD中，AB=AD,Z BAD=90°,点E,F分别在边BC,CD上，Z EAF=45°.若Z B,Z D都不是直角，则当Z B与Z D满足等量关系时，EF=BE+DF 仍然成立，请证明．（3）联想拓展如图③，在A ABC中，Z BAC=90°,AB=AC，点D,E均在边BC上，且Z DAE=45°.猜想BD,DE,EC应满足的等量关系，并写出证明过程．7如图1已知AABC是等腰直角三角形，/BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上，连接AE,BG.(1)求证:AE=BG(2)将正方形DEFG绕点D逆时针方向旋转a(0°<aW360°)如图2所示，判断(1)中的结论是否仍然成立？如果仍成立，请给予证明；如果不成立，请说明理由；⑶若BC=DE=4,当旋转角a为多少度时，AE取得最大值？直接写出AE取得最大值时a的度数，并利用备用图画出这时的正方形DEFG,最后求出这时AF的值．8.如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为(6,6)，将正方形ABCO绕点C逆时针旋转角度a(0°<a<90°)，得到正方形CDEF，ED交线段AB 于点G，ED的延长线交线段OA于点H，连结CH、CG．F(1)求证：CG平分心DCB；(2)在正方形ABCO绕点C逆时针旋转的过程中，求线段HG、OH、BG之间的数量关系；(3)连结BD、DA、AE、EB，在旋转的过程中，四边形AEBD是否能在点G满足一定的条件下成为矩形？若能，试求出直线DE的解析式；若不能，请说明理由．9.已知正方形ABCD中，E为对角线BD上一点，过E点作EFLBD交BC于F,连接DF,G为DF中点，连接EG，CG.SF C B E B图①图②圄⑹⑴求证：EG=CG；(2)将图①中ABEF绕B点逆时针旋转45°,如图②所示，取DF中点G,连接EG,CG.问⑴中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；(3)将图①中ABEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问(1)中的结论是否仍然成立？通过观察你还能得出什么结论(均不要求证明)．10如图，四边形ABCD是正方形，E是边AB上一点，连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F.(1)如图1，求证：DE=DF；(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PHLCH交AB于点P,求证：E为AP中点；(3)如图3,在(2)的条件下，连接AC交EF于点G,连接BG,BH,若BG二V5,AB=3,求线段BH的长。