统计学第八版贾俊平指导书勘误
- 格式:docx
- 大小:38.20 KB
- 文档页数:5

(1N69)統計學(概要)(97年10月20日二版)勘誤表P.1第二段第二行第一個字 「及」應改為「計」。
P.31第13題解析(f +1-f M0)應更正為(f M0-f +1)。
P.7第18題答案修正為(A )P.10第(5)項原:資料歸屬應包含上限而不包含下限 修正為:資料歸屬應包含下限而不包含上限P.30第9題題目修正為:下列何者敘述「正確」? 答案修正為(全)解析更正為,資料的歸屬應包含下限而不包含上限P.97第5題選項(C )修正為0.376 解析修正為:X 服從二項分配(10,0.2)()()()91101100108.02.08.02.01C C X P +=≤=0.3758(約0.376)P.102第23題 答案修正為無解P.125第15題選項(C)應改為0.0228,另外更正解析(2)0.0228P Z ≥=P.127第20題選項(A)應改為75,100,另外更正解析22[(7075)..........]5100S =-+÷=P.127 第23題本題答案選項(C)0.6844,更正為0.6736。
【解析】220-225/125開根號=5/11.1803398874=0.4472=>四捨五入後約0.45P(Z≧-0.45)=0.6736P.153第22題本題答案更正為「無解」。
P.174第2題【解析】型I 誤差(type Ierror)當虛無假設H0為真,卻因抽樣誤差導致決策為拒絕H0,此種誤差稱為型I誤差。
型II誤差(type II error)當虛無假設H0為假,卻因抽樣誤差導致決策不拒絕H0,此種誤差稱為型II誤差。
故本題答案,應修正為(B)P.203第9題本題答案選項(C)3.94,更正為(C)3.54。
解析中,3.94更正為3.54P.203第10題本題答案選項(B)F0=36.548,應更正為40.678。
【解析】分子:32/2=16分母:3.54/9=0.3933333計算:16/0.3933333=40.678P.251第6題選項(C)修正為「有,Q=14.749」解析修正為:P.252 第四行Q =(28-33.33)233.33 +(48-36.67)236.67 +(19-10)210 +(32-33.33)233.33 …=19.249 修正為:Q =(28-33.33)233.33 +(48-36.67)236.67 +(4-10)210 +(32-33.33)233.33 …=14.749刪除下段文字:→採H 0的決策,即此五種牌子的洗髮精之品質並無差異。



统计学重点笔记第一章导论一、比较描述统计和推断统计:数据分析是通过统计方法研究数据,其所用的方法可分为描述统计和推断统计。
(1)描述性统计:研究一组数据的组织、整理和描述的统计学分支,是社会科学实证研究中最常用的方法,也是统计分析中必不可少的一步。
内容包括取得研究所需要的数据、用图表形式对数据进行加工处理和显示,进而通过综合、概括与分析,得出反映所研究现象的一般性特征。
(2)推断统计学:是研究如何利用样本数据对总体的数量特征进行推断的统计学分支。
研究者所关心的是总体的某些特征,但许多总体太大,无法对每个个体进行测量,有时我们得到的数据往往需要破坏性试验,这就需要抽取部分个体即样本进行测量,然后根据样本数据对所研究的总体特征进行推断,这就是推断统计所要解决的问题。
其内容包括抽样分布理论,参数估计,假设检验,方差分析,回归分析,时间序列分析等等。
(3)两者的关系:描述统计是基础,推断统计是主体二、比较分类数据、顺序数据和数值型数据:根据所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
(1)分类数据是只能归于某一类别的非数字型数据。
它是对事物进行分类的结果,数据表现为类别,是用文字来表达的,它是由分类尺度计量形成的。
(2)顺序数量是只能归于某一有序类别的非数字型数据。
也是对事物进行分类的结果,但这些类别是有顺序的,它是由顺序尺度计量形成的。
(3)数值型数据是按数字尺度测量的观察值。
其结果表现为具体的数值,现实中我们所处理的大多数都是数值型数据。
总之,分类数据和顺序数据说明的是事物的本质特征,通常是用文字来表达的,其结果均表现为类别,因而也统称为定型数据或品质数据;数值型数据说明的是现象的数量特征,通常是用数值来表现的,因此可称为定量数据或数量数据。
三、比较总体、样本、参数、统计量和变量:(1)总体是包含所研究的全部个体的集合。
通常是我们所关心的一些个体组成,如由多个企业所构成的集合,多个居民户所构成的集合。


统计学(贾俊平版)重点第一章统计:收集、处理、分析、解释数据并从数据中得出结论的科学。
数据1. 分类数据对事物进行分类的结果数据,表现为类别,用文字来表述.例如,人口按性别分为男、女两类2. 顺序数据对事物类别顺序的测度,数据表现为类别,用文字来表述例如,产品分为一等品、二等品、三等品、次品等3. 数值型数据对事物的精确测度,结果表现为具体的数值.例如:身高为175cm ,168cm,183cm总体–所研究的全部元素的集合,其中的每一个元素称为个体–分为有限总体和无限总体.有限总体的范围能够明确确定,且元素的数目是有限的.无限总体所包括的元素是无限的,不可数的样本–从总体中抽取的一部分元素的集合–构成样本的元素数目称为样本容量参数:描述总体特征。
有总体均值( )、标准差(σ)总体比例(π)统计量:描述样本特征。
样本标准差(s),样本比例(p)变量:说明现象某种特征,分类,顺序,数值型:离散型,连续型。
经验,理论变量描述统计研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计是研究如何利用样本数据进行推断总体特征第二章间接数据(查询的)与直接数据:调查(通常是对社会现象而言的)普查信息全面完整。
再一个是实验。
概率抽样:也称随机抽样。
按一定的概率以随机原则抽取样本,抽取样本时使每个单位都有一定的机会被抽中–每个单位被抽中的概率是已知的,或是可以计算出来的–当用样本对总体目标量进行估计时,要考虑到每个样本单位被抽中的概率简单随机抽样:从总体N个单位中随机地抽取n个单位作为样本,每个单位入抽样本的概率是相等的分层抽样:优点:保证样本的结构与总体的结构比较相近将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本,从而提高估计的精度–组织实施调查方便–既可以对总体参数进行估计,也可以对各层的目标量进行估计整群抽样:将总体中若干个单位合并为组(群),抽样时直接抽取群,然后对中选群中的所有单位全部实施调查优点:抽样时只需群的抽样框,可简化工作量–调查的地点相对集中,节省调查费用,方便调查的实施–缺点是统计的精度较差系统抽样:将总体中的所有单位(抽样单位)按一定顺序排列,在规定的范围内随机地抽取一个单位作为初始单位,然后按事先规定好的规则确定其它样本单位–先从数字1到k之间随机抽取一个数字r作为初始单位,以后依次取r+k,r+2k…等单位操作简便,可提高估计的精度多阶段抽样:先抽取群,但并不是调查群内的所有单位,而是再进行一步抽样,从选中的群中抽取出若干个单位进行调查–群是初级抽样单位,第二阶段抽取的是最终抽样单位。

第1章导论一、思考题1.什么是统计学?答:统计学是关于数据的科学,它所提供的是一套有关数据收集、处理、分析、解释并从数据中得出结论的方法,统计研究的是来自各领域的数据。
数据收集也就是取得统计数据;数据处理是将数据用图表等形式展示出来;数据分析则是选择适当的统计方法研究数据,并从数据中提取有用信息进而得出结论。
2.解释描述统计和推断统计。
答:数据分析所用的方法可分为描述统计方法和推断统计方法。
(1)描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计方法。
比如,对产品的质量进行检验,往往是破坏性的,不可能对每个产品进行测量。
这就需要抽取部分个体即样本进行测量,然后根据获得的样本数据对所研究的总体特征进行推断,这就是推断统计要解决的问题。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?答:统计数据是对现象进行测量的结果,可以从不同角度对统计数据进行分类:(1)按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
①在分类数据中,各类别之间是平等的并列关系,无法区分优劣或大小,各类别之间的顺序是可以改变的;②顺序数据也表现为类别,但这些类别之间是可以比较顺序的;③数值型数据具有分类数据和顺序数据的特点,并且还可以进行加、减、乘、除运算。
(2)按照统计数据的收集方法,可以将其分为观测数据和实验数据。
①观测数据是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的,有关社会经济现象的统计数据几乎都是观测数据;②实验数据则是在实验中控制实验对象而收集到的数据,自然科学领域的大多数数据都为实验数据;(3)按照被描述的现象与时间的关系,可以将统计数据分为截面数据和时间序列数据。
①截面数据是在相同或近似相同的时间点上收集的数据,这类数据通常是在不同的空间上获得的,用于描述现象在某一时刻的变化情况;②时间序列数据是在不同时间上收集到的数据,这类数据是按时间顺序收集到的,用于所描述现象随时间变化的情况。

《统计学》课后答案(第二版,贾俊平版)附录答案第6章-9章方差分析第6章方差分析6.1 0215.86574.401.0=<=F F (或01.00409.0=>=-αvalue P ),不能拒绝原假设。
6.2 579.48234.1501.0=>=F F (或01.000001.0=<=-αvalue P ),拒绝原假设。
6.3 4170.50984.1001.0=>=F F (或01.0000685.0=<=-αvalue P ),拒绝原假设。
6.4 6823.37557.1105.0=>=F F (或05.0000849.0=<=-αvalue P ),拒绝原假设。
6.5 8853.30684.1705.0=>=F F (或05.00003.0=<=-αvalue P ),拒绝原假设。
85.54.14304.44=>=-=-LSD x x B A ,拒绝原假设;85.58.16.424.44=<=-=-LSD x x C A ,不能拒绝原假设;85.56.126.4230=>=-=-LSD x x C B ,拒绝原假设。
6.6554131.3478.105.0=<=F F (或05.0245946.0=>=-αvalue P ),不能拒绝原假设。
第7章相关与回归分析7.1 (1)散点图(略),产量与生产费用之间正的线性相关关系。
(2)920232.0=r 。
(3)检验统计量2281.24222.142=>=αt t ,拒绝原假设,相关系数显著。
7.2 (1)散点图(略)。
(2)8621.0=r 。
7.3 (1)0?β表示当0=x 时y 的期望值。
(2)1?β表示x 每变动一个单位y 平均下降0.5个单位。
(3)7)(=y E 。
7.4 (1)%902=R 。
(2)1=e s 。
7.5 (1)散点图(略)。
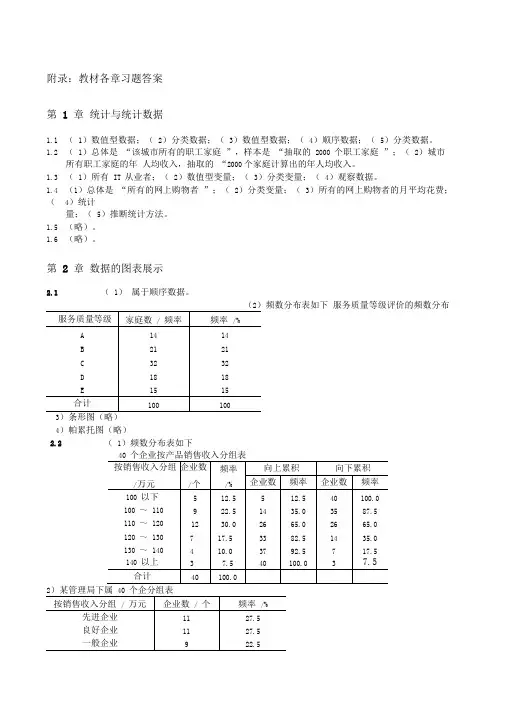
附录:教材各章习题答案第1 章统计与统计数据1.1(1)数值型数据;(2)分类数据;(3)数值型数据;(4)顺序数据;(5)分类数据。
1.2(1)总体是“该城市所有的职工家庭”,样本是“抽取的2000 个职工家庭”;(2)城市所有职工家庭的年人均收入,抽取的“2000个家庭计算出的年人均收入。
1.3(1)所有IT 从业者;(2)数值型变量;(3)分类变量;(4)观察数据。
1.4(1)总体是“所有的网上购物者”;(2)分类变量;(3)所有的网上购物者的月平均花费;(4)统计量;(5)推断统计方法。
1.5(略)。
1.6(略)。
第2 章数据的图表展示2.1 (1)属于顺序数据。
(2)频数分布表如下服务质量等级评价的频数分布3)条形图(略)4)帕累托图(略)2.2 (1)频数分布表如下402)某管理局下属40 个企分组表2.3 频数分布表如下某百货公司日商品销售额分组表2.4茎叶图如下茎叶数据个数1 8 8 93 2 0 1 1 3 3 6 8 8 8 9 9 912 3 13 5 6 95 4 1 2 36 67 6 50 1 2 74箱线图(略) 2.5 ( 1)排序略(2)频数分布表如下1数分布34)茎叶图如下茎叶65 66 67 68 5 5 6 6 6 7 7 8 8 8 8 9 970 7169720 1 2 2 5 6 7 8 9 973 3 5 674 1 4 72.6(1)频数分布表如下按重量分组频率/包40~42 242~44 344~46 746~48 1648~50 1752~52 1052~54 2054~56 856~58 1058~60 460~62 3合计100 (2)直方图(略)。
(3)食品重量的分布基本上是对称的2.7(1)频数分布表如下按重量误差分组频数/个10~20 020~30 530~40 740~50 850~60 1360~70 970~80 680~90 2合计50 2)直方图(略)2.8 (1)属于数值型数据( 2 )分组结果如下分组天数/天-25~-20 6-20~-15 8-15~-10 10-10~-5 13-5~0 120~5 45~10 7合计60( 3 )直方图(略)。

8.2 一种元件,要求其使用寿命不得低于700小时。
现从一批这种元件中随机抽取36件,测得其平均寿命为680小时。
已知该元件寿命服从正态分布,σ=60小时,试在显著性水平0.05下确定这批元件是否合格。
解:H 0:μ≥700;H 1:μ<700 已知:x =680 σ=60由于n=36>30,大样本,因此检验统计量:x z ==-2 当α=0.05,查表得z α=1.645。
因为z <-z α,故拒绝原假设,接受备择假设,说明这批产品不合格。
8.38.4 糖厂用自动打包机打包,每包标准重量是100千克。
每天开工后需要检验一次打包机工作是否正常。
某日开工后测得9包重量(单位:千克)如下:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5已知包重服从正态分布,试检验该日打包机工作是否正常(a =0.05)?解:H 0:μ=100;H 1:μ≠100 经计算得:x =99.9778 S =1.21221检验统计量:x t =-0.055 当α=0.05,自由度n -1=9时,查表得()29t α=2.262。
因为t <t α,样本统计量落在接受区域,故接受原假设,拒绝备择假设,说明打包机工作正常。
8.5 某种大量生产的袋装食品,按规定不得少于250克。
今从一批该食品中任意抽取50袋,发现有6袋低于250克。
若规定不符合标准的比例超过5%就不得出厂,问该批食品能否出厂(a =0.05)?解:解:H 0:π≤0.05;H 1:π>0.05已知: p =6/50=0.12检验统计量:Z ==2.271当α=0.05,查表得z α=1.645。
因为z >z α,样本统计量落在拒绝区域,故拒绝原假设,接受备择假设,说明该批食品不能出厂。
8.68.7 某种电子元件的寿命x(单位:小时)服从正态分布。
现测得16只元件的寿命如下: 159 280 101 212 224 379 179 264222 362 168 250 149 260 485 170问是否有理由认为元件的平均寿命显著地大于225小时(a =0.05)?解:H 0:μ≤225;H 1:μ>225 经计算知:x =241.5 s =98.726检验统计量:x t =0.669 当α=0.05,自由度n -1=15时,查表得()15t α=1.753。

第4页倒数第9行 将“……是基本事件的概率的可能性”改为“….是基本事件的概率的等可能性”第7页的第6行和第8行的公式中的“A μ”和“A μ”及“S μ”分别改为“()A μ”和“()A μ”及“()S μ”。
第10页中倒数第11行中“(3!12!)(4!4!4!4!)⨯”改为“(3!12!)(4!4!4!)⨯”第13页倒数第3行“贝叶斯公式可得”改为“由贝叶斯公式可得” 第14页第11行“概率均为…”改为“概率为…”,将例1-14中附图的数字改标为如下图的形式第15页中例1-16和第16页中例1-17中的“A μ”和“S μ”分别改为“()A μ”和“()S μ” 第16页中倒数第10行和第13行中的“()P AB ”均改为“()P AB ”第16页中最后一行中将“…生日同在各个月份…”改为“…生日在各个月份…” 第19页中第17行中的“()()()()A B A B A B A B ++++”改为 “()()()()A B A B A B A B ”第19页中倒数第9行中将“()()A B AB Ω- ”改为“()()A B S AB - ” 第20页中倒数第10行中的“(B )()AC B ”改为“(B )()AC B ” 第20页中倒数第9行中的“则()( )P AB =”改为“则()( )P AB =” 第21页第6行中将“()()P AB P AB =”改为“()()P AB P AB =” 第25页第15行中将“{}()(1),0,1,2,,kkn kk k n kn n n P k P X k C p p C p q k n --===-== ”改为“{}()(1),0,1,2,,kkn kn n P k P X k C p p k n -===-= ”第25页第19行中将“lim (),0,1,2,,!kn n P k e k n k λλ-→∞== ”改为lim ()lim (1),0,1,2,!kkk n kn n nn n n P k C p p e k k λλ--→∞→∞=-==第28页倒数第3行中将“0, 0(), 011, 1x Y g X x x x ≤⎧⎪==<≤⎨⎪>⎩”改为“0, 0(), 011, 1x y g x x x x ≤⎧⎪==<≤⎨⎪>⎩”第34页中倒数第10行中将“…第一路线较短…”改为“…第一条路线较短…”第36页第12行中将“…应选择第二条路线.”改为“…应选择第一条路线.” 第37页第9行中将“{}(1), 1,2,k P Y k p p k ==-= ”改为 “{}(1), 0,1,2,k P Y k p p k ==-= ”第40页中倒数第5行中公式中的“⨯”号改为“⋅”号第45页第8行中将“…独立性及不相关性的概念,了解这两个概念间的联系与区别,”改为“…独立性的概念,”第63页第14行中将“2231(60060), 010,150001()(20), 1020,150000, .Z z z z z f z z z ⎧-+≤<⎪⎪⎪=-≤<⎨⎪⎪⎪⎩其它”改为 “2331(60060), 010,150001()(20), 1020,150000, .Z z z z z f z z z ⎧-+≤<⎪⎪⎪=-≤<⎨⎪⎪⎪⎩其它” 第63页中倒数第4行将“}222)|y x y a +≤,如图3-7所示. 显然有(,)(,)GSf x y dxdy f x y dxdy ≤⎰⎰⎰⎰”改为“}222)|2y x y a +≤,如右图3-7.因为(,)0,,,f x y x y >-∞<<+∞显然有(,)(,)GSf x y dxdy f x y dxdy <⎰⎰⎰⎰,” 第64页第5行中将“22221x aa aedx e ---⎛⎫=-⎪⎪⎭⎰”改为“22221x aa aedx e ---⎛⎫<-⎪⎪⎭”第64页第722x aaedx --=⎰22x aaedx --<⎰第64页倒数第2行中将“220, 01,02()(,)30, X xy x dy x y f x f x y dy +∞-∞⎧⎛⎫+<<<<⎪ ⎪==⎝⎭⎨⎪⎩⎰⎰其它.” 改为“220, 01,()(,)30, X xy x dy x f x f x y dy +∞-∞⎧⎛⎫+<<⎪ ⎪==⎝⎭⎨⎪⎩⎰⎰其它.” 第67页第9行中将“…222cos 2222sin 12x y r x r Z y r ed erdr θπσσθθπσ+=--=⋅=⎰⎰”改为“…22cos 222sin12r x r zy r d erdr θπσθθπσ=-=⋅=⎰⎰”第67页第10行中将“22222220()12z r zr red e σσ--=--=-+⎰”改为“222222220()12r z zred e σσσ--=--=-+⎰”第67页第12行中将“2222'222()(1)z z Z z f z ee r σσ--=-+=”改为“2222222()(1)z z Z z f z ee σσσ--'=-+=”第67页第14行中将“2222, 0,()0, z Z z e z f z r σ-⎧⎪≥=⎨⎪⎩其他.”改为“2222, 0,()0, z Z z e z f z σσ-⎧⎪≥=⎨⎪⎩其他.”第69页倒数第4行中将“()f S ”改为“()f s ”第71页将第5行中“…关判断X 和Y 是…”改为“…并判断X 和Y 是…”第76页将第9行中“[(())][(())] (,1,2,,)ij i i j j E X E X X E X i j n σ=--= ”改为 “[(())(())] (,1,2,,)ij i i j j E X E X X E X i j n σ=--= ” 第83页将第14行中“1,X Y X Y μμσσ--==”改为“11,X Y X Y μμσσ--==”第88页倒数第5行中将“2()i i D X σ=i α(1,i =”改为“2()i i D X σ=,i α(1,i =”第89页第2行中将“22111()n n nn i i i i i i i i i D X D X ααασ===⎡⎤==⎢⎥⎣⎦∑∑∑”改为“222111()n n ni i i i i i i i i D X D X ααασ===⎡⎤==⎢⎥⎣⎦∑∑∑”第89页第4行中将“2121(,,,)nn n i i i f αααασ==∑ ”改为“22121(,,,)nn i ii f αααασ==∑ ”第89页第10行中将“2111ni iλσ==-∑”改为“2112ni iλσ==-∑”第90页第15行中将“{}11nkk n P X k ===∑∑”改为“{}11kk n P X k ∞===∑∑”第91页第5行中将“1()()1f x dx f x dx ∞-∞==⎰⎰”改为“120()()132a bf x dx ax bx c dx c ∞-∞=++=++=⎰⎰” 第92页倒数第5行中将“111{2,1}0{2}{1}428P X Y P X P =-==≠=-==⨯=”改为 “111{2,1}0{2}{1}428P X Y P X P Y =-==≠=-==⨯=” 第94页第21行中将“有奖购物问题”改为“有奖购物的应对策略”第98页第8行中将“22lim ()lim n t i x n n n X n F x P x e dt μ--∞→∞→∞⎧⎫-⎪⎪⎪=≤=⎬⎪⎪⎪⎩⎭∑⎰”改为“22lim ()lim n t i xn n n X n F x P x e dt μ--∞→∞→∞⎧⎫-⎪⎪⎪=≤=⎬⎪⎪⎪⎩⎭∑”第104页第5行中将“P X⎧=>⎨⎩”改为“P => ”第106页倒数第16行中将“计算同时用电户…”改为“同时用电户…” 第116页第1行中将“211~(0,),n n n X X N n σ++-”改为“211~(0,),n n n X X N nσ++-” 第128页倒数第9行中将“(1,)X B p -”改为“~(1,)X B p ” 第129页例7-5中将所有的“2u α”全部都改为“2z α”第133页第12行中将“12(1)(,,....,),n n x x x αα=+⋅ ”改为“12(1)(....),n n x x x αα=+⋅ ”第133页中第13行中将“1ln(,,)n x x α+ ”改为“1ln()n x x α+ ”第133页倒数第3行中将“1ˆmax{}i i nx θ≤≤=”改为“1ˆmin{}ii nx θ≤≤=” 第134页倒数第7,8,9,10行中的“1E θ∧,2E θ∧,3E θ∧,4E θ∧”分别改为“1ˆE θ,2ˆE θ,3ˆE θ,4ˆE θ” 第135页第7行中将“E θ∧,D θ∧”分别改为“ˆE θ,ˆD θ” 第135页第15行中将“⨯”号改为点乘号“⋅”第135页倒数第8行中将“12Y aX bX =+”改为“12Y aX bX =+”第135页倒数第6行中将“1EX μ=, 2EX μ=”改为“1EX μ=, μ=2X E ” 第135页倒数第4行中将“12Y aX bX =+”改为“21X b X a Y +=”第149页中将第6,7行中每个数字后的“次/min ”全部去掉第159页倒数第9行中将“此时拒绝域为”改为“此时接受域为”第163页第6行中将“问是否可以推论安装…”改为“问是否可以推断安装…” 第164页第11行中将“…有小一部分…”改为“…有一小部分…” 第178页倒数第4行中将“11n ≥”改为“171n ≥” 第179页第5行中将“(1)(D )”改为“(1)(B )” 第182页第10行中将“(5)1”改为“(5)12” 第184页倒数第10行中将“2ˆln X μ=矩”改为“2ˆln X μ=矩”。
统计学第八版贾俊平指导书勘误摘要:一、引言二、统计学第八版贾俊平指导书勘误概述1.勘误列表2.错误原因分析三、重要章节勘误及解析1.第一章:数据与统计思维1) 内容概述2) 勘误及解析2.第二章:概率论基础1) 内容概述2) 勘误及解析3.第三章:抽样分布与抽样分布律1) 内容概述2) 勘误及解析4.第四章:参数估计1) 内容概述2) 勘误及解析5.第五章:假设检验1) 内容概述2) 勘误及解析6.第六章:回归分析与相关分析1) 内容概述2) 勘误及解析7.第七章:时间序列分析与预测1) 内容概述2) 勘误及解析8.第八章:统计软件与应用1) 内容概述2) 勘误及解析四、总结与建议正文:一、引言随着统计学在我国各领域的广泛应用,贾俊平教授的《统计学》第八版成为了广大读者学习统计学的经典教材。
然而,在教材的编写和印刷过程中,难免会出现一些勘误。
本文旨在梳理并分析这些勘误,以助于读者更好地学习和掌握统计学知识。
二、统计学第八版贾俊平指导书勘误概述1.勘误列表根据读者反馈和网上讨论,我们整理出以下勘误列表:(1)部分公式编号错误;(2)部分符号、公式书写不规范;(3)部分例题解答错误;(4)部分章节内容重复或顺序混乱;(5)部分图表、数据有误。
2.错误原因分析(1)编撰过程中疏漏所致;(2)排版、校对失误;(3)教材更新迅速,部分内容未能及时修订。
三、重要章节勘误及解析1.第一章:数据与统计思维(1)内容概述:本章主要介绍数据的概念、分类、收集、整理、分析及统计思维的方法。
(2)勘误及解析:部分内容重复,建议删减或调整顺序。
2.第二章:概率论基础(1)内容概述:本章主要讲解概率论的基本概念、条件概率、独立性、贝叶斯定理等。
(2)勘误及解析:部分公式编号错误,符号书写不规范。
建议校对并更正。
3.第四章:参数估计(1)内容概述:本章主要介绍最大似然估计、矩估计、区间估计等方法。
(2)勘误及解析:部分例题解答错误,建议重新解答并校对。
第1章统计与统计数据一、学习指导统计学是处理和分析数据的方法和技术,它几乎被应用到所有的学科检验领域。
本章首先介绍统计学的含义和应用领域,然后介绍统计数据的类型及其来源,最后介绍统计中常用的一些基本概念。
本章各节的主要内容和学习要点如下表所示。
章节主要内容学习要点1.1 统计及其应用领域什么是统计学④概念:统计学,描述统计,推断统计。
统计的应用领域④统计在工商管理中的应用。
④统计的其他应用领域。
1.2 数据的类型分类数据、顺序数据、数值型数据④概念:分类数据,顺序数据,数值型数据。
④不同数据的特点。
观测数据和实验数据④概念:观测数据,实验数据。
截面数据和时间序列数据④概念:截面数据,时间序列数据。
1.3 数据来源数据的间接来源④统计数据的间接来源。
④二手数据的特点。
数据的直接来源④概念:抽样调查,普查。
④数据的间接来源。
④数据的收集方法。
调查方案设计④调查方案的内容。
数据质量④概念。
抽样误差,非抽样误差。
④统计数据的质量。
1.4 统计中的几个基本概念总体和样本④概念:总体,样本。
参数和统计量④概念:参数,统计量。
变量④概念:变量,分类变量,顺序变量,数值型变量,连续型变量,离散型变量。
二、主要术语1. 统计学:收集、处理、分析、解释数据并从数据中得出结论的科学。
2. 描述统计:研究数据收集、处理和描述的统计学分支。
3. 推断统计:研究如何利用样本数据来推断总体特征的统计学分支。
4. 分类数据:只能归于某一类别的非数字型数据。
5. 顺序数据:只能归于某一有序类别的非数字型数据。
6. 数值型数据:按数字尺度测量的观察值。
7. 观测数据:通过调查或观测而收集到的数据。
8. 实验数据:在实验中控制实验对象而收集到的数据。
9. 截面数据:在相同或近似相同的时间点上收集的数据。
10. 时间序列数据:在不同时间上收集到的数据。
11. 抽样调查:从总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来推断总体特征的数据收集方法。
统计学第八版贾俊平指导书勘误引言统计学是一门重要的学科,对于各个领域的研究和实践都具有重要的指导作用。
而《统计学第八版贾俊平指导书》作为一本经典的统计学教材,对于学习统计学的人来说具有重要的参考价值。
然而,任何书籍都难免会存在一些错误和疏漏,因此本文将对《统计学第八版贾俊平指导书》进行勘误,以期提供更准确、完整的统计学知识。
勘误内容第一章:统计学导论1.在第3页,第2段的第一句话中,“统计学是一门研究数据收集、整理、处理、分析、解释和推断的科学”中的“解释”一词应更正为“解读”。
第二章:统计学中的数据1.在第15页,第2段的第一句话中,“数据可以分为定量数据和定性数据”中的“定性”一词应更正为“质性”。
第三章:概率1.在第38页,第2段的第二句话中,“概率是指某个事件在多个重复试验中发生的相对频率”中的“重复试验”一词应更正为“独立试验”。
第四章:离散型随机变量与概率分布1.在第69页,第3段的第二句话中,“二项分布是指在n个相互独立的伯努利试验中成功次数的概率分布”中的“成功次数”一词应更正为“事件发生次数”。
第五章:连续型随机变量与概率分布1.在第96页,第1段的第一句话中,“连续型随机变量的概率分布可以通过概率密度函数来描述”中的“概率密度函数”一词应更正为“密度函数”。
第六章:多个随机变量的概率分布1.在第128页,第3段的第一句话中,“联合分布函数可以由边缘分布函数推导而来”中的“联合分布函数”一词应更正为“联合密度函数”。
第七章:样本及抽样分布1.在第157页,第1段的第一句话中,“样本是从总体中抽取的一部分观察值”中的“观察值”一词应更正为“个体”。
第八章:点估计1.在第185页,第2段的第一句话中,“点估计是利用样本数据来估计总体参数的方法”中的“参数”一词应更正为“未知参数”。
第九章:区间估计1.在第213页,第1段的第一句话中,“区间估计是利用样本数据给出总体参数估计范围的方法”中的“总体参数”一词应更正为“未知参数”。
第一章导论.1(1)数值型变量。
(2)分类变量。
(3)离散型变量。
(4)顺序变量。
(5)分类变量。
(1)总体是该市所有职工家庭的集合;样本是抽中的2000个职工家庭的集合。
(2)参数是该市所有职工家庭的年人均收入;统计量是抽中的2000个职工家庭的年人均收入。
(1)总体是所有IT从业者的集合。
(2)数值型变量。
(3)分类变量。
(4)截面数据。
(1)总体是所有在网上购物的消费者的集合。
(2)分类变量。
(3)参数是所有在网上购物者的月平均花费。
(4)参数(5)推断统计方法。
第二章数据的搜集1.什么是二手资料?使用二手资料需要注意些什么?与研究内容有关的原始信息已经存在,是由别人调查和实验得来的,并会被我们利用的资料称为“二手资料”。
使用二手资料时需要注意:资料的原始搜集人、搜集资料的目的、搜集资料的途径、搜集资料的时间,要注意数据的定义、含义、计算口径和计算方法,避免错用、误用、滥用。
在引用二手资料时,要注明数据来源。
2.比较概率抽样和非概率抽样的特点,举例说明什么情况下适合采用概率抽样,什么情况下适合采用非概率抽样。
概率抽样是指抽样时按一定概率以随机原则抽取样本。
每个单位被抽中的概率已知或可以计算,当用样本对总体目标量进行估计时,要考虑到每个单位样本被抽中的概率,概率抽样的技术含量和成本都比较高。
如果调查的目的在于掌握和研究总体的数量特征,得到总体参数的置信区间,就使用概率抽样。
非概率抽样是指抽取样本时不是依据随机原则,而是根据研究目的对数据的要求,采用某种方式从总体中抽出部分单位对其实施调查。
非概率抽样操作简单、实效快、成本低,而且对于抽样中的专业技术要求不是很高。
它适合探索性的研究,调查结果用于发现问题,为更深入的数量分析提供准备。
非概率抽样也适合市场调查中的概念测试。
3.调查中搜集数据的方法主要有自填式、面方式、电话式,除此之外,还有那些搜集数据的方法?实验式、观察式等。
4. 自填式、面方式、电话式调查个有什么利弊?自填式优点:调查组织者管理容易,成本低,可以进行较大规模调查,对被调查者可以刻选择方便时间答卷,减少回答敏感问题的压力。
贾俊平统计学思考题答案(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章:1、什么是统计学统计学是一门收集、分析、表述、解释数据的科学和艺术。
2、描述统计:研究的是数据收集、汇总、处理、图表描述、概括与分析等统计方法。
推断统计:研究的是如何利用样本数据来推断总体特征。
3、统计学据可以分成哪几种类型,个有什么特点按照计量尺度不同,分为:分类数据、顺序数据、数值型数据。
分类数据:只能归于某一类别的,非数字型数据。
顺序数据:只能归于某一有序类别的,非数字型数据。
数值型数据:按数字尺度测量的观察值,结果表现为数值。
按收集方法不同。
分为:观测数据、和实验数据观测数据:通过调查或观测而收集到的数据;不控制条件;社会经济领域实验数据:在试验中收集到的数据;控制条件;自然科学领域。
按时间不同,分为:截面数据、时间序列数据截面数据:在相同或近似相同的时间点上收集的数据。
时间序列数据:在不同时间收集的数据。
4、举例说明总体、样本、参数、统计量、变量这几个概念。
总体:是包含全部研究个体的集合,包括有限总体和无限总体(范围、数目判定)样本:从总体中抽取的一部分元素的集合。
参数:用来描述总体特征的概括性数字度量。
(平均数、标准差、比例等)统计量:用来描述样本特征的概括性数字度量。
(平均数、标准差、比例等)变量:是说明样本某种特征的概念,其特点:从一次观察到下一次观察结果会呈现出差别或变化。
(商品销售额、受教育程度、产品质量等级等)(对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
)5、变量可以分为哪几类分类变量:说明事物类别;取值是分类数据。
《统计学第八版贾俊平指导书勘误》序统计学作为一门重要的应用数学学科,对于理解和处理数据具有至关重要的地位。
而贾俊平编著的《统计学第八版》作为一本经典教材,被广泛应用于统计学教学和研究中。
然而,即使是经典之作也难免存在一些错误或疏漏,因此勘误也就显得至关重要。
本文将对《统计学第八版贾俊平指导书》进行全面评估,并提供相关的勘误内容,以帮助读者更好地理解和应用该教材。
一、对于《统计学第八版贾俊平指导书》的全面评估在对《统计学第八版贾俊平指导书》进行全面评估时,我们首先需要对其内容进行深入理解和分析。
该教材系统全面地介绍了统计学的基本概念、原理和方法,涵盖了概率论、数理统计和应用统计等内容,对于统计学初学者和进阶者都具有很大的参考价值。
然而,在阅读过程中,我们也发现了一些可能存在的错误或疏漏,这就需要我们进行勘误和修正。
二、《统计学第八版贾俊平指导书》的勘误内容1. 第xx页,第x行:“xxx”应更正为“xxx”。
在该页面和行数处出现了一个概念或术语的错误使用,正确的表述应当是“xxx”。
2. 第xx页,第x段,第x句:“xxx”应更正为“xxx”。
在该段落中出现了一个公式或推导的错误,正确的表述应当是“xxx”。
3. 第xx页,第x章,第x节:“xxx”应更正为“xxx”。
在该章节中出现了一个概念或原理的错误理解,正确的表述应当是“xxx”。
通过以上勘误内容的整理,我们可以更好地理解和应用《统计学第八版贾俊平指导书》,避免在学习和研究中出现错误或误解。
三、对于《统计学第八版贾俊平指导书》的个人观点和理解作为我个人来说,《统计学第八版贾俊平指导书》是一本非常重要的统计学教材,它系统地介绍了统计学的基本概念和方法,对于我在统计学领域的学习和研究具有很大的指导作用。
通过对该教材进行勘误和修正,我可以更加准确地理解和应用其中的知识,从而提高自己在统计学领域的能力和水平。
总结通过本文对《统计学第八版贾俊平指导书》的全面评估和勘误内容的整理,我们可以更好地理解和应用该教材,避免在学习和研究中出现错误或误解。
统计学第八版贾俊平指导书勘误
第八版《统计学》贾俊平指导书勘误全解析
序号: 1
在统计学领域,贾俊平教授的第八版《统计学》指导书被广泛认可为一本经典之作。
然而,就像任何一本重要的参考书籍一样,难免会有一些错误或疏忽之处。
在本文中,我将全面评估第八版《统计学》贾俊平指导书中的勘误,探讨这些错误或疏忽对于读者的影响,并分享个人对于该主题的观点和理解。
序号: 2
在评估贾俊平指导书的勘误之前,让我们先简要回顾统计学的基本概念。
统计学是一门关于数据收集、分析和解释的学科,旨在帮助我们理解和解释现实世界中的现象和变化。
在现代社会中,统计学在各个领域都起着重要的作用,从医学研究到市场调查,从环境科学到经济学,都依赖于统计学的方法和理论。
序号: 3
回到贾俊平指导书的勘误上来,我们不能忽视这些错误对读者的影响。
一个错误的公式或解释可能导致读者产生误解,进而影响他们对统计
学的理解和应用。
及时发现和纠正这些错误对于保持学科的准确性和
可靠性至关重要。
序号: 4
在第八版《统计学》贾俊平指导书的勘误中,我注意到了一些重要的
错误和疏忽。
在第三章的公式3.2中,分母的符号应为负号而非正号,这个错误可能会导致读者在计算中产生错误结果。
在第五章的表格5.3中,有一个数据单元的数值缺失,这可能会造成读者对该表格的误解。
这些错误和疏忽可能会对读者的学习和应用产生不必要的困扰,因此
应该尽快进行勘误和修正。
序号: 5
然而,尽管贾俊平指导书中存在一些错误和疏忽,我仍然认为这本书
是一本优秀的参考书。
贾俊平教授对统计学的深入理解和干货满满的
解释使其成为一本不可或缺的学习资料。
当我们阅读该指导书时,我
们应该保持批判性思维并对其中的错误进行评估和修正,以确保我们
真正理解统计学的核心概念和原则。
序号: 6
总结回顾一下,第八版《统计学》贾俊平指导书的勘误虽然存在一些
错误和疏忽,但这并不否定其作为一本经典参考书的价值。
作为读者,我们应该保持对这些错误的警惕,并主动寻找并修正其中的错误。
通
过批判性思维和主动学习,我们能够更加全面、深刻和灵活地理解统
计学的核心概念和原则。
序号: 7
个人观点和理解方面,我认为统计学的学习和应用是一个不断发展的
过程。
我们应该持续关注最新的研究成果和方法,以保持对统计学知
识的更新。
我们也应该把握统计学的核心原则和方法,以便在实际问
题中能够正确地收集、分析和解释数据。
序号: 8
在本文中,我详细评估了第八版《统计学》贾俊平指导书的勘误,强
调了错误和疏忽对于读者的影响,并分享了个人对于该主题的观点和
理解。
无论在统计学领域还是其他领域,我们都应该始终保持批判性
思维和主动学习的态度,以不断提高我们的知识水平和能力。
序号: 9
参考文献:
贾俊平. 统计学(第8版). 清华大学出版社, 2020.统计学作为一门学科,具有广泛的应用价值和深远的影响力。
然而,正如前文所述,统
计学的参考书籍中常常存在错误和疏忽。
这并不意味着我们应该抛弃
这些经典参考书,而是需要保持警惕并进行修正。
在阅读统计学相关参考书籍时,我们应该保持批判性思维。
批判性思
维是指对于所学知识持有独立、深入和有追求真理精神的思考方式。
在发现歧义、矛盾或错误时,我们应该主动进行验证和修正。
这需要
我们积极地查阅其他参考书籍、文献、论文以及与专业人士进行交流,以获得更准确的信息和理解。
只有通过批判性思维,我们才能获得更
加全面、准确和深入的统计学知识。
另外,我们也应该保持主动学习的态度。
主动学习是指积极主动地参
与学习过程,通过自主学习、实践和反思,不断提高自己的知识水平
和能力。
统计学是一门实践性很强的学科,光靠 passively learning (被动学习)很难获得深刻的理解。
我们应该主动利用各种学习资源,如在线课程、学术论坛、数据分析平台等,进行实践和探索,以加深
对统计学原理和方法的理解。
随着科技和学术研究的不断发展,统计学的理论和方法也在不断更新。
作为学习者,我们应该持续关注最新的研究成果和方法。
通过阅读最
新的论文、参加学术会议和交流活动,我们可以及时了解和掌握最新
的统计学知识。
我们也需要不断巩固和掌握统计学的核心原则和方法,以便在实际问题中能够基于准确的数据收集、分析和解释进行决策。
统计学的学习和应用是一个不断发展的过程,需要我们保持批判性思
维和主动学习的态度。
通过批判性思维,我们能够发现和修正参考书
中的错误和疏忽,以获得更准确的统计学知识。
通过主动学习,我们
能够深入理解统计学的核心原则和方法,并将其应用于实际问题当中。
只有不断更新知识,我们才能不断提高自己的能力,并更好地为社会
和科学做出贡献。
参考文献:
贾俊平. 统计学(第8版). 清华大学出版社, 2020.。