2地下水动力学基本理论_208909758

流体的地下水动力学流体的地下水动力学是研究地下水流动行为以及地下水运动规律的学科，涉及专业知识较多，包括水文地质学、地下水动力学等。

本文将介绍地下水动力学的基本概念、流体在地下的运动规律以及地下水资源管理等相关内容。

一、地下水动力学的基本概念地下水动力学是描述地下水流动行为的学科，它研究地下水的运动规律、影响因素以及地下水流体力学和传质过程等问题。

地下水动力学的研究对于水资源的合理开发和利用具有重要意义。

地下水动力学的基本概念包括：1. 地下水的来源和补给：地下水主要来源于降水的入渗和地表水的补给，其中入渗是地下水的重要补给方式。

2. 渗透率和孔隙度：地下岩层对水的渗透能力称为渗透率，而孔隙度则是描述岩层中可存储水的空隙比例。

3. 地下水流速和流量：地下水流速是单位时间内地下水通过单位面积的速度，流量是单位时间内通过某一断面的地下水体积。

4. 地下水压力和水头：地下水压力是地下水对岩层施加的压力，水头则是用来描述地下水压力差的概念。

5. 地下水流场和流线：地下水在地下岩层中的流动形态称为地下水流场，而地下水流场中各点连成的线路称为流线。

二、流体在地下的运动规律地下水动力学研究了流体在地下的运动规律，主要涉及泊松方程和达西定律等基本原理。

1. 泊松方程：泊松方程是描述地下水压力分布的方程，它描述了地下水压力与地下水位（或水头）之间的关系。

泊松方程可以帮助我们了解地下水的压力分布情况，并对地下水流动进行数值模拟和分析。

2. 达西定律：达西定律是描述地下水流速与水头梯度之间关系的定律，也称为达西-普朗克方程。

根据达西定律，地下水流速正比于水头梯度，并且与渗透率和孔隙度等因素有关。

3. 流体力学和传质过程：地下水流体力学是研究地下水流动行为的分支学科，它涉及地下水流速、流量、流体力与单位面积上岩石壁面作用力之间的关系。

此外，地下水中还存在着溶质的传质过程，即溶质在地下流体中的传输现象，它涉及浓度分布、扩散速率等问题。

内容主要有：（1）渗流理论基础；（2）地下水向河渠的稳定运动；（3）地下水向完整井的稳定运动；（4）地下水向完整井的非稳定运动；（5）地下水向边界附近井的稳定和非稳定运动。

重点考核地下水运动的基本概念、基本原理和方法。

题目类型有名词解释、判断题、作图题和计算题等，其中计算题占试题总分数的65%。

《地下水动力学》复习要点第一章 渗流理论基础一、基本内容1、基本概念：多孔介质、贮水率、贮水系数（弹性给水度）、渗流、渗流速度及与实际速度关系、水头（位置水头、测压管水头）、水力坡度、渗透系数、渗透率、导水系数、各向异性介质、各向同性介质、均质与非均质、水流折射原理、流网、dupuit 假设、第一类边界条件、第二类边界条件等2、基本定律：达西定律及适用范围3、描述地下水运动的方程：渗流连续性方程、承压水运动的基本微分方程、潜水运动的基本微分方程、越流含水层地下水非稳定流运动方程4、定解条件（初始条件、边界条件），数值方法基本思想二、要求1、理解并掌握上述概念和理论2、用达西定律分析水头线的变化或根据流网分析水文地质条件变化；3、给定水文地质条件，能正确画出反映地下水运动特点的流网图；4、给定水文地质模型和水文地质条件，写出反映地下水运动的基本方程（给定假设条件，建立数学模型，包括初始条件、边界条件）第二章 河间地块地下水的稳定运动一、基本内容有入渗时河间地块潜水的稳定运动问题（水文地质模型、假设条件、数学模型、流网、任意过水断面流量、分水岭移动规律、水头线）、无入渗时潜水的稳定运动、承压水的稳定运动，水在承压—无压含水层中的运动，非均质含水层中水的运动问题。

二、学习要求根据给定问题的水文地质条件，用相关公式计算过水断面流量或水位。

三、常用公式 1、承压含水层（达西定律） l H H m m kq 21212++= x lH H H H 211--= 2、无入渗潜水含水层（达西定律）l h h h h k q 21212-+= x lh h h h 2122212-+= 3、有入渗时潜水 wx wl l h h k q +--=2122221 )(22122212x lx kw x l h h h h -+-+= 4、分水岭位置 l h h w k l a 222221--= 5、其它流动问题（水平层状含水层、非均质含水层、承压—无压含水层、厚度或水流厚度沿流向变化等）第三章 地下水向完整井的稳定运动一、 基本概念：完整井、不完整井、水井及周围水位（水头）、稳定井流条件（定水头边界、越流、入渗补给）、井损与水跃、影响半径与引用影响半径、叠加原理、均匀流及平面或剖面流网二、学习要求1、掌握地下水向承压水井和潜水井运动问题的假设条件、数学模型、平面或剖面流网特征2、利用有关公式计算抽水量、降深或利用抽水试验资料（已知降深或水位），求含水层参数（导水系数或渗透系数）3、应用叠加原理地下水向完整井群的稳定运动问题。

（完整版）地下⽔动⼒学知识点总结基本问题潜⽔含⽔层的贮⽔能⼒可表⽰为Q=HF；承压含⽔层的贮⽔能⼒可表⽰为Q=HF；式中Q——含⽔层⽔位变化时H的贮⽔能⼒，H——⽔位变化幅度；F——地下⽔位受⼈⼯回灌影响的范围。

从中可以看出，因为承压含⽔层的弹性释⽔系数远远⼩于潜⽔含⽔层的给⽔度，因此在相同条件下进⾏⼈⼯回灌时，潜⽔含⽔层的贮⽔能⼒远远⼤于承压含⽔层的贮⽔能⼒。

⽔跃：抽⽔井中的⽔位与井壁外的⽔位之间存在差值的现象（seepage face）。

井损（well loss）是由于抽⽔井管所造成的⽔头损失。

①井损的存在：渗透⽔流由井壁外通过过滤器或缝隙进⼊抽⽔井时要克服阻⼒，产⽣⼀部分⽔头损失h1。

②⽔进⼊抽⽔井后，井内⽔流井⽔向⽔泵及⽔笼头流动过程中要克服⼀定阻⼒，产⽣⼀部分⽔头差h2。

③井壁附近的三维流也产⽣⽔头差h3。

通常将（h1+h2+h3）统称为⽔跃值.趋于等速下降。

113承压⽔井的Dupuit公式的⽔⽂地质概念模型(1)含⽔层为均质、各向同性，产状⽔平、厚度不变（等厚）、，分布⾯积很⼤，可视为⽆限延伸；或呈圆岛状分布，岛外有定⽔头补给；(2)抽⽔前地下⽔⾯是⽔平的，并视为稳定的；含⽔层中的⽔流服从Darcy’s Law，并在⽔头下降的瞬间将⽔释放出来，可忽略弱透⽔层的弹性释⽔；（3）完整井，定流量抽⽔，在距井⼀定距离上有圆形补给边界，⽔位降落漏⽃为圆域，半径为影响半径；经过较长时间抽⽔，地下⽔运动出现稳定状态；(4)⽔流为平⾯径向流，流线为指向井轴的径向直线，等⽔头⾯为以井为共轴的圆柱⾯，并和过⽔断⾯⼀致；通过各过⽔断⾯的流量处处相等，并等于抽⽔井的流量。

123承压⽔井的Dupuit公式的表达式及符号含义或式中，s w—井中⽔位降深，m；Q—抽⽔井流量，m3/d；M—含⽔层厚度，m；K—渗透系数，m/d；r w—井半径，m；R—影响半径（圆岛半径），m。

133Theim公式的表达式若存在两个观测孔，距离井中⼼的距离分别为r1，r2，⽔位分别为H1，H2，在r1到r2区间积分得：式中s1、s2分别为r1和r2处的⽔位降深。

高等地下水动力学1. 简介高等地下水动力学是研究地下水流动和传质过程的一门学科，主要涉及地下水的流速、压力、渗透率以及污染物在地下水中的迁移和扩散等方面。

本文将从以下几个方面介绍高等地下水动力学的基本理论和应用。

2. 地下水流动地下水是指土壤或岩石中填充的孔隙中充满的水。

地下水流动是指地下水在孔隙中由高压区向低压区运动的过程。

其流动规律可以通过达西定律来描述，即根据渗透性差异产生压差，使得地下水在渗透性较好的介质内形成流线，并遵循贝尔纳利方程进行运动。

3. 地下水传质地下水传质是指溶解物质在地下水中通过扩散、对流和反应等方式进行迁移和转化的过程。

其中扩散是指溶质由高浓度区向低浓度区沿浓度梯度进行自发性运动，对流则是指由于外部作用力（如水力压力）引起的溶质的迁移。

此外，地下水中的溶质还会通过化学反应进行转化，如酸碱中和、氧化还原等。

4. 地下水动力学模型为了定量描述地下水流动和传质过程，需要建立相应的地下水动力学模型。

通常采用连续介质假设，将地下储层视为连续均匀介质，并利用守恒方程和运动方程来描述地下水流动和传质的物理过程。

在实际建模中，需要考虑多种因素，如渗透率分布、边界条件、初值条件等。

5. 高等地下水动力学应用高等地下水动力学在环境工程和地下水资源管理方面具有重要应用价值。

它可以用于预测地下水污染物的迁移路径和浓度分布，评估污染源对周围环境的影响，并指导相应的污染治理措施。

同时，高等地下水动力学也可以用于优化地下水资源开发利用方案，提高供水效率，并保护地下水资源的可持续利用。

6. 结论高等地下水动力学是研究地下水流动和传质过程的重要学科，具有广泛的理论基础和应用价值。

通过建立地下水动力学模型，可以定量描述地下水的流动和传质特性，并为环境工程和地下水资源管理提供科学依据。

在今后的研究中，需要进一步深化对高等地下水动力学理论的认识，并结合实际工程问题进行应用研究，以推动该领域的发展与创新。

参考文献：1. Freeze, R. Allan, and John A. Cherry. “Groundwater.” (1979). 2. Bear, Jacob. “Dynamics of fluids in porous media.” Courier Corporation, 2013.以上是关于高等地下水动力学的简要介绍，希望对您有所帮助。

1，地下水动力学：研究地下水在孔隙岩石，裂隙岩石和岩溶（喀斯特）岩石中运动规律的科学第一章渗流理论基础2，多孔介质：在地下水动力学中，把具有孔隙的岩石称为多孔介质3有效空隙：互相连通的，不为结合水所占据的那一部分空隙4，有效孔隙度：有效孔隙体积与多孔介质总体积之比5，贮水率：又称释水率面积为一个单位，厚度为一个单位，当水头降低一个单位时所能释放出的水量贮水系数（释水系数）=贮水率乘以含水层厚度表示面积为一个单位，厚度为含水层全厚度的含水层主体中，当水头改变一个单位时弹性释放或贮存的水量贮水率与贮水系数相互关系：1，都是表示含水层弹性释水能力的参数2，对于承压含水层，只要水头不降低到隔水底板以下，水头降低只会引起弹性释水，可用贮水系数表示这种释水能力3，对于潜水含水层，当水头下降时可引起两部分水的排出（1，在上部潜水面下降引起重力排水，用给水度表示重力排水的能力2，在下部饱水部则引起弹性释水，用贮水率表示这一部分的释水能力）弹性释水和重力排水的不同点：1，影响范围不同（弹性释水影响整个承压含水层，重力释水影响潜水含水层和包气带）2，和时间有关（1 弹性释水瞬时完成不随时时间变化2 重力释水存在滞后效应是时间的函数）3 两只大小不同（弹性释水系数多在0.001-0.00005之间重力排水参数在0.1-0.01之间）7 渗流：假设这种假想水流运动时，在任意岩石体积内所受的阻力等于真是水流所受的阻力，通过任意断面的流量及任一点的压力或水头均和实际水流相同，这种假想水流称为渗流渗流与实际水流相比相同点：阻力相同水头相同流量相同8 渗流速度：代表渗流在过水断面上的平均流速，时一种假想流速实际平均流速：在空隙中的不同地点，地下水运动的方向和速度可能不同平均速度称为实际平均速度测压管水头：H_z=z+p/r水位：一般用在野外，基准面相同（黄海水位标高）水头：基准面可任意选定水位是一种特殊的水头运动要素：表征渗流运动的物理量，主要有渗流量Q，渗流速度V ，压强P，水头H等按运动要素和时间的关系分为：（1）稳定流：运动要素不随时间变化；（2）非稳定流：运动要素随时间变化按地下水运动方向和空间坐标的关系：一维运动，二维运动，三维运动12，层流：流速较小时，液体质点做有条不紊的线性运动，彼此不相掺混紊流：流速较大时，液体质点的运动轨迹曲折混乱，互相掺混13，Dacry在此处键入公式。

第一章 渗流理论基础§1-1 渗流的基本概念一、渗流及连续介质假说1 多孔介质(porous medium)与连续介质(continuous medium)多孔介质很难给出其精确定义，在地下水动力学中，把具有孔隙的岩石称为多孔介质。

它包括孔隙介质和裂隙介质。

一般来说，具有以下特点的物质就称为多孔介质。

（1）该物体为多相体：固体相-骨架，流体相-空隙；（2）固体相的分布遍及整个多相体所占据的区域；（3）空隙空间具有连通性。

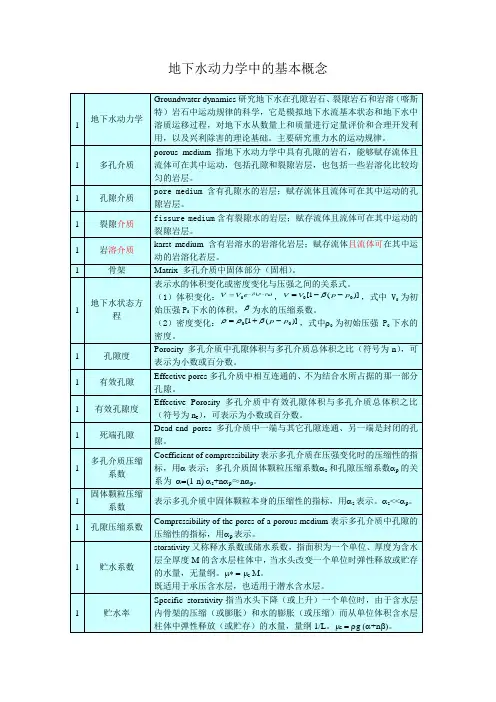
多孔介质由连续分布的多孔介质质点(图1-2)组成—多孔连续介质.此时孔隙度的表示公式为:--为数学点P 处多孔介质的表征体积元（简称为表征体元-REV ），将其所包含的所有流体质点与固体颗粒0v ∆的总体称为多孔介质质点.将其所包含的所有流体质点称为多孔介质流体质点。

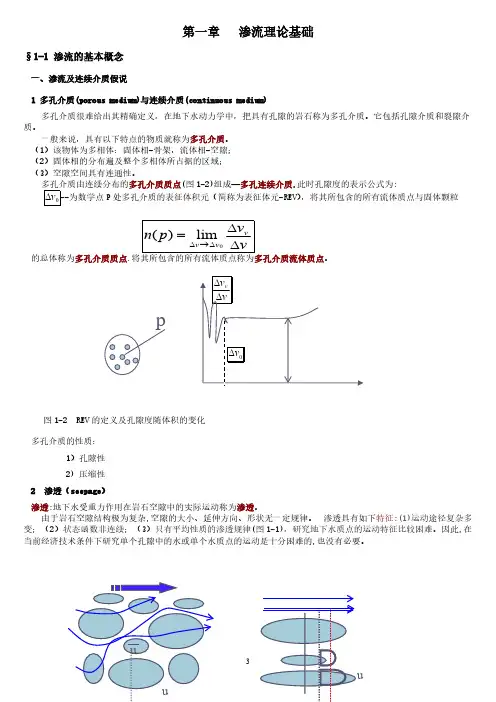
图1-2 REV 的定义及孔隙度随体积的变化多孔介质的性质：1）孔隙性2) 压缩性2 渗透（seepage ）渗透:地下水受重力作用在岩石空隙中的实际运动称为渗透。

由于岩石空隙结构极为复杂,空隙的大小、延伸方向、形状无一定规律。

渗透具有如下特征:(1)运动途径复杂多变；（2）状态函数非连续；（3）只有平均性质的渗透规律(图1-1)，研究地下水质点的运动特征比较困难。

因此,在当前经济技术条件下研究单个孔隙中的水或单个水质点的运动是十分困难的,也没有必要。

vv p n v v v ∆∆=∆→∆0lim)(图1-2岩石中地下水的渗透针对这种极为复杂的地下水运功，在地下水动力学中一般可采用两种研究方法。

1) 研究微观情况下的运动，即研究地下水在以孔隙介质中的骨架为边界孔隙或裂隙中的运动。

由于空隙介质的结构具有随机性，所以用统计平均方法来确定地下水运动的宏观规律性；2) 从宏观角度出发，采用试验及数学分析方法，对大量微观运动进行宏观研究得出各种运动条件下地下水运动的基本规律。

3 渗流(seepage flow)前面已经提到,要研究实际的渗透十分困难,因此,我们用一种假想水流来代替真实水流,这种假想水流是在连续介质的基础上通过概化得出的:(1)假定水流充满整个含水层空间(既包括空隙所占据的空间,也包括颗粒/骨架所占据的空间);(2)只考虑水流运动的总体方向,不考虑水流实际运动途径的复杂变化.将通过上述概化后所得到的假想水流—渗流。

1. 地下水动力学是研究地下水在孔隙岩石、裂隙岩石、和喀斯特岩石中运动规律的科学。

它是模拟地下水流基本状态和地下水中溶质运移过程，对地下水从数量和质量上进行定量评价和合理开发利用，以及兴利除害的理论基础。

2. 流量:单位时间通过过水断面的水量称为通过该断面的渗流量。

3. 渗流速度（比流量）:假设水流通过整个岩层断面（骨架+空隙）时所具有的虚拟平均流速，定义为通过单位过水断面面积的流量。

4. 实际速度：孔介质中地下水通过空隙面积的平均速度；地下水流通过含水层过水断面的平均流速，其值等于流量除以过水断面上的空隙面积，量纲为L/T。

4. 渗流场:发生渗流的区域称为渗流场。

由固体骨架和岩石空隙中的水两者组成5. 层流:水质点作有秩序、互不混杂的流动。

6. 紊流:水质点作无秩序、互相混杂的流动。

7. 稳定流与非稳定流:若流场中所有空间点上一切运动要素都不随时间改变时，称为稳定流，否则称为非稳定流。

8. 雷诺数:表征运动流体质点所受惯性力和粘性力的比值。

9. 雷诺数的物理意义:水流的惯性力与黏滞力之比。

10. 渗透系数:在各项同性介质（均质）中，用单位水力梯度下单位面积上的流量表示流体通过孔隙骨架的难易程度，称之为渗透系数。

11. 流网：在渗流场中，由流线和等水头线组成的网络称为流网。

12. 折射现象:地下水在非均质岩层中运动，当水流通过渗透系数突变的分界面时，出现流线改变方向的现象。

13. 裘布依假设：绝大多数地下水具有缓变流的特点。

14. 缓变流：各流线接近于平行直线的运动14. 完整井:贯穿整个含水层，在全部含水层厚度上都安装有过滤器并能全断面进水的井。

15. 非完整井:未揭穿整个含水层、只有井底和含水层的部分厚度上能进水或进水部分仅揭穿部分含水层的井。

16. 水位降深:抽水井及其周围某时刻的水头比初始水头的降低值。

17. 水位降落漏斗:抽水井周围由抽水（排水）而形成的漏斗状水头（水位）下降区，称为降落漏斗。

地质学中的地下水资源与地下水动力学地下水是地质学研究中重要的组成部分之一，它在地球系统中起着至关重要的作用。

地下水资源的开发利用和地下水动力学的研究成为地质学领域的重要课题。

本文将围绕地下水资源的形成、分布、开发利用以及地下水动力学的基本理论展开论述。

一、地下水资源的形成地下水是地球表面降水的重要去向之一。

它的形成主要受到降水量、地表水径流和土壤水分等因素的影响。

当降水量超过地表蒸发和植被蒸腾的量时，剩余的水分会渗入地下，形成地下水资源。

地下水资源的形成与地球的水循环密切相关。

二、地下水资源的分布地下水资源的分布具有一定的地域性和差异性。

它受到地质构造、岩石渗透性、地下水补给和排泄等多种因素的影响。

一般来说，地下水资源丰富的地区多为地质构造较为复杂、岩石渗透性较高的地方。

而地下水贫乏的地区则可能受到地下水补给不足或者地下水排泄过快的影响。

三、地下水资源的开发利用地下水资源的开发利用是为了满足人类的日常生活和工业农业用水需求。

根据地下水的深度、水质和开采技术的不同，可以采取不同的开发利用方式。

例如，浅层地下水资源可以通过打井和挖掘水井等方式进行开发利用；深层地下水资源则需要借助抽水机械和钻井技术等进行有效开采。

四、地下水动力学的基本理论地下水动力学是研究地下水流动规律和水文地质问题的学科。

它涉及到地下水的输运、扩散和水力特性等方面。

地下水动力学的研究可以借助数学模型和地球物理探测等方法来进行。

研究者可以通过模拟计算分析地下水流动的速度、路径和污染程度等，为地下水资源的合理开发和保护提供科学依据。

五、地下水资源的保护与利用地下水资源是有限的，它的开发利用必须与保护环境相协调。

为了保护地下水资源，需要加强对地下水的监测和管理，制定科学合理的开发方案，合理利用地下水资源。

此外，要加强环境教育和宣传，提高公众对地下水资源及其保护的意识。

六、地下水资源的挑战与未来发展随着人口的增加和工业农业的发展，地下水资源的利用面临着诸多挑战。

岩土中的地下水动力学分析地下水动力学是岩土工程中的重要分析内容之一。

地下水动力学研究地下水的运动规律和特性，在工程设计和施工中起到关键作用。

本文将对岩土中的地下水动力学进行深入分析，并探讨其在实际工程中的应用。

一、地下水动力学概述地下水动力学是研究地下水运动规律和特性的学科，通过分析水流速度、水头分布、渗透性等参数，来揭示地下水流动的机理。

地下水动力学在岩土工程中具有重要意义，它对于水库、地铁、隧道等工程的设计和施工具有指导作用。

二、地下水动力学的基本原理1. 达西定律达西定律是地下水动力学的基本原理之一。

它认为地下水的流动速度与渗透系数和水力坡度成正比。

在岩土工程中，通过测量地下水流速和水头分布，可以利用达西定律计算地下水的渗透系数，从而判断渗流的强弱。

2. 渗透性渗透性是地下水动力学中的重要参数，它直接影响地下水的流动性质。

渗透性可以通过实验室试验和场地观测获得。

在岩土工程中，需要根据渗透性的大小来选择合适的抗渗措施，保证工程的安全。

3. 水力坡度水力坡度指地下水流动的水头差与流动距离的比值。

水力坡度越大，地下水流速越快。

在岩土工程中，合理设计水力坡度可以提高地下水流动速度，减小渗流压力，减少工程灾害的发生。

三、地下水动力学的应用1. 工程设计地下水动力学对工程设计具有重要影响。

通过对地下水流场的分析，可以预测工程建设过程中可能遇到的地下水问题，为工程设计提供依据。

例如，在水利工程中，需要根据地下水动力学的分析来确定水库的导流能力和坝体的抗渗性能。

2. 施工监测地下水动力学分析还可以用于工程施工的监测。

在岩土工程施工过程中，地下水对施工有着直接影响。

通过监测地下水的流速和压力变化，可以及时预警施工风险，采取相应的措施进行调整。

3. 地质灾害防治地下水动力学也对地质灾害防治起到重要作用。

通过分析地下水流场的变化，可以预测地质灾害的发生，并采取相应的防治措施。

例如，在山区隧道工程中，地下水动力学分析可以帮助工程师判断隧道施工过程中的地下水涌泉风险，从而采取相应的排水措施。