胡寿松自动控制原理第五版

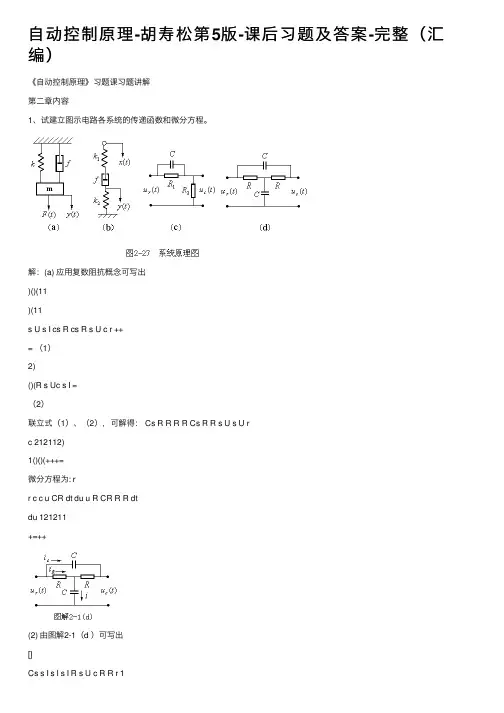
⾃动控制原理-胡寿松第5版-课后习题及答案-完整（汇编）《⾃动控制原理》习题课习题讲解第⼆章内容1、试建⽴图⽰电路各系统的传递函数和微分⽅程。

解：(a) 应⽤复数阻抗概念可写出)()(11)(11s U s I cs R cs R s U c r ++= （1）2)()(R s Uc s I =（2）联⽴式（1）、（2），可解得： Cs R R R R Cs R R s U s U rc 212112)1()()(+++=微分⽅程为: rr c c u CR dt du u R CR R R dtdu 121211+=++(2) 由图解2-1（d ）可写出[]Cs s I s I s I R s U c R R r 1)()()()(++= （5）)()(1)(s RI s RI Cs s I c R c -= （6）[]Cs s I s I R s I s U c R c c 1)()()()(++= （7）联⽴式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c微分⽅程为 r r r c c c u R C dt du CR dt du u R C dt du CR dt du 222222221213++=++2、试建⽴图⽰电路各系统的传递函数解：由图可写出s C R s U c 221)(+ = s C R s C R s C R s U r 111112111)(+?++ 整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 3、试⽤结构图等效化简求图2-32所⽰各系统的传递函数)()(s R s C 。

解（a ）所以： 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++=（b ）所以： H G G G s R s C 2211)()(--=（c ）所以：32132213211)()(G G G G G G G G G G s R s C +++= （d ）所以：2441321232121413211)()(H G G G G G G H G G H G G G G G G G s R s C ++++++= （e ）所以： 2321212132141)()(H G G H G H G G G G G G s R s C ++++=4、电⼦⼼脏起博器⼼律控制系统结构图如题3-49图所⽰，其中模仿⼼脏的传递函数相当于⼀纯积分环节。

第 一 章1-1 图1-2是液位自动控制系统原理示意图。

在任意情况下，希望液面高度c 维持不变，试说明系统工作原理并画出系统方块图。

图1-2 液位自动控制系统解：被控对象：水箱；被控量：水箱的实际水位；给定量电位器设定水位r u （表征液位的希望值r c ）；比较元件：电位器；执行元件：电动机；控制任务：保持水箱液位高度不变。

工作原理：当电位电刷位于中点（对应r u ）时，电动机静止不动，控制阀门有一定的开度，流入水量与流出水量相等，从而使液面保持给定高度r c ，一旦流入水量或流出水量发生变化时，液面高度就会偏离给定高度r c 。

当液面升高时，浮子也相应升高，通过杠杆作用，使电位器电刷由中点位置下移，从而给电动机提供一定的控制电压，驱动电动机，通过减速器带动进水阀门向减小开度的方向转动，从而减少流入的水量，使液面逐渐降低，浮子位置也相应下降，直到电位器电刷回到中点位置，电动机的控制电压为零，系统重新处于平衡状态，液面恢复给定高度r c 。

反之，若液面降低，则通过自动控制作用，增大进水阀门开度，加大流入水量，使液面升高到给定高度r c。

系统方块图如图所示：1-10 下列各式是描述系统的微分方程，其中c(t)为输出量，r (t)为输入量，试判断哪些是线性定常或时变系统，哪些是非线性系统?（１）222)()(5)(dt t r d t t r t c ++=；（２）)()(8)(6)(3)(2233t r t c dt t dc dt t c d dt t c d =+++； （３）dt t dr t r t c dt t dc t )(3)()()(+=+； （４）5cos )()(+=t t r t c ω； （５）⎰∞-++=t d r dt t dr t r t c ττ)(5)(6)(3)(；（６）)()(2t r t c =；（７）⎪⎩⎪⎨⎧≥<=.6),(6,0)(t t r t t c解：（1）因为c(t)的表达式中包含变量的二次项2()r t ，所以该系统为非线性系统。

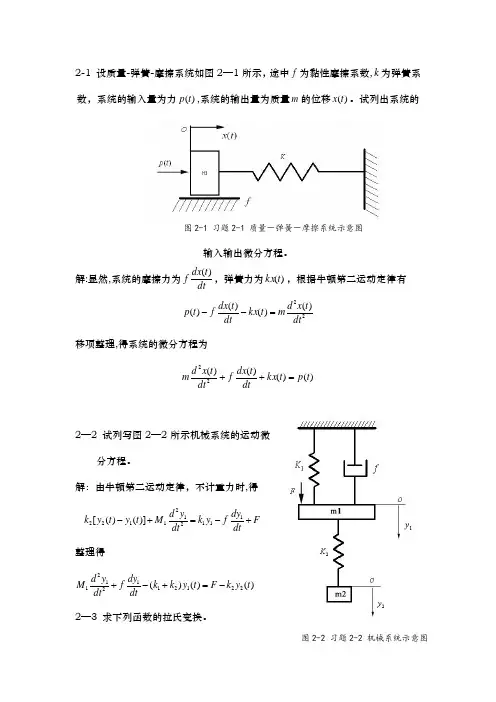
2-1 设质量-弹簧-摩擦系统如图2—1所示，途中f 为黏性摩擦系数,k 为弹簧系数，系统的输入量为力()p t ,系统的输出量为质量m 的位移()x t 。

试列出系统的输入输出微分方程。

解:显然,系统的摩擦力为dtt dx f)(，弹簧力为)(t kx ，根据牛顿第二运动定律有 22)()()()(dtt x d m t kx dt t dx f t p =-- 移项整理,得系统的微分方程为)()()()(22t p t kx dtt dx f dt t x d m =++2—2 试列写图2—2所示机械系统的运动微分方程。

解：由牛顿第二运动定律，不计重力时,得2112211112[()()]d y dyk y t y t M k y f F dt dt-+=-+整理得2111121222()()()d y dyM f k k y t F k y t dt dt+-+=-2—3 求下列函数的拉氏变换。

图2-1 习题2-1 质量－弹簧－摩擦系统示意图图2-2 习题2-2 机械系统示意图（1))sin 1(3)(t t f -= （2）at te t f =)( (3）)43cos()(π-=t t f解：（1）[()][3(1sin )]L f t L t =-2223([1][sin ])113()13(1)(1)L L t s s s s s s =-=-+-+=+ (2)at te t f =)(21[]L t s=21[()][]()at L f t L te s a ==-(3）()cos(3))cos(3)]42f t t t t π=-=+[()])cos(3)]2L f t t t =+222[sin(3)][cos(3)])3)29939L t L t s s s s s =+=++++=+2—4 求下列函数的拉氏反变换 （1）)5)(2(1)(++-=s s s s F(2）)3(6)(2+-=s s s s F（3）)1(152)(22++-=s s s s s F解：(1)112()(2)(5)25s F s s s s s --==+++++1112[()][]25L F s L s s ---=+++ 112512[]2[]252ttL L s s e e ----=-+++=-+ (2)226211()(3)3s F s s s s s s --==++++ 112211[()][]3L F s L s s s ---=+++ 111231112[][][]321t L L L s s s t e ----=+-+=+- （3)22225115()(1)1s s s F s s s s s -+-==+++ 11215[()][]1s L F s L s s ---=++11215[][]11cos 5sin s L L s s t t ---=++=+-2—5 试分别列写图2—3中各无源网络的微分方程（设电容C 上的电压为)(t u c ，电容1C 上的电压为)(1t u c ，以此类推）。

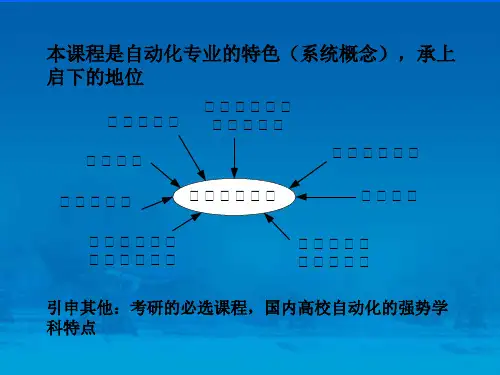
2—1 设水位自动控制系统的原理方案如图1—18 所示，其中Q1 为水箱的进水流量，Q2 为水箱的用水流量，H 为水箱中实际水面高度。

假定水箱横截面积为F，希望水面高度为H0 ，与H对应的水流量为Q，试列出水箱的微分方程。

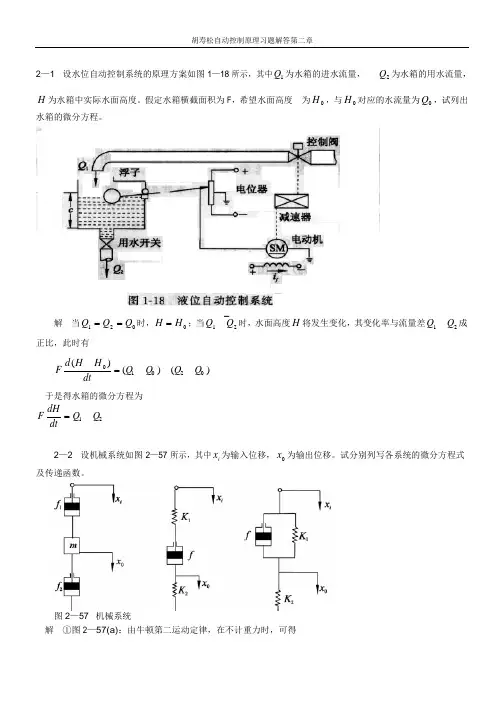
解当Q1 =Q2=Q时，H =H；当Q1⎺Q2时，水面高度H 将发生变化，其变化率与流量差Q1Q2成正比，此时有F d (H H)= (Q Q ) (Q Q ) dt 1 0 2 0于是得水箱的微分方程为F dH=Q Qdt 1 22—2 设机械系统如图2—57 所示，其中x i 为输入位移，x0 为输出位移。

试分别列写各系统的微分方程式及传递函数。

图2—57 机械系统解①图2—57(a)：由牛顿第二运动定律，在不计重力时，可得2 1f 1 ( x &i x &0 ) f 2 x &0 = m &x&0整理得m d x 0+ ( f + f ) dx 0 = f dx i dt 2 1 2 dt 1 dt将上式进行拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得[ms 2+ ( f + f 2)s ]X 0(s ) = f 1sX i(s )于是传递函数为X 0 (s ) =X i (s ) f 1 ms + f 1 + f 2②图 2—57(b)：其上半部弹簧与阻尼器之间，取辅助点 A ，并设 A 点位移为 x ，方向朝下；而在其下半部工。

引出点处取为辅助点 B 。

则由弹簧力与阻尼力平衡的原则，从 A 和 B 两点可以分别列出如下原始方程：K 1 ( x i x ) =f ( x & x &0 )K 2 x 0 = f ( x & x&0 )消去中间变量 x ，可得系统微分方程f (K + K ) dx 0 + K K x= K f dx i 1 2 dt 1 2 0 1 dt对上式取拉氏变换，并计及初始条件为零，得系统传递函数为X 0 (s ) =X i (s ) fK 1 s f (K 1 + K 2 )s + K 1 K 2③图 2—57(c)：以 x 0 的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：K 1 ( x i x ) + f ( x &i x&0 ) = K 2 x 0移项整理得系统微分方程f dx 0+ (K dt 1 + K2 ) x 0 = f dx i dt+ K 1 x i对上式进行拉氏变换，并注意到运动由静止开始，即x i (0) = x 0 (0) = 0则系统传递函数为X 0 (s ) =X i (s ) fs + K 1 fs + (K 1 + K 2 )2-3 试证明图2-58(ａ)的电网络与(b)的机械系统有相同的数学模型。

自动控制原理课后答案1 请解释下列名字术语：自动控制系统、受控对象、扰动、给定值、参考输入、反馈。

解：自动控制系统：能够实现自动控制任务的系统，由控制装置与被控对象组成；受控对象：要求实现自动控制的机器、设备或生产过程扰动：扰动是一种对系统的输出产生不利影响的信号。

如果扰动产生在系统内部称为内扰；扰动产生在系统外部，则称为外扰。

外扰是系统的输入量。

给定值：受控对象的物理量在控制系统中应保持的期望值参考输入即为给定值。

反馈：将系统的输出量馈送到参考输入端，并与参考输入进行比较的过程。

2 请说明自动控制系统的基本组成部分。

解：作为一个完整的控制系统，应该由如下几个部分组成：①被控对象：所谓被控对象就是整个控制系统的控制对象；②执行部件：根据所接收到的相关信号，使得被控对象产生相应的动作；常用的执行元件有阀、电动机、液压马达等。

③给定元件：给定元件的职能就是给出与期望的被控量相对应的系统输入量（即参考量）；④比较元件：把测量元件检测到的被控量的实际值与给定元件给出的参考值进行比较，求出它们之间的偏差。

常用的比较元件有差动放大器、机械差动装置和电桥等。

⑤测量反馈元件：该元部件的职能就是测量被控制的物理量，如果这个物理量是非电量，一般需要将其转换成为电量。

常用的测量元部件有测速发电机、热电偶、各种传感器等；⑥放大元件：将比较元件给出的偏差进行放大，用来推动执行元件去控制被控对象。

如电压偏差信号，可用电子管、晶体管、集成电路、晶闸管等组成的电压放大器和功率放大级加以放大。

⑦校正元件：亦称补偿元件，它是结构或参数便于调整的元件，用串联或反馈的方式连接在系统中，用以改善系统的性能。

常用的校正元件有电阻、电容组成的无源或有源网络，它们与原系统串联或与原系统构成一个内反馈系统。

3 请说出什么是反馈控制系统，开环控制系统和闭环控制系统各有什么优缺点？解：反馈控制系统即闭环控制系统，在一个控制系统，将系统的输出量通过某测量机构对其进行实时测量，并将该测量值与输入量进行比较，形成一个反馈通道，从而形成一个封闭的控制系统；开环系统优点：结构简单，缺点：控制的精度较差；闭环控制系统优点：控制精度高，缺点：结构复杂、设计分析麻烦，制造成本高。

第 一 章1-1 图1-2是液位自动控制系统原理示意图。

在任意情况下，希望液面高度c 维持不变，试说明系统工作原理并画出系统方块图。

图1-2 液位自动控制系统解：被控对象：水箱；被控量：水箱的实际水位；给定量电位器设定水位r u （表征液位的希望值r c ）；比较元件：电位器；执行元件：电动机；控制任务：保持水箱液位高度不变。

工作原理：当电位电刷位于中点（对应r u ）时，电动机静止不动，控制阀门有一定的开度，流入水量与流出水量相等，从而使液面保持给定高度r c ，一旦流入水量或流出水量发生变化时，液面高度就会偏离给定高度r c。

当液面升高时，浮子也相应升高，通过杠杆作用，使电位器电刷由中点位置下移，从而给电动机提供一定的控制电压，驱动电动机，通过减速器带动进水阀门向减小开度的方向转动，从而减少流入的水量，使液面逐渐降低，浮子位置也相应下降，直到电位器电刷回到中点位置，电动机的控制电压为零，系统重新处于平衡状态，液面恢复给定高度r c。

反之，若液面降低，则通过自动控制作用，增大进水阀门开度，加大流入水量，使液面升高到给定高度r c。

系统方块图如图所示：1-10 下列各式是描述系统的微分方程，其中c(t)为输出量，r (t)为输入量，试判断哪些是线性定常或时变系统，哪些是非线性系统?（１）222)()(5)(dt t r d tt r t c ++=；（２）)()(8)(6)(3)(2233t r t c dt t dc dt t c d dt t c d =+++；（３）dt t dr t r t c dt t dc t )(3)()()(+=+； （４）5cos )()(+=t t r t c ω；（５）⎰∞-++=t d r dt t dr t r t c ττ)(5)(6)(3)(；（６）)()(2t r t c =；（７）⎪⎩⎪⎨⎧≥<=.6),(6,0)(t t r t t c解：（1）因为c(t)的表达式中包含变量的二次项2()r t ，所以该系统为非线性系统。