自动控制原理-胡寿松第5版-课后习题及答案-完整(汇编)
- 格式:doc
- 大小:962.50 KB
- 文档页数:24

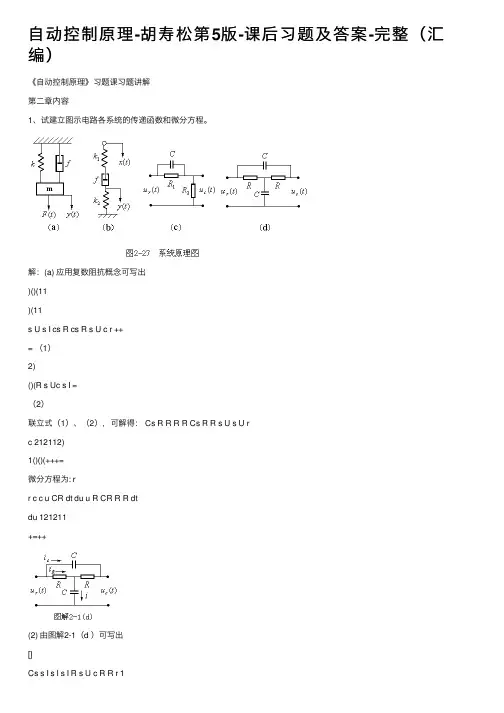
⾃动控制原理-胡寿松第5版-课后习题及答案-完整(汇编)《⾃动控制原理》习题课习题讲解第⼆章内容1、试建⽴图⽰电路各系统的传递函数和微分⽅程。
解:(a) 应⽤复数阻抗概念可写出)()(11)(11s U s I cs R cs R s U c r ++= (1)2)()(R s Uc s I =(2)联⽴式(1)、(2),可解得: Cs R R R R Cs R R s U s U rc 212112)1()()(+++=微分⽅程为: rr c c u CR dt du u R CR R R dtdu 121211+=++(2) 由图解2-1(d )可写出[]Cs s I s I s I R s U c R R r 1)()()()(++= (5))()(1)(s RI s RI Cs s I c R c -= (6)[]Cs s I s I R s I s U c R c c 1)()()()(++= (7)联⽴式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c微分⽅程为 r r r c c c u R C dt du CR dt du u R C dt du CR dt du 222222221213++=++2、试建⽴图⽰电路各系统的传递函数解:由图可写出s C R s U c 221)(+ = s C R s C R s C R s U r 111112111)(+?++ 整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 3、试⽤结构图等效化简求图2-32所⽰各系统的传递函数)()(s R s C 。
解(a )所以: 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++=(b )所以: H G G G s R s C 2211)()(--=(c )所以:32132213211)()(G G G G G G G G G G s R s C +++= (d )所以:2441321232121413211)()(H G G G G G G H G G H G G G G G G G s R s C ++++++= (e )所以: 2321212132141)()(H G G H G H G G G G G G s R s C ++++=4、电⼦⼼脏起博器⼼律控制系统结构图如题3-49图所⽰,其中模仿⼼脏的传递函数相当于⼀纯积分环节。



第 一 章1-1 图1-2是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c 维持不变,试说明系统工作原理并画出系统方块图。
图1-2 液位自动控制系统解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位r u (表征液位的希望值r c );比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
工作原理:当电位电刷位于中点(对应r u )时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度r c ,一旦流入水量或流出水量发生变化时,液面高度就会偏离给定高度r c 。
当液面升高时,浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到电位器电刷回到中点位置,电动机的控制电压为零,系统重新处于平衡状态,液面恢复给定高度r c 。
反之,若液面降低,则通过自动控制作用,增大进水阀门开度,加大流入水量,使液面升高到给定高度r c。
系统方块图如图所示:1-10 下列各式是描述系统的微分方程,其中c(t)为输出量,r (t)为输入量,试判断哪些是线性定常或时变系统,哪些是非线性系统?(1)222)()(5)(dt t r d t t r t c ++=;(2))()(8)(6)(3)(2233t r t c dt t dc dt t c d dt t c d =+++; (3)dt t dr t r t c dt t dc t )(3)()()(+=+; (4)5cos )()(+=t t r t c ω; (5)⎰∞-++=t d r dt t dr t r t c ττ)(5)(6)(3)(;(6))()(2t r t c =;(7)⎪⎩⎪⎨⎧≥<=.6),(6,0)(t t r t t c解:(1)因为c(t)的表达式中包含变量的二次项2()r t ,所以该系统为非线性系统。

胡寿松版完整答案自动控制原理第五版课后习题答案2-1设质量-弹簧-摩擦系统如图2-1所示,途中f为黏性摩擦系数,k为弹簧系数,系统的输入量为力p(t),系统的输出量为质量m的位移x(t)。
试列出系统的图2-1练习2-1质量弹簧摩擦系统示意图输入输出微分方程。
解决方案:显然,系统的摩擦力是FDX(T),弹簧力是KX(T)。
根据牛顿第二运动定律,有dtdx(T)d2x(T)P(T)吗?Fkx(t)?系统的微分方程是d2x(t)dx(t)m?f?kx(t)?p(t)dt2dt2-2试列写图2-2所示机械系统的运动微分方程式解:由牛顿第二运动定律,不计重力时,得d2y1dyk2[y2(t)?y1(t)]?m12?k1y1?f1?Fdtdt整理得d2y1dym12?f1?(k1?k2)y1(t)?Fk2y2(t)dtdt2-3求下列函数的拉氏变换。
图2-2练习2-2机械系统示意图(1)f(t)?3(1?sint)(2)f(t)?teat(3)f(t)?cos(3t??4)解决方案:(1)l[f(T)]?l[3(1?辛特)]3(l[1]l[sint])113(2)ss13(s2s1)s(s21)(2)f(t)?teatl[t]?12s12(s?a)l[f(t)]?l[乳头]??2[sin(3t)?cos(3t)](3)f (t)?cos(3t?)?42l[f(t)]?2[sin(3t)?cos(3t)]22(l[sin(3t)]?l[cos(3t)]223s?(2?2)2s?9秒?92秒?3.2s2?9?2-4求下列函数的拉氏反变换(1)f(s)?s?1(s?2)(s?5)s?6s2(s?3)(2)f(s)?2s2?5秒?1(3)f(s)?s(s2?1)解:(1)f(s)?s?1?12??(s?2)(s?5)s?2秒?5l?1[f(s)]?L1[?12?] s2秒?512]? 2l?1.s?2秒?5.2e?5t??L1[?e?2t(2)f(s)?s?621?122s(s?3)sss?3l?1[f (s)]?L1[21?1??] 2sss?311? 11? 1]? l[]?l.[s2ss]?3.2t?1.E3t?2l?1[2s2?5s?11s?5?2(3)f(s)?2s(s?1)ss?11s?5l?1[f(s)]?L1[?2]ss?11s?5?l?1[]?l?1[2]ss?1?1?cost?5sint2-5试着在图2-3中写下每个无源网络的微分方程(让电容器C上的电压为UC(T),电容器C1上的电压为uc1(T),依此类推)。

3.4 已知二阶系统的单位阶跃响应为)6.1sin(5.1210)(1.532.1︒-+-=t t h et试求系统的超调量σ%,峰值时间t p 和调节时间 t s 。
解:t e t t t heeettt6.1sin 25)6.1cos(20)6.1sin(15)(2.12.12.11.531.53-︒-︒-=+-+=44.240)]([)(2++==s s t hL s φ 阻尼比ξ= 0.6, 自然频率2=w n,阻尼振荡频率wd=6.16.01212=-⨯=-=ξw w n d因为0<ξ<1,所以系统是欠阻尼状态。
1. 峰值时间tp的计算96.16.1===ππwt dp2. 调节时间ts的计算9.226.05.35.3=⨯==w t ns ξ3. 超调量σ%的计算%48.9%1006.0%100%221/6.01/=⨯=⨯=-⨯---eeππξξσ3-8设控制系统如图3-9所示。
要求:(1) 取,1.0,021==ττ计算测速反馈校正系统的超调量,调节时间和速度误差;图3-9 控制系统解答:(1)取120,0.1ττ==时,系统的传递函数为()210()210()210G s s s s s s =+Φ=++由开还传递函数可知,此系统是一个I 型系统,其速度系数为5v K =,由静态误差系数法可得系统的速度误差为10.2ss ve K ==由闭环传递函数可知,13.16,0.3163.16n ωζ====,故 超调量%35.09%e σ-==调节时间 3.53.5s nt ζω==超调量%76%d t ζσ-==调节时间3-9 已知系统特征方程为432310520s s s s ++++=试用劳思判据和赫尔维茨判据确定系统的稳定性。
并写出正实部根和负实部根及虚根数。
解答:首先用劳思判据来判定系统的稳定性,列出劳思表如下:43210 3 5 2 10 1472 10153472s s s s s -显然,由于表中第一列元素的符号有两次改变,所以该系统在s 右半平面有两个闭环极点。


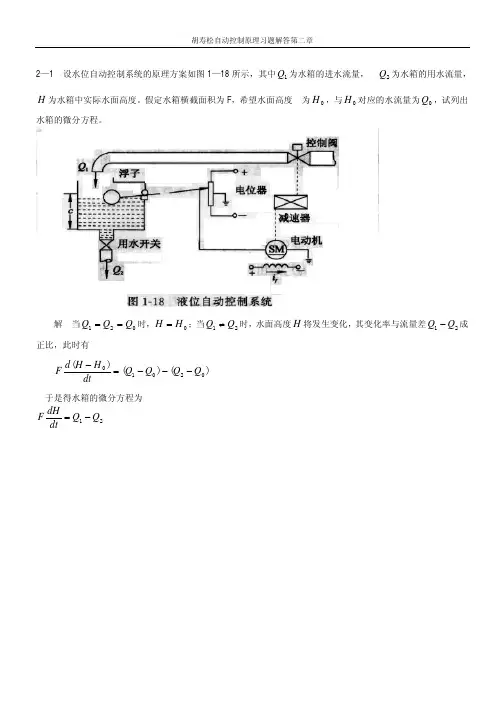
2—1 设水位自动控制系统的原理方案如图1—18 所示,其中Q1 为水箱的进水流量,Q2 为水箱的用水流量,H 为水箱中实际水面高度。
假定水箱横截面积为F,希望水面高度为H,与H对应的水流量为Q,试列出水箱的微分方程。
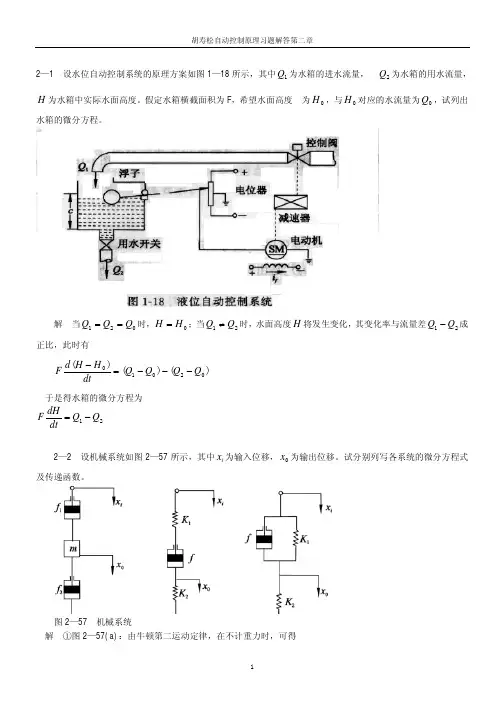
解当Q1=Q2=Q时,H =H;当Q1⎺Q2时,水面高度H 将发生变化,其变化率与流量差Q1Q2成正比,此时有Fd (H H)= (Q Q ) (QQ )dt 1 0 2 0于是得水箱的微分方程为FdH=Q Qdt 1 22—2 设机械系统如图2—57 所示,其中x i 为输入位移,x0 为输出位移。
试分别列写各系统的微分方程式及传递函数。
图2—57 机械系统解①图2—57(a):由牛顿第二运动定律,在不计重力时,可得2 1f 1 ( x &i x &0 ) f 2 x &0 = m &x&0整理得m d x 0 + ( f + f ) dx 0 = f dx i dt 2 1 2dt 1 dt将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[ms 2+ ( f + f 2)s ]X 0(s ) = f 1sX i(s )于是传递函数为X 0 (s ) =X i (s ) f 1ms + f 1 + f 2②图 2—57(b):其上半部弹簧与阻尼器之间,取辅助点 A ,并设 A 点位移为 x ,方向朝下;而在其下半部工。
引出点处取为辅助点 B 。
则由弹簧力与阻尼力平衡的原则,从 A 和 B 两点可以分别列出如下原始方程:K 1 ( x i x ) =f ( x & x &0 )K 2 x 0 = f ( x& x &0 )消去中间变量 x ,可得系统微分方程f (K + K ) dx 0 + K K x= K f dx i1 2 dt 1 2 01 dt对上式取拉氏变换,并计及初始条件为零,得系统传递函数为X 0 (s ) =X i (s ) fK 1 s f (K 1 + K 2 )s + K 1 K 2③图 2—57(c):以 x 0 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:K 1 ( x i x ) + f ( x&i x &0 ) = K 2 x 0移项整理得系统微分方程f dx0 + (K dt 1+ K 2) x 0= f dx i dt+ K 1 x i对上式进行拉氏变换,并注意到运动由静止开始,即x i (0) = x 0 (0) = 0则系统传递函数为X 0 (s ) =X i (s ) fs + K 1fs + (K 1 + K 2 )2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t25.1e0125.0)t (k -=,试求系统闭环传递函数)s (Φ。
解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 设某高阶系统可用下列一阶微分方程)t (r )t (r )t (c )t (c T +τ=+••近似描述,其中,1)T (0<τ-<。
试求系统的调节时间s t 。
解 设单位阶跃输入ss R 1)(= 当初始条件为0时有:1Ts 1s )s(R )s (C ++τ= 1Ts T s 1s 11Ts 1s )s (C +τ--=⋅++τ=∴ T/t e T T 1)t (h )t (c -τ--==T )0(h τ=,1)(h =∞,20T T )]0(h )(h [05.0τ-=-∞=∆求 s tT/t s s eTT 1)0(h )]0(h )(h [95.0)t (h -τ--=+-∞= 3T 05.ln0T t s ==∴3-2 一阶系统结构如图所示。
要求单位阶跃输入时调节时间4.0t s ≤s (误差带为5%),稳态 输出为2,试确定参数21k ,k 的值。
解 由结构图写出闭环系统传递函数1k k sk 1k k s k sk k 1s k )s (212211211+=+=+=Φ闭环增益2k 1k 2==Φ, 得:5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==,得:15k 1≥。
3-4 在许多化学过程中,反应槽内的温度要保持恒定, 下图(a )和(b )分别为开环和闭环温度控制系统结构图,两种系统正常的K 值为1。
解 (1)对(a )系统: 1s 1011s 10K )s (G a +=+=, 时间常数 10T = 632.0)T (h = (a )系统达到稳态温度值的63.2%需要10秒;对(b )系统:1s 10110101100101s 10100)s (b+=+=Φ, 时间常数 10110T = 632.0)T (h = (b )系统达到稳态温度值的63.2%需要0.099秒。
《自动控制原理》习题课习题讲解第二章内容1、试建立图示电路各系统的传递函数和微分方程。
解:(a) 应用复数阻抗概念可写出)()(11)(11s U s I cs R cs R s U c r ++= (1)2)()(R s Uc s I =(2)联立式(1)、(2),可解得: Cs R R R R Cs R R s U s U rc 212112)1()()(+++=微分方程为: rr c c u CR dt du u R CR R R dtdu 121211+=++(2) 由图解2-1(d )可写出[]Cs s I s I s I R s U c R R r 1)()()()(++= (5))()(1)(s RI s RI Cs s I c R c -= (6)[]Cs s I s I R s I s U c R c c 1)()()()(++= (7)联立式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c微分方程为 r r r c c c u R C dt du CR dt du u R C dt du CR dt du 222222221213++=++2、试建立图示电路各系统的传递函数解:由图可写出s C R s U c 221)(+ = s C R s C R s C R s U r 111112111)(+⋅++ 整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R3、试用结构图等效化简求图2-32所示各系统的传递函数)()(s R s C 。
解 (a )所以: 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++=(b )所以: H G G G s R s C 2211)()(--=(c )所以:32132213211)()(G G G G G G G G G G s R s C +++= (d )所以:2441321232121413211)()(H G G G G G G H G G H G G G G G G G s R s C ++++++= (e )所以: 2321212132141)()(H G G H G H G G G G G G s R s C ++++=4、电子心脏起博器心律控制系统结构图如题3-49图所示,其中模仿心脏的传递函数相当于一纯积分环节。
(1) 若5.0=ξ对应最佳响应,问起博器增益K 应取多大?(2) 若期望心速为60次/min ,并突然接通起博器,问1s 钟后实际心速为多少?瞬时最大心速多大?解 依题,系统传递函数为2222205.005.0105.0)(n n n s s K s s Ks ωξωω++=++=Φ⎪⎪⎩⎪⎪⎨⎧⨯==n n K ωξω205.0105.0 令 5.0=ξ可解出 ⎩⎨⎧==2020nK ω 将 s t 1=代入二阶系统阶跃响应公式()βωξξξω+---=-t e t h n t n 221sin 11)(可得 m in 00145.60000024.1)1(次次==s h5.0=ξ时,系统超调量 %3.16%=σ,最大心速为m in78.69163.1163.01(次次)==+=s t h p5、 机器人控制系统结构图如图3-50所示。
试确定参数21,K K 值,使系统阶跃响应的峰值时间5.0=p t s ,超调量%2%=σ。
解 依题,系统传递函数为222121212112)1()1()1(1)1()(n n n s s K K s K K s K s s s K K s s K s ωξωωΦΦ++=+++=++++=由 ⎪⎩⎪⎨⎧=-=≤=--5.0102.0212n p oo t e ωξπσξπξ 联立求解得 ⎩⎨⎧==1078.0nωξ 比较)(s Φ分母系数得⎪⎩⎪⎨⎧=-===146.0121001221K K K n n ξωω6、 某典型二阶系统的单位阶跃响应如图3-51所示。
试确定系统的闭环传递函数。
解 依题,系统闭环传递函数形式应为2222.)(nn ns s K s ωξωω++=ΦΦ由阶跃响应曲线有:21)(lim )()(lim (0==⋅Φ=Φ=∞Φ→→K s s s s R s s h s s )⎪⎪⎩⎪⎪⎨⎧=-===-=--o oo o n p e t 25225.221212ξξπσξωπ联立求解得 ⎩⎨⎧==717.1404.0nωξ所以有95.239.19.5717.1717.1404.02717.12)(2222++=+⨯⨯+⨯=Φs s s s s7、 已知系统的特征方程,试判别系统的稳定性,并确定在右半s 平面根的个数及纯虚根。
(1)01011422)(2345=+++++=s s s s s s D (2)0483224123)(2345=+++++=s s s s s s D (3)022)(45=--+=s s s s D (4)0502548242)(2345=--+++=s s s s s s D解(1)1011422)(2345+++++=s s s s s s D =0 Routh : S 5 1 2 11S 4 2 4 10S 3 ε 6S 2 εε124- 10S6S 0 10第一列元素变号两次,有2个正根。
(2)483224123)(2345+++++=s s s s s s D =0 Routh : S 5 1 12 32S 43 24 48S 3 3122434⨯-= 32348316⨯-= 0 S 2 424316412⨯-⨯= 48 S1216448120⨯-⨯= 0 辅助方程 124802s +=,S 24 辅助方程求导:024=sS 0 48系统没有正根。
对辅助方程求解,得到系统一对虚根 s j 122,=±。
(3)022)(45=--+=s s s s DRouth : S 5 1 0 -1S 4 2 0 -2 辅助方程 0224=-sS 3 8 0 辅助方程求导 083=sS 2 ε -2S ε16S 0 -2第一列元素变号一次,有1个正根;由辅助方程0224=-s 可解出:))()(1)(1(2224j s j s s s s -+-+=-))()(1)(1)(2(22)(45j s j s s s s s s s s D -+-++=--+=(4)0502548242)(2345=--+++=s s s s s s D Routh : S 5 1 24 -25S 4 2 48 -50 辅助方程 05048224=-+s sS 3 8 96 辅助方程求导 09683=+s sS 2 24 -50S 338/3S 0 -50第一列元素变号一次,有1个正根;由辅助方程05048224=-+s s 可解出:)5)(5)(1)(1(25048224j s j s s s s s -+-+=-+)5)(5)(1)(1)(2(502548242)(2345j s j s s s s s s s s s s D -+-++=--+++=8、 系统结构图如图3-57所示。
试求局部反馈加入前、后系统的静态位置误差系数、静态速度误差系数和静态加速度误差系数。
解 局部反馈加入前,系统开环传递函数为)1()12(10)(2++=s s s s G ∞==∞→)(lim s G K s p ∞==→)(lim 0s sG K s v10)(lim 2==→s G s K s a局部反馈加入后,系统开环传递函数为)20()12(1012011(1012)(2+++=+++⋅+=s s s s s s s s s s G )()∞==→)(lim 0s G K s p5.0)(lim 0==→s sG K s v)(lim 2==→s G s K s a9、 已知单位反馈系统的开环传递函数为)22)(4()1(7)(2++++=s s s s s s G 试分别求出当输入信号t t t r ),(1)(=和2t 时系统的稳态误差[)()()(t c t r t e -=]。
解)22)(4()1(7)(2++++=s s s s s s G ⎩⎨⎧==187v K由静态误差系数法)(1)(t t r =时, 0=ss et t r =)(时, 14.178===K A e ss 2)(t t r =时, ∞=ss e10、单位反馈系统的开环传递函数为)5(25)(+=s s s G求各静态误差系数和25.021)(t t t r ++=时的稳态误差ss e ;解 (1))5(25)(+=s s s G ⎩⎨⎧==15v K∞=+==→→)5(25lim)(lim 00s s s G K s s p5525lim )(lim 00=+==→→s s G s K s s v525lim )(lim 020=+==→→s ss G s K s s a)(1)(1t t r =时, 0111=+=pss K et t r 2)(2=时,4.0522===v ss K A e 235.0)(t t r =时,∞===013a ss K A e由叠加原理 ∞=++=321ss ss ss ss e e e e11、已知开环零、极点如图4-22所示,试绘制相应的根轨迹。
(a) (b) (c) (d)(e) (f) (g) (h) 题4-22图 开环零、极点分布图解 根轨如图解4-2所示:12、已知单位反馈系统的开环传递函数,试概略绘出系统根轨迹。
⑴)15.0)(12.0()(++=s s s Ks G⑵)3)(2()5()(*+++=s s s s K s G ⑶)12()1()(++=s s s K s G解 ⑴)2)(5(10)15.0)(12.0()(++=++=s s s Ks s s K s G系统有三个开环极点:01=p ,22-=p ,53-=p ① 实轴上的根轨迹: 图解4-2 根轨迹图(]5,-∞-,[]0,2-② 渐近线: ⎪⎪⎩⎪⎪⎨⎧±=+=-=--=πππϕσ,33)12(373520k aa ③ 分离点:021511=++++d d d解之得:88.01-=d ,7863.32-d (舍去)。
④ 与虚轴的交点:特征方程为 010107)(23=+++=k s s s s D令⎩⎨⎧=+-==+-=010)](Im[0107)](Re[32ωωωωωj D k j D 解得⎩⎨⎧==710k ω与虚轴的交点(0,j 10±)。