静电场和高斯定理
- 格式:ppt
- 大小:1.82 MB
- 文档页数:71

关于静电场的高斯定理和静电场的环路定理静电场的高斯定理和静电场的环路定理是库仑定律的推论,所以称之为定理。
由于库仑定律是静电场的基本规律,适用于静电场,所以库仑定律的推论也适用于静电场。
电场有许多种:静电场(由静止电荷激发)、恒定电场(由运动然而空间分布不随时间改变的电荷体系激发的电场)、位电场(可以在其中建立电位函数的电场,位电场的电场强度等于电位的负梯度,分为恒定的与时变的,静电场和恒定电场就属于恒定的位电场)、涡旋电场。
静电场的高斯定理的文字表述是:静电场中,电场强度穿出闭合曲面的通量等于该闭合曲面所包围的总电量除以真空电容率。
静电场的高斯定理的数学表述式是:in 0d i S qE S ε⋅=∑⎰ 。
英国著名物理学家麦克斯韦首先假设静电场的高斯定理的数学表示式in 0d i S q E S ε⋅=∑⎰ 适用于一切电场,也就是说,实际的电场强度(即总电场强度)穿出闭合曲面的通量等于闭合曲面内的总电量除以真空电容率。
这个假设后来被实验证实了。
正因为这个原因,数学表示式in 0d i S qE S ε⋅=∑⎰ 也叫做高斯定律。
由于德国数学家高斯根据库仑定律推出的这个静电场规律的数学表示式是普遍适用的,这让高斯在电磁学中享有很高的声誉。
in 0d i S q E S ε⋅=∑⎰ 有好几个称谓:高斯定理、高斯通量定理、电场的高斯定理、电场的高斯通量定理、高斯定律、高斯通量定律、电场的高斯定律、电场的高斯通量定律。
对于静电场,这个规律叫做静电场的高斯定理,或者静电场的高斯通量定理。
高斯在数学方面有一项重要成就,叫做高斯公式(也可以叫做高斯通量公式或者高斯散度公式)。
高斯公式的数学表示式是d d S Vf S f V ⋅=∇⋅⎰⎰ 。
其含义是:矢量场穿出闭合曲面的通量等于矢量场的散度在闭合曲面所包围的空间区域内的体积分。
高斯定理是电(磁)学规律,高斯公式是纯粹数学规律,两者截然不同。
但是把两者结合起来,就可以推出0E ρε∇⋅= 。




静电场中的高斯定理:高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ (1)高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用:例1:一半径为R 的带电球体,其电荷体密度分布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量。


真空中静电场的高斯定理
真空中静电场高斯定理:在真空静电场中,通过任意的闭合曲面电通量等于该闭合曲面内所包围的电荷的代数和除以真空介电常量。
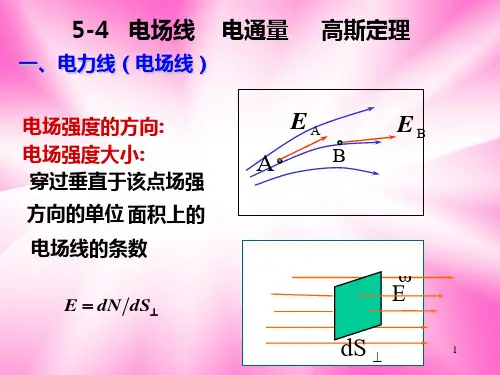
电通量Φ所代表的物理含义是通过电场中某一给定曲面的电场线的总条数。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。

静电场的高斯定理静电场是物质中因电荷分布不平衡而引起的电场。
而高斯定理是一种用于计算电场的方法,通过将闭合曲面内的电场通量与被围绕电荷的总量之间建立关系。
本文将介绍静电场的概念、高斯定理的原理及应用,并探讨高斯定理在不同情况下的适用性。
一、静电场的概念静电场是指不随时间变化的电场。
它产生于电荷分布不均匀的物体周围,并以电场线的形式表现出来。
静电场的特点是力线密集并始终相互垂直,电荷分布越密集,电场力线越密集。
静电场的强度由电场强度表示,它是单位正电荷所受到的电场力。
在真空中,静电场的强度与电荷的大小和距离成反比。
二、高斯定理的原理高斯定理是由德国物理学家高斯提出的,它是静电学中的基本定理。
根据高斯定理,通过一个闭合曲面的电场通量与该曲面所围绕的电荷量成正比。
具体来说,通过一个闭合曲面的电场通量等于该曲面内的电荷量除以真空介电常数。
这一定理表明了计算静电场的电荷分布时,可以通过测量闭合曲面上的电场通量得出曲面内的电荷情况。
三、高斯定理的应用高斯定理在电场的计算与分析中具有重要的应用价值。
首先,它可以用于确定由各种不均匀电荷分布所产生的电场。
通过选择合适的闭合曲面,将电场通量与曲面上的电荷量建立起关系,可以准确计算出电场分布。
其次,高斯定理还能用于计算均匀电荷分布所产生的电场。
例如,对于均匀带电球面,通过选择一个球面作为闭合曲面,可以利用高斯定理快速计算出球面内外的电场分布情况。
四、高斯定理的适用性高斯定理在一些特殊情况下不适用。
例如,当电荷分布不对称或不规则时,闭合曲面的选择就变得困难,无法简单地使用高斯定理求解电场分布。
此外,在存在导体或电介质时,由于电荷的表面分布不明显,也不能直接应用高斯定理进行分析。
在这些情况下,需要采用其他方法,如电场叠加原理或边界条件等,来求解电场问题。
总结:静电场的高斯定理是一种用于计算电场的重要方法,通过建立闭合曲面内的电场通量与曲面所围绕的电荷量之间的关系,可以准确计算静电场的电荷分布。

静电场中的高斯定理:高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/ni i S E ds q φε==∙=∑⎰⎰ (1)高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合 曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用:例1:一半径为R 的带电球体,其电荷体密度分布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量。

静电场的高斯定理内容
静电场的高斯定理内容
静电场的高斯定理是由德国数学家恩斯特·高斯发现的一条定理,用来解释各种物理现象,尤其是静电场的分布。
高斯定理可以用来求出任意一点上的电荷密度。
高斯定理的正式表述为:对任意一个由完全导体组成的闭合曲面,外面的电荷数量和里面的电荷数量是相等的。
也就是说,外面的电荷数量等于里面曲面内电荷的和。
由于高斯定理的正式表述有些复杂,所以经常用另一种形式来描述静电场的分布,即:任一点上的电荷密度等于任一点上的电荷流出量,其积分为零。
这就是静电场的高斯定理的内容,它可以用来解释各种物理现象,特别是静电场的分布。
它也是德国数学家恩斯特·高斯发现的一条定理,现在仍然是物理学中一个重要的定理。
静电场高斯定理一、静电场是什么大家应该都听说过静电吧,特别是在干燥的冬天,摸到门把手或者某些金属物体时,电一下子就蹦出来了。
那种刺痛感,有没有?没错,那就是静电!其实静电就是一种电荷不动的状态,没错,不动。
想象一下,如果你在地毯上走来走去,脚下摩擦产生的电荷积累到你身上,你就成了一个“电气人”。
而周围的一些物体、你接触的物体如果带有相反的电荷,电荷会跳跃过去,哇,那一瞬间多像电影里的特效,啪啪作响。
静电的存在让我们在日常生活中时不时就能感受到它的“威力”,它不仅仅只是“电”那么简单,它也是个无形的、可以随时爆发的能量源。
这么一说,大家对静电是不是有了点感觉?对了,不是所有电都像你家插座里那样“活蹦乱跳”的,静电其实是很“静”很“安静”的,直到它突然跳起来,给你一个“电击”的惊喜!二、什么是高斯定理说到静电,我们就不得不提一个非常有意思的定理——高斯定理。
对,有没有觉得很厉害的名字?一听就知道不是普通的定理,不是随便一个数学家就能发明的东西。
这高斯定理是德国数学家高斯(CarlFriedrichGauss)搞出来的,简直就是个天才。
这个定理听起来好像挺复杂,实际上它的意思不难理解。
简单来说,高斯定理告诉我们,如果你把一个电荷放在某个地方,电场就像是围绕它的一团空气或者一层看不见的“气场”。
换句话说,电荷不只是在自己周围产生电场,还能影响到周围的一大块区域。
更神奇的是,这个影响是可以通过一些数学方式来量化的。
它说什么呢?就是说,穿过一个闭合曲面的电场通量,和这个闭合曲面包围的总电荷成正比。
听起来是不是有点绕?其实就是说,我们可以通过这个曲面内的电荷量,直接算出它对外界的影响力。
就像你拿个透明的气泡罩子罩住一个电池,罩子里的电场到底有多强,其实只要知道罩子里面的电池的电荷数就行了。
是不是觉得这定理还挺神奇的,啥都不用看,就可以从电荷数量推算出来电场的强度。
三、高斯定理的实际应用说到这里,你肯定会想,这个定理到底怎么用啊?能不能拿来做点实实在在的事?别急,等着。
静电场的高斯定理的数学表达式为静电场的高斯定理是物理学中一个重要的定理,它可以帮助我们了解和描述电场的变化以及电荷(电荷量或电荷密度)与它们之间的关系。
该定理以19世纪德国数学家卡尔高斯(Karl Gauss)命名,他在1813年发表了第一个有关静电场的论文。
高斯定理有几种不同的数学表达式,它们可以描述不同类型的物理系统。
首先,让我们来看看静电场的概念。
电场是一种场,它由一组随时间变化的电荷产生的电力线组成。
这些线描述电力在某个空间区域内的分布。
在这里,我们只考虑静电场,它是由平衡状态的电荷产生的(即不会随时间变化)。
此外,静电场在电磁学中也被称为电场,是由平衡状态的电荷产生的。
接下来,我们来看看静电场的高斯定理的数学表达式。
该定理建立在一个有限空间上,它表明,在该空间内,电场的总变化量可以用电荷的总量来表示,也就是说,电场的总变化量可以用电荷的总量来描述。
以下是静电场的高斯定理的数学表达式:begin{equation}vecabla cdot vec E = rho/epsilon_0end{equation} 其中,$vec E$代表了一维空间上电场的分量;$vecabla$表示空间离散梯度;$rho$是电荷密度,$epsilon_0$是真空介电常数。
通过这个定理,可以表示电荷密度与电力线的关系,并且可以使用它来求解静电场。
通常情况下,可以利用它来计算某个特定点处的电力线的密度和方向。
总的来说,静电场的高斯定理的数学表达式是一种强有力的工具,它可以帮助我们理解和描述电场的变化以及电荷和它们之间的关系。
该定理的数学表达式也可以用来求解静电场的电力线的方向和密度,这有时对物理系统的研究是非常有价值的。