一笔画和最短路线问题
- 格式:ppt
- 大小:5.79 MB
- 文档页数:60


年级三年级学科奥数版本通用版课程标题奇妙的一笔画(二)现在我们了解了什么是一笔画和一笔画图形的一些特点,接下来我们深入学习利用一笔画知识解决实际问题的方法,并且扩展出多笔画问题。
希望同学们能够对这类有趣的问题产生兴趣。
一、多笔画问题:我们把不能一笔画成的图,归纳为多笔画。
多笔画图形的笔画数恰等于奇点个数的一半。
事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成。
奇点数÷2=笔画数,即2n÷2=n。
二、对于一笔画问题的应用,我们首先要理解题意,然后常需要改画图形,把代表实际的图形简化成能明确看出奇偶点的图形。
例1 观察下面的图形,看各至少用几笔画成?分析与解:图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要6笔画出,图(3)能一笔画出。
例2 18世纪的哥尼斯堡是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来。
如果游人要一次走过这七座桥,而且每座桥只许走一次,问如何走才能成功?分析与解:图a中,用A,D表示两个小岛,点B,C表示河的左右两岸,若再用连结两点的线表示桥,从而得到一个由四个点和七条线组成的图形,点A、B、C、D四个点均为奇点,显然不能一笔画出这个图形。
考虑如果再架一座桥,游人能否走遍所有这八座桥:若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时图形可以一笔画出,如我们可以选择奇点B、D之间连一条线,如图b。
考虑架设几座桥可以使游人走遍所有的桥回到出发地:再在另外两个奇点A、C之间连一条线,使这两个奇点也变成偶点,如图c,可以以任意点为起点,最后仍回到这个点。
例3 有一个邮局,负责21个村庄的信件投递工作,图中的点表示村庄,线段表示道路。
邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析与解:图中有两个奇点,所以该图可以一笔画出,但因为邮局所在点为奇点,所以要一笔画出就不可能回到邮局。

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空例题精讲知识点拨4-1-5.奇妙的一笔画【关键词】华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
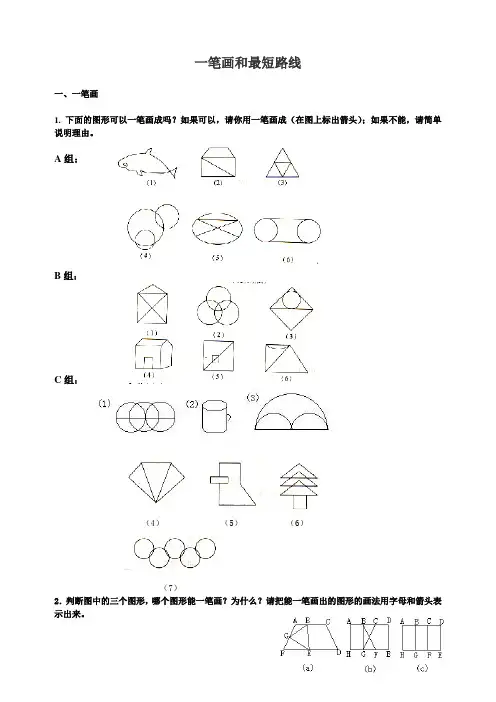
一笔画和最短路线一、一笔画1. 下面的图形可以一笔画成吗?如果可以,请你用一笔画成(在图上标出箭头);如果不能,请简单说明理由。
A组:B组:C组:(4)(5)(6)(7)2.判断图中的三个图形,哪个图形能一笔画?为什么?请把能一笔画出的图形的画法用字母和箭头表示出来。
3.有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路。
邮递员从邮局出发,能不重复地经过每一个村庄,最后回到邮局么?如果可以,请你用一笔画成(在图上标出箭头);如果不能,请简单说明理由。
4.下图是一个公园的道路平面图,要使游客走遍每条路且不重复,问出、入口应设在哪里?5.一张纸上画有如下所示的图,你能否用剪刀连续剪下图中的三个正方形和两个三角形?二、最短路线1.甲、乙、丙是三个镇,中间有一条河把甲、丙和乙隔开,如图13—12,要使这三个镇中任何两个镇之间都有最短通路,除了在甲、丙之间修一条直线型公路外,还需要在河面上架两座桥,使甲与乙、乙与丙之间也有通路.这两座桥应架在什么地方最合理.2.有两条通讯路线A和B,如图13—13,通讯员从C处出发,查完两条线后到D处,作图表示他怎样走路程最短(假设到达通讯线路的任何一处都可完成查线工作)?3.要在两条街道(如图13—14)A和B上各设立一个邮筒,M处是邮局,问邮筒设在哪里才能使邮递员从邮局出发,到两个邮筒取完信再回到邮局的路程最短?4.一个小虫从圆柱体(如图13—15)的A点处绕圆柱体侧面一周,最后爬到顶点B处.请画出小虫从A点绕到圆柱体侧面到达B点的最短路线.5.如图13—16,A、B、C三点分别是正方体三条棱的中点.假设一只蚂蚁沿着正方体的表面从中点A爬到中点C,图中所示路线是否为蚂蚁爬行的最短路线,为什么?答案仅供参考:1.如图13-1’所示,桥应架在AB、CD位置上.2.如图13-2’所示,沿C→P→Q→D走路程最短.3.如图13-3’所示,邮筒应设在E、F两点,沿M→E→F→M路线为最短.4.将圆柱体的侧面展开成一个长方形,如图13-4’.从A到B的直线段最短,把侧面展开图卷成圆柱,那么直线段AB就变成圆柱体侧面上的曲线AB,小虫沿着这条曲线爬行是最短路线.5.要求A到C的最短路线,可以先把立方体展开,使它相邻两个面处于同一平面内.蚂蚁从A到C有两条路线可以选择:(1)将朝上的一面与朝前的一面展开在同一平面内,连结AC,则AC一定过中点B,如图13-5’.假设正方体的棱长为2个长度单位,则由勾股定理,得:AC2=22+22=8(2)把朝前和朝右的一面展开在同一平面内,连结AC,如图13-6’.同样可以求得AC2=12+(2+1)2=10比较两种路线,由于8小于10,所以沿第一条路线从A到C的路线为最短,即图13-21所示路线是蚂蚁爬行的最短路线.6、甲、乙两村之间隔一条河,如图13—1.现在要在小河上架一座桥,使得这两村之间的行程最短,桥应修在何处?分析:设甲、乙两村分别用点A、B表示.要在河上架桥,关键是要选取一个最佳建桥的位置,使得从甲村出发经过桥到乙村的路程最短.即从甲村到甲村河边的桥头的距离加上桥长(相当于河的宽度),再加上乙村到乙村河边的桥头的距离尽可能短,这是一个求最短折线的问题.直接找出这条折线很困难,能否可以把它转化为直线问题呢?由于河的宽度不变,不论桥修在哪里,桥都是必经之路,且桥长相当于河宽,是一个定值,所以可以预先把这段距离扣除,只要使两镇到河边桥头的距离最短就可以了.所谓预先将桥长扣除,就是假设先走完桥长,即先把桥平移到甲村,先过了桥,到C点,如图13—2,找出C到B 的最短路线,实际上求最短折线问题转化为直线问题.解:如图13—2.过A点作河岸的垂线,在垂线上截取AC的长等于河宽.连BC交与乙村的河岸于F点,作EF垂直于河的另一岸于E点,则EF为架桥的位置,也就是AE+EF+FB是两村的最短路线.7、如图13—3,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?8、如图13—6,河流EF与公路FD所夹的角是一个锐角,某公司A在锐角EFD内.现在要在河边建一个码头,在公路边修建一个仓库,工人们从公司出发,先到河边的码头卸货,再把货物转运到公路边的仓库里去,然后返回到A处,问仓库、码头各应建在何处,使工人们所行的路程最短.分析:工人们从A出发先到河边码头,再到公路的仓库,然后回到A处,恰好走一个三角形,现在要求三角形的另外两个顶点分别建在河岸与公路的什么位置能使这个三角形的三边之和为最小,利用轴对称原理作图.解:过A分别作河岸、公路的对称点A′、A″,如图13—7,连结A′A″,交河岸于M,交公路于N,则三角形AMN各边之和等于直线A′A″的长度,所以仓库建在N处,码头建在M处,使工人们所行的路程最短.9、如图13—8是一个长、宽、高分别为4分米、2分米、1分米的长方体纸盒.一只蚂蚁要从A点出发在纸盒表面上爬到B点运送食物,求蚂蚁行走的最短路程.分析:因为是在长方体的表面爬行,求的是立体图形上的最短路线问题,往往可以转化为平面上的最短路线问题.将蚂蚁爬行经过的两个面展开在同一平面上,如图13—9,在展开图中,AB间的最短路线是连结这两点的直线段,但要注意,蚂蚁可沿几条路线到达B点,需对它们进行比较.解:蚂蚁从A点出发,到B点,有三条路线可以选择:(1)从A点出发,经过上底面然后进入前侧面到达B点,将这两个平面展开在同一平面上,这时A、B间的最短路线就是连线AB,如图13—9(1),AB是直角三角形ABC的斜边,根据勾股定理,AB2=AC2+BC2=(1+2)2+42=25(2)从A点出发,经过左侧面,然后进入前侧面到达B点,将这两个面展开在同一平面上,如图13—9(2),同理AB2=22+(1+4)2=29(3)从A点出发,经过上底面,然后进入右侧面到达B点,将这两个面展开在同一平面上,如图13—9(3),得AB2=(2+4)2+12=37比较这三条路线,25最小,所以蚂蚁按图13—9(1)爬行的路线最短,最短路程为5分米.10、如图13—10,在圆柱形的木桶外,有一个小甲虫要从桶外的A点爬到桶内的B点.已知A点到桶口C点的距离为1 4厘米,B点到桶口D点的距离是10厘米,而C、D两点之间的弧长是7厘米.如果小甲虫爬行的是最短路线,应该怎么走?路程是多少?分析:先设想将木桶的圆柱展开成矩形平面,如图13—11,由于B点在桶内,不便于作图,利用轴对称原理,作点B关于直线CD的对称点B′,这就可以用B′代替B,从而找出最短路线.解:如图13—11,将圆柱体侧面展成平面图形.作点B关于直线CD的对称点B′,连结AB′,AB′是A、B′两点间的最短距离,与桶口边交于O点,则OB′=OB,AB′=AO+OB,那么A、B之间的最短距离就是AO+OB,所以小甲虫在桶外爬到O点后,再向桶内的B点爬去,这就是小甲虫爬行的最短路线.延长AC到E,使CE=B′D,因为△AEB′是直角三角形,AB′是斜边,EB′=CD=7厘米,AE=14+10=24(厘米),根据勾股定理:AB′2=AE2+EB′2=242+72=625所以AB′=25(厘米)即小甲虫爬行的最短路程是25厘米.11、一个邮递员投送信件的街道如图141,图上数字表示各段街道的千米数.他从邮局出发,要走遍各街道,最后回到邮局.问走什么样的路线最合理,全程要走多少千米?12、图143是一个城市道路图,数字表示各段路的路程(单位:千米),求出图中从A到F的最短路程.13、某乡有八个行政村,如图144,点表示村的位置,线表示村与村之间的道路,路的长度由线旁的数字表示.现在要在这个乡建立通讯网,沿道路架设电线,问沿怎样的路线架设电线最省(单位:千米)?解:根据剪圈法将圈形网络图144转化成了树形网络图145,此网络的总长度为:13+12+4+6+16+8=69(千米)由于通讯线路是双线,所以电线的总长度为69×2=138(千米).14、仍取图144中八个行政村的位置和线路图,乡政府要在全乡沿村与村之间的道路挖渠修道,建立排灌系统.全乡的地势是西高东低,即A村最高,依次为B、F、G、H、E、C、D,水源在A村,问沿什么路线修道最合理?分析:由题意,要确定一条合理的挖渠路线,而且要省工省料,并符合“水往低处流”的客观规律.由于所修水渠是连通的,渠道可以看作是网络,而且也是树形网络.只是在本题中增加了“地势不同”这一条件,所以,力求树形网络总长尽可能短的情况下,所求的树形网络的方向应该是由西向东,以A为起点,以距离A最远的D为终点.采取“取短法”,所谓取短法就是剪去长线,留取短线.并根据方向的限制,从地势最低点开始考虑(也可从其它点入手考虑).D的临近点有E、H、C,它们都比D地势高,所以,这三点处的水都可以流入D,则只需取一条最短的即可,ED=16最短,留ED,将HD、CD去掉.再看C点,有两条通道HC、BC(这里所说的通道是指地势高的点通向地势低的点的道路),HC 比BC短,去掉BC,保留HC.E点有三条通道FE、GE、HE,其中HE最短,保留HE,去掉FE、GE.H点有两条通道BH、GH,其中GH最短,保留GH,去掉BH,最后剩下地势较高的三点B、F、G,它们与A都各有一条通道,不存在取舍问题,这样得到,挖渠的最佳方案.解:利用取短法并根据方向的限制,得到图146所示的挖渠的最佳方案.最佳方案的挖渠总长为:17+15+13+4+7+6+16=78(千米)例5有八栋居民楼AA2、…、A8分布在公路的两侧,如图147,由一些小路与公路相连,要在公路1、上设一个汽车站,使汽车站到各居民楼的距离之和最小,车站应设在哪里?。

二年级一笔画的题目以下是一些二年级的一笔画题目:画出从A点到B点的最短路径,只能沿着直线走,不能拐弯。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,但是可以经过其他点。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,但是可以经过其他点,而且经过的点越多越好。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,而且不能经过其他点。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,而且不能经过其他点,但是可以经过A点或B点。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,而且不能经过其他点,但是可以经过A点或B点,而且经过的点越多越好。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,而且不能经过其他点,但是可以经过A点或B点,而且经过的点越多越好,但是最后一个点必须是B点。
画出从A点到B点的最短路径,只能沿着直线走,不能拐弯,而且不能经过其他点,但是可以经过A点或B点,而且经过的点越多越好,但是最后一个点必须是B点,而且必须经过A点和B点的所有相邻点。
希望这些题目能够满足您的需求。
以下是一些二年级一笔画题目的例子:有一个村庄,村长家在村子的一头,村民家在村子的另一头。
现在我们要从村长家走到村民家,只能沿着村庄的街道走,不能拐弯。
请问,我们如何找到最短的路径?在一个城市的地图上,A大厦和B大厦是两个点。
我们只能沿着街道走,不能拐弯,而且不能重复走相同的路线。
请问,我们如何找到从A大厦到B大厦的最短路径?在一个公园的地图上,A点和B点是两个景点。
游客只能沿着小路走,不能拐弯,而且不能重复走相同的路线。
请问,游客如何找到从A点到B点的最短路径?在一个工业园区的地图上,A工厂和B工厂是两个点。
物流车只能沿着道路走,不能拐弯,而且不能重复走相同的路线。
请问,物流车如何找到从A工厂到B工厂的最短路径?希望这些例子能够帮助您更好地理解二年级一笔画题目。
对于二年级的一笔画题目,以下是一些答题技巧:观察图形:首先仔细观察题目中的图形,了解图形的结构、线条和交点。

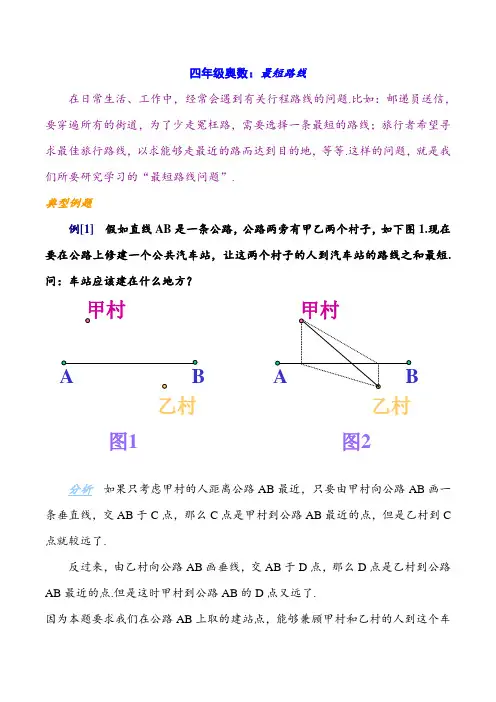
四年级奥数:最短路线在日常生活、工作中,经常会遇到有关行程路线的问题.比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等.这样的问题,就是我们所要研究学习的“最短路线问题”.典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1.现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短.问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最近的点,但是乙村到C 点就较远了.反过来,由乙村向公路AB 画垂线,交AB 于D 点,那么D 点是乙村到公路AB 最近的点.但是这时甲村到公路AB 的D 点又远了.因为本题要求我们在公路AB 上取的建站点,能够兼顾甲村和乙村的人到这个车甲村 乙村乙村 图1图2站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB 交点P ,就是所求的公共汽车站的建站点了(图2).解 用直线把甲村、乙村连起来.因为甲村乙村在公路的两侧,所以这条连线必与公路AB 有一个交点,设这个交点为P ,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短.例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数.他从邮局出发,要走遍各街道,最后回到邮局.问:走什么样的路线最合理?全程要走多少千米?分析 选择最短的路线最合理.那么,什么路线最短呢?一笔画路线应该是最短的.邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点.因此,要能一笔把路线画出来,必须途径的各点全是偶点.但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的.要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点.如果有不同的添法,3就还要考虑哪一种添法能使总路程最短.为使8个奇点变成偶点,我们可以用图4的4种方法走重复的路线.图4中添虚线的地方,就是重复走的路线.重复走的路程分别为: (a )3×4=12(千米) (b ) 3×2+2×2=10(千米) (c ) 2×4=8(千米) (d ) 3×2+4×2=14(千米)当然,重复走的路程最短,总路程就最短.从上面的计算不难找出最合理的路线了.解 邮递员应按图4(c )所示的路线走,这条路重复的路程最短,所以最合理.全程为:(1+2+4+2+1)×2+3×6+2×4 =20+18+83333( a )( b )( c )( d )图4=46(千米)例[3] 图5中的线段表示的是小明从家到学校所能经过的所有街道.小明上学走路的方向都是向东或向南,因为他不想偏离学校的方向而走冤枉路.那么小明从家到学校可以有多少条不同的路线?分析 为了叙述的方便,我们在各交叉点标上字母(见图6).我们从小明家出发,顺序往前推.由于从小明家到A 、B 、C 、D 各处都是沿直线行走,所以都只有一种走法.我们分别在交叉点处标上“1”.而从小明家到E 处,就有先到A 或先到D 的两种走法,正好是两个对角上标的数1+1的和.从小明家到F 点,则有3条路线,又正好是两个对角上标的数1+2的和.标在各交叉点的数,就是依次顺序推出的到各交叉点能有多少种不同的路线的数.从中我们可以看出,每个格内上右角与下左角两个对角上的数的和,正好等学校小明家A B F EF D EF于下右角上的数.解 从小明家到学校有13条不同的路线.如图7所示.图7学校H MNK。

第十二讲一笔画问题例2下图是国际奥委会的会标,你能一笔把它画出来吗?分析与解答一个图能否一笔画出,关键取决于这个图中奇点的个数.通过观察可以发现,上图中所有的结点都是偶点,因此,这个图可以一笔画出.画时可以任一结点作为起点。
例3下图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析与解答本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C。
容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和。
仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C。
例4(1)能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?(2)能否用剪刀一次连续剪下右下图中六个三角形?【解析】:上面两个图形都只有两个奇点(红色交点),都是一笔画图形,但用笔画和用剪刀剪,这两种操作是有区别的。
第一、用笔画,笔要经过图中的每一条线段,用剪刀剪只能剪图形内部线段,四周的边框是不能剪的;第二,用笔画一条经过某个点的直线后,图形还是完整的,用剪刀沿直线经过某个点剪一刀后,这个图形会被剪成两段。
因此在剪的过程中要注意技巧,可以分别准备好这样的两张纸片,在纸片上画出对应的线段,让孩子在剪纸的操作中慢慢体验这一点。
这两个图形都可以按题目要求一次连续剪下。
上面左边图形在剪的时候注意:可以从图形左边奇点开始先向右剪,遇到第一个交点后拐弯向上,再向右下,再向左剪,最后向下到第二个奇点结束。
例5 下图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析与解答这种应用题,表面看起来不易解决,事实上,只要认真分析,就可以发现:我们并不关心展室的大小以及路程的远近,关心的只是能否一次不重复地走遍所有的门,与七桥问题较为类似.因此,仿照七桥问题的解法,我们可以把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A。

一笔画问题及解决策略一、问题提出一笔画是一个大问题,为了更好的解决这个问题,我们从生活提出一笔画问题。
我们先看一个公路检查员的问题:他为了检查几个城市之间的若干公路,希望在这些城市和公路组成的公路系统中找出一条路线,使他能不重复地恰好通过每条公路一次,而经过每个城市的次数不限.这就是拓扑学中的数学问题。
二、问题解决(一) 数学化我们把这问题数学化,以点表示城市,以弧表示公路,这样构成的网络图就表示某个简单公路系统。
(二)点线图用点线图表示四个不同的公路系统。
如图所示:(三)一笔画的含义一个图形由一笔构成叫一笔画.对于平面图形的一笔画与多笔画问题,通常的几何方法是无能为力的,因为一个图形能否一笔画,与图形的大小、形状等几何概念都没有关系,而是与图形中线段的数目及连接关系有关,我们可以随意地将图形拉伸、压缩或弯曲,甚至在保持端点不动的前提下,还可以将某些线段“搬家”,只要图形的整体结构不变,能否一笔画的性质也就不会改变.(四)一笔画图形的判别著名的哥尼斯堡七桥问题实质上就是一个一笔画问题。
欧拉最终证明了这个图形是不能一笔画成的,并在关于七桥问题的报告中得到了任一网络图能否一笔画的判别法则。
1。
必要条件一个网络图是由有限个点和有限条曲线组成的平面图形,这些点和线分别称为网络的顶点和弧。
如果从网络的一个顶点出发,一条弧连着一条弧地把所有的弧都画出,且每条弧都只画一次,而经过每个顶点的次数不限,就称该网络能一笔画.当一个网络能一笔画时,只有两种情形:一是开放图形,只有起点和终点的指数为奇数,其余顶点的指数均为偶数;二是封闭图形,所有顶点的指数均为偶数。
我们称指数为奇数的顶点为奇顶点,指数为偶数的顶点为偶顶点,那么当一个网络能一笔画时,奇顶点个数必为0或2,所以,连通且奇顶点的个数是0或2,是一个网络图能一笔画的必要条件。
(1)。
凡是由偶点组成的连通图,一定可以一笔画成.画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。

小学数学《一笔画》练习题(含答案)什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.判断图形能否一笔画的规律:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.(一) 一笔画以及多笔画【例1】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.(f)(e)(d)JIH G F ED C BAJ K IHGFED CB A分析:(a )图:可以一笔画,因为只有两个奇点A 、B ;画法为A →头部→翅膀→尾部→翅膀→嘴. (b )图:不能一笔画,因为此图不是连通图.(c )图:不能一笔画,因图中有四个奇点:A 、B 、C 、D.(d )图:可以一笔画,因为只有两个奇点;画法为:A →C →D →A →B →E →F →G →H →I →J →K →B. (e )图:可以一笔画,因为没有奇点;画法可以是:A →B →C →D →E →F →G →H →I →J →B →D →F →H →J →A.(f )图:不能一笔画出,因为图中有八个奇点.[注意]在上面能够一笔画出的图中,画法并不是惟一的.事实上,对于有两个奇点的图来说,任一个奇点都可以作为起点,以另一个奇点作为终点;对于没有奇点的图来说,任一个偶点都可以作为起点,最后仍以这点作为终点.[巩固]判断下列图a 、图b 、图c 能否一笔画.E分析:图a是一个连通的图形,图中只有点A和点F两个奇点,所以它能一笔画,其中一种画法如下:A —M—N—A—F—B—C—B—K—C—D—E—D—L—E—F.‘图b是一个不连通的图形,所以不能一笔画.图c是连通图,图中所有点都是偶点,所以能一笔画.其中一种画法如下:A—B—C—D—E—F—D—A—F —C—A.【例2】右图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达 C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析:本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.[巩固]在六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?分析:许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D点,因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E,D两个奇点,所以从E到D可以一笔画出,而从B到D却不能,因此E点的蚂蚁获胜.[数学小游戏] 用一笔画成四条线段把所有的点连起来,怎样画?分析:通过试画,似乎不可以画,但通过仔细观察,对照一笔画的规律,便可发现,若添上两个辅助点,就可画成.如右图:FE DCB AEDCBA我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.公式如下: 奇点数÷2=笔画数,即2n ÷2=n.【例3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IH G FED CBA 图aH G I KLJ F EDCBA 图b DC HG EFBA图c分析:图a :原图有四个奇点,所以不能一笔画,在B,D 两点之间加一条线后,图中只有两个奇点,故可以一笔画出,如图d 所示.画法:H →A →B →C →D →E →F →I →D →B →I →H →G →F .图b :原图有四个奇点,所以不能用一笔画.去掉K ,L 两点之间的连线,图中只有两个奇点,故 可以一笔画出,如图e 所示.画法:B →C →D →E →F →→J →H →G →I →A →B →K →I →L →E .图c :原图有四个奇点,所以不能用一笔画.在B ,C 两点之间加一条线后,图中只有两个奇点, 故可以一笔画出,如图f 所示.画法:A →E →D →H →A →B →F →C →G →B →C →D注意:a 、b 、c 三个图都是连通的图形,但由于每个图的奇点个数均超过两个,所以都不能一笔画.图dA BCD EFG H IH GI KLJ F EDCB A 图eDC HG EFBA图f[前铺]观察下面的图,看各至少用几笔画成?分析:(1)图中有8个奇点,因此需用4笔画成. (2)图中有12个奇点,需6笔画成. (3)图是无奇点的连通图,可一笔画成.【例4】 将下图改为一笔画.DC BA(2)(1)FEC DB A分析:图(1)中有6个奇点,因此可添上两条(或3条)边后可改为一笔画;又因为这个图中,把这6个奇点任意分为3对后,最多只有两对奇点间有边相连,因此,可去掉两条边后改为一笔画,举例如图(3)~(6).图(2)中有4个奇点,因此,可添上2条(或1条)边后改为一笔画;又因为把奇点按A 与B ,C 与D (或A 与D ,B 与C )分为两对后,每对间均有边相连,因此,可去掉两条(或1条)边后改为一笔画.举例如图(7)~(8).说明:图(6)运用了两种方法,去掉边BC ,添上边AD 与EF.(二)一笔画的实际应用【例5】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?:这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在. 下面,我们考虑如下两个问题:(1)如果再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由. (2)架设几座桥可以使游人走遍所有的桥回到出发地?而得到一个由四个点和七条线组成的图形(如图b).在图b 中,点A ,B ,C ,D 四个点均为奇点,显然不能一笔画出这个图形.若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时,图形可以一笔画出.如我们可以选择奇点B ,D ,在B ,D 之间连一条线(架一座桥),如图c .在图c 中只有点A 和C 两个奇点,那么我们可以以A 为起点,C 为终点将图形一笔画出.其中一种画法为:A →C →A →B →A →D →B →D →C所以,如果在河岸B 与小岛D 之间架一座桥,游人就可以不重复地走遍所有的桥.(2)在(1)的基础上,再在另外两个奇点A 与C 之间连一条线(即架一座桥),使这两个奇点也变成偶点,如图d .那么A ,B ,C ,D 四个点均为偶点,所以图d 可以一笔画出,并且可以以任意点为起点,最后 仍回到这个点.其中一种画法为:A →C →A →C →D →A →B →D →B →A这表明:在河岸B 与小岛D 之间架一座桥后,再在小岛A 与河岸C 之间架一座桥,共架设两座桥,就可以使游人不重复地走遍所有的桥并回到出发地.[巩固]如图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?分析:用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,有2个奇点,所以该图可以一笔画,即可以一次不重复地走遍这七座桥.例如右下图的走法.EDCBA【例6】 有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析:图中有两个奇点,所以该图可以一笔画,但因为邮局所在点为奇点,所以要一笔画就不可能回到邮局.又图中A,B,C,D,E,F,G,H,I,J十点均有4条线段与之相连,如果我们将上图一笔画的话,就要经过以上十点各两次,这也不满足题目的要求,所以要将这些点相连的线段去掉一些,使得与这些点相连的线段均只有两条,并且将两个奇点也变成只有两条线段与之相连,这样得到的图形即可一笔画,又只经过每个点一次,并且可以回到邮局,一种可行路线如下:邮局I JHGF E D C B A 邮局邮局【例7】 右图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径;若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?分析:我们把展厅A,B,C,D,E 及馆外F 看成某个图中的点,把两个展厅之间的门看作是连接表示这两个展厅的点的线.根据题中条件知,馆外F 与A ,B ,C ,D ,E 各展厅相通,这样将点F 与点A ,B ,C ,D ,E 用线连接;展厅A 与展厅B ,C ,D 相通,将点A 与点B ,C ,D 用线连接;展厅B 除与A 相通外,它还与D ,E 展厅相通,将B 与D ,E 连接;除此之外,展厅C ,D 相通,展厅D ,E 相通,将点C ,D 连接,再将点D ,E 连接(如图a).于是本题要解决的问题就变成了能否将图a 一笔画的问题.可以看出:图a 中共有六个点,其中有四个奇点,它们分别为C ,D ,E ,F ,由一笔画的规律可知,图a 不能一笔画.也就是说,参观者不能够不重复地一次穿过每一扇门.如果允许关闭某一扇门,这相当于在图a 中去掉一条线,那么参观者就有可能不重复地一次穿过每一扇门.我们知道,在图a 中有四个奇点C ,D ,E ,F 为了把图a 改成一笔画图形,我们设法减少奇点个数,使奇点数变为两个.为此,我们可以去掉一条连接两个奇点的线,如去掉E 与F 间的连线,相应的图a 就变成了图b .在图b 中,除了原来的C 和D 是奇点外,其余点全部是偶点,故图b 可以一笔画.其中一种画法为:C →F →D →E →B →F →A →B →D →A →C →D .上面的分析表明,如果关闭连接E 、F 两展厅之间的门,参观者就可以不重复地一次穿过每一扇开着的门. 本题与七桥问题类似,只是将行人过桥换成了参观者穿过每一扇门.我们将这个问题转化为一笔画问题来研究.[前铺]右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? FFF F E C D BA EB A分析:我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到下图.能否不重复地穿过每扇门的问题,变为下图是否一笔画问题.EDC BA图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走. 【例8】 已知长方体木块的长是80厘米,宽40厘米,高80厘米(如右图),并且要求蜘蛛在爬行过程中只能前进,不能后退,同一条棱不能爬两次.请问这只蜘蛛最多要爬行多少厘米?分析:图中八个顶点均为奇点,所以不能一笔画,要使其能一笔画,至少要去掉三条棱,使上图只有两个奇点,就可以满足一笔画的条件.长方体的棱长总和一定,(80+80+40)×4=800(厘米),因此去掉的三条棱越短,蜘蛛爬过的距离就越远.所以我们去掉三条棱长为40厘米的棱,于是可知,蜘蛛爬行的最远距离为: 800-40×3=680(厘米).蜘蛛的爬行路径为:G →F →C →D →G →H →A →B →E →H(如右图).[注意]这是一个立体图形,它有八个顶点,我们把长方体的棱看作顶点与顶点之间的连线,蜘蛛只能前进不能后退,并且每一条棱不能爬两次,这实质上是一个一笔画问题.【例9】 右图是某小区的街道分布图,街道长度如图所示(单位:公里),图中各点表示不同楼的代号.一辆垃圾清扫车从垃圾站(垃圾站位于C 楼与D 楼之间的P 处)出发要清扫完所有街道后仍回到垃圾站,问怎样走路线最短,最短路线是多少公里?分析:为了少走冤枉路和节省时间,题目中要求最短路线,根据一笔画原理,我们知道一笔画路线就是最短路线.本题要求清扫车从P点出发,仍回到P 点.通过观察上图可知,图中有六个奇点,根据一笔画规律可知,清扫车想清扫完所有街道而又不走重复的路是不可能的.要使清扫车从P 点出发,最后仍回到P 点,就必须把图中所有的奇点都变成偶点,即在两奇点之间添加一条线.在实际问题中,就是清扫车在哪些街道上重复走的问题,由于每条街道的长度不同,因此需要我们考虑清扫车重复走哪条街道才使总路线最短.为使六个奇点都变成偶点,我们可以有下图中的四种方法表示清扫车所走的重复路线,其中填虚线的地方表示的是重复路线.重复的路程分别为:图a :2×2+3=7;图b :3+4×2=11;图C :3×3=9; 图d :3+6×2=15.显然,重复走的路线最短,总路程就最短.从上述计算中就可找到最短路线图,即下面四个图中的图a .408080H G F ED C BA804080H GFED CBA图b 图a图d图c在图a 中,所有点均为偶点,是一笔画图形.清扫车可按如下路径走:P →D →G →D →E →F →G →H →L →H →C →B →L →M →A →B →C →P ,全程为:(1+2+4+2)×2+3×5+2×2+3=40(公里).【例10】 邮递员李文投送邮件的街道以及街道的长度如右图所示(单位:千米),每天小李要从邮局出发,走遍所有街道后回到邮局.请你帮他设计一条最短路线,并计算出这条路线有多少千米?分析:本题仍可以用一笔画图形的方法来解决.在图a 中共有六个奇点E ,F ,G ,H ,I ,J ,把这些奇点配对,每对之间用虚线连接(如图a),其中要用到D 点,这样图中就没有奇点了,从而可以不重复地走遍所有的街道.由于邮递员李文要重复走一些路段,因此重复走的路越短越好,即添上去的重复线段的总长度越短越好.在图a 中H 与E 之间有重叠,这样势必会增加李文所走路程的长度,应作调整.经调整后,将重叠部分去掉便得图b .在图b 的圈形闭路IHGJI 中,I ,J ,G ,H 各点没有连线时是奇点,连线后变成偶点,增加长度为50×2=100千米.而如果连IJ 和HG ,增加的长度仅为10×2=20,由此可知图b 需继续作调整,改成图c ,这种连接方法是最好的,它使李文行走的路线最短.根据以上分析,为了保证添上去的线段之和最短,应遵循下面的两条原则:(1)连线不能有重叠的线段;(2)在每一个圈形闭路上,连线长度之和不能超过 这个闭路总圈长的一半.经过分析可以知道,图c 的连接方法能使邮递员李文行走路线最短,而且能保证李文从邮局出发又回到邮局.这时他的行走路线为:邮局→A →I →J →I →H →G →H →E →D →F →D →G →J →B →C →D →E →邮局 他行走的全程为: (50+15)×4+20×4+10×6+20×2=440(千米).图a图b图c[小结]本题中采用的方法叫做“奇偶点图上作业法”,用这种方法来确定最短路线比较简便实用.此方法可以用下面的口诀来描述:画出路线图,确定奇偶点;奇点对对连,连线不重叠;闭路添连线.不得过半圈.[巩固]右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A 出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理? 分析:这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K 是中间点,因此必须成为偶点,这样洒水车必须重复走KC 这条边(如下左图).至此,奇点的个数并未减少,仍是6个.容易得出,洒水车必须重复走的路线有:GF 、IJ 、BC.即洒水路线如下右图.全程45+3+6=54(里).1. (例1)判断下列各图能否一笔画.图aG I H F ECD BA图bF ED CBA分析:图a 中九个点全是偶点,因此可以一笔画,其中一种画法为:A →F →B →G →C →H →D →E →H →l →→F →G →l →E →A .图b 中A ,B ,C ,D 四个点均为奇点,故不可以一笔画.图c 中,只有A,C 为奇点,故可一笔画.其中一种画法为:A →D →E →C →H →N →G →M →F →A →B →C .2. (例3)下列各图至少要用几笔画完?分析:(1)4笔;(2)4笔;(3)2笔;(4)1笔;(5)1笔;(6)1笔.3.(例6)右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析:把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.4.(例7)一辆清洁车清扫街道,每段街道长1公里,清洁车由A出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?分析:清洁车走的路径为: ABCNPBCDEFMNEFGHOLMHOIJKPLJKA. 即:清洁车必须至少重复走4段1公里的街道,如下图.最短路线全程为28公里.5.(例10)一个邮递员的投递范围如右图,图上的数字表示各段街道的长度.请你设计一条最短的投递路线,并求出全程是多少?分析:邮递员的投递路线如下图,即:路线为:ABCDEDOBOMNLKLGLNEFGHIMOJIJA.最短路线的全程为39+9=48.。
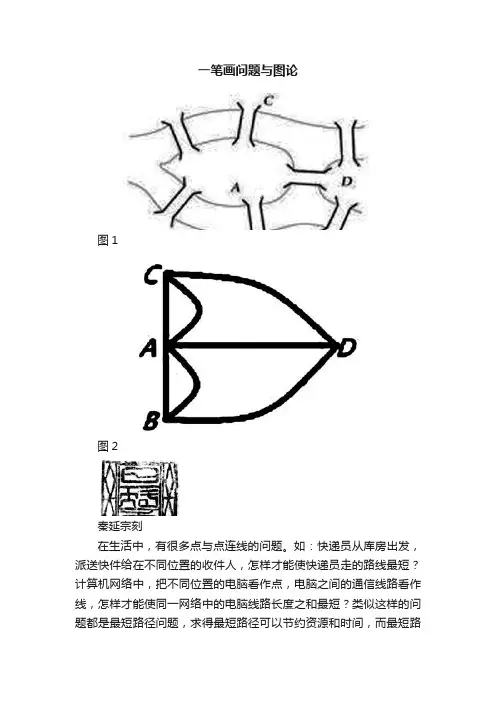
一笔画问题与图论图1图2秦延宗刻在生活中,有很多点与点连线的问题。
如:快递员从库房出发,派送快件给在不同位置的收件人,怎样才能使快递员走的路线最短?计算机网络中,把不同位置的电脑看作点,电脑之间的通信线路看作线,怎样才能使同一网络中的电脑线路长度之和最短?类似这样的问题都是最短路径问题,求得最短路径可以节约资源和时间,而最短路径问题与图论密切相关。
快递员最短路径、计算机网络最短路径,这两个问题有些复杂。
为了理解图论的基本原理,我们先看一个简单的一笔画问题:对一个有若干个点(大于等于2)和若干条线的图形,从一个点开始,能否用一支笔,在不离开纸面的情况下,不遗漏、不重复地沿线画完图形。
你或许求解过很多一笔画问题,但有没有想过这类问题是否有统一的解答方法呢?即:什么样的一笔画问题可求解?可求解的一笔画问题有没有确定的解法?最先给出一笔画问题统一解法的是瑞士数学家欧拉。
欧拉对图论的研究是从哥尼斯堡七桥问题开始的。
18世纪初普鲁士的哥尼斯堡(今俄罗斯加里宁格勒)有一条河穿过,河上有两个小岛(A和D),有七座桥把两个岛与河岸(B和C)连接起来(如图1)。
当地居民有一个休闲活动,就是从一块陆地出发,怎样才能不重复、不遗漏地一次走完七座桥,再回到出发点。
当地的人们试验了无数多次,都没有人做到。
1735年,有几名大学生写信给数学家欧拉,请他帮忙解决这一问题。
欧拉在亲自观察了哥尼斯堡的七座桥后,认真思考走法,也没能成功,于是他怀疑七桥问题是不是原本就无解。
在经过一年的研究之后,欧拉写出了《哥尼斯堡七桥问题》的论文,圆满地解决了这一问题,同时开创了新的数学分支——图论。
欧拉的解法是:将四块陆地看作四个点,分别记作A、B、C、D;将七座桥看作连接陆地的线,将与偶数条线相连的点叫做偶点,与奇数条线相连的点叫作奇点,如图2所示。
在图2中,每一个点都与奇数条线相连,每一个点都是奇点,这样的图不可能不重复地一笔画完,因此哥尼斯堡七桥问题无解。
所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
2019国家公务员考试行测备考:几何问题中的最短线路问题2019国家公务员考试行测备考:几何问题中的最短线路问题。
几何问题是行测考试中相对来说比较常考的问题,因为几何问题涉及到的知识点非常多,范围非常广泛,能够更全面的考察学员的能力。
而在几何问题中,有一类题目是将几何问题和图形推理中的一笔画问题相结合的,那就是最短线路问题。
那什么是最短线路问题呢?某社区道路如下图所示,社区民警早上9点整从A处的办公室出发,以每分钟50米的速度对社区内每一条道路进行巡查(要求完整走过整个社区内的每一段道路),问他最早什么时候能完成任务返回办公室?想要解决这个问题,我们就得思考怎么走才能够才能保证走的距离最短,也就是最早回到办公室。
因为题干中要求必需巡查每一条道路,所以如果能够按照一笔画图形去走的话应该是最短的。
而且题干中要求要回到A点,那就还要考虑一笔画问题中的画法问题。
1.一笔画:当奇点的个数为0或者2时,这个图形可以由一遍画完成。
2.画法:当奇点的个数为0时,所有的点都是偶点,可以从任意点出发,完成一笔画并且回到原点;当奇点的个数为2时,必须从奇点出发,回到另外一个奇点,才能完成一笔画。
所以由以上的结论可知,先要构成一笔画,则奇点的个数必须为0或者2,而本题中要求回到原点,则奇点的个数必须为0。
我们可以将某些奇点连接起来,将奇点的个数降为0,如图:当然在连接的时候,还要尽量保证所连接的线段或者线段和是最小的,所以该民警走的最短距离为:350×4+350+350+150+200+250=2700米,最短时间:2700÷50=54分钟,回到办公室的最早时间是9点54分。
玉溪中公教育提醒:广大考生一定要注意各学科以及各知识点之间的联系,做题时才能更加得心应手。
When you are old and grey and full of sleep,And nodding by the fire, take down this book,And slowly read, and dream of the soft lookYour eyes had once, and of their shadows deep;How many loved your moments of glad grace,And loved your beauty with love false or true,But one man loved the pilgrim soul in you,And loved the sorrows of your changing face;And bending down beside the glowing bars,Murmur, a little sadly, how love fledAnd paced upon the mountains overheadAnd hid his face amid a crowd of stars.The furthest distance in the worldIs not between life and deathBut when I stand in front of youYet you don't know thatI love you.The furthest distance in the worldIs not when I stand in front of youYet you can't see my loveBut when undoubtedly knowing the love from both Yet cannot be together.The furthest distance in the worldIs not being apart while being in loveBut when I plainly cannot resist the yearningYet pretending you have never been in my heart. The furthest distance in the worldIs not struggling against the tidesBut using one's indifferent heart To dig an uncrossable riverFor the one who loves you.。
一笔画问题(教师必备)一、欧拉的一笔画原理是:(1)一笔画必须是连通的(图形的各部分之间连接在一起);(2)没有奇点的连通图形是一笔画,画时可以以任一偶点为起点,最后仍回到这点;(3)只有两个奇点的连通图形是一笔画,画时必须以一个奇点为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形不是一笔画。
利用一笔画原理,七桥问题很容易解决。
因为图中A,B,C,D都是奇点,有四个奇点的图形不是一笔画,所以一个散步者不可能不重复地一次走遍这七座桥。
二、顺便补充两点:(1)一个图形的奇点数目一定是偶数。
因为图形中的每条线都有两个端点,所以图形中所有端点的总数必然是偶数。
如果一个图形中奇点的数目是奇数,那么这个图形中与奇点相连接的端点数之和是奇数(奇数个奇数之和是奇数),与偶点相连的线的端点数之和是偶数(任意个偶数之和是偶数),于是得到所有端点的总数是奇数,这与前面的结论矛盾。
所以一个图形的奇点数目一定是偶数。
(2)有K个奇点的图形要K÷2笔才能画成。
例如:下页左上图中的房子共有B,E,F,G,I,J六个奇点,所以不是一笔画。
如果我们将其中的两个奇点间的连线去掉一条,那么这两个奇点都变成了偶点,如果能去掉两条这样的连线,使图中的六个奇点变成两个,那么新图形就是一笔画了。
将线段GF和BJ去掉,剩下I和E两个奇点(见右下图),这个图形是一笔画,再添上线段GF和BJ,共需三笔,即(6÷2)笔画成。
一个K(K>1)笔画最少要添加几条连线才能变成一笔画呢?我们知道K笔画有2K个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点。
如左下图中的B,C两个奇点在右下图中都变成了偶点。
所以只要在K笔画的2K个奇点间添加(K-1)笔就可以使奇点数目减少为2个,从而变成一笔画。
三、到现在为止,我们已经学会了如何判断一笔画和多笔画,以及怎样添加连线将多笔画变成一笔画,看下面的例题:1.下列图形分别是几笔画?怎样画?2.能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?3.从A点出发,走遍右上图中所有的线段,再回到A点,怎样走才能使重复走的路程最短?4.下图是国际奥林匹克运动会的会标,能一笔画吗?如果能,请你把它画出来。
所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形; (2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点:D H J O 偶点:A B CEFG I【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。