当前位置：文档之家 › 角动量例题

角动量例题

  • 格式：ppt
  • 大小：466.50 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

刚体角动量 功能例题.ppt

刚体角动量 功能例题.ppt

l 6
3g l l 3g 6l
1 6 1 2
3gl，水平向左． g，竖直向上．
第四章 刚体的转动
9
物理学
第五版
4-3 角动量 角动量守恒定律
思考：如何用刚体定轴转动的动能定理解第二问？
Md
0
1 2
J 2
1 2
J0 2
2
mg
l
cosd
1
J 2
06
2
1 mgl 1 1 ml22
6
29
得 3g
4-3 角动量 角动量守恒定律
v1 2a1h 2h
R1
R1
R1
解得
2h
2(m1R1 m2R2 )g
R1 (M1 2m1)R12 (M 2 2m2 )R22
方法二：Rh机1 械能守h恒 定R2律求RR解12 h
同轴圆柱体、两重物（含绳）、地球组成的系统，机械能守恒。
m1gh
m2 g
mg 1 l 1 J2 1 1 ml22
62
29
得 3g
＝M 0
l
J
(3) vA
rA
l 3
3g 1 l3
3gl，水平向右．
aAn
rA 2
l 3
3g l
g，竖直向下．
vB rB
aBn rB 2
2l 3 2l
3
3g l 3g l
2 3
3gl，水平向左．vC rC
2g，竖直向上． aCn rC 2
物理学
第五版
4-3 角动量 角动量守恒定律
例1：留声机的转盘绕通过盘心垂直盘面的轴在水平面内以
角速率ω 作匀速转动．放上唱片后，唱片将在摩擦力作用下

第8讲 刚体角动量典型例题

第8讲 刚体角动量典型例题
解 子弹、细棒系统的角动量守恒
mv0 y J
y
其中
J
J棒
J子弹
1 3
ML2
my2
mv0 y 1 ML2 my2
3
v0
m
15
刚体转动的典型例题
例10.上题中，若子弹和杆共同偏转30o，子弹的质量为 m ,速度为 v0 。 求 子弹的初速度v0 。
解 由机械能守恒有
1 J2 mgy L Mg (mgy L Mg )cos
11 M Jω0 (t1 t2 )
22
刚体转动的典型例题
例16.求一半径R 50cm 的飞轮对过其中心轴的
转动惯量，在飞轮上绕以细绳，绳末端挂一重物, 其
质量 m1 8.0kg 的让其从 h 2.0m 处静止下落,
测得下落时间 t1 16s ；若用质量 m2 4.0kg 的
重物时, t2 25s , 假定摩擦力矩 Mf 是一个常量 ,
m
S 1 r r sin
F
G
ms m
r
r3
t 2 t
lim S 1 rvsin 1 L
t0 t 2
2m
L C 所以相等的时间内扫过相等的面积。
26
刚体转动的典型例题
例18. 一滑冰者开始转动时 Ek0 J002 2 ，然后
将手臂收回，使转动惯量减少为原来的 1/3，求此时的
转动角速度.
由因为： v2 2ah v 2 mgh
M 2m
6
刚体转动的典型例题
解2 圆盘受力矩 FTR 作用
利用刚体的动能定理, 得
0
FT Rd
1 2
J 2
1 2
J02
绳与圆盘间无相对滑动 v = Rω

角动量计算题

角动量计算题

角动量计算题
角动量是描述物体旋转运动的物理量，它的计算公式是角动量等于物体质量乘以物体的角速度与距离旋转中心的垂直距离的乘积。

角动量的单位是千克·米/秒。

在实际的物理问题中，常常需要计算物体的角动量，以便分析物体的旋转运动规律和研究力学、天体物理等领域的问题。

下面就来看几个角动量计算题：
1. 一个质量为2千克的物体以每秒5转的角速度绕一个固定的点旋转，旋转半径为1.5米。

求该物体的角动量。

解析：根据角动量的计算公式，角动量L = mvr，其中m为物体的质量，v为角速度，r为旋转半径。

将已知数据代入计算公式得到L = 2kg × (5 × 2π rad/s) × 1.5m = 30π kg·m/s。

2. 一个刚体以每秒2.5转的角速度绕自己的对称轴旋转，刚体的质量为3千克，旋转半径为0.8米。

求该刚体的角动量。

解析：同样根据角动量的计算公式，角动量L = mvr，将已知数据代入计算公式得到L = 3kg × (2.5 × 2π rad/s) × 0.8m = 12π kg·m/s。

以上两个例题都是求解物体或刚体在旋转运动中的角动量，通过角动量的计算可
以得到物体或刚体的旋转动量大小。

角动量的大小与物体的质量、角速度和旋转半径有关，所以在计算角动量时要对这些因素进行合理的选择和计算。

同时，还需要注意角速度的单位为弧度/秒，旋转半径的单位为米，质量的单位为千克。

角动量例题

角动量例题
第5章 角动量变化定理与角动量守恒
理学院 物理系 陈强
[例] 试利用角动量守恒定律 证明关于行星运动的开普 例 试利用角动量守恒定律,证明关于行星运动的开普 勒第二定律:任一行星和太阳之间的联线, 勒第二定律:任一行星和太阳之间的联线,在相等的 时间内扫过的面积相等,即掠面速度不变. 时间内扫过的面积相等,即掠面速度不变. [证明] 证明] 行星对太阳O的角动量 行星对太阳 的角动量 的大小为
L = r × p = r m v sin θ
之间的夹角. 其中θ 是径矢 r与行星的动量 p或速度v之间的夹角. 内行星所走过的弧长, 用 s表示时间 t内行星所走过的弧长,则有 s L = lim ( r m sin θ ) t → 0 t
第5章 角动量变化定理与角动量守恒
理学院 物理系 陈强
第5章 角动量变化定理与角动量守恒
理学院 物理系 陈强
考试题:如图所示,一个小物体, 考试题:如图所示,一个小物体,位于光滑的水平桌 面上,与一绳的一端相连结, 面上,与一绳的一端相连结,绳的另一端穿过桌面中 心的小孔O. 该物体原以角速度ω在半径为 在半径为R的园周上 心的小孔 该物体原以角速度 在半径为 的园周上 旋转.今将绳从小孔缓慢往下拉 绕O旋转 今将绳从小孔缓慢往下拉,则物体 旋转 今将绳从小孔缓慢往下拉, (A)动能不变 动量改变. (A)动能不变,动量改变. 动能不变, (B) 动量不变,动能改变 动量不变,动能改变. (C) 角动量不变,动量不变 角动量不变,动量不变. (D) 角动量改变,动量改变 角动量改变,动量改变. (E) 角动量不变,动能,动量都改变 角
�
表示从O到速度矢 若用 r⊥表示从 到速度矢 的垂直距离, 量v 的垂直距离,则有
r sin θ s = r⊥ s = 2 S

牛顿力学中的角动量守恒练习题及

牛顿力学中的角动量守恒练习题及

牛顿力学中的角动量守恒练习题及解答牛顿力学中的角动量守恒练习题及解答在牛顿力学中，角动量守恒是一个重要的概念。

它指的是如果一个物体受到的合外力矩为零，则该物体的角动量将保持不变。

本文将介绍一些关于角动量守恒的练习题，并提供解答。

练习题一：一个半径为r的质点以速度v绕一个定点做匀速圆周运动。

求该质点的角动量。

解答一：根据角动量的定义：L = r × p其中，r为质点与定点的距离，p为质点的动量。

由于质点做匀速圆周运动，所以其速度和角动量的方向是沿着圆周平面的法向量。

而质点的动量则是质量和速度的乘积，即p = mv。

所以，角动量的大小为L = r × mv = mvr角动量的方向与速度方向垂直，并由右手法则确定。

对于这道题目，要求的只是角动量的大小，所以最终答案为L = mvr。

练习题二：一个竖直绕一个定点转动的细长杆长L，质量为m。

当杆的角速度为ω时，求杆的角动量。

解答二：根据角动量的定义：L = r × p其中，r为质点与定点的距离，p为质点的动量。

对于细长杆，可以将其看作是质点，且该质点的动量为质量乘以质点的速度，即p = mLω（ω为角速度）。

而关于杆的角速度，根据直线运动的关系可得：v = ωr（v为线速度，r为质点与定点的距离）。

将v代入p = mv中，得到：p = mLωr将以上结果代入角动量的定义中，可得到：L = r × p = r × (mLωr) = mL²ω所以杆的角动量大小为L = mL²ω。

练习题三：一个质量为m的质点，以速度v沿一条与水平方向夹角θ的斜面下滑，质点的轨迹是一条半径为R的圆弧，求质点的角动量。

解答三：首先需要计算质点的速度与轨迹的关系。

根据斜面的性质和牛顿力学的知识，可以得到：mgsinθ = mv²/R其中，g为重力加速度。

将以上结果代入角动量的定义中，可得到：L = r × p = mRsinθ × mv = m²R²sinθ所以质点的角动量大小为L = m²R²sinθ。

角动量——精选推荐

角动量——精选推荐

⾓动量⾓动量、刚体习题4-1 如本题图，⼀质量为m的质点⾃由降落，在某时刻具有速度v．此时它相对于A、B、C三参考点的距离分别为d1、d2、d3。

求：(1)质点对三个点的⾓动量；(2)作⽤在质点上的重⼒对三个点的⼒矩。

4-2 ⼀质量为m的粒⼦位于(x，y)处，速度为v=v x i+ v y j，并受到⼀个沿-x⽅向的⼒f．求它相对于坐标原点的⾓动量和作⽤在其上的⼒矩。

4-3 电⼦的质量为9.1×10-31kg，在半径为5.3×10-11m的圆周上绕氢核作匀速率运动。

已知电⼦的⾓动量为h/2π，(h为普朗克常量，等于6.63×10-34J?s)，求其⾓速度。

4-4 如本题图，圆锥摆的中央⽀柱是⼀个中空的管⼦，系摆锤的线穿过它，我们可将它逐渐拉短。

设摆长为l1时摆锤的线速度为v1，将摆长拉到l2时，摆锤的速度v2为多少？圆锥的顶⾓有什么变化？4-5 如本题图，在⼀半径为R、质量为m的⽔平转台上有⼀质量是它⼀半的玩具汽车。

起初⼩汽车在转台边缘，转台以⾓速度ω绕中⼼轴旋转。

汽车相对转台沿径向向⾥开，当它⾛到R/2处时，转台的⾓速度变为多少，动能改变多少？能量从哪⾥来？4-6 在上题中若转台起初不动，玩具汽车沿边缘开动，当其相对于转台的速度达到v时，转台怎样转动？4-7 两质点的质量分别为m1、m2(m1> m2)，拴在⼀根不可伸长的绳⼦的两端，以⾓速度ω在光滑⽔平桌⾯上旋转。

它们之中哪个对质⼼的⾓动量⼤？⾓动量之⽐为多少？4-8 在上题中，若起初按住m2不动，让m1绕着它以⾓速度ω旋转。

然后突然将m2放开，求以后此系统质⼼的运动，绕质⼼的⾓动量和绳中的张⼒。

设绳长为l。

4-9 两个滑冰运动员，体重都是60kg，他们以6.5m/s的速率垂直地冲向⼀根10m长细杆的两端，并同时抓住它，如本题图所⽰。

若将每个运动员看成⼀个质点，细扦的质量可以忽略不计。

(1)求他们抓住细杆前后相对于其中点的⾓动量；(2)他们每⼈都⽤⼒往⾃⼰⼀边收细杆，当他们之间距离为5.0m时，各⾃的速率是多少？(3)求此时细杆中的张⼒；(4)计算每个运动员在减少他们之间举例的过程中所作的功，并证明这功恰好等于他们动能的变化。

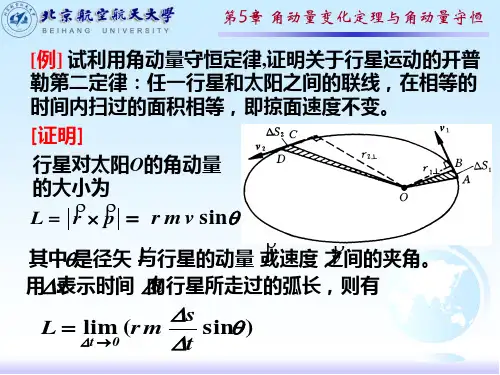
第五章质点角动量例题

J2
半径为 R 的大圆盘对 O 点的转动惯量为
1 R R 3 m2 ( ) 2 m2 ( ) 2 mR 2 2 2 2 24
13 总转动惯量 J J1 J 2 mR 2 24
1 1 m 4 J1 MR 2 (m ) R 2 mR 2 2 2 3 6
R O
R/2
O`
8
四、转动定律的应用
例5-8 阿特伍德机 （1）如图所示,不计绳子的质量和滑轮的质量及半径，滑轮与 绳间只滚不滑，不计滑轮与轴间的摩擦力。且 m1 m2 。 求 重物释放后，物体的加速度和绳的张力。 A
m1
C
M
m2
B
9
（2）如图所示,不计绳子的质量，滑轮的质量与半径分别为M
和 R ， 滑轮与绳间只滚不滑，不计滑轮与轴间的摩擦力 。
1
5-2
A( . O ,
R ,
O . . ,
.
. ), A B
m
M mgR cos
dL mgR cos dt
2
dL mgR cos dt
dL mgRcos dt
L mR v mR , d dt
2
LdL m gR cosd
2 3

L
0
LdL m gR
o
r
R
A
1 2 p mv mgt gt 2 1 LA r p mt 3 g g 0 2 (2) 对 O 点的角动量 r
r
m
mv
r R r
LO r p (R r) p R p R mgt
Rg
LO Rmgt
确定质点有无角动量，要看位矢是否存在绕参考点的转动。

动量 角动量 质心相关例题


二、 一枚返回式火箭以 2.5103 m·s-1 的速率相对惯性系 S 沿水平方 向飞行．空气阻力不计．现使火箭分离为两部分, 前方的仪器舱质
量为 100 kg，后方的火箭容器质量为 200 kg，仪器舱相对火箭容器的 水平速率为 1.0103 m·s-1．求仪器舱和火箭容器相对惯性系的速度．
v1 v2 v'
mv m mv1
1 2 1 1 2 mv m mv12 kx0 2 2 2
x0
mm v k m m
四、如图所示，在光滑的水平面上有一轻质弹簧(其劲度系数为k)， 它的一端固定，另一端系一质量为m′的滑块.最初滑块静止时，弹簧 今有一质量为m 的子弹以速度v0 沿水平方向并垂直 呈自然长度 l0 ， 于弹簧轴线射向滑块且留在其中，滑块在水平面内滑动，当弹簧被拉 伸至长度l 时，求滑块速度v 的大小和方向.
dP mac 提示：利用质心运动定理 F dt
(m1 m2 ) v m1v1 m2 v2
v2 v
m1 v' 2.17 103 m s 1 m1 m2
v1 3.17 103 m s 1
三、如图所示,质量为m、速度为v 的钢球,射向质量为m′的靶,靶 中心有一小孔 , 内有劲度系数为 k 的弹簧 , 此靶最初处于静止状态 , 但 可在水平面上作无摩擦滑动．求子弹射入靶内弹簧后,弹簧的最大压 缩距离．
40
3 2 2 mr0 0 2
W
九、 （练习题）如图所示,质量分别为m1 ＝10.0 kg和m2 ＝6.0 kg 的两小球A 和B,用质量可略去不计的刚性细杆连接,开始时它们静止 在Oxy 平面上,在图示的外力F1 ＝(8.0 N) i 和F2 ＝(6.0 N) j 的作用 下运动．试求：(1)它们质心的坐标与时间的函数关系；(2)系统总动 量与时间的函数关系．

中学物理竞赛讲义角动量例题

5.3角动量例题例1、在一根长为3l的轻杆上打一个小孔，孔离一端的距离为l，再在杆的两端以及距另一端为l处各固定一个质量为M的小球。

然后通过此孔将杆悬挂于一光滑固定水平细轴O上。

开始时，轻杆静止，一质量为m的铅粒以v0的水平速度射入中间的小球，并留在其中。

求杆摆动的最大高度。

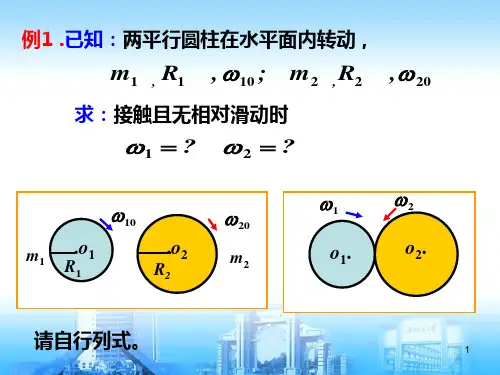
例2、质量m＝1.1 kg的匀质圆盘，可以绕通过其中心且垂直盘面的水平光滑固定轴转动．圆盘边缘绕有绳子，绳子下端挂一质量m1＝1.0 kg的物体，如图所示．起初在圆盘上加一恒力矩使物体以速率v0＝0.6 m/s匀速上升，如撤去所加力矩，问经历多少时间圆盘开始作反方向转动．例3、两个质量均为m的质点，用一根长为2L的轻杆相连。

两质点以角速度ω绕轴转动，轴线通过杆的中点O与杆的夹角为θ。

试求以O为参考点的质点组的角动量和所受的外力矩。

例4、小滑块A位于光滑的水平桌面上，小滑块B位于桌面上的小槽中，两滑块的质量均为m，并用长为L、不可伸长、无弹性的轻绳相连。

开始时，A、B之间的距离为L/2，A、B间的连线与小槽垂直。

突然给滑块A一个冲击，使其获得平行与槽的速度v0，求滑块B开始运动时的速度例5、有一半径为R的圆形平板平放在水平桌面上，平板与水平桌面的摩擦系数为μ，若平板绕通过其中心且垂直板面的固定轴以角速度ω0开始旋转，它将在旋转几圈后停止？例6、一质量为M a，半径为a的圆筒A，被另一质量为M b，半径为b的圆筒B同轴套在其外，均可绕轴自由旋转。

在圆筒A的内表面上散布了薄薄的一层质量为M o的沙子，并在壁上开了许多小孔。

在t＝0时，圆筒A以角速度ω0绕轴匀速转动，而圆筒B静止。

打开小孔，沙子向外飞出并附着于B筒的内壁上。

设单位时间内喷出的沙子质量为k，若忽略沙子从A筒飞到B筒的时间，求t 时刻两筒旋转的角速度。

*例7、如图，CD、EF均为长为2L的轻杆，四个端点各有一个质量为m的质点，CE、DF为不可伸长的轻绳，CD的中点B处用一细线悬于天花板A点。

高中物理力学中角动量守恒问题的解题技巧

高中物理力学中角动量守恒问题的解题技巧在高中物理力学学习中，角动量守恒是一个非常重要的概念。

它在解决一些与旋转运动有关的问题时起着至关重要的作用。

本文将通过具体题目的举例，来说明角动量守恒问题的解题技巧，并且尝试给出一些一般性的指导。

例题1：一质点质量为m，在水平光滑桌面上以速度v做匀速圆周运动，半径为r。

一个质量为M的物体以速度V撞击该质点，并与其发生完全弹性碰撞。

碰撞后，质点的圆周运动半径变为R。

求M与m的质量比。

解析：这道题目涉及到了角动量守恒和动量守恒两个重要的物理定律。

我们可以首先分析碰撞前后的角动量和动量是否守恒。

碰撞前，质点的角动量为L1 = mvr，物体的角动量为L2 = MRV。

由于碰撞是完全弹性碰撞，所以碰撞后质点和物体的速度方向不变，仅仅改变了大小。

因此，碰撞后质点的角动量为L3 = mVR，物体的角动量为L4 = MRv。

根据角动量守恒定律，碰撞前后的总角动量应该相等，即L1 + L2 = L3 + L4。

代入数值，得到mvr + MRV = mVR + MRv。

同样地，根据动量守恒定律，碰撞前后的总动量也应该相等，即mv + MV = mV + Mv。

通过以上两个方程，我们可以解得M与m的质量比。

这道题目的解题关键在于正确运用角动量守恒和动量守恒的定律，并将它们转化为数学方程进行求解。

在解题过程中，需要注意将碰撞前后的角动量和动量分别表示出来，并且注意角动量的正负方向。

例题2：一个物体以速度v绕一个半径为r的固定点做匀速圆周运动。

现在将该物体的速度加倍，求此时物体的角动量相对于原来增加了多少倍。

解析：这道题目考察的是角动量与动量的关系。

根据角动量的定义，L = mvr，其中m为物体的质量，v为物体的速度，r为物体到固定点的距离。

当物体的速度加倍时，新的角动量为L' = 2mv(r/2) = 2L。

可以看出，物体的角动量相对于原来增加了2倍。

这道题目的解题关键在于理解角动量与动量的关系，即角动量正比于动量。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
代入数据可, 得
r远 日 5.26 1012 m
7.如图所示，一个长为l 、质量为M 的 匀质杆可绕支点o自由转动.一质量为m 、速 率为v 的子弹以与水平方向成角 600的方向射 入杆内距支点为a 处，使杆的偏转角为 300. 问子弹的初速率为多少？ 解 把子弹和匀质杆作为 0 一个系统, 分析可知在碰 30 撞过程中角动量守恒. 0v 设子弹射入杆后与杆 60 ,则 一同前进的角速度为 1 2 0 2 m v cos 60 a Ml ma 3
6. 哈雷慧星绕太阳运行时的轨道是一个 椭圆，如图所示，它距离太阳最近的距离是 4 -1 10 v 5 . 46 10 m s r近 日 8.75 10 m , 速率 近 日 2 -1 ；它离太阳最远时的速率 v远 日 9.08 10 m s ，这时它离太阳的距离 r远 日 ？ v远 日
8. 如图所示，一根质量为M 、长为2l 的 均匀细棒，可以在竖直平面内绕通过其中心 的光滑水平轴转动，开始时细棒静止于水平 位置. 今有一质量为m 的小球，以速度 u 垂 直向下落到了棒的端点，设小球与棒的碰撞 为完全弹性碰撞. 试求碰撞后小球的回跳速 度 v 及棒绕轴转动的角速度 . m u M o
r近 日
r远 日
v近 日
解 彗星受太阳引力的作用，而引力通过了 太阳，所以对太阳的力矩为零，故彗星在运 行的过程中角动量守恒. 于是有 r近 日 v近 日 r远 日 v远 日 因为 r近日 v近日，r远日 v远日
r近日v近日 所以 r远日 v远日
l
lLeabharlann 解 分析可知,以棒和小球组成的系统的角动 量守恒. 由于碰撞前棒处于静止状态，所以 碰撞前系统的角动量就是小球的角动量 lmu ; 由于碰撞后小球以速度v 回跳，棒获得的角 速度为 ，所以碰撞后系统的角动量为 1 2 lmv Ml 3 由角动量守恒定律得 1 2 lmu lmv Ml 3 由题意知，碰撞是完全弹性碰撞，所以 碰撞前后系统的动能守恒，即
o R M

T
h
G
a
a R 物体m 落下h 高度时的速率为
v 2ah
圆盘的转动惯量为 1 J MR 2 2 联立以上五式，可得物体m 落下h 高度 时的速率为 mgh v2 M 2m 小于物体自由下落的速率 2 gh.
解法二 利用动能定理求解. 对于物体m 利用质点的动能定理有
角动量守恒定律
若：M 0 即系统所受的合外力矩为零.
——角动量守恒的条件
则：dL d J 0 ， 或L J 常量.
——角动量守恒的内容 注意：在推导角动量守恒定律的过程中 受到了刚体、定轴等条件的限制，但它的适 用范围却远远超过了这些限制. 如: 滑冰运动员的表演.
1.求长为L ，质量为m 的均匀细棒AB 的 转动惯量. （1）对于通过棒的一端与棒垂直的轴； （2）对于通过棒的中点与棒垂直的轴. 解 （1）如图所示，以过A 端垂直于棒的 oo 为轴，沿棒长方向为x 轴，原点在轴上，在 棒上取长度元 dx ，则由转动惯量的定义有: J 端 点 x 2dm m o x dx B x L m x 2 dx A 0 dm L 1 2 L o mL 3
a
l
子弹在射入杆后与杆一起摆动的过程中 只有重力做功，所以由子弹、杆和地球组成 的系统机械能守恒，因此有
1 1 2 2 2 Ml ma 2 3 l mga1 cos 30 Mg 1 cos 300 2
0
联立上述这两个方程得子弹的初速率为
2 2 3 v g Ml 2ma Ml 2 3ma 2 ma 6
1 1 2 1 1 2 2 2 mu mv Ml 2 2 2 3
联立以上两式，可得小球的速度为 3m M v u 3m M 棒的角速度为 6m u 3m M l 讨论: 要保证小球回跳v 0 ，则必须保证 M 3m .
5. 如图所示，一质 量为M 、半径为R 的匀 质圆盘形滑轮，可绕一 无摩擦的水平轴转动. 圆盘上绕有质量可不计 绳子，绳子一端固定在 滑轮上，另一端悬挂一 质量为m 的物体，问物 体由静止落下h 高度时, 物体的速率为多少？
R
M
h
解法一 用牛顿第二运动 定律及转动定律求解.分 析受力如图所示. 对物体m用牛顿第二 运动定律得 mg T ma 对匀质圆盘形滑轮用 转动定律有 TR J 物体下降的加速度的 大小就是转动时滑轮边缘 上切向加速度，所以
mgh v2 M 2m
解法三 利用机械能守恒定律求解.
若把滑轮、物体和地球看成一个系统， 则在物体落下、滑轮转动的过程中，绳子的 拉力T 对物体做负功（ Th），对滑轮做正 功（ Th ）即内力做功的代数和为零，所以 系统的机械能守恒. 若把系统开始运动而还没有运动时的状 态作为初始状态，系统在物体落下高度h 时 的状态作为末状态，则 2 1 1 1 2 2 v MR mv mgh 0 2 2 R 2 解之可得物体 m 落下h 高度时的速率.
J r 2dm

m R
0
1 1 4 r 2r ldr R l mR 2 2 2
2
4.一绳跨过定滑轮，两端分别系有质量 分别为m 和M 的物体，且 M m . 滑轮可 看作是质量均匀分布的圆盘，其质量为 m ， 半径为R ，转轴垂直于盘面通过盘心，如 图所示.由于轴上有摩擦，滑轮转动时受到 了摩擦阻力矩 M阻 的作用. 设绳不可伸长 且与滑轮间无相对滑动.求物体的加速度及 绳中的张力.
R o M阻 m

据题意可知，绳与滑轮间无相对滑动， 所以滑轮边缘上一点的切向加速度和物体的 加速度相等，即
a a1 a2 a R
联立以上三个方程，得
M阻 ( M m)g R a m M m 2
mM阻 m ( 2 M )mg 2 R T1 m( g a ) m M m 2 MM阻 m ( 2m ) Mg 2 R T2 M ( g a ) m M m 2 注意：当不计滑轮的质量和摩擦阻力矩 时，此时有 T1 T2 ，物理学中称这样的滑轮 为“理想滑轮”，称这样的装置为阿特伍德 机.
2
2.试求质量为m 、半径为R 的匀质圆环 对垂直于平面且过中心轴的转动惯量. 解 作示意图如右,由于质 量连续分布，所以由转动 惯量的定义得
J R 2dm
m
dm
o
R

2R 0
m R dl 2R
2
mR 2
3.试求质量为m 、半径为R 的匀质圆盘 对垂直于平面且过中心轴的转动惯量. dr 解 如图所示, 由于质 量连续分布，设圆盘的 R l o r 厚度为l，则圆盘的质量 密度为 m 2 R l
解 受力分析如图所示. 对于上下作平动的两物体， 可以视为质点，由牛顿第 二运动定律得
T1 对m ：T1 mg ma1 T2 a1 对 M ： Mg T Ma 2 2 m 若以顺时针方向转的 M 力矩为正，逆时针转的方 a2 Gm 向为负，则由刚体定轴转 GM 动的转动定律得 1 2 T2 R T1 R M阻 J m R 2
1 1 2 2 mgh Th mv mv0 2 2 其中 v0 和 v 是物体的初速度和末速度.
对于滑轮由刚体定轴转动的转动定理有 1 1 2 2 TR J J 0 2 2 其中 是在拉力矩TR 的作用下滑轮转 过的角度， 0 和 是滑轮的初末角速度.
由于滑轮和绳子间无相对滑动，所以物 体落下的距离应等于滑轮边缘上任意一点所 经过的弧长，即 h R . 1 又因为v0 0, 0 0, v R, J MR 2 . 2 联立以上各式，可得物体 m 落下h 高度 时的速率为
（2）如图所示，以过中点垂直于棒的oo 为轴，沿棒长方向为x 轴，原点在轴上，在 棒上取长度元 dx ，则由转动惯量的定义有: o x dx B x A dm L L o 2 2
J 端 点 x dm
2 m
L 2 L 2
m 1 mL2 x dx L 12