习题课6-力矩与角动量

理解角动量与力矩在物理学中，角动量和力矩是两个重要的概念，它们在描述物体运动和旋转方面发挥着至关重要的作用。

本文将对角动量和力矩进行解释和探讨，并分析它们之间的关系。

一、角动量的概念与性质角动量是描述物体自旋状态的物理量，它的大小与物体的质量、旋转速度以及旋转轴的位置有关。

角动量的定义可以表示为L=Iω，其中L表示角动量，I表示转动惯量，ω表示角速度。

转动惯量与物体的形状和质量分布有关，在不同的旋转轴上转动，转动惯量也会发生变化。

角速度则是物体旋转的快慢程度。

角动量有一些重要的性质。

首先，角动量是矢量量，具有大小和方向。

方向垂直于旋转平面，并遵循右手定则。

其次，角动量守恒是一个重要的物理定律。

在没有外力或力矩作用的情况下，物体的角动量保持不变。

这一定律被广泛应用于天体力学、量子力学等领域的研究中。

二、力矩的概念与计算方法力矩是描述物体受力作用下旋转状态的物理量，它的大小与力的大小、力臂的长度以及力的作用方向有关。

计算力矩可以使用以下公式：τ = r × F，其中τ表示力矩，r表示力臂，F表示力。

力矩的单位是牛顿米（N·m）。

力矩也满足一些重要的性质。

首先，力矩也是矢量量，具有大小和方向。

其方向垂直于力臂和力的平面，并遵循右手定则。

其次，力矩的大小可以通过将力矢量与力臂矢量的叉乘来计算。

三、角动量与力矩的关系角动量与力矩之间存在着密切的关系。

力矩可以导致物体的角动量发生变化，进而影响物体的旋转状态。

根据牛顿力学定律，力矩等于物体的转动惯量乘以加速度矢量。

由于角速度与加速度之间存在关系，即ω=αt，其中α表示角加速度，t表示时间，因此可以将力矩表示为τ=Iα。

根据以上推导，可以得到角动量的变化率与力矩的关系，即dL/dt=τ。

这表明，力矩的作用可以改变物体的角动量，从而影响旋转运动的状态。

当力矩为零时，物体的角动量保持不变，符合角动量守恒定律。

四、实际应用与例子分析角动量和力矩的理论在物理学中有广泛的应用。

第一节力矩和角动量【知识要点】一、力矩的定义1.对轴的力矩对轴的力矩可推动物体绕轴转动或改变物体绕轴转动的角速度.力矩的大小不仅与力的大小和方向有关，而且与力的作用点有关.当力的作用线在垂直于轴的平面（π）上时（图5-1-1),力矩τ的大小与力的作用点P和轴的距离ρ成正比，与力在垂直于ρ方向上的分量Fφ成正比，因为力在ρ方向上的分量Fρ对物体的绕轴转动无作用，于是有τ=ρFφ=Fρsinθ（5. 1-1)式中θ是F与ρ的夹角，ρ就是从轴与平面π的交点O'指向P点的矢量，由于在力矩作用下引起的转动有两个可能的方向，力矩也有正、负两种取向.例如，先任意规定轴的正方向，当逆着轴的正方向去看力矩作用下所引起的物体的转动时，若物体沿逆时针方向转动，对应的力矩就取为正，反之为负.由于ρsinθ=d就是力的作用线与轴的距离，（5. 1-1)式又可写成τ = Fd （5. 1-1a)d常称为力臂，这正是大家所熟知的力矩表达式.当力的作用线不在垂直于轴的平面(π)上时，可将和垂直于轴的分量F⊥力F分解为平行于轴的分量F∥两部分，其中F1-1b)这里的θ是F⊥与ρ的夹角（图5-1-2).2.对参考点的力矩可将上述对轴的力矩的概念推广到对点的力矩.在选定的参照系中，从参考点0指向力的作用点P的矢量r与作用力F的矢积称为作用力对于参考点0的力矩，即Τ=r×F(5-1-2)r也可称为作用点相对参考点的位矢.当参考点是坐标原点时，r就是力的作用点的位矢.根据矢积的意义，力矩的大小等于以r 和F 两矢量为邻边所构成的平行四边形的面积，方向与r 、F 所在平面垂直并与r 、F 成右手螺旋。

二、作用于质点的力矩和作用于质点系的力矩1.作用于质点的力矩当质点m 受力F 作用时，F 对参考点〇的力矩即为质点受到的力矩，这时力矩表达式中的r 就是参考点指质点的矢量，当参考点为坐标原点时，r 就是质点的位矢.当质点受F 1、F 2、…、F NN 个力同时作用时，诸力对某参考点的力矩的矢量和等于合力F=F 1+F 2+…+F N 对同一参考点的力矩，即r ×F 1+r ×F 2+…+r×F N =r×(F 1+F 2+…+F N )=r×F （5. 1-3)2. 作用于质点系的力矩力矩概念也可应用于作用于质点系上的作用力.一般讲来，质点系内各质点受到的作用力有外力和内力的区别，因此应分别考察外力的力矩和内力的力矩(1)外力的力矩当质点系受多个外力作用时，若第i 个质点受到的合外力为F i ，该质点相对某一给定参考点的位矢为r i ，则其力矩为τi 外= r i ×F i ，各质点所受力矩的矢量和，即质点系所受的总力矩为∑∑⨯==i ii i i F r 外外ττ （）由于各外力作用在不同质点上，各质点的位矢r i 各不相同，因而外力对质点系的总力矩一般不能通过外力矢量和的力矩来计算.但当质点系处在重力场中时，各质点所受重力与质点的质量成正比，方向又都相同，因而作用于质点系的重力相对某一参考点的力矩，根据式为∑∑⨯=⨯=⨯=i iC i i i i Mg r g r m g m r ）（重力τ （5. 1-5)即作用于质点系的重力相对某参考点的力矩等于重力的矢量和作用于质心上时对该参 考点的力矩.在平动非惯性系中的惯性力显然也具有这种性质.(2)内力的力矩若f i 为作用于质点系中第i 个质点上的合内力，r i 为该质点的位矢，则内力的总力矩为∑∑∑≠⨯=⨯=i i i r ij ji i i f f r 内τ由于内力总是成对出现，因而上式可写成∑⨯+⨯=ji )( ij j ji i f r f r 内τ根据牛顿第三定律（强形式），任一对内力f ji 和f ij 必定等值反向，且沿同一直线，因而对任一给定参考点O 来说，力矩也必等值反向，两者相互抵消，即0=⨯+⨯ij j ji i f r f r因而内力的总力矩为零 0)(ji =⨯+⨯=∑ ij j ji i f r f r 内τ （5. 1-6)这一结果与内力的冲量相似，但与内力的功不同.三、 冲量矩在明确了力矩的概念以后，可引出冲量矩的概念.t t 0t t L ∆=∆+=∆+=∆=∆外外内外）（）（τττττ （5. 1-7)此式对质点系适用.若对质点只需把外τ改为τ即可.在一段时间内质点或质点系所受的冲量矩为这段时间内冲量矩的累加：∑∑∆=∆=∆t L L 外总τ （5. 1-8)总L ∆为矢量，方向与外τ相同，单位是ｓｍＮ••。

力矩与角动量力矩和角动量是物理学中重要的概念，在许多领域中都有广泛的应用。

本文将从基本定义、计算公式、应用领域等方面对力矩和角动量进行论述。

一、力矩的定义与计算公式力矩是描述物体受力作用时转动效果的物理量，它是由作用在物体上的力产生的。

力矩的定义是力对物体作用的垂直距离和力的大小的乘积。

如果将物体迅速转动，则力矩的大小决定了物体转动的快慢。

力矩的计算公式是M = Fd，其中M表示力矩，F表示作用在物体上的力，d表示力作用点到转轴的垂直距离。

这个公式可以简单理解为力乘以力臂的乘积。

二、角动量的定义与计算公式角动量是描述物体旋转状态的物理量，它是由旋转物体的质量、转动轴和运动速度决定。

角动量的定义是物体质量与线速度的乘积与物体到转移轴的距离的乘积。

在物理学中，角动量是守恒的，当物体在没有外力作用和无摩擦的情况下，其角动量将保持不变。

角动量的计算公式是L = rp，其中L表示角动量，r表示物体到转动轴的距离，p表示物体的动量。

这个公式可以理解为物体离转动轴的距离乘以物体的动量。

三、力矩和角动量的应用领域1.力矩在机械方面的应用力矩在机械中有广泛的应用，特别是在杠杆、摇杆、螺旋等机构的设计中。

通过调整不同长度的杆臂或者改变力的大小，可以实现不同程度的力矩作用，从而达到理想的运动效果。

2.角动量在天体物理学中的应用角动量在天体物理学中有着重要的应用。

例如，行星绕太阳运动时的角动量守恒定律可以解释行星运动的稳定性和轨道形状。

3.角动量在核物理学中的应用角动量在核物理学中扮演着重要的角色，尤其是在原子核的结构和核反应等方面。

核物理学家利用角动量来解释原子核的稳定性、核衰变、核裂变等现象。

4.力矩和角动量在运动学中的应用力矩和角动量在运动学中有广泛的应用。

例如，力矩可以用来描述地球自转的影响、物体平衡的条件等。

而角动量则可以用来描述刚体转动、旋转力矩等现象。

总结：力矩和角动量是物理学中的重要概念，对于理解物体的旋转和转动效果有着重要的意义。

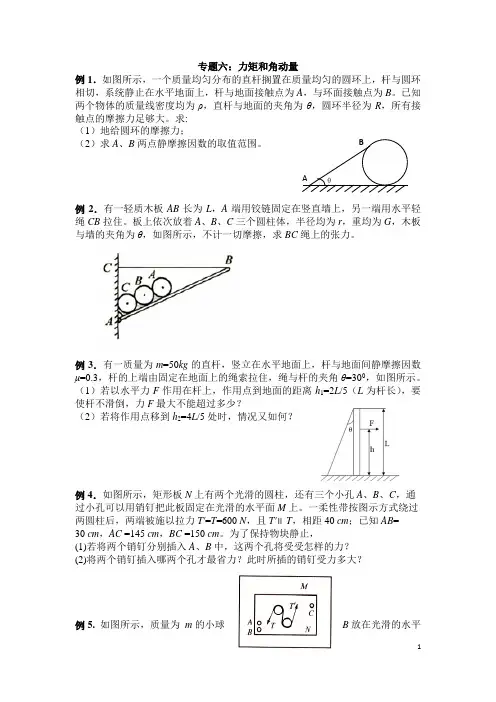
专题六：力矩和角动量例1．如图所示，一个质量均匀分布的直杆搁置在质量均匀的圆环上，杆与圆环相切，系统静止在水平地面上，杆与地面接触点为A ，与环面接触点为B 。

已知两个物体的质量线密度均为ρ，直杆与地面的夹角为θ，圆环半径为R ，所有接触点的摩擦力足够大。

求:（1）地给圆环的摩擦力；（2）求A 、B 两点静摩擦因数的取值范围。

例2．有一轻质木板AB 长为L ，A 端用铰链固定在竖直墙上，另一端用水平轻绳CB 拉住。

板上依次放着A 、B 、C 三个圆柱体，半径均为r ，重均为G ，木板与墙的夹角为θ，如图所示，不计一切摩擦，求BC 绳上的张力。

例3．有一质量为m =50kg 的直杆，竖立在水平地面上，杆与地面间静摩擦因数μ=0.3，杆的上端由固定在地面上的绳索拉住，绳与杆的夹角θ=300，如图所示。

（1）若以水平力F 作用在杆上，作用点到地面的距离h 1=2L /5（L 为杆长），要使杆不滑倒，力F 最大不能超过多少？（2）若将作用点移到h 2=4L /5处时，情况又如何？例4．如图所示，矩形板N 上有两个光滑的圆柱，还有三个小孔A 、B 、C ，通 过小孔可以用销钉把此板固定在光滑的水平面M 上。

一柔性带按图示方式绕过 两圆柱后，两端被施以拉力T'=T =600 N ，且T'∥T ，相距40 cm ；已知AB = 30 cm ，AC =145 cm ，BC =150 cm 。

为了保持物块静止，(1)若将两个销钉分别插入A 、B 中，这两个孔将受受怎样的力？(2)将两个销钉插入哪两个孔才最省力？此时所插的销钉受力多大？例5. 如图所示，质量为 m 的小球 B 放在光滑的水平A B θ槽内，现以一长为l 的细绳连接另一质量为m 的小球A ，开始时细绳处于松弛状态, A 与B 相距为l /2。

球A 以初速度v 0在光滑的水平地面上向右运动。

当A 运动到图示某一位置时细绳被拉紧，试求B 球开始运动时速度v B 的大小。

大学物理角动量和力矩（一）引言概述：大学物理中，角动量和力矩作为重要的概念之一，对于研究物体的运动和旋转有着重要的影响。

角动量是描述物体旋转运动状态的物理量，而力矩则是描述旋转物体所受到的力和力臂的乘积。

本文将从角动量和力矩的基本概念入手，通过各个角度的阐述和分析，深入探讨角动量和力矩的原理及其在物理中的应用。

正文：一、角动量的基本概念1. 角动量的定义和量纲2. 角动量的计算方法及其守恒定律3. 角动量和动量的关系4. 角动量的矢量性质及其坐标表示5. 角动量的多体系下的计算方法二、力矩的基本概念1. 力矩的定义和量纲2. 力矩与力的关系3. 力矩的计算方法及其守恒定律4. 力矩的矢量性质及其坐标表示5. 力矩的多体系下的计算方法三、角动量和力矩的物理意义1. 角动量的物理意义及其应用领域2. 力矩的物理意义及其应用领域3. 角动量和力矩在自然界中的实际案例4. 角动量和力矩在机械工程中的应用5. 角动量和力矩在天文学研究中的应用四、角动量和力矩的数学推导和分析1. 角动量守恒定律的动力学推导2. 力矩与角加速度的关系及其推导3. 角动量和力矩的相互作用机制分析4. 角动量和力矩的转动惯量及其数学解析5. 角动量和力矩的数学计算公式及其推导五、角动量和力矩的实验测量方法1. 实验测定角动量的装置和方法2. 实验测定力矩的装置和方法3. 角动量和力矩的实验数据处理和分析4. 角动量和力矩实验的误差分析和改进措施5. 角动量和力矩实验的应用案例和展望总结：通过对角动量和力矩的深入讨论，我们可以更好地理解物体的旋转运动以及受到的力和力臂的影响。

角动量和力矩的物理意义在不同的领域中得到广泛应用，并通过数学推导和实验测量方法得以验证和实践。

未来，随着科学技术的不断进步，角动量和力矩的研究将继续向更深层次发展，为人们认识世界的运动规律提供更多的突破点和启示。

高中物理中的力矩与角动量问题解析在高中物理学习过程中，力矩与角动量是两个重要的概念。

力矩是描述物体受力情况下的转动效应的物理量，而角动量则是描述物体旋转状态的物理量。

本文将对这两个概念进行解析，并探讨其在物理学中的应用。

一、力矩的概念与计算方法力矩是描述物体受力情况下的转动效应的物理量。

它是由力的大小、作用点到转轴的距离以及力与转轴的夹角共同决定的。

力矩的计算公式为M = F × r × sinθ，其中M表示力矩，F表示力的大小，r表示力的作用点到转轴的距离，θ表示力与转轴的夹角。

力矩的方向垂直于力的方向和力臂的平面，遵循右手定则。

当力矩的方向与物体的旋转方向一致时，力矩将促使物体继续旋转；当力矩的方向与物体的旋转方向相反时，力矩将阻碍物体的旋转。

力矩在物理学中有着广泛的应用。

例如，力矩可以解释为什么杠杆可以放大力的作用。

当我们用杠杆来举起一个重物时，通过改变力臂的长度，可以使得力矩增大，从而减小所需的力的大小。

此外，力矩还可以解释为什么一个物体在受到外力作用时会发生旋转。

二、角动量的概念与计算方法角动量是描述物体旋转状态的物理量。

它是由物体的质量、角速度以及物体质心到转轴的距离共同决定的。

角动量的计算公式为L = I × ω，其中L表示角动量，I表示物体的转动惯量，ω表示物体的角速度。

角动量的方向垂直于物体的旋转轴，遵循右手定则。

当角动量的方向与物体的旋转方向一致时，角动量将促使物体继续旋转；当角动量的方向与物体的旋转方向相反时，角动量将阻碍物体的旋转。

角动量在物理学中也有着广泛的应用。

例如，角动量可以解释为什么旋转物体在没有外力作用时仍然保持旋转状态。

这是因为旋转物体的角动量守恒，即旋转物体的角动量在没有外力作用时保持不变。

此外，角动量还可以解释为什么旋转物体在改变自身转动惯量时会发生角速度的变化。

三、力矩与角动量的关系力矩与角动量有着密切的关系。

当物体受到外力作用时，力矩将改变物体的角动量。

力矩与角动量的概念和计算方法在物理学中，力矩和角动量是两个非常重要的概念，它们在理解物体的旋转运动方面起着关键作用。

接下来，让我们逐步深入了解这两个概念以及它们的计算方法。

一、力矩力矩，简单来说，就是使物体绕着某个轴转动的力的效果。

想象一下，当我们试图转动一扇门时，我们施加在门把手上的力就是产生力矩的力。

力矩的大小等于力的大小与力臂的乘积。

力臂是从转动轴到力的作用线的垂直距离。

如果用 M 表示力矩，F 表示力，L 表示力臂，那么力矩的计算公式就是 M ＝ F × L 。

为了更清楚地理解力矩，我们来看一个例子。

假设我们有一个水平放置的杠杆，杠杆的一端施加一个垂直向下的力F ，杠杆的长度为L ，转动轴位于杠杆的中点。

那么力臂就是杠杆长度的一半，即 L ／ 2 ，此时的力矩 M ＝ F ×（ L ／ 2 ）。

力矩的方向也很重要。

根据右手定则，当右手的四指沿着力绕轴的转动方向弯曲时，大拇指所指的方向就是力矩的方向。

在实际生活中，力矩的概念有着广泛的应用。

比如螺丝刀的使用，我们通过施加在手柄上的力产生力矩，从而拧紧或松开螺丝。

汽车的方向盘也是利用力矩来控制车轮的转向。

二、角动量角动量是描述物体绕轴旋转状态的物理量。

它类似于描述物体直线运动状态的动量。

角动量的大小等于转动惯量与角速度的乘积。

转动惯量取决于物体的质量分布和旋转轴的位置。

角速度则是物体旋转的快慢程度。

如果用 L 表示角动量，I 表示转动惯量，ω 表示角速度，那么角动量的计算公式为 L ＝I × ω 。

转动惯量的计算相对复杂一些，对于一个质点，其转动惯量 I ＝ m × r²，其中 m 是质点的质量，r 是质点到转轴的距离。

对于一个连续分布的物体，需要通过积分来计算转动惯量。

角动量也有方向，其方向同样可以通过右手定则来确定。

右手弯曲的四指沿着物体的转动方向，大拇指所指的方向就是角动量的方向。

角动量在很多自然现象和工程应用中都起着重要作用。

力矩定理与角动量的计算力矩定理和角动量是力学中非常重要的概念，它们在解释物体运动和力的作用时起着至关重要的作用。

本文将探讨力矩定理和角动量的计算方法，并探讨它们在实际生活中的应用。

力矩定理是描述物体受力矩作用时的平衡条件的定理。

力矩是由力在物体上施加的力臂引起的，力臂是力作用点到物体某一点的垂直距离。

力矩定理的数学表达式是：力矩 = 力 ×力臂。

根据力矩定理，当物体受到的力矩之和为零时，物体将保持平衡。

要计算力矩，我们需要知道作用力的大小和方向，以及力臂的长度。

例如，考虑一个杆子，上面有一个质量为5千克的物体。

如果有一个力以20牛的大小施加在杆子上，使得物体保持平衡，我们可以计算出力矩。

假设力臂的长度为1米，那么力矩 = 20牛 × 1米 = 20牛米。

这意味着物体受到的力矩为20牛米，因此保持平衡。

角动量是描述物体旋转运动的物理量。

它是由物体的质量、速度和旋转半径决定的。

角动量的数学表达式是：角动量 = 质量 ×速度 ×旋转半径。

当物体受到外力或扭矩的作用时，角动量会发生变化。

根据角动量守恒定律，当物体在没有外力作用下旋转时，角动量守恒。

要计算角动量，我们需要知道物体的质量、速度和旋转半径。

例如，考虑一个半径为2米的转盘，上面有一个质量为10千克的物体。

如果物体以5米/秒的速度沿着转盘旋转，我们可以计算出角动量。

角动量 = 10千克 × 5米/秒 × 2米 = 100千克米/秒。

这意味着物体的角动量为100千克米/秒。

力矩定理和角动量的计算方法在实际生活中有广泛的应用。

在机械工程中，我们可以使用力矩定理来计算机械装置的平衡条件。

例如，在设计一个平衡杆时，我们可以使用力矩定理来确定所需的力矩，以保持杆的平衡。

在物理学中，我们可以使用角动量来解释天体运动。

例如，地球绕太阳旋转时，地球的角动量守恒，这解释了地球保持在轨道上的原因。

此外，力矩定理和角动量的计算方法还可以应用于运动力学和动力学的研究中。