当前位置：文档之家 › 第3章 地震作用计算-1

第3章 地震作用计算-1

  • 格式：pdf
  • 大小：4.55 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

第三章1-单自由度体系的弹性地震反应分析与地震作用

第三章1-单自由度体系的弹性地震反应分析与地震作用


1 k

x g (t )
上式与振动方程（3.4b）完全相同。
17
3. 振动方程的简化
令： = k m (3.6) (3.7)
=
c 2 m
代入式（3.4b）得 即 (t ) 2 x (t ) 2 x (t ) = g (t ) x x (3.5)
式中 ：称为自振频率
x (t )
建立振动方程有两种方法： 刚度法和柔度法
m
k
fD
m
fS
fI
x g (t )
14
1. 刚度法
地震时，任意时刻质点m的相对位移为x(t ) 任意时刻基础的位移为xg (t ) 质点m的绝对加速度为： x(t ) xg (t ) 取质点m为脱离体，则其所受 到的作用力有：
xg (t )
t
30
振动方程的特解——续
2 x 2 x = g x x
观察振动方程，可将方程右边项 xg (t )看作单位质量(m = 1)上 的动力荷载。
g (t )曲线划分成若 现将 x 干个瞬时荷载（如图）。
当t = 时： 体系的质量 m = 1 g ( ) 1 瞬时荷载为 P = x g ( ) d 瞬时冲量为 Pdt = x
x(t ) = et (c1 cosDt c2 sin Dt )
D = 1 2
D : 有阻尼单自由度体系的 自振频率
一般工程为欠阻尼情况： 边界条件： 代入上式：
x0 = x(0), x 0 = x(0)
c1 = x0



代入上式导数式： c = 2
x 0 x0
6
地震作用计算ppt课件

地震作用计算ppt课件


0.9 0.05 - 0.5 5
1——直线下降段的斜率调整系数； 1 0 . 0 2 ( 0 . 0 5 - ) / 8
2——阻尼调整系数，小于0.55时，
应取0.55。
2
1
0.05 - 0.06 1.7
8
二、 多质点体系水平地震作用
结构总的地震作用
F E k a 1G e q
0 0.1 Tg
T(s)
5Tg
6.0
4
a
第五章 地震作用 第三节 2amax 单质a 点(TTg体) 系2am水ax 平地震作用
0.45a max
a [2 0.2 -1(T - 5Tg )]amax
0 0.1 Tg
T (s)
5Tg
6.0
曲线由四部分组成
➢0＜T＜0.1区段，a为向上倾斜的直线
➢0.1＜T＜Tg区段，a为水平线
16
质点i的竖向地震作用标准值
Fvi
GiH i
n
FEvk
GiH i
i 1
规范要求：9度时，高层建筑楼层 的竖向地震作用效应应乘以1.5的增大 系数。
17
（二）大跨度结构的竖向地震计算
F E vk vG E
v ——竖向地震作用系数，按表采用；
GE ——重力荷载代表值。
结构类型
平板型网架、 钢屋架
➢Tg＜T＜5Tg区段，a为下降的曲线
➢5Tg＜T＜6.0s区段，a为下降直线
5
a
第五章 地震作用 第三节 2amax 单质a 点(TTg体) 系2am水ax 平地震作用
0.45a max
a [2 0.2 -1(T - 5Tg )]amax
0 0.1 Tg
第3章高层建筑结构的荷载和地震作用.

第3章高层建筑结构的荷载和地震作用.

第3章高层建筑结构的荷载和地震作用[例题] 某高层建筑剪力墙结构，上部结构为38层，底部1-3层层高为4m,其他各层层高为3m，室外地面至檐口的高度为120m，平面尺寸为30m⨯40m，地下室采用筏形基础，埋置深度为12m，如图3.2.4(a)、(b)所示。

已知基本风压为w0=0.45kNm，建筑场地位于大城市郊区。

已计算求得作用于突出屋面小塔楼上的风荷载标准值的总值为800kN。

为简化计算，将建筑物沿高度划分为六个区段，每个区段为20m，近似取其中点位置的风荷载作为该区段的平均值，计算在风荷载作用下结构底部（一层）的剪力和筏形基础底面的弯矩。

2解：（1）基本自振周期：根据钢筋混凝土剪力墙结构的经验公式，可得结构的基本周期为： T1=0.05n=0.05⨯38=1.90sw0T12=0.45⨯1.92=1.62kN⋅s2m2（2）风荷载体型系数：对于矩形平面，由附录1可求得μs1=0.80H⎫120⎫⎛⎛⎪=- 0.48+0.03⨯⎪=-0.57 L40⎝⎭⎝⎭（3）风振系数：由条件可知地面粗糙度类别为B类，由表3.2.2可查得脉动增大系数ξ=1.502。

脉动影响系数ν根据H/B和建筑总高度H由表3.2.3确定，其中B 为迎风面的房屋宽度，由H/B=3.0可从表3.2.3经插值求得ν=0.478；由于结构属于质量和刚度沿高度分布比较均匀的弯剪型结构，可近似采用振型计算点距室外地面高度z与房屋高度H的比值，即ϕz=Hi/H，Hi为第i层标高；H为建筑总高度。

则由式（3.2.8）可求得风振系数为：ξ ν ϕzξνHi1.502⨯0.478Hiβz=1+=1+⋅=1+⋅μzμzHμzH（4）风荷载计算：风荷载作用下，按式（3.2.1）可得沿房屋高度分布的风荷载标准值为：q(z)=0.45×(0.8+0.57)×40μzβz=24.66μzβzμs2=- 0.48+0.03按上述公式可求得各区段中点处的风荷载标准值及各区段的合力见表3.2.4，如图3.2.4(c)所示。

第3章-1 抗震 等级 场地 分类

第3章-1 抗震 等级 场地 分类


3.1.2 三水准抗震设防目标

3水准 小震
地震设防要达到的目标－三水准： “小震不坏、中震可修、大震不倒”
烈度 多遇烈度 众值烈度 基本烈度 偶遇烈度 罕遇烈度 超越概率 (重现期) 63.2% (50年) 10% (475年) 2~3% (2000年) 要求具有变形特征 弹性(或轻微损伤) 相应的烈度值 基本烈度－1.55度
建筑类别建筑的重要性抗震措施地震作用计算甲类特殊要求的建筑特殊考虑特殊考虑乙类国家重点抗震城市生命线工程的建筑提高一度9度适当提高设防烈度甲乙丁类以外的一般建筑设防烈度设防烈度次要的建筑降低一度6度不降设防烈度311建筑物抗震类别与设防标准按抗震规范对i类场地可降低一度一级注册结构师考题一级注册结构师考题抗震设计概要前两项合并称为抗震措施p51312三水准抗震设防目标通过抗震设防减轻建筑的破坏避免人员死亡减轻经济损失
为此要确定工程场地的设计地震动参数。
场地划分与场地区划的概念



场地：工程群体所在地，具有相似的反应谱特 征。其范围相当于厂区、居民小区、自然村的 或不小于1.0km2的平面面积。(规范中的定义) 场地土：在场地范围内的地基土。场地土是场 地表层土的简称。 场地的以下方面对地震灾害有显著影响

不利地段
危险地段

《规范》3.3.1 对不利地段，应提出避开要求； 当无法避开时，应采取有效措施；不应在危险地 段建造甲、乙、丙类建筑。
水边地的地下 水位较高，土质也 较松软，容易在地 震时产生土壤滑动 或地层液化。
山坡地在地震 时会产生土壤滑动 冲积地的土质 松软，地震时容易 塌陷，如果此处有 地下水层，还容易 发生液化。

“*”按抗震规范，对I类场地可不提高 “**”按抗震规范，对I类场地可降低一度
地震作用计算

地震作用计算


1．0．5 一般情况下，建筑的抗震设
防烈度应采用根据中国地震动参数区 划图确定的地震基本烈度(本规范设计 基本地震加速度值所对应的烈度值)。
设防烈度的确定——抗规附录A
（3）确定抗震设防烈度的目的
确定设计基本地震加速度和设计特征周期
或设计地震动参数
3．2．2 抗震设防烈度和设计基本地震加速度取值的对应关系， 应符合表3．2．2的规定。设计基本地震加速度为0.15g和0.30g 地区内的建筑，除本规范另有规定外，应分别按抗震设防烈度7 度和8度的要求进行抗震设计。
1.抗震设防的三水准目标——抗规GB50011-2010
1．0．1 按本规范进行抗震设计的建筑，其基本 的抗震设防目标是：当遭受低于本地区抗震设防 烈度的多遇地震影响时，主体结构不受损坏或不 需修理可继续使用；当遭受相当于本地区抗震设 防烈度的设防地震影响时，可能发生损坏，但经 一般性修理仍可继续使用；当遭受高于本地区抗 震设防烈度的罕遇地震影响时，不致倒塌或发生 危及生命的严重破坏。使用功能或其他方面有专 门要求的建筑，当采用抗震性能化设计时，具有 更具体或更高的抗震设防目标。
限批准作为一个地区抗震设防依据的地震 烈度。一般情况，取50年内超越概率10％ 的地震烈度。 抗震设防标准 ——衡量抗震设 防要求高低的尺度，由抗震设防烈度或设 计地震动参数及建筑抗震设防类别确定。
（2）设防依据——抗规
1．0．4 抗震设防烈度必须按国家规
定的权限审批、颁发的文件(图件)确 定。
3．3．2 建筑场地为Ⅰ类时，对甲、乙类的建筑应允许仍
3．3．3 建筑场地为Ⅲ、Ⅳ类时，对设计基本地震加速度
C.建筑物使用功能的设防标准 ——自身 条件问题。
3．1．1 抗震设防的所有建筑应按现行国家
震主要分析方法 - 3 - 1(时程反应分析)

震主要分析方法 - 3 - 1(时程反应分析)



自由度 有限元方法的基本思想
14
层模型
层模型取层为基本计算单元。视结构为悬臂杆。将结构 质量集中于各楼层处，合并整个结构的竖向承重构件成一根 竖向杆。用结构每层的侧移刚度代表竖向杆刚度，形成一底 部嵌固的串联质点系模型即称为层模型。采用层恢复力模型 以表征地震过程中层刚度随层剪力的变化关系。 层模型的基本假定：（1）建筑各层楼板在其自身平面内 刚度无穷大，水平地震作用下同层各竖向构件侧向位移相同； （2）建筑刚度中心与其质量中心重合，水平地震作用下无绕 竖轴扭转发生。 根据结构侧向变形状况不同，层模型可分为三类．即剪 切型、弯曲型与剪弯型，如图所示，若结构侧向变形主要为 层间剪切变形（如强梁弱柱型框架等)，则为剪切型，若结构 侧向变形以弯曲变形为主（加剪力墙结构等），则为弯曲型； 若结构侧向变形为剪切变形与弯曲变形综合而成（如框剪结 构、强柱弱梁框架等），则为剪弯型。 15
结构时程分析的计算模型
结构分析时要根据结构形式、构造、受 力特点、计算量、要求精度等各种因素，选 择既能较真实地描述结构中力－变形性质， 又能使用简便的力学计算模型。 这里将介绍最常用的层模型、杆模型以 及较为精细的有限元模型。
13
基本概念

节点 单元（梁柱单元、壳单元、实体单元、 弹簧单元）
25
时程分析方法的一些实例
模型中包含 20532 梁单元 24048壳单元 3496 连接单元
单元?
台北101 / 台北金融中心
Hong Fan et al. Journal of Constructional Steel Research , 2009
26
模态分 析结果
顶层位移反 应分析结果
27
层模型
桥梁结构抗震计算-1

桥梁结构抗震计算-1

1桥梁结构抗震Seismic Design for Bridge Structures土木工程学院2010.8第三章地震作用计算Seismic Action Calculation3. 1 概述3.2 静力法3.3 单自由度体系的地震反应3.4 单自由度体系的水平地震作用-反应谱法3.5 多自由度体系的地震反应3.6 多自由度体系的水平地震作用-振型分解反应谱法3.7 竖向地震作用计算3.8 地震反应时程分析法的概念3.9 结构自振频率的近似计算3.1 概述一、地震作用二、结构地震反应结构地震反应：三、结构动力计算简图及体系自由度a、水塔建筑d、多、高层建筑3.2 静力法静力法明显的优点是简单，其缺点是完全没有反映地基和结构的动力特征。

静力法只对刚度较大，且较低矮的结构才是合适的。

一般认为对于自振周期小于0.5秒的结构按静力法计算地震作用时，误差不会很大。

日本从20世纪20年代起始用静力法以来，为了表示场地、结构动力特性等众多因素的影响，对静力法作过多次修正，乘以多个系数，称之为震度法，并沿用至今。

我国鉴于当前路基和挡土墙、坝体等土木工程结构的动力观测资料和自振特性的试验研究尚少，故对它们的抗震验算，仍采用静力法计算地震作用。

3.3 单自由度体系的地震反应-----------------------单自由度体系的振动f cv cx=−=− f =−I f ma mx=−=−单自由度体系无阻尼自由振动：mxA:振幅单自由度体系无阻尼自由振动：2ξωωξ特征方程：（3）若一、运动方程二、运动方程的解初始条件:初始位移例题3-12.方程的特解II——冲击强迫振动图地面冲击运动地面冲击运动：⎩⎨⎧>≤≤=dtdt x xg g τττ00)(对质点冲击力：⎩⎨⎧>≤≤−=dtdtx m P g ττ0质点加速度（0～dt）：自由振动初速度为t x)(图体系自由振动3.方程的特解III ——动⎪⎩⎪⎨⎧≥−−<=−−ττωωττττξωt t d x e t t dx D D g t )(sin )(0)()( 地面运动脉冲引起的反应tdte xt x D Dtg ωωξωsin )(−−=叠加：体系在t 时刻的地震反应为：⎪⎨≥−−=−−ττωωτξωt t e t dx Dt )(sin )()(单自由度体系的水平地震作用一、水平地震作用的定义二、地震反应谱地震（加速度）反应谱可理解为一个确定的地面运动，通过一组相同但自振周期t地震动的影响频谱：地面运动各种频率（周期）成分与加速度幅值的对应关系不同场地条件下的平均反应谱不同震中距条件下的平均反应谱地震反应谱峰值对应的周期也越长场地越软震中距越大地震动主要频率成份越小（或主要周期成份越长）G —体系的重量；—地震系数；—动力系数。

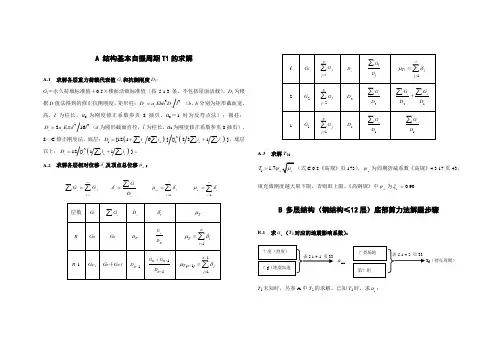
地震作用计算

地震作用计算

A 结构基本自振周期T1的求解A.1 求解各层重力荷载代表值G i 和抗侧刚度D i ：G i ＝永久荷载标准值＋0.5×楼面活载标准值（按5.1.3条，不包括屋面活载）。

D i 为根据D 值法得到的修正抗侧刚度，矩形柱：33i c i D a Ebh D l = （b 、h 分别为矩形截面宽、高，l 为柱长，a c 为刚度修正系数参页8插页，a c ＝1时为反弯点法）；圆柱：43316i c D a E dl π=（d 为圆形截面直径，l 为柱长，a c 为刚度修正系数参页8插页）。

S —C 修正刚度法，底层：()()211[1216][231]cbbciiD ii l ii =++∑∑∑∑，底层以上：()212[11]i i bciD l ii =+∑∑。

A.2 求解各层相对位移i δ及顶点总位移T μ：nijj iGG==∑∑ ii iGD δ=∑ 1iT i jj μδ==∑ 1nT ii μδ==∑A.3 求解T 1：1 1.7TT ψ=（式C.0.2《高规》页173），T ψ为周期折减系数《高规》4.3.17页43，填充墙刚度越大取下限，否则取上限。

《高钢规》中T ψ为0.90T ξ=B 多层结构（钢结构≤12层）底部剪力法解题步骤B.1 求1α（T 1对应的地震影响系数）：T 1未知时，另参A 中T 1的求解。

已知T 1时，求1α：m axαg （特征周期）B.2 求G i 、iG ∑、eq G 、Ek F 、n δ、n F ∆、i F 、E ki V ：G i ＝永久荷载标准值＋0.5×楼面活载标准值（不包括屋面活载）；i G ∑＝1G ＋2G ＋…＋n G （n 为楼层总数包括小塔楼）；0.85eq i G G =⨯∑；1Ek eq F G α=⨯；分别根据T g 和T 1查表5.2.1（页36）得n δ、1n δ-（小塔楼层数为1）：n F ∆＝n δ×Ek F （无小塔楼时）；11n n Ek F F δ--∆=⨯（小塔楼层数为1），内框架0.2n δ=，砖混底框0n δ=。

风荷载及地震作用

风荷载及地震作用


风荷载的特点
风力作用与建筑物外形有直接关系，圆形与正方形受到的风力较合理
风力受到建筑物周围环境影响较大，处于高层建筑群中的高层建筑，有 时会出现受力更为不利的情况 风力作用具有静力、动力两重性质。 风力在建筑物表面的分布很不均匀，在角区和建筑物内收的局部区域， 会产生较大的风力。 与地震作用相比，风力作用持续时间较长，其作用更接近于静力，但建 筑物的使用期限出现较大风力的次数较多。
高层建筑与抗震设计-风荷载与地震作用
平均风压与波动风压图
高层建筑与抗震设计-风荷载与地震作用
《高层建筑混凝土结构技术规程》（JGJ3-2002)中规 定： 当建筑物高度>30m、高宽比>1.5时，考虑风振 系数：
振型系数
脉动增大系数，按下表采用：
脉动影响系数 按照不同的地面粗糙度A类地形、 B类地形、 C类地 形和D类地形取值。见《高层建筑混凝土结构技术规 程》（JGJ3-2002)中的规定。 风压高度变化系数，按下表采用：
Z
风 压 高 度 变 化 系 数
离地面或海平 面高度（m)
5 15 50
地面粗糙度类别
A 1.17 1.52 2.03 B 1.00 1.14 1.67 C 0.74 0.74 1.25 D 0.62 0.62 0.84
300
3.12
2.97
2.75
2.45
高层建筑与抗震设计-风荷载与地震作用
C Z 0.616
由于有较长期的气象观测，大风的重现期很短，所以风力大小的估计比 地震作用大小的估计较为可靠。而且抗风设计具有较大的可靠性。
高层建筑与抗震设计-风荷载与地震作用
3-1 风荷载
1、高层建筑风荷载的特点
地震作用标准值计算

地震作用标准值计算

地震作⽤标准值计算地震作⽤标准值计算(1)各层总重⼒荷载代表值计算1．屋⾯层总重⼒荷载代表值⼥⼉墙重量：(1.95+0.51+0.875)×[(11.4+0.2)×2+(25+0.2)×2-(2.5+0.4×10+0.5×4)]=217.11kN屋⾯板重量：6.4×(4-0.2-0.15)×(11.4-0.2-0.3-0.2)×2=499.90kN7.7×(6-0.15×2)×(11.4-0.2-0.3-0.2)×2=939.25kN5.9×[(6-0.2-0.15)×(2.5-0.3)×2+(2.5-0.3)×(3.6-0.3)]+6.4×(1.8-0.25)×(2.5-0.3)=211.33kN499.90+939.25+211.33=1650.48kN电梯机房重量：0.91+2.366+1.333+3.465+1.43+3.887+25×0.3×0.3×1.5×2+ 25×0.2×0.2×(1.8×2+2.5×2)+5.9×1.6×2.3=50.453kN楼梯间重量：(7.275+15.132+3.958)×2+(1.275+1.716+0.449+1.62)+ (2.61+5.148+1.346+0.486)=67.38kN4.5×[(2.5-0.4)+(2.5-0.25-0.2)+(5.4-0.3-0.25)+(5.4-0.3-0.2)]=62.55kN3.89+4.031+0.432+0.571=8.924kN25×3×(0.4×0.4×3+0.5×0.5)=54.75kN5.9×(5.4-0.35)×(2.5-0.3)=65.55kN67.38+62.55+8.924+54.75+65.55=259.15kN楼梯板重量：25×(0.3×0.15/2×1.1×9+3×1.1×0.12+0.2×0.3×2.5)+3×1.1×2.3+ 17×0.02×[1.1×2.3+2.3×(0.2+0.2+0.2)+1.1×3]+2.12=31.38kN8层柱重量：25×1.5×(0.4×0.4×9+0.5×0.5×5)=100.88kN17×0.02×1.5×(0.4×4×9+0.5×4×5-0.2×2×14)=9.59kN100.88+9.59=110.47kN梁重量：4.5×[(11.4+0.2)×7-0.4×12-0.5×8-0.3)]=324.45kN4.5×[(25+0.2)×3-0.4×12-0.5×8]=300.6kN1.5×(2.5-0.3)=3.3kN2.122×2+4.243×2+3.89+4.031+3.89+4.972+1.428×2+2.418×2+0.432+0.714×2+1.18×2+0.571+0.443=42.44kN324.45+300.6+3.3+42.44=670.79kN7层墙、门、窗重量：54.253×2+28.925×2+42.844+41.342+40.291+14.463×2+ 15.826×2+18.378+11.172×2+8.629+14.463×2+23.598×2+5.573+8.374+8.439×2+15.06×2+10.184+8.706×2+26.611+5.597×2=603.23kN7层柱重量：25×3×(0.4×0.4×12+0.5×0.5×8)=294kN17×0.02×3×(0.4×4+0.7×4+1.7×2+1×2+0.6×3+1.4×2+0.9×2+1)=17.544kN294+17.544=311.544kN因屋⾯可变载不计⼊重⼒荷载代表值，故屋⾯层的重⼒荷载代表值为：G=217.11+1650.48+50.453+259.15+31.38+110.47+670.79+603.23/2+311.544/2 7 =3447.22kN2-6层重⼒荷载代表值楼⾯板重量：3.5×(4-0.35)×(11.4-0.2-2.25-0.2)×2=223.563kN3.0×[(2-0.25)×(2.5-0.3)+(4-0.25)×(2.5-0.3)+(6-0.3)×(2.9-0.25)+(2.5-0.3)×(6-0.55)+(2-0.25)×(4-0.55)]×2+3.0×(3.6-0.3)×(2.5-0.3)=296.325kN4.8×(6-0.3)×(6-0.35)×2=309.168kN3.5×(1.5-0.2)×(6-0.3)×2=51.87kN223.563+296.325+309.168+51.87=880.93kN柱重量：25×3×(0.4×0.4×12+0.5×0.5×8)=294kN17×0.02×3×(0.4×4+0.7×4+1.7×2+1×2+0.6×3+1.4×2+0.9×2+1)=17.544kN294+17.544=311.544kN楼梯板重量：31.38×2=62.76kN梁重量：[1.5×(2.5-0.3)+3×(6-0.3)+1.5×(4-0.35)+3×(6-0.3)+1×(2-0.25)]×2+1×(5-0.6)=93.85kN4.5×1.5×4=27kN0.431×2+2.267×2+0.422+0.305+0.384+2.648×2+0.22×2+0.676×4=14.947kN 670.79+93.85+27+14.947=806.59kN墙、门、窗、栏杆重量：603.23+1.06×4+4.239×2=615.948kN楼⾯可变荷载：2.0×[(25-0.1)×(11.4-0.1)-1.8×2.5]+2.5×6×1.5×2=598.74kN因楼⾯可变荷载按等效均布荷载计算，要乘以组合值系数0.5，故2-6层的总重⼒荷载G=880.93+311.544+62.76+806.59+615.948+0.5×598.74=2977.14kN代表值为：621层重⼒荷载代表值楼⾯板重量：3.5×(4-0.35)×(11.4-0.2-2.25-0.2)×2=223.563kN3.0×[(2-0.25)×(2.5-0.3)+(4-0.25)×(2.5-0.3)+(6-0.3)×(2.9-0.25)+(2.5-0.3)×(6-0.55)+(2-0.25)×(4-0.55)]×2+3.0×(3.6-0.3)×(2.5-0.3)=296.325kN4.8×(6-0.3)×(6-0.35)×2=309.168kN3.5×(1.5-0.2)×(6-0.3)×2=51.87kN223.563+296.325+309.168+51.87=880.93kN柱重量：25×3.8×(0.4×0.4×12+0.5×0.5×8)=372.4kN372.4+17.544=389.944kN楼梯板重量：31.38×2=62.76kN梁重量：[1.5×(2.5-0.3)+3×(6-0.3)+1.5×(4-0.35)+3×(6-0.3)+1×(2-0.25)]×2+1×(5-0.6)=93.85kN4.5×1.5×4=27kN0.431×2+2.267×2+0.422+0.305+0.384+2.648×2+0.22×2+0.676×4=14.947kN670.79+93.85+27+14.947=806.59kN墙、门、窗、栏杆重量：因1层平⾯布置与标准层⼤致相同，此项荷载相差不⼤，故⼤⼩取同标准层此项荷载，为615.948kN楼⾯可变荷载：2.0×[(25-0.1)×(11.4-0.1)-1.8×2.5]+2.5×6×1.5×2=598.74kN因楼⾯可变荷载按等效均布荷载计算，要乘以组合值系数0.5，故1层的总重⼒荷载代表值为：G=880.93+(389.944+311.544)/2+62.76+806.59+615.948+0.5×598.74=3016.34kN 1(2)全楼横向⽔平地震作⽤计算 1．结构基本⾃振周期计算采⽤顶点位移法计算，此⽅法计算周期必须先求出结构在重⼒荷载代表值⽔平作⽤于各质点产⽣的顶点位移，计算过程见表3-2-15。

第三章 地震作用与抗震验算(4)

第三章 地震作用与抗震验算(4)

3.地震波选取 ◆强震持时
一般为结构基本周期的5～10倍，且≥12s。
强震持续时间
地震加速度记录
3.11 时程分析法
3.地震波选取
加速度（g）
0.3
0.2 0.1 0
0.1
0.2 0.3 0 5 10 15 20 25时间（s）
［美］英佩里亚尔谷地震
1940年El Centro地震的加速度记录（南-北分量）
动荷载下钢材的应力-应变关系
3.13 抗震验算
2.承载力验算
S
R
RE 承载力抗震调整系数
或
RE S R
3.13 抗震验算
2.承载力验算
地震作用效应与其他作用效应基本组合
S G S EG Eh S Ehk Ev S Evk w w S wk
1.2 不利 G 1.0 有利
T1 折减系数 T T 1 附加周期△T(s) 场地类别 Ⅲ类 当高宽比 烈度 大于3时，顶 0.08 8度 层不折减。
9度 0.10
0.9
Ⅳ类 0.20 0.25
3.13 抗震验算
1.确定地震作用计算方向
◆一般情况下，应允许在建筑结构的两个主轴方向分 别计算水平地震作用并进行抗震验算，各方向的水 平地震作用应由该方向抗侧力构件承担。 ◆有斜交抗侧力构件的结构；当相交角度大于15° 时，应分别计算各抗侧力构件方向的水平地震作 用。 ◆质量和刚度分布明显不对称的结构，应计入双向水 平地震作用下的扭转影响；其他情况，应允许采用 调整地震作用效应的方法计入扭转影响。 ◆8、9度时的大跨度和长悬臂结构及9度时的高层建 筑，应计算竖向地震作用。
动力方程 ti 1 Cx t i 1 Kxt i 1 m g ti 1 m x x

第三章 计算水平地震作用的振型分解反应谱法(第9节课讲义)


地震特征周期分组的特征周期值（s）
场地类别
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一组 0.25
0.35
0.45 0.65
第二组 0.30
0.40
0.55 0.75
第三组 0.35
0.45
0.65 0.90
（2）计算各振型的地震影响系数
查表得 max 0.16
Tg 0.4s
第一振型 Tg T1 5Tg
第二振型 0.1s T2 Tg
---t时刻第j振型i质点的水平地震作用
Fji Fji (t) max mi x ji j j (t) xg (t) max
---体系j振型i质点水平地震作用标准值
单自由度体系水平地震作用：
F
F (t ) max
m x(t) xg (t) max
G
多自由度体系j振型i质点水平地震作用：
mx cx kx m1xg (t)
mN
mi
xi
m2
m1
xg(t)
mi mi (xi xg )
Si (t)
Ri (t)
D j
(t )
2
j
j
D j
2 j
D
j
(t )
X
T j
M
1
X
T j
M
X
j
xg
(t )
n
j
X
T j
M
1
X
T j
M
X
j
mi x ji
i 1
n
mi
x
2 ji
i 1
---j振型的振型参与系数
335.8 671.6 845.8
组合后各层地震剪力

地震作用计算

地震作用计算一、确定计算前提：烈度：甲类建筑按安评报告且应高于本地设防烈度，乙、丙类按本地设防烈度。

（高层适用）方向：两个主轴方向+斜交抗侧力构件方向（斜交角度大于15度）双向地震：质量刚度明显不对称（1）从平面形状上判别：平面为L 形，T形等属于平面不规则的结构为明显不对称的结构，位移比无论为何值，均应考虑双向地震作用（2）位移比大于1.2（或1.3，尚无定论）的结构属平面不规则中的扭转不规则，无论平面形状对称与否，均应考虑双向地震作用。

（3）从竖向形状上判别：大地盘结构为明显的质量及刚度竖向不对称应考虑双向地震作用（4）竖向质量和刚度明显不对称的结构，如上下刚度差别较大，或上下的质量差别较大的结构应考虑双向地震作用。

竖向地震：7度半（高层）、8度、9度的大跨度和长悬臂结构，9度时的高层考虑。

8、9度时的隔震结构偶然偏心：(高层、单向地震考虑，多层不考虑，双向地震不考虑)二、选择计算方法：底部剪力法、振型分解反应谱发、时程分析法。

三、计算重力荷载代表值：采用半层集中法，屋面活荷载和软钩吊车荷载不计入，书库、档案馆等活载组合系数取0.8楼顶计算: 楼板+下半层墙体重力+活荷载×0+雪荷载×0.5+积灰荷载×0.5每层计算:楼板+上下半墙重量+等效均布活载×0.5（书库、档案活载×0.8）+实际情况的楼活载×1.0四、计算水平地震作用效应：地震效应Fi计算楼层剪力计算考虑扭转耦联作用边榀构件地震效应放大（采用扭转耦联振型分解法的除外）考虑地基与结构相互作用地震效应折减薄弱层放大系数1.25剪重比调整0.2V0调整（框剪）筒体结构调整。

框支柱调整（部分框支剪力墙）地震作用标准值五、计算竖向地震作用效应：（1）9度高层：Geq=0.75Ge (水平地震计算时，Geq=0.85Ge)ɑvmax=0.65ɑmax地震效应按各构件所承受的重力荷载代表值分配，并宜乘以1.5的放大系数。

水平地震作用计算

上海市工程建设规范《建筑抗震设计规程》(DGJ08-9-2013)强制性条文3 抗震设计的基本要求3.1.1 抗震设防的所有建筑应按现行国家标准《建筑工程抗震设防分类标准》GB 50223 确定其抗震设防类别及其抗震设防标准。

3.3.1选择建筑场地时，应根据工程需要和地震活动情况、工程地质和地震地质的有关资料，对抗震有利、一般、不利和危险地段做出综合评价。

对不利地段，应提出避开要求，当无法避开时应采取有效的措施。

对危险地段，严禁建造甲、乙类的建筑，不应建造丙类的建筑。

3.4.1建筑设计应根据抗震概念设计的要求明确建筑形体的规则性。

不规则的建筑应按规定采取加强措施；特别不规则的建筑应进行专门研究和论证，采取特别的加强措施；严重不规则的建筑不应采用。

注：形体指建筑平面形状和立面、竖向剖面的变化。

3.5.2结构体系应符合下列各项要求：1应具有明确的计算简图和合理的地震作用传递途径。

2应避免因部分结构或构件破坏而导致整个结构丧失抗震能力或对重力荷载的承载能力。

3应具备必要的抗震承载力，良好的变形能力和消耗地震能量的能力。

4对可能出现的薄弱部位，应采取措施提高其抗震能力。

3.7.1 非结构构件，包括建筑非结构构件和建筑附属机电设备，自身及其与结构主体的连接，应进行抗震设计。

3.7.4框架结构的围护墙和隔墙，应估计其设置对结构抗震的不利影响，避免不合理设置而导致主体结构的破坏。

3.9.1抗震结构对材料和施工质量的特别要求，应在设计文件上注明。

3.9.2 结构材料性能指标，应符合下列要求：1 砌体结构材料应符合下列规定：1)普通砖和多孔砖的强度等级不应低于MU10，其砌筑砂浆强度等级不应低于M5；2)混凝土小型空心砌块的强度等级不应低于MU7.5，其砌筑砂浆强度等级不应低于Mb7.5。

2混凝土结构的材料应符合下列规定：1) 混凝土的强度等级，框支梁、框支柱及抗震等级为一级的框架梁、柱、节点核芯区，不应低于C30；构造柱、芯柱、圈梁及其它各类构件不应低于C20；2) 抗震等级为一级、二级、三级的框架和斜撑构件(含梯段)，其纵向受力钢筋采用普通钢筋时，钢筋的抗拉强度实测值与屈服强度实测值的比值不应小于1.25；钢筋的屈服强度实测值与屈服强度标准值的比值不应大于1.3，且钢筋在最大拉力下的总伸长率实测值不应小于9%。

第3章 建筑抗震计算原理


α
自振周期T 自振周期
谱曲线
α max
水平地震影响系数最大值.根据结 水平地震影响系数最大值 根据结 构阻尼比制定,见 构阻尼比制定 见表3-2 ζ = 0.05 场地特征周期.与设计地震分组有关, 场地特征周期 与设计地震分组有关 有关 见表3-3 阻尼调整系数
等高单层厂房及其计算简图
3．2．2运动方程的建立 ． ． 运动方程的建立
为了研究单质点弹性体系的水平地震反应，根据结构 为了研究单质点弹性体系的水平地震反应， 单质点弹性体系的水平地震反应 的计算简图并进行受力分析， 的计算简图并进行受力分析，从而建立体系在水平地 震作用下的运动方程（动力平衡方程） 震作用下的运动方程（动力平衡方程）
FI (t ) + Fd (t ) + Fe (t ) = 0
ɺ mɺɺ(t ) + cx(t ) + kx(t ) = − mɺɺ (t ) x x
g
两边同除 以m
ɺɺ(t ) + 2ζωx(t ) + ω x(t ) = − ɺɺg (t ) ɺ x x
2
式中: 式中
结构振动圆频率 (自振圆频率 自振圆频率) 自振圆频率
1．方程的齐次解——自由振动位移反应 ．方程的齐次解 自由振动位移反应
ɺɺ(t ) + 2ζωx(t ) + ω x(t ) = 0 ɺ x
2
采用动力 学方法求 解
x (t ) = e
−ζωt
ɺ x0 + ζωx0 sin ω d t x0 cos ω d t + ωd
ζ = 0.01 ~ 0.1
F ≈| kx(t ) | max =| mω 2 x(t ) | max

第3章 结构地震反应分析


I (t ) (m mg ) x x
m
kx
x g (t )
阻尼力
运动方程
R(t ) cx
m cx kx mg x x
二、单自由度体系动力学分析回顾
1.单自由度体系自由振动 （1）无阻尼时
m kx 0 x
2
2 x 0 x
3.1.2
地震作用
结构工程中“作用”一词，指能引起 结构内力、变形等反应的各种因素。按引 起结构反应的方式不同，“作用”可分为 直接作用与间接作用。各种荷载（如重力、 风载、土压力等）为直接作用，而各种非 荷载作用（如温度、基础沉降等）为间接 作用。结构地震反应是地震动通过结构惯 性引起的，因此地震作用（即结构地震惯 性力）是间接作用，而不称为荷载。
0 t

d 0 2 t g ( )e (t ) sin d (t )d 0 x d
2 2 2
t
g ( )e (t ) sin d (t )d x
质点相对于地面的最大加速度反应为
S a (t ) g x x
§3.2 单自由度弹性体系的地震反应分析
一、地震作用下单自由度体系的运动方程
X (t ) x(t ) xg (t ) 质点加速度 X (t ) (t ) g (t ) x x
质点位移 惯性力 弹性恢复力
m
m( g ) x x
cx
x(t )
S (t ) kx
x(t ) ( x0 cos t
k m
（2）有阻尼时
m cx kx 0 x
2
k c , m 2m

x0
sin t )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Sa(T)
ξ=ξ
0
T1
T2
T3
T4
T5
T
T1
地震作用的计算方法
确定性方法
非确定性方法——随机振动分析
静态分析（最不利状态分析）
动力分析法（全过程时程分析）
静力法
反应谱理论
弹性全过程分析 弹塑性全过程分析
底部剪力法
振型分解反应谱法
三、结构动力计算简图及体系自由度 描述结构质量的两种方法 1. 连续化描述（分布质量） 2. 集中化描述（集中质量） 工程上常用
自由振动的振幅将不 断衰减，直至消失。
例题3-1 已知一水塔结构，可简化为单自由 度体系（见图）。
h
h
m 10000kg
k 1kN/cm
求该结构的自振周期。 解：直接由式
2 m T 2 k
并采用国际单位可得:
m 10000 T 2 2 1.99 s 3 2 k 1 10 / 10
3.1 概 述 一、地震作用 作用：能引起结构内力、变形等反应的各种因素
直接作用 ——各种荷载：如重力、风载、土压力等
作用分类
间接作用 ——各种非荷载作用：如温度、基础沉降、地震等
由于地面运动引起的对结构的动力作用称为地震作用。
与一般荷载不同，地震作用不仅与外来干扰作用的大小及其随
时间的变化规律有关，而且还与结构的动力特性，如结构的自振 频率、阻尼等有密切关系。 确定地震作用要比确定一般荷载复杂的多。
单质点体系
d、多、高层建筑
e、烟囱
主要质量：楼盖部分
结构无主要质量部分
结构分成若干区域 集中到各区域质心
多质点体系
3.2 静力法 静力法始于意大利，发展于日本。结构抗 震定量计算由此开始。日本学者大森房吉是第 一个试图对结构在地震作用下提出完整计算理 论的人，结构抗震静力法的创始人。静力理论 大森房吉(Omori Fusakichi) 是假定结构为绝对的刚体，当受到地震作用时， 1868-1923 处于水平振动状态，因此在任何瞬间结构上各 x 点的加速度都相等，惯性力在结构上的分布与 质量分布成正比，结构所受到得地震力等于结 构自重乘以一个地震系数。 gh |max | x | | x 水平地震系数 k F W khW g x g
x(t )
g dte t x
D
sin D t
0 t g ( )d x dx(t) e(t ) sinD (t ) t D
地面运动脉冲引起的反应
叠加：体系在t时刻的地震反应为：
1 t x(t) dx(t) xg ( )e(t ) sin D (t )d 0 D 0
单自由度体系无阻尼自由振动：
cx kx 0 mx
k m
2
kx 0 mx
k m
2 x x 0
x (t ) c1 cos t c2 sin t
, 初始速度
0 x ( 0) x
初始位移 则
x 0 x ( 0)
c1 x 0
f r kx
fI fc fr 0
c k m 2 m
cx kx m g m x x
2 x 2 x g x x
二、运动方程的解 1.方程的齐次解——自由振动
2 x 2x 0 x 齐次方程：
P g dt V dt x m
dt时刻的位移：
1P d (dt ) 2 0 2m
地面冲击作用后，体系不再受外界任何作用，将做自由振动。
自由振动初速度为
g dt V x
t
x (t ) e
0 x 0 x [ x 0 cos D t sin D t ] D
c r 2m
c cr
临界阻尼比（简称阻尼比）：
单自由度体系的地震反应 一、运动方程 作用在质点上的三种力：
惯性力 f I 、阻尼力 f c 、弹性恢复力 f r
＊惯性力 ＊阻尼力
g ) f I m( x x
f c cx
＊弹性恢复力 ——由结构弹性变形产生
x(t ) c1 cos t c2 sin t
e cos t i sin t
（2）若 0 1 ，r1 r 2 为共轭复数
e
it
cos t i sin t
其中 D 1 2
欠阻尼状态——衰减振动
x (t ) e t (c1 cos D t c 2 sin D t )
单自由度体系运动方程
cx kx m g m x x
kx ) m( xg x ) (cx
m( x g x)
max
kx max cx
位移最大 地震作用
0 x
g ) F = m( x x
max
k x
（3）若 1 ，r1 r2
x ( t ) ( c 1 c 2 t ) e t
临界阻尼状态——体系不振动
（4）若
1 ，r1 、r 2 为负实数
x ( t ) c 1 e r1 t c 2 e r 2 t
过阻尼状态——体系不振动 当 1时 临界阻尼系数：
桥梁结构抗震
Seismic Design for Bridge Structures 土木工程学院
2010.8
1
第三章 地震作用计算
Seismic Action Calculation
3. 1 概述 3.2 静力法 3.3 单自由度体系的地震反应 3.4 单自由度体系的水平地震作用-反应谱法 3.5 多自由度体系的地震反应 3.6 多自由度体系的水平地震作用-振型分解反应谱法 3.7 竖向地震作用计算 3.8 地震反应时程分析法的概念 3.9 结构自振频率的近似计算
0 1 ，r1 r 2
D 1 2
x (t ) e t ( c1 cos D t c 2 sin D t )
其中
欠阻尼状态——衰减振动
x(t)
1
1
0
0 1
t
图 各种阻尼下单自由度体系的自由振动
阻尼比是结构的重要参数，变化范围在0.01-0.10之间，通 常取0.05。可通过对结构进行振动试验确定。
r 2 2 r 2 0
自由振动：在没有外界激励的 情况下结构体系的运动
方程的解：
特征根
特征方程
r2 2 1
r1
2
1
（1）若
0
x (t ) c1 cos t c2 sin t
为共轭复数
无阻尼——简谐振动
（2）若
2
1
特征方程： r
2
2 r 2 0
r2 2 1
特征根
r1 2 1
（1）若 0
x(t ) c1 cos t c2 sin t
无阻尼——简谐振动
x De rt
it
x D1e i t D2 e i t
max
求得地震作用后，即可按静力分析方法计算结构的最大位移反应 。
二、地震反应谱
F max k x max m 2 x max
t 0
k m
2
m | x g ( )e ( t ) sin (t )d |max =mSa
质点加速度最大绝对值
单自由度体系无阻尼自由振动：
cx kx 0 mx
令
x 0 x 2 x
2
假定：
k m
c 2 m
x De
rt
特征方程： r
2
2 r 2 0
特征根
r2 2 1
r1
g ( )e (t ) sin (t )d |max Sa | x
0 t
称为加速度反应谱
地震（加速度）反应谱可理解为一个确定的地面运动，通过一组阻尼比 相同但自振周期各不相同的单自由度体系，所引起的各体系最大加速度反应 与相应体系自振周期间的关系曲线
初始条件: 初始位移 则
c1 x 0
x 0 x ( 0)
x 0 x 0 c2 D
t
, 初始速度
0 x ( 0) x
体系有阻尼 自由振动 的位移时程
x (t ) e

0 x 0 x [ x 0 cos D t sin D t ] D
0 x c2 0
(0) x x (t ) x (0) cos t sin t
x (t ) A sin(t )
A:振幅 ：初始相位角 ：
2 x 2 A x0 02
x (t ) A sin(t )
x0 tan 0 / x
2.方程的特解II——冲击强迫振动 地面冲击运动：
g x g ( ) x 0
对质点冲击力：
0 dt dt
g x m P 0
0 dt dt
图 地面冲击运动
质点加速度（0～dt）：
P g a x m
dt时刻的速度：
t
单自由度体系的地震反应：
杜哈美积分(Duhamel
Integral)
体系地震反应(通解)=自由振动(齐次解)+强迫振动(特解)
初位移、初速度引起 迅速衰减，可不考虑 地面运动 引起
单自由度体系的水平地震作用-反应谱法