最新二计量经济学模型

我国居民消费水平的计量分析通过对我国居民消费水平的历史及现状研究，建立了居民消费水平的经济模型，并研究了模型中主要变量对模型的影响程度，在此基础上对我国居民消费水平进行计量分析同时提出了提高居民消费水平的对策建议。

消费水平是指一个国家一定时期内人们在消费过程中对物质和文化生活需要的满足程度。

笔者以分析居民消费水平为目的，同时考虑了其他一些指标的分析需要，根据计量经济学模型的构思，在建模时作了如下处理：1、该模型为线性模型。

2、主要采集的样本是1978年以后的，因为改革开放以后，我国的经济运行机制有了极大的改变，人民生活水平也有了极大的提高，故这一时期的样本更能反映这种变化。

3、模型中将居民消费水平作为被解释变量，根据经验引入国内生产总值、城乡居民人均收入、人口自然增长率、居民消费价格指数，对模型进行回归分析，以求能使模型具有更高的可操作性一、收集数据二、建立模型为了研究居民消费水平和经济发展水平的关系，我们把国内生产总值作为经济发展水平的代表性指标。

由经济理论分析可知，经济发展水平与居民消费水平有密切关系。

因此，我们设定居民消费水平Y 与国内生产总值X 1的关系为：μββ++=110X Y三、模型检验其中，可决系数2R =0.9993。

从回归结果可以看出，模型拟合度很好，可决系数很高，这也表明国内生产总值确实对居民消费水平有显著影响。

其中，GDP 每增长1亿元，居民消费水平平均增加0.04元。

2、居民人均收入对居民消费水平的影响如果说国内生产总值是宏观影响因素，那么居民的人均收入就是微观影响因素。

由于我国城乡差距比较显著，于是在这里分别考察了城镇居民和农村居民的可支配收入对消费水平的影响。

设城镇居民人均可支配收入为2X ，农村居民人均纯收入为3X ，它们与居民消费水平的关系为：221X Y μββ++=332Y μββ++=X运用OLS 法估计结果如下：城镇居民可支配收入对居民消费水平的影响25304.06297.9X Y t +=（0.5142） （100.2944） 2R =0.9977农村居民纯收入对居民消费水平的影响34918.14612.113X Y t +-=（-3.9590） （68.7807） R ²=0.9952由数据分析的结论可知，农村居民人均纯收入对居民消费水平的影响大大超过了城镇居民人均可支配收入对居民消费水平的影响。

计量经济学模型的核心内容计量经济学是经济学的一个重要分支，旨在通过建立经济学模型来解释和预测经济现象。

计量经济学模型是计量经济学研究的核心内容，它能够帮助研究者对经济现象进行量化分析和预测。

下面将介绍计量经济学模型的核心内容。

一、模型的假设计量经济学模型建立在一系列假设的基础上，这些假设是为了简化和抽象经济现象，使得模型能够更好地描述实际情况。

常见的假设包括理性行为假设、市场均衡假设、完全竞争假设等。

这些假设为模型提供了基本的框架，使得研究者能够对经济问题进行具体的分析和预测。

二、模型的变量计量经济学模型中包含多个变量，这些变量代表了经济现象中的各个要素。

常见的变量包括经济产出、价格、就业率、利率等。

通过对这些变量的测量和分析，可以揭示它们之间的关系和相互影响，进而理解和解释经济现象的发生和演变。

三、模型的结构计量经济学模型的结构是指模型中各个变量之间的关系和相互作用方式。

常见的模型结构包括线性模型、非线性模型、动态模型等。

线性模型假设模型中的变量之间存在线性关系，非线性模型则允许变量之间存在非线性关系。

动态模型则考虑了时间的因素，使得模型能够更好地反映经济现象的变化和演化。

四、模型的估计计量经济学模型的估计是指通过实证分析来确定模型中的参数值。

估计模型参数的方法有很多种，常见的方法包括最小二乘法、极大似然法、广义矩估计法等。

通过对模型参数的估计，可以得到模型对经济现象的解释和预测结果。

五、模型的检验计量经济学模型的检验是指通过统计方法对模型的有效性和适用性进行检验。

常见的检验方法包括假设检验、拟合优度检验、残差分析等。

通过对模型的检验，可以评估模型在描述和预测经济现象方面的准确性和可靠性。

六、模型的应用计量经济学模型的应用范围广泛，可以用于解释和预测各种经济现象。

例如，可以利用计量经济学模型来研究货币政策对经济增长的影响，分析贸易政策对国际贸易的影响，预测股票市场的走势等。

通过应用计量经济学模型，可以更好地理解和解释经济现象，并为政策制定提供科学依据。

计量经济学GMM模型计量经济学GMM模型是指基于计量经济学的Generalized Method of Moment(GMM)模型。

它是一种基于有限数学参数来解释经济现象的模型，它利用最优估计技术来拟合大量数据，预测和分析隐藏在它们背后的模式。

为了使用GMM模型来估计价格、需求、收入、消费、投资和其他宏观变量，需要对其进行调整和运行。

一、计量经济学GMM模型基本原理计量经济学GMM模型的基本原理建立在极大似然估计(MLE)的基础之上。

它假设某一经济现象的行为是由一个有限、可估计参数的定量模型来建模的，这些参数的估计值可以使模型的残差最小化。

模型除了参数之外，还规定了模型对应的经济现象的一般特征（比如相关性）。

因此，计量经济学GMM模型是通过最小化函数来拟合实验数据，以确定参数值的一种方法。

二、计量经济学GMM模型特点1.有效性：由于GMM模型能够在有限数据情况下得到准确估计，因此是一种十分可靠的估计方法。

2.准确性：与其他经济数据加工方法（如典型回归模型）相比，GMM的准确性要好得多，能够提供更精确的参数估计。

3.便捷性：GMM模型也是一种简单便捷的预测方法，可以轻易地从历史数据中抽取出参数，从而把它们应用到现实经济中。

4.减小噪音：GMM模型能够准确地对数据进行拟合，可以有效地压制测量误差的影响。

三、计量经济学GMM模型的应用1. 价格预测：GMM模型可以通过利用时间序列上的历史数据、均衡条件以及其他特征，预测出最终的物价变动情况；2. 投资分析：使用GMM模型，可以施行完整性的投资分析，以便估计未来对投资报酬的影响程度；3. 消费预测：使用此模型预测消费行为，可以估计预算支出，并调节它以达到给定的消费预算。

4. 估计协整模型：GMM模型可以被用来估计协整模型，这样可以用来衡量不同的经济变量是否存在协整关系。

总之，计量经济学GMM模型对于对数据拟合和通过数据估计市场变量都具有重要意义。

它具有有效性、准确性、便捷性和减少噪音的特点；并且可以被广泛用于价格预测、投资分析、消费预测和估计协整模型等领域。

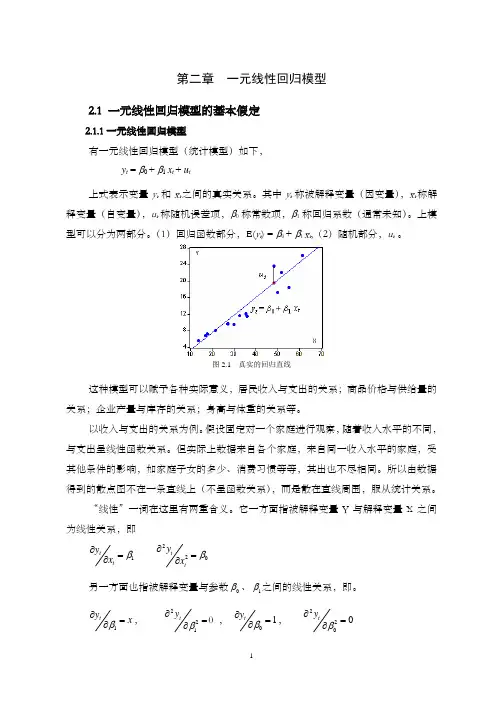
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型（统计模型）如下， y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。

其中y t 称被解释变量（因变量），x t 称解释变量（自变量），u t 称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t ) = β0 + β1 x t ,（2）随机部分，u t 。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，居民收入与支出的关系；商品价格与供给量的关系；企业产量与库存的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自同一收入水平的家庭，受其他条件的影响，如家庭子女的多少、消费习惯等等，其出也不尽相同。

所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

“线性”一词在这里有两重含义。

它一方面指被解释变量Y 与解释变量X 之间为线性关系，即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系，即。

1ty x β∂=∂，221ty β∂=∂0 ，1ty β∂=∂，2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

随机误差项u t 正是计量模型与其它模型的区别所在，也是其优势所在，今后咱们的很多内容，都是围绕随机误差项u t 进行了。

回归模型的随机误差项中一般包括如下几项内容： （1）非重要解释变量的省略， （2）数学模型形式欠妥， （3）测量误差等，（4）随机误差（自然灾害、经济危机、人的偶然行为等）。

第二章经典单方程计量经济学模型：一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法（OLS）的学习与掌握。

同时，也介绍了极人似然估计法（ML）以及矩估计法（MM）。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”, 第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包扌舌两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成：第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则oGoss-niarkov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包扌舌被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为kids= 00 + P i educ+ “（1）随机扰动项〃包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变卞的影响吗？请解释。

计量经济学did模型计量经济学DID模型引言计量经济学是经济学中的一个重要分支，通过运用统计学和数学方法来解决经济问题。

DID模型（Difference-in-Differences）是计量经济学中一种常用的分析方法，用于评估政策或其他干预措施对某一特定群体或地区的影响。

本文将介绍DID模型的基本原理、应用领域以及一些相关的注意事项。

一、DID模型的基本原理DID模型是一种自然实验设计，通过比较两个群体或地区在政策干预前后的差异，来评估政策对实验组的影响。

其中，实验组是受到政策干预的群体或地区，对照组是没有受到政策干预的群体或地区。

通过比较实验组和对照组在政策干预前后的差异，可以得出政策对实验组的效应。

DID模型的基本原理可以通过以下公式表示：Y_it = α + β*T_i + γ*D_t + δ*(T_i*D_t) + ε_it其中，Y_it表示观测单位i在时间t的结果变量；T_i表示观测单位i 是否受到政策干预的虚拟变量（Treatment）；D_t表示时间t是否为政策干预的虚拟变量（Difference）；α、β、γ、δ分别表示常数项和各个系数；ε_it表示误差项。

二、DID模型的应用领域DID模型在计量经济学中有广泛的应用领域。

以下列举了一些常见的应用案例：1. 教育政策评估：DID模型可以用于评估教育政策对学生学业成绩的影响。

通过比较政策实施前后不同学校或学生群体的学业成绩差异，可以评估教育政策的效果。

2. 劳动力市场研究：DID模型可以用于研究最低工资政策对就业率的影响。

通过比较实施最低工资政策的地区和没有实施最低工资政策的地区的就业率变化，可以评估最低工资政策的效果。

3. 医疗政策评估：DID模型可以用于评估医疗政策对健康指标的影响。

通过比较实施医疗政策的地区和没有实施医疗政策的地区的健康指标变化，可以评估医疗政策的效果。

4. 环境政策研究：DID模型可以用于研究环境政策对环境污染的影响。

计量经济学4种常用模型计量经济学是经济学的一个重要分支，主要研究经济现象的数量关系及其解释。

在计量经济学中，常用的模型有四种，分别是线性回归模型、时间序列模型、面板数据模型和离散选择模型。

下面将对这四种模型进行详细介绍。

第一种模型是线性回归模型，也是计量经济学中最常用的模型之一。

线性回归模型是通过建立自变量与因变量之间的线性关系来解释经济现象的模型。

在线性回归模型中，自变量通常包括经济学理论认为与因变量相关的变量，通过最小二乘法估计模型参数，得到经济现象的解释。

线性回归模型的优点是简单易懂，计算方便，但其前提是自变量与因变量之间存在线性关系。

第二种模型是时间序列模型，它主要用于分析时间序列数据的模型。

时间序列模型假设经济现象的变化是随时间演变的，通过分析时间序列的趋势、周期性和随机性，可以对经济现象进行预测和解释。

时间序列模型的常用方法包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）等。

时间序列模型的优点是能够捕捉到时间的动态变化，但其局限性是对数据的要求较高，需要足够的时间序列观测样本。

第三种模型是面板数据模型，也称为横截面时间序列数据模型。

面板数据模型是将横截面数据和时间序列数据结合起来进行分析的模型。

面板数据模型可以同时考虑个体间的差异和时间的变化，因此能够更全面地解释经济现象。

面板数据模型的常用方法包括固定效应模型、随机效应模型等。

面板数据模型的优点是能够控制个体间的异质性，但其需要对个体间的相关性进行假设。

第四种模型是离散选择模型，它主要用于分析离散选择行为的模型。

离散选择模型假设个体在面临多种选择时，会根据一定的规则进行选择，通过建立选择概率与个体特征之间的关系，可以预测和解释个体的选择行为。

离散选择模型的常用方法包括二项Logit模型、多项Logit模型等。

离散选择模型的优点是能够分析个体的选择行为，但其局限性是对选择行为的假设较强。

综上所述，计量经济学中常用的模型有线性回归模型、时间序列模型、面板数据模型和离散选择模型。

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述（1）确定性关系或函数关系：变量之间有唯一确定性的函数关系。

其一般表现形式为：一、回归模型的一般形式变量间的关系经济变量之间的关系，大体可分为两类：（2.1)（2）统计关系或相关关系：变量之间为非确定性依赖关系。

其一般表现形式为：(2.2)例如：函数关系：圆面积S =统计依赖关系/统计相关关系：若x和y之间确有因果关系，则称(2.2)为总体回归模型，x(一个或几个）为自变量（或解释变量或外生变量），y为因变量（或被解释变量或内生变量），u为随机项，是没有包含在模型中的自变量和其他一些随机因素对y的总影响。

一般说来，随机项来自以下几个方面：1、变量的省略。

由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。

2、统计误差。

数据搜集中由于计量、计算、记录等导致的登记误差；或由样本信息推断总体信息时产生的代表性误差。

3、模型的设定误差。

如在模型构造时，非线性关系用线性模型描述了；复杂关系用简单模型描述了；此非线性关系用彼非线性模型描述了等等。

4、随机误差。

被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。

若相互依赖的变量间没有因果关系，则称其有相关关系。

对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。

他们各有特点、职责和分析范围。

相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析，但在大多数情况下，则是和回归分析结合在一起，进行综合分析，作为回归分析方法的补充。

回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。