回归分析相关系数计算

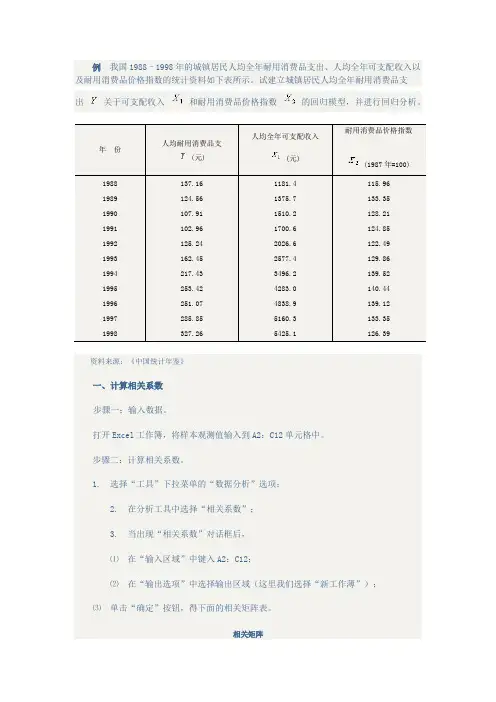
例我国1988–1998年的城镇居民人均全年耐用消费品支出、人均全年可支配收入以及耐用消费品价格指数的统计资料如下表所示。

试建立城镇居民人均全年耐用消费品支
出关于可支配收入和耐用消费品价格指数的回归模型，并进行回归分析。

人均耐用消费品支
(元)人均全年可支配收入
(元)
耐用消费品价格指数
(1987年=100)
资料来源：《中国统计年鉴》
一、计算相关系数
步骤一：输入数据。

打开Excel工作簿，将样本观测值输入到A2：C12单元格中。

步骤二：计算相关系数。

1. 选择“工具”下拉菜单的“数据分析”选项；
2. 在分析工具中选择“相关系数”；
3. 当出现“相关系数”对话框后，
⑴在“输入区域”中键入A2：C12；
⑵在“输出选项”中选择输出区域（这里我们选择“新工作薄”）；
⑶单击“确定”按钮，得下面的相关矩阵表。

相关矩阵
二、回归分析
我们继续说明如何利用Excel进行回归分析。

1. 选择“工具”下拉菜单的“数据分析”选项；
2. 在分析工具中选择“回归”；
3. 当出现对话框后，
⑴在“Y值输入区域”方框中键入A2：A12；
⑵在“X值输入区域”方框中键入B2：C12；
⑶在“输出选项”中选择输出区域（这里我们选择“新工作薄”）；
⑷单击“确定”按钮，得到的结果如下表所示：
从表中得到的主要结果有：
复相关系数：，
判定系数：，
估计的回归方程为：
根据括号内的统计量的值可知：对有显著影响，而对没有显著影响。

根据统计量的值可知：回归方程是显著的。

回归分析lxy公式直线回归是用直线回归方程表示两个数量变量间依存关系的统计分析方法,属双变量分析的范畴.1. 直线回归方程的求法（1）回归方程的概念:直线回归方程的一般形式是l=a+bx,其中x为自变量,一般为资料中能精确测定和控制的量,Y为应变量,指在x规定范围内随机变化的量.a为截距,是回归直线与纵轴的交点,b为斜率,意为x每改变一个单位时的变化量.(2)直线回归方程的求法确定直线回归方程利用的是最小二乘法原理,基本步骤为：1）先求b,基本公式为b=lxy/lxx=SSxy/SSxx ,其中lxy为X,Y的离均差积和,lxx为X的离均差平方和；2）再求a,根据回归方程a等于Y的均值减去x均值与b 乘积的差值.(3)回归方程的图示:根据回归方程,在坐标轴上任意取相距较远的两点,连接上述两点就可得到回归方程的图示.应注意的是,连出的回归直线不应超过x的实测值范围.2. 回归关系的检验回归关系的检验又称回归方程的检验,其目的是检验求得的回归方程在总体中是否成立,即是否样本代表的总体也有直线回归关系.方法有以下两种：(1)方差分析其基本思想是将总变异分解为SS回归和SS剩余,然后利用F检验来判断回归方程是否成立.(2)t检验其基本思想是利用样本回归系数b与总体均数回归系数?进行比较来判断回归方程是否成立,实际应用中因为回归系数b的检验过程较为复杂,而相关系数r的检验过程简单并与之等价,故一般用相关系数r的检验来代替回归系数b的检验.3. 直线回归方程的应用(1)描述两变量之间的依存关系；利用直线回归方程即可定量描述两个变量间依存的数量关系(2)利用回归方程进行预测；把预报因子（即自变量x）代入回归方程对预报量（即因变量Y）进行估计,即可得到个体Y值的容许区间.(3)利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标.如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度.4. 应用直线回归的注意事项(1)做回归分析要有实际意义；(2)回归分析前,最好先作出散点图；(3)回归直线不要外延.。

数据分析技巧Excel中的回归分析和相关性计算在Excel中，回归分析和相关性计算是数据分析中常用的技巧。

通过这些分析方法，我们可以了解变量之间的关系，以及预测和解释数据的趋势。

本文将介绍Excel中回归分析和相关性计算的基本原理和操作方法。

一、回归分析回归分析是用于研究因变量和一个或多个自变量之间关系的方法。

在Excel中，我们可以使用“数据分析”功能来进行回归分析。

下面以一个示例来说明回归分析的具体步骤。

假设我们想研究一个人的身高与体重之间的关系。

首先，将收集到的身高和体重数据录入Excel表格中，如下所示：身高（cm）体重（kg）160 50165 55170 60175 65180 70接下来，在Excel的菜单栏中选择“数据”→“数据分析”→“回归”功能。

然后，选择“输入Y范围”为体重数据，选择“输入X范围”为身高数据。

点击“确定”，Excel会生成回归分析的结果。

回归分析的结果包括了斜率、截距、相关系数等信息。

通过这些信息，我们可以得出一个回归方程，用于预测体重。

例如，回归方程可能是：体重 = 0.5 ×身高 + 25。

通过回归分析，我们可以得到身高与体重之间的关系，并进行相关的预测和解释。

二、相关性计算相关性是用来描述两个变量之间关系的统计指标。

在Excel中，我们可以使用相关性函数来计算两个变量之间的相关系数。

下面以一个示例来说明相关性计算的具体操作。

假设我们有两列数据，分别是销售额和广告费用。

我们想知道这两个变量之间是否存在相关关系。

首先，在Excel表格中录入这两列数据，如下所示：销售额（万元）广告费用（万元）10 212 315 518 620 8然后，在Excel的一个空白单元格中输入“=CORREL(A2:A6, B2:B6)”并按下回车键，Excel会自动计算出这两个变量的相关系数。

相关系数的取值范围在-1到1之间。

相关系数为正值表示正相关，即当一个变量增加时，另一个变量也随之增加；相关系数为负值表示负相关，即当一个变量增加时，另一个变量会减少；相关系数为0表示没有线性关系。

回归方程的相关系数公式(一)回归方程的相关系数公式在统计学中，回归分析是一种用于探索变量之间关系的方法。

回归分析可用于预测和解释因变量与一个或多个自变量之间的关系。

相关系数是回归分析中常用的指标，用于衡量自变量与因变量之间的关联程度。

下面是回归方程的相关系数公式及其解释说明。

简单线性回归的相关系数公式在简单线性回归中，只有一个自变量和一个因变量。

相关系数（也称为皮尔逊相关系数）表示自变量和因变量之间的线性关系强度。

相关系数公式如下：r=∑(x−x)(y−y)i i其中，r为相关系数，x i和y i分别表示第i个观测值的自变量和因变量值，x和y分别为自变量和因变量的均值。

多元线性回归的相关系数公式多元线性回归中，有多个自变量和一个因变量。

相关系数矩阵可以用来衡量每个自变量与因变量之间的关联程度。

相关系数矩阵公式如下：R=(X T X)−1(X T Y)其中，R为相关系数矩阵，X为自变量矩阵，Y为因变量矩阵。

示例说明假设我们想要研究某个城市的房价与以下两个因素的关系：房屋面积和距离市中心的距离。

我们收集了10个房屋的数据，如下所示：房屋编号 | 面积（平方米） | 距离市中心（公里） | 房价（万元） || | | |1 | 80 | 5 | 200 |2 | 90 | 4 | 220 |3 | 95 | 7 | 230 |4 | 100 | 6 | 250 |5 | 110 | 3 | 270 |6 | 120 | 8 | 290 |7 | 130 | 2 | 310 |8 | 140 | 9 | 330 |9 | 150 | 1 | 350 |10 | 160 | 10 | 370 |我们可以使用多元线性回归模型来分析房屋面积和距离市中心与房价之间的关系。

根据相关系数矩阵公式，我们可以计算出相关系数矩阵R：R=(X T X)−1(X T Y)其中，X是由房屋面积和距离市中心组成的自变量矩阵，Y是房价的因变量矩阵。

回归方程相关系数r公式
回归方程相关系数r是一种统计指标，用于衡量两个变量之间的线性关系。

它是一种反映变量之间线性关系的统计指标，可以用来衡量两个变量之间的相关性。

回归方程相关系数r的取值范围从-1到1，其中-1表示完全负相关，1表示完全正相关，0表示没有线性关系。

回归方程相关系数r的计算公式为：r=Σ(x-x̅)(y-y̅)/√[Σ(x-
x̅)^2]*[Σ(y-y̅)^2]，其中x和y分别表示两个变量，x̅和y̅分别表示两个变量的均值。

回归方程相关系数r的计算可以帮助我们了解两个变量之间的线性关系，从而更好地分析数据。

它可以帮助我们判断两个变量之间是否存在线性关系，以及线性关系的强度。

回归方程相关系数r的计算可以帮助我们更好地理解数据，从而更好地分析数据。

回归方程相关系数r的计算是一种重要的统计指标，它可以帮助我们更好地理解数据，从而更好地分析数据。

它可以帮助我们判断两个变量之间是否存在线性关系，以及线性关系的强度。

因此，回归方程相关系数r的计算是统计分析中不可或缺的一部分。

相关系数与回归分析打开数据分析的⼤门，从感性⾛向理性。

“概率统计”正确理解，才能正确应⽤！本专栏从最通俗易懂的⾓度，⽤最易于理解的⽅法，真正内化吸收概率统计的核⼼思想与算法，帮助您在⼯作⽣活中正确应⽤概率统计知识。

“相关”想象⼀下，如果⽼师说——“数学考试中，读题能⼒很重要，所以语⽂学得好的同学更容易数学也学得好。

”如何从统计学⾓度来分析这件事呢？我们拿到了全班同学的数学和语⽂成绩，有的同学两科成绩都好，有的同学两科成绩者差，但也存在偏科的同学啊。

你怎么能说，语⽂学得好，则数学也容易学得好呢？这样吧，我把所有成绩画成“散点图”看看：分析关系的散点图，有时也称为“相关图”可以感受到：语⽂成绩 X 与数学成绩 Y 之间存在某种关系，但是⼜“不能说存在因果关系”，这⾥就说 X 与 Y “相关”（Correlation）。

从图中基本可以看出，X 越⼤，Y 也就有越⼤的趋势，称为“正相关”；反之，X 越⼤，Y 越⼩，则称为“负相关”。

相关系数为了“定量地描述相关关系的强弱”，数学家们发明了“相关系数”。

相关系数有⼀个特点，它在区间 [-1,1] 范围内，也就是说：相关系数为1——“最强正相关”相关系数为-1——“最强负相关”相关系数为0——“完全不相关”下图可以让我们对相关系数的值与散点模式之间的关系有⼀个直观认识。

各种散点模式及其相关系数⾄此可以总结，相关，显⽰的是两个随机变量之间线性关系的强度和⽅向。

相关系数公式与理解（1）计算公式如下：相关系数(X,Y) = 协⽅差(X,Y) /（标准差(X)*标准差(Y)）协⽅差（Covariance）⽤于衡量两个变量的总体误差——协⽅差公式从这个公式和上⾯的例⼦套⽤，怎么求出的相关度就很明显了，因为每⼀项为——（语⽂分-语⽂平均分）*（数学分-数学平均分）意思是说，语⽂好数学也好的，该项结果为正；语⽂差数学也差的，该项结果也为正；⽽偏科的该项结果为负。

最后再把这些项取平均值，看看整体为正还是为负。

回归分析与相关性检验方法引言回归分析和相关性检验方法是统计学中常用的两种分析方法。

它们主要用于研究变量之间的关联程度和预测某一变量对其他变量的影响。

在实际应用中，回归分析和相关性检验方法具有广泛的应用领域，例如经济学、医学、社会科学等。

本文将对回归分析和相关性检验方法进行详细介绍，并给出相应的案例应用。

一、回归分析回归分析是一种统计学方法，用于研究因变量和一个或多个自变量之间关系的强度和方向。

回归分析有两种基本类型：简单线性回归和多元线性回归。

1. 简单线性回归简单线性回归是指当因变量和自变量之间存在一种线性关系时使用的回归分析方法。

简单线性回归的模型可以表示为：$y = \\beta_0 + \\beta_1x + \\epsilon$，其中y表示因变量，x表示自变量，$\\beta_0$和$\\beta_1$是回归系数，表示截距和斜率，$\\epsilon$表示误差项。

简单线性回归的关键是通过最小二乘法估计回归系数，然后进行显著性检验和模型拟合度的评估。

通过显著性检验可以确定回归系数是否显著不为零，进而得出自变量对因变量的影响是否显著。

2. 多元线性回归多元线性回归是指当因变量和多个自变量之间存在一种线性关系时使用的回归分析方法。

多元线性回归的模型可以表示为：$y = \\beta_0 + \\beta_1x_1 +\\beta_2x_2 + ... + \\beta_nx_n + \\epsilon$，其中y表示因变量，x1,x2,...,x n表示自变量，$\\beta_0, \\beta_1, \\beta_2, ..., \\beta_n$表示回归系数，$\\epsilon$表示误差项。

多元线性回归的关键也是通过最小二乘法估计回归系数，并进行显著性检验和模型拟合度的评估。

多元线性回归可以通过检验回归系数的显著性，判断各个自变量是否对因变量产生显著影响。

二、相关性检验方法相关性检验方法是用于检测变量之间关系的非参数统计学方法。

统计学中的回归分析与相关系数统计学中，回归分析和相关系数是两个重要的概念和方法，它们可以帮助我们理解数据之间的关系、预测未来趋势以及评估变量之间的相互作用。

本文将介绍回归分析的基本原理和应用，以及相关系数的定义和计算方法。

一、回归分析回归分析是一种统计方法，用于研究两个或多个变量之间的关系，并建立一个数学模型来描述这种关系。

在回归分析中，我们通常将一个变量称为因变量（dependent variable），将其他变量称为自变量（independent variable）。

回归分析的目标是找到一个关系模型，使得自变量能够解释因变量的变化。

在简单线性回归中，我们假设只有一个自变量和一个因变量之间存在线性关系。

回归模型可以表示为：Y = α + βX + ε其中，Y表示因变量，X表示自变量，α和β是待估计的参数，ε表示误差项。

通过最小二乘法估计参数α和β，我们可以得到最佳拟合直线，以描述自变量和因变量之间的关系。

除了简单线性回归，我们还可以进行多元线性回归，其中自变量可以是多个。

多元线性回归将回归模型拓展为：Y = α + β₁X₁ + β₂X₂ + ... + βₖXₖ + ε通过最小二乘法，我们可以估计所有的参数β₁，β₂，...，βₖ。

多元线性回归分析可以帮助我们更全面地理解多个自变量对因变量的影响。

回归分析不仅可以用于探索变量之间的关系，还可以用于预测未来的数值。

通过已知的自变量值，我们可以利用回归模型来预测因变量的值。

这使得回归分析在实际应用中非常有用，例如经济学、金融学、市场营销等领域。

二、相关系数相关系数是衡量两个变量之间线性关系强度的统计指标，常用于描述变量之间的相关程度。

最常用的相关系数是皮尔逊相关系数，表示为r。

皮尔逊相关系数的取值范围为-1到1之间，其中1表示完全正相关，-1表示完全负相关，0表示无线性关系。

皮尔逊相关系数可以通过以下公式计算：r = Σ((Xᵢ - X)(Yᵢ - Ȳ)) / √(Σ(Xᵢ - X)²Σ(Yᵢ - Ȳ)²)其中，Xᵢ和Yᵢ分别表示X和Y的观测值，X和Ȳ分别表示X和Y的平均值。