简单线性回归模型试题及答案

线性模型练习题(含答案)练题一设有线性回归模型：$ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 $，其中 $x_1$、$x_2$ 和 $x_3$ 是自变量，$y$ 是因变量。

已知模型的参数估计值如下：$ \hat{\beta}_0 = 2.5 $$ \hat{\beta}_1 = 0.8 $$ \hat{\beta}_2 = -1.2 $$ \hat{\beta}_3 = 1.3 $请判断以下哪个自变量与因变量的关系最为显著：A. $x_1$B. $x_2$C. $x_3$D. 无法确定答案：B. $x_2$练题二下面是一个简单的线性回归模型：$ y = 3x_1 + 4x_2 + 2x_3 + 1 $已知模型的参数估计值如下：$ \hat{\beta}_1 = 2.1 $$ \hat{\beta}_2 = 1.8 $$ \hat{\beta}_3 = 0.9 $请根据模型参数估计值计算预测值 $ \hat{y} $，当 $x_1 = 2$，$x_2 = 3$，$x_3 = 1$ 时的结果。

答案：$ \hat{y} = 3(2) + 4(3) + 2(1) + 1 = 23 $练题三某研究人员运用线性回归模型分析了一个因变量 $y$ 和四个自变量 $x_1$、$x_2$、$x_3$ 和 $x_4$ 的关系，得到模型方程如下：$ y = 2.6x_1 + 1.9x_2 - 1.4x_3 + 0.5x_4 - 1 $已知 $x_1 = 3$，$x_2 = 2$，$x_3 = 4$，$x_4 = 1$，请计算对应的预测值 $ \hat{y} $。

答案：$ \hat{y} = 2.6(3) + 1.9(2) - 1.4(4) + 0.5(1) - 1 = 2.9 $练题四以下是一个多元线性回归模型的参数估计值摘录：$ \hat{\beta}_0 = 1.2 $$ \hat{\beta}_1 = -0.8 $$ \hat{\beta}_2 = 0.5 $$ \hat{\beta}_3 = 1.0 $$ \hat{\beta}_4 = 0.3 $$ \hat{\beta}_5 = -0.6 $请写出该线性回归模型的方程。

2.2 简单线性回归模型参数的估计一、判断题1.使用普通最小二乘法估计模型时，所选择的回归线使得所有观察值的残差和达到最小。

（F)2.随机扰动项和残差项是一回事。

（F ）3.在任何情况下OLS 估计量都是待估参数的最优线性无偏估计。

（F ）4.满足基本假设条件下，随机误差项i μ服从正态分布，但被解释变量Y 不一定服从正态分 布。

（ F ）5.如果观测值i X 近似相等，也不会影响回归系数的估计量。

（ F ）二、单项选择题1．设样本回归模型为i 01i i ˆˆY =X +e ββ+，则普通最小二乘法确定的iˆβ的公式中，错误的是（ D ）。

A ．()()()i i 12i X X Y -Y ˆX X β--∑∑＝ B ．()i i i i 122i i n X Y -X Y ˆn X -X β∑∑∑∑∑＝C ．i i 122iX Y -nXY ˆX -nX β∑∑＝ D ．i i i i 12x n X Y -X Y ˆβσ∑∑∑＝ 2．以Y 表示实际观测值，ˆY 表示回归估计值，则普通最小二乘法估计参数的准则是使（ D ）。

A ．i i ˆY Y 0∑（－）＝B ．2i i ˆY Y 0∑（－）＝C ．i i ˆY Y ∑（－）＝最小D ．2i i ˆY Y ∑（－）＝最小 3．设Y 表示实际观测值，ˆY 表示OLS 估计回归值，则下列哪项成立（ D ）。

A ．ˆYY ＝ B ．ˆY Y ＝ C ．ˆY Y ＝ D ．ˆY Y ＝ 4．用OLS 估计经典线性模型i 01i i Y X u ββ+＝＋，则样本回归直线通过点（ D ）。

A ．X Y （，）B ． ˆX Y （，）C ．ˆX Y （，）D ．X Y （，） 5．以Y 表示实际观测值，ˆY表示OLS 估计回归值，则用OLS 得到的样本回归直线i 01iˆˆˆY X ββ+＝满足（ A ）。

A ．i i ˆY Y 0∑（－）＝B ．2i i Y Y 0∑（－）＝ C ． 2i i ˆY Y 0∑（－）＝ D ．2i i ˆY Y 0∑（－）＝6．按经典假设，线性回归模型中的解释变量应是非随机变量，且（ A ）。

2.4 回归系数的区间估计和假设检验一、判断题1.如果零假设H 0：B 2=0，在显著性水平5%下不被拒绝，则认为B 2一定是0。

（F ）2.k β的置信度为()α-1的置信区间指真实参数落入该区间的概率是()α-1。

(F)3.假设检验为单侧检验还是双侧检验本质上取决于备择假设的形式。

（F ）4.回归系数的显著性检验是用来检验解释变量对被解释变量有无显著解释能力的检验。

（T ）二、单项选择题1．对回归模型i i 10i u X Y ++=ββ进行检验时，通常假定i u 服从（ C ）。

A ．()2i 0N σ, B ．()2n t - C ．()20N σ, D ．()n t2．用一组有30个观测值的样本估计模型i i 10i u X Y ++=ββ，在0.05的显著性水平下对1β的显著性作检验，则1β显著地不等于零的条件是其统计量大于（ D ）。

A ．()30t 050. B ．()30t 0250.) C ．()28t 050. D ．()28t 0250. 3．回归模型i i i u X Y ++=10ββ中，关于检验010=β：H 所用的统计量)ˆ(ˆ111βββVar -，下列说法正确的是（ D ）。

A ．服从）（22-n χB ．服从）（1-n tC ．服从）（12-n χ D ．服从）（2-n t 4.用一组有30个观测值的样本估计模型后，在0.05的显著性水平上对的显著性作检验，则显著地不等于零的条件是其统计量大于等于（ C ） A. B. C. D. 三、简答题1.当α给定后，回归系数2β的置信区间是什么样的？答：总体方差2σ已知时，置信区间为⎥⎥⎦⎤⎢⎢⎣⎡+-∑∑2i 22i2x z xz σβσβˆ,ˆ；总体方差2σ未知则使用2n e 2i2-=∑σˆ估计2σ：①样本容量充分大时，统计量仍服从正态，则置信区间为t t 01122t t t t y b b x b x u =+++1b t 1b t )30(05.0t )28(025.0t )27(025.0t )28,1(025.0F⎥⎥⎦⎤⎢⎢⎣⎡+-∑∑2i 22i 2x z x z σβσβˆˆ,ˆˆ；②样本容量较小时，统计量服从t 分布，则置信区间为⎥⎥⎦⎤⎢⎢⎣⎡+-∑∑2i 222i22x t xt σβσβααˆˆ,ˆˆ 。

2.5 回归模型预测一、判断题1.fY ˆ是对个别值f Y 的点估计。

（F ） 2.预测区间的宽窄只与样本容量n 有关。

（F ）3.fY ˆ对个别值f Y 的预测只受随机扰动项的影响。

（F ） 4.一般情况下，平均值的预测区间比个别值的预测区间宽。

（F ）5.用回归模型进行预测时，预测普通情况和极端情况的精度是一样的。

（F ）二、单项选择题1．某一特定的X 水平上，总体Y 分布的离散度越大，即2σ越大，则（ A ）。

A ．预测区间越宽，精度越低B ．预测区间越宽，预测误差越小C 预测区间越窄，精度越高D ．预测区间越窄，预测误差越大2.在缩小参数估计量的置信区间时，我们通常不采用下面的那一项措施（D ）。

A.增大样本容量nB. 预测普通情形而非极端情形C.提高模型的拟合优度D.提高样本观测值的分散度三、多项选择题1．计量经济预测的条件是（ABC ）A ．模型设定的关系式不变B ．所估计的参数不变C.解释变量在预测期的取值已作出预测 D ．没有对解释变量在预测期的取值进行过预测 E ．无条件2.对被解释变量的预测可以分为（ABC ）A.被解释变量平均值的点预测B.被解释变量平均值的区间预测C.被解释变量的个别值预测D.解释变量预测期取值的预测四、简答题1.为什么要对被解释变量的平均值以及个别值进行区间预测？答：由于抽样波动的存在，用样本估计出的被解释变量的平均值fY ˆ与总体真实平均值()f f X Y E 之间存在误差，并不总是相等。

而用fY ˆ对个别值f Y 进行预测时，除了上述提到的误差，还受随机扰动项的影响，使得总体真实平均值()f f X Y E 并不等于个别值f Y 。

一般而言，个别值的预测区间比平均值的预测区间更宽。

2.分别写出()f f X Y E 和f Y 的置信度为α-1的预测区间。

答：()f f X Y E ：()⎪⎪⎪⎭⎫ ⎝⎛-+±∑22f 2f i x X X n 1t Y σαˆˆ；f Y ：()⎪⎪⎪⎭⎫ ⎝⎛-++±∑22f 2f i x X X n 11t Y σαˆˆ。

13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投1021．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗(1)(2)请根据上表提供的数据，求出y 关于x 的回归直线方程； (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投10[答案] 25[解析] x 甲＝6＋7＋7＋8＋75＝7，x 乙＝6＋7＋6＋7＋95＝7，∴s 2甲＝(6－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(7－7)25＝25， s 2乙＝(7－6)2＋(7－7)2＋(7－6)2＋(7－7)2＋(7－9)25＝65， 21．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗(1)(2)请根据上表提供的数据，求出y 关于x 的回归直线方程；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？[解析] (1)散点图如图．(2)x －＝4.5，y －＝3.5，b ^＝∑x i y i －4x － y －∑x 2i －4x －2＝66.5－6386－81＝0.7，a ^＝3.5－0.7×4.5＝0.35，∴回归直线方程为y ^＝0.7x ＋0.35. (3)90－(0.7×100＋0.35)＝19.65(t) ∴降低了19.65吨．教你如何用WORD 文档标签： 杂谈1. 问：WORD答：分节，不同。

2. 问：请问word 部改了？答：在插入分隔符里，个字来。

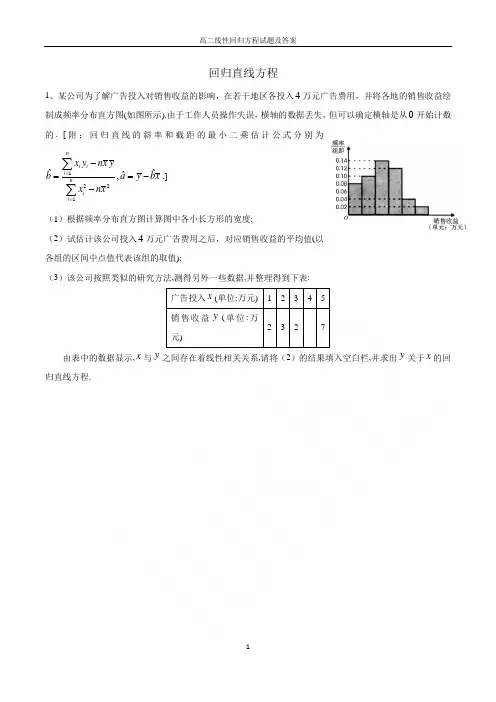
回归直线方程1、某公司为了解广告投入对销售收益的影响，在若干地区各投入万元广告费用，并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从开始计数的. [附：回归直线的斜率和截距的最小二乘估计公式分别为.] （1）根据频率分布直方图计算图中各小长方形的宽度;（2）试估计该公司投入万元广告费用之后，对应销售收益的平均值(以各组的区间中点值代表该组的取值);（3）该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将（2）的结果填入空白栏,并求出关于的回归直线方程.401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x2、某校在规划课程设置方案的调研中，随机抽取160名理科学生，想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性，调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等，且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人，根据调（）完成列联表，并判断在犯错误的概率不超过的前提下，能否认为选题与性 别有关.（Ⅰ）按照分层抽样的方法，从选择“坐标系与参数方程”与选择“不等式选讲”的学生中共抽取8人进行问卷.若从这8人中任选3人，记选择“坐标系与参数方程”与选择“不等式选讲”的人数的差为，求的分布列及数学期望． 附： ，其中．ξξE ξ()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++3、面向全市招聘事业编工作人员，由人事、劳动、纪检等部门联合组织招聘考试，招聘考试分为两个阶段：笔试和面试.现将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．（Ⅰ）求出上表中的x，y，z，s，p的值；（Ⅱ）按规定，笔试成绩不低于90分的应聘人员可以参加面试，且面试的方式采用单循环，以参加面试人员胜出的场数决定是否录用（即参加面试的所有人员中每两人必需进行一个场次的PK比赛）．已知松山区有两名应聘人员取得面试资格，在所有的比赛中，求有松山区选手参加比赛的概率．答案1、某公司为了解广告投入对销售收益的影响，在若干地区各投入万元广告费用，并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从开始计数的. [附：回归直线的斜率和截距的最小二乘估计公式分别为.] （1）根据频率分布直方图计算图中各小长方形的宽度;（2）试估计该公司投入万元广告费用之后，对应销售收益的平均值(以各组的区间中点值代表该组的取值);（3）该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将（2）的结果填入空白栏,并求出关于的回归直线方程.解：（1）设各小长方形的宽度为,由频率分布直方图中各小长方形的面积总和为1,可知,故，即图中各小长方形的宽度为2. …3分（2）由（1）知各小组依次是, 其中点分别为,对应的频率分别为,故可估计平均值为.7分 （3）由（2）可知空白栏中填5.由题意可知, ，401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x m (0.080.10.140.120.040.02)0.51m m +++++⋅==2m =[0,2),[2,4),[4,6),[6,8),[8,10),[10,12]1,3,5,7,9,110.16,0.20,0.28,0.24,0.08,0.0410.1630.250.2870.2490.08110.045⨯+⨯+⨯+⨯+⨯+⨯=12345232573, 3.855x y ++++++++====,,根据公式,可求得 ………………10分, ………………11分 所以所求的回归直线方程为. ………………12分2、某校在规划课程设置方案的调研中，随机抽取160名理科学生，想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性，调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等，且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人，根据调51122332455769i ii x y=⨯+⨯+⨯+⨯+⨯==∑522222211234555ii x==++++=∑26953 3.8121.2,555ˆ310b-⨯⨯===-⨯3.8 1.230ˆ.2a=-⨯= 1.20.2y x =+，故不能认为选题与性别有关．…………………5分（Ⅱ）选择“坐标系与参数方程”与选择“不等式选讲”的人数比例为100：60＝5：3， 所以抽取的8人中倾向“坐标系与参数方程”的人数为5，倾向“不等式选讲”的人 数为3．依题意，得，，，， ． …………………9分 故的分布列如下:所以． …………………12分 3、面向全市招聘事业编工作人员 ，由人事、劳动、纪检等部门联合组织招聘考试，招聘考试分为两个阶22160(9001800) 3.74 5.0241055510060K -=≈<⨯⨯⨯3,1,1,3=--ξ33381(3)56C P C =-==ξ12533815(1)56C C P C =-==ξ21533830(1)56C C P C ===ξ30533810(3)56C C P C ===ξξ115301033(1)135********E =-⨯+-⨯+⨯+⨯=ξy = 50×0.38 = 19， Z = 50﹣9﹣19﹣16 = 6， S = = 0.12 ----------------------------------------------------------6分（Ⅱ）由（Ⅱ）知，参加面试的应聘人员共6人.若参加面试的6人分别记为：S 1 , S 2 , a , b , c , d .( 其中S 1 , S 2 表示松山区的参赛选手，a , b , c , d 表示其他旗、县的选手)则所有的比赛为： （S 1 , S 2 ） （S 1 , a ） （S 1 ,b ） （S 1 ,c ） （S 1 , d ） （S 2 , a ） （S 2 , b ） （S 2 , c ） （S 2 ,d ） （a , b ） （ a , c ） （ a , d ） （ b , c ） （b , d ） （c , d ） 共十五个场次的比赛，有松山区选手出现的比赛有9场. 若有松山区选手参加比赛的事件为：A 则P650。

线性回归习题答案线性回归是统计学中一种常见的数据分析方法，用于建立自变量与因变量之间的线性关系模型。

在实际应用中，线性回归模型常用于预测、趋势分析和关联度分析等领域。

下面将通过一些典型的线性回归习题来探讨其应用。

习题一：某公司根据过去几年的销售数据，建立了一个线性回归模型来预测未来的销售额。

已知公司的广告费用与销售额之间存在着一定的线性关系。

根据模型，当广告费用为1000元时，预测的销售额为15000元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示销售额，x表示广告费用。

根据已知条件，可以得到一个方程：15000 = a + 1000b。

进一步，如果再给出另外一个广告费用与销售额的数据点，就可以求解出回归方程的具体参数a和b。

习题二：某城市的房价与房屋面积之间存在一定的线性关系。

已知一套房子的面积为120平方米，根据线性回归模型预测其价格为80万元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示房价，x表示房屋面积。

根据已知条件，可以得到一个方程：80 = a + 120b。

同样地，如果再给出另外一个房屋面积与价格的数据点，就可以求解出回归方程的具体参数a和b。

习题三：某公司根据市场调研数据，建立了一个线性回归模型来分析产品销售量与价格之间的关系。

已知当产品价格为10元时，预测的销售量为1000个。

根据该模型，求当产品价格为15元时的预测销售量。

解答：假设回归方程为y = a + bx，其中y表示销售量，x表示产品价格。

根据已知条件，可以得到一个方程：1000 = a + 10b。

根据该方程，可以求解出参数a和b的具体值。

然后，将x取15，代入回归方程中，即可得到当产品价格为15元时的预测销售量。

通过以上习题的解答，我们可以看到线性回归模型在实际问题中的应用。

通过建立合适的回归方程，我们可以通过已知的自变量值来预测因变量的取值。

这对于企业决策、市场分析以及经济预测等方面都具有重要意义。

2.3拟合优度的度量一、判断题1.当()∑-2i y y 确定时，()∑-2iy y ˆ越小，表明模型的拟合优度越好。

（F ） 2.可以证明，可决系数高意味着每个回归系数都是可信任的。

（F ） 3.可决系数的大小不受到回归模型中所包含的解释变量个数的影响。

（F ） 4.任何两个计量经济模型的都是可以比较的。

（F ）5.拟合优度的值越大，说明样本回归模型对数据的拟合程度越高。

（ T ）6.结构分析是高就足够了，作预测分析时仅要求可决系数高还不够。

（ F ）7.通过的高低可以进行显著性判断。

（F ）8.是非随机变量。

（F ）二、单项选择题1．已知某一直线回归方程的可决系数为0.64，则解释变量与被解释变量间的线性相关系数为（ B ）。

A ．±0.64B ．±0.8C ．±0.4D ．±0.32 2．可决系数的取值范围是（ C ）。

A ．≤-1B ．≥1C ．0≤≤1D ．－1≤≤1 3.下列说法中正确的是：（ D ）A 如果模型的2R 很高，我们可以认为此模型的质量较好B 如果模型的2R 较低，我们可以认为此模型的质量较差C 如果某一参数不能通过显著性检验，我们应该剔除该解释变量D 如果某一参数不能通过显著性检验，我们不应该随便剔除该解释变量三、多项选择题1．反映回归直线拟合优度的指标有（ ACDE ）。

A ．相关系数B ．回归系数C ．样本可决系数D ．回归方程的标准差E ．剩余变差（或残差平方和）2．对于样本回归直线i 01i ˆˆˆY X ββ+＝，回归变差可以表示为（ ABCDE ）。

A ．22i i i i ˆY Y -Y Y ∑∑　（－）　（－） B ．221ii ˆX X β∑（－） C ．22iiRY Y ∑（－） D ．2iiˆY Y ∑（－） E ．1iiiiˆX X Y Y β∑（－（）－） 3．对于样本回归直线i 01iˆˆˆY X ββ+＝，ˆσ为估计标准差，下列可决系数的算式中，正确的有（ ABCDE ）。

一、单选题1、假设检验采用的逻辑推理方法是A.归纳推理法B.类比推理法C.反证法D.演绎推理法正确答案：C2、在Eviews软件操作中，预测是用（）命令。

A.GENERATEB.PLOTC.FORECASTD.SCAT正确答案：C3、对任意两个随机变量X和Y，若EXY=EX*EY,则（）A.X和Y不独立B.X和Y相互独立C.Var(XY)=VarX*VarYD.Var(X+Y)=VarX+VarY正确答案：D4、设随机变量X1,X2,...,Xn（n>1）独立同分布，且方差σ2>0。

令随机变量Y=1n ∑X ini=1，则()A.Var(X1+Y)=n+2nσ2B.Cov(X1,Y)=1nσ2C. Var(X1−Y)=n+2nσ2D. Cov(X1,Y)=σ2正确答案：B5、设随机变量X~t(n)(n>1),Y=1X，则A. Y~F(1,n)B. Y~F(n,1)C. Y~χ2(n−1)D. Y~χ2(b)正确答案：B二、多选题1、变量的显著性T检验的步骤有哪些？A.以原假设H0构造T统计量B.对总体参数提出假设C.给定显著性水平α，查t分布表得临界值tα/2(n-2)D.比较t统计量和临界值正确答案：A、B、C、D2、随机误差项的主要影响因素是A.变量观测值的观测误差的影响B.在解释变量中被忽略的因素的影响C.都不是D.模型关系的设定误差的影响正确答案：A、B、D3、下列中属于最小二乘法基本假设的有A.解释变量X是确定性变量，不是随机变量B.m服从零均值、同方差、零协方差的正态分布：μi~N(0,σμ2) i=1,2, …,nC.随机误差项μ与解释变量X之间不相关：Cov(Xi,μi)=0i=1,2, …,nD.随着样本容量的无限增加，解释变量X的样本方差趋于一有限常数。

正确答案：A、B、C、D4、最小二乘估计量的性质A.有效性B.无偏性C.一致性D.线性性正确答案：A、B、D5、缩小置信区间的途径有哪些A.增大样本容量B.降低模型的拟合优度C.提高模型的拟合优度D.减小样本容量正确答案：A、C三、判断题1、可以通过散点图来确定模型的形式。

回归分析期末试题及答案一、简答题1. 请解释回归分析的基本思想。

回归分析是一种统计学方法，用于研究变量之间的关系。

其基本思想是通过建立一个数学模型来描述一个或多个自变量对因变量的影响，并根据观察数据对模型进行拟合和推断。

2. 请解释简单线性回归和多元线性回归的区别。

简单线性回归是建立在一个自变量和一个因变量之间的基础上的回归模型。

多元线性回归则是在两个或更多个自变量和一个因变量之间建立的回归模型。

3. 请解释残差的含义。

残差是指建立回归模型后，观测值与模型预测值之间的差异。

残差可以用来评估模型的拟合程度，如果残差较大，则说明模型无法很好地解释观察数据的变化。

4. 请解释R平方的含义及其优缺点。

R平方是一个用来衡量回归模型拟合程度的指标，其值介于0和1之间。

R平方越接近1，说明模型对观察数据的拟合越好；而R平方越接近0，则说明模型对观察数据的拟合越差。

R平方的优点是简单直观，易于理解，但其缺点是不适用于比较不同自变量的模型。

5. 请简要说明什么是多重共线性问题。

多重共线性问题指的是在多元线性回归中，自变量之间存在高度相关性的情况。

多重共线性会导致回归系数的估计不准确，难以解释自变量与因变量之间的关系。

二、计算题1. 已知一个简单线性回归模型为：Y = 2 + 3X，回归系数的解释是什么？回归系数3表示自变量X每增加1个单位，因变量Y会增加3个单位。

而常数项2表示当自变量X为0时，因变量Y的取值为2。

2. 使用最小二乘法求解简单线性回归模型的参数估计值。

最小二乘法是一种常用的回归分析方法，用于估计回归模型中的参数值。

以简单线性回归模型Y = β0 + β1X 为例，最小二乘法通过最小化观测值Y与模型预测值之间的平方差来估计β0和β1。

3. 请计算多元线性回归模型的回归系数。

多元线性回归模型可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn。

回归系数β1、β2、...、βn可以使用最小二乘法来估计，通过最小化观测值Y与模型预测值之间的平方差来得出。

、判断题2 21. 当y y确定时，？ y越小，表明模型的拟合优度越好。

（F）2. 可以证明，可决系数R2高意味着每个回归系数都是可信任的。

（F）3. 可决系数R2的大小不受到回归模型中所包含的解释变量个数的影响。

（F）4. 任何两个计量经济模型的R2都是可以比较的。

（F）5. 拟合优度R2的值越大，说明样本回归模型对数据的拟合程度越高。

（T）6. 结构分析是R2高就足够了，作预测分析时仅要求可决系数高还不够。

（F ）7.通过R2的高低可以进行显著性判断。

(F)8.R2是非随机变量。

（F）二、单项选择题1. 已知某一直线回归方程的可决系数为0.64 , 则解释变量与被解释变量间的线性相关系数为(B )。

A.± 0.64B.± 0.8C.± 0.4D. ± 0.322. 可决系数R2的取值范围是（C）。

A.R2< -1B. R2> 1C.0< R2< 1D.—1 < R2< 13.下列说法中正确的是：（D ）A如果模型的R2很高，我们可以认为此模型的质量较好B如果模型的R2较低，我们可以认为此模型的质量较差C如果某一参数不能通过显著性检验，我们应该剔除该解释变量D如果某一参数不能通过显著性检验，我们不应该随便剔除该解释变量三、多项选择题1. 反映回归直线拟合优度的指标有（ACDE ）。

A. 相关系数 B .回归系数 C.样本可决系数D.回归方程的标准差E.剩余变差（或残差平方和）2•对于样本回归直线Y?= ?）?X j ,回归变差可以表示为（ABCDE ）。

A. （丫厂Y i）2 - （Y i- Y?）2B . ?2（X i - X）2C. R2（Y i-Y i）2 D . （Y?i-Y）2E.? （X i-X（Y i—Y i）2.3拟合优度的度量3•对于样本回归直线丫j=乙F列可决系数的算式中，正确的有(ABCDE )。

线性回归方程检测试题（附答案）高中苏教数学③2.4线性回归方程测试题一、选择题1．下列关系属于线性负相关的是（）Ａ．父母的身高与子女身高的关系Ｂ．身高与手长Ｃ．吸烟与健康的关系Ｄ．数学成绩与物理成绩的关系答案：Ｃ2．由一组数据得到的回归直线方程，那么下面说法不正确的是（）Ａ．直线必经过点Ｂ．直线至少经过点中的一个点Ｃ．直线a的斜率为Ｄ．直线和各点的总离差平方和是该坐标平面上所有直线与这些点的离差平方和中最小的直线答案：Ｂ3．实验测得四组的值为，则y与x之间的回归直线方程为（）Ａ．Ｂ．Ｃ．Ｄ．答案：Ａ4．为了考查两个变量x和y之间的线性关系，甲、乙两位同学各自独立作了10次和15次试验，并且利用线性回归方法，求得回归直线分别为l1，l2，已知两人所得的试验数据中，变量x和y的数据的平均值都相等，且分别是，那么下列说法正确的是（）Ａ．直线和一定有公共点Ｂ．直线和相交，但交点不一定是Ｃ．必有直线Ｄ．和必定重合答案：Ａ二、填空题5．有下列关系：（1）人的年龄与他（她）拥有的财富之间的关系（2）曲线上的点与该点的坐标之间的关系（3）苹果的产量与气候之间的关系（4）森林中的同一种树木，其断面直径与高度之间的关系（5）学生与他（她）的学号之间的关系其中，具有相关关系的是．答案：（1）（3）（4）6．对具有相关关系的两个变量进行的方法叫做回归分析．用直角坐标系中的坐标分别表示具有的两个变量，将数据表中的各对数据在直角坐标系中描点得到的表示具有相关关系的两个变量的一组数据的图形，叫做．答案：统计分析；相关关系；散点图7．将一组数据同时减去3.1，得到一组新数据，若原数据的平均数、方差分别为，则新数据的平均数是，方差是，标准差是．答案：；；8．已知回归直线方程为，则可估计x与y增长速度之比约为．答案：三、解答题9．某商店统计了近6个月某商品的进价x与售价y（单位：元）的对应数据如下：352891246391214求y对x的回归直线方程．解：，，，，，，回归直线方程为．10．已知10只狗的血球体积及红血球的测量值如下：45424648426.536.309.257.5806.9935584039505.909.496.206.557.72x（血球体积，ml），y（红血球数，百万）（1）画出上表的散点图；（2）求出y对x的回归直线方程并且画出图形．解：（1）见下图（2），，，设回归直线方程为，则，．图形如下：11．某医院用光电比色计检验尿汞时，得尿汞含量（毫克/升）与消光系数如下表：尿汞含量：246810消光系数64134205285360（1）画出散点图；（2）如果y与x之间具有线性相关关系，求回归直线方程；（3）估计尿汞含量为9毫克/升时的消光系数．解：（1）（2）由散点图可知与线性相关，设回归直线方程为．列表：12345246810 64134205285360 128536123022803600，．回归直线方程为．（3）当时，．。

2.2 简单线性回归模型参数的估计一、判断题1.使用普通最小二乘法估计模型时，所选择的回归线使得所有观察值的残差和达到最小。

（F)2.随机扰动项和残差项是一回事。

（F ）3.在任何情况下OLS 估计量都是待估参数的最优线性无偏估计。

（F ）4.满足基本假设条件下，随机误差项i μ服从正态分布，但被解释变量Y 不一定服从正态分 布。

（ F ）5.如果观测值i X 近似相等，也不会影响回归系数的估计量。

（ F ）二、单项选择题1．设样本回归模型为i 01i i ˆˆY =X +e ββ+，则普通最小二乘法确定的iˆβ的公式中，错误的是（ D ）。

A ．()()()i i 12i X X Y -Y ˆX X β--∑∑＝ B ．()i i i i 122i i n X Y -X Y ˆn X -X β∑∑∑∑∑＝C ．i i 122i X Y -nXY ˆX -nX β∑∑＝D ．i i i i 12xn X Y -X Y ˆβσ∑∑∑＝ 2．以Y 表示实际观测值，ˆY 表示回归估计值，则普通最小二乘法估计参数的准则是使（ D ）。

A ．i i ˆY Y 0∑（－）＝B ．2i i ˆY Y 0∑（－）＝C ．i i ˆY Y ∑（－）＝最小D ．2i i ˆY Y ∑（－）＝最小 3．设Y 表示实际观测值，ˆY 表示OLS 估计回归值，则下列哪项成立（ D ）。

A ．ˆYY ＝ B ．ˆY Y ＝ C ．ˆY Y ＝ D ．ˆY Y ＝ 4．用OLS 估计经典线性模型i 01i i Y X u ββ+＝＋，则样本回归直线通过点（ D ）。

A ．X Y （，）B ． ˆX Y （，）C ．ˆX Y （，）D ．X Y （，） 5．以Y 表示实际观测值，ˆY表示OLS 估计回归值，则用OLS 得到的样本回归直线i 01iˆˆˆY X ββ+＝满足（ A ）。

A ．i i ˆY Y 0∑（－）＝B ．2i i Y Y 0∑（－）＝ C ． 2i i ˆY Y 0∑（－）＝ D ．2i i ˆY Y 0∑（－）＝6．按经典假设，线性回归模型中的解释变量应是非随机变量，且（ A ）。

2.1回归分析与回归函数一、判断题1. 总体回归直线是解释变量取各给定值时被解释变量条件期望的轨迹。

（T ）2. 线性回归是指解释变量和被解释变量之间呈现线性关系。

（ F ）3. 随机变量的条件期望与非条件期望是一回事。

（F ）4、总体回归函数给出了对应于每一个自变量的因变量的值。

（F ）二、单项选择题1．变量之间的关系可以分为两大类，它们是（ A ）。

A ．函数关系与相关关系B ．线性相关关系和非线性相关关系C ．正相关关系和负相关关系D ．简单相关关系和复杂相关关系2．相关关系是指（ D ）。

A ．变量间的非独立关系B ．变量间的因果关系C ．变量间的函数关系D ．变量间不确定性的依存关系3．进行相关分析时的两个变量（ A ）。

A ．都是随机变量B ．都不是随机变量C ．一个是随机变量，一个不是随机变量D ．随机的或非随机都可以4．回归分析中定义的（ B ）。

A.解释变量和被解释变量都是随机变量B.解释变量为非随机变量，被解释变量为随机变量C.解释变量和被解释变量都为非随机变量D.解释变量为随机变量，被解释变量为非随机变量5．表示x 和y 之间真实线性关系的总体回归模型是（ C ）。

A ．01ˆˆˆt t Y X ββ=+B ．01()t t E Y X ββ=+C ．01t t t Y X u ββ=++D ．01t t Y X ββ=+6.一元线性样本回归直线可以表示为（ C ）A ．i i X Y u i 10++=ββ B. i 10X )(Y E i ββ+=C. i i e X Y ++=∧∧i 10ββ D. i 10X i Y ββ+=∧7．对于i 01i i ˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有（ D）。

A ．ˆ0r=1σ＝时，B ．ˆ0r=-1σ＝时，C ．ˆ0r=0σ＝时，D ．ˆ0r=1r=-1σ＝时，或8．相关系数r 的取值范围是（ D ）。

13．(09·江苏理）某校甲、乙两个班级各有5名编号为1,2，3,4，5的学生进行投篮练习,每人投10次,投中的次数如下表:学生1号2号3号4号5号甲组67787乙组67679则以上两组数据的方差中较小的一个为s2＝______.21．（本题满分12分）下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据x3456y 2.534 4.5（1)请画出上表数据的散点图；(2)请根据上表提供的数据,求出y关于x的回归直线方程；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？13．(09·江苏理)某校甲、乙两个班级各有5名编号为1，2,3,4，5的学生进行投篮练习，每人投10学生1号2号3号4号5号甲组67787乙组67679s2［答案] 错误!［解析] 错误!甲＝错误!＝7，错误!乙＝错误!＝7，∴s错误!＝错误!＝错误!，s错误!＝错误!＝错误!，21．（本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x(y3456y 2.534 4.5(1)(2）请根据上表提供的数据,求出y关于x的回归直线方程；(3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2）求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?[解析］（1）散点图如图．(2）错误!＝4.5,错误!＝3.5， 错误!＝错误!＝错误!＝0。

7, 错误!＝3.5－0。

7×4.5＝0.35,∴回归直线方程为错误!＝0。

7x ＋0.35。

(3）90－（0.7×100＋0.35)＝19.65(t) ∴降低了19.65吨．分组频数频率[122,126)50.04[126,130)80.07[130,134)100.08[134,138)220.18[138,142)330.28[142,146)200.17[146,150)110.09[150,154)60.05[154,158)50.04合计1201122 126 130 134 138 142 146 150 158 154 身高（cm ）o0.01 0.02 0.03 0.04 0.05 0.06 0.07 频率/组距。