下载文档原格式
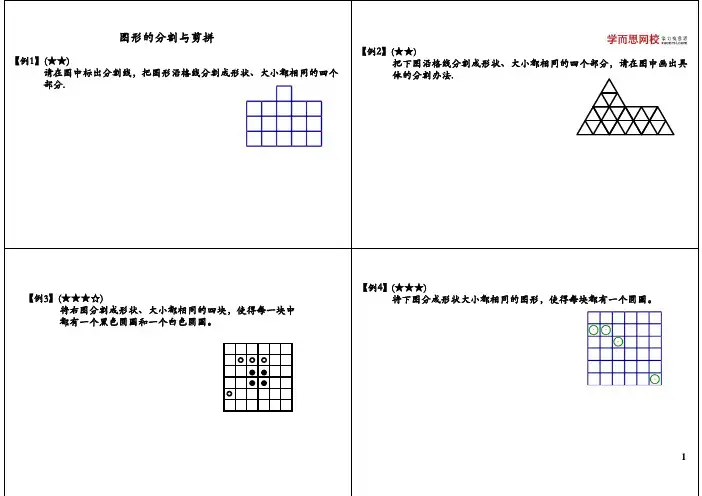
部分
部分.
图都图，得每都有个
将下图分成形状大小都相同的图形，使得每块都有一个圆圈。
用若干个边长为1，2，3，4的正方形纸片互不重叠地拼成一个边长为
个，，，拼个
5的大正方形，那么最少需要纸片____张。
图。
请你选取其中的一些或者全部，分别拼出一个五边形和一个七边
2cm2cm
下图是一个9×4的长方形，请把它分割成完全相等的两块，并拼成右图的方形请在左图中出分割线在右图中出拼接线
图的正方形，请在左图中画出分割线，在右图中画出拼接线。
如图，在5×8的长方形中，挖去了一个1×4的小长方形(阴影部分)，图，中，个(影部)，请你将它划分成两部分，使它们能拼成一个正方形。
第五讲图形的分割与拼接教学目标本章内容比较抽象，在这一讲中我们主要学习几种图形处理方法：1、理解掌握图形的分割；2、理解掌握图形的拼合；3、理解图形的剪拼；4、利用剪拼图形计算、解决问题.本章中很多类型的题目还要求同学们去动手尝试．通过本章知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．有8个相等的直角三角形，你能拼成下图中的空心正八角星吗？想挑战吗分析：把一个直角三角形的斜边与另一个直角三角形的直角边的一部分重合，但顶点均不重合，依次摆放下去，便可由这八个相等的直角三角形组成如右图所示的空心正八角星．专题精讲把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．（一）图形的分割【例1】（★★★）如右图所示是由三个正方形组成的图形，请把它分成大小、形状都相同的四个图形？→→分析：要求把原来三个正方形分成四个大小、形状都相同的四个图形，先不考虑形状，大小相同也就是面积相等，也就是把整个图形的面积分成四份，分割后的每一部分占一份，可以考虑把每一个正方形的面积分成四份，再把三个正方形中的每一个小正方形合成要求的图形，如右上图所示.[拓展]把如右图这样由五个正方形组成的图形，分成四块大小、形状都相同的图形→→分析：从面积考虑，把整个图形的面积分成四份，分割后的每一部分占一份.正方形，则可把每个正方形分成四个面积相等的小正方形，每块图形应有五个这样的小正方形，如右上图所示.[巩固]右图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分?分析：如果不考虑分成的四个图形的形状，只考虑它们的面积，这就要求把原来五个正方形分成四个面积相等的图形，每个图形的面积应是1个多正方形．我们把每个正方形各分成四个面积相等的小正方形，分成的每块图形应有五个这样的小正方形．根据图形的对称性，我们很快就能得到如右上图的分法.【例2】（★★★★）把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法．的面积必定相等．而要得到这4个等底等高的小三角形，只需把原三角形的某条边四等分，再将各分点与这边相对的顶点连接起来就行了.根据上面的分析，可得如左上图所示的三种分法．又因为4＝l×4＝2×2，所以，如果我们把每一个小三角形的面积看做1，那么1×4就可以视为把三角形的面积直接分成4等份，即分成4个面积为1的小三角形；而2×2可以视为先把原三角形分成两等份，再把每一份分别分成两等份．根据前面的分析，在每次等分时，都要想办法找等底等高的三角形．根据上面的分析，又可以得到如右上图的另两种分法．[前铺] 把任意一个三角形分成面积相等的2个小三角形，有许多种分法．请你画出4种不同的分法．分析：根据等底等高的三角形面积相等这一结论，只要把原三角形分成2个等底等高的小三角形，它们的面积必定相等．而要得到这2个等底等高的小三角形，只需找出原三角形的某条边的中点与这边相对的顶点连接起来就行了.根据上面的分析，可得如下图所示的三种分法．[拓展]怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.→分析：（1）分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成一半，得到如左上图所示的图形.（2）分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右上图所示的符合条件的图形.【例3】（★★★★）如下图所示，请将这个正方形分切成两块，使得两块的形状、大小都相同，并且每一块都含有学而思奥数五个字.→图1 图2分析：图中有相同汉字挨在一起的情况，肯定要从它们之间切开（图1），因此，首先要在它们之间划出切分线.因为要将这个正方形切开成两块形状和大小都一样的图形，所以其中一块绕中心点旋转180°必定与另一块重合.要是把切分线也绕中心点旋转180°就可得到一些新的切分线（图2）.这就为我们解决问题提供了线索，本题的两种解法如上图所示.[拓展] 如右图所示的正方形是由36个小正方格组成的.如图那样放着4颗黑子，4颗白子，现在要把它切割成形状、大小都相同的四块，并使每一块中都有一颗黑子和一颗白子.试问如何切割？分析：首先在相同颜色的棋子之间划出切分线，以中心旋转90°、180°、270°之后，得一些新的切分线，同时考虑到每块包含有一颗黑子和一颗白子的要求，以及每一块面积应该是36÷4=9，即含有9个小正方格，先找到符合要求的一块后，让它绕中心旋转90°、180°、270°便得到其他三块，如右上图.（二）图形的拼合【例4】（★★★）将方格纸剪成面积是4的图形，形状只有七种，如下图所示．其中有哪几种自身可以拼成面积是16的正方形?分析：面积是16的正方形，其边长等于4，用图形(5)和(7)显然能拼成边长是4的正方形(如左上图所示)．用图形(1)、(2)和(6)也能拼成边长为4的正方形(如右上图所示)．通过观察与试验，无法用所给图中的(3)和(4)拼成题目要求的正方形．因此，用所给图中的七种图形，共可以拼成5种面积是16的正方形．[巩固]下面哪些图形自身用4次就能拼成一个正方形？分析：用4块图（4）和图（5）那样的图形显然能够拼成一个大正方形．其实用图（1）、图（2）、图（3）也能拼成一个大正方形，拼法见右上图．【例5】（★★★★）用6个完全一样的等腰直角三角形拼图，要求边与边完全重合．你能拼出几种图形?把它们画出来．分析：建议用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合，或者准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上，见下图[前铺]用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形?分析：这种类型的题需要学生亲自操作，建议教师准备材料与学生互动。
小学数学《图形的分割与拼接》练习题(含答案)本文介绍了图形的分割、拼合和剪拼的概念和方法。
在图形分割中，可以使用染色法来找到对称点，保持每个小方格的完整。
在图形拼合中，需要注意每条边的长度，先拼少的，再拼多的。
在剪拼图形时，要确保剪、拼前后图形的面积相等，通过分析推理和计算确定剪拼的方法。
例1中给出了一个3×4的方格纸，要求用四种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整。
因为要分割成完全相同的两块，即大小、形状完全相同，所以可以使用染色法，先选中一个小格，找它关于中心点或中心线的对称位置，标上相应的符号。
例2中给出了一个正三角形形状的土地上有四棵大树，要把这块正三角形的土地分成和它形状相同的四小块，并且要求每块地中都要有一棵大树。
可以先将正三角形分成四个小三角形，然后在每个小三角形中心画一个小圆，这样每个小块中就有一棵大树了。
例4】下图是一个直角梯形，请画一条线段，把它分成两个形状相同并且面积相等的四边形。
要把这个直角梯形分成两个相同的四边形，首先需要保证它们的面积相等。
我们可以找到梯形中一条边可以分成上底和下底的长度之和，即AD边长为3.然后，我们在AD边上找到三等分点E，连接EF，再找到BC的中点F，这样就可以把梯形分成两个完全相同的部分，如右上图所示。
例5】用两块大小一样的等腰直角三角形能拼成几种常见的图形？我们可以使用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合。
或者，我们可以准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上。
如下图所示，可以拼成几种形状。
拓展]用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形？这种类型的题需要学生亲自操作，建议教师准备材料与学生互动。
一共可以拼成如下图的几种形状：例6】用下面左边的3个图形，拼成右边的大正方形。
首先数一数所有的空格数，一共只有16个，只能组成4×4的正方形。
使用目标倒推法，在右边的大正方形中拼图，使用染色法，把已知图形往右边的大正方形中放，这样就很容易拼合了，如下图所示。
4-2-3.圖形的分割與拼接知識點撥本講主要學習三大圖形處理方法：1．理解掌握圖形的分割；2．理解掌握圖形的拼合；3．理解圖形的剪拼．本講中很多類型的題目還要求同學們去動手嘗試．通過本講知識的學習，讓同學們瞭解不同圖形的分割、拼合、剪拼的方法，鍛煉同學們的平面想像能力以及增強學生的動手操作能力．把一個幾何圖形按某種要求分成幾個圖形，就叫做圖形的分割．反過來，按一定的要求也可以把幾個圖形拼成一個完美的圖形，就叫做圖形的拼合．將一個或者多個圖形先分割開，再拼成一種指定的圖形，則叫做圖形的剪拼．我們在圖形的分割、拼合和剪拼的過程中，都要結合所提供的圖形特點來思考．如果把一個圖形分割成若干個大小、形狀相等的部分，那麼就要想辦法找圖形的對稱點，把圖形先分少，再分多．圖形中，如果有數量方面的要求，可以先從數量入手，找出平分後每塊上所含數量的多少，再結合數量來分割圖形．如果是要把幾個圖形拼合成一個大圖形，要特別注意每條邊的長度，把相等的邊長拼合在一起，先拼少的，再拼多的．如果是剪拼圖形，要抓住“剪、拼前後圖形的面積相等”這個關鍵，根據已知條件和圖形的特點，通過分析推理和必要的計算，確定剪拼的方法．模組一、圖形的分割【例 1】用一條線段把一個長方形平均分割成兩塊，一共有多少種不同的分割法？BA O【考點】圖形的分割與拼接【難度】2星【題型】解答【解析】怎樣把一個圖形按照規定的要求分割成若干部分呢？這就是圖形的分割問題．按照規定的要求合理分割圖形，是很講究技巧的，多做這種有趣的訓練，可以培養學生的創造性思維，發展空間觀念，豐富想像，提高觀察能力．這道題要求把長方形平均分割成兩塊，過長方形中心的任意一條直線都可以把長方形平均分割成兩塊，根據這點給出如下分法(如右圖)：⑴做長方形的兩條對角線，設交點為O⑵過O點任作一條直線AB，直線AB將長方形平均分割成兩塊．可見用線段平分長方形的分法是無窮多的．【答案】⑴做長方形的兩條對角線，設交點為O⑵過O點任作一條直線AB，直線AB將長方形平均分割成兩塊．用線段平分長方形的分法有無窮多種。
本讲主要学习三大图形处理方法：
1．理解掌握图形的分割；
2．理解掌握图形的拼合；
3．理解图形的剪拼．
本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．
把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．
我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．
图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．
如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．
如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．
板块一图形的分割
【例 1】用一条线段把一个长方形平均分割成两块，一共有多少种不同的分割法？
B
A O
【例 2】把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法．【例 3】怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形．
→
【例 4】下图是一个直角梯形，请你画一条线段，把它分成两个形状相同并且面积相等的四边形．
3
2
1
D
C
B A
1
F
E 2
2
1
D
C
B
A
【例 5】 在一块长方形的地里有一正方形的水池(如下图)．试画一条直线把除开水池外的这块地平分成两块．
A
O
【例 6】 把下图四等分，要求剪成的每个小图形形状、大小都一样．除了剪正方形外，你还有别的方法吗？
20
60
40
20
【例 7】 下图是一个34 的方格纸，请用四种不同的方法将它分割成完全相同的两部分，但要保持每个小方
格的完整．
【例 8】 下图是一个被挖去了为总面积四分之一小正方形的大正方形，请你将它分成大小形状完全一样的四
部分．
【例 9】 下图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分？
【例 10】
已知左下图是由同样大小的5个正方形组成的．试将图形分割成4块形状、大小都一样的图形．
【例 11】
下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形．
【例 12】 一个正三角形形状的土地上有四棵大树(如下图所示)，现要把这块正三角形的土地分成和它形
状相同的四小块，并且要求每块地中都要有一棵大树．应怎样分？
【例 13】
将下图分割成大小、形状相同的三块，使每一小块中都含有一个○．
【例 14】 请把下面这个长方形沿方格线剪成形状、大小都相同的4块，使每一块内都含有“奥数读本”
这四个字中的一个，该怎么剪？
本
读数
奥
【例 15】 (2008年第八届“春蕾杯”小学数学邀请赛初赛)请把下面的图形分成形状、大小都相同的4块，
使每一块里面都有“春蕾杯赛”4个字．
春春蕾杯
赛
春春蕾
蕾
蕾杯
杯杯赛赛
赛第13题
【例 16】
学习与思考对小学生的发展是很重要的，学习改变命运，思考成就未来，请你将下图分成形状
和大小都相同的四个图形，并且使其中每个图形都含有“学习思考”这四个字．应怎样分？
学
习思考学
习思考学习
思考
考思习学
【例 17】 如下图所示，请将这个正方形分切成两块，使得两块的形状、大小都相同，并且每一块都含有
学而思奥数五个字．
学
而
思
奥
数
数
奥思而学 →
【例 18】 如图，甲、乙是两个大小一样的正方形．要求把每一个正方形分成四块，两个正方形共分为八
块，使每块的大小和形状都相同，而且都带一个○．
甲 乙
【例 19】 正三角形ABC 的面积是1平方米，将三条边分别向两端各延长一倍，连结六个端点得到一个六
边形(如右图)，求六边形的面积．
C
B
A
【巩固】正方形ABCD 的面积是1平方米，将四条边分别向两端各延长一倍，连结八个端点得到一个正方形(如
图)，求大正方形的面积．
D
C
B A
【例 20】 (第九届“中环杯”小学生思维能力训练活动初赛)如图，它是由15个边长为1厘米的小正方形
组成的．
⑴ 请在原图中沿正方形的边线，把它划分为5个大小形状完全相同的图形，分割线用笔描粗．
⑵分割后每个小图形的周长是厘米．
⑶分割后5个小图形的周长总和与原来大图形的周长相差厘米．
第3题
【例 21】如何把下图中的三个图形分割成两个相同的部分(除了沿正方形的边进行分割外，还可沿正方形的对角线进行分割)．
【例 22】(2003年《小学生数学报》数学邀请赛)如图，将一个等边三角形分割成互相不重叠的23个较小的等边三角形(这些较小的等边三角形的大小不一定都相同)，请在图中画出分割的结果．
【例 23】(2005年《小学生数学报》数学邀请赛)如图，将一个正方形分割成互相不重叠的21个小正方形，这些小正方形的大小不一定相同，请画图表示．
板块二图形的拼合
【例 24】用两块大小一样的等腰直角三角形能拼成几种常见的图形？
【例 25】下面哪些图形自身用4次就能拼成一个正方形？
【例 26】用下面的3个图形，拼成右边的大正方形．
【例 27】有6个完全相同的，你能将它们拼成下面的形状吗？
【例 28】(保良局亚洲区城市小学数学邀请赛)三种塑料板的型号如图：
(A) (B) (C)
已有A型板30块，要购买B、C两种型号板若干，拼成55
正方形10个，B型板每块价格5元，C型板每块价格为4元．请你考虑要各买多少块，使所花的总钱数尽可能少，那么购买B、C两种板要花多少元？
【例 29】试用图a中的8个相等的直角三角形，拼成图b中的空心正八边形和图c中的空心正八角星．
板块三图形的剪拼
【例 30】试将一个正方形分成相同的四块，然后用这四块分别拼成三角形、平行四边形和梯形．
【例 31】把两个小正方形剪开以后拼成一个大正方形．
【例 32】将下图分成4个形状、大小都相同的图形，然后拼成一个正方形．
【例 33】试将一个49
的长方形分割成两个大小相等、形状相同的图形，然后拼成一个正方形．
【例 34】将下图分成两块，然后拼成一个正方形．
【例 35】将图1分成4个形状、大小都相同的图形，然后拼成一个正方形．
图1图2图3
【例 36】小龙的妈妈在街上卖边角布料的地摊上，买回了一块形状是等腰直角三角形的绸布，想用它来做长方形的窗帘，为了不把布剪的太碎，裁剪的块数就要尽可能的少，请问小龙的妈妈应该怎样剪拼呢？
【例 37】试将任意一个三角形分成三块，然后拼成一个长方形．
【例 38】把一个正方形分成8块，再把它们拼成一个正方形和一个长方形，使这个正方形和长方形的面积相等．
【例 39】有一块长8米、宽3米的长方形地毯，现在要把它移到长6米、宽4米的新房间里．请找出一种剪裁方法，使剪后的各块拼合后正好能铺满房间的地面，为了使剪后的地毯尽量完整，就要使剪裁的块数尽可能地少，应怎样剪拼？
【例 40】如何把一个长20厘米、宽12厘米的长方形切成两块，拼成一个长16厘米、宽15厘米的新长方形．
→
【例 41】长方形长24厘米，宽15厘米．把它剪成两块，使它们拼成一个长20厘米，宽18厘米的长方形．
4
4 4
4 3
43
3
4
3
3
24
15
【例 42】如下图长方形的长、宽分别为120厘米、90厘米，正中央开有小长方形孔，长为80厘米，宽为10厘米，要拼成面积为100平方厘米的正方形．问如何切分，能使划分的块数最少．
【例 43】把下图中两个图形中的某一个分成三块，最后都拼在一起，使它们成为一个正方形．
【例 44】如下图两个正方形的边长分别是a和b(a b
)，将边长为a的正方形切成四块大小、形状都相同的图形，与另一个正方形拼在一起组成一个正方形．
a
b b
a
【例 45】如下图所示，这是一张十字形纸片，它是由五个全等正方形组成，试沿一直线将它剪成两片，然后再沿另一直线将其中一片剪成两片，使得最后得到的三片拼成两个并列的正方形．
乙 ’
甲’
乙
甲。
