下载文档原格式
非线性规划非线性规划问题是比线性规划问题更一般的数学规划问题，它的目标函数或约束函数中至少含有一个非线性函数，非线性规划就是研究非线性规划问题的有关理论和方法的学科。
非线性规划是运筹学的一个重要分支，它在军事、经济、工程、管理以及最优设计等方面都有着广泛的应用。
本部分介绍无约束非线性规划和约束非线性规划的基本理论和方法。
第三章 无约束优化方法无约束非线性规划问题是指可行域是整个决策空间的非线性规划问题。
本章首先分析无约束非线性规划问题的一阶和二阶最优性条件，包括必要条件和充分条件，然后讨论一维搜索问题，最后介绍无约束优化的求解方法，包括最速下降法，Newton 法共轭梯度法和拟Newton 法等。
补充：最优性条件现在考虑无约束非线性规划问题)(min x xf (UNP)其中决策变量n R ∈x ，目标函数1:R R f n →。
我们先引进下降方向的概念，并研究其充分条件，由此建立(UNP)的一阶和二阶最优性条件。
补.1 下降方向定义补.1 设函数1:R R f n →，n R ∈x ，nR ∈s 是非零方向。
若存在δ>0，使()(f f λ+<x s x ，(0,)λδ∀∈则称s 是f 在x 处的下降方向。
注补.1 设*x 是(UNP)的局部最优解，则f 在*x 处不存在下降方向。
定理补.1 设)(x f 在x 处可微，nR ∈s 是非零方向。
若()Tf ∇x s <0，则s 是f 在x 处的下降方向。
证明：对任意的λ>0，因为)(x f 在x 处可微，故由)(x f 在x 处的一阶Taylor 展开式知，()()()()()[()()/]T T f f f o f f o λλλλλλ+=+∇+=+∇+x s x x s x x s (补.1)根据条件()Tf ∇x s <0和0()lim0o λλλ→=知，存在δ>0，使()()0T o f λλ∇+<x s ，(0,)λδ∀∈代入(补.1)并由λ>0得到，()(f f λ+<x s x ，(0,)λδ∀∈由此知s 是f 在x 处的下降方向。
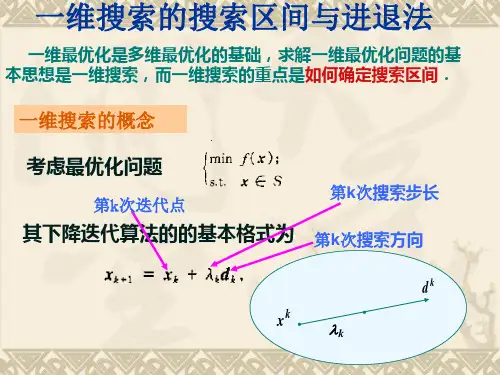
§4.3 一维搜索方法一维搜索问题：目标函数为单变量的非线性规划问题，即)(min max00t t t t ϕ≤≤≥ （4.3.1）对t 的取值为0≥t 的（4.3.1）称为一维搜索问题，即 )(min 0t t ϕ≥ ；对t 的取值为max 0t t ≤≤的（4.3.1）称为有效一维搜索问题，即 )(minmax0t t t ϕ≤≤。
1、0.618法（近似黄金分割法）单谷函数：称函数)(t ϕ是区间],[b a 上的单谷函数，若存在 ],[*b a t ∈，使得)(t ϕ在],[*t a 上严格递减，且在],[*b t 上严格递增。
区间],[b a 称为)(t ϕ的单谷区间。
求解一维搜索问题的方法：先设法给出一个搜索区间],[b a ，然后通过迭代不断缩小搜索区间，当区间的长度充分小是，可取这个区间中的任一点作为一个近似极小点。
考虑问题)(min t bt a ϕ≤≤ （4.3.2）其中],[b a 是)(t ϕ的单谷区间， 下面将通过迭代不断缩小搜索区间， 获得)(t ϕ的唯一极小点 *t 的近似解。
在],[b a 内任取两点 21,t t ，设 21t t <，由于)(t ϕ是区间],[b a 上的单谷函数，所以有<1> 若)()(21t t ϕϕ≤，则 ],[2*t a t ∈；<2> 若)()(21t t ϕϕ≥，则 ],[1*b t t ∈。
证<1>：若],[2*t a t ∉，则 2*t t >，所以*21t t t a <<<，因为)(t ϕ在],[*t a 上严格递减，所以)()(21t t ϕϕ>，矛盾。
同理可证 <2>。
通过比较)(1t ϕ和)(2t ϕ的大小，可将搜索区间缩小为],[2t a 或],[1b t 。
不妨设为],[2t a ，则在],[2t a 只需另找一个点 2t '，比较 1t 和2t '的目标函数值，又可以进一步缩小搜索区间。
机械优化设计课后答案【篇一：机械优化设计第5章习题参考答案】?4000.333?时， f(x*)??cjxj??5.567。
t第2题答案：x??2024840 0?，z??428。
*t第3题提示：求解方法可参考第四节中的应用实例。
第4题提示：如果设x1、x2、x3、x4、x5分别以Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五种下料方式所用钢材的件数，则此问题的数学模型是：求一组xj(j?1,2,?,5)的值，满足下列限制条件x1?2x2 ?x4 ?100?2x3?2x4?x5 ?100???3x1?x2?2x3 ?3x5?100?xj?0 (j?1,2,?,5)??使总的尾料z?0.1x2?0.2x3?0.3x4?0.8x5 达到最小。
【篇二：《机械优化设计》复习题答案】xt>一、填空题1、用最速下降法求f(x)=100(x2- x12) 2+(1- x1) 2的最优解时，设x（0）＝[-0.5,0.5]t，第一步迭代的搜索方向为 [-47,-50]t。
2、机械优化设计采用数学规划法，其核心一是，二是。
3、当优化问题是的情况下，任何局部最优解就是全域最优解。
4、应用进退法来确定搜索区间时，最后得到的三点，即为搜索区间的始点、中间点和终点，它们的函数值形成高－低－高趋势。
5、包含n个设计变量的优化问题，称为维优化问题。
6、函数 1txhx?btx?c的梯度为。
28模型的基本要素。
9、对于无约束二元函数f(x1,x2)，若在x0(x10,x20)点处取得极小值，其必要条件是10约束函数梯度的非负线性组合。
11、用黄金分割法求一元函数f(x)?x2?10x?36的极小点，初始搜索区间[a,b]?[?10,10]，经第一次区间消去后得到的新区间为12、优化设计问题的数学模型的基本要素有、。
?1?h13、牛顿法的搜索方向dkkgk，其计算量且要求初始点在极小点置。
14、将函数f(x)=x12+x22-x1x2-10x1-4x2+60表示成1txhx?btx?c 的形式215、存在矩阵h，向量 d1，向量 d2，当满足t d1和向量 d2是关于h共轭。
第5章 一维搜索§5.1 最优化算法的简单介绍1．算法概念在解非线性规划时，所用的计算方法，最常见的是迭代下降算法． 迭代：从一点)(k x 出发，按照某种规则A 求出后继点)1(+k x．用1+k 代替k ，重复以上过程，产生点列}{)(k x。
规则A 是在某个空间X 中点到点的映射，即对每一个X xk ∈)(，有点X xA xk k ∈=+)()()1(．更一般地，把A 定义为点到集的映射，即对每个点X x k ∈)(，经A 作用，产生一个点集X xA k ⊂)()(.任意选取一个点)()()1(k k xA x∈+，作为)(k x的后继点．定义1: 算法A 是定义在空间X 上的点到集映射，即对每一个点X x ∈，给定－个子集X x A ⊂)(.例1 考虑线性规划：1s.t. min 2≥x x最优解1=x ．设计一个算法A 求出这个最优解．⎪⎪⎩⎪⎪⎨⎧<⎥⎦⎤⎢⎣⎡+≥⎥⎦⎤⎢⎣⎡+=1 ,1 ),1(211 ,)1(21 ,1x x x x A 从一点出发，经A 作用得到一个闭区间.从此区间中任取一点作为后继点，得到一个点列.在一定条件下，该点列收敛于问题的解．利用算法A 可以产生不同的点列，如以3=x 为起点可产生点列:{} ,5/4 ,3/2 ,2 ,3其聚点是问题的最优解．在许多情况下，要使算法产生的点列收敛于全局最优解是比较困难的．因此，一般把满足某些条件的点集定义为解集合.当迭代点属于这个集合时，就停止迭代．无约束最优化问题可以定义解集合为}0)(|{=∇=Ωx f x约束最优化问题可以定义解集合为}T -K 为|{点x x =Ω2. 算法收敛问题设Ω为解集合，X X A →:是一个算法，集合X Y ⊂.若以任一初点Y x∈)1(开始，算法产生的序列其任一收敛子序列的极限属于Ω，则称算法映射A 在Y 上收敛．收敛速率: 定义2: 设序列}{)(k γ收敛于*γ，定义满足∞<=--≤+∞→βγγγγpk k k *)(*)1(lim的非负数p 的上确界为序列}{)(k γ的收敛级．若序列的收敛级为p ，就称序列是p 级收敛的．若1=p 且1<β，则称序列是以收敛比β 线性收敛的． 若1>p 或者1=p 且0=β，则称序列是超线性收敛的． 例2 序列{}10 ,<<a a k.0→ka 1lim1<=+∞→a aakk k序列{}ka以收敛比a 线性收敛于零．例3 序列{}10 ,2<<a ak02→ka[]1lim2221=+∞→kk a ak序列{}ka 2是2 级收敛的．注1：收敛级取决于当∞→k 时该序列所具有的性质，它反映了序列收敛的快慢． 收敛级p 越大，序列收敛得越快．当收敛级p 相同时，收敛比β越小，序列收敛得越快。
§5.2 一维搜索基本概念5.2.1 基本概念在许多迭代下降算法中，得到点)(k x 后，需要按某种规则确定一个方向)(k d，再从)(k x出发，沿方向)(k d在直线（或射线）L 上求目标函数的极小点，从而得后继点)1(+k x ．求目标函数在直线上的极小点，称为一维搜索，或称为线搜索．一维搜索可归结为单变量函数的极小化问题．求目标函数)(x f 在直线L 上极小点转化为求一元函数)()()()(k k dxf λλφ+=的极小点．一维搜索大体可分成两类：试探法： 按某种方式找试探点．通过一系列试探点来确定极小点．函数逼近法，或插值法：用某种较简单的曲线逼近本来的函数曲线，通过求逼近函数的极小点来估计目标函数的极小点．这两类方法一般只能求得极小点的近似值，称为非精确一维搜索．5.2.2 搜索区间及其确定方法一维搜索需要事先给定一个包含极小点的区间，此区间称为搜索区间。
搜索区间确定方法：进退法．进退法是一种试探法：从一点出发，按一定的步长，试图确定出函数值呈现“高-低-高”的三点。
一个方向不成功，就退回来．再沿相反方向寻找．进退法的计算步骤： (l)给定初点1)0(R x∈，初始步长00>h ．置0h h =，)0()1(xx=，计算)()1(xf ，并置0=k .(2)令h xx+=)1()4(，计算)()4(xf ，置1:+=k k .(3)若)()()1()4(xf x f <，则转步骤（4）；否则，转步骤（5）． (4)令)1()2(x x=, )4()1(xx=, )()()1()2(xf xf =, )()()4()1(xf xf =，置02:h h =，转步骤（2）.(5) 若1=k ，则转步骤（6）；否则，转步骤（7）. (6) 置h h -=:, )4()2(xx =，)()()4()2(xf x f =，转步骤（2）.(7) 令)2()3(xx=,)1()2(xx=，)4()1(x x=，停止计算．得到含有极小点的区间],[)3()1(xx 或者],[)1()3(xx ．注2：实际应用中，为了获得合适的0h ，有时需要做多次试探才能成功．5.2.3 单峰函数及其性质定义3: 设f 是定义在闭区间],[b a 上的一元实函数, x 是f 在],[b a 上的极小点，并且对任意的],[,)2()1(b a x x ∈，)2()1(xx<，有当x x≤)2(时，)()()2()1(xf xf >，当)1(xx ≤时，)()()1()2(xf xf >，则称f 是在闭区间],[b a 上的单峰函数．单峰函数的性质：通过计算区间],[b a 内两个不同点处的函数值，就能确定一个包含极小点的子区间．定理1: 设f 是区间],[b a 上的单峰函数，],[,)2()1(b a xx ∈,且)2()1(xx <.如果)()()2()1(xf xf >，则对每一个],[)1(xa x ∈，有)()()2(xf x f >；如果)()()2()1(x f xf ≤，则对每一个],[)2(b x x ∈，有)()()1(xf x f >.根据定理1，只需选择两个试探点，就可将包含极小点的区间缩短．§5.3 0.618法和Fibonacci 法5.3.1 0.618法0.618 法（黄金分割法）适用于单峰函数．基本思想：通过取试探点使包含极小点的区间（不确定区间）不断缩短，当区间长度小到一定程度时，区间上各点的函数值均接近极小值，因此任意一点都可作为极小点的近似．试探点计算公式：设)(x f 在],[11b a 上单峰，极小点],[11b a x ∈.设进行第k 次迭代时，有],[k k b a x ∈．为缩短包含极小点的区间，取两个试探点],[,k k k k b a ∈μλ,并规定k k μλ<．)(382.0k k k k a b a -+=λ （1）)(618.0k k k k a b a -+=μ （2）计算步骤：（1）置初始区间],[11b a 及精度要求0>L ，计算试探点1λ和1μ，计算函数值)(1λf 和)(1μf ．计算公式：)(382.01111a b a -+=λ )(618.01111a b a -+=μ令1=k .（2）若L a b k k <-，则停止计算．否则，当)()(k k f f μλ>时，转步骤（3）；当)()(k k f f μλ≤时，转步骤（4）.（3）置k k a λ=+1，k k b b =+1，k k μλ=+1, )(618.01111++++-+=k k k k a b a μ 计算函数值)(1+k f μ，转步骤（5）.（4）置k k a a =+1，k k b μ=+1，k k λμ=+1, )(382.01111++++-+=k k k k a b a λ 计算函数值)(1+k f λ，转步骤（5）.（5）置1:+=k k ，返回步骤（2）.例4：解下列问题：12)(min 2--=x x x f 。
初始区间]1 ,1[],[11-=b a ，精度16.0=L .kk a k b k λ k μ )(k f λ )(k f μ1 -1 1 -0.236 0.236 -0.653 -1.1252 -0.236 1 0.236 0.528 -1.125 0.9703 -0.236 0.528 0.056 0.236 -1.050 -1.1254 0.056 0.528 0.236 0.348 -1.125 -1.106 5 0.056 0.348 0.168 0.236 -1.112 -1.125 6 0.168 0.348 0.236 0.279 -1.125 -1.123 70.1680.279经6次迭代达到L a b <=-111.077,极小点]279.0,168.0[∈x .该问题的最优解25.0*=x ．可取23.02/)279.0168.0(=+=x 作为近似解．5.3.2 Fibonacci 法Fibonacci 法与0.618法类似，也是用于单峰函数. Fibonacci 法与0.618法的主要区别：（1）区间长度缩短比率不是常数，而是由Fibonacci 数确定． （2）需要事先知道计算函数值的次数. 定义4：设有数列}{k F ，满足条件：（1）110==F F ；（2）),2,1( 11 =+=-+k F F F k k k 则称}{k F 为Fibonacci 数列．k0 1 2 3 4 5 6 7 8 9 ⋯ k F11235813213455⋯Fibonacci 法在迭代中计算试探点的公式：1,,1 ),(11-=-+=+---n k a b F F a k k k n k n k k λ (3)1,,1 ),(1-=-+=+--n k a b F F a k k k n k n k k μ (4)n 是计算函数值的次数.利用（3）式和（4）式计算试探点时，第k 次迭代区间长度的缩短比率恰为1/+--k n k n F F . 给定初始区间长度11a b -及精度要求L ，可求出计算函数值的次数n （不包括初始区间端点函数值的计算）．由下式La b F n 11-≥求出Fibonacci 数n F ，根据n F 确定计算函数值的次数n .Fibonacci 法与0.618 法的关系: (1)0.618法可作为Fibonacci 法极限形式:618.0lim1≈-∞→nn n F F(2)Fibonacci 法精度高于0.618 法．在计算函数值次数相同条件下，0.618法的最终区间大约比使用Fibonacci 法长17%．(3)Fibonacci 法缺点是要事先知道计算函数值次数．0.618 法不需要事先知道计算次数，且收敛速率与Fibonacci 法比较接近.在解决实际问题时，一般采用0.618法．§5.4 插值法(二次)5.4.1 牛顿法(一点二次插值法)基本思想：在极小点附近用二阶Taylor 多项式近似目标函数)(x f ，进而求出极小点的估计值．考虑问题1),(min R x x f ∈ (5)令 2)()()()(')())(("21))(()()(k k k k k xx xf x x x f xf x -+-+=ϕ又令 0))((")()()()()(''=-+=k k k xx xf xf x ϕ得到)(x φ的驻点，记作)1(+k x，则)(")(')()()()1(k k k k xf x f xx-=+ （6）在点)(k x 附近，)()(x x f ϕ≈，因此可用函数)(x ϕ的极小点作为目标函数)(x f 极小点的估计．如果)(k x 是)(x f 极小点的一个估计，那么利用（6）式可以得到极小点的一个进一步的估计.利用迭代公式（6）可以得到一个序列}{)(k x．可以证明，在一定条件下，这个序列收敛于问题（5）的最优解，而且是2级收敛． 牛顿法的计算步骤： (1)给定初点)0(x ，允许误差0>ε，置0=k .(2)若ε<|)('|)(k x f ，则停止迭代，得到点)(k x.(3)计算点)1(+k x,)(")(')()()()1(k k k k xf x f xx-=+,置1:+=k k ，转步骤(2).注3：运用牛顿法时，如果初始点靠近极小点，则可能很快收敛；如果远离极小点，迭代产生的点列可能不收敛于极小点．5.4.2 割线法(二点二次插值法)基本思想：用割线逼近目标函数的导函数的曲线)('x f y =，把割线的零点作为目标函数的驻点的估计.迭代公式：)(')(')(')()1()()1()()()1(k k k k k k k xf x f xf xx xx--+---=得到序列}{)(k x．可以证明，在一定的条件下，这个序列收敛于解（收敛级为1.618）．注4：与牛顿法相比，收敛速率较慢，但不需要计算二阶导数．注5：缺点与牛顿法类似，都不具有全局收敛性，如果初点选择得不好，可能不收敛．5.4.3 抛物线法(三点二次插值法)基本思想：在极小点附近，用二次三项式)(x ϕ逼近目标函数)(x f ，令)(x ϕ与)(x f 在三点)3()2()1(xxx<<处有相同的函数值，并假设)()()2()1(x f xf >，)()()3()2(xf xf <.令 2)(cx bx a x ++=ϕ 又令)()()1(2)1()1()1(x f cx bxa x=++=ϕ （7） )()()2(2)2()2()2(x f cx bx a x =++=ϕ （8） )()()3(2)3()3()3(xf cxbxa x=++=ϕ （9）解方程组（7）-(9)，求二次逼近函数)(x ϕ的系数b 和c ．为书写方便，记)()()1(2)3(2)2(1x f x x B -= )()()1()3()2(1x f xxC -= )()()2(2)1(2)3(2x f x x B -= )()()2()1()3(2xf xx C -=)()()3(2)2(2)1(3xf xxB -= )()()3()2()1(3xf xxC -=))()(()1()3()3()2()2()1(xxxx xxD ---=由方程（7）-(9)得到D B B B b /)(321++= (10) D C C C c /)(321++-= (11))(x ϕ的极小点对应的驻点为cb x 2-=.把驻点x 记作)(k x ，则)(2321321)(C C C B B B xk ++++=（12）把)(k x作为)(x f 的极小点的一个估计．再从)1(x ，)2(x，)3(x，)(k x中选择目标函数值最小的点及其左、右两点，给予相应的上标，代入（12）式，求出极小点的新的估计值)1( k x.以此类推，产生点列}{)(k x.注6：在一定条件下，这个点列收敛于问题的解，其收敛级为1. 3．。
