扭转应力计算
- 格式:ppt
- 大小:5.91 MB
- 文档页数:30

长方形扭转切应力公式
摘要:
1.长方形扭转切应力的概念
2.长方形扭转切应力公式的推导
3.公式的应用和意义
4.总结
正文:
长方形扭转切应力公式是机械工程领域中一个重要的公式,它用于描述扭转过程中长方形截面上产生的切应力分布。
下面我们将详细介绍长方形扭转切应力的概念、公式的推导、应用和意义。
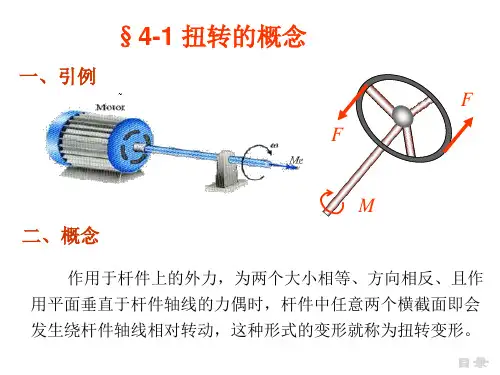
一、长方形扭转切应力的概念
长方形扭转切应力是指在长方形截面上,由于扭转作用而产生的剪切应力。
当长方形截面绕其中心轴线扭转时,截面上的应力分布呈非均匀状态。
在距离中心轴线越远的地方,切应力越大。
长方形扭转切应力公式可以帮助我们更好地了解这种应力分布规律。
二、长方形扭转切应力公式的推导
长方形扭转切应力公式为:
τ= ω × (t/r)
其中:
τ——切应力(单位:帕);
ω——角速度(单位:弧度/秒);
t——截面厚度(单位:米);
r——距离中心轴线的半径(单位:米)。
通过对该公式的推导,我们可以发现长方形扭转切应力与距离中心轴线的半径成反比,与角速度成正比。
这意味着,在扭转过程中,距离中心轴线越远的地方,切应力越大;角速度越高,切应力也越大。
三、公式的应用和意义
长方形扭转切应力公式在工程领域具有广泛的应用。
通过计算长方形截面上的切应力,我们可以了解零件在扭转过程中的应力分布状况,从而为零件的设计和强度分析提供依据。
此外,该公式还可以用于评估材料的抗扭性能,为材料的选择提供参考。
四、总结
长方形扭转切应力公式是一个重要的力学公式,它描述了扭转过程中长方形截面上切应力的分布规律。

04、基本知识 怎样推导轴向拉压和扭转的应力公式、变形公式(供参考)同学们学习下面内容后,一定要向老师回信(****************),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1 * 问题的提出 ........................................................................................................................... 1 2 下面就用统一的步骤,研究轴向拉压和扭转的应力公式和变形公式。
........................... 2 3 1.1 轴向拉压杆的应力公式推导 ............................................................................................ 2 4 1.2 轴向拉压杆的变形公式推导 ............................................................................................ 4 5 1.3 轴向拉压杆应力公式和变形公式的简要推导 ................................................................ 4 6 1.4 轴向拉压杆的强度条件、刚度条件的建立 .................................................................... 4 7 2.1 扭转轴的应力公式推导 .................................................................................................... 5 8 2.2 扭转轴的变形公式推导 .................................................................................................... 7 9 2.3 扭转轴应力公式和变形公式的简要推导 ........................................................................ 7 10 2.4 扭转的强度条件、刚度条件的建立 ............................................................................ 8 11 3. 轴向拉压、扭转、梁的弯曲剪切,应力公式和变形公式推导汇总表 .. (9)1* 问题的提出在材料力学里,分析杆件的强度和刚度是十分重要的,它们是材料力学的核心内容。




工程力学中的扭转力学分析扭转力学是工程力学中的一个重要分支,研究物体在受到扭转力作用时产生的变形和应力分布。
在工程实践中,扭转力学的应用非常广泛,特别是在建筑、机械、航空航天等领域。
一、引言扭转力学研究的对象是物体在受到外界扭转力矩作用下的行为。
扭转力学涉及到以下几个关键概念:扭转角、扭转应变、扭转应力等。
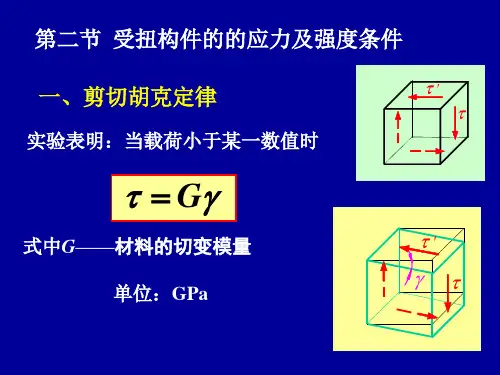
二、基本原理与公式推导在扭转力学分析中,我们需要借助一些基本原理和公式来描述扭转的行为。
其中,最基本的原理是胡克定律,它表明物体在弹性阶段的扭转行为与受到的扭转力矩成正比。
公式推导过程如下:(1)胡克定律:θ = T / (G * J)其中,θ表示物体的扭转角,T表示扭转力矩,G表示切变模量,J 表示抗扭转性能指标。
(2)扭转应变:γ = θ * r / L其中,γ表示扭转应变,r表示被扭转物体的半径,L表示物体的长度。
(3)扭转应力:τ = G * γ其中,τ表示扭转应力。
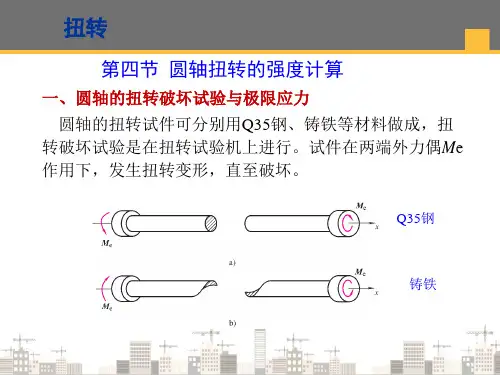
三、典型扭转问题的分析在工程实践中,我们常常遇到一些典型的扭转问题,如轴材料的扭转分析、螺旋桨的扭转分析等。
下面以轴材料的扭转分析为例,介绍典型问题的求解过程:(1)问题描述:一根长度为L,半径为r的均质轴材料,在受到扭转力矩T作用下,求解轴的扭转角和轴的最大扭转应力。
(2)解答过程:首先,根据胡克定律可以得到轴的扭转角:θ = T / (G * J),其中G 为轴材料的切变模量,J为轴的惯性矩。
然后,根据扭转应变公式可以得到轴的扭转应变:γ = θ * r / L。
最后,根据扭转应力公式可以得到轴的扭转应力:τ = G * γ。
四、工程应用示例扭转力学在工程中的应用非常广泛,例如在机械工程中,通过对扭转力学的分析,我们可以设计出更加合理的轴、齿轮等零件;在建筑工程中,我们可以通过扭转力学的分析,预测结构在风荷载下的变形和损伤等。
五、总结扭转力学是工程力学中的重要分支,研究物体在受到扭转力作用下的变形和应力分布。
本文通过引言、基本原理与公式推导、典型扭转问题的分析以及工程应用示例的介绍,对扭转力学的相关内容进行了阐述。