双曲线的简单几何性质人教A版高中数学选修第一册优质课件

离心率 e=c∈(1,+∞)
a
渐近线 y=±bax
y=±ba x
-4-
2.2.2 双曲线的简单几何性质
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
-5-
2.2.2 双曲线的简单几何性质
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
-21-
2.2.2 双曲线的简单几何性质
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
探究一
探究二
探究三
(2)依题意得 e=ac = 5,所以ac22=5,
即a
2 +b a2
2
=5,解得ba =2.
若双曲线焦点在 x 轴上,则其渐近线方程为 y=±bax,即
2.2.2 双曲线的简单几何性质
-1-
2.2.2 双曲线的简单几何性质
首页
X D 新知导学 INZHIDAOXUE
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
学习目标
思维脉络
1.掌握双曲线的范围、对称性、 双曲线的几何性质
顶点、渐近线、离心率等几何性 范围
质. 2.能够利用双曲线的标准方程画 出双曲线的图形.
答疑解惑
AYIJIEHUO
D当堂检测 ANGTANGJIANCE
探究三双曲线的渐近线与离心率问题
【例 3】(1)过双曲线的一个焦点 F2 作垂直于实轴的弦 PQ,F1 是另一焦点,若∠PF1Q=π2,则双曲线的离心率等于( )

(2)由双曲线的渐近线方程为
2
− 4 =1.
1
2 2
y=±2x,可设双曲线方程为 2 -y =λ(λ≠0).
的形式,
在a≠0的情况下可得:
(1)Δ>0时,直线与双曲线有两个不同的公共点;
(2)Δ=0时,直线与双曲线只有一个公共点;
(3)Δ<0时,直线与双曲线没有公共点.
此外,当直线平行于双曲线的渐近线时,直线与双曲线只有一个公共点,故
直线与双曲线只有一个公共点是直线与双曲线相切的必要不充分条件.
重难探究·能力素养速提升

9 12
- =
2 2
42
∴所求的双曲线方程为
9
=
25
,
9
解得
1,
2
− =1.
4
2
=
9
,
4
2 = 4.
3 );
(3)已知双曲线的渐近线方程为2x±3y=0,且两顶点间的距离是6.
2
2
4
9
解 设双曲线方程为 4x -9y =λ(λ≠0),即 − =1(λ≠0),由题意得 a=3.
4
−
6
2 =1.

2
=
4
,
3
2 = 3.
2
− =1.
3
5
(2)已知双曲线的焦点在x轴上,离心率为 3 ,且经过点M(-3,2
解
2
设所求双曲线方程为 2

2
5

∵e= ,∴e2= 2
3


∴

=
=
−
2
2 =1(a>0,b>0).

1
=1
答案:B
-5-
2.2.2
双曲线的简单 几何性质
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
1
2
【做一做 1-2】 A.y=± ������B. ������ = C.y=± =
2 3 3 ������D. ������ 2
> 1, 离心率越大, =
������ 2 -1就越大,双
曲线“张口”越大.
-4-
2.2.2
双曲线的简单 几何性质
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
1
2
【做一做 1-1】 中心在原点,实轴长为 10,虚轴长为 6 的双曲线 的标准方程是( )
2.2.2
双曲线的简单几何性质
-1-
2.2.2
双曲线的简单 几何性质
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
1.了解双曲线的范围、对称性、顶点、离心率、渐近线等几何 性质. 2.能解决一些简单的双曲线问题.
3 5 . 5 2 5
答案:2 5 4 ������ = ±
2 5 ������ 5
3 5 5
-8-
2.2.2
双曲线的简单 几何性质

双曲线的渐近线方程？

=−


2 2
对于双曲线 2 − 2 = 1和它的渐近线 = ± ，




=

y
(, )
将方程中的与互换，就得到双曲线


即 = ± ．
− 2 = 1 的渐近线方程 = ± ，
2



2
2
(−, )
规律方法：由双曲线方程求渐近线方程，只需把1变成0,

∴当 ∈
2
+
2


2
> 1.
=

(1, +∞)时，

∈

1+

2

(0, +∞),且增大, 也增大

b
离心率越大, 渐近线y x的斜率越大 双曲线的“张口”越大
a
新知探究
方程
2 2
− 2=1
2


2 2
− 2=1
2


图像
范围
对称性
≤ −，或 ≥
≤ −，或 ≥
≤ −，或 ≥
关于轴、轴、原点对称
（ − ，），（，） （， − ），（，）
a
b
y x
y x
渐近线
b
a

= >
离心率

顶点
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
2
2
x
y
2
2
2
2
2
2
(1) x 8 y 32; (2) 9 x y 81; (3) x y 4; (4)

如图,某工厂有一双曲线型自然通风塔,其外形是双曲线 的一部分绕其虚轴旋转所成的曲面,已知该塔最小半径为 12 米,下口半径为 25 米,下口半径到最小圆面距离为 45 米,整个 通风塔高为 55 米.问在建造该塔的过程中,上口半径大约应该建多少米?
预学 1:双曲线的几何性质
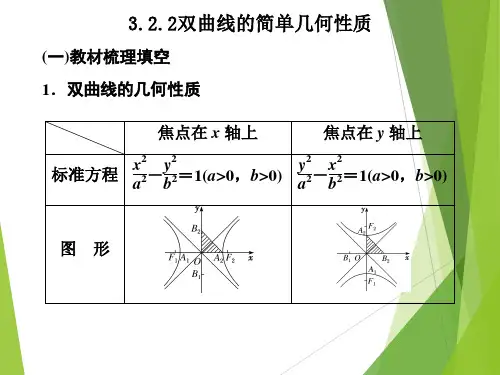
标准方程
x2 y2
- =1(a>0,b>0) a2 b2
������ 2 1 + ������ 2 .故当
也越大,所以 e 反
映了双曲线开口的大小,即双曲线的离心率越大,它的开口就越大.
预学 4:实轴和虚轴长相等的双曲线叫作等轴双曲线,它的渐 近线方程为 y=±x,离心率 e= 2.
1.双曲线 9y -16x =144 的渐近线方程为(
4 A.y= x 3 4 B.x= y 3 4
第 5 课时
双曲线的简单几何性质
知识 目标 能力 目标 素养 目标
1.掌握双曲线的简单几何性质 2.给出双曲线的方程能够得到其几何性质,反之由双曲线的几何 性质也能得到该双曲线的方程 通过学习双曲线简单的几何性质培养学生灵活应对、适当转化的 能力;利用双曲线的性质求解双曲线的标准方程、渐近线、离心 率培养学生灵活应用知识探究问题和解决问题的能力 通过学习双曲线的简单几何性质结合双曲线的图象培养数学抽象 素养,通过求解双曲线的标准方程、渐近线、离心率培养数学运 算素养
时,焦点在 y 轴上.
预学 2:椭圆与双曲线的几何性质的异同 (1)椭圆与双曲线的离心率都为 e=������ .椭圆的离心率 e∈(0,1),双曲 线的离心率 e∈(1,+∞). (2)椭圆中长轴长大于短轴长,即 2a>2b;双曲线中虚轴长 2b 和实轴 长 2a 大小关系不确定. (3)焦点在坐标轴,中心为原点时,椭圆与双曲线的焦点坐标形式一 2 2 2 2 2 2 致,即(±c,0)或(0,±c).在椭圆中,c =a -b ,在双曲线中,c =a +b . (4)椭圆无渐近线,双曲线有渐近线.

(3)设所求双曲线方程为2������42 − 4������02=λ(λ≠0),过点 M(3 2,
λ=1284
−
10 40
=
12.
故双曲线方程为������2
24
−
������2 40
=
12,即1������22
−
2������02=1.
10),有
一 二三四
知识精要
典题例解
迁移应用
(4)方法一:首先确定所求双曲线的标准类型,可在图中判断一下
一 二三四
知识精要
典题例解
迁移应用
若双曲线的焦点在 y 轴上,设������������22 − ������������22=1(a>0,b>0).
同理,有������������22
=
5 4
,
2 ������2
−
���9���2=1,a2+b2=c2.
解得 b2=-127(舍去).
∴双曲线的焦点只能在 x 轴上,故所求双曲线方程为 x2-4y2=1.
(2)若是根据双曲线的渐近线求标准方程,设法为:
若双曲线的渐近线方程为 y=±������������x,则双曲线方程可表示为
������2 ������2
−
������������22=λ(λ≠0).
一 二三四
知识精要
典题例解
迁移应用
【例 2】 根据以下条件,求双曲线的标准方程.
(1)虚轴长为 12,离心率为54;
目标导航
预习导引
12
顶点
性
轴长
质
离心率
渐近线
A1(-a,0),A2(a,0)
实轴长=2a,虚轴长=2b e=ac ∈(1,+∞)

第二章 圆锥曲线与方程
2.1.5 双曲线的简单几何性质
1．掌握双曲线的简单的几何性质， 2．能灵活的运用性质解决问题．
1.双曲线的定义是怎样的？ 2.双曲线的标准方程是怎样的？
x2 a2
y2 b2
1
y2 a2
x2 b2
1
知识导学
双曲线的几何性质 1.双曲线的几何性质
t;0，b>0)
9k k
9k k
把(3,9 2)代入②，得 k＝9，
故所求双曲线方程为 y2 －x2＝1. 81 9
(2)方法一 首先确定所求双曲线的标准类 型，可在图中判断一下点 P(2，－1)在渐近线 y＝－3x 的上方还是下方．如图所示，x＝2 与 y＝－3x 交点为 Q(2，－6)，P(2，－1)在 Q(2，－6)的上方，所以焦点在 x 轴上．
∴所求的距离为 d 3 5 3 ． 32 42
4．（已知双曲线 x2 ky2 1 的一个焦点是 ( 5, 0) ，则其渐近线的方程
为（ ）
A．
y
1 4
x
【答案】D
B． y 4x
C．
y
1 2
x
D． y 2x
【解析】双曲线 x2 y2 1 的一个焦点是 ( 5, 0) ， 1 k
∴1 1 5 ，即 k 1 ， ∴渐近线的方程为 y 2x ．
因此顶点为 A1(－3,0)，A2(3,0)，
焦点坐标 F1(－ 13，0)，F2( 13，0)， 实轴长是 2a＝6，虚轴长是 2b＝4，离心率 e＝c＝ 13，
a3 渐近线方程 y＝±bx＝±2x.
a3
问题探究
探究2：与双曲线离心率相关的问题
例
2、已知 F1
，F2

[典例 4] 已知双曲线 3x2－y2＝3，过点 P(2,1)作一直线交 双曲线于 A，B 两点，且 P 为 AB 的中点.
(1)求直线 AB 的方程； (2)求弦 AB 的长．
[解] (1)法一：由题意知直线 AB 的斜率存在， 设直线 AB 的方程为 y－1＝k(x－2)， 联立双曲线方程 3x2－y2＝3，得 (3－k2)x2＋2k(2k－1)x－4k2＋4k－4＝0. 设 A(x1，y1)，B(x2，y2)， 则 x1＋x2＝－2k32－k－k2 1＝4，解得 k＝6. 所以直线 AB 的方程为 y－1＝6(x－2)， 即 6x－y－11＝0.
[方法技巧] 求双曲线的标准方程的方法与技巧
(1)根据双曲线的某些几何性质求双曲线方程，一般用待定 系数法转化为解方程(组)，但要注意焦点的位置，从而正确选择 方程的形式．
(2)巧设双曲线方程的六种方法与技巧： ①焦点在 x 轴上的双曲线的标准方程可设为xa22－by22＝1(a>0， b>0)； ②焦点在 y 轴上的双曲线的标准方程可设为ay22－xb22＝1(a>0， b>0)；
(二)基本知能小试
1．判断正误
(1)双曲线的离心率越大，双曲线的开口越开阔． ( )
(2)以 y＝±2x 为渐近线的双曲线有 2 条．
()
(3)
双
曲
线
x2 b2
－
y2 a2
＝
1(a>0
，
b>0)
的
离
心
率
e
＝
c a
(其
中
c＝
a2＋b2)．
()
答案：(1)√ (2)× (3)×
2．双曲线1x62－y2＝1 的顶点坐标是

双曲线是否具有类似的性质呢?
一、双曲线的简单几何性质
yห้องสมุดไป่ตู้
Q B2 A1 N M
1.范围:
两直线x=±a的外侧
x2.对称性:
O
b A2 a
B1
关于x轴, y轴,原点对称
原点是双曲线的对称中心
x y - 2 =1 2 a b
2 2
对称中心叫双曲线的中心
一.双曲线的简单几何性质
y
Q B2 A1 N M
∴ 双曲线方程为
y x 4. 求与椭圆 1 有共同焦点，渐近线方程为 16 8
2
2
x 3y 0 的双曲线方程。
解： 椭圆的焦点在x轴上，且坐标为
F ， 0)，F （ ， 0） 1 (2 2 2 2 2

双曲线的焦点在x轴上，且c 2 2
3 双曲线的渐近线方程为 y x 3 b 3 ，而c 2 a 2 b 2 ， a 2 b 2 8 a 3 解出 a 2 6，b 2 2 x2 y2 双曲线方程为 1 6 2
• 例3：双曲线型冷却塔的外形，是双曲线 的一部分绕其虚轴旋转所成的曲面，它 的最小半径为12m，上口半径为13m，下 口半径25m，高为55m，试选择适当的坐 标系，求出此双曲线的方程。
• 例4：点M（x,y)到定点F（5，0） 的距离和它到定直线l:x=16/5 的距离的比是常数5/4，求点M 的轨迹。
b A2 a
B1
(2)直线的方程: y=±－ a x
x
渐渐接近但永不相交
x2 y 2 - 2 =1 2 a b
•
y
Q B2 A1 N M
5.离心率
(1)概念:焦距与实轴长之比

返
首
页
·
29
·
情
课
景
堂
导
小
学 探
法二：设所求双曲线方程为x92－1y62 ＝λ(λ≠0)，
·
结 提
新
素
知
养
合
将点(－3,2 3)代入得 λ＝14，
作
课
探 究
释
所以双曲线方程为x92－1y62 ＝14，即49x2－y42＝1.
时 分 层 作
疑
业
难
返 首 页
·
30
·
情
课
景
堂
导
小
学
结
探
1．由几何性质求双曲线标准方程的解题思路
[解]
方程 4x2－9y2＝－4 可化为标准方程y42－x2＝1，焦点在 y
·
提 素 养
9
合
作 探 究
轴上，这里 a2＝49，b2＝1，c2＝49＋1＝193.
课 时 分
层
释
作
疑 难
所以顶点坐标为0，23，0，－23.Biblioteka 业返 首 页·
21
·
情
课
景 导 学
焦点坐标为0，
313，0，－
313.
堂 小 结
学 ________.
·
结
探
提
新
素
知 合
5 [∵双曲线的标准方程为ax22－y92＝1(a>0)，
养
作
课
探 究
∴双曲线的渐近线方程为 y＝±3ax.
时 分 层
释
作
疑 难
又双曲线的一条渐近线方程为 y＝35x，∴a＝5.]