双曲线的简单几何性质总结归纳(人教版)

一．基本概念1 双曲线定义：①到两个定点F 1与F 2的距离之差的绝对值等于定长（＜|F 1F 2|）的点的轨迹（21212F F a PF PF <=-（为常数））这两个定点叫双曲线的焦点．②动点到一定点F 的距离与它到一条定直线l 的距离之比是常数e (e ＞1)时，这个动点的轨迹是双曲线这定点叫做双曲线的焦点，定直线l 叫做双曲线的准线 2、双曲线图像中线段的几何特征：⑴实轴长122A A a =，虚轴长2b,焦距122F F c = ⑵顶点到焦点的距离：11A F =22A F c a =-，12A F =21A F a c =+⑶顶点到准线的距离：21122 a A K A K a c ==-；21221 a A K A K a c ==+⑷焦点到准线的距离：2211221221 a a F K F K c F K F K c c c==-==+或 ⑸两准线间的距离: 2122a K K c=⑹21F PF ∆中结合定义a PF PF 221=-与余弦定理21cos PF F ∠，将有关线段1PF 、2PF 、21F F 和角结合起来，12212cot2PF F F PF S b ∆∠= ⑺离心率：121122121122PF PF A F A F c e PM PM A K A K a ======∈（1，+∞）⑻焦点到渐近线的距离：虚半轴长⑼通径的长是a b 22，焦准距2b c ，焦参数2b a（通径长的一半）其中222b a c +=a PF PF 221=-3 双曲线标准方程的两种形式：①22a x －22b y =1，c =22b a +，焦点是F 1（－c ，0），F 2（c ，0） ②22a y －22bx =1，c =22b a +，焦点是F 1（0，－c ）、F 2（0，c ） 4、双曲线的性质：22a x －22by =1（a ＞0，b ＞0）⑴范围：|x |≥a ，y ∈R⑵对称性：关于x 、y 轴均对称，关于原点中心对称 ⑶顶点：轴端点A 1（－a ，0），A 2（a ，0） ⑷渐近线：①若双曲线方程为12222=-b y a x 渐近线方程⇒=-02222b y a x x aby ±=②若渐近线方程为x a b y ±=0=±bya x 双曲线可设为λ=-2222b y a x③若双曲线与12222=-b y a x 有公共渐近线，可设为λ=-2222by a x（0>λ，焦点在x 轴上，0<λ，焦点在y 轴上）④特别地当⇔=时b a 离心率2=e 两渐近线互相垂直，分别为y=，此时双曲线为等轴双曲线，可设为λ=-22y x ；y =a b x ，y =－abx ⑸准线：l 1：x =－c a 2，l 2：x =c a 2，两准线之距为2122a K K c=⋅⑹焦半径：21()a PF e x ex a c =+=+，（点P 在双曲线的右支上x a ≥）；22()a PF e x ex a c=-=-，（点P 在双曲线的右支上x a ≥）；当焦点在y 轴上时，标准方程及相应性质（略）⑺与双曲线12222=-b y a x 共渐近线的双曲线系方程是λ=-2222by a x )0(≠λ⑻与双曲线12222=-by a x 共焦点的双曲线系方程是12222=--+k b y k a x ⑼双曲线上过焦点的弦，当弦的两端点在双曲线的同一支上时，过焦点且垂直于实轴的弦最短，当弦的两端点在双曲线的两支上时，以实轴长最短。

双曲线的简单几何性质【知识点1】双曲线22a x -22b y ＝1的简单几何性质(1)范围：｜x ｜≥a,y∈R.(2)对称性：双曲线的对称性与椭圆完全相同，关于x 轴、y 轴及原点中心对称.(3)顶点：两个顶点：A 1(-a,0),A 2(a,0)，两顶点间的线段为实轴长为2a ，虚轴长为2b ，且(4)＝1中的1(5)(6)e ＝2(7)注意：且λ（2）与椭圆2a +2b ＝1(a ＞b ＞0)共焦点的曲线系方程可表示为λ-2a -λ-2b ＝1(λ＜a 2,其中b 2-λ＞0时为椭圆，b 2＜λ＜a 2时为双曲线)（3）双曲线的第二定义：平面内到定点F(c,0)的距离和到定直线l :x ＝c a 2的距离之比等于常数e ＝a c(c ＞a ＞0)的点的轨迹是双曲线，定点是双曲线的焦点，定直线是双曲线的准线，焦准距(焦参数)p ＝c b 2，与椭圆相同.1、写出双曲线方程1254922-=-y x 的实轴长、虚轴的长，顶点坐标，离心率和渐近线方程2、已知双曲线的渐近线方程为x y 43±=，求双曲线的离心率3、求以032=±y x 为渐近线，且过点p （1,2）的双曲线标准方程4、已知双曲线的中心在原点，焦点在y 轴上，焦距为16，离心率为43，求双曲线的标准方程。

5、求与双曲线221169x y -=共渐近线，且经过()23,3A -点的双曲线的标准方及离心率．【知识点2】弦长与中点弦问题（1）．直线和圆锥曲线相交时的一般弦长问题：一般地，若斜率为k 的直线被圆锥曲线所截得的弦为AB ，A 、B 两点分别为A(x 1，y 1)、B(x 2，y 2)，则弦长]4))[(1(1212212122x x x x k x x k AB -++=-⋅+=]4)[()11(11212212122y y y y ky y k -+⋅+=-⋅+=,这里体现了解析几何“设而不求”的（2）设A(x 1；对于y 2【变1变4】7、过双曲线2212y x -=的右焦点F 作直线l 交双曲线于A,B 两点,若|AB|=4,这样的直线有几条？【题型2】双曲线离心率的求法一、根据离心率的范围，估算e ：即利用圆锥的离心率的范围来解题，有时可用椭圆的离心率e ∈()01，，双曲线的离心率e >1，抛物线的离心率e =1来解决。

疱丁巧解牛知识·巧学双曲线的几何性质1.双曲线的范围、对称性及顶点（1）双曲线在不等式x≥a 与x≤-a 所表示的区域内. 如果双曲线的焦点在y 轴上，则双曲线的范围是y≥a 与y≤-a.（2）双曲线关于每个坐标轴和原点都对称，这时，坐标轴是双曲线的对称轴，原点是双曲线的对称中心，双曲线的对称中心叫双曲线中心.判断曲线关于原点，关于x 轴、关于y 轴对称的依据：若把方程中的x 换成-x ，y 换成-y ，方程不变，则曲线关于原点对称；若把方程中的y 换成-x ，方程不变，则曲线关于x 轴对称；若把方程中的x 换成-y ，方程不变，则曲线关于y 轴对称.（3）双曲线和它的对称轴有两个交点A 1(-a,0)、A 2(a,0)，它们叫做双曲线的顶点.线段A 1A 2叫双曲线的实轴，它的长等于2a,a 叫做双曲线的实半轴长；线段B 1B 2叫双曲线的虚轴，它的长等于2b,b 叫做双曲线的虚半轴长.疑点突破 如果双曲线的中心不在原点，是不是还是对称图形？答案是肯定的，椭圆的对称性与选择的坐标系没有关系. 2.双曲线的渐近线及离心率（1）把两条直线y=±x ab 叫做双曲线的渐近线.与双曲线2222b y a x -=1共渐近线的双曲线系方程可表示为2222by a x -=λ(λ≠0且λ为待定常数)；与椭圆2222by a x +(a ＞b ＞0)共焦点的曲线系方程可表示为λλ---2222b y a x =1(λ＜a 2,其中b 2-λ＞0时为椭圆， b 2＜λ＜a 2时为双曲线）.（2）等轴双曲线：实轴和虚轴等长的双曲线叫做等轴双曲线. （3）双曲线的焦距与实轴长的比e=ac，叫双曲线的离心率. 深化升华 ①由c>a>0可得e>1；②双曲线的离心率越大，它的开口越阔.③焦半经:已知F 1(-c,0)、F 2(c,0))，点p(x 0,y 0)在双曲线2222by a x -=1的右支上时，|PF 1|=ex 0+a,|PF 2|=ex 0-a;P 在左支上时，则|PF 1|=-（ex 0+a ）,|PF 2|=-（ex 0-a ）.问题·探究问题1 学习双曲线的简单几何性质时应注意什么？探究:（1）由给定条件求双曲线的方程，常用待定系数法.首先是根据焦点位置设出方程的形式（含有参数），再由题设条件确定参数值，应特别注意： ①当焦点位置不确定时，方程可能有两种形式，应防止遗漏； ②已知渐近线的方程bx±ay=0，求双曲线方程，可设双曲线方程为b 2x 2-a 2y 2=λ（λ≠0），根据其他条件确定λ的值.若求得λ＞0，则焦点在x 轴上，若求得λ＜0，则焦点在y 轴上.（2）由已知双曲线的方程求基本量，注意首先应将方程化为标准形式，再计算，并要特别注意焦点位置，防止将焦点坐标和准线方程写错.问题2 给定了双曲线方程，就可求得确定的两条渐近线.但已知渐近线方程，是不是可以直接求出双曲线方程？探究:给定了双曲线方程，就可求得确定的两条渐近线.但已知渐近线方程只是限制了双曲线张口的大小，不能直接写出双曲线方程.但若已知渐近线方程是bya x ±=0，则可把双曲线方程表示为2222b y a x -=λ（λ≠0），再根据已知条件确定λ的值，求出双曲线的方程. 典题·热题例1 求以曲线2x 2+y 2-4x-10=0和y 2=2x-2的交点与原点的连线为渐近线，且实轴长为12的双曲线的标准方程．思路分析：先求出渐近线方程，确定出其斜率，结合已知条件确定所求双曲线方程中的字母系数．解：∵⎪⎩⎪⎨⎧==+2,-2x y 0,10-4x -y 2x 222∴⎩⎨⎧==2y 3,x 或⎩⎨⎧==-2.y 3,x∴渐近线方程为y=±x 32. 当焦点在x 轴上时，由32=a b 且a=6，得b=4． ∴所求双曲线方程为163622y y -=1. 当焦点在y 轴上时，由32=b a ，且a=6,得b=9． ∴所求双曲线方程为813622x y -=1. 方法归纳 （1）“定量”与“定位”是求双曲线标准方程的两个过程，解题过程中应准确把握. （2）为避免上述的“定位”讨论，可以用有相同渐近线的双曲线系方程去解．例2 求证:双曲线2222by a x -=1(a>0,b>0)上任何一点到两条渐近线的距离之积为定值.思路分析：可以在双曲线上任意找一点，把这点到两条渐近线的距离表示出来，化简即可看出.证明:设双曲线上任一点P(asecθ,btanθ),∵双曲线的两条渐近线方程为bx+ay=0和bx-ay=0, ∴点P 到直线bx+ay=0的距离d 1=2222|tan sec ||tan sec |ba ab ba ab ab ++=++θθθθ;点P 到直线bx-ay=0的距离d 2=2222|tan sec |tan sec ba ab ba ab ab +-=+-θθθθ.∴d 1·d 2=22222222222222|tan sec ||tan sec |tan sec |ba b a b a b a b a ab ba ab +=+-=+-=++θθθθθθ. ∴双曲线上任一点到两条渐近线的距离之积为定值.方法归纳 (1)所谓定值,是与P 点在曲线上的位置无关的,为了达到目标明确,可先通过特殊的情况,求出一个常数,猜想其定值.(2)双曲线2222b y a x -=1(a>0,b>0)的参数方程为⎩⎨⎧==θθtan ,sec b y a x (θ为参数),不作过高要求,在解题中灵活应用,类似于换元法解题,将可达到一元化的目的.例3 在双曲线131222x y -=1的一支上有三个点A （x 1，y 1）、B （x 2,6）、C(x 3,y 3)与焦点F （0,5）的距离成等差数列． (1)求y 1+y 3；(2)求证线段AC 的垂直平分线经过某个定点，并求出定点的坐标．思路分析：利用双曲线的第二定义解(1)，利用点差法结合(1)的结果证(2)． (1)解：依题意，得B 在双曲线上支上，故A 、B 、C 三点都在双曲线的上支，且上准线的方程为y=512． |AF|，|BF|，|CF|成等差数列，根据双曲线的第二定义，得)512(1)512(1)5126(231-+-=-y e y e e .故y 1+y 3=12． (2)证明:由点A 、C 在双曲线上，故113122121=-x y ,13122323x y -=1． 两式相减，得13))((12))((31313131x x x x y y y y -+--+=0．∴13)(13)(123131313131x x y y x x x x y y +=++=--． ∴AC 的垂直平分线的斜率为3113x x +-．又AC 的中点坐标为（231x x +,6），故AC 的垂直平分线方程为 y-6=)2(133131x x x x x +-+-.当x=0时，y=225，故AC 的垂直平分线过定点（0,225）． 误区警示 本题属定值问题，存在的问题是一方面对定值的概念和求法弄不清楚，摸不出头绪；论另一方面不会运用式子的变换和曲线的定义．方法归纳 关于定值问题，一般通过计算证明其值与曲线的点的位置无关，或与直线的斜率无关．为了证明的目的更明确，可通过特殊情况，求出一个常数，猜想出这个定值．不同的设法，可以得到不同的证法．例4 已知双曲线b y a x 222-=1（a ＞0，b ＞0）的右焦点为F ，右准线与一条渐近线交于点A ，△OAF 的面积为22a （O 为原点），则两条渐近线的夹角为（ ）A ．30°B ．45°C ．60°D ．90°思路分析：可以利用△OAF 的面积为22a ，求出a 点的坐标，判断a 、b 的关系可以求出两条渐近线的夹角.2222b y a x -=1（a>0,b>0）的焦点F （c,0）,右准线方程x=c a 2,渐近线y=x a b ，则A(c ab c a ,2),所以S △OAF =21×c×22a c ab =.求得a=b,所以双曲线为等轴双曲线,则两条渐近线夹角为90°.答案：D。

四、双曲线一、双曲线及其简单几何性质（一）双曲线的定义：平面内到两个定点F 1，F 2的距离差的绝对值等于常数2a （0＜2a ＜|F 1F 2|）的点的轨迹叫做双曲线。

定点叫做双曲线的焦点；|F 1F 2|=2c ，叫做焦距。

● 备注：① 当|PF 1|-|PF 2|=2a 时，曲线仅表示右焦点F 2所对应的双曲线的一支（即右支）；当|PF 2|-|PF 1|=2a 时，曲线仅表示左焦点F 1所对应的双曲线的一支（即左支）；② 当2a=|F 1F 2|时，轨迹为以F 1，F 2为端点的2条射线； ③ 当2a ＞|F 1F 2|时，动点轨迹不存在。

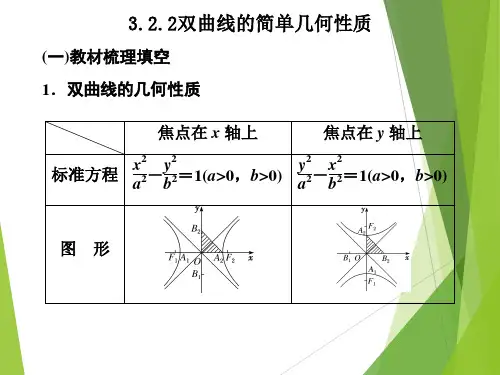
双曲线12222=-b y a x 与12222=-bx a y （a>0,b>0）的区别和联系（二）双曲线的简单性质1．范围： 由标准方程12222=-by a x （a ＞0，b ＞0），从横的方向来看，直线x=-a,x=a 之间没有图象，从纵的方向来看，随着x 的增大，y 的绝对值也无限增大。

x 的取值范围________ ,y 的取值范围______2. 对称性： 对称轴________ 对称中心________ 3．顶点：(如图) 顶点：____________特殊点：____________实轴：21A A 长为2a, a 叫做半实轴长虚轴：21B B 长为2b ，b 叫做半虚轴长双曲线只有两个顶点，而椭圆则有四个顶点4．离心率：双曲线的焦距与实轴长的比a ca c e ==22，叫做双曲线的离心率 范围：___________________双曲线形状与e 的关系：1122222-=-=-==e a c a a c a b k ，e 越大，即渐近线的斜率的绝对值就越大，这时双曲线的形状就从扁狭逐渐变得开阔 由此可知，双曲线的离心率越大，它的开口就越阔5．双曲线的第二定义：到定点F 的距离与到定直线l 的距离之比为常数)0(>>=a c a ce 的点的轨迹是双曲线 其中，定点叫做双曲线的焦点，定直线叫做双曲线的准线 常数e 是双曲线的离心率． 准线方程：对于12222=-b y a x 来说，相对于左焦点)0,(1c F -对应着左准线c a x l 21:-=， 相对于右焦点)0,(2c F 对应着右准线c a x l 22:=； 6．渐近线过双曲线12222=-b y a x 的两顶点21,A A ，作x 轴的垂线a x ±=，经过21,B B 作y 轴的垂线b y ±=，四条直线围成一个矩形 矩形的两条对角线所在直线方程是____________或（0=±b ya x ），这两条直线就是双曲线的渐近线双曲线无限接近渐近线，但永不相交。

第二课时问题探究双曲线离心率对其渐近线有何影响?对双曲线有何影响?思路分析:双曲线22a x -22by =1的离心率越大,则由a b =e 2-1知,渐近线y=±a b x 的斜率绝对值越大,进而双曲线的开口越开阔.自学导引1.双曲线的第二定义：动点M 与定点F(c,0)的距离和它到定直线l: x=ca 2的距离的比为常数ac (c ＞a ＞0)，则动点M 的轨迹是 ______.定直线l 叫做 __________ . 2.双曲线的焦半径公式为|PF|=______________ (或________________).答案:1.双曲线 双曲线的准线2.|a±ex 0| |ex 0±a|疑难剖析1.双曲线第二定义的应用利用第二定义计算焦半径或过焦点的弦长应注意向“到准线距离”转化.【例1】 已知双曲线22a x -22by =1(a ＞0，b ＞0)的焦点坐标是F 1(-c,0)和F 2(c,0),P （x 0,y 0）是双曲线上的任一点，求证:｜PF 1｜=｜a+ex 0｜,｜PF 2｜=｜a-ex 0｜，其中e 是双曲线的离心率.证明:双曲线22a x -22by =1的两焦点为F 1(-c,0)、F 2(c,0)，相应的准线方程分别是x=-c a 2和x=ca 2. ∵双曲线上任一点到焦点的距离与它到相应准线的距离的比等于这个双曲线的离心率， ∴||||201c a x PF +=e ，||||202ca x PF -=e. 化简得｜PF 1｜=｜a+ex 0｜,｜PF 2｜=｜a-ex 0｜.温馨提示:｜PF 1｜、｜PF 2｜都是双曲线上的点到其焦点的距离，通常称作焦半径.｜PF 1｜=｜a+ex 0｜,｜PF 2｜=｜a-ex 0｜称作焦半径公式.【例2】 在双曲线162x -92y =1上求一点P ，使它到左焦点的距离是它到右焦点距离的两倍. 解析:设P 点的坐标为(x,y)，F 1、F 2分别为双曲线的左、右焦点.∵双曲线的准线方程为x=±165,∴|516|||1+x PF =|516|||2-x PF . ∵｜PF 1｜=2｜PF 2｜,∴P 在双曲线的右支上. ∴516||22+x PF =516||2-x PF .∴x=548. 把x=548代入方程162x -92y =1得 y=±53119. 所以，P 点的坐标为(548，±53119). 温馨提示:此题也可设P(x 0,y 0),列方程进行解答.【类题演练1】(1)双曲线92x -72y =1的焦点到准线的距离是( ) A.47 B.425 C. 47或425 D. 423或49 (2)如果双曲线642x -362y =1上一点P 到它的右焦点的距离为8，求P 到它的右准线的距离.2.双曲线几何性质的综合应用【例3】 求证:双曲线22a x -22by =1(a>0,b>0)上任何一点到两条渐近线的距离之积为定值. 证法一:设P(x 0,y 0)是双曲线上任意一点,由双曲线的两条渐近线方程为bx+ay=0和bx-ay=0,可得P 到bx+ay=0的距离d 1=2200||b a ay bx ++;P 到bx-ay=0的距离d 2=2200||b a ay bx +-.∴d 1d 2=2200||b a ay bx ++·2200||ba ay bx +-=22202202||b a y a x b +-. 又P 在双曲线上,∴220a x +220by =1,即b 2x 02-a 2y 02=a 2b 2. ∴d 1·d 2=2222b a b a +,即P 到两条渐近线的距离之积为定值. 证法二:设双曲线上任一点P(asec θ,btanθ),∵双曲线的两条渐近线方程为bx+ay=0和bx-ay=0,∴点P 到直线bx+ay=0的距离d 1=22|tan sec |b a ab ab ++θθ =22|tan sec |b a ab ++θθ,点P 到直线bx-ay=0的距离d 2= 22|tan sec |b a ab ab +-θθ=22|tan sec |b a ab +-θθ.∴d 1·d 2=22|tan sec |b a ab ++θθ·22|tan sec |b a ab +-θθ =222222|tan sec |b a b a +-θθ=2222ba b a +. ∴双曲线上任一点到两条渐近线的距离之积为 定值 .温馨提示:(1)所谓定值,是与P 点在曲线上的位置无关,为了达到目标明确,可先通过特殊的情况,求出一个常数,猜想其定值.(2)双曲线22a x -22b y =1(a>0,b>0)的参数方程为⎩⎨⎧==θθtan sec b y a x (θ为参数),不作过高要求.在解题中灵活应用即可,类似于换元法解题,将可达到一元化的目的.【例4】 过双曲线22a x -22by =1(a>0,b>0)的一个焦点F 作x 轴的垂线,交双曲线的一支于P 、Q 两点,又过F 作一直线平行于双曲线的一条渐近线,交双曲线于R,求证:|PQ|=4|FR|.证明:设F 点的坐标为(c,0),将x=c 代入双曲线方程22a x -22by =1, 得y 2=24a b , ∴|PQ|=ab 22. 过点F(c,0)且与双曲线的渐近线bx+ay=0平行的直线为y=-ab (x-c), 代入双曲线方程,得22a x -22)]([bc x ab -- =1. 解之得x=cc a 222+,代入y=-a b (x-c), 得y=-a b (c c a 222+-c),即y=-acc a b 2)(22-. ∴|FR|2=(x-c)2+y 2=(c c a 222+-c)2+22224)(c a c a b - =22224)(c c a - +22224)(c a c a b -=22224)(c c a -·(1+22ab ) =244c b ·22a c =244a b . 故|FR|=ab 22,∴|PQ|=4|FR|. 温馨提示:证|PQ|等于4|FR|,需用双曲线的基本量a 、b 表示它们.【类题演练2】(1)双曲线2mx 2-my 2=2的一条准线是y=1,求m 的值.(2)双曲线的焦距是两准线间距离的4倍，求此双曲线的离心率.1.(1)解析:∵a 2=9,b 2=7,∴c=4.∴双曲线的焦点坐标是(±4，0)，准线方程是x=±49. ∴双曲线的焦点到准线的距离为4-49=47 和4+49=425 答案: C (2)解析:双曲线的离心率e=a c =810=45,设所求距离为d,则d 8=45,∴d=532. 2.(1)解析:可知双曲线的焦点在y 轴上,∴m ＜0. 双曲线方程可化为m y 22--mx 12- =1,因此 a 2=-m 2, b 2=-m 1, c 2=-m3. ∵准线是y=1,∴a 2=c,即-m 2=m3-. 解得m=-34. (2)解析:∵2c=4×ca 22,∴c 2=4a 2. ∴e 2=22a c =4,e=2. 拓展迁移【拓展点】 已知双曲线22a x -22by =1的离心率e>1+2,左、右焦点分别为F 1、F 2,左准线为l,能否在双曲线的左支上找到一点P,使得|PF 1|是P 到l 的距离d 与|PF 2|的等比中项? 解析:设在左支上存在P 点,使|PF 1|2=|PF 2|·d.由双曲线的第二定义,知d PF ||1=||||12PF PF =e,即|PF 2|=e|PF 1|.① 再由双曲线的第一定义,得|PF 2|-|PF 1|=2a.②由①②解得|PF 1|=12-e a ,|PF 2|=12-e ac . 在△PF 1F 2中,有|PF 1|+|PF 2|≥2c,即12-e a +12-e ac ≥2c.③ 利用e=a c ,由③式得e 2-2e-1≤0. 解得1-2≤e≤1+2.又由e>1,得1<e≤1+2.与已知e>1+2矛盾. 因此符合条件的点P 不存在.。

高二数学双曲线的几何性质人教版【本讲教育信息】一. 教学内容：双曲线的几何性质二.1. 2.三.[例1] N （1）18021=∠+∠N MA N MA （2）N A MA 21⊥，N A MA 12⊥又x NA x NA 21,∠∠均为锐角 ∴ x NA x NA 2190∠-=∠即9021=∠+∠x NA x NA根据对称性，∴18021=∠+∠M NA M NA （2）仿（1）可求得),(22a b b M --∴ 1222221-=--⋅+--=⋅ab a b a b a b k k N A MA ∴ N A MA 21⊥，同理可证N A MA 12⊥[例2] 已知双曲线12222=-by a x )0,0(>>b a 的焦点坐标是)0,(1c F -和)0,(2c F ，),(00y x P 是双曲线上的任一点，求证：||||01ex a PF +=，||||02ex a PF -=，其中e 是双曲线的离心率。

证明：双曲线12222=-by a x 的两焦点为)0,(1c F -、)0,(2c F ，相应的准线方程分别是c a x 2-=和ca x 2=。

∵ 双曲线上任一点到焦点的距离与它到相应准线的距离的比等于这个双曲线的离心率∴ e c a x PF =+||||201，e ca x PF =-||||202 化简得||||01ex a PF +=，||||02ex a PF -=[例3] 在双曲线191622=-y x 上求一点P ，使它到左焦点的距离是它到右焦点距离的两倍。

解：设P 点的坐标为),(y x ，1F 、2F 分别为双曲线的左、右焦点。

∵ 双曲线的准线方程为516±=x ∴ |516||||516|||21-=+x PF x PF ∵ ||2||21PF PF = ∴ P 在双曲线的右支上∴ 516||516||222-=+x PF x PF ∴ 548=x 把548=x 代入方程191622=-y x 得 11953±=y 所以P 点的坐标为)11953,548(±[例4] 已知双曲线方程为122=-y x ，双曲线左支上一点),(b a P 到直线x y =的距离是2，求b a +。