第3章)傅里叶变换的性质
- 格式:ppt
- 大小:2.23 MB
- 文档页数:45
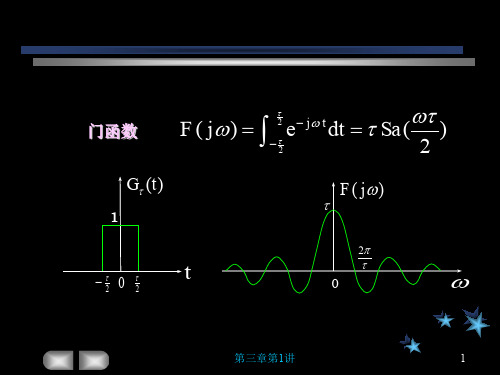


§3–4傅里叶变换的性质设f(t) ←→F(jω),f1(t) ←→F1(jω),f2(t) ←→F2(jω);α、α1、α2为实数,则有如下性质:一、线性:α1 f1(t) + α2 f2(t)←→α1F1(jω) + α2 F2(jω)二、对称性:F(jt)←→2πf(-ω)证明:将上式中的t换为ω,将原有的ω换为t,或:,即:F(jt)←→2π f(-ω)P.67例3-3:已知,再令==> ←→2πG(-ω)三、尺度变换:(α≠0的实数)可见信号持续时间与占有频带成反比(此性质易由积分变量代换证得)。
推论(折叠性):f(-t) ←→F(-jω)四、时移性:(此性质易由傅氏变换的定义证得)推论(同时具有尺度变换与时移):P.69-70例3-4请大家浏览。
五、频移性:(此性质易由傅氏变换的定义证得) π.70例3-5请大家浏览。
频移性的重要应用——调制定理:欧拉公式?例如门信号的调制:显然,当ω0足够大时,就可使原频谱密度函数被向左、右复制时几乎不失真。
六、时域卷积:f1(t)* f2(t) ←→F1(jω)F2(jω)证明:时域卷积的重要应用——求零状态响应的频域法:时域:yf(t) = f(t)* h(t) ==> 频域:Y f(jω) = F(jω)H(jω)七、频域卷积:f1(t). f2(t) ←→1/2π[F1(jω)*F2(jω)]八、时域微分性:df(t)/dt←→ jωF(jω) (其证明请自学P.72-73有关内容)推论:条件:例如:d(t) ←→1 ==>δ'(t) ←→jω九、时域积分性:证:故信号t轴上、下面积相等时F(0)=0,否则微分性与积分性是不可逆的。
十、频域微分性:例如:十一、频域积分性:f(0)=0时频域微分性与频域积分性才是可逆的。
十二、帕塞瓦尔定理:若f(t)为实函数,则能量表3-2傅里叶变换的基本性质下面再举几个例子说明性质的综合运用。

傅里叶变换的性质本质就是信号的时域运算关系在傅里叶变换域中的体现,也是求解信号傅里叶变换的基本手段。
傅里叶变换具有唯一性。
傅氏变换的性质揭示了信号的时域特性和频域特性之间的确定的内在联系。
讨论傅里叶变换的性质,目的在于:1. 了解特性的内在联系2. 用性质求3. 了解在通信系统领域中的实用这些性质在内容和形式上具有某种程度的对称性。
§3.7.1对称性质1.性质2.意义例3-7-1例3-7-2例3-7-3§3.7.2 线性1.性质2.说明§3.7.3 奇偶虚实性奇偶虚实性实际上在§3.4的“傅里叶变换的特殊形式”中已经介绍过。
1.证明:由定义可以得到2.若,则证明:设f(t)是实函数(为虚函数或复函数情况相似,略)显然§3.7.4 尺度变换性质1. 性质:2. 证明:综合上述两种情况3.意义(1) 0<a<1 时域扩展,频带压缩。
脉冲持续时间增加a倍,信号变化减缓,信号在频域的频带压缩a倍。
因此高频分量减少,幅度上升a倍。
(2) a>1 时域压缩,频域扩展a倍。
持续时间短,变化加快。
信号在频域高频分量增加,频带展宽,各分量的幅度下降a倍。
此例说明:信号的持续时间与信号占有频带成反比,有时为加速信号的传递,要将信号持续时间压缩,则要以展开频带为代价。
§3.7.5 时移特性性质幅度频谱无变化,只影响相位频谱,例3-7-8求下图所示函数的傅里叶变换。
解:由对称关系求,又因为得幅频、相频特性分别如下图所示。
幅度频谱无变化,只影响相位频谱§3.7.6 时移+尺度变换1.性质:2. 证明:(仿的证明过程)当时,设,则例3-7-9方法一:先标度变换,再时延方法二:先时延再标度变换§3.7.7 频移特性1.性质2.证明3.说明4.应用通信中调制与解调,频分复用§3.7.8 频移特性1.性质2.证明3.说明4.应用通信中调制与解调,频分复用§3.7.9 时域微分性质2. 证明即3. 特别注意如果f(t)中有确定的直流分量,应先取出直流分量单独求傅里变换,余下部分再用微分性质。

第3章 离散时间傅里叶变换在信号与系统中,分析连续时间信号可以采用时域分析方法和频域分析方法,它们之间是通过连续时间的傅里叶变换来完成从时域到频域的变换,它们之间是完成了一种域的变换,从而拓宽了分析连续时间信号的途径。
与连续时间系统的分析类似,在离散时间系统中,也可以采用离散傅里叶变换,将时间域信号转换到频率域进行分析,这样,不但可以得到离散时间信号的频谱,而且也可以使离散时间信号的分析方法更具有多元化。
本章将介绍离散时间系统的频域分析方法。
3.1 非周期序列的傅里叶变换及性质3.1.1 非周期序列傅里叶变换1.定义一个离散时间非周期信号与其频谱之间的关系,可用序列的傅里叶变换来表示。
若设离散时间非周期信号为序列)(n x ,则序列)(n x 的傅里叶变换(DTFT)为:正变换: ∑∞-∞=ω-ω==n nj j en x e X n x DTFT )()()]([ (3-1-1)反变换: ⎰ππ-ωωω-ωπ==d e e X n x e X DTFT n j j j )(21)()]([1 (3-1-2)记为:)()(ω−→←j Fe X n x当然式(3-1-2)等式右端的积分区间可以是)2,0(π或其它任何一个周期。
[例3-1] 设序列)(n x 的波形如图3-1所示,求)(n x 的傅里叶变换)(ωj e X解:由定义式(3-1-1)可得ωω=--=--===ω-ω-ωω-ω-ωω-ω-ω-ω-=ω-∞-∞=ω∑∑21sin 3sin )()(11)()(25212121333656j j j j j j j j j nj n nj n j ee e e e e e e e een R e X 2.离散时间序列傅里叶变换存在的条件:离散时间序列)(n x 的傅里叶变换存在且连续的条件为)(n x 满足绝对可和。
即:∞<∑∞-∞=)(n x n (3-1-3)反之,序列的傅里叶变换存在且连续,则序列一定是绝对可和的。

傅里叶变换的性质与应用傅里叶变换(Fourier Transform)是一种在信号和图像处理领域中广泛应用的数学工具。
它通过将一个函数表示为一系列正弦和余弦函数的线性组合来描述时域和频域之间的关系。
在本文中,我们将探讨傅里叶变换的性质以及其在各个领域中的应用。
一、傅里叶变换的性质1. 线性性质傅里叶变换具有线性性质,即对于任意常数a和b以及函数f(t)和g(t),有以下等式成立:F(af(t) + bg(t))= aF(f(t))+ bF(g(t))其中F(f(t))表示对函数f(t)进行傅里叶变换后得到的频域函数。
2. 对称性质傅里叶变换具有一系列对称性质。
其中最为重要的对称性质为奇偶对称性。
当函数f(t)为实函数并满足奇偶对称时,其傅里叶变换具有如下关系:F(-t)= F(t)(偶对称函数)F(-t)= -F(t)(奇对称函数)3. 尺度变换性质傅里叶变换可以对函数的尺度进行变换。
对于函数f(a * t)的傅里叶变换后得到的频域函数为F(w / a),其中a为正数。
二、傅里叶变换的应用1. 信号处理傅里叶变换在信号处理中被广泛应用。
它可以将时域信号转换为频域信号,使得信号的频率成分更加明确。
通过傅里叶变换,我们可以分析和处理各种信号,例如音频信号、图像信号和视频信号等。
在音频领域中,傅里叶变换可以用于音乐频谱分析、滤波器设计和音频压缩等方面。
在图像处理领域中,傅里叶变换可以用于图像增强、图像去噪和图像压缩等方面。
2. 通信系统傅里叶变换在通信系统中具有重要的应用。
通过傅里叶变换,我们可以将信号转换为频域信号,并根据频域特性进行信号调制和解调。
傅里叶变换可以用于调制解调器的设计、信道估计和信号的频谱分析等方面。
在无线通信系统中,傅里叶变换也广泛应用于OFDM(正交频分复用)技术,以提高信号传输效率和抗干扰性能。
3. 图像处理傅里叶变换在图像处理中有广泛的应用。
通过将图像转换到频域,我们可以对图像进行滤波、增强和去噪等操作。
傅里叶变换的11个性质公式傅里叶变换的11个性质公式是傅立叶变换的基本性质,由他们可以推出其它性质。
其中包括线性性质、有穷性质、周期性质、旋转性质、折叠性质、应变性质、平移性质、对称性质、频域算子性质、滤波性质、压缩性质等共11条。
1、线性性质:如果x(t)和y(t)是两个信号,则有:X(ω)=F[x(t)],Y(ω)=F[y(t)],则有:X(ω)+Y(ω)=F[x(t)+y(t)];αX(ω)=F[αx(t)];X(ω)*Y(ω)=F[x(t)*y(t)]。
2、有穷性质:如果x(t)是有穷的,则X(ω)也是有穷的。
3、周期性质:如果x(t)在周期T内无穷重复,则X(ω)也在周期2π/T内无穷重复。
4、旋转性质:X(ω-ω0) = F[x(t)e^(-jω0t)],即信号x(t)经过相位旋转成x(t)e^(-jω0t),其傅里叶变换也会经过相位旋转成X(ω-ω0)。
5、折叠性质:X(ω+nω0)=F[x(t)e^(-jnω0t)],即信号x(t)经过频率折叠后变为x(t)e^(-jnω0t),其傅里叶变换也会经过频率折叠成X(ω+nω0)。
6、应变性质:X(aω)=F[x(at)],即信号x(t)经过时间应变成x(at),其傅里叶变换也会经过频率应变成X(aω)。
7、平移性质:X(ω-ω0) = F[x(t-t0)],即信号x(t)经过时间平移成x(t-t0),其傅里叶变换也会经过频率平移成X(ω-ω0)。
8、对称性质:X(-ω) = X*(-ω),即傅里叶变换的实部和虚部对称。
9、频域算子性质:X(ω)Y(ω)=F[h(t)*x(t)],即傅里叶变换不仅可以表示信号,还可以表示系统的频域表示,即h(t)*x(t),其傅里叶变换为X(ω)Y(ω)。
10、滤波性质:H(ω)X(ω)=F[h(t)*x(t)],即傅里叶变换可以用来表示滤波器的频域表示,即h(t)*x(t),其傅里叶变换为H(ω)X(ω)。