2019版同步优化探究文数(北师大版)练习:第四章 第一节 平面向量的概念及其线性运算
- 格式:doc
- 大小:251.00 KB
- 文档页数:11

课时作业 A 组——基础对点练1.(2017·杭州模拟)在△ABC 中,已知M 是BC 中点,设CB →=a ,CA →=b ,则AM →=( )A.12a -b B.12a +b C .a -12bD .a +12b解析:AM→=AC →+CM →=-CA →+12CB →=-b +12a ,故选A.答案:A2.已知AB→=a +2b ,BC →=-5a +6b ,CD →=7a -2b ,则下列一定共线的三点是( )A .A ,B ,C B .A ,B ,D C .B ,C ,DD .A ,C ,D解析:因为AD→=AB →+BC →+CD →=3a +6b =3(a +2b )=3AB →,又AB →,AD →有公共点A .所以A ,B ,D 三点共线. 答案:B3.已知向量a ,b ,c 中任意两个都不共线,但a +b 与c 共线,且b +c 与a 共线,则向量a +b +c =( ) A .a B .b C .cD .0解析:依题意,设a +b =mc ,b +c =na ,则有(a +b )-(b +c )=mc -na ,即a -c =mc -na .又a 与c 不共线,于是有m =-1,n =-1,a +b =-c ,a +b +c =0. 答案:D4.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=( )A.BC→ B.12AD →C.AD →D.12BC →解析:如图,EB→+FC →=EC →+CB →+FB →+BC →=EC →+FB →=12(AC →+AB →)=12·2AD→=AD →. 答案:C5.已知O ,A ,B ,C 为同一平面内的四个点,若2 AC →+CB →=0,则向量OC →等于( )A.23OA →-13OB → B .-13OA →+23OB → C .2 OA→-OB → D .-OA→+2 OB → 解析:因为AC →=OC →-OA →,CB →=OB →-OC →,所以2 AC →+CB →=2(OC →-OA →)+(OB →-OC →)=OC →-2 OA →+OB →=0,所以OC →=2 OA →-OB →. 答案:C6.已知点G 是△ABC 的重心,过点G 作一条直线与AB ,AC 两边分别交于M ,N 两点,且AM→=x AB →,AN →=y AC →,则xy x +y 的值为( )A .3 B.13 C .2D.12解析:由已知得M ,G ,N 三点共线,所以AG→=λ AM →+(1-λ)AN →=λx AB →+(1-λ)y AC →.∵点G 是△ABC 的重心,∴AG →=23×12(AB →+AC →)=13(AB →+AC →), ∴⎩⎪⎨⎪⎧λx =13,(1-λ)y =13,即⎩⎪⎨⎪⎧λ=13x ,1-λ=13y ,得13x +13y =1,即1x +1y =3,通分得x +y xy =3,∴xy x +y=13.答案:B7.在△ABC 中,已知D 是AB 边上的一点,若AD→=2DB →,CD →=13CA →+λCB →,则λ等于( ) A.23 B.13 C .-13D .-23解析:∵AD→=2DB →,即CD →-CA →=2(CB →-CD →),∴CD→=13CA →+23CB →,∴λ=23. 答案:A8.设a ,b 都是非零向量,下列四个条件中,使a |a |=b|b |成立的充分条件是( ) A .a =-b B .a ∥bC .a =2bD .a ∥b 且|a |=|b |解析:a |a |=b |b |⇔a =|a |b|b |⇔a 与b 共线且同向⇔a =λb 且λ>0.B ,D 选项中a 和b 可能反向.A 选项中λ<0,不符合λ>0. 答案:C9.设D 为△ABC 所在平面内一点,BC →=3CD →,则( )A.AD→=-13AB →+43AC → B.AD→=13AB →-43AC →C.AD→=43AB →+13AC →D.AD→=43AB →-13AC →解析:由题意得AD→=AC →+CD →=AC →+13BC →=AC →+13AC →-13AB →=-13AB →+43AC →,故选A. 答案:A10.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+y AC →,则x= ;y = .解析:∵AM →=2MC →,∴AM →=23AC →. ∵BN→=NC →,∴AN →=12(AB →+AC →), ∴MN→=AN →-AM →=12(AB →+AC →)-23AC → =12AB →-16AC →.又MN→=xAB →+yAC →,∴x =12,y =-16. 答案:12 -1611.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA→+OC →=OB →+OD →,则四边形ABCD 的形状为 . 解析:由OA→+OC →=OB →+OD →得OA →-OB →=OD →-OC →,所以BA →=CD →,所以四边形ABCD 为平行四边形. 答案:平行四边形12.在矩形ABCD 中,O 是对角线的交点,若BC →=5e 1,DC →=3e 2,则OC →= .(用e 1,e 2表示)解析:在矩形ABCD 中,因为O 是对角线的交点,所以OC→=12AC →=12(AB →+AD →)=12(DC →+BC →)=12(5e 1+3e 2). 答案:52e 1+32e 213.已知A (1,0),B (4,0),C (3,4),O 为坐标原点,且OD→=12(OA →+OB →-CB →),则|BD→|等于 . 解析:由OD→=12(OA →+OB →-CB →)=12(OA →+OC →),知点D 是线段AC 的中点,故D (2,2),所以BD→=(-2,2),故|BD →|=(-2)2+22=2 2.答案:2 2B 组——能力提升练1.已知e 1,e 2是不共线向量,a =me 1+2e 2,b =ne 1-e 2,且mn ≠0,若a ∥b ,则mn 等于( ) A .-12 B.12 C .-2D .2解析:∵a ∥b ,∴a =λb ,即me 1+2e 2=λ(ne 1-e 2),则⎩⎪⎨⎪⎧λn =m -λ=2,故mn =-2.答案:C2.在△ABC 中,AN →=14NC →,若P 是直线BN 上的一点,且满足AP→=m AB →+25AC →,则实数m 的值为( ) A .-4 B .-1 C .1D .4解析:根据题意设BP →=n BN →(n ∈R),则AP →=AB →+BP →=AB →+n BN →=AB →+n (AN →-AB →)=AB →+n ⎝ ⎛⎭⎪⎫15AC →-AB →=(1-n )AB →+n 5AC →,又AP →=m AB →+25AC →,∴⎩⎨⎧1-n =m ,n 5=25,解得⎩⎪⎨⎪⎧n =2,m =-1,故选B.答案:B3.在平面上,AB 1→⊥AB 2→,|OB 1→|=|OB 2→|=1,AP →=AB 1→+AB 2→.若|OP →|<12,则|OA →|的取值范围是( ) A .(0,52] B .(52,72] C .(52,2]D .(72,2]解析:由题意得点B 1,B 2在以O 为圆心的单位圆上,点P 在以O 为圆心、半径为12的圆内,又AB 1→⊥AB 2→,AP →=AB 1→+AB 2→,所以点A 在以B 1B 2为直径的圆上,当点P 与点O 重合时,|OA→|最大,为2,当点P 在半径为12的圆周上时,|OA →|最小,为72,故选D. 答案:D4.在△ABC 中,BD →=3 DC →,若AD →=λ1 AB →+λ2 AC →,则λ1λ2的值为( )A.116B.316C.12D.109解析:由题意得,AD→=AB →+BD →=AB →+34BC →=AB →+34(AC →-AB →)=14AB →+34AC →,∴λ1=14,λ2=34,∴λ1λ2=316. 答案:B5.若点M 是△ABC 所在平面内的一点,且满足5 AM →=AB →+3 AC →,则△ABM与△ABC 的面积的比值为( ) A.15 B.25 C.35D.45解析:设AB 的中点为D ,如图,连接MD ,MC ,由5 AM →=AB →+3 AC→,得5 AM →=2 AD →+3 AC → ①,即AM →=25AD →+35AC →,即25+35=1,故C ,M ,D 三点共线,又AM→=AD →+DM → ②,①②联立,得5 DM→=3 DC →,即在△ABM 与△ABC 中,边AB 上的高的比值为35,所以△ABM 与△ABC 的面积的比值为35.答案:C6.设M 是△ABC 所在平面上的一点,且MB→+32MA →+32MC →=0,D 是AC 的中点,则|MD →||BM →|的值为( ) A.13 B.12 C .1D .2解析:∵D 是AC 的中点,延长MD 至E ,使得DE =MD (图略),∴四边形MAEC 为平行四边形,∴MD→=12ME →=12(MA →+MC →).∵MB→+32MA →+32MC →=0,∴MB →=-32(MA →+MC →)=-3MD →,∴|MD →||BM →|=|MD →||-3MD →|=13,故选A. 答案:A7.如图所示,矩形ABCD 的对角线相交于点O ,E 为AO 的中点, 若DE→=λ AB →+μ AD →(λ,μ为实数),则λ2+μ2=( )A.58B.14 C .1D.516解析:DE →=12DA →+12DO →=12DA →+14DB →=12DA →+14(DA →+AB →)=14AB →-34AD →,所以λ=14,μ=-34,故λ2+μ2=58,故选A. 答案:A8.在△ABC 上,点D 满足AD →=2AB →-AC →,则( )A .点D 不在直线BC 上B .点D 在BC 的延长线上 C .点D 在线段BC 上 D .点D 在CB 的延长线上 解析:AD →=2AB →-AC →=AB →+AB →-AC → =AB →+CB →; 如图,作BD ′→=CB →,连接AD ′,则: AB →+CB →=AB →+BD ′→=AD ′→=AD →; ∴D ′和D 重合;∴点D 在CB 的延长线上. 答案:D9.如图,在直角梯形ABCD 中,AB =2AD =2DC ,E 为BC边上一点,BC →=3 EC →,F 为AE 的中点,则BF →=( ) A.23AB →-13AD → B.13AB →-23AD →C .-23AB →+13AD →D .-13AB →+23AD →解析:如图,取AB 的中点G ,连接DG ,CG ,则易知四边形DCBG 为平行四边形,所以BC →=GD →=AD →-AG →=AD →-12AB →,∴AE →=AB →+BE →=AB →+23BC →=AB →+23⎝ ⎛⎭⎪⎫AD →-12AB →=23AB →+23AD →,于是BF→=AF →-AB →=12AE →-AB →=12⎝ ⎛⎭⎪⎫23AB →+23AD →-AB →=-23AB →+13AD →,故选C. 答案:C10.设D 为△ABC 所在平面内一点,且BC→=3BD →,则AD →=( )A.23AB →+13AC →B.13AB →+23AC →C.43AB →+13AC →D.23AB →+53AC → 解析:∵BC→=3BD →∴BD →=13BC →=13(AC →-AB →),则AD→=AB →+BD →=AB →+13(AC →-AB →)=23AB →+13AC →. 答案:A11.已知O 为坐标原点,B 、D 分别是以O 为圆心的单位圆与x 轴正半轴、y 轴正半轴的交点,点P 为单位圆劣弧BD 上一点,若OB →+OD →=xDB →+yOP →,∠BOP =π3, 则x +y =( ) A .1 B. 3 C .2D .4-3 3解析:如图,DB→=OB →-OD →,∴OB→+OD →=x (OB →-OD →)+yOP →, ∴yOP→=(1-x )OB →+(1+x )OD →,① ∵∠BOP =π3,∴OP →=12OB →+32OD →, ∴yOP →=y 2OB →+32yOD →,② 由①②得⎩⎪⎨⎪⎧1-x =y2,1+x =32y ,解得x =2-3,y =23-2,∴x +y =3,故选B. 答案:B12.已知向量e 1、e 2是两个不共线的向量,若a =2e 1-e 2与b =e 1+λe 2共线,则λ= .解析:因为a 与b 共线,所以a =xb ,⎩⎪⎨⎪⎧x =2λx =-1,故λ=-12. 答案:-1213.如图,在△ABC 中,AB =2,BC =3,∠ABC =60°,AH ⊥BC 于点H ,M 为AH 的中点.若AM →=λAB →+μBC →,则λ+μ= .解析:因为AB =2,∠ABC =60°,AH ⊥BC ,所以BH =1.因为点M 为AH 的中点,所以AM →=12AH →=12(AB →+BH →)=12⎝ ⎛⎭⎪⎫AB →+13BC →=12AB →+16BC →,又AM→=λAB →+μBC →,所以λ=12,μ=16,所以λ+μ=23.答案:2314.(2018·临汾模拟)如图,△ABC 中,GA →+GB →+GC →=0,CA →=a ,CB→=b .若CP →=ma ,CQ →=nb ,CG ∩PQ =H ,CG →=2CH →,则1m +1n = .解析:由GA→+GB →+GC →=0,知G 为△ABC 的重心,取AB 的中点D (图略),则CH →=12CG →=13CD →=16(CA →+CB →)=16m CP →+16n CQ →,由P ,H ,Q 三点共线,得16m +16n =1,则1m +1n =6. 答案:615.如图,在△ABC 中,AN →=13NC →,P 是BN 上的一点,若AP →=mAB →+211AC →,则实数m 的值为 .解析:由AN →=13NC →,可知AN →=14AC →,又∵AP →=mAB →+211AC →=mAB →+811AN →,且B 、P 、N 共线,∴m +811=1,∴m =311. 答案:311。

课时作业A 组——基础对点练1.已知|a |=6,|b |=3,向量a 在b 方向上的投影是4,则a ·b 为( )A .12B .8C .-8D .2解析:∵|a |cos 〈a ,b 〉=4,|b |=3,∴a ·b =|a ||b |·cos 〈a ,b 〉=3×4=12.答案:A2.已知向量a =(1,m ),b =(3,-2),且(a +b )⊥b ,则m =( )A .-8B .-6C .6D .8解析:由向量的坐标运算得a +b =(4,m -2),由(a +b )⊥b ,(a +b )·b =12-2(m -2)=0,解得m =8,故选D.答案:D3.(2018·云南五市联考)在如图所示的矩形ABCD 中,AB =4,AD =2,E 为线段BC 上的点,则AE →·DE →的最小值为( )A .12B .15C .17D .16解析:以B 为坐标原点,BC 所在直线为x 轴,BA 所在直线为y 轴,建立如图所示的平面直角坐标系,则A (0,4),D (2,4),设E (x,0)(0≤x ≤2),所以AE →·DE →=(x ,-4)·(x -2,-4)=x 2-2x +16=(x -1)2+15,于是当x =1,即E 为BC 的中点时,AE →·DE →取得最小值15,故选B.答案:B4.(2018·昆明市检测)已知a ,b 为单位向量,设a 与b 的夹角为π3,则a 与a -b 的夹角为( ) A.π6B.π3C.2π3D.5π6解析:由题意,得a ·b =1×1×cos π3=12,所以|a -b |2=a 2-2a ·b +b 2=1-2×12+1=1,所以cos 〈a ,a -b 〉=a ·〈a -b 〉|a ||a -b |=a 2-a ·b 1×1=1-12=12,所以〈a ,a -b 〉=π3,故选B. 答案:B5.在△ABC 中,BC =5,G ,O 分别为△ABC 的重心和外心,且OG →·BC →=5,则△ABC 的形状是( )A .锐角三角形B .钝角三角形C .直角三角形D .上述三种情况都有可能解析:设M 为BC 的中点,G 在BC 上的射影为H ,A 在BC 上的射影为N ,由OG →·BC →=5,又BC =5,知OG →在BC →上的投影为1,即MH =1,∴HC =1.5,又MG GA =12<11.5,A 在BC 上的射影在MC 的延长线上,∴△ABC 为钝角三角形,故选B. 答案:B6.已知平面向量a =(2,4),b =(1,-2),若c =a -(a ·b )·b ,则|c |=__________.解析:由题意可得a ·b =2×1+4×(-2)=-6,∴c =a -(a ·b )·b =a +6b =(2,4)+6(1,-2)=(8,-8),∴|c |=82+(-8)2=8 2. 答案:8 27.已知两个单位向量a ,b 的夹角为60°,c =t a +(1-t )b .若b·c =0,则t =________.解析:由题意,将b·c =[t a + (1-t )b ]·b 整理得ta ·b +(1-t )=0,又a·b =12,所以t =2. 答案:28.(2018·九江市模拟)若向量a =(1,1)与b =(λ,-2)的夹角为钝角,则λ的取值范围是。


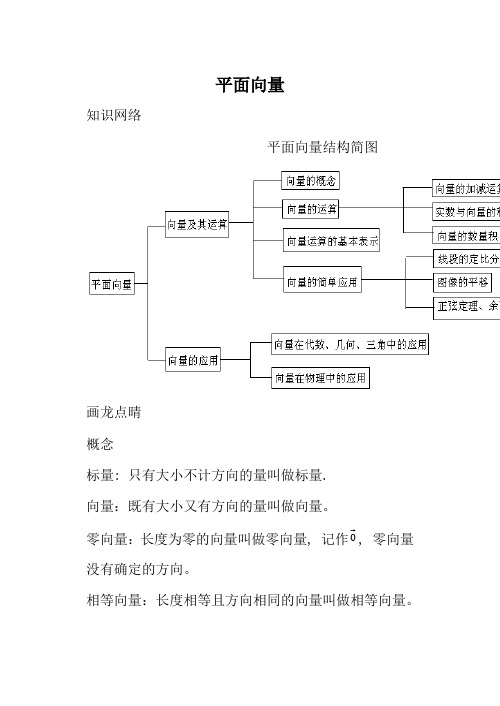
平面向量知识网络平面向量结构简图画龙点晴概念标量: 只有大小不计方向的量叫做标量.向量:既有大小又有方向的量叫做向量。
零向量:长度为零的向量叫做零向量, 记作0, 零向量没有确定的方向。
相等向量:长度相等且方向相同的向量叫做相等向量。
向量的模: 向量a 的大小(或长度)叫做向量的模, 记作|a |.负向量: 与已知的向量a 的模相等且方向相反的向量叫做已知向量a 的负向量, 记作-a .自由向量: 只有大小和方向而无特定位置的向量叫做自由向量.有向线段: 具有方向的线段叫做有向线段. 通常在有向线段的终点处画上箭头表示它的方向. 以A 为起点, B 为终点的有向线段记作AB . 起点、方向、长度是有向线段的在要素。
用有向线段表示向量:已知向量a 与有向线段AB . 当|a |=|AB |且a 与AB 同向时, 向量a 可用有向线段AB 表示, 叫做向量AB .向量加法:求两个向量的和的运算,叫做向量的加法。
向量加法的平行四边形: 平面上任意两个向量a 、b ,从同一点O 出发分别作向量OA =a ,OB =b ,以OA 、OB 为一组邻边作平行四边形OACB ,则平行四边形的对角线OC 所代表的向量OB OA OC +== a+b 。
向量加法的三角形法则: 平面上任意两个向量a 、b ,任取一个起点O ,从O 出发作向量OA =a ,再从A 出发作向量AB =b ,则OB =OA +AB =a+b 。
说明:(1)“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点;(2)可以推广到n 个向量连加,和向量就是以第一个向量的起点为起点,最后一个向量的终点为终点的向量; (3)a a a =+=+00;(4)不共线向量都可以采用这种法则——三角形法则.向量的加法运算律: (1)交换律:a +b =b +a ; (2)向量加法的结合律:(a +b ) +c =a + (b +c ). 向量的减法: 平面上任意两个向量a 、b ,从同一点O出发分别作向量OA =a ,OB =b ,作向量BA , 则向量BA 叫做向量a 与b 的差, 记作a-b , 即BA = a-b. [活用实例][例1] 试用向量方法证明:对角线互相平分的四边形是平行四边形。

课时作业A 组——基础对点练1.(2017·高考天津卷)设集合A ={1,2,6},B ={2,4},C ={1,2,3,4},则(A ∪B )∩C =( )A .{2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6}解析:由题意知A ∪B ={1,2,4,6},∴(A ∪B )∩C ={1,2,4}.答案:B2.(2018·成都市模拟)设集合A ={0,1},B ={x |(x +2)(x -1)<0,x ∈Z},则A ∪B =( )A .{-2,-1,0,1}B .{-1,0,1}C .{0,1}D .{0} 解析:因为集合A ={0,1},B ={x |(x +2)(x -1)<0,x ∈Z}={-1,0},所以A ∪B ={-1,0,1}.故选B.答案:B3.设集合A ={x |x <2},B ={y |y =2x -1},则A ∩B =( )A .(-∞,3)B .[2,3)C .(-∞,2)D .(-1,2)解析:A ={x |x <2},因为y =2x -1>-1,所以B ={y |y =2x -1}=(-1,+∞),所以A ∩B =(-1,2),故选D.答案:D4.设a ,b ∈R ,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,则b -a =( ) A .1B .-1C .2D .-2解析:根据题意,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,b a ,b ,又∵a ≠0,∴a +b =0,即a =-b ,∴b a =-1,b =1.故a =-1,b =1,则b -a =2.故选C.答案:C5.已知集合A ={-2,-1,0,1,2,3},B ={x |x +1x -2<0},则A ∩B =( ) A . {-2,-1,0,1,2,3}B .{-1,0,1,2}C .{-1,2}D .{0,1}解析:由题意,得B={x|-1<x<2},所以A∩B={0,1},故选D.答案:D6.已知集合A={1,2,3,4},B={y|y=3x-2,x∈A},则A∩B=()A.{1} B.{4}C.{1,3} D.{1,4}解析:由题意,得B={1,4,7,10},∴A∩B={1,4}.答案:D7.(2018·长沙市模拟)已知集合P={x|-2 016≤x≤2 017},Q={x| 2 017-x<1},则P∩Q =()A.(2 016,2 017) B.(2 016,2 017]C.[2 016,2 017) D.(-2 016,2 017)解析:由已知可得Q={x|0≤2 017-x<1}=(2 016,2 017],则P∩Q=(2 016,2 017].答案:B8.(2018·石家庄模拟)函数y=x-2与y=ln(1-x)的定义域分别为M,N,则M∪N=() A.(1,2] B.[1,2]C.(-∞,1]∪[2,+∞) D.(-∞,1)∪[2,+∞)解析:使x-2有意义的实数x应满足x-2≥0,∴x≥2,∴M=[2,+∞),y=ln(1-x)中x 应满足1-x>0,∴x<1,∴N=(-∞,1),所以M∪N=(-∞,1)∪[2,+∞),故选D.答案:D9.(2018·沈阳市模拟)设全集U=R,集合A={x|x≥2},B={x|0≤x<6},则集合(∁U A)∩B =()A.{x|0<x<2} B.{x|0<x≤2}C.{x|0≤x<2} D.{x|0≤x≤2}解析:∵U=R,A={x|x≥2},∴∁U A={x|x<2}.又B={x|0≤x<6},∴(∁U A)∩B={x|0≤x<2}.故选C.答案:C10.(2018·天津模拟)设集合M={0,1,2},N={x|x2-3x+2≤0},则M∩N=() A.{1} B.{2}C.{0,1} D.{1,2}解析:N={x|x2-3x+2≤0}={x|1≤x≤2},又M={0,1,2},所以M∩N={1,2}.答案:D11.已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=()A.{1,4} B.{2,3}C.{9,16} D.{1,2}解析:n=1,2,3,4时,x=1,4,9,16,∴集合B={1,4,9,16},∴A∩B={1,4}.答案:A12.(2018·长春市模拟)已知集合A={x|x2-x+4>x+12},B={x|2x-1<8},则A∩(∁R B)=()A.{x|x≥4} B.{x|x>4}C.{x|x≥-2} D.{x|x<-2或x≥4}解析:由题意易得,A={x|x<-2或x>4},B={x|x<4},则A∩(∁R B)={x|x>4}.故选B. 答案:B13.已知集合A={-1,2,3,6},B={x|-2<x<3},则A∩B=________.答案:{-1,2}14.已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∪(∁U B)=________.解析:∁U B={2},∴A∪∁U B={1,2,3}.答案:{1,2,3}15.集合{-1,0,1}共有__________个子集.解析:集合{-1,0,1}的子集有∅,{-1},{0},{1},{-1,0},{-1,1},{0,1},{-1, 0,1},共8个.答案:816.已知集合U={1,2,3,4,5},A={1,3},B={1,3,4},则A∪(∁U B)=__________.答案:{1,2,3,5}B组——能力提升练1.已知全集U={0,1,2,3},∁U M={2},则集合M=()A.{1,3} B.{0,1,3}C.{0,3} D.{2}解析:M={0,1,3}.答案:B2.已知集合A={0,1,2},B={1,m}.若A∩B=B,则实数m的值是()A.0 B.2C.0或2 D.0或1或2解析:∵A∩B=B,∴B⊆A,∴m=0或m=2.答案:C3.(2018·南昌市模拟)已知集合A ={x ∈R|0<x ≤5},B ={x ∈R|log 2x <2},则(∁A B )∩Z =( )A .{4}B .{5}C .[4,5]D .{4,5}解析:∵集合A ={x ∈R|0<x ≤5},B ={x ∈R|log 2x <2}={x |0<x <4},∴∁A B ={x |4≤x ≤5},∴(∁A B )∩Z ={4,5},故选D.答案:D4.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x -1x +2≤0,B ={x |y =lg(-x 2+4 x +5)},则A ∩(∁R B )=( ) A .(-2,-1]B .[-2,-1]C .(-1,1]D .[-1,1]解析:依题意,A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x -1x +2≤0={x |-2<x ≤1},B ={x |y =lg(-x 2+4x +5)}={x |-x 2+4x +5>0}={x |-1<x <5},∴∁R B ={x |x ≤-1或x ≥5},A ∩(∁R B )=(-2,-1],选A.答案:A5.(2018·惠州模拟)已知集合A ={0,1},B ={z |z =x +y ,x ∈A ,y ∈A },则集合B 的子集的个数为( )A .3B .4C .7D .8解析:由题意知,B ={0,1,2},则集合B 的子集的个数为23=8.故选D.答案:D6.(2018·太原市模拟)已知全集U =R ,集合A ={x |x (x +2)<0},B ={x ||x |≤1},则如图所示的阴影部分表示的集合是( )A .(-2,1)B .[-1,0]∪[1,2)C .(-2,-1)∪[0,1]D .[0,1]解析:因为集合A ={x |x (x +2)<0},B ={x ||x |≤1},所以A ={x |-2<x <0},B ={x |-1≤x ≤1},所以A ∪B =(-2,1],A ∩B =[-1,0),所以阴影部分表示的集合为∁A ∪B (A ∩B )=(-2,-1)∪[0,1],故选C.答案:C7.(2018·郑州质量预测)设全集U={x∈N*|x≤4},集合A={1,4},B={2,4},则∁U(A∩B)=()A.{1,2,3} B.{1,2,4}C.{1,3,4} D.{2,3,4}解析:因为U={1,2,3,4},A∩B={4},所以∁U(A∩B)={1,2,3},故选A.答案:A8.(2018·广雅中学测试)若全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的Venn图是()解析:由题意知,N={x|x2+x=0}={-1,0},而M={-1,0,1},所以N M,故选B.答案:B9.已知集合A满足条件{1,2}⊆A,则集合A的个数为()A.8 B.7C.4 D.3解析:由题意可知,集合A中必含有元素1和2,可含有3,4,5中的0个、1个、2个,则集合A可以为{1,2},{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},共7个.故选B.答案:B10.已知集合A={2,0,1,4},B={k|k∈R,k2-2∈A,k-2∉A},则集合B中所有的元素之和为()A.2 B.-2C.0 D. 2解析:若k2-2=2,则k=2或k=-2,当k=2时,k-2=0,不满足条件,当k=-2时,k-2=-4,满足条件;若k2-2=0,则k=±2,显然满足条件;若k2-2=1,则k=±3,显然满足条件;若k2-2=4,得k=±6,显然满足条件.所以集合B中的元素为-2,±2,±3,±6,所以集合B中的元素之和为-2,故选B.答案:B11.给出下列四个结论:①{0}是空集;②若a ∈N ,则-a ∉N ;③集合A ={x |x 2-2x +1=0}中有两个元素;④集合B =⎩⎨⎧⎭⎬⎫x ∈Q ⎪⎪6x ∈N 是有限集. 其中正确结论的个数是( )A .0B .1C .2D .3解析:对于①,{0}中含有元素0,不是空集,故①错误;对于②,比如0∈N ,-0∈N ,故②错误;对于③,集合A ={x |x 2-2x +1=0}={1}中有一个元素,故③错误;对于④,当x ∈Q 且6x ∈N 时,6x 可以取无数个值,所以集合B =⎩⎨⎧⎭⎬⎫x ∈Q ⎪⎪6x ∈N 是无限集,故④错误.综上可知,正确结论的个数是0.故选A.答案:A12.已知集合A ={(x ,y )|x 2+y 2≤1,x ,y ∈Z},B ={(x ,y )||x |≤2,|y |≤2,x ,y ∈Z},定义集合A B ={(x 1+x 2,y 1+y 2)|(x 1,y 1)∈A ,(x 2,y 2)∈B },则A B 中元素的个数为( )A .77B .49C .45D .30解析:集合A ={(x ,y )|x 2+y 2≤1,x ,y ∈Z},所以集合A 中有5个元素(即5个点),即图中圆内及圆上的整点.集合B ={(x ,y )||x |≤2,|y |≤2,x ,y ∈Z}中有25个元素(即25个点),即图中正方形ABCD 内及正方形ABCD 上的整点.集合A B ={(x 1+x 2,y 1+y 2)|(x 1,y 1)∈A ,(x 2,y 2)∈B }中的元素可看作正方形A 1B 1C 1D 1内及正方形A 1B 1C 1D 1上除去四个顶点外的整点,共7×7-4=45个.答案:C13.设全集U ={n ∈N|1≤n ≤10},A ={1,2,3,5,8},B ={1,3,5,7,9},则(∁U A )∩B =________. 解析:依题意得U ={1,2,3,4,5,6,7,8,9,10},∁U A ={4,6,7,9,10},(∁U A )∩B ={7,9}. 答案:{7,9}14.集合A ={x ∈R||x -2|≤5}中的最小整数为________.解析:由|x -2|≤5,得-5≤x -2≤5,即-3≤x ≤7,所以集合A 中的最小整数为-3. 答案:-315.若集合A ={x |(a -1)x 2+3x -2=0,x ∈R}有且仅有两个子集,则实数a 的值为________. 解析:由题意知,方程(a -1)x 2+3x -2=0,x ∈R ,有一个根,∴当a =1时满足题意,当a ≠1时,Δ=0,即9+8(a -1)=0,解得a =-18. 答案:1或-18。
平面向量及向量的运算 同步练习一、选择题1.以下说法错误的是( )A .零向量与任一非零向量平行 B.零向量与单位向量的模不相等 C.平行向量方向相同 D.平行向量一定是共线向量 2.下列四式不能化简为AD 的是( )A .;)++(BC CD AB B .);+)+(+(CM BC MB AD C .-+ D .; 3.设四边形ABCD 中,有=21,且||=||,则这个四边形是( ) A.平行四边形 B.矩形 C.等腰梯形 D.菱形 4.已知=(3,4),=(5,12),与 则夹角的余弦为( )A .6563 B .65 C .513 D .13 5. 已知a 、b 均为单位向量,它们的夹角为60°,那么|a+ 3b| =( )A .7B .10C .13D .46.已知向量a (cos ,sin )θθ=,向量b 1)=-,则|2a -b|的最大值、最小值分别是( )A .0,24B .24,4C .16,0D .4,07.已知)(),点=(),,-=(-21x,P 1,1ON 32OM 在线段NM 的中垂线上,则x 等于( )A .;-25B .;-23C .;-27 D .-3;8.在平面直角坐标系中,已知两点A (cos80o,sin80o),B(cos20o,sin20o),则|AB |的值是( )A .;21B .;22 C .;23 D .1; 9.|a|=3,|b|=4,向量a+43b 与a -43b 的位置关系为( )A .平行B .垂直C .夹角为3π.不平行也不垂直10.在边长为2的正三角形ABC 中,设AB =c, =a, =b,则a ·b+b ·c+c ·a 等 于( ) A .0 B .1 C .3 D .-3二、填空题11.若),4,3(=AB A点的坐标为(-2,-1),则B点的坐标为 . 12.已知(3,4),(2,3)=-=a b ,则2||3-⋅=a a b .13.与向量a =(12,5)平行的单位向量为 .14. 已知向量OP X OB OA OP 是直线设),1,5(),7,1(),1,2(===上的一点(O 为 坐标原点),那么XB XA ⋅的最小值是___________________.三、解答题15.向量),1,(),2,1(x b a ==(1)当2+与-2平行时,求x ; (2)当b a 2+与b a -2垂直时,求x .16.已知61)b a (2)b 3a (23,|b |4,a =+∙==-||, (1)求∙的值; (2)求b a 与的夹角θ; (3)求||b a +的值.17.设、是两个不共线的非零向量(R t ∈)(1)记),(31,,b a OC b t OB a OA +===那么当实数t 为何值时,A 、B 、C 三点共线?(2)若 1201||||夹角为与且==,那么实数x 为何值时||x -的值最小?附加题:已知A 、B 、C 的坐标分别是A (3,0),B (0,3),C (cos α,sin α).(1) 若AC BC =,求角α的值;(2)若1,AC BC ⋅=- 求22sin sin 21tan ααα++的值.参考答案一、选择题二、填空题11.(1,3) 12. 28 13.)135,1312(或 )135,1312(-- 14. -8三、解答题15.(1)21, (2)27或-2 16.(1)-6(2)32π(3)1317.(1)t=21(2)x=21-时最小附加题. (1))(,4Z k k ∈+=ππα(2)95-。
课时作业组——基础对点练.(·高考天津卷)设集合={},={},={},则(∪)∩=( ).{}.{}.{}.{}解析:由题意知∪={},∴(∪)∩={}.答案:.(·成都市模拟)设集合={},={(+)(-)<,∈},则∪=( ).{-}.{-,-}.{}.{}解析:因为集合={},={(+)(-)<,∈}={-},所以∪={-}.故选.答案:.设集合={<},={=-},则∩=( ).(-∞,).[).(-).(-∞,) 解析:={<},因为=->-,所以={=-}=(-,+∞),所以∩=(-),故选.答案:.设,∈,集合{,+,}=,则-=( ).-..-.解析:根据题意,集合{,+,}=,又∵≠,∴+=,即=-,∴=-,=.故=-,=,则-=.故选.答案:.已知集合={-,-},={<},则∩=( ). {-,-}.{-}.{}.{-}解析:由题意,得={-<<},所以∩={},故选.答案:.已知集合={},={=-,∈},则∩=( ).{}.{}.{}.{}解析:由题意,得={},∴∩={}.答案:.(·长沙市模拟)已知集合={-≤≤ },={-)<},则∩=( ).( ).( ].(-).[ )解析:由已知可得={≤-<}=( ,],则∩=( ].答案:.(·石家庄模拟)函数=与=(-)的定义域分别为,,则∪=( ).[].(].(-∞,)∪[,+∞).(-∞,]∪[,+∞) 解析:使有意义的实数应满足-≥,∴≥,∴=[,+∞),=(-)中应满足->,∴<,∴=(-∞,),所以∪=(-∞,)∪[,+∞),故选.答案:.(·沈阳市模拟)设全集=,集合={≥},={≤<},则集合(∁)∩=( ).{<≤}.{<<}.{≤≤}.{≤<} 解析:∵=,={≥},∴∁={<}.又={≤<},∴(∁)∩={≤<}.故选.答案:.(·天津模拟)设集合={},={-+≤},则∩=( ).{}.{}.{}.{}解析:={-+≤}={≤≤},又={},所以∩={}.答案:.已知集合={},={=,∈},则∩=( ).{}.{}.{}.{}解析:=时,=,∴集合={},∴∩={}.答案:.(·长春市模拟)已知集合={-+>+},={-<},则∩(∁)=( ).{>}.{≥}.{<-或≥}.{≥-}解析:由题意易得,={<-或>},={<},则∩(∁)={>}.故选.答案:.已知集合={-},={-<<},则∩=.答案:{-}.已知集合={},={},={},则∪(∁)=.解析:∁={},∴∪∁={}.答案:{}。
课时作业A组一一基础对点练1. (2017杭州模拟)在厶ABC中,已知M是BC中点,设CB= a, CA= b,则AM =()11A.qa —bB.qa + b11C. a —2b D . a+-bf f f f f1 1解析:AM = AC+ CM = —CA + 2CB = —b + qa,故选A.答案:Af f f2.已知AB = a+ 2b, BC= —5a + 6b,CD = 7a—2b,则下列一定共线的三点是(A. A, B, CB. A, B, DC. B, C, D D . A, C, Df f f f f f f解析:因为AD = AB + BC + CD = 3a + 6b = 3(a + 2b)= 3AB,又AB , AD有公共点A.所以A, B, D三点共线.答案:B3. 已知向量a, b, c中任意两个都不共线,但a + b 与c共线,且b+ c与a共线,则向量a+ b + c=( )A . aB . bC. c D . 0解析:依题意,设a+ b= me, b+ c= na,则有(a + b) —(b + c)= me—na, 即卩a—c= me—na.又a 与c 不共线,于是有m = —1, n = —1, a+ b = —c, a+ b + c= 0.答案:Df f4. 设D, E, F分别为△ ABC的三边BC, CA, AB的中点,贝U EB+ FC =( )f fA.BC1B.^ADf fC.AD1D.^BC解析:AC.- 3D. - 31 1如图,EB+ FC = EC+ CB+ FB + BC= EC + FB = q(AC + AB) = - 2AD = AD.答案:Cf f f5.已知O, A, B,C为冋一平面内的四个点,若 2 AC+ CB = 0,则向量OC等于()f f f f2 1A.3OA —3OB B . 1 2-3OA+3OBf f f fC. 2O A —OB D . —OA + 2 OBf f f f f f f f f f f f f解析:因为AC= OC—OA, CB = OB —OC,所以2AC + CB = 2(OC —OA) + (OB —OC)=OC —f f f f f2 OA + OB = 0,所以0C= 2 OA—OB.答案:C6.已知点G是厶ABC的重心,过点G作一条直线与AB, AC两边分别交于M , N两点,f f f f且AM = x AB, AN= y AC,则鶯的值为()A. 31B.1C. 21f f f f解析:由已知得M , G , N三点共线,所以AG =入AM + (1 —;)AN=入xAB + (1 —答案:B7.在△ ABC中,已知D是AB边上的一点,若AD = 2DB,2 於AC「.•点G是厶ABCf f f2 1的重心,••• AG = 3 X ^(AB + AC)f f1=3(AB+ AC),入x 3,亠3X,1-匕3y,1 1 1 1得3X+矿1,即X+1= 3,通分得xy x+ y13.f f f1CD = 3CA + QB,贝V入等于(C.- 3D. - 3A・3C.- 3D. - 3f f f f f f解析:T AD = 2DB,即CD —CA= 2(CB —CD),f f f••• CD = 3CA+ |CB,「・匕|.答案:Aa b&设a, b都是非零向量,下列四个条件中,使 a =肯成立的充分条件是()A . a= —bB . a// bC. a = 2b D . a / b 且ai= |b|解析:a= £? a=警?a与b共线且同向? a =入I且A> O.B, D选项中a和b可能反向.A |a| |b| |b|选项中入v 0,不符合X> 0.答案:Cf f9. 设D ABC所在平面内一点,BC = 3CD,则()f f f f f f1 4 1 4A.AD = —|AB + |ACB.AD = |AB —|ACf f f f f fC.AD = 4AB+ 1ACD.AD = 4AB —£A Cffff ff f f f f1 11 14解析:由题意得AD = AC+ CD = AC + |BC= AC + |AC —|AB= —|AB+ |AC,故选A.答案:Af ffff f f10. __________________________________________________________________________ 在△ ABC 中,点M, N 满足AM = 2MC , BN= NC.若MN = xAB + yAC,贝V x= ______________y= __________ .f f f f2 解析:•/ AM = 2MC ,• AM = |AC.f f f f f1•/ BN = NC ,• AN= |(AB + AC),f f f f f f1 MN = AN —AM =-(AB+ AC) —2A C2f f1 1 =2AB —6AC.f f f1 1又MN = xAB + yAC,• x=—, y =—一2 6_ 1—6fff fO 为四边形ABCD 所在平面内一点,且向量OA, OB , OC , 0D 满足等式OA + OC =OB + OD ,则四边形 ABCD 的形状为 ____________ .TTTTTTT TT T解析:由OA + OC = OB + OD 得OA - OB = OD — OC ,所以BA = CD ,所以四边形 ABCD 为平 行四边形.答案:平行四边形TTT12. _____________________________________________________________________ 在矩形ABCD 中,O 是对角线的交点,若BC = 5e i , DC = 3勺,则OC = ______________________ .(用印, e 2表示)TT T T T T1 1 1解析:在矩形ABCD 中,因为O 是对角线的交点,所以OC = I II AC = 2(AB + AD) = *DC + BC) =2(5 e i +3e 2).答案:芬+ 3e 2TT T TT1TT T TT TT解析:由OD = *0A + OB — CB) = ;(OA + OC),知点D 是线段AC 的中点,故D(2,2),所以BDT=(—2,2),故 |BD|= , — 2 2+ 22= 2 2. 答案:2 2B 组一一能力提升练1.已知e 1, e 2是不共线向量,a = m& + 2e 2, b = ne 1 — e 2,且mn ^ 0,若a // b ,则半等于( )II 1 A . — 2 B.2 C .— 2D . 2入n mm解析:T a / b ,— a =入 b 即卩 me 〔 + 2e 2= X ne 〔 一 e 2),则 i,故—=—2.I —入=2n答案:C答案:1 2 11.已知 T T13. 已知A(1,0), B(4,0) , C(3,4), O 为坐标原点,且OD = -(OA + OB —CB),则|BD|等于1 一3.在平面上,AB 1 丄 AB 2,|0B 1|= |0B 2|= 1, AP = AB 1+ AB 2.若 |0P|<2,则 |OA|的取值范围是( A . (0, — ———— — 又AB 1± AB 2, AP = AB 1 + AB 2,所以点A 在以B 1B 2为直径的圆上,当点P 与点0重合时,|0A1最大,为,2,当点P 在半径为2的圆周上时, —|0A|最小,为#故选D.答案:D4.在△ ABC 中, — — — — —BD = 3 DC ,若AD =入AB + h AC ,贝U 入乃的值为( )1 A~ 16 B .16 16C 1 C.210 D .?解析:由题意得, — — — — — — — — — —33 1 3AD = AB + BD = AB + :BC = AB + [(AC — AB) = [AB +•-入=4, ^=4‘二 “= 答案:B— — —5. 若点M 是厶ABC 所在平面内的一点,且满足 5 AM = AB + 3人6则厶ABM 与厶ABC 的2.在△ ABC 中,1 AN =4NC,若p 是直线BN 上的一点,且满足2AP = m AB + AC ,则实数 m5的值为(C . 1根据题意设 BP = n BN(n € R),则 AP = AB + BP = AB + n BN = AB + n(AN — AB)= AB +/ — —、 — —— n 1 " -AC — AB =(1.-— n —n)AB + 5AC , 又 AP = m '■■5选B.答案:B— — — — —— — 「1 n = m .2 1n =2,AB + ?C ,・ • f n 2 解得5 in = 5, m = —1,— — — —C .(解析:由题意得点B 1, B 2在以0为圆心的单位圆上,点1P 在以o 为圆心、半径为2的圆内,解析: 故If面积的比值为( )1 A.5 3 C.3D 三点共线,又AM = AD + DM ②,①②联立,得5 DM = 3 DC ,即在△ ABM 与厶ABC 中,33 边AB 上的高的比值为3,所以△ ABM 与厶ABC 的面积的比值为3.55答案:Cf fff6. 设M 是厶ABC 所在平面上的一点,且 MB + |M A + 3MC = 0, D 是AC 的中点,贝V 的|BM|值为()11 A.3B.1 C . 1D . 2解析: •/ D 是AC 的中点,延长MD 至E ,使得DE = MD (图略),•四边形 MAEC 为平行四f f f f边形,•• 1 1 -MD = 2ME = 2(MA + MC).ffffff f3 3 3••• MB + 2MA + 2MC = 0,二 MB = —,(MA + MC) = — 3MD ,...碑=」》丄=3,故选A.~f ~f 3|BM| |— 3MD|答案:Afff7. 如图所示,矩形 ABCD 的对角线相交于点 O , E 为AO 的中点,若DE =入AB +卩AD (人 □为实数),则*+ f=( )2 B.2 4 D・4解析:设AB 的中点为D ,如图,连接MDMC , 得 5 AM = 2 AD + 3AC ①,即 ff2 _ AM = 5AD+ 5AC ,2 3即-+ 3= 1,故 C , M , 5 5由 5 AM = AB + 3 AC ,A.55D .{6111111 AO 1 3 1 3DE =-DA + -DO =-DA +jDB = -DA + :(DA + AB)= AB — AD ,所以 X=-, 尸一:,222424 4 4 4 4f=5,故选A.8答案:A&在△ ABC 上,点 D 满足AD = 2AB — AC ,则( )A .点D 不在直线BC 上B .点D 在BC 的延长线上 C .点D 在线段BC 上 D .点D 在CB 的延长线上ff f解析:AD = 2AB — ACf f f =AB + AB — ACf f=AB + CB ;如图,f f作BD ' = CB ,连接AD ',则:f f ffffAB + CB = AB + BD ' = AD ' = AD ; ••• D '和D 重合;•••点D 在CB 的延长线上. 答案:Dff9.如图,在直角梯形 ABCD 中,AB = 2AD = 2DC , E 为BC 边上一点,BC = 3 EC , F 为AEf的中点,贝U BF =( )C . 1解析:T T1 2D . —-AB+3AD解析:如图,取AB的中点G,连接DG, CG,则易知四边形DCBG为平行四边形,所以BCT T T T T T T T T T T1 2 2=GD = AD —AG= AD —|AB,「・AE= AB+ BE= AB + _BC = AB+ - AD —_AB T T T T T1 1于是BF = AF —AB= |AE—AB = |答案:T TA.|AB-1A D10.设 D ABC所在平面内一点,且BC = 3BD , 则AD =( )T- 1A.§AB+ 3AC1 -B.3AB + -AC3’T T4 1C.3AB+ 3ACT T2 5解析:•/ BC= 3BDT T T T••• BD = 3BC= 3(AC —AB),贝U AD = AB+ BD = AB+T〜1—AB)= 3AB + 3AC.答案:A2 1C.—3AB + 3ADT T=細+[AD ,,故选C.11. 已知0为坐标原点,B 、D 分别是以O 为圆心的单位圆与 x 轴正半轴、y 轴正半轴的交•'•OB + OD = x(OB — OD) + yOP ,TTT•yOP = (1 — x)OB + (1 + x)OD ,①解得 x = 2— 3, y = 2工:3— 2,「. x + y = , 3,故选 B. 答案:B12. ___________________________________________________________________________ 已知向量e 1、e?是两个不共线的向量, 右a = 2e 1 — e ?与b = e 1 +入e 共线,贝卩入=_____________________________________________________________________________________________■x = 2解析:因为a 与b 共线,所以a = xb ,, I入 x — 1故 A - 2.13. 如图,在厶ABC 中,AB = 2, BC = 3, Z ABC = 60 ° AH 丄BC 于点H , M 为AH 的中点.若TTT点,点P 为单位圆劣弧 BD 上一点,A . 1 C . 2ff解析:如图,DB = OB — OD ,T T T T TT TTTn若0B + OD = xDB + yOP , / BOP =-,3B.-D . 4— 3,3则 x + y =(n••ZBOP =-,TTTOP = *0B + ~2-OD ,T •yOP =TT;OB + ~2-yOD ,®由①②得1 — .1 + x =x =y 2,y ,AM = ?AB+ 迟C,则 + [i=____________ .答案:小1 1nb,CG n PQ=H,CG=2CH,则m+n=f f f f1 1 解析:由AN= 3NC,可知AN = 4AC,f f f f f又AP= mAB+121AC= mAB+塔AN,且B P、N 共线,••• m+11= 1,••• m= 3解析:因为点M为AH的中点, ;AB +JJ BC,所以入=6,1+ BH)= 2严+ 3BC ,f f1 1=-AB+R BC ,2 6又AM =尸6,所以14.(2018临汾模拟)如图,△ ABC 中, GA + GB+ GC = 0, CA= a,CB = b.若CP= ma,CQ =解析:f f f由GA+ GB+ GC = 0,知G ABC的重心,取AB的中点f1D(图略),贝U CH = ^CG =答案: f f f f+C B)=6m CP+6n CQ,由P, H , Q三点共线,得11= 1,则丄 +1= 6.6m 6n m nf115.如图,在△ ABC 中,AN = 3NC ,f f fP是BN上的一点,若AP= mAB + ^AC,则实数m的值因为AB = 2,Z ABC= 60°f f f f所以AM = 1A H =6答案:3 1 1。
向量一、选择题1.已知平行四边形ABCD 中,AD =(3,7), AB =(-2,3),对角线AC 、BD 交于O ,则CO 的坐标是( ) A.(- 21,5) B.(- 21, -5) C.( 21),-5) D.( 21,5) 2.设点P 分21P P 的比为λ,若|21P P |=4|2PP |,则λ的值为( )A..-5或3B.-4或2C.5或-3D.4或-23.三点A(x 1,y 1)、B(x 2,y 2)、C(x 3,y 3)共线的充要条件是( )A.x 1y 2-x 2y 1=0B.x 1y 3-x 3y 1=0C.(x 2-x 1)(y 3-y 1)=(x 3-x 1)(y 2-y 1)D.(x 2-x 1)(x 3-x 1)=(y 2-y 1)(y 3-y 1)4.已知点A(1,8),B(5,0)且|PA |=3|PB |,(A 、B 、P 三点共线)则点P 的坐标为( )A.(4,2)B.(7,-4)C.(4,2)或(7,-4)D.不存在5.设=(23,sin α), =(cos α,31)且∥,则锐角α为( ) A.30°B.60°C.45°D.75° 6.点P 分有向线段21P P 成定比λ,若λ∈(-∞,-1),则λ所对应点,P 的集合是( )A.线段P 1P 2B.线段P 1P 2的延长线C.射线P 2P 1D.线段P 1P 2的反向延长线7.已知向量AB =(6,1), BC =(x,y), CD =(-2,-3),则DA =( )A.(x+4,2-y)B.(x-4,2-y)C.(x-4,y-2)D.(-4-x,-y+2)8.已知M(-1,0),N(5,6),P(3,4),P 为MN 的定比分点,则λ的值是( ) A.31 B.3 C. 21 D.29.已知=(1,2), =(x,1),当+2与2-共线时,x 值为( )A.1B.2C. 31D. 21 10.在△ABC 中,A(3,1),AB 中点为D(2,4),三角形的重心G(3,4),则B 、C 坐标分别为( )A.(1,7)、(4,5)B.(1,7)、(5,4)C.(7,1)、(4,5)D.(7,1)、(5,4)11.如果1e 、2e 是平面α内所有向量的一组基底,那么( )A.若实数λ1、λ2,使λ11e +λ22e =,λ1=λ2=0B.空间任一向量a 可以表示为a =λ11e +λ22e ,这里λ1、λ2是实数C.对实数λ1、λ2,λ11e +λ22e )不一定在平面α内D.对平面α内的任一向量a ,使a =λ11e +λ22e 的实数λ1、λ2有无数对.12.已知:平面上有三个点A(-2,1)、B(1,4)、D(4,-3),又有一点C 在线段AB 上,使||=2||,连结DC 并延长至E ,使||=4||,则点E 的坐标为( )A.(0,1)B.(-83 ,311)C.(0,1)或(-38,311)D.(-8,-35) 二、填空题:1.已知1e 、2e 是一对不共线的非零向量,若=1e +λ2e , b =-2λ1e -2e ,且、共线,则λ= .2.若向量=(1,-2)的终点在原点,那么这个向量的始点坐标是 .3. 在△ABC 中,已知=a ,CA =c ,O 是△ABC 的重心,则OB +OC = .4.已知△ABC 的顶点A(4,5),重心G(-1,2),则BC 边的中点D 坐标为三、解答题:1.已知=,B(1,0), =(-3,4), =(-1,1),且=3-2,求点A 的坐标.2.已知△ABC ,A(7,8)、B(3,5)、C(4,3),M 、N 是AB 、AC 的中点,D 是BC 中点,MN 与AD 交于F ,求DF .3.已知A(1,-2),B(2,1),C(3,2)和D(-2,3),以、为一组基底来表示++. 4.已知两点A(3,-4)、B(-9,2),在直线AB 上求一点P ,使得|AP |=31|AB |. 5.正方形ABCO ,按顺时针方向依次为A →B →C →O ,O 为坐标原点=(1,3),求向量,OC 的坐标.6.已知点M(2,3)、N(8,4),点P 在线段MN 内,且MP =λPN =λ2MN ,求λ的值及P 点的坐标.附加题1、已知,不共线,=+, =2-,将符合下列条件的向量写成m +n )的形式:(1)点C 分所成的比λ=2,则= .(2)点C 分所成的比λ=-3,则= .2、已知平行四边形三个顶点是(3,-2),(5,2),(-1,4),则第四个顶点的坐标为 .3、已知A(2,3)、B(0,1)、C(3,0),点D 、E 分别在AB 、AC 上,DE ∥BC ,且DE 平分△ABC 的面积,求点D 的坐标. 向量测试01 一、选择题 BACCC BDDDB AB 二、填空 1.±22 2. (-1,2) 3. 31 (a -c ) 4. (- 27,21) 三、解答题: 1.(8,-10) 2. DF =-21 AD =(47,2) 3.32AB -22AC 4、.P(-1,-2)或P(7,-6)5、OA =(231-,231+), OC =2 (462+,62-) 6、λ=215-,P(11-35,259-) 附加题1、解:(1)由AC =λCB ,有OC -OA =λ(OB -OC )有OC =λ+11OA +λλ+1OB 所以OC =211+OA +212+OB =31 (a +b )+32(a -b )=35a -31b (2) OC =λ+11 OB +λλ+1OA =-21 (2a -b )+23( a +b )=21a +2b 2、解:如图,设OA =(3,-2), OB =(5,-2), OC =(-1,4), OD =(x,y)依题意,AB =DC 或AC =DB 或AB =CD由AB =DC ,可得:OB -OA =OC -OD即(5,2)-(3,2)=(-1,4)-(x,y) ⇔ (2,4)=(-1-x,4-y)∴D(-3,0)同理,若=可得:(-4,6)=(5-x,2-y).∴x=9,y=-4, ∴D(9,4)若=可得:(2,4)=(x+1,y-4)∴x=1,y=8. ∴D(1,8)∴点D 的坐标为(-3,0)或(9,-4)或(1,8)3、解:因为DE ∥BC ,则有△ADE ∽△ABC.有ABC ADE S S △△=(ABAD )2 由已知,有(AB AD )2=21,即AB AD =21以点D 分所成的比为λ,利用分点定义可得λ=121-=2+1所以得点D 的横、纵坐标为 x=1212++=2-2,y=121123++++=3-2则点D 的坐标为(2-2,3-2)。
课时作业 A 组——基础对点练1.(2017·杭州模拟)在△ABC 中,已知M 是BC 中点,设CB →=a ,CA →=b ,则AM →=( )A.12a -b B.12a +b C .a -12bD .a +12b解析:AM →=AC →+CM →=-CA →+12CB →=-b +12a ,故选A.答案:A2.已知AB →=a +2b ,BC →=-5a +6b ,CD →=7a -2b ,则下列一定共线的三点是( ) A .A ,B ,C B .A ,B ,D C .B ,C ,DD .A ,C ,D解析:因为AD →=AB →+BC →+CD →=3a +6b =3(a +2b )=3AB →,又AB →,AD →有公共点A .所以A ,B ,D 三点共线. 答案:B3.已知向量a ,b ,c 中任意两个都不共线,但a +b 与c 共线,且b +c 与a 共线,则向量a +b +c =( ) A .a B .b C .cD .0解析:依题意,设a +b =mc ,b +c =na ,则有(a +b )-(b +c )=mc -na ,即a -c =mc -na .又a 与c 不共线,于是有m =-1,n =-1,a +b =-c ,a +b +c =0. 答案:D4.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=( )A.BC →B.12AD →C.AD →D.12BC →解析:如图,EB →+FC →=EC →+CB →+FB →+BC →=EC →+FB →=12(AC →+AB →)=12·2AD →=AD →.答案:C5.已知O ,A ,B ,C 为同一平面内的四个点,若2 AC →+CB →=0,则向量OC →等于( )A.23OA →-13OB →B .-13OA →+23OB →C .2 OA →-OB →D .-OA →+2 OB →解析:因为AC →=OC →-OA →,CB →=OB →-OC →,所以2 AC →+CB →=2(OC →-OA →)+(OB →-OC →)=OC →-2 OA →+OB →=0,所以OC →=2 OA →-OB →. 答案:C6.已知点G 是△ABC 的重心,过点G 作一条直线与AB ,AC 两边分别交于M ,N 两点,且AM →=x AB →,AN →=y AC →,则xyx +y 的值为( )A .3 B.13 C .2D.12 解析:由已知得M ,G ,N 三点共线,所以AG →=λ AM →+(1-λ)AN →=λx AB →+(1-λ)y AC →.∵点G 是△ABC 的重心,∴AG →=23×12(AB →+AC →)=13(AB →+AC →),∴⎩⎨⎧λx =13,(1-λ)y =13,即⎩⎨⎧λ=13x,1-λ=13y,得13x +13y =1,即1x +1y =3,通分得x +y xy =3,∴xy x +y =13. 答案:B7.在△ABC 中,已知D 是AB 边上的一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ等于( )A.23B.13 C .-13D .-23解析:∵AD →=2DB →,即CD →-CA →=2(CB →-CD →), ∴CD →=13CA →+23CB →,∴λ=23.答案:A8.设a ,b 都是非零向量,下列四个条件中,使a |a |=b|b |成立的充分条件是( )A .a =-bB .a ∥bC .a =2bD .a ∥b 且|a |=|b |解析:a |a |=b |b |⇔a =|a |b|b |⇔a 与b 共线且同向⇔a =λb 且λ>0.B ,D 选项中a 和b 可能反向.A选项中λ<0,不符合λ>0. 答案:C9.设D 为△ABC 所在平面内一点,BC →=3CD →,则( )A.AD →=-13AB →+43AC →B.AD →=13AB →-43AC →C.AD →=43AB →+13AC →D.AD →=43AB →-13AC →解析:由题意得AD →=AC →+CD →=AC →+13BC →=AC →+13AC →-13AB →=-13AB →+43AC →,故选A.答案:A10.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________.解析:∵AM →=2MC →,∴AM →=23AC →.∵BN →=NC →,∴AN →=12(AB →+AC →),∴MN →=AN →-AM →=12(AB →+AC →)-23AC →=12AB →-16AC →. 又MN →=xAB →+yAC →,∴x =12,y =-16.答案:12 -1611.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA →+OC →=OB →+OD →,则四边形ABCD 的形状为________.解析:由OA →+OC →=OB →+OD →得OA →-OB →=OD →-OC →,所以BA →=CD →,所以四边形ABCD 为平行四边形. 答案:平行四边形12.在矩形ABCD 中,O 是对角线的交点,若BC →=5e 1,DC →=3e 2,则OC →=________.(用e 1,e 2表示)解析:在矩形ABCD 中,因为O 是对角线的交点,所以OC →=12AC →=12(AB →+AD →)=12(DC →+BC →)=12(5e 1+3e 2). 答案:52e 1+32e 213.已知A (1,0),B (4,0),C (3,4),O 为坐标原点,且OD →=12(OA →+OB →-CB →),则|BD →|等于__________.解析:由OD →=12(OA →+OB →-CB →)=12(OA →+OC →),知点D 是线段AC 的中点,故D (2,2),所以BD→=(-2,2),故|BD →|=(-2)2+22=2 2.答案:2 2B 组——能力提升练1.已知e 1,e 2是不共线向量,a =me 1+2e 2,b =ne 1-e 2,且mn ≠0,若a ∥b ,则mn 等于( )A .-12B.12 C .-2D .2解析:∵a ∥b ,∴a =λb ,即me 1+2e 2=λ(ne 1-e 2),则⎩⎪⎨⎪⎧λn =m -λ=2,故mn=-2.答案:C2.在△ABC 中,AN →=14NC →,若P 是直线BN 上的一点,且满足AP →=m AB →+25AC →,则实数m的值为( ) A .-4 B .-1 C .1D .4 解析:根据题意设BP →=n BN →(n ∈R),则AP →=AB →+BP →=AB →+n BN →=AB →+n (AN →-AB →)=AB →+n ⎝ ⎛⎭⎪⎫15AC →-AB →=(1-n )AB →+n 5AC →,又AP →=m AB →+25AC →,∴⎩⎪⎨⎪⎧1-n =m ,n 5=25,解得⎩⎪⎨⎪⎧n =2,m =-1,故选B. 答案:B3.在平面上,AB 1→⊥AB 2→,|OB 1→|=|OB 2→|=1,AP →=AB 1→+AB 2→.若|OP →|<12,则|OA →|的取值范围是( )A .(0,52] B .(52,72] C .(52,2] D .(72,2] 解析:由题意得点B 1,B 2在以O 为圆心的单位圆上,点P 在以O 为圆心、半径为12的圆内,又AB 1→⊥AB 2→,AP →=AB 1→+AB 2→,所以点A 在以B 1B 2为直径的圆上,当点P 与点O 重合时,|OA →|最大,为2,当点P 在半径为12的圆周上时,|OA →|最小,为72,故选D.答案:D4.在△ABC 中,BD →=3 DC →,若AD →=λ1 AB →+λ2 AC →,则λ1λ2的值为( )A.116B.316C.12D.109解析:由题意得,AD →=AB →+BD →=AB →+34BC →=AB →+34(AC →-AB →)=14AB →+34AC →,∴λ1=14,λ2=34,∴λ1λ2=316.答案:B5.若点M 是△ABC 所在平面内的一点,且满足5 AM →=AB →+3 AC →,则△ABM 与△ABC 的面积的比值为( ) A.15 B.25 C.35D.45解析:设AB 的中点为D ,如图,连接MD ,MC ,由5 AM →=AB →+3 AC →,得5 AM →=2 AD →+3 AC →①,即AM →=25AD →+35AC →,即25+35=1,故C ,M ,D 三点共线,又AM →=AD →+DM →②,①②联立,得5 DM →=3 DC →,即在△ABM 与△ABC 中,边AB 上的高的比值为35,所以△ABM 与△ABC 的面积的比值为35.答案:C6.设M 是△ABC 所在平面上的一点,且MB →+32MA →+32MC →=0,D 是AC 的中点,则|MD →||BM →|的值为( ) A.13 B.12 C .1D .2 解析:∵D 是AC 的中点,延长MD 至E ,使得DE =MD (图略),∴四边形MAEC 为平行四边形,∴MD →=12ME →=12(MA →+MC →).∵MB →+32MA →+32MC →=0,∴MB →=-32(MA →+MC →)=-3MD →,∴|MD →||BM →|=|MD →||-3MD →|=13,故选A. 答案:A7.如图所示,矩形ABCD 的对角线相交于点O ,E 为AO 的中点,若DE →=λ AB →+μ AD →(λ,μ为实数),则λ2+μ2=()A.58B.14 C .1D.516解析:DE →=12DA →+12DO →=12DA →+14DB →=12DA →+14(DA →+AB →)=14AB →-34AD →,所以λ=14,μ=-34,故λ2+μ2=58,故选A.答案:A8.在△ABC 上,点D 满足AD →=2AB →-AC →,则( )A .点D 不在直线BC 上B .点D 在BC 的延长线上 C .点D 在线段BC 上 D .点D 在CB 的延长线上解析:AD →=2AB →-AC →=AB →+AB →-AC →=AB →+CB →; 如图,作BD ′→=CB →,连接AD ′,则: AB →+CB →=AB →+BD ′→=AD ′→=AD →; ∴D ′和D 重合;∴点D 在CB 的延长线上. 答案:D9.如图,在直角梯形ABCD 中,AB =2AD =2DC ,E 为BC 边上一点,BC →=3 EC →,F 为AE的中点,则BF →=( )A.23AB →-13AD → B.13AB →-23AD →C .-23AB →+13AD →D .-13AB →+23AD →解析:如图,取AB 的中点G ,连接DG ,CG ,则易知四边形DCBG 为平行四边形,所以BC →=GD →=AD →-AG →=AD →-12AB →,∴AE →=AB →+BE →=AB →+23BC →=AB →+23⎝ ⎛⎭⎪⎫AD →-12AB →=23AB →+23AD →,于是BF →=AF →-AB →=12AE →-AB →=12⎝ ⎛⎭⎪⎫23AB →+23AD →-AB →=-23AB →+13AD →,故选C.答案:C10.设D 为△ABC 所在平面内一点,且BC →=3BD →,则AD →=( )A.23AB →+13AC →B.13AB →+23AC →C.43AB →+13AC → D.23AB →+53AC →解析:∵BC →=3BD →∴BD →=13BC →=13(AC →-AB →),则AD →=AB →+BD →=AB →+13(AC →-AB →)=23AB →+13AC →.答案:A11.已知O 为坐标原点,B 、D 分别是以O 为圆心的单位圆与x 轴正半轴、y 轴正半轴的交点,点P 为单位圆劣弧BD 上一点,若OB →+OD →=xDB →+yOP →,∠BOP =π3, 则x +y =( )A .1 B. 3 C .2D .4-3 3 解析:如图,DB →=OB →-OD →, ∴OB →+OD →=x (OB →-OD →)+yOP →,∴yOP →=(1-x )OB →+(1+x )OD →,① ∵∠BOP =π3,∴OP →=12OB →+32OD →,∴yOP →=y 2OB →+32yOD →,②由①②得⎩⎨⎧1-x =y2,1+x =32y ,解得x =2-3,y =23-2,∴x +y =3,故选B.答案:B12.已知向量e 1、e 2是两个不共线的向量,若a =2e 1-e 2与b =e 1+λe 2共线,则λ=________.解析:因为a 与b 共线,所以a =xb ,⎩⎪⎨⎪⎧x =2λx =-1,故λ=-12.答案:-1213.如图,在△ABC 中,AB =2,BC =3,∠ABC =60°,AH ⊥BC 于点H ,M 为AH 的中点.若AM →=λAB →+μBC →,则λ+μ=________.解析:因为AB =2,∠ABC =60°,AH ⊥BC ,所以BH =1.因为点M 为AH 的中点,所以AM →=12AH →=12(AB →+BH →)=12⎝ ⎛⎭⎪⎫AB →+13BC →=12AB →+16BC →,又AM →=λAB →+μBC →,所以λ=12,μ=16,所以λ+μ=23.答案:2314.(2018·临汾模拟)如图,△ABC 中,GA →+GB →+GC →=0,CA →=a ,CB →=b .若CP →=ma ,CQ →=nb ,CG ∩PQ =H ,CG →=2CH →,则1m +1n =________.11解析:由GA →+GB →+GC →=0,知G 为△ABC 的重心,取AB 的中点D (图略),则CH →=12CG →=13CD →=16(CA →+CB →)=16m CP →+16n CQ →,由P ,H ,Q 三点共线,得16m +16n =1,则1m +1n=6. 答案:615.如图,在△ABC 中,AN →=13NC →,P 是BN 上的一点,若AP →=mAB →+211AC →,则实数m 的值为________.解析:由AN →=13NC →,可知AN →=14AC →, 又∵AP →=mAB →+211AC →=mAB →+811AN →,且B 、P 、N 共线,∴m +811=1,∴m =311. 答案:311。