北师大版高二年级上学期数学期中试卷文科

2024-2025学年五年级上学期数学北师大版期中模拟检测（1~4单元）学校:___________姓名：___________班级：___________等级：___________一．填空题1．有一个四位数，它的最高位上是最小的质数，百位上是最大的一位数，十位上是最小的合数，个位上的数既是偶数又是质数。

这个四位数是 。

2．有74千克的油，每个油桶最多装6千克油，至少要 个油桶才能把油装完。

3．如果一个两位小数的近似数是7.9，那么这个两位小数最大是 ，最小是 。

4．7个3.4是 ，9.6是16的 倍。

5．等边三角形有 条对称轴， 三角形有一条对称轴。

6．一场演出9：00开始，12：00结束，会场时钟上的时针从演出开始到结束沿 方向旋转了　度。

7．511至少加上 才是3的倍数，至少减去 才是2和5的倍数．8．一块平行四边形麦田占地面积2公顷，已知它的高是50米，底是 米。

二．选择题9．在计算除法时，如果要求得数精确到十分位，通常商应除到（ ）A．十分位B．百分位C．千分位D．万分位10．图形的平移没有改变图形的( )。

A．形状和大小B．位置和大小C．位置和形状D．方向和位置11．20以内所有质数的和是（ ）A．76B．77C．78D．8012．下面各组数中，三个连续自然数都是合数的是（ ）A．13、14、15B．7、8、9C．14、15、1613．如图，两条平行线间的甲、乙两个梯形的面积相等，梯形乙的上底是（ ）cm。

A．3B．4C．4.514．自然数中，凡是17的倍数（ ）三．判断题15．平行四边形的底和高分别扩大到原来的2倍，面积也扩大到原来的2倍。

（ ）16．因为7×3=21，所以7和3都是因数，21是倍数。

（ ）17．循环小数都是无限小数，无限小数都是循环小数． ．18．一个自然数（0除外）的倍数有无限个，其中最小的倍数是它本身． ．19．直接写出得数。

0.1﹣0.03＝0.6÷0.12＝0.24×0.5＝1﹣0.2÷0.2＝0.32÷0.04＝0×3.75＝0.3+0.44＝ 2.5+0.5×0.7＝1.111÷1.01＝ 1.8×1.01＝2÷0.4＝2.5×4×8＝四．计算题20．直接写出得数。

高二数学（期中试卷） 宝鸡铁一中 孙敏一、选择题（本大题共12小题，每小题4分，共48分；每小题所给的四个选项中只有一个选项符合题意）1、在数列{}n a 中，111012,221,n n a a a a +==+则的值为（ ）A ．49B ．50C ．51D ．52 2、63x y -<不在4表示的平面区域内的点是（） A ．()00， B ．()12， C ．()21， D ．()31，3、x y y =若1，，，z,25五个数成等比数列，则（） A ．5 B ．5- C ．5± D ．24、已知a ，b ，c ，d ∈R ，则下列命题中必然成立的是（）A ．若a >b ，c >b ，则a >cB ．若a >－b ，则c －a <c +bC ．若a 2>b 2，则－a <－bD ．若a >b ，c >d ，则>a bc d5、{}9n n a a n =数列的通项公式该数列的前项和等于，则n=（ ）A ．98B ．99C ．96D ．97 6、{}202,023axbax b x x x x ++>>>--不等式的解集为则不等式 的解集为（ ） A.{}213x x x -<<->或 B ．{}321x x x -<<->或 C.{}123x x x -<<>或 D ．{}231x x x <<<-或7、222sin sin ,cos cos 0,ABC A B C b B c C ∆=+⋅-⋅=已知中，sin 则ABC ∆是（ ）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形 8、()()222240a x a x x R -+--<∈若不等式对一切恒成立，则a 的取值范围是（ ）A ．(]2-∞，B ．(]22-，C ．[]22-，D ．()2-∞， 9、4,ABC ABC a b ∆∆==已知中，,则S =（ ）A．19 BC ．4819D．1910、{}138n n a a n S 在等差数列中，=-25，S =S ,则前项和的最小值为（ ）A ．-75B ．-80C ．-76D ． -7411、()()21x y xy x x ⊕=-⊕+定义运算，则的最大值是（ ）A ．1B ．12 C． D ．1412、00,23x y x y x y x y y a -≤⎧⎪+≥+⎨⎪≤⎩若实数、满足且z=的最大值是，则a =( )A ．1B ．1-C ．0D ．2、填空题（本大题共4小题，每小题5分，共20分。

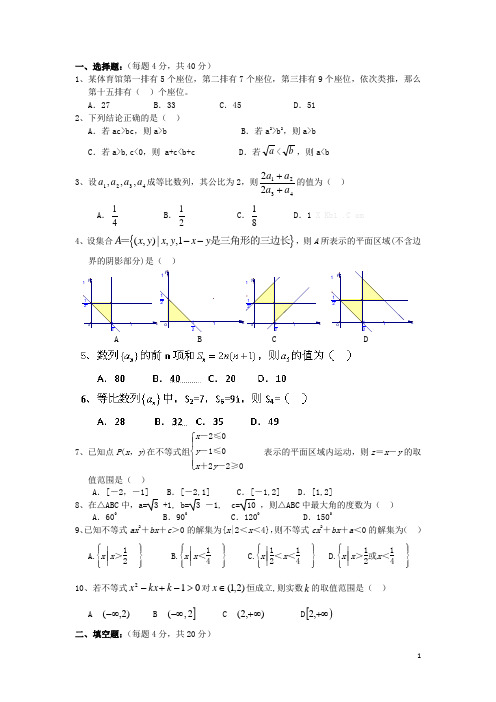
一、选择题：（每题4分，共40分）1、某体育馆第一排有5个座位，第二排有7个座位，第三排有9个座位，依次类推，那么第十五排有（ ）个座位。

A ．27B ．33C ．45D ．51 2、下列结论正确的是（ ）A ．若ac>bc ，则a>bB ．若a 2>b 2，则a>b C ．若a>b,c<0，则 a+c<b+c D ．若a <b，则a<b 3、设4321,,,a a a a 成等比数列，其公比为2，则432122a a a a ++的值为（ ）A ．41 B ．21 C ．81D ．1 X Kb1 .C om 4、设集合{}(,)|,,1A x y x y x y --＝是三角形的三边长，则A 所表示的平面区域(不含边界的阴影部分)是（ ）121112oyx 121112oyx121112oyx121112oyxA B C D7、已知点P (x ，y )在不等式组⎩⎪⎨⎪⎧x －2≤0y －1≤0x ＋2y －2≥0表示的平面区域内运动，则z ＝x －y 的取值范围是（ ）A ．[－2，－1]B ．[－2,1]C ．[－1,2]D ．[1,2]8、在△ABC 中，a= 3 +1, b= 3 －1, c=10 ，则△ABC 中最大角的度数为（ ）A ．600B ．900C ．1200D ．15009、已知不等式ax 2＋bx ＋c ＞0的解集为{x |2＜x ＜4}，则不等式cx 2＋bx ＋a ＜0的解集为（ ）A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＞12 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜14 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12＜x ＜14 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＞12或x ＜14 10、若不等式012>-+-k kx x 对)2,1(∈x 恒成立,则实数k 的取值范围是（ ） A )2,(-∞ B ]2,(-∞ C ),2(+∞ D [)+∞,2 二、填空题：（每题4分，共20分）11、已知数列{ a n }满足条件a 1 = –2 , a n + 1 =2 +nna 1a 2-, 则a 5 = 12、不等式13x x+<的解集为 13、设,x y R +∈且191x y+=,则x y +的最小值为________. 14、等差数列{}n a 中，01>a ，且13853a a =，则}{n S 中最大项为 15、一船以每小时15km 的速度向东航行，船在A 处看到一个灯塔B 在北偏东60，行驶4h 后，船到达C 处，看到这个灯塔在北偏东15，这时船与灯塔的距离为__ km ． 三、解答题：（共60分）18、（10分）某工厂家具车间造A 、B 型两类桌子，每张桌子需木工和漆工两道工序完成已知木工做一张A 、B 型桌子分别需要1小时和2小时，漆工油漆一张A 、B 型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张A 、B 型桌子分别获利润2千元和3千元，试问工厂每天应生产A 、B 型桌子各多少张，才能获得利润最大？ 19、（12分）已知△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ，若a 、b 、c 成等差数列，且2cos2B-8cosB+5=0,求角B 的大小并判断△ABC 的形状.20、（14分）设数列{}n a 的前项n 和为n S ，若对于任意的正整数n 都有n a S n n 32-=. （1）设3n n b a =+，求证：数列{}n b 是等比数列，并求出{}n a 的通项公式。

河南省青桐鸣2024-2025学年高二上学期10月联考数学试卷（北师大版）一、单选题1．在正三棱柱111ABC A B C -中，则平面ABC 内不可能存在一条直线与直线1AC （ ） A ．平行B ．垂直C ．相交D ．异面2．已知角θ∈R ，直线()1cos 12y x θ=-的倾斜角的取值范围是（ ） A ．3π,π4⎡⎫⎪⎢⎣⎭B ．π0,4⎡⎤⎢⎥⎣⎦C ．3π,π4⎡⎤⎢⎥⎣⎦D ．{}3π,π04⎡⎫⎪⎢⎣⎭U3．已知tan 2α=-，则2sin cos 1cos sin cos ααααα+=+（ ）A ．3B ．-3C ．2D ．-24．已知直线l 过点()1,2，且直线l 与直线1y ax =-平行，与直线11y x a a ⎛⎫=++ ⎪⎝⎭垂直，0a ≠，则直线l 的方程为（ ） A ．20x y +-= B ．240x y +-=C ．20x y --=D ．240x y --=5．已知在ABC V 中， D ，E 分别为AC ，AB 的中点， BD b =u u u r r ，CE c =r u u u r ，则AB u u u r可以用含b r ，c r的式子表示为（ ）A ．1433b c --r rB ．4233b c --r rC ．2433b c +r rD ．4233b c +r r6．将函数()2πsin 03y x ωω⎛⎫=+> ⎪⎝⎭的图象向左平移π6个单位长度后所得图象关于直线π12x =-对称，则ω的最小值为（ ）A ．8B ．9C ．10D ．127．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，a 45A =︒，则下列说法错误的是（ ）A ．若60B =︒，则b =B ．若120B =︒，则bC ．若32b =，则B 有两解 D ．若2b =，则B 有两解8．在正四棱柱1111ABCD A B C D -中， 2AB =，14AA =，M 是该正四棱柱表面上的一动点，且满足1DM BD ⊥，则点M 的运动轨迹的长度为（ ）A ．8B ．C ．D ．二、多选题9．已知复数()i ,,0z a b a b b =+∈≠R ，z 为z 的共轭复数，则下列说法正确的是（ ） A ．若2i1i z=+，则1i z =+ B ．若2i z z =-，则1b = C ．z z =D ．若()2i z -为实数，则2a b =10．已知函数()()()()2sin 0,0,2πf x x ωϕωϕ=+>∈在π5π,36⎡⎤⎢⎥⎣⎦上单调，且π13f ⎛⎫= ⎪⎝⎭，5π26f ⎛⎫=- ⎪⎝⎭，则下列说法正确的是（ ） A ．1ω= B ．43ω=C ．29πϕ=D ．718πϕ=11．已知圆M 过点()1,3A ，()2,4B -，且圆心M 在x 轴上，则下列说法正确的是（ ）A ．圆心M 的坐标为5,03⎛⎫- ⎪⎝⎭B ．圆M 的标准方程为22514539x y ⎛⎫++= ⎪⎝⎭C ．圆M 与y 轴的交点坐标为0,⎛ ⎝⎭D ．圆M 上一点到点10,03⎛⎫ ⎪⎝⎭距离的最大值为5三、填空题12．在平面直角坐标系中，向量()1,3a =r，()1,2b =-r ，且满足()()a b a b λλ+⊥-r r r r ，其中0λ>，则λ=.13．已知0θ360<<o o ，且角θ终边上有一点()tan200,1-o，则角θ=.14．已知角α，0,2πβ⎛⎫∈ ⎪⎝⎭，tan tan 2αβ=，()5sin 13αβ-=，则()cos αβ+=.四、解答题15．在平面直角坐标系中，点A 的坐标为()2,3-，直线l ：()()22130x y λλλ++-+-=，R λ∈.(1)若直线l 过点A ，求λ的值； (2)求点A 到直线l 距离的最大值.16．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且s i n s i n s i n s i n a A b B a B c C +-=.(1)求角C 的值；(2)若2c =，求ABC V 周长的最大值.17．已知函数()22sin cos 3cos f x x x x x =++. (1)求()f x 的值域；(2)求()f x =[]0,2πx ∈上所有实数根的和.18．已知圆22:1O x y +=，M 为直线:34100l x y +-=上一动点，直线MA ，MB 分别切圆O 于点A ，B .(1)若AB M 的坐标； (2)求cos AMB ∠的最小值.19．如图，在正三棱台111ABC A B C -中， 1122AB A B ==，11AB BC ⊥.(1)求1AA 的长度；(2)求三棱台111ABC A B C -的体积.。

2024-2025学年九年级数学上学期期中模拟卷（陕西专用）（考试时间：120分钟试卷满分：120分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

4．测试范围：北师大版九年级（九上全册）。

5．难度系数：0.69。

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．下列函数不是反比例函数的是（ ）A．y＝3x﹣1B．y=―x3C．xy＝5D．y=12x2．如图是某个几何体的三视图，则该几何体是（ ）A．圆锥B．长方体C．三棱柱D．圆柱3．若双曲线y=k―1x的图象经过第二、四象限，则k的取值范围是（ ）A．k＞1B．k＜1C．k＝1D．不存在4．在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.7左右，则布袋中白球可能有（ ）A．15个B．20个C．30个D．35个5．如图，AD∥BE∥CF，若AB＝2，AC＝5，EF＝4，则DE的长度是（ ）A ．6B ．23C ．53D ．836．在长为30m ，宽为20m 的长方形田地中开辟三条入口宽度相等的道路，已知剩余田地的面积为468m 2，求道路的宽度设道路的宽度为x （m ），则可列方程（ ）A ．（30﹣2x ）（20﹣x ）＝468B ．（20﹣2x ）（30﹣x ）＝468C ．30×20﹣2×30x ﹣20x ＝468D ．（30﹣x ）（20﹣x ）＝4687．如图，正方形四个顶点分别位于两个反比例函数y =3x和y =n x 的图象的四个分支上，则实数n 的值为（ ）A ．﹣3B ．―13C ．13D ．38．如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE AE =34，BE ＝1，F 是BC 的中点．现有下列四个结论：①DE ＝3；②四边形DEBC 的面积等于9；③（AC +BD ）（AC ﹣BD ）＝80；④DF ＝DE ．其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个二、填空题（共5小题，每小题3分，计15分）9．广场上，一个大型字母宣传牌垂直于地面放置，其投影如图所示，则该投影属于__________.（填“平行投影”或“中心投影”）10．反比例函数y =k x的图象经过点（1，6）和（m ，﹣3），则m ＝__________．11．已知等腰三角形的两边长是方程x 2﹣9x +18＝0的两个根，则该等腰三角形的周长为__________．12．如图，在菱形ABCD 中，AC ＝24，BD ＝10．E 是CD 边上一动点，过点E 分别作EF ⊥OC 于点F ，EG⊥OD 于点G ，连接FG ，则FG 的最小值为__________．13．如图，在Rt △ABC 中，∠C ＝90°，AC ＝10cm ，BC ＝8cm ．点P 从点C 出发，以2cm /s 的速度沿着CA向点A 匀速运动，同时点Q 从点B 出发，以1cm /s 的速度沿BC 向点C 匀速运动，当一个点到终点时，另一个点随之停止．经过__________秒后，△PCQ 与△ABC 相似．三、解答题（共13小题，计81分．解答应写出过程）14．（5分）解方程：x 2﹣4x +1＝0．15．（5分）已知：a 2=b 3=c 4≠0，且2a ﹣b +c ＝10．求a 、b 、c 的值．16．（5分）一个几何体由一些大小相同的小正方块儿搭建，如图是从上面看到的这个几何体的形状如图，小正方形的数字表示在该位置的小正方块儿的个数，请在网格中画出从正面和左面看到的几何体的形状图．．17．（5分）如图所示，BE，CF是△ABC的高，D是BC边的中点，求证：DE＝DF．18．（5分）已知矩形ABCD中，AB＝2，在BC中取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，求AD的长．19．（5分）如图，小明用自制的直角三角形纸板DEF测量水平地面上树AB的高度，已知两直角边EF：DE＝2：3，他调整自己的姿势和三角形纸板的位置，使斜边DF保持水平，并且边DE与点B在同一直线上，DM垂直于地面，测得AM＝21m，边DF离地面的距离为1.6m，求树高AB．20．（5分）如图所示某地铁站有三个闸口．（1）一名乘客随机选择此地铁闸口通过时，选择A闸口通过的概率为 ．（2）当两名乘客随机选择此地铁闸口通过时，请用树状图或列表法求两名乘客选择不同闸口通过的概率．21．（6分）如图，小亮利用所学的数学知识测量某旗杆AB的高度．（1）请你根据小亮在阳光下的投影，画出旗杆AB在阳光下的投影．（2）已知小亮的身高为1.72m，在同一时刻测得小亮和旗杆AB的投影长分别为0.86m和6m，求旗杆AB的高．22．（7分）如图，在平面直角坐标系中，每个小正方形的边长都是1个单位长度，△ABC的顶点都在格点上．（1）以原点O 为位似中心，在第三象限内画出将△ABC 放大为原来的2倍后的位似图形△A 1B 1C 1；（2）已知△ABC 的面积为72，则△A 1B 1C 1的面积是__________．23．（7分）实验数据显示，一般成人喝50毫升某品牌白酒后，血液中酒精含量y （毫克/百毫升）与时间x（时）变化的图象如图（图象由线段OA 与部分双曲线AB 组成）所示．国家规定，车辆驾驶人员血液中的酒精含量大于或等于20（毫克/百毫升）时属于“酒后驾驶”，不能驾车上路．（1）求部分双曲线AB的函数表达式；（2）参照上述数学模型，假设某驾驶员晚上22：00在家喝完50毫升该品牌白酒，第二天早上6：30能否驾车去上班？请说明理由．24．（8分）如图所示，A、B、C、D是矩形的四个顶点，AB＝16cm，AD＝6cm，动点P，Q分别从点A，C 同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止，点Q以2cm/s的速度向点D移动（1）P，Q两点从出发开始到几秒时，四边形PBCQ的面积为33cm2？（2）P，Q P和点Q的距离第一次是10cm？25．（8分）如图，已知四边形ABCD为正方形，AB＝E为对角线AC上一动点，连接DE，过点E 作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG 是正方形；（2）探究：CE +CG 的值是否为定值？若是，请求出这个定值；若不是，请说明理由．26．（10分）如图，12y kx =+的图象与反比例函数2y mx =图象相交于A 、B 两点，已知点B 坐标为（3，﹣1）．（1）求一次函数和反比例函数的表达式；（2）求得另一个交点A（﹣1，3），观察图象，请直接写出不等式kx+2≤mx的解集；（3）P为y轴上的点，Q为反比例函数图象上的点，若以ABPQ为顶点的四边形是平行四边形，求出满足条件的点P的坐标．。

（新课标）最新北师大版高中数学必修五总分：150分 考试时间：120分钟 共21题注意事项：本卷为文理共用卷，若标明文科题，则仅文科生做，若标明理科题，则仅理科生做，未作标注的文理科均要做！！！一、选择题：(每题5 分共50分) 1.在直角坐标系中，直线的倾斜角是 （ ）A ．B ．C ．D ．2．已知直线l 方程为2x-5y+10=0,且在x 轴上的截距为a,在y 轴上的截距为b ，则︱a+b ︱等于（ ）A 3B 7C 10D 5 3．圆1)1(22=+-y x 的圆心到直线x y 33=的距离是 （ ） A ．21B ．23C ．1D ．34．抛物线281x y -=的焦点坐标是 （ ）A ．(0,－4)B ．(0,－2)C ．)0,21(-D ． ⎪⎭⎫⎝⎛-0,321 5．已知焦点在x 轴上的椭圆的离心率为21，它的长轴长等于圆x 2+y 2－2x －15=0的半径，则椭圆的标准方程是（ ） A ．1121622=+y x B. 1422=+y x C. 141622=+y x D.13422=+y x 6．R ∈θ，则方程4sin 22=+θy x 表示的曲线不可能是 （ ） A 、圆 B 、椭圆 C 、双曲线 D 、抛物线 7．（文科） 两条直线2x + 3y －k = 0和x －ky + 12 = 0的交点在y 轴上，那么k 的值是 （ ）A －24B 6C ±6D 24（理科）直线L ：y=kx-1与曲线y x --=2112不相交，则k 的取值范围是( )A ．12或3B ．12C ．3D ．[12，3]8．直线03=+y x 绕原点按顺时针方向旋转30°所得直线与圆3)2(22=+-y x 的位置关系是 （ ）.(A)直线与圆相切 (B) 直线与圆相交但不过圆心 (C)直线与圆相离 (D) 直线过圆心9．直线143x y+=与椭圆221169x y +=相交于A 、B 两点，该椭圆上点P 使PAB ∆的面积 等于6，这样的点P 共有 （ ）A.1个B.2个C.3个D.4个10．一束光线从点A(-1，1)出发经X 轴反射到圆C ：1)3()2(22=-+-y x 上的最短路程是（ ）A. 4B. 5C. 123-D. 62二、填空题(每题5 分共25分)11、经过两点A(－m ，6)、B(1，3m)的直线的斜率是12，则m 的值为。

2024-2025学年八年级数学上学期期中模拟卷（深圳专用）（考试时间：90分钟 试卷满分：100分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

4．测试范围：北师大八上第一章勾股定理+第二章实数+第三章位置与坐标+第四章一次函数。

5．难度系数：0.70。

第一部分（选择题 共24分）一、选择题（本大题共8小题，每小题3分，满分24分．在每个小题给出的四个选项中，只有一项符合题目要求的）1．在实数 3.14，0，2p ，227，0.1616616661¼（两个1之间依次多一个6）中，无理数的个数是（ ）A ．5B ．4C ．3D ．22．下列二次根式中，是最简二次根式的是（ ）A B C D 3．如图，根据尺规作图痕迹，图中标注在点A 处所表示的数为（ ）A ．B ．1C ．1-+D ．1-4．三角形ABC 中，A Ð，B Ð，C Ð的对边分别记为a ，b ，c ，由下列条件不能判定三角形ABC 为直角三角形的是（ ）A ．AB C=+∠∠∠B ．::1:1:2A B C ÐÐÐ=C ．222b a c =+D ．::1:1:2a b c =5．已知点P 的坐标为()2,36a a -+，且点P 到两坐标轴的距离相等，则点P 的坐标是（ ）A ．()3,3B ．()3,3-C ．()6,6-D ．()3,3或()6,6-6．在同一平面直角坐标系中，一次函数2y ax a =+与2y a x a =+的图像可能是（ ）A ．B ．C ．D ．7．某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为BAF Ð时，顶部边缘B 处离桌面的高度BC 为7cm ，此时底部边缘A 处与C 处间的距离AC 为24cm ，小组成员调整张角的大小继续探究，最后发现当张角为DAF Ð时（D 是B 的对应点），顶部边缘D 处到桌面的距离DE 为20cm ，则底部边缘A 处与E 之间的距离AE 为（ ）A ．15cmB ．18cmC ．21cmD ．24cm8．如图，直线483y x =-+分别与x ，y 轴交于点A ，B ，点C 在线段OA 上，将BOC V 沿BC 翻折，点O 恰好落在AB 边上的点D 处．则点C 的坐标为（ ）A ．8,03æöç÷èøB ．5,03æöç÷èøC ．()20，D ．()30，第二部分（非选择题 共76分）二、填空题（本大题共5小题，每小题3分，满分15分）9的算术平方根为 ．10．已知x 的整数部分，y xy 的值 ．11．如图是勾股树衍生图案，它由若干个正方形和直角三角形构成，1S ，2S ，3S ，S ₄分别表示其对应正方形的面积，若已知上方左右两端的两个正方形的面积分别是64，9，则1234S S S S -+-的值为12．如图，已知等边AOC △的边长为1，作OD AC ^于点D ，在x 轴上取点1C ，使1CC DC =，以1CC 为边作等边11A CC △；作111CD A C ^于点1D ，在x 轴上取点2C ，使1211C C D C =，以12C C 为边作等边212A C C V ；作1222C D A C ^于点2D ，在x 轴上取点3C ，使2322C C D C =，以23C C 为边作等边323A C C △；…，且点123,,,A A A A ，…都在第一象限，如此下去，则点2023D 的坐标为 ．13．数形结合是数学的重要思想和解题方法，如：“当012x <<值”可看作两直角边分别为x 和2的Rt ACP V 12x -和3的Rt BDP V 的斜边长．于是将问题转化为求AP BP +的最小值，如图所示，当AP 与BP 共线时，AP BP +为最小．请你解决问题：当04x <<的最小值是 ．三、解答题（本大题共7小题，满分61分．解答应写出文字说明，证明过程或演算步骤）14．（8分）计算：(1)0(2023)1|p -+-(2)+-．15．（7分）已知2x +的一个平方根是2-，21x y +-的立方根是3；(1)求x y 、的值；(2)的算术平方根．16．（7分）如图，在平面直角坐标系中，△ABC 顶点分别是()0,2A ，()2,2B -，()4,1C -．(1)在图中作出△ABC 关于y 轴对称的111A B C △；(2)直接写出对称点坐标1B ________，1C ________；(3)在图中第一象限格点中找出点D ，使AD =且同时CD （无需计算过程，请把点画清楚一些）17．（8分）如图，在三角形ABC 中，90ABC Ð=°，20AC =，12BC =．(1)设点P 在线段AB 上，连接PC ，若PAC PCA Ð=Ð，求AP 的长；(2)设点M 在线段AC 上，若MBC △是等腰三角形，求AM 的长．18．（10分）综合与实践【问题情境】在平面直角坐标系中，有不重合的两点()11,A x y 和点()22,B x y ，若12x x =，则AB y ∥轴，且线段AB 的长度为12y y -：若12y y =，则AB x ∥轴，且线段AB 的长度为12x x -．【知识应用】（1）若点()1,1A -，()2,1B ，则AB x ∥轴，AB 的长度为________；【拓展延伸】我们规定：平面直角坐标系中，任意不重合的两点()11,M x y ，()22,N x y 之间的折线距离为()1212,d M N x x y y =-+-．例如：图1中，点()1,1M -与点()1,2N -之间的折线距离为()(),1112235d M N =--+--=+=．【问题解决】（2）如图2，已知()2,0E ，若()1,1F --，则(),d E F =________；（3）如图2，已知()2,0E ，()1,G t ，若(),3d E G =，则t 的值为________；（4）如图3，已知()2,0E ，()0,2H ，点P 是EOH △的边上一点，若(),d E P =P 的坐标．19．（10分）问题情境：在学习了《勾股定理》和《实数》后，某班同学们以“已知三角形三边的长度，求三角形面积”为主题开展了数学活动，同学们想到借助曾经阅读的数学资料进行探究：材料1．古希腊的几何学家海伦（Heron ，约公元50年），在他的著作《度量》一书中，给出了求其面积的海伦公式S =（其中a b c ，，为三角形的三边长，2a b c p ++=，S 为三角形的面积）．S a b c ，，，三角形的面积为S ．（1）利用材料1解决下面的问题：当3a b c ===，（2）利用材料2解决下面的问题：已知ABC V 24-，记ABC V 的周长为ABC C V ．①当2x =时，请直接写出ABC V 中最长边的长度；②若x 为整数，当ABC C V 取得最大值时，请用秦九韶公式求出△ABC 的面积．20．（11分）如图，点(0,)A a ，点(,0)B b 分别为y 轴正半轴、x 轴负半轴上的点，以点B 为直角顶点在第二象限作等腰Rt ABC △．(1)如图1，若a 、b 满足()230a -=，求点C 的坐标；(2)在x 轴上是否存在点P ，使PAB V 是以AB 为腰的等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．(3)如图2，点M 在AC 上，点N 在CA 的延长线上，45MBN Ð=°，探究线段CM 、AN 和MN 之间的关系，并加以证明．。

2023-2024学年安徽省A10联盟（北师大版）高二（上）期中数学试卷一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知直线l 的方程为√3x +y −1=0，则直线的倾斜角为（ ） A ．π6B ．π3C ．2π3D ．5π62．若双曲线y 22−x 2m=1的焦点与椭圆x 24+y 29=1的焦点重合，则m 的值为（ ） A ．2B ．3C ．6D ．73．以A （2，0），B （0，﹣4）两点为直径的两个端点的圆的方程为（ ） A ．（x +1）2+（y ﹣2）2＝20 B ．（x +1）2+（y ﹣2）2＝5C ．（x ﹣1）2+（y +2）2＝20D ．（x ﹣1）2+（y +2）2＝54．已知圆（x ﹣1）2+y 2＝4上有四个点到直线y ＝x +b 的距离等于1，则实数b 的值不可能为（ ） A ．1B ．0C ．−√2D ．−√35．若圆x 2+y 2﹣2x +4y +1＝0被直线ax ﹣2by ﹣2＝0（a ＞0，b ＞0）平分，则1a+4b的最小值为（ ） A ．9+4√22B ．16C ．17D ．2526．已知抛物线y 2＝8x ，过焦点F 的直线与抛物线交于A ，B 两点，过A ，B 分别作y 轴的垂线，垂足分别为C ，D ，则AC +BD 的最小值为（ ） A ．2B ．4C ．6D ．87．已知在△ABC 中，顶点A （1，1），点B 在直线l ：x ﹣y +2＝0上，点C 在x 轴上，则△ABC 的周长的最小值为（ ） A ．√5B ．2√5C ．4√5D ．5√528．已知底边BC 长为2的等腰直角三角形ABC ，D 是平面ABC 内一点，且满足DB ：DC =√3：1，则△ABD 面积的最大值是（ ）A ．3+√62B ．3−√62C ．3√2+2√32D ．3√2−2√32二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求全部选对的得5分，部分选对的得2分，有选错的得0分.） 9．若方程x 25−t+y 2t−1=1所表示的曲线为C ，则（ ）A ．曲线C 可能是圆B ．若C 为椭圆，且焦点在x 轴上，则1＜t ＜3 C ．若1＜t ＜5，则C 为椭圆D ．若C 为双曲线，且焦点在y 轴上，则t ＞510．已知椭圆C ：x 225+y 216=1的左、右焦点分别为F 1，F 2，A ，B 两点都在C 上，且A ，B 关于坐标原点对称，则（ ） A ．AB 的最大值为10 B ．C 的焦距是短半轴长的34C ．|AF 2|+|BF 2|为定值D ．存在点A ，使得AF 1⊥AF 211．下列有关直线与圆的结论正确的是（ ）A ．过点（3，4）且在x ，y 轴上的截距相等的直线方程为x ﹣y ﹣7＝0B ．若直线 kx ﹣y ﹣k ﹣1＝0 和以M （2，1），N （3，2）为端点的线段相交，则实数k 的取值范围为[32，2]C ．若点P （a ，b ）是圆x 2+y 2＝r 2（r ＞0）外一点，直线l 的方程是ax +by ＝r 2，则直线l 与圆相离D ．若圆C 1：x 2+y 2=1与圆C 2：(x −3)2+(y +4)2=a(a ＞0)恰有3条公切线，则a ＝1612．已知O 为坐标原点，F 1，F 2分别为双曲线C ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)，的左、右焦点，C 的一条渐近线l 的方程为y =√3x ，且F 1到l 的距离为3√3，P 为C 在第一象限上的一点，点Q 的坐标为（2，0），PQ 为∠F 1PF 2的平分线，则下列说法正确的是（ ） A ．双曲线C 的方程为x 29−y 227=1 B ．双曲线C 的离心率为2 C ．|PF 1|＝3|PF 2|D ．点P 到x 轴的距离为3√152三、填空题（本题共4小题，每小题0分，共20分.）13．已知圆C ：x 2+y 2＝4，过点P （1，1）的直线被圆C 截得弦长最短时，直线的方程为 ． 14．已知双曲线C ：x 2a 2−y 2b 2=1的离心率是√5，F 1，F 2分别为双曲线C 的左、右焦点，过点F 2且垂直于x 轴的垂线在x 轴上方交双曲线C 于点M ，则tan ∠MF 1F 2的值为 ．15．如图，探照灯反射镜由抛物线的一部分绕对称轴旋转而成，光源位于抛物线的焦点处，这样可以保证发出的光线经过反射之后平行射出．已知当灯口圆的直径为80cm 时，灯的深度为50cm ．为了使反射的光更亮，增大反射镜的面积，将灯口圆的直径增大到88cm ，并且保持光源与顶点的距离不变，此时探照灯的深度为 cm ．16．过直线l ：x ﹣y +4＝0上任意点P 作圆O ：x 2+y 2＝4的两条切线，切点分别为A ，B ，直线AB 过定点 ；记线段AB 的中点为Q ，则点Q 到直线l 的距离的最小值为 ．四、解答题（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．（10分）已知△ABC 的三个顶点分别是A （4，0），B （6，7），C （0，3）． （1）求边BC 的高所在的直线方程；（2）求平分△ABC 的面积且过点B 的直线的方程． 18．（12分）已知双曲线C ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)的一条渐近线与直线x +2y ＝0垂直，且右顶点A 到该条渐近线的距离为2√55． （1）求双曲线C 的方程；（2）若直线l 与双曲线C 交于A 、B 两点，线段AB 的中点为M （3，2），求直线l 的斜率． 19．（12分）已知点P （4，0），圆C 的圆心在直线x ﹣y ﹣4＝0上，且圆C 与y 轴切于点M （0，﹣2）． （1）求圆C 的方程；（2）若直线l 过点P 且被圆C 截得的弦长为2√2，求直线l 的方程．20．（12分）已知抛物线Γ的顶点在原点，对称轴为坐标轴，且过（1，﹣2），(14，1)，（﹣2，﹣2）三点中的两点．（1）求抛物线Γ的方程；（2）已知F 是抛物线Γ的焦点，P 为抛物线Γ上任意一点，M 是线段PF 上的点，且PM →=3MF →，求直线OM 的斜率的最大值（O 为坐标原点）．21．（12分）一动圆与圆C 1：x 2+y 2+6x +5＝0外切，同时与圆C 2：x 2+y 2﹣6x ﹣91＝0内切，动圆圆心的轨迹为曲线E ．（1）求曲线E 的方程；（2）点P 为E 上一动点，点O 为坐标原点，曲线E 的右焦点为F ，求|PO |2+|PF |2的最小值． 22．（12分）已知椭圆C ：x 2a 2+y 2b 2=1（a ＞b ＞0）的左、右焦点分别为F 1，F 2，该椭圆的离心率为12，且椭圆上动点M 与点F 1的最大距离为3． （1）求椭圆C 的方程；（2）如图，若直线l 与x 轴、椭圆C 顺次交于P ，Q ，R （点P 在椭圆左顶点的左侧），且∠PF 1Q +∠PF 1R ＝π，求△RQF 1面积的最大值．2023-2024学年安徽省A10联盟（北师大版）高二（上）期中数学试卷参考答案与试题解析一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知直线l 的方程为√3x +y −1=0，则直线的倾斜角为（ ） A ．π6B ．π3C ．2π3D ．5π6解：因为直线l 的方程为√3x +y −1=0，即y =−√3x +1， 所以直线的斜率为k =−√3，所以直线的倾斜角为2π3．故选：C ． 2．若双曲线y 22−x 2m=1的焦点与椭圆x 24+y 29=1的焦点重合，则m 的值为（ ） A ．2 B ．3C ．6D ．7解：因为椭圆x 24+y 29=1的焦点为(0，√5)，(0，−√5)，所以双曲线y 22−x 2m=1的焦点为(0，√5)，(0，−√5)，故2+m ＝5，解得m ＝3．故选：B ．3．以A （2，0），B （0，﹣4）两点为直径的两个端点的圆的方程为（ ） A ．（x +1）2+（y ﹣2）2＝20 B ．（x +1）2+（y ﹣2）2＝5C ．（x ﹣1）2+（y +2）2＝20D ．（x ﹣1）2+（y +2）2＝5解：依题意，圆心坐标为AB 中点，即（1，﹣2），半径为12|AB|=12√(2−0)2+(0+4)2=√5，所以圆的方程为（x ﹣1）2+（y +2）2＝5． 故选：D ．4．已知圆（x ﹣1）2+y 2＝4上有四个点到直线y ＝x +b 的距离等于1，则实数b 的值不可能为（ ） A ．1B ．0C ．−√2D ．−√3解：由圆的方程（x ﹣1）2+y 2＝4，可得圆心为原点O （1，0），半径为2， 若圆上有4个点到直线l 的距离等于1，则O 到直线y ＝x +b 的距离d 小于1， 又直线的一般方程为x ﹣y +b ＝0， 所以√1+11，所以|1+b |＜√2，所以−√2−1＜b ＜﹣1+√2，所以实数b 的取值范围为（−√2−1，﹣1+√2）． 故选：A ．5．若圆x 2+y 2﹣2x +4y +1＝0被直线ax ﹣2by ﹣2＝0（a ＞0，b ＞0）平分，则1a+4b的最小值为（ ）A ．9+4√22B ．16C ．17D ．252解：由题意知，圆x 2+y 2﹣2x +4y +1＝0被直线ax ﹣2by ﹣2＝0（a ＞0，b ＞0）平分， 即圆心（1，﹣2）在直线ax ﹣2by ﹣2＝0（a ＞0，b ＞0）上，故a +4b ﹣2＝0，即a +4b ＝2， 故1a +4b =（1a +4b ）•12（a +4b ）=12（1+16+4b a +4a b ）≥12（17+2√4a b ×4b a ）=252， 当且仅当4b a =4a b，结合a +4b ＝2，即a ＝b =25时取等号，所以1a+4b的最小值为252．故选：D ．6．已知抛物线y 2＝8x ，过焦点F 的直线与抛物线交于A ，B 两点，过A ，B 分别作y 轴的垂线，垂足分别为C ，D ，则AC +BD 的最小值为（ ） A ．2 B ．4C ．6D ．8解：如图，∵抛物线的方程为y 2＝8x ， ∴焦点F （2，0），准线x ＝﹣2，由抛物线的定义可知|AC |+|BD |＝|AF |+|FB |﹣4＝|AB |﹣4， 即当且仅当|AB |取得最小值，|AC |+|BD |取得最小值，依据抛物线的定义可知当|AB |为通径时，即|AB |＝2p ＝8时为最小值， ∴|AC |+|BD |的最小值为4． 故选：B ．7．已知在△ABC 中，顶点A （1，1），点B 在直线l ：x ﹣y +2＝0上，点C 在x 轴上，则△ABC 的周长的最小值为（ ） A ．√5B ．2√5C ．4√5D ．5√52解：如图示：，设A （1，1）点关于直线x ﹣y +2＝0的对称点为A ′（a ，b ），则{b−1a−1=−1a+12−b+12+2=0，解得：{a =−1b =3，故A ′（﹣1，3），点A 关于x 轴的对称点A ″（1，﹣1）， 则|A ′A ″|=√4+16=2√5，故A ′A ″的长即△ABC 周长的最小值． 故选：B ．8．已知底边BC 长为2的等腰直角三角形ABC ，D 是平面ABC 内一点，且满足DB ：DC =√3：1，则△ABD 面积的最大值是（ ） A ．3+√62B ．3−√62C ．3√2+2√32D ．3√2−2√32解：以BC 的中点O 为原点，以BC 所在直线为x 轴，BC 的垂直平分线为y 轴，建立直角坐标系，如图，则A （0，1），B （﹣1，0），C （1，0），设D （x ，y ），因为DB ：DC =√3：1，所以2222=√3，化简整理得：（x +1）2+y 2＝3（x ﹣1）2+3y 2，即（x ﹣2）2+y 2＝3， 所以点D 的轨迹为以（2，0）为圆心，以√3为半径的圆， 当点D 与直线AB 距离最大时，△ABD 面积最大， 直线AB 的方程为x ﹣y +1＝0，且|AB|=√2， 设圆心到直线的距离为d ，则点D 到直线AB 的最大距离为d +r =2+√3=3√2+2√32，所以△ABD 面积的最大值为12×√2×3√2+2√32=3+√62． 故选：A ．二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求全部选对的得5分，部分选对的得2分，有选错的得0分.） 9．若方程x 25−t+y 2t−1=1所表示的曲线为C ，则（ ）A ．曲线C 可能是圆B ．若C 为椭圆，且焦点在x 轴上，则1＜t ＜3 C ．若1＜t ＜5，则C 为椭圆D ．若C 为双曲线，且焦点在y 轴上，则t ＞5解：对A 选项，当5﹣t ＝t ﹣1＞0，即t ＝3时，曲线C 是圆，∴A 选项正确；对B 选项，若C 为椭圆，且焦点在x 轴上，则5﹣t ＞t ﹣1＞0，∴1＜t ＜3，∴B 选项正确； 对C 选项，若C 为椭圆，则{5−t ＞0t −1＞05−t ≠t −1，∴1＜t ＜5且t ≠3，∴C 选项错误；对D 选项，若C 为双曲线，且焦点在y 轴上，则{t −1＞05−t ＜0，∴t ＞5，∴D 选项正确．故选：ABD ． 10．已知椭圆C ：x 225+y 216=1的左、右焦点分别为F 1，F 2，A ，B 两点都在C 上，且A ，B 关于坐标原点对称，则（ ） A ．AB 的最大值为10 B ．C 的焦距是短半轴长的34C ．|AF 2|+|BF 2|为定值D ．存在点A ，使得AF 1⊥AF 2解：∵在椭圆C ：x 225+y 216=1中，a ＝5，b ＝4，c ＝3， 又A ，B 两点都在C 上，且A ，B 关于坐标原点对称， ∴AB 的最大值为2a ＝10，∴选项正确；∴C 的焦距为2c ＝6，短半轴长为4，而6≠4×34，∴B 选项错误； 根据椭圆的对称性可知|BF 2|＝|AF 1|，∴|AF 2|+|BF 2|＝|AF 2|+|AF 1|＝2a ＝10，∴C 选项正确； 根据椭圆的几何性质可得：当A 为短轴顶点时∠F 1AF 2最大，设∠F 1AF 2＝2θ，而当∠F 1AF 2＝2θ最大时，tan θ=cb =34＜1，θ∈（0，π2），∴θ＜π4，∴∠F 1AF 2＝2θ的最大角小于π2，∴椭圆C 上不存在点A ，使得AF 1⊥AF 2，∴D 选项错误．故选：AC ．11．下列有关直线与圆的结论正确的是（ ）A ．过点（3，4）且在x ，y 轴上的截距相等的直线方程为x ﹣y ﹣7＝0B ．若直线 kx ﹣y ﹣k ﹣1＝0 和以M （2，1），N （3，2）为端点的线段相交，则实数k 的取值范围为[32，2]C ．若点P （a ，b ）是圆x 2+y 2＝r 2（r ＞0）外一点，直线l 的方程是ax +by ＝r 2，则直线l 与圆相离D ．若圆C 1：x 2+y 2=1与圆C 2：(x −3)2+(y +4)2=a(a ＞0)恰有3条公切线，则a ＝16 解：当截距不为0时，设直线xa +y a=1，将点（3，4）代入得，3a+4a=1，∴a ＝7，则直线方程为x +y﹣7＝0，当截距为0时，设直线y ＝kx ，将点（3，4）代入得，4＝3k ，∴k =43，则直线方程为4x ﹣3y ＝0， 则直线方程为x +y ﹣7＝0和4x ﹣3y ＝0，故A 错误； 对于B ，已知直线kx ﹣y ﹣k ﹣1＝0过定点A （1，﹣1）， 又直线AM ，AN 的斜率为k AM =1+12−1=2，k AN =2+13−1=32， 所以直线kx ﹣y ﹣k ﹣1＝0和以M （2，1），N （3，2）为端点的线段相交， 实数k 的取值范围为[32，2]，故B 正确；对于C ，点P （a ，b ）是圆x 2+y 2＝r 2外一点，所以a 2+b 2＞r 2， 所以圆心（0，0）到直线的距离d =r 2√a 2+b r ，所以直线与圆相交，故C 不正确；圆C 1：x 2+y 2=1与圆C 2：(x −3)2+(y +4)2=a(a ＞0)恰有3条公切线， 所以圆C 1与圆C 2相外切，所以|C 1C 2|＝1+√a ，又√(3−0)2+(4−0)2=5， 所以1+√a =5，解得a ＝16，故D 正确． 故选：BD ．12．已知O 为坐标原点，F 1，F 2分别为双曲线C ：x 2a 2−y 2b2=1(a ＞0，b ＞0)，的左、右焦点，C 的一条渐近线l 的方程为y =√3x ，且F 1到l 的距离为3√3，P 为C 在第一象限上的一点，点Q 的坐标为（2，0），PQ 为∠F 1PF 2的平分线，则下列说法正确的是（ ） A ．双曲线C 的方程为x 29−y 227=1 B ．双曲线C 的离心率为2 C ．|PF 1|＝3|PF 2|D ．点P 到x 轴的距离为3√152解：对于A ，由F 1（﹣c ，0）到渐近线y =√3x 的距离为3√3，得√3c2=3√3，解得c ＝6，由渐近线方程为y =√3x ，得ba=√3，结合a 2+b 2＝c 2可得a ＝3，b =3√3，则双曲线C 的方程为x 29−y 227=1，故A 正确．对于B ，e =ca=2，故B 正确． 对于C ，PQ 为∠F 1PF 2的平分线，则|PF 1||PF 2|=|QF 1||QF 2|=84=2，故C 错误．对于D ，由双曲线定义可得|PF 1|﹣|PF 2|＝6，则可得|PF 1|＝12，|PF 2|＝6，在△PF 1F 2中，cos ∠F 1PF 2=122+62−1222×12×6=14，sin ∠F 1PF 2=√1−cos 2∠F 1PF 2=√154，设点P 到x 轴的距离为d ，则|PF 2|•sin ∠F 1PF 2 即12×12×d =12×12×6×√154，解得d =3√152，故D 正确．故选：ABD ．三、填空题（本题共4小题，每小题0分，共20分.）13．已知圆C ：x 2+y 2＝4，过点P （1，1）的直线被圆C 截得弦长最短时，直线的方程为 x +y ﹣2＝0 ． 解：圆C ：x 2+y 2＝4的圆心为（0，0），半径为2，则依题意有k CP =1−01−0=1， 当直线与CP 垂直时，该直线被圆C 截得的弦长最短， 所以所求直线的斜率为k ＝﹣1，所以直线方程为y ﹣1＝﹣（x ﹣1），即x +y ﹣2＝0，所以过点P （1，1）的直线被圆C 截得弦长最短时，直线的方程为 x +y ﹣2＝0． 故答案为：x +y ﹣2＝0． 14．已知双曲线C ：x 2a 2−y 2b 2=1的离心率是√5，F 1，F 2分别为双曲线C 的左、右焦点，过点F 2且垂直于x 轴的垂线在x 轴上方交双曲线C 于点M ，则tan ∠MF 1F 2的值为 2√55． 解：已知双曲线C ：x 2a 2−y 2b 2=1的离心率是√5，则ca=√5，不妨令a ＝t ，t ＞0，则c =√5t ，b ＝2t ，又F 1，F 2分别为双曲线C 的左、右焦点，过点F 2且垂直于x 轴的垂线在x 轴上方交双曲线C 于点M ，由双曲线的性质可得：|MF 2|=b 2a ，则tan ∠MF 1F 2=|MF 2||F 1F 2|=4t 2t×2√5t =2√55．故答案为：2√55． 15．如图，探照灯反射镜由抛物线的一部分绕对称轴旋转而成，光源位于抛物线的焦点处，这样可以保证发出的光线经过反射之后平行射出．已知当灯口圆的直径为80cm 时，灯的深度为50cm ．为了使反射的光更亮，增大反射镜的面积，将灯口圆的直径增大到88cm ，并且保持光源与顶点的距离不变，此时探照灯的深度为 60.5 cm ．解：在反射镜的轴截面上建立平面直角坐标系，以抛物线的顶点为原点，以旋转轴为x 轴（抛物线开口方向是x 轴的正方向），则可设抛物线的标准方程为y 2＝2px （p ＞0）灯口圆与轴截面在第一象限内的交点的坐标为（50，40）， 代入抛物线方程得402＝2p ×50，解得p ＝16，所以抛物线方程为y 2＝32x ，光源应安置在与顶点相距16cm 处，当灯口圆的直径增大到88cm 时，灯口圆与轴截面在第一象限的交点的纵坐标变为882=44，故将y ＝44代入y 2＝32x 中，求得x =1212=60.5， 此时，探照灯的深度为60.5cm ．16．过直线l ：x ﹣y +4＝0上任意点P 作圆O ：x 2+y 2＝4的两条切线，切点分别为A ，B ，直线AB 过定点 （﹣1，1） ；记线段AB 的中点为Q ，则点Q 到直线l 的距离的最小值为 √2 ． 解：设P （x 0，y 0），因为P 是直线l ：x ﹣y +4＝0上一点，所以y 0＝x 0+4， 以OP 为直径的圆的方程为x （x ﹣x 0）+y （y ﹣y 0）＝0，即x 2+y 2﹣x 0x ﹣y 0y ＝0， 所以x 0x +y 0y ＝4，即直线AB 的方程为x 0x +y 0y ＝4，又y 0＝x 0+4，∴直线AB 的方程为x 0（x +y ）+4y ﹣4＝0，故直线AB 过定点（﹣1，1）． 设Q （x ，y ），直线AB 过定点为M ，则M （﹣1，1），由MQ →⋅OQ →=0， 得（x +1）x +（y ﹣1）y ＝0，整理得点Q 的轨迹方程为(x +12)2+(y −12)2=12，因为点(−12，12)到直线l ：x ﹣y +4＝0的是距离d =|−12−12+4|√2=3√22＞√22，所以直线l ：x ﹣y +4＝0与圆(x +12)2+(y −12)2=12相离， 所以点Q 到直线的距离的最小值为|−12−12+4|√2−√22=3√22−√22=√2．故答案为：（﹣1，1）；√2．四、解答题（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．（10分）已知△ABC 的三个顶点分别是A （4，0），B （6，7），C （0，3）． （1）求边BC 的高所在的直线方程；（2）求平分△ABC 的面积且过点B 的直线的方程． 解：（1）由题意可得：直线BC 的斜率k BC =3−70−6=23， 则边BC 的高所在的直线的斜率k =−32，所求直线方程为y −0=−32(x −4)，即3x +2y ﹣12＝0． （2）由题意可知：所求直线即为边AC 的中线所在的直线，则线段AC 的中点为D(2，32)，可得直线BD 的斜率k BD =7−326−2=118，所以直线BD 的方程为y −32=118(x −2)，即11x ﹣8y ﹣10＝0． 18．（12分）已知双曲线C ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)的一条渐近线与直线x +2y ＝0垂直，且右顶点A 到该条渐近线的距离为2√55． （1）求双曲线C 的方程；（2）若直线l 与双曲线C 交于A 、B 两点，线段AB 的中点为M （3，2），求直线l 的斜率． 解：（1）因为双曲线C 的一条渐近线与直线x +2y ＝0垂直，且直线x +2y ＝0的斜率为−12，因为双曲线C 的渐近线为y =±b a x ，所以−12⋅ba =−1，解得b a=2，则双曲线C 的渐近线方程为y ＝±2x ，即2x ±y ＝0，因为右顶点（a ，0）到该条渐近线的距离为2√55，所以√5=2√55，解得a ＝1，可得b ＝2， 所以双曲线C 的方程为x 2−y 24=1；（2）若直线l ⊥x 轴，此时A ，B 两点关于x 轴对称，可得线段AB 的中点在x 轴上，不符合题意； 若直线l 与x 轴不垂直，不妨设A （x 1，y 1）、B （x 2，y 2），直线l 的斜率为k ，此时{x 12−y 124=1x 22−y 224=1，即(x 12−x 22)−y 12−y 224=0， 此时(x 1+x 2)(x 1−x 2)−(y 1+y 2)(y 1−y 2)4=0，整理得y 1+y 2x 1+x 2⋅y 1−y 2x 1−x 2=4． 因为线段AB 的中点为M （3，2），所以x 1+x 2＝6，y 1+y 2＝4，则46⋅k =4，解得k ＝6， 故直线l 的斜率为6．19．（12分）已知点P （4，0），圆C 的圆心在直线x ﹣y ﹣4＝0上，且圆C 与y 轴切于点M （0，﹣2）． （1）求圆C 的方程；（2）若直线l 过点P 且被圆C 截得的弦长为2√2，求直线l 的方程． 解：（1）设圆心坐标为C （a ，b ），因为圆C 的圆心在直线x ﹣y ﹣4＝0上，且圆C 与y 轴切于点M （0，﹣2）， 所以{a −b −4=0b =−2，解得{a =2b =−2，所以C （2，﹣2），半径r ＝|MC |＝2， 所以圆C 的方程为（x ﹣2）2+（y +2）2＝4；（2）由题意得，圆心C （2，﹣2）到直线l 的距离为√4−2=√2， 若直线l 的斜率存在，设直线l 的方程为y ＝k （x ﹣4）， 则√k 2+1=√2，解得k =2+√3或k =2−√3，当直线l 的斜率不存在，l 的方程为x ＝4，此时圆心C （2，﹣2）到直线l 的距离为2，不满足题意，舍去， 综上，直线l 的方程为y =(2+√3)(x −4)或y =(2−√3)(x −4)．20．（12分）已知抛物线Γ的顶点在原点，对称轴为坐标轴，且过（1，﹣2），(14，1)，（﹣2，﹣2）三点中的两点．（1）求抛物线Γ的方程；（2）已知F 是抛物线Γ的焦点，P 为抛物线Γ上任意一点，M 是线段PF 上的点，且PM →=3MF →，求直线OM 的斜率的最大值（O 为坐标原点）．解：（1）若抛物线Γ经过A （1，﹣2）、B (14，1)，则抛物线开口向右，设抛物线Γ方程为y 2＝2px （p ＞0），代入A 点坐标，得（﹣2）2＝2p ×1，解得p ＝2， 故抛物线Γ方程为y 2＝4x ，恰好经过点B (14，1)，符合题意； 若抛物线Γ经过A （1，﹣2）、C （﹣2，﹣2），则抛物线开口向下，设抛物线Γ方程为x 2＝﹣2py （p ＞0），找不到p 值，使A 、C 两点都满足该方程；而B (14，1)在第一象限，C （﹣2，﹣2）在第三象限，不存在抛物线，使B 、C 两点都在抛物线上． 综上所述，抛物线Γ经过A （1，﹣2）、B (14，1)两点，方程为y 2＝4x ．（2）作出示意图，设点P （x 0，y 0）为抛物线Γ上任意一点，点M 是线段PF 上的点，且PM →=3MF →，①若P 点在第四象限，则直线OM 的斜率为负数，不能达到最大值；②若P 点在第一象限，则F （1，0），x 0=y 024，y 0＞0，设M （s ，t ），由OM →=OF →+FM →=OF →−14PF →=OF →−14(OF →−OP →)=14OP →+34OF →，得{s =14x 0+34×1=y 0216+34t =14y 0+34×0=14y 0， 所以M 的坐标为(y 0216+34，14y 0)，可得直线OM 的斜率k =14y 0y 0216+34=y 0y 024+3≤02√y 04×3=√33，当且仅当y 024=3，即x 0＝3，y 0=2√3时，直线OM 的斜率有最大值√33．综上所述，当抛物线Γ上的点P 坐标为(3，2√3)时，直线OM 的斜率有最大值√33． 21．（12分）一动圆与圆C 1：x 2+y 2+6x +5＝0外切，同时与圆C 2：x 2+y 2﹣6x ﹣91＝0内切，动圆圆心的轨迹为曲线E ．（1）求曲线E 的方程；（2）点P 为E 上一动点，点O 为坐标原点，曲线E 的右焦点为F ，求|PO |2+|PF |2的最小值． 解：（1）不妨设动圆圆心为M （x ，y ），半径为R ，易知圆C 1：(x +3)2+y 2=4，圆C 2：(x −3)2+y 2=100， 当动圆M 与圆C 1外切时，|C 1M |＝R +2； 当动圆M 与圆C 2内切时，|C 2M |＝10﹣R ， 所以|C 1M |+|C 2M |＝12＞|C 1C 2|，则点M 的轨迹是焦点为C 1（﹣3，0），C 2（3，0），长轴长为12的椭圆， 不妨设该椭圆的长轴为2a ，短轴为2b ，焦距为2c ， 此时2c ＝6，2a ＝12，解得c ＝3，a ＝6，则b 2＝36﹣9＝27， 故动圆圆心轨迹方程为x 236+y 227=1；（2）由（1）知F （3，0），不妨设P （x ，y ）， 此时|PO |2+|PF |2＝x 2+y 2+（x ﹣3）2+y 2＝2x 2﹣6x +9+2y 2， 因为点P 在椭圆上，所以x ∈[﹣6，6]，y 2=27−34x 2， 此时|PO|2+|PF|2=12x 2−6x +63=12(x −6)2+45， 易知当x ＝6时，|PO |2+|PF |2取得最小值，最小值为45． 22．（12分）已知椭圆C ：x 2a 2+y 2b 2=1（a ＞b ＞0）的左、右焦点分别为F 1，F 2，该椭圆的离心率为12，且椭圆上动点M 与点F 1的最大距离为3． （1）求椭圆C 的方程；（2）如图，若直线l 与x 轴、椭圆C 顺次交于P ，Q ，R （点P 在椭圆左顶点的左侧），且∠PF 1Q +∠PF 1R ＝π，求△RQF 1面积的最大值．解：（1）因为椭圆C 的离心率为12，所以e =c a =12，即a ＝2c ，①因为椭圆上动点M 与点F 1的最大距离为3， 所以a +c ＝3，② 又b =√a 2−c 2，③联立①②③，解得a ＝2，c ＝1，b =√3， 则椭圆C 的方程为x 24+y 23=1；（2）不妨设Q （x 1，y 1），R （x 2，y 2）， 由（1）知F 1（﹣1，0）， 因为∠PF 1Q +∠PF 1R ＝π， 所以k QF 1+k RF 1=0， 即y 1x 1+1+y 2x 2+1=0，整理得x 1y 2+y 2+x 2y 1+y 1＝0，不妨设直线PQ 的方程为x ＝my +n （m ≠0），联立{x =my +n x 24+y 23=1，消去x 并整理得（3m 2+4）y 2+6mny +3n 2﹣12＝0，此时Δ＝36m 2n 2﹣4（3m 2+4）（3n 2﹣12）＞0， 解得n 2＜3m 2+4，由韦达定理得y 1+y 2=−6mn 3m 2+4，y 1y 2=3n 2−123m 2+4，又x 1＝my 1+n ，x 2＝my 2+n ，所以x 1y 2+y 2+x 2y 1+y 1＝2my 1y 2+（n +1）（y 1+y 2）＝0，即2m ⋅3n 2−123m 2+4+(n +1)(−6mn3m 2+4)=0， 因为m ≠0，所以n ＝﹣4，则直线PQ 的方程为x ＝my ﹣4（m ≠0）， 此时点F 1（﹣1，0）到直线PQ 的距离d =|−1+4|√1+m 2=3√1+m 2，所以S △F 1QR=12|QR|d =12√1+m 2⋅√(y 1+y 2)2−4y 1y 2⋅3√1+m 2=18√m 2−43m 2+4， 因为n 2＜3m 2+4，n ＝﹣4， 所以3m 2+4＞16，即m 2＞4， 不妨令√m 2−4=t ，t ＞0， 此时m 2＝t 2+4，所以√m 2−43m 2+4=t 3(t 2+4)+4=t 3t 2+16=13t+16t≤2√3t⋅t=8√3，当且仅当3t =16t 时，等号成立， 此时m 2=t 2+4=283，直线l 存在， 综上，△RQF 1面积的最大值为18×183=3√34．。

2024-2025学年八年级上学期北师大版数学期中考试模拟试卷一、单选题1π，131.626626662……中，无理数的个数是（）A ．1个B ．2个C ．3个D ．4个2．一次函数73y x =-的图象不经过的象限是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．一等腰三角形，腰长10cm ，底长16cm ，则底边上的高是（）A ．8cmB ．6cmC ．10cmD ．12cm4．已知a ，b ，c 是三角形的三边长，如果满足()26|10|0a c --=，则三角形的形状是（）A ．等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形5．下列计算正确的是（）A=B ．3-=C =D ．2=6．△ABC 的三边长分别为a ，b ，c ，由下列条件不能判断△ABC 是直角三角形的是（）A ．∠A ＝2∠B ＝3∠C B ．∠A ＝∠C ﹣∠B C ．a ：b ：c ＝12D ．a 2＝（b ＋c ）（b ﹣c ）7．一个正比例函数的图象经过()2,4A -，(),2B m -两点，则m 的值为（）A ．2-B ．1-C ．2D ．18．在平面直角坐标系中，若点(231)P a +-，与点(51)Q b -，关于x 轴对称，则a b +的值是（）A ．1B ．2C ．3D ．49．如图，Rt ABC △中，90ACB ∠=︒，以Rt ABC △的三边为边向外作正方形，其面积分别是1S ，2S ，3S ，且14S =，216S =，则3S =（）A ．20B ．12C ．D ．10．如图，在平面直角坐标系xOy 中，O 为坐标原点，(4,0)A ，(4,2)B ，(0,2)C ，将OAB △沿直线OB 折叠，使得点A 落在点D 处，OD 与BC 交于点E ，则点D 的纵坐标为（）A ．165B ．125C ．95D ．4二、填空题1115（填“>、<、或=”）12．若点(x 1，y 1)和(x 2，y 2)都在直线y =−3x +b 上，且x 1<x 2，则y 1、y 2的大小关系是．13．将直线y ＝﹣12x +6向下平移2个单位，平移后的直线分别交x 轴、y 轴于A 、B 两点，点O 为坐标原点，则S △ABO ＝．14．中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位，体现了数学研究中的继承和发展．下图是3世纪我国汉代的数学家赵爽在注解《周髀算经》时给出的图案，人们称它为“赵爽弦图”．此图中四个全等的直角三角形可以围成一个大正方形，中空的部分是一个小正方形．如果大正方形的面积是25，小正方形的面积是1，则()2a b +的值是．15．实数a b ，||a b +化简结果为．16．已知－2<x<1化简的结果是.三、解答题17．计算：|4|+18．求下列各式中x 的值(1)()2419x +=；(2)()31342x +=-．19．已知2x -的平方根是2±，27x y ++的立方根是3，求22x y +的平方根．20．已知1x =-，1y =．()1求22x xy y ++；()2若a 是x 的小数部分，b 是y 的整数部分，求1ba b a-+的值．21．已知：在四边形ABCD 中，连接AC ，BC AB =，2222CD AD AB +=，AD CD ⊥．(1)试判断AB 与BC 的位置关系，并说明理由；(2)当13CD AB =，17AD =，求四边形ABCD 的周长．22．如图，一架云梯AB 斜靠在一竖直的墙AO 上，这时20AO =米，云梯AB 的长度比OB 的长度（云梯底端离墙的距离）大10米，AO BO ⊥，设OB 的长度为x 米．(1)求OB 的长度；(2)若云梯的顶端A 沿墙下滑了5米到达点C 处，通过计算说明云梯的底部B 往外移动多少米．23．学校首届海棠文化节启动暨原创校园歌曲《京广路86号》现场发布仪式于4月2日在京广校区举行，海棠文化节系列活动也伴随启动仪式同步开展．为奖励积极参与活动的班级与个人，学校计划购买A 、B 两种奖品，若购买A 种奖品3个和B 种奖品2个共需要130元；若购买A 种奖品5个和B 种奖品4个共需要230元．(1)A 、B 两种奖品的单价；(2)按照学校计划，准备购买A 、B 两种奖品共20个，且A 种奖品的数量不少于B 种奖品的数量的2倍，请你设计出最省钱的购买方案，并说明理由．24．如图，直线24y x =-+交x 轴和y 轴于点A 和点B ，点(0,2)C -在y 轴上，连接AC ．(1)求直线AC 的解析式；(2)若点P 是直线AB 上一点，若BPC 的面积为3，求点P 的坐标；(3)在x 轴上是否存在一点D ，使得ABD △是等腰三角形，若存在，请直接写出点D 坐标，若不存在，请说明理由．25．如图1，已知直线24y x =+与y 轴，x 轴分别交于A ，B 两点，以B 为直角顶点在第二象限作等腰Rt ABC △．(1)求点C 的坐标，并求出直线AC 的关系式；(2)如图2，直线CB 交y 轴于E ，在直线CB 上取一点D ，连接AD ，若AD AC =，求证：BE DE =；(3)如图3，在（1）的条件下，直线AC 交x 轴于点M ，7,2P a ⎛⎫- ⎪⎝⎭是线段BC 上一点，在x轴上是否存在一点N ，使BPN △面积等于BCM 面积的一半？若存在，请求出点N 的坐标；若不存在，请说明理由．。

2024-2025学年七年级数学上学期期中测试卷（一）（考试时间：120分钟试卷满分：120分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

4．测试范围：新北师版（2024）七年级上册第一章~第三章。

5．难度系数：0.85。

一、选择题（本题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．如果收入10元记作+10元，那么支出5元记作（）A．+5元B．−5元C．+10元D．−10元【答案】B【分析】本题主要考查了正负数的意义，掌握正负数的意义是解题的关键．根据正负数的意义，收入为正，那么支出为负进行选择即可．【详解】解：由题意可知：收入为正，那么支出为负，支出5元记作−5元．故选：B2．如图是一个正方体展开图，将其围成一个正方体后，与“罩”字相对的是（）．A．勤B．洗C．手D．戴【答案】C【分析】本题要有一定的空间想象能力，可通过折纸或记口诀的方式找到“罩”的对面应该是“手”．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“罩”相对的面是“手”；故选：C．【点睛】可以通过折一个正方体再给它展开，通过结合立体图形与平面图形的转化，建立空间观念，解决此类问题．还可以直接记口诀找对面：＂跳一跳找对面；找不到，拐个弯＂．3．2024年春节小长假期间旅游创新高，达到474000000人次，同比上涨34.3%，将474000000用科学记数法表示为（）A．0.474×109B．474×106C．4.74×108D．47.4×107【答案】C【分析】本题考查科学记数法，解题的关键是熟记科学记数法的定义：将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于或等于10时，n是正整数；当原数的绝对值小于1时，n是负整数．【详解】解：将474000000用科学记数法表示为4.74×108．故选：C．4．下列运算正确的是（）A．3a+4a=7a B．−2x+6x=8x C．9x−7x=2D．m+n=mn【答案】A【分析】根据合并同类项法则逐个进行判断即可．【详解】解：A、3a+4a=7a，故A正确，符合题意；B、−2x+6x=4x，故B不正确，不符合题意；C、9x−7x=2x，故C不正确，不符合题意；D、m与n不是同类项，不能合并，故D不正确，不符合题意；故选：A．【点睛】本题主要考查了合并同类项法则，解题的关键是掌握相关运算法则并熟练运用．5．已知代数式3m−2n的值是3，则代数式6m−4n−2的值是（）A．1B．4C．−8D．不能确定【答案】B【分析】把原式化为：2(3m−2n)−2,再整体代入求值即可.【详解】解：∵3m−2n=3,∴6m−4n−2=2(3m−2n)−2=2×3−2=4,故选B【点睛】本题考查的是代数式的求值，掌握整体代入法求解代数式的值是解题的关键.6．有理数a，b在数轴上的对应点的位置如图所示，则下列各式成立的是（）A．a+b>0B．b−a<0C．ab>0D．|a+b|<|a|+|b|【答案】D【分析】根据a，b在数轴上的对应点的位置得到−2<a<−1<0<b<1，进行逐一判断即可．【详解】解：由数轴可得：−2<a<−1<0<b<1，则|a|>|b|，∴a+b<0，b−a>0，ab<0，|a+b|<|a|+|b|，故A、B、C错误，D正确，故选D．【点睛】本题考查了有理数的乘法、数轴、绝对值、有理数的加法，解决本题的关键是掌握有理数的乘法、数轴、绝对值、有理数的加法．7．若x m y3与9x2y n是同类项，则m+n的值是（ ）A．5B．6C．4D．3【答案】A【分析】把字母相同，且相同字母的指数也相同的几个项叫做同类项，由同类项的定义可得m与n的值，则可得m+n的值．【详解】由于x m y3与9x2y n是同类项，则m=2，n=3，所以m+n=2+3=5．故选：A．【点睛】本题考查了同类项的概念及求代数式值，关键是掌握同类项的概念．8．下列说法正确的是（）A．−3xy25系数是−35，次数是2B．−2π2a3b是六次单项式C．3与π是同类项D．x2+1x−3是二次三项式【答案】C【分析】此题主要考查了同类项、多项式与单项式，正确把握多项式的次数确定方法是解题关键．9．若|x|=5，|y|=2且|x−y|=x−y，则x+y=（）A．3或−7B．−7或−3C．7或3D．−3或7【答案】C【分析】首先根据绝对值的性质可得x=±5，y=±2，然后由x>y，求出x和y的值，分别代入x+y 即可求解．【详解】解：∵|x|=5，|y|=2，∴x=±5，y=±2，又∵|x−y|=x−y∴x>y，∴x=5，y=2，或x=5，y=−2，当x=5，y=2时，x+y=5+2=7；当x=5，y=−2时，x+y=5−2=3；∴x+y的值为7或3．故选：C．【点睛】本题主要考查代数式求值、有理数的加法和绝对值的计算，根据题意分情况计算是解题的关键．10．观察下列等式：21=2，22=4，23=8，24=16，25=32，26=64，根据这个规律，则21+22+23+24+ (22018)末位数字是A．6B．4C．2D．0【答案】A【分析】根据题目中的式子可以知道，末位数字出现的2、4、8、6的顺序出现，从而可以求得21+22 +23+24+...+22018的末位数字，本题得以解决.【详解】∵21=2,22=4,23=8,24=16,25=32,26=64,...,∴2018÷4=504...2，∵(2+4+8+6)×504+2+4=10086，∴21+22+23+24+...+22018末位数字是6，故选A.【点睛】本题考查尾数特征，解答本题的关键是发现题目中的尾数的变化规律，求出相应的式子的末尾数字.二、填空题（本题共6小题，每小题3分，共18分．）11．比较大小：−38−49．（填“>”、“=”或“<”）12．当x=时，式子2x+1与3x−6的值互为相反数．【答案】1【分析】利用相反数的性质列出方程，求出方程的解即可得到x的值．【详解】解：根据题意得：2x+1+3x﹣6＝0，移项得：2x+3x＝6﹣1，合并同类项得：5x＝5，解得：x＝1．故答案为：1．【点睛】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项，合并同类项，把未知数系数化为1，熟练掌握解一元一次方程的步骤是解题的关键．13．把5.296精确到百分位的近似数是．【答案】5.30【分析】本题主要考查了求一个数的近似数．精确到百分位只需要对千分位上的数字6进行四舍五入即可．【详解】解：5.296精确到百分位的近似数是5.30，故答案为：5.30．14．单项式−3x2y3的系数是．515．九宫格起源于中国古代的神秘图案河图和洛书．如图，将3，2，1，0，−1，−2，−3，−4，−5填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则a的值为．16．你喜欢吃拉面吗？拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉成了许多细的面条，如下面草图所示．这样捏合到第次后可拉出2048根细面条．【答案】11【分析】本题考查了数字类规律探究，有理数的乘方，先探究规律：第n 次捏合可拉出2n 根细面条，然后根据规律列式计算，理解乘方的意义是解题的关键．【详解】解：根据题意有，第一次捏合可拉出21=2根细面条，第二次捏合可拉出22=4根细面条，第三次捏合可拉出23=8根细面条，…，第n 次捏合可拉出2n 根细面条，令：2n =2048，解得：n =11，故答案为：11．三．解答题（本题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）计算：(1)(−5)+10−2+(−1)；(2)−22+[12−(−3)×2]÷2；(3)−112+13÷|−124|；(4)112×57−−×212+−÷125．18．（6分）化简求值：(2x2y−3xy2)−3(x2y−2xy2)+2(x2y−4xy2)，其中x=−1，y=2．【答案】xy(x−5y);22【分析】先去括号，合并同类项化简原式，再将x，y代入求值即可.【详解】原式=(2x2y−3xy2)−(3x2y−6xy2)+(2x2y−8xy2)=2x2y−3x y2−3x2y+6x y2+2x2y−8x y2=x2y−5x y2=xy(x−5y)当x=−1，y=2时，原式=(−1)×2×(−1−5×2)=(−1)×2×(−11)=22【点睛】本题主要考查代数式的化简求值，掌握去括号，合并同类项的法则是解题的关键.19．（6分）如图是一个几何体从三个方向看所得到的形状图.（1）写出这个几何体的名称；（2）若从正面看的长为10cm，从上面看到的圆的直径为4cm，求这个几何体的表面积（结果保留π）．【答案】（1）圆柱；（2）48πcm2．【分析】（1）根据该几何体的主视图与左视图是矩形，俯视图是圆可以确定该几何体是圆柱；（2）根据告诉的几何体的尺寸确定该几何体的表面积即可；【详解】(1)由三视图判断出该几何体是圆柱.(2)∵从正面看的长为10cm，从上面看的圆的直径为4cm，∴该圆柱的底面半径径为2cm，高为10cm，∴该几何体的侧面积为2πrh=2π×2×10=40πcm2，底面积为：2πr2=8πcm2.∴该几何体的表面积为40π+8π=48πcm2．【点睛】本题考查了由三视图判断几何体及几何体的表面积问题，解题的关键是了解圆柱的表面积的计算方法．20．（8分）小虫从某点O出发在一条直线上来回爬行，假定向右爬行的路程记为正，向左爬行的路程记为负，爬过的路程依次为（单位：厘来）：−5，+8，−14，+5，+6，−9，+10．问：(1)小虫是否回到出发点O？(2)小虫离开出发点O最远是多少厘米？(3)在爬行过程中，如果每爬行1厘米奖励2粒芝麻，则小虫共可得到多少粒芝麻？【答案】(1)小虫没有回到出发点O(2)小虫离开出发点O最远是11厘米(3)小虫共可得到114粒芝麻【分析】本题考查了正负数的意义，有理数的四则运算等知识；（1）向左、向右爬行的距离相加即可作出判断；（2）依次计算出前2个、前3个、前4个、…、前6个、7个数的和，其中最大的数即是小虫离开出发点O最远的距离；（3）所有路程绝对值的和与2的积即可奖励的芝麻数．【详解】（1）解：−5+8+(−14)+5+6+(−9)+10=+1所以小虫没有回到出发点O．（2）解：−5+8=+3，+3+(−14)=−11，−11+5=−6，−6+6=0，0+(−9)=−9，−9+10=+1所以小虫离开出发点O最远是11厘米．（3）解：(|−5|+|+8|+|−14|+|+5|+|+6|+|−9|+|+10|)×2=57×2=114所以小虫共可得到114粒芝麻．21．（10分）阅读材料：我们知道，4x−2x+x=(4−2+1)x=3x，类似地，我们把(a+b)看成一个整体，则4(a+b)−2(a+b) +(a+b)=(4−2+1)(a+b)=3(a+b)．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用：(1)把(a−b)2看成一个整体，合并6(a−b)2−2(a−b)2+3(a−b)2=；(2)已知x2−2y=4，求3x2−6y−21的值；(3)拓广探索：已知a−5b=3，5b−3c=−5，3c−d=10，求(a−3c)+(5b−d)−(5b−3c)的值．【答案】(1)7(a−b)2(2)−9(3)8【分析】（1）利用整体的思想进行合并即可；（2）先对3x2−6y−21进行变形，然后整体代入即可；（3）首先根据题意将原式进行变形，然后整体代入即可．【详解】（1）解：6(a−b)2−2(a−b)2+3(a−b)2=(6−2+3)(a−b)2=7(a−b)2；故答案为：7(a−b)2；（2）解：∵x2−2y=4，∴3x2−6y−21=3(x2−2y)−21=12−21=−9；（3）∵a−5b=3,5b−3c=−5,3c−d=10，∴(a−3c)+(5b−d)−(5b−3c)=a−3c+5b−d−5b+3c=(a−5b)+(5b−3c)+(3c−d)=3−5+10=8．【点睛】本题主要考查代数式求值和整式的加减运算，掌握整体代入法是解题的关键．22．（10分）11×2=1−12，12×3=12−13，13×4=13−14，14×5=14−15=⋯，(1)第5个式子是_____；第n个式子是_____；(2)从计算结果中找规律，利用规律计算：11×2+12×3+13×4+14×5+⋯+12023×2024；(3)计算：（由此拓展写出具体过程）：11×3+13×5+15×7+⋯+199×101．23．（10分）甲乙两家体育用品店出售同款羽毛球拍和羽毛球．每副羽毛球拍定价80元，每个羽毛球2元．甲商店推出的优惠方案是：买一副球拍赠送5个羽毛球；乙商店的优惠方案是：按总价的九折优惠．某学校想购买20副羽毛球拍和x个羽毛球（其中x≥100）．(1)若到甲商店购买，应付多少元？（用含x的代数式表示）(2)若到乙商店购买，应付多少元？（用含x的代数式表示）(3)当x=200时，应选择去哪家商店购买更合算？为什么？【答案】(1)(2x+1400)元(2)(1.8x+1440)元(3)去任意一家商店购买即可，理由见解析【分析】本题考查列代数式，代数式求值：（1）根据甲商店的优惠方法，列出代数式即可；（2）根据乙商店的优惠方案，列出代数式即可；（3）求出x=200时，两家需花费的费用，进行比较即可．【详解】（1）解：20×80+2(x−20×5)=(2x+1400)元；（2）(80×20+2x)×0.9=(1.8x+1440)元（3）去任意一家商店购买即可，理由如下：当x=200时，2x+1400=400+1400=1800元；1.8x+1440=1.8×200+1440=1800元；故选择甲、乙商店购买的费用相同．24．（10分）若点A在数轴上对应的数为a，点B在数轴上对应的数为b，我们把A、B两点之间的距离表示为AB，记AB=|a−b|，且a，b满足|a−1|+(b+2)2=0．(1)a=；b=；线段AB的长=；(2)点C在数轴上对应的数是c，且c与b互为相反数，在数轴上是否存在点P，使得PA+PB=PC?若存在，求出点P对应的数；若不存在，请说明理由；(3)在（1）、（2）的条件下，点A、B、C开始在数轴上运动，若点B以每秒1个单位长度的速度向左运动，同时点A和点C分别以每秒4个单位长度和9个单位长度的速度向右运动，t秒钟后，若点A和点C之间的距离表示为AC，点A和点B之间的距离表示为AB，那么AB−AC的值是否随着时间t的变化而变化?若变化，请说明理由；若不变，请求出AB−AC的值．【答案】(1)1，−2，3；(2)−3或−1；(3)AB−AC的值不随着时间t的变化而变化，值为2．【分析】（1）根据绝对值及平方的非负性，求出a，b的值，从而求出线段AB的长；（2）设P对应的数为y，再由PA+PB=PC，可得出点P对应的数；（3）根据A，B，C的运动情况即可确定AB，AC的变化情况，即可确定AB−AC的值．【详解】（1）∵|a−1|+(b+2)2=0，∴a−1=0，b+2=0，解得：a=1，b=−2，∴线段AB的长为：1−(−2)=3，故答案为：1，−2，3；（2）由（1）得：b=−2，∴c=2，设P对应的数为y，由图知：①P在A右侧时，不可能存在P点；②P在B左侧时，1−y−2−y=2−y，解得: y=−3，③当P在A、B中间时，3=2−y，解得: y=−1，故点P对应的数是−3或−1；（3）AB−AC的值不随着时间t的变化而变化，理由如下：t秒钟后，A点位置为：1+4t，∴B点的位置为: −2−t，C点的位置为: 2+9t，∴AB=1+4t−(−2−t)=5t+3AC=2+9t−(1+4t)=5t+1，∴AB–AC=5t+3−(5t+1)=2，∴AB−AC的值不随着时间t的变化而变化，值为2．【点睛】此题考查了非负数的应用，数轴的应用，数轴上的距离，理解数轴上点的距离是解题的关键．。