山东省滨州市惠民县2017-2018学年八年级上学期期末数学试题(原卷版)

FDBCAE 八年级数学试题上学期期末考试一、选择题（每小题3分,共30分） 1．下列图形中轴对称图形是（ ）Ａ Ｂ Ｃ Ｄ２,.已知三角形的三边长分别是3，8，x ，若x 的值为偶数，则x 的值有( )A.6个B.5个C.4个D.3个３.一个多边形截去一个角后，形成的多边形的内角和是2520°，则原多边形的边数是( )A.15或16B.16或17C.15或17D.15.16或174.如图，△ACB ≌△A'CB'，∠BCB'＝30°，则∠ACA'的度数为( )A.20°B.30°C.35°D.40°５, 等腰三角形的两边长分别为5cm 和 10cm ，则此三角形的周长是（ ）A.15cmB. 20cmC. 25cmD.20cm 或25cm6.如图，已知∠CAB ＝∠DAB ，则添加下列一个条件不能使△ABC ≌△ABD 的是( ) A.AC ＝AD B.BC ＝BD C.∠C ＝∠D D.∠ABC ＝∠ABD7.如图，已知在△ABC 中，CD 是AB 边上的高，BE 平分∠ABC ，交CD 于点E ，BC ＝5，DE ＝2，则△BCE 的面积等于( )A.10B.7C.5D.4 8．若()22316m x x+-+是完全平方式,则m 的值等于( )A. 3B. -5C.7D. 7或-19．如图，在△ABC 中，AB =AC ，BE=CD ，BD =CF ，则∠EDF 的度数为 （ ） A ．1452A ︒-∠ B ．1902A ︒-∠ C ．90A ︒-∠ D ．180A ︒-∠第10题 10．如上图，等腰Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，∠ABC 的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交BC 于点N ，连接DM ，下列结论：① DF ＝DN ；② △DMN 为等腰三角形；③ DM 平分∠BMN ；④ AE ＝32EC ；⑤ AE ＝NC ，其中正确结论的个数是（ ）A ．2个B ．3个C ．4个D ．5个二、填空题（每小题3分,共24分）11．计算:()()312360.1250.2522⨯-⨯⨯- = 12,在实数范围内分解因式:3234a ab - = 13.若2,3,mn xx ==则2m nx+=14．若A （x ，3）关于y 轴的对称点是B （﹣2，y ），则x=__________，y=__________，点A 关于x 轴的对称点的坐标是__________．15,如图，△ABC 中，DE 是AC 的垂直平分线，AE ＝3 cm ，△ABD 的周长是13 cm ，则△ABC 的周长为 _________第15题图 第17题图16,已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°，求此等腰三角形的顶角为17．如图，∠AOB ＝30°，点P 为∠AOB 内一点，OP ＝8．点M 、N 分别在OA 、OB 上，则△PMN 周长的最小值为__________18. 如图所示，在△ABC 中，∠A =80°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于A 1点，∠A 1BC 与∠A 1CD 的平分线相交于A 2点，依此类推，∠A 4BC 与∠A 4CD 的平分线相交于A 5点，则∠A 5的度数是 。

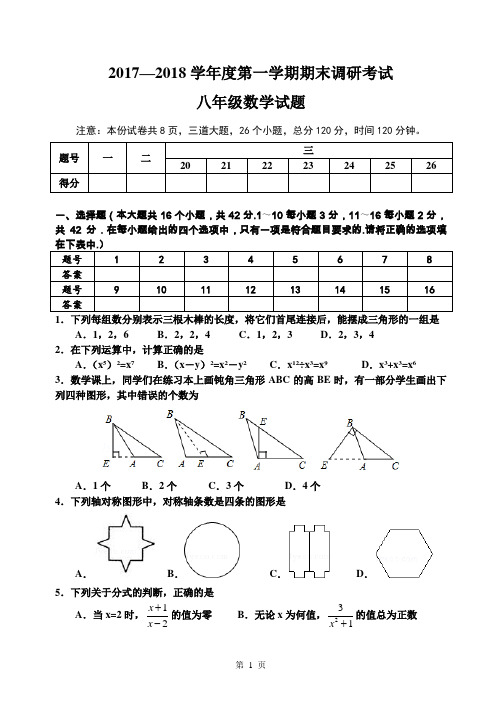
2017—2018学年度第一学期期末调研考试八年级数学试题注意：本份试卷共8页，三道大题，26个小题，总分120分，时间120分钟。

一、选择题（本大题共16个小题，共42分.1～10每小题3分，11～16每小题2分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的选项填在A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，42．在下列运算中，计算正确的是A．（x5）2=x7B．（x－y）2=x2－y2C．x12÷x3=x9D．x3+x3=x63．数学课上，同学们在练习本上画钝角三角形ABC的高BE时，有一部分学生画出下列四种图形，其中错误的个数为A．1个B．2个C．3个D．4个4．下列轴对称图形中，对称轴条数是四条的图形是A．B．C．D．5．下列关于分式的判断，正确的是A．当x=2时，12xx+-的值为零B．无论x为何值，231x+的值总为正数C ．无论x 为何值，31x +不可能得整数值 D ．当x≠3时，3x x -有意义6．如图，已知AB=AC ，AD=AE ，若要得到“△ABD ≌△ACE”，必须添加一个条件，则下列所添条件不恰当的是A ．BD=CEB ．∠ABD=∠ACEC ．∠BAD=∠CAED ．∠BAC=∠DAE 7．若把分式2x yxy+中的x 和y 都扩大3倍，且x+y≠0，那么分式的值 A ．扩大3倍 B ．不变 C ．缩小3倍 D ．缩小6倍 8．若x=－2，y=12，则y （x+y ）+（x+y ）（x －y ）－x 2的值等于 A ．－2 B ．12C ．1D ．－19．如图，在△ABC 中，DE 是AC 的垂直平分线，AC=6cm ，且△ABD 的周长为13cm ，则△ABC 的周长为A ．13cmB ．19cmC ．10cmD ．16cm10.观察等式（2a ﹣1）a+2=1，其中a 的取值可能是A ．﹣2B ．1或﹣2C ．0或1D ．1或﹣2或0 11．下列计算中正确的是A ．22155b a a b ab -⨯=-- B ．32x y x y ya b a b a b+--=+++ C ．m m n m n n m n ÷⨯= D ．1224171649xy xy a xy a -⎛⎫⎛⎫÷=⎪ ⎪⎝⎭⎝⎭12．如图，C 在AB 的延长线上，CE ⊥AF 于E ，交FB 于D ，若∠F=40°，∠C=20°，则∠FBA 的度数为A ．50°B ．60°C ．70°D ．80°13．若y －x=－1，xy=2，则代数式－12x 3y+x 2y 2－12xy 3的值是 A ．2 B ．－2 C ．1 D ．－114．图1是一个长为 2a ，宽为2b （a ＞b ）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积是A ．a 2－b 2B ．（a －b ）2C ．（a+b ）2D ．ab15．如图，△ABC的顶点坐标分别为A（4，4）、B（2，1）、C（5，2），沿某一直线作△ABC的对称图形，得到△A′B′C′，若点A的对应点A′的坐标是（3，5），那么点B的对应点B′的坐标是A．（0，3）B．（1，2）C．（0，2）D．（4，1）16．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED=90°②∠ADE=∠CDE ③DE=BE ④AD=AB+CD，四个结论中成立的是A．①②④B．①②③C．②③④D．①②二、填空题（本大题共3小题，共10分.17～18小题各3分；19小题有2个空，每空2分.把答案写在题中横线上）17．一个多边形的每一个外角都为36°，则这个多边形是边形．18．若x2+2（m－3）x+16是一个完全平方式，那么m应为．19．对于实数a、，b，定义运算⊗如下：a⊗b=()(),0,0bba ab aa ab a-⎧>≠⎪⎨≤≠⎪⎩，例如：2⊗4=2－4=116，计算[4⊗2] =，[2⊗2]×[3⊗2]=．三、解答题（本大题共7小题，共68分．解答应写出文字说明、证明过程或演算步骤）20．计算（本题满分8分）如图，在平面直角坐标中，△ABC各顶点都在小方格的顶点上．（1）画出△ABC关于x轴对称的图形△A1B1C1；（2）在y轴上找一点P，使PA+PB1最短，画出图形并写出P点的坐标．21．（本题满分9分）先化简，再求值：2214411a aa a a-+⎛⎫-÷⎪--⎝⎭，其中－2＜a≤2，请选择一个a的合适整数代入求值．22．（本题满分9分）两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，（1）请找出图②中的全等三角形，并给予证明（结论中不得含有未标识的字母）；（2）求证：DC⊥BE．23．（本题满分9分）先阅读以下材料，然后解答问题．将一个多项式分组后，可提公因式或运用公式继续分解的方法是因式分解中的分组分解法，一般的分组分解法有四种形式，即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等．如“2+2”分法：ax+ay+bx+by=（ax+ay）+（bx+by）=a（x+y）+b（x+y）=（x+y）（a+b）请你仿照以上方法，探索并解决下列问题：（1）分解因式：x2－y2－x－y；（2）分解因式：9m2－4x2+4xy－y2；24．（本题满分10分）如图，已知BD平分∠ABC，AB=AD，DE⊥AB，垂足为E．（1）求证：AD∥BC；（2）若DE=6cm，求点D到BC的距离；（3）当∠ABD=35°，∠DAC=2∠ABD时，①求∠BAC的度数；②证明：AC=AD．25．（本题满分11分)随着城际铁路的正式开通，从甲市经丙市到乙市的高铁里程比普快里程缩短了90km，运行时间减少了8h，已知甲市到乙市的普快列车里程为1220km．高铁平均时速是普快平均时速的2.5倍．（1）求高铁列车的平均时速；（2）某日王先生要从甲市去距离大约780km的丙市参加14：00召开的会议，如果他买到当日9：20从甲市到丙市的高铁票，而且从丙市火车站到会议地点最多需要1小时．试问在高铁列车准点到达的情况下，它能否在开会之前20分钟赶到会议地点？26．(本题满分12分)如图1，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的是速度都为1厘米/秒．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（秒）．（1）当运动时间为t秒时，BQ的长为厘米，BP的长为厘米；（用含t 的式子表示）（2）当t为何值时，△PBQ是直角三角形；（3）如图2，连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．参考答案及评分标准说明：1.在阅卷过程中，如果考生还有其它正确解法，可参照评分参考酌情给分；2.填空题缺少必有的单位或答案不完整不得分；3.坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误，就不给分；4.解答右端所注分数，表示正确做到这一步应得的累积分数.一、(本大题有16小题，共43分.1~10每小题各3分，11~16每小题各2分)二、(本大题有3个小题，共10分.17~18小题个3分；19小题有2个空，每空2分) 17．十；18．－1或7；19．16，．三、（本大题有7小题，共68分）20.解：（1）如图所示：△A1B1C1为所求作的三角形；……………………….……4分（2）如图，……………………………………………………………………..…..……7分点P的坐标为：（0，1）．………………………………………………………...………8分21．解：原式=……………………………………………………….2分=……………………………………………………………………………4分=，………………………………………………………………………………………6分当a=－1时，…………………………………………………………………….…………8分原式=．……………………………………………..……………………………9分22．（1）解：△BAE≌△CAD，证明如下：……………………………………………1分∵△ABC，△DAE是等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°．……………………………..……………2分∠BAE=∠DAC=90°+∠CAE，………………………………………………………...…4分在△BAE和△DAC中∴△BAE≌△CAD（SAS）．………………………………………………………………6分（2）证明：∵△ABC，△DAE是等腰直角三角形，∴∠B=45°，∠BCA=45°，……………………………………………………………..…7分∵△BAE≌△CAD．∴∠DCA=∠B=45°．………………………………………………………………………8分∴∠BCD=∠BCA+∠DCA=90°，∴DC⊥BE．…………………………………………………………………………………9分23．解：（1）原式=（x2－y2）－（x+y）…………………………………………………2分=（x+y）（x－y）－（x+y）…………………………….……………………………….…3分=（x+y）（x－y－1）；……………………………………………….………………………4分（2）原式=9m2－（4x2－4xy+y2）……………………………………………………….6分=（3m）2－（2x－y）2…………………………………………………………………….8分=（3m+2x－y）（3m－2x+y）. ……………………………………………………….……9分24．（1）证明：∵AB=AD，∴∠ADB=∠ABD…………………………………………………….………..……………1分又∵BD平分∠ABC，即∠ABD=∠DBC，∴∠ADB =∠DBC，…………………………………………………………..……………2分∴AD∥BC；…………………………………………………………………………………3分（2）解：作DF⊥BC交BC的延长线于F．∵BD平分∠ABC，DE⊥AB，DF⊥BC，∴DF=DE=6cm；即点D到BC的距离为6cm. ……………………………………………………..……5分（3）①解：∵BD平分∠ABC，∴∠ABC=2∠ABD=70°，…………………………………………………………..….…6分∵AD∥BC，∴∠ACB=∠DAC=70°，……………………………………………………………….…7分∴∠BAC=180°－∠ABC－∠ACB=180°－70°－70°=40°．……………………………8分②证明：∵∠ABC=70°，∠ACB=70°，∴∠ABC=∠ACB，∴AB=AC，…………………………………………………………………………………9分又∵AB=AD，∴AC=AD．………………………………………………………………………………..10分25．解：（1）设普快的平均时速为x千米/小时，高铁列车的平均时速为2.5x千米/小时，根据题意得，……………..……………………………………………………..…………1分－=8，…………………………………………..………………….……4分解得：x=96，……………..………………5分经检验，x=96是原分式方程的解，且符合题意，……………..………………………6分则2.5x=240，答：高铁列车的平均时速为240千米/小时；………………………………..…………7分（2）780÷240=3.25，则坐车共需要3.25+1=4.25（小时），……………………………………..…………..…9分从9：20到13：40，共计4小时，………………………………...…………………10分因为4小时＞4.25小时，所以王先生能在开会之前到达．………………………………………………..………11分26．解：（1）t；（5－t）；………………………..………………….…………..………2分（2）∵△ABC是等边三角形，∴∠B=60°．①当∠PQB=90°时，∵∠B=60°，∴∠BPQ=30°，∴PB=2BQ，得5－t=2t，解得，t=，………………………………………………………………………………4分②当∠BPQ=90°时，∵∠B=60°，∴∠BQP=30°，∴BQ=2BP，得t=2（5－t），解得，t=，………………………………………………………………...…………6分∴当t的值为或时，△PBQ为直角三角形；…………………………..………7分（3）∠CMQ不变，∠CMQ=60°理由如下：………………………………….……8分∵△ABC是等边三角形，∴AB=AC，∠B=∠BAC=60°，由题意可知：AP=BQ，在△ABQ与△CAP中，，∴△ABQ≌△CAP（SAS），…………………………………………………..………10分∴∠BAQ=∠ACP，∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°，∴∠CMQ不会变化，总为60°．………………………..……………………………12分。

山东省滨州市八年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）以下列各数为边长，不能组成直角三角形的是（）A . 3，4，5B . 4，5，6C . 5，12，13D . 6，8，102. （2分）下列实数中，为无理数的是（）A . 0.2B .C .D . -53. （2分） (2019七下·永川期中) 下列说法中正确的是（）A . 9的平方根是3B . 4平方根是C . 的算术平方根是4D . -8的立方根是4. （2分）下列二次根式中，取值范围是的是（）A .B .C .D .5. （2分） (2016八上·永登期中) 已知点A（4，﹣3），则它到y轴的距离为（）A . ﹣3B . ﹣4C . 3D . 46. （2分） (2020七下·越秀期中) 下列说法中，正确的是（）A . －(－3)2＝9B . |－3|＝－3C . ＝±3D . ＝7. （2分）如图，七年级（下）教材第4页给出了利用三角尺和直尺画平行线的一种方法，能说明AB∥DE 的条件是（）A . ∠CAB=∠FDEB . ∠ACB=∠DFEC . ∠ABC=∠DEFD . ∠BCD=∠EFG8. （2分） (2016七上·乳山期末) 如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，BE=4，则AD的长是（）A . 4B . 2C . 6D . 29. （2分） (2018九上·建平期末) 已知一次函数y=mx+n与反比例函数y= 其中m、n为常数，且mn＜0，则它们在同一坐标系中的图象可能是（）A .B .C .D .10. （2分）(2020·杭州模拟) 已知反比例函数y＝的图象在每一个象限内，y随x的增大而增大，那么一次函数y＝kx+2的大致图象是（）A .B .C .D .二、填空题 (共6题；共6分)11. （1分） (2019七下·濉溪期末) 计算： - =________．12. （1分） (2019八上·漳州月考) 一个正数的平方根为x+3与2x 6，则这个正数是________．13. （1分）(2018·攀枝花) 样本数据1，2，3，4，5．则这个样本的方差是________．14. （1分）计算：= ________15. （1分） (2016八上·抚宁期中) 如图，在△ABC中，AB=AC，AD⊥BC于D，DE⊥AB于E，DF⊥AC于F，若DE=3，则DF=________．16. （1分）(2020·宿迁) 如图，在矩形ABCD中，AB=1，AD= ，P为AD上一个动点，连接BP，线段BA 与线段BQ关于BP所在的直线对称，连接PQ，当点P从点A运动到点D时，线段PQ在平面内扫过的面积为________.三、解答题 (共9题；共65分)17. （5分） (2020八下·延平月考) 计算：．18. （5分）已知关于x、y的二元一次方程组与的解相同，求a、b的值．19. （5分）(2019·周至模拟) 如图，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF=DE.求证：AE∥CF.20. （5分） (2016八上·思茅期中) 为了抓住市文化艺术节的商机，某商店决定购进A，B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．求购进A，B两种纪念品每件各需多少元？21. （5分）解方程：x-=1-22. （10分） (2019八上·铁锋期中) 如图所示，边长为1的正方形网格中，的三个顶点A、B、C 都在格点上.（1）作关于关于x轴的对称图形，（其中A、B、C的对称点分别是D、E、F），并写出点D 坐标；（2） P为x轴上一点，请在图中画出使的周长最小时的点P（不写画法，保留画图痕迹），并直接写出点P的坐标.23. （10分）．（1）请在如图的直角坐标系中作出y=2x+1，y=3x的图象；（2）利用你所画的图象，直接写出方程组的解．24. （10分）(2017·润州模拟) 王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：（1）根据图中提供的数据列出如下统计表：平均成绩（分）中位数（分）众数（分）方差（S2）王华 80 b 80 d张伟 a 85 c 260则a=________，b=________，c=________，d=________，（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是________．（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？25. （10分） (2016九上·兖州期中) 如图，抛物线y=ax2+bx﹣4（a≠0）与x轴交于A（4，0），B（﹣1，0）两点，过点A的直线y=﹣x+4交抛物线于点C．（1）求此抛物线的解析式；（2）在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共6分)11-1、12-1、答案：略13-1、14-1、15-1、16-1、三、解答题 (共9题；共65分)17-1、答案：略18-1、答案：略19-1、20-1、答案：略21-1、22-1、答案：略22-2、答案：略23-1、答案：略23-2、答案：略24-1、24-2、24-3、25-1、答案：略25-2、答案：略。

山东省滨州市—第一学期期末考试八年级数学试题第Ⅰ卷 选择题一、选择题：（本大题共12小题，在每小题的四个选项中只有一个是正确的，请把正确的选项选出来，并将其字母标号填写在答题栏内） 1.下列图形具有稳定性的是（ ）A. 正方形B. 长方形C. 直角三角形D. 平行四边形 2.已知图中的两个三角形全等，则∠α度数是（ ）A. 50°B. 58°C. 60°D. 72°3.若等腰三角形中有一个角等于50，则这个等腰三角形的顶角的度数为（ ）A ．50B ．80C ．65或50D ．50或804.下列计算中，结果正确的是 ( ) A ．236a a a =· B ．()()26a a a =·3 C ．()326a a = D ．623a a a ÷=5.下列图形中，不是轴对称图形的是（ ）6.使分式14-x 有意义，则x 的取值范围是( ) A ．x ≠ 1 B．x ＞1 C ．x ＜1 D ．x ≠－17．如图，画△ABC 中AB 边上的高，下列画法中正确的是（ ） A. B. C. D.8．下列判定两个直角三角形全等的方法，错误的是 ( ) A ．两条直角边对应相等 B ．斜边和一锐角对应相等 C ．斜边和一直角边对应相等D ．两锐角对应相等9．下列运用平方差公式计算，错误．．的是（ ）。

A ．22))((b a b a b a -=-+ B ．1)1)(1(2-=-+x x x C ．12)12)(12(2-=-+x x x D ．49)23)(23(2-=--+-x x x 10．若分式112x y -=，则分式4543x xy yx xy y+---的值等于( ) A ．－35 B ．35 C ．－45 D ．4511．如图，已知△ABC，O 是△ABC 内的一点，连接OB 、OC ，将∠ABO、∠ACO 分别记为∠1、∠2，则∠1、∠2、∠A、∠O 四个角之间的数量关系是（ ）A ．∠1+∠0=∠A+∠2B ．∠1+∠2+∠A+∠O=180°C ．∠1+∠2+∠A+∠O=360°D ．∠1+∠2+∠A=∠O12．如图，AB=AC ，AB 的垂直平分线交AB 于D ，交AC 于E ，BE 恰好平分ABC ∠，有以下结论：（1）ED=EC ；（2）BEC ∆的周长等于2AE+EC ； (3)图中共有3个等腰三角形； （4）36A ∠=，其中正确的共有（ ）A ．4个B ．3个C ．2个D ．1个题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题：13.一个多边形的内角和等于其外角和的3倍，则这个多边形是 边形。

山东省滨州市惠民县2017-2018学年八年级上学期期末数学试题一、单选题(★) 1 . 下列根式中不是最简二次根式的是A．B．C．D．(★★) 2 . 无论 a取何值时，下列分式一定有意义的是A．B．C．D．(★★★) 3 . 如图，,要使,还需添加一个条件，那么在① ；② ；③ ；④ 这四个关系中可以选择的是A．①②③B．①②④C．①③④D．②③④(★★) 4 . 如图是用直尺和圆规作一个角等于已知角的示意图，则说明∠A′O′B′＝∠AOB的依据是A．SSS B．SAS C．ASA D．AAS(★★★) 5 . 如图，, ,则图中等腰三角形的个数是A．5B．6C．8D．9(★) 6 . 下列运算：（1）；（2）；（3）；（4）.其中错误的个数是A．1B．2C．3D．4(★★★) 7 . 若，则A等于A．B．C．D．(★) 8 . 练习中，小亮同学做了如下4道因式分解题，你认为小亮做得正确的有① ②③ ④A．1个B．2个C．3个D．4个(★★★) 9 . 关于的分式方程的解，下列说法正确的是A．不论取何值，该方程总有解B．当时该方程的解为C．当时该方程的解为D．当时该方程的解为(★) 10 . 如果把分式中的x和y的值都扩大为原来的3倍，那么分式的值A．扩大为原来的3倍B．扩大6倍C．缩小为原来的12倍D．不变(★★★) 11 . 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=4，BC=8，则△BC′F的周长为A．12B．16C．20D．24(★★★) 12 . 如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2EC，给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AB＝3BF，其中正确的结论共有A．①②③B．①③④C．②③D．①②③④二、填空题(★★★) 13 . 在△ABC中，∠C=90°，BC=16，∠BAC的平分线交BC于D，且BD：DC=5：3，则D到AB的距离为_____________．(★★★) 14 . 已知等腰三角形的一个内角为 50°，则顶角为____________．(★★★) 15 . 分解因式：=__________________________________. (★★★) 16 . 若x 2-mx+36是一个完全平方式，则m=____________________.(★) 17 . 当x的值为_______________，分式的值为0.(★★★) 18 . 如果直角三角形的三边长为10、6、 x，则最短边上的高为______．三、解答题(★★★) 19 . （1）计算：.（2）计算：(★★★) 20 . 根据要求，解答下列问题：（1）计算：（2）化简：.(★★★) 21 . 如图，已知点E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足.连接CD，且交OE于点F．（1）求证：OE是CD的垂直平分线．（2）若∠AOB=60°，求证：OE=4EF．(★★★) 22 . 如图，已知 B、 C、 E三点在同一条直线上，△ ABC与△ DCE都是等边三角形.其中线段BD交AC于点G，线段AE交CD于点F.求证：（1）△ACE≌△BCD；（2）△GFC是等边三角形.(★★★★★) 23 . 如图，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2秒后，求△ABP的周长．（2）问t为何值时，△BCP为等腰三角形？（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？(★★★)24 . 如图所示，港口A位于灯塔C的正南方向，港口B位于灯塔C的南偏东60°方向，且港口B在港口A的正东方向的135公里处.一艘货轮在上午8时从港口A出发，匀速向港口B航行.当航行到位于灯塔C的南偏东30°方向的D处时，接到公司要求提前交货的通知，于是提速到原来速度的1.2倍，于上午12时准时到达港口B，顺利完成交货.求货轮原来的速度是多少？。

2016—2017学年第一学期期末学业水平测试八年级数学试题第Ⅰ卷（选择题）一、选择题：本大题共12小题，共36分，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分. 1.下列图形：线段、角、正方形、圆，其中是轴对称图形个数的为（ ） A.1 B. 2C. 3D. 42.某个三角形的三边长有可能是（ ）A. 20,16,2016B. 2，2,4C. 2,2,2D. 1,2,4 3.如果一个多边形的每一个外角都是60°，那么这个多边形是（ ）A. 四边形B. 五边形C. 六边形D.八边形 4.若一个等腰三角形的两边长分别是3和7，则它的周长为（ ）A ．17B ．15C ．13D ．13或17 5.下列结论正确的是（ ）A.分式 有意义的条件是B. 与 的最简公分母是C.－0.000 0064用科学记数法表示为D.等式成立的条件是6.下列等式一定成立的是（ ）A. B.C. D.7.如果把分式中的x 和y 的值都扩大为原来的2倍，那么分式的值（ ） A.扩大为原来的2倍B.扩大4倍C.缩小为原来的2倍D.不变8.已知 ， ，则 的值为（ ）A.4B.C.2D. 9.下列式子由左到右的变形中，是因式分解且结果正确的为（ ）A. ＝x （x ﹣5）+ 6B.＝（x ﹣2）（x ﹣3） 1(1)x x -22x y x y-+22xy x y -222()()x y x y --20(9)1x -=632a a a ÷=235a a a +=y x x 23y2-5233()()xy xy x y -÷-=-2336(2)6xy x y =2m n x -41214=m x 8=nx 652+-x x 652+-x x 01x x ≠≠或66.410--⨯3x =±C.（x ﹣2）（x ﹣3）＝D. ＝（x + 2）（x + 3） 10.如图,已知△ABE ≌△ACD,且∠B=∠C,则下列结论： （1）∠1=∠2；（2）∠BAD=∠CAE ；（3）AD=AE ；（4）DB=EC. 其中错误的个数为（ ）A.0B.1C.2D.311.如果多项式能因式分解为 ，那么下列结论正确的是（ ） A. B. C. D.12.图（1）是一个长为，宽为 的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分（阴影部分）的面积是（ ）A. B. C. D.第Ⅱ卷（非选择题）二、填空题：本大题共6小题，共24分，只要求填写最后结果，每小题填对得4分．13.等腰三角形的一个角是70°，则它的底角是 . 14.如图，∠1=∠2，要使△ABE ≌△ACE ，还需添加一个条件是 （填上你认为适当的一个条件即可）．15.已知 ，则m = .16.当m = 时,分式 的值为零.第12题图（1）第12题图（2）652+-x x 652+-x x 22mx nx --(32)()x x p ++1n =3mnp =2p =-6m =2()b a b >ab2()a b +2()a b -22a b -2(1)(3)32m m m m ---+21119273m m -⨯=2a17.如图，在 中， ， 是 的垂直平分线， 交 于 点，交 于 点．已知 ，则 的大小为 . 18.已知，则 = . 三、解答题：本大题共6个小题，满分60分．解答时请写出必要的演推过程． 19.（每小题5分，满分10分）分解因式： （1）22)72()23(+--x x（2）20.（满分8分）当 取何值时， 的值比 的值大3？21.（每小题5分，满分10分）根据要求解答下列问题： （1）符号a b cd称为二阶行列式，规定它的运算法则为：a bcdad bc =-.依据以上法则，化简下列二阶行列式：bb a 42+ba ba 25.0--.（2）先化简，再求值：， 其中1x =-．22.（满分10分）一台汽车开往距离出发地180km 的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40分钟到达目的地，求汽车原来的速度.Rt ABC △ο90=∠B ED AC AC D BC E ο10=∠BAE C∠21322a a -+13a a-=22882ab b a--13(22)x --1(1)x --x22214()2442x x x x x x x x ----÷++++23.（满分10分）如图，点 是 的交点，点 是 的中点.试判 断和 的位置关系，并给出证明.24.（满分12分）已知：如图，∠B=∠C=90°，M 是BC 的中点，且DM 平分∠ADC. （1）求证：AM 平分∠DAB.（2）试说明线段DM 与AM 有怎样的位置关系？并证明你的结论．A BCDE O第23题图AB E ,AD BC O ,,BAC ABD AC BD ∠=∠=OE AB参考答案一、选择题（本大题12个小题，每小题3分，共36分.请选出唯一正确答案的代号填在下面的答题栏内）二、填空题（本大题6个小题，每小题4分，共24分）13.55°或70°； 14.酌情判分； 15.2； 16.3； 17.40°； 18. 三、解答题（本大题6个小题，共60分） 19.（每小题5分，满分10分）解：（1）原式＝［(3x －2)＋(2x ＋7)］［(3x －2)－(2x ＋7)］…………… 2分＝(3x －2＋2x ＋7)(3x －2－2x －7) ………………………… 3分 ＝(5x ＋5)(x －9) ………………………………………………4分 ＝5(x ＋1)(x －9). ……………………………………………5分 （2）原式= ……………………2分. …………………………5分20．（本小题满分8分） 解：根据题意列方程得……………3分 方程两边乘 ，得………………4分 解得 x= ……………6分 检验：当x= 时， ≠0. ……………7分 所以，原分式方程的解为x= . 答：当x 取 时， 的值比 的值大3. ………8分21.（每小题5分，满分10分）21-222(44)a ab b =--+22882ab b a --22(2)a b =--313221x x=+--2(1)x -326(1)x =-+-1161162(1)x -1161(1)x --13(22)x --116解:（1）原式 ……………………2分 222424b ab b a +--= ……………………4分 ab a 22-= . …………………………………5分（2） 原式= ……………2分 = ……………3分= ……………4分当x=－1时原式= = =-1 ……………5分22．（本小题满分10分）解：设汽车原速度为x 千米/时，依题意，得3215.11180180=⎪⎭⎫ ⎝⎛+--x x x . ……………5分 解得60=x ……………8分 经检验60=x 是原方程的解.答：（略）. ……………10分 23.（本小题满分10分）解：OE ⊥AB ……………2分证明：在ABC ∆和BAD ∆中AB BABAC ABD AC BD =⎧⎪∠=∠⎨⎪=⎩∴ABC ∆≌BAD ∆ ………………5分 ∴ABC BAD ∠=∠ ………………6分 ∴OA OB = ………………7分 ∴OAB ∆是等腰三角形 ………………8分 又E 是AB 的中点)5.0(4)2)(2(b a b b a b a ---+=2(2)(2)(1)4(2)2x x x x x x x x -+---÷++212x x+22242(2)4x x x x x x x --+++-g 21(1)2(1)-+⨯-112-∴OE⊥AB. ………………10分24.（本小题满分12分）证明：（1）作ME⊥AD. ……………………………………2分∵DM平分∠ADC，∠C=90°，∴ME=MC. ……………………………………4分又M是BC的中点，∴MB=MC. ……………………………………5分∴MB=ME. …………………………………6分又ME⊥AD，∠B=90°，∴点M在∠DAB的平分线上，即AM平分∠DAB. …………………………………7分（2）DM⊥AM，…………………………………8分∵∠B=∠C=90°，∴CD∥AB，…………………………………9分∴∠DAB+∠ADC=180°. …………………………………10分又∵DM平分∠ADC，AM平分∠DAB，∴½（∠DAB+∠ADC）=90°. …………11分∴∠AMD=90°，即MD⊥AM. ………………………………12分。

A B C D 2017--2018学年度八年级 （上）数学期末测试一、选择题（每小题3分，共36分）1．下列平面图形中，不是轴对称图形的是 （ ）2．下列运算中，正确的是（ ）A 、 (x 2)3=x 5B 、3x 2÷2x=xC 、 x 3·x 3=x 6D 、(x+y 2)2=x 2+y 43．已知：在Rt △ABC 中，∠C =90°，AD 平分∠BAC 交BC 于D ，若BC =32，且BD ：DC =9：7，则D 到AB 边的距离为 （ ）A ．18B ．16C ．14D ．124．下列各式由左边到右边的变形中，是分解因式的为（ ）A 、a (x + y) =a x + a yB 、x 2－4x+4=x(x －4)+4C 、10x 2－5x=5x(2x －1)D 、x 2－16+3x=(x －4)(x+4)+3x 5．如图，C F BE ,,,四点在一条直线上，,,D A CF EB ∠=∠=再添一个条件仍不能证明⊿ＡＢＣ≌⊿ＤＥＦ的是（ ）A ．AB=DEB ．.DF ∥AC C ．∠E=∠ABCD ．AB ∥DE 6．将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（ ）A ．1、2、3B ．2、3、4C ．3、4、5D ．4、5、6 7．已知m 6x =，3n x =，则2m n x-的值为（ ） A 、9 B 、 12 C 、 43 D 、34 8．已知：如图，△ABC 与△DEF 是全等三角形，则图中相等的线段的组数是 （ ）A ．3B ． 4C ．5D ．6（第8题） （第9题） （第10题）9．如图，在∠AOB 的两边上截取AO=BO ，CO=DO ，连接AD ，BC 交于点P ，那么在结论①△AOD ≌△BOC ；②△APC ≌△BPD ；③点P 在∠AOB 的平分线上．其中正确的是 （ ）A ．只有①B ． 只有②C ． 只有①②D ． ①②③ABE CF D O D C A B P A B D CE α γ β A BF E C D10．如图，D ，E 分别是△ABC 的边BC ，AC ，上的点，若AB=AC ，AD=AE ，则 （ ）A ．当∠B 为定值时，∠CDE 为定值 B ．当∠α为定值时，∠CDE 为定值C ．当∠β为定值时，∠CDE 为定值D ．当∠γ为定值时，∠CDE 为定值11．已知等腰三角形一边长为4，一边的长为10，则等腰三角形的周长为（ ）A 、14B 、18C 、24D 、18或2412．若分式方程xa x a x +-=+-321有增根，则a 的值是（ ） A ．1 B ．0 C ．—1 D ．—2二、填空题（每小题3分，共24分）13.用科学记数法表示—0.000 000 0314= ．14．如图，△ABC ≌△ADE ，∠EAC =25°，则∠BAD = °15．如图，D ，E 是边BC 上的两点，AD =AE ，请你再添加一个条件： 使△ABE ≌△ACD 16.计算(－3a 3)·(－2a 2)＝________________17．已知,2,522-=+=+b ab ab a 那么=-22b a ． 18．等腰三角形一腰上的高与另一腰的夹角为40°，则它的顶角的度数为 °．19．如图,△ABC 中,DE 是AC 的垂直平分线,AE =3cm ,△ABD 的周长为13cm ,则△ABC 的周长为__________cm ．20．如图，在△ABC 中，∠ACB =90°，BE 平分∠ABC ，CF 平分∠ACB ，CF ,BE 交于点P ，AC =4cm ，BC =3cm ，AB =5cm ，则△CPB 的面积为 2cm三、解答题（本大题共60分）21．①（5分） 因式分解：33ab b a -B AC D E A C B F E P （第20题） A D B E C B D E C A （第14题） （第15题） （第19题）② （5分）化简求值：[]{})24(32522222b a ab ab b a b a ----其中5.0,3=-=b a22．（5分）如图,A 、B 、C 三点表示3个村庄，为了解决村民子女就近入学问题，计划新建一所小学，要使学校到3个村庄的距离相等，请你在图中有尺规确定学校的位置．(保留作图痕迹,不写画法)23．（7分）一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？24．（8分）如图,BD 平分∠MBN ,A ，C 分别为BM ,BN 上的点,且BC >BA ,E 为BD 上的一点,AE =CE ,求证 ∠BAE +∠BCE =180°C A B · · · B C NDE MAA D BE FC 25.(8分) 如图,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,求△ABC 各角的度数.26．（10分）如图，已知AC ⊥CB ，DB ⊥CB ，AB ⊥DE ，AB =DE ，E 是BC 的中点．（1）观察并猜想BD 和BC 有何数量关系？并证明你猜想的结论．（2）若BD =6cm ，求AC 的长．27.（12分）如图，在△ABC 中，∠ACB =90°，CE ⊥AB 于点E ，AD=AC ，AF 平分∠CAB •交CE 于点F ，DF 的延长线交AC 于点G ，求证：（1）DF ∥BC ；（2）FG =FE ．A D C B2017--2018学年度八年级 （上）数学期末测试3参考答案一、选择题（每小题3分，共36分）ACACACBBDACD二、填空题（每小题3分，共24分）13.-3.14×610-14.25°15.∠B=∠C16.65a17.918.5019.19cm20.1.5三、解答题（本大题共60分） 21．①（5分） 因式分解： 33ab b a -=ab(2a -2b )=ab(a+b)(a-b)② （5分）化简求值：[]{})24(32522222b a ab ab b a b a ----其中5.0,3=-=b a 解：原式=[]{})24(32522222b a ab ab b a b a ----=ab(5a-b)=138.522.答案略23.设江水的流速为x 千米/时，则可列方程xx -=+306030100 解得：x=7.5答：江水的流速为7.5千米/时.24.提示（过E 点分别BA 与BC 的垂线，即可证明）25.∠A=36°,∠ABC=∠C=72°26.解（1）BD 和BC 相等。

2017—2018学年度第一学期期末考试八年级数学试题温馨提示：1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共4页.满分100分，考试用时90分钟.考试结束后，将试题卷和答题卡一并交回.2.答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在试题卷和答题卡规定的位置上.3.第Ⅰ卷每小题选出答案后，必须用0.5毫米黑色签字笔将该答案选项的字母代号填入答题卡的相应表格中，不能答在试题卷上.4.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷（选择题共30分）一、选择题：本大题共10个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来，并将该选项的字母代号填入答题卡的相应表格中.每小题选对得3分,满分30分. 1．在下列长度的三条线段中，能组成三角形的是A．1,2,3 B．3,8,4 C．10,6,5 D．2,4,22．下列图形：①角，②线段，③等腰三角形，④直角三角形，其中是轴对称图形的有A．①②③④ B．①②③C．②④D．①③3．△ABC中，若∠B =∠A+10°，∠C=∠B+10°，则下列结论错误的是A．∠C=∠A+20°B．∠A=50°C．∠B的外角是130°D．△ABC是一个锐角三角形4．下列数据能唯一确定三角形的形状和大小的是A．∠A=50°，∠B =60°，∠C=70°B．AB=6，∠B =70°，∠C=60°C．AB=4，BC =5，∠C=60°D．AB=4，BC =5，CA=105．下列运算正确的是A ．2222x x x =B ．326()x x =C ．3412(2)8x x -=D ．734()()x x x -÷-=-6．下列各因式分解正确的是A ．22(2)(2)(2)x x x -+-=-+B ．2221(1)x x x +-=-C ．22441(21)x x x -+=-D ．242(2)(2)x x x x -=+-7．若分式12x x -+的值为0,则x 应满足的条件是 A ．x =-2 B ．x =0 C.x =1或x =-2 D ．x =18.下列计算错误的是A ．0.220.77a b a b a b a b++=--B ．3223x y x x y y=C ．1a bb a-=--D ．123c c c+= 9．如图，为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等，应修建在△ABC 的 A ．两条中线的交点处B ．两条角平分线的交点处C ．两条高的交点处D ．两条边的垂直平分线的交点处10．如图，△ABC 的周长为30cm ，把△ABC 的边AC 对折，使顶点C 和点A 重合，折痕交BC 边于点D ，交AC 边于点E ，连接AD ，若AE =4cm ，则△ABD 的周长是 A ．22 cm B ．20 cm C ．18 cm D ．15 cm（第9题图）第Ⅱ卷（非选择题 共70分）二、填空题：本大题共8个小题，每小题3分，满分24分. 11．点（-7,9）关于y 轴对称的点的坐标是 ．12．计算：0220183--+-（）= ． 13．如果216x kx ++可运用完全平方公式进行因式分解，那么k 的值是 ． 14．张明3小时清点完一批图书的一半，李强加入清点另一半图书的工作，两人合作1.2小时清点完另一半图书.如果李强单独清点这批图书需要 小时． 15．一个多边形的内角和比它的外角和的3倍多180°，则它是 边形． 16．如图，∠1=∠2，∠3=∠4，∠BDC =130°，则∠A = ．17．在Rt△ABC 中，∠ACB =90°，BC =2.1cm ，CD ⊥AB ，在AC 上取一点E ，使EC =BC ，过点E 作EF ⊥AC 交CD 的延长线于点F ，若EF =4cm ，则AE = cm ． 18．如图，∠A =61°，∠C ′=47°,△ABC 与△A ′B ′C ′关于直线l 对称，则∠B =____ ．三、解答题：本大题共7个小题，满分46分. 解答时请写出必要的演推过程.19．先化简，再求值：222693293x x x x x x-+-÷--+，其中2018x =-.20．计算：（1）23215)()ab ab a b --÷-（； （2）222)()()6x y x y x y y +-+--（. 21．分解因式：（1）4811m -； （2）43242025ab ab ab -+.22. 两个小组同时开始攀登一座600m 高的山，第一组的攀登速度是第二组的1.2倍，他们比第二组早20min 到达顶峰，两个小组的攀登速度各是多少m/min ？如果山高是h m ，第一组的攀登速度是第二组的a 倍，并比第二组早t min 到达峰顶，则请直接写出两组的攀登速度各是多少m/min ？23. 如图，在平面直角坐标系中，点A 的坐标为（-2,0），△AOB 是等边三角形，点C 为OA 延长线上的一个动点，以BC 为边在第二象限中作等边△BCE ，连接EA 并延长EA 交y 轴于点F .（1）求∠EAB 的度数；（2）如果点C 再向左移动3个单位长度，则点F 的位置变化情况是 .24. 如图，在△ABC 中，AD ⊥BC ，BE ⊥AC ，垂足分别为D ，E ，AD 和BE 相交于点F ，DF =EF ，延长CF 交AB 于点G .（1）图中共有 个等腰三角形，共有 对全等三角形； （2）求证：CG 垂直平分AB .G FEDCBA（第23题图）（第24题图）2017—2018学年第一学期八年级数学试题参考答案及评分标准二、填空题：（每题3分，共24分）11.(7,9)； 12．89-； 13．±8； 14．4； 15．九； 16.80°； 17．1.9； 18.72°. 三、解答题：（共46分）19.解：222693293x x x x x x-+-÷--+ =2(3)(3)2(3)(3)3x x x x x x -+-+-- ……………………………………… 4分 = 2x -. ……………………………………… 5分 当2018x =-时，原式=-2018-2=-2020. …………………………… 6分20．解：（1）23215)()ab ab a b --÷-（ =362215a b a b a b --÷ ………………………………… 2分=321625a b ---- ………………………………… 3分 =1b. ………………………………… 4分（2）222)()()6x y x y x y y +-+--（ =22222446x xy y x y y ++-+- ……………………………………6分 =24xy y -. ……………………………………7分 21．解：（1）4811m -=22(91)(91)m m +- ………………………………… 2分 =2(91)(31)(31)m m m ++-. ………………………………… 4分（2）43242025ab ab ab -+=22(42025)ab b b -+ ………………………………… 5分=22(25)ab b - . ………………………………… 7分 22．解：设第二组的攀登速度为x m/min ，根据题意，列出方程600600201.2x x+=……………………………… 3分 解得 x =20 ……………………………… 4分经检验，x =20是原方程的解. ……………………………… 5分此时，1.2x =24 ……………………………… 6分 答：第一组的速度为24m/min 第二组的速度为20m/min ；如果山高是h m ，第一组的攀登速度是第二组的a 倍，并比第二组早t min 到达峰顶，则第一组的速度为ah h t -m/min 第二组的速度为ah hat-m/min. …………………… 8分 23．（1）解：∵△AOB 和△BCE 是等边三角形，∴BE =BC ,BA =BO ，∠EBC =∠ABO =∠AOB =60°，…………………… 3分 ∴∠EBC +∠ABC =∠ABO +∠ABC ，即∠EBA =∠CBO ，…………………… 4分 ∴△EBA ≌△CBO (SAS) …………………………………… 5分 ∴∠EAB =∠AOB =60°. …………………………………… 6分（2）如果点C 再向左移动3个单位长度，则点F 的位置变化情况是 保持不变 .…………………………………… 8分24． （1）图中共有 2 个等腰三角形，共有 6 对全等三角形；……2分 （2）证明：∵AD ⊥BC ，BE ⊥AC ，∴∠AEF =∠CEF =90°, ∠BDF =∠CDF =90°，∴∠CEF =∠CDF =90°, ∠AEF =∠BDF =90°，………………3分 在△CEF 和△CDF 中90,CEF CDF EF DF CF CF ∠=∠=︒⎧⎪=⎨⎪=⎩，∴△CEF ≌△CDF (HL) …………………………………… 5分 ∴∠ACG =∠BCG ，CE =CD . ………………………………… 6分 在△AEF 和△BDF 中90,AEF BDF EF DF EFA DFB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，∴△AEF ≌△BDF (ASA) …………………………………… 8分 ∴AE =BD ,∴CE +AE =CD +BD ，即AC =BC ，…………………………… 9分 又∠ACG =∠BCG ，∴CG 垂直平分AB . …………………………………… 10分。