徐州市初中数学圆的经典测试题含解析
- 格式:doc
- 大小:763.00 KB
- 文档页数:17
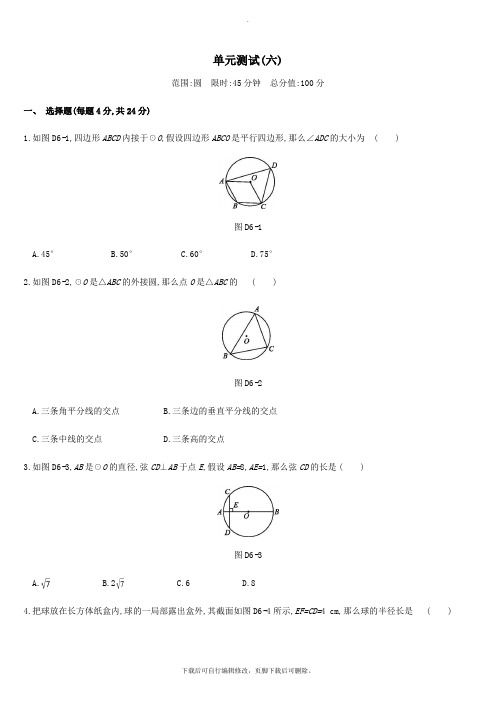
单元测试(六)范围:圆限时:45分钟总分值:100分一、选择题(每题4分,共24分)1.如图D6-1,四边形ABCD内接于☉O,假设四边形ABCO是平行四边形,那么∠ADC的大小为()图D6-1A.45°B.50°C.60°D.75°2.如图D6-2,☉O是△ABC的外接圆,那么点O是△ABC的()图D6-2A.三条角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点3.如图D6-3,AB是☉O的直径,弦CD⊥AB于点E,假设AB=8,AE=1,那么弦CD的长是()图D6-3A.B.2C.6D.84.把球放在长方体纸盒内,球的一局部露出盒外,其截面如图D6-4所示,EF=CD=4 cm,那么球的半径长是()图D6-4A.2 cmB.2.5 cmC.3 cmD.4 cm5.如图D6-5,等腰直角三角形ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于点D,那么阴影局部的面积为(结果保留π)()图D6-5A.24-4πB.32-4πC.32-8πD.166.如图D6-6,☉O是以原点为圆心,2为半径的圆,点P是直线y=-x+8上的一点,过点P作☉O的一条切线PQ,Q为切点, 那么切线长PQ的最小值为()图D6-6A.4B.2C.8-2D.2二、填空题(每题4分,共24分)7.如图D6-7,四边形ABCD内接于☉O,∠CBE=70°,那么∠ADC的度数是.图D6-78.如图D6-8,正五边形ABCDE的边长为2,分别以点C,D为圆心,CD长为半径画弧,两弧交于点F,那么的长为.(结果保存π)图D6-89.圆锥的底面周长为6π cm,高为4 cm,那么该圆锥的全面积是cm2;侧面展开图的扇形的圆心角是.10.如图D6-9,AB是☉O的直径,且经过弦CD的中点N,过CD延长线上一点E作☉O的切线,切点为F.假设∠ACF=65°,那么∠E= .图D6-911.如图D6-10,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,那么阴影局部的面积是(结果保存π).图D6-1012.如图D6-11,在直角坐标系xOy中,点A(0,1),点P在线段OA上,以AP为半径的☉P的周长为1,点M从点A开场沿☉P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).图D6-11(1)当m=时,n= ;(2)随着点M的转动,当m从变化到时,点N相应移动的路径长为.三、解答题(共52分)13.(12分)如图D6-12,正方形ABCD内接于☉O,M为的中点,连接BM,CM.(1)求证:BM=CM;(2)当☉O的半径为2时,求的长.图D6-1214.(12分)如图D6-13,AB为☉O的直径,C为☉O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.(1)求证:AC平分∠DAB;(2)假设BE=3,CE=3,求图中阴影局部的面积.图D6-1315.(14分)如图D6-14,AB是☉O的直径,弦CD与直径AB相交于点F.点E在☉O外,作直线AE,且∠EAC=∠D.(1)求证:直线AE是☉O的切线;(2)假设∠BAC=30°,BC=4,cos∠BAD=,CF=,求BF的长.图D6-1416.(14分)如图D6-15,△ABC中,AB=AC,以AB为直径作☉O,交BC于点D,交CA的延长线于点E,连接AD,DE.(1)求证:D是BC的中点;(2)假设DE=3,BD-AD=2,求☉O的半径;(3)在(2)的条件下,求弦AE的长.图D6-15参考答案1.C[解析] 设∠ADC=α,∠ABC=β.∵四边形ABCO是平行四边形,∴∠ABC=∠AOC.∵∠ADC=∠AOC=β,即α=β,而α+β=180°,∴解得β=120°,α=60°,即∠ADC=60°,应选C.2.B3.B[解析] 连接OC,那么OC=4,OE=3,在Rt△OCE中,CE===.因为AB⊥CD,所以CD=2CE=2.4.B5.A6.B7.70°8.π9.24π216°10.50°[解析] 如图,连接BC,OF.∵AB是☉O的直径,∴∠ACB=90°.∵∠ACF=65°,∴∠BCF=25°,∴∠BOF=50°.又∵EF是☉O的切线,∴∠OFE=90°.∵AB是☉O的直径,且经过弦CD的中点N, ∴CD⊥OA,即∠OND=90°.∵四边形ONEF的内角和是360°,∴∠NOF+∠E=180°.∵∠BOF+∠NOF=180°,∴∠E=∠BOF=50°.11.3-π12.-113.解:(1)证明:∵四边形ABCD是正方形, ∴AB=CD,∴=,∵M为中点,∴=,∴+=+,即=,∴BM=CM.(2)∵☉O的半径为2,∴☉O的周长为4π,∴的长=×4π=π.14.解:(1)证明:连接OC.∵CD与☉O相切于点C,∴OC⊥DE.又∵AD⊥CD,∴AD∥CO.∴∠DAC=∠ACO.∵OA=OC,∴∠ACO=∠CAO.∴∠DAC=∠CAO,即AC平分∠DAB.(2)设☉O的半径为r.∵在Rt△OEC中,OC2+EC2=OE2,∴r2+27=(r+3)2,解得r=3,∴∠COE=60°.∴S阴影=S△COE-S扇形COB=-.15.解:(1)证明:∵AB是☉O的直径,∴∠BCA=90°,∴∠B+∠BAC=90°,∵∠D=∠B,∠EAC=∠D,∴∠EAC=∠B,∴∠EAC+∠BAC=90°,即∠BAE=90°,∴BA⊥AE,∵BA是☉O的直径,∴直线AE是☉O的切线.(2)如图,作FH⊥BC于点H,∵∠BAD=∠BCD,cos∠BAD=,∴cos∠BCD=,在Rt△CFH中,∵CF=,∴CH=CF·cos∠BCD=×=, ∵BC=4,∴BH=BC-CH=4-=,∵AB是☉O的直径,∴∠BCA=90°,∵∠BAC=30°,∴∠B=60°,∴BF===3.16.解:(1)证明:∵AB是☉O的直径,∴∠ADB=90°,即AD⊥BC.∵AB=AC,∴BD=CD,即D是BC的中点.(2)∵AB=AC,∴∠B=∠C.又∵∠E=∠B,∴∠E=∠C,∴CD=ED=3.∵D是BC的中点,∴BD=CD=3.∵BD-AD=2,∴AD=1.∵∠ADB=90°,∴AB2=BD2+AD2=9+1=10.∵AB>0,∴AB=,∴r=AB=.(3)过点D作DF⊥CE交CE于点F.在Rt△ABD中,∠ADB=90°,∴cos B===.∵∠C=∠B,∴cos C=..在Rt△CDF中,∠DFC=90°,∴cos C===,∴CF=.∵DE=DC,DF⊥CE,∴CE=2CF=.又∵AC=AB=,∴AE=CE-AC=-=.。

江苏省徐州市中考数学专题题型复习07:圆的有关计算与证明姓名:________ 班级:________ 成绩:________一、解答题 (共7题;共55分)1. (10分)如图,为了测量河宽,小华采用的办法是:在河的对岸选取一点A,在河的这岸选一点B,使AB 与河的边缘垂直,然后在AB的延长线上取一点C,并量得BC=30米;在河的这边取一点D,并量得BD=20米;最后在射线AD上取一点E,使得,并量得DE=40米.小华这种做法,她能根据已有的数据求出河宽AB吗?若能,请求出河宽AB;若不能,她还必须测量哪一条线段的长?假设这条线段的长是m米,请你用含m的代数式表示河宽AB.2. (5分)如图,△ABC的三条内角平分线相交于点O,过点O作OE⊥BC于E点,(1)求证:∠BOD=∠COE.(2)如果AB=17,AC=8,BC=15,利用三角形内心性质及相关知识,求OE长.3. (5分)如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).4. (5分) (2017八下·黑龙江期末) 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D.F分别在边AB、AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.5. (10分) (2018九上·库伦旗期末) 如图,⊙O的直径AB=2,AM、BN是它的两条切线,CD与⊙O相切于点E,与BN、AM交于点C、D,设AD=x,BC=y。
(1)求证:AM∥BN。
(2)求y关于x的函数关系式。
(3)若x、y是关于t的方程2t -5t+m=0的两根,且xy= ,求x、y的值。
6. (10分)(2018·西华模拟) 为了对一棵倾斜的古杉树AB进行保护,需测量其长度,如图,在地面上选取一点C,测得∠ACB=45 ,AC=24 m,∠BAC=66.5 ,求这棵古杉树AB的长度.(结果精确到0.1 m.参考数据:sin66.5 ≈0.92,cos66.5 ≈0.40,tan66.5 ≈2.30)7. (10分) (2016九上·老河口期中) 如图,AB是⊙O的直径,C,E是⊙O上的两点,CD⊥AB于D,交BE 于F, = .求证:BF=CF.二、综合题 (共20题;共210分)8. (10分) (2016九下·澧县开学考) 如图,已知二次函数y=ax2+ x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+ x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.9. (10分)(2016·北仑模拟) 如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.(1)求m的值和该二次函数的表达式.P为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.(2)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.10. (10分)(2017·上思模拟) 如图,AB是△ABC外接圆⊙O的直径,D是AB延长线上一点,且BD= AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、EF.(1)求证:CD是⊙O的切线;(2)求:tan∠BFE的值.11. (10分)(2017·洪山模拟) 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F 两点,且CD= ,以O为圆心,OC为半径作,交OB于E点.(1)求⊙O的半径OA的长;(2)计算阴影部分的面积.12. (10分)(2012·义乌) 如图1,已知直线y=kx与抛物线y= 交于点A(3,6).(1)求直线y=kx的解析式和线段OA的长度;(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?13. (15分)(2017·长春模拟) 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.(1)求证:BC是⊙O的切线;(2)若已知AE=9,CF=4,求DE长;(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.14. (10分)(2018·深圳) 如图:在中,BC=2,AB=AC,点D为AC上的动点,且 .(1)求AB的长度;(2)求AD·AE的值;(3)过A点作AH⊥BD,求证:BH=CD+DH.15. (10分) (2018九上·灌阳期中) 如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,(1)求点B的坐标;(2)当点P运动什么位置时,使得∠CPD =∠OAB,且,求这时点P的坐标;(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。

初中圆的考试题及答案一、选择题1. 圆的周长公式为C=2πr,其中 r 代表圆的半径。
如果一个圆的半径是 5 厘米,那么它的周长是多少?A. 10π 厘米B. 20π 厘米C. 25π 厘米D. 30π 厘米答案:B2. 圆的面积公式为A=πr²,其中 r 代表圆的半径。
如果一个圆的半径是 4 厘米,那么它的面积是多少?A. 16π 平方厘米B. 32π 平方厘米C. 64π 平方厘米D. 100π 平方厘米答案:A3. 圆的标准方程是 (x-a)²+(y-b)²=r²,其中 (a,b) 是圆心的坐标,r 是半径。
如果一个圆的圆心坐标是 (3,4),半径是 2 厘米,那么这个圆的方程是什么?A. (x-3)²+(y-4)²=4B. (x-3)²+(y-4)²=9C. (x-3)²+(y-4)²=16D. (x-3)²+(y-4)²=25答案:A二、填空题4. 已知圆的直径是 10 厘米,求这个圆的半径。
答案:5 厘米5. 已知圆的周长是 31.4 厘米,求这个圆的半径。
答案:5 厘米6. 已知圆的面积是 78.5 平方厘米,求这个圆的半径。
答案:5 厘米三、解答题7. 一个圆的半径是 7 厘米,求这个圆的周长和面积。
答案:周长为44π 厘米,面积为49π 平方厘米。
8. 一个圆的直径是 14 厘米,求这个圆的周长和面积。
答案:周长为14π 厘米,面积为49π 平方厘米。
9. 一个圆的面积是 50.24 平方厘米,求这个圆的半径。
答案:半径为 4 厘米。

圆的测试题及答案初中一、选择题(每题3分,共30分)1. 圆的周长公式为:A. C=2πrB. C=πr^2C. C=πdD. C=2πd答案:A2. 圆的面积公式为:A. S=πr^2B. S=2πrC. S=πd^2D. S=2πd答案:A3. 圆的直径是半径的:A. 2倍B. π倍C. 1/2倍D. 1/π倍答案:A4. 圆的半径扩大到原来的2倍,其面积扩大到原来的:A. 2倍B. 4倍C. π倍D. 2π倍答案:B5. 圆的周长与直径的比值称为:A. 半径B. 直径C. 周长D. 圆周率答案:D6. 圆心到圆上任意一点的距离称为:A. 直径B. 半径C. 周长D. 面积答案:B7. 圆的切线垂直于:A. 半径B. 直径C. 周长D. 面积答案:A8. 圆内接四边形的对角线:A. 相等B. 互补C. 垂直D. 平行答案:B9. 圆的内切圆半径与外接圆半径的关系是:A. 相等B. 互补C. 垂直D. 互为倒数答案:A10. 圆的内角和为:A. 180°B. 360°C. 720°D. 1440°答案:B二、填空题(每题3分,共30分)1. 半径为3cm的圆的周长是_______。
答案:18.84cm2. 半径为4cm的圆的面积是_______。
答案:50.24cm²3. 直径为5cm的圆的半径是_______。
答案:2.5cm4. 圆的周长是其直径的_______倍。
答案:π5. 圆的面积是其半径的平方乘以_______。
答案:π6. 圆的切线与半径_______。
答案:垂直7. 圆内接四边形的对角线互相_______。
答案:平分8. 圆的内切圆半径与外接圆半径相等,说明该四边形是_______。
答案:正方形9. 圆的内角和为_______度。
答案:36010. 圆的外接圆半径是内切圆半径的_______倍。
答案:2三、解答题(每题20分,共40分)1. 已知一个圆的半径为6cm,求该圆的周长和面积。

课时训练(二十七)圆的基本概念和性质(限时:30分钟)|夯实基础|1。
到三角形三个顶点的距离都相等的点是这个三角形的()A.三条高的交点B.三条角平分线的交点C。
三条中线的交点D。
三条边的垂直平分线的交点2。
如图K27-1,在半径为5 cm的☉O中,弦AB=6 cm,OC⊥AB于点C,则OC= ()图K27-1A。
3 cm B.4 cm C.5 cm D。
6 cm3.如图K27-2,AB为☉O的直径,点C在☉O上,若∠ACO=50°,则∠B的度数为()图K27—2A.60° B。
50° C.40° D。
30°4.[2017·苏州]如图K27-3,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的☉O交AB 于点D,E是☉O上一点,且=,连接OE,过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为()图K27-3A。
92° B.108° C.112°D.124°5.如图K27-4所示,点P在以AB为直径的半圆O内,连接AP,BP,并延长分别交半圆于点C,D,连接AD,BC,并延长交于点F,作直线PF,与AB交于点E,下列说法一定正确的是()图K27-4①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF。
A。
①③ B.①④C。
②④D。
③④6.[2018·无锡]如图K27—5,点A,B,C都在☉O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= 。
图K27-57.[2018·南通]如图K27—6,AB是☉O的直径,点C是☉O上的一点,若BC=3,AB=5,OD⊥BC 于点D,则OD的长为.图K27-68。
[2018·嘉兴]如图K27—7,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10 cm,点D在量角器上的读数为60°,则该直尺的宽度为cm.图K27-79.[2016·扬州]如图K27—8,☉O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为.图K27-810.[2017·盐城]如图K27—9,将☉O沿弦AB折叠,点C在上,点D在上,若∠ACB=70°,则∠ADB= °.图K27-911.[2017·南京]如图K27—10,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE,若∠D=78°,则∠EAC= 。

[中考12年]徐州市2001-2012年中考数学试题分类解析专题11:圆一、选择题1. (2002年江苏徐州4分)如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM长的取值范围是【】A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5【答案】A。
【考点】动点问题,垂直线段的性质,垂径定理,勾股定理2. (2003年江苏徐州4分)如图所示,⊙O的直径EF为10cm,弦AB,CD分别为6cm和8cm,且AB∥EF∥CD,则图中阴影部分的面积和为【】A.252πcm2 B.253πcm2 C.758πcm2 D.17512πcm2【答案】A。
【考点】平行线的性质,垂径定理,勾股定理,全等三角形的判定和性质。
3. (2005年江苏徐州4分)如图,PA是⊙O的切线,A为切点,PBC是过点O的割线。
若PA=8㎝,PB = 4㎝,则⊙O的直径为【】A.6㎝ B.8㎝ C.12㎝ D.16㎝4. (2008年江苏徐州2分)⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是【】A.内含B.内切C.相交D.外切【答案】B。
【考点】两圆的位置关系。
5. (2012年江苏徐州3分)如图,A、B、C是⊙O上的点,若∠AOB=700,则∠ACB的度数为【】A.700 B.500 C.400D.350二、填空题1. (2001年江苏徐州2分)两圆的半径分别为3和5,若两圆相交,则圆心距d的取值范围是▲。
2. (2001年江苏徐州2分)如图,⊙O中,弦AB、CD相交于点P,若PA=PB=6,PC=4,则PD=▲。
3. (2003年江苏徐州4分)如图,AB是⊙O的直径,CD是弦,且CD⊥AB,垂足是P,如果CP=2,PB=l,那么AP= ▲ ,OP= ▲ .4. (2004年江苏徐州2分)如图,AB为⊙O的直径,弦AC=4cm,BC=3cm,CD⊥AB,垂足为D,那么CD的长为▲ cm.【答案】125。
2023年江苏省徐州市中考数学测试试题学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.相交两圆的公共弦长为 6,两圆的半径分别为32和 5,则这两个圆的圆心距等于()A.1 B.2 或 6 C.7 D.1 或72.若⊙O1圆心坐标为(2,0),半径为1;⊙O2的圆心坐标为(-1,0),半径为3,则这两圆的位置关系是()A.相交B.相切C.相离D.内含3.如图,下列各组图形是相似形的是()A.①③④B.①②③C.②③④D.①②④4.在同一坐标系中,函数2y ax bx=+的图象与byx=的图象大致为()A.B.C.D.5.下列说法错误的是()A.错误的判断也是命题B.命题有真命题和假命题两种C.定理是命题D.命题是定理6.已知△ABC在平面直角坐标系中的位置如图所(图中小方格的边长均代表1个单位),将△ABC向右平移2个单位,则平移后的点B的坐标是()A.(-l,1)B.(1,-l)C.(1,-2)D.(0,2)7.“5·12”汶川大地震导致某铁路隧道被严重破坏.为抢修其中一段120米的铁路,施工队每天比原计划多修5米,结果提前4天开通了列车.问原计划每天修多少米?设原计划每天修x 米,所列方程正确的是( )A .12012045x x -=+B .12012045x x -=+C .12012045x x-=- D .12012045x x -=- 8.一只小猫在如图的方砖上走来走去,最终停在阴影方砖上的概率是( ) A .154 B .31 C .51 D .152 9.下列各式的因式分解中,正确的是( )A .236(36)m m m m m -=-B .2()a b ab a a ab b ++=+C .2222()x xy y x y -+-=--D .222()x y x y +=+ 10.三角形的三边长都是整数,并且唯一的最长边是5,则这样的三角形共有( )A 1个B .2个C .3个D .4个11.如图,直线AB 、CD 相交于点O .OE 平分∠AOD ,若∠BOC =80°,则∠AOE 的度数是( )A .40°B .50°C .80°D . 100°12.在 1.414、2-2π32、23113这些实数中,无理数有( ) A . 4个 B .3个 C .2个 D .1个二、填空题13.如图,△ABC 中,AD 是 BC 上中线,M 是AD 的中点,BM 延长线交AC 于 N ,则AN NC= . 14.某超市一月份的营业额为200万元,第一季度的营业额共1000万元,如果平均每月增长率为x ,则有题意列方程为 .15.一个内角和为1260°的凸多边形共有 条对角线.16.在一次班长选举中,甲得了50票中的45票,这个事件中,频数是 ,频率是 .17.一个印有“嫦娥一号卫星”字样的立方体纸盒表面展开图如图所示,则与印有“娥”字面 相对的表面上印有 字.18.多项式24ax a -与多项式244x x -+的公因式是 .19.在1:1000000的地图上,A ,B 两地相距10cm ,则A ,B 两地的实际距离是_____千米.20.太阳的半径约是69660千米,用科学记数法表示(保留3个有效数字)约是 千米.三、解答题21. 如图,△ABC 是边长为 2 的正三角形,以 BC 为直径作⊙O 交AB ,AC 于D 、E , 连结 DE .求:(1)⌒DE 的度数;(2)DE 的长.22.已知抛物线y = x 2-2x -8,若该抛物线与x 轴的两个交点分别为A 、B ,且它的顶点为P ,求△ABP 的面积.△ABP 面积为27.23.已知:四边形ABCD 中,AB=CD ,E ,F ,G 分别是AD ,BC ,AC 的中点.求证:∠GEF=∠GFE .24.已知:如图,△ABC 为正三角形,D 是BC 延长线上一点,连结AD ,以AD 为边作等边△ADE ,连结CE .(1)请你说明△ABD ≌△ACE ;(2)探索AC 、CD 、CE 三条线段的长度有何关系?请说明理由. E D C B A(1)略;(2)AC+CD=CE ,略25.下列各个分式中的字母满足什么条件时,分式有意义?(1)251y -;(2)1|1|a -;(3)1||1b -26.图形设计:如图所示是一个10×10格点正方形组成的网格.△ABC 是格点三角形(顶点网格交点处),请你完成下面的两个问题:(1)在图①中画出与△ABC 相似的格点△A 1B 1C l ,且△A 1B 1C l 和△ABC 的相似比是2;(2)在图②中用与△ABC 和△A 1B 1C l 全等的格点三角形(每个三角形至少使用一次),拼出一个你熟悉的图案,并在图案下配一句贴切的解说词.27.如图所示,把方格纸上的四边形ABCD 作相似变换,使所成的像是原图形的2倍.28.在如图所示的6个箭头中,哪几个箭头是可以通过平移得到的,请你们指出它们的序号.29.有这样一道题:“计算322323323(232)(2)(3)x x y xy x xy y x x y y ----++-+-的值,其中12x =,1y =-.” 甲同学把“12x =”错抄成“12x =-”, 但他计算的结果也是正确的,你能说出这是什么原因?30.借助计算器计算下列各题.31=3312+333123++33331234+++从上面计算结果,你发现了什么规律?你能把发现的规律进行拓展吗?【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.D2.A3.B4.D5.D6.B7.B8.B9.C10.D11.A12.A二、填空题13.1214.200+200(1+x)+200(1+x)2=100015.2716.45,0.917.卫18.2x 19.10020.6.97×104三、解答题21.(1)连结 OD、OE,∵∠ B= ∠C= 60°,OB= OD=OE=OC,∴∠BOD=∠COE=∠EOD=60°,∴⌒DE的度数为60°(2)∵∠BOD=∠GOE=∠EOD=60°,∴BD= DE= EC,∵∠DOE=60°,OD=OE,∴∠ODE= ∠BDO=60°,∠ADE=60°,∴DE∥BC.∴∠ADE=∠B=∠C= ∠AED=∠A= 60°,AD= DE=AE= BD,∵AB=2,∴DE=12AB=1.22.23.EG=12DC=12AB=GF24.25.(1)1y≠±;(2)1a≠;(3)1b≠±26.略27.图略28.①与⑤可以通过平移得到29.化简得32y-,不含字母x,所以其值与x无关30.(1) 1 (2) 3 (3) 6 (4) 10 3123n n++=++++。
2020年江苏省徐州市中考数学经典试题 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.主视图、左视图、俯视图都是圆的几何体是( )A . 圆锥B . 圆柱C . 球D .空心圆柱2.在Rt △ABC 中, ∠C=90°,若AB=2AC,则cosA 的值等于( )A .3B . 23C . 21D . 333. 如图,在300 m 高的峭壁上测得一塔顶与塔基的俯角分别为 30°和 60°,则塔高 CD 约为( )A .100mB .200mC .150mD .180m4.下列图形不相似的是( )A . 所有的圆B .所有的正方形C .所有的等边三角形D .所有的菱形5.下面这几个车标中,是中心对称图形而不是轴对称图形的共有( )A .1个B .2个C .3个D .4个6.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开,得到的图形是( )A .B .C .D .7.下列变化过程中存在函数关系的是( )A .人的身高与年龄B .y=k-3xC .3x+y+1D .速度一定,汽车行驶的路程与时间8.下列各组所述的几何图形中,一定全等的是( )A .有一个角是45°的两个等腰三角形B .两个等边三角形C .腰长相等的两个等腰直角三角形D .各有一个角是40°,腰长都为5cm 的两个等腰三角形9.下列调查中,不适合采用普查而适合采用抽样调查的是( )A .审核书稿中的错别字B .对五名同学的身高情况进行调查C .对中学生目前的睡眠情况进行调查D .对某社区的卫生死角进行调查10.若两条平行直线被第三条直线所截得的八个角中有一个角的度数已知. 则( )A .只能求出其余三个角的度数B .只能求出其余五个角的度数C .只能求出其余六个角的度数D .能求出其余七个角的度数11.如图,△ABC ≌△BAD ,A 与B ,C 与D 是对应点,若AB=4cm ,BD=4.5cm ,AD=1.5cm ,则BC 的长为( )A .4cmB .4.5cmC .1.5cmD .不能确定 12.化简(-2x )3·y 4÷12x 3y 2的结果是( ) A .61y 2 B .-61y 2 C .-32y 2 D .-32xy 2 13.如图所示,绕旋转中心旋转60°后能与自身重合的是( )14.下列物体的形状,类似于圆柱的个数是( )①篮球②书本③标枪头④罐头 ⑤水管A .1个B .2个C .3个D .4个二、填空题15.如图,四圆两两相切,⊙O 的半径为 a ,⊙O 1、⊙O 2半径为 12a ,则⊙O 3的半径为 .16.如图是一张电脑光盘的表面,两个圆的圆心都是点O ,大圆的弦AB 所在直线是小圆的切线,切点为C .已知大圆的半径为5cm ,小圆的半径为1cm ,则弦AB 的长度为 cm .17.如图,△ABC 内接于⊙O ,点D 是CA 的延长线上一点,若∠BOC= 120°,则∠BAD 等于 .18. 如图,△ABC 中,∠C=90°,∠ABC=60°,BD 平分∠ABC ,若AD=6,则CD= .19.根据下列数轴上所表示的x 的解集,在下面的横线上分别填出满足解的特殊解:(1) 自然数x 的值 ;(2)小于零的最大整数x 的值 ; (3)正整数x 的值 .20.有14个顶点的直棱柱是直 棱柱,有 条侧棱,相邻两条侧棱互相 .21.已知一个三角形的三边长分别为3k ,4k ,5k (k 是为自然数),则这个三角形为 ,理由是 .22.2121)2(422+⨯-÷--x x x x = . 23.若一个正方体的棱长为3(21)a +,则这个正方体的体积为 .24.请写出是轴对称图形的英文字母(至少写出五个) .25.已知A 、B 是数轴上两点,AB=2,点B 表示-1,那么点A 表示 .26.已知a 是一个无理数,则 2a 是 ,a-1是 .27. 用“<”、“=”或“>”把下列每组中的两数连接起来. (1) 0 -5 ;-8 -7;(3)2- 2+.三、解答题28.如图,AB ∥CD ,AE 交CD 干点C ,DE ⊥AE ,垂足为点E ,∠A=37°,求∠D 的度数.29.计算:(1)432114212121a a a a a a +----+++;(2)2242n mn m mn m n m n n m ------;(3)22()()()()xy yz x y x z x y z x +----; (4)2b ac b c a b c b a c b a c+-+--+----30.x 为何值时,式子32x -与式子13x -+满足下面的条件? (1)相等(2)互为相反数(3)式子32x -比式子13x -+的值小 1【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.C3.B4.D5.B6.C7.D8.C9.C10.D11.C12.C13.A14.B二、填空题15.1a16.317.60 度18.319.(1)0,l;(2)-1;(3)1,220.7,7,平行21.直角三角形;如果一个三角形较小的两边的平方和等于最大边的平方,那么这个三角形是直角三角形22.123.9(21)a 24.A,C,E,H,K等25.-3或l26.无理数,无理数27.>,<,=三、解答题28.∵AB∥CD,∴∠ECD=∠A=37°,∵DE⊥AE,∴∠CED=90°.∴∠D=90°-∠ECD=90°-37°=53°.29.(1)3;(2)m n-;(3)2yyχ-;(4)-230.(1)245x= (2)12x= (3)185x=。
提分专练(七)以圆为背景的计算题与证明题|类型1| 平面直角坐标系中的圆1.如图T7-1,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧MN 的长为π,直线y=-x+4与x轴、y轴分别交于点A,B.(1)求证:直线AB与☉O相切;(2)求图中所示的阴影局部的面积(结果用π表示).图T7-12.[2021·酒泉] 如图T7-2,AN是☉M的直径,NB∥x轴,AB交☉M于点C.(1)假设点A,N,∠ABN=30°,求点B的坐标;(2)假设D为线段NB的中点,求证:直线CD是☉M的切线.图T7-2|类型2| 垂径定理与勾股定理联手3.[2021·金华] 如图T7-3,:AB是☉O的直径,点C在☉O上,CD是☉O的切线,AD⊥CD于点是AB延长线上的一点,CE交☉O于点F,连接OC,AC.(1)求证:AC平分∠DAO.(2)假设∠DAO=105°,∠E=30°.①求∠OCE的度数;②假设☉O的半径为2,求线段EF的长.图T7-3|类型3| 与圆有关的图形的面积4.[2021·达州] ,如图T7-4,以等边三角形ABC的边BC为直径作☉O,分别交AB,AC于点D,E,过点D作DF⊥AC于点F.(1)求证:DF是☉O的切线;(2)假设等边三角形ABC的边长为8,求由,DF,EF围成的阴影局部的面积.图T7-4|类型4| 与圆的切线有关的问题5.[2021·扬州] 如图T7-5,▱OABC的三个顶点A,B,C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB,AO的延长线于点D,E,AE交半圆O于点F,连接CF.(1)判断直线DE与半圆O的位置关系,并说明理由.(2)①求证:CF=OC;②假设半圆O的半径为12,求阴影局部的周长.图T7-5|类型5| 圆与四边形结合的问题6.正方形ABCD内接于☉O,如图T7-6所示,在劣弧AB上取一点E,连接DE,BE,过点D作DF∥BE交☉O于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;(2)DG=BE.图T7-6|类型6| 圆与三角函数结合的问题7.如图T7-7,AB是☉O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.(1)判断BD与☉O的位置关系,并说明理由;(2)假设CD=15,BE=10,tan A=,求☉O的直径.图T7-7|类型7| 圆与相似三角形结合的问题8.[2021·黄冈] :如图T7-8,MN为☉O的直径,ME是☉O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.求证:(1)DE是☉O的切线;(2)ME2=MD·MN.图T7-8参考答案1.解:(1)证明:作OD⊥AB于D,如下图:∵劣弧MN的长为π,∴=π,解得OM=,即☉O的半径为,∵直线y=-x+4与x轴、y轴分别交于点A,B,当y=0时,x=3;当x=0时,y=4,∴A(3,0),B(0,4),∴OA=3,OB=4,∴AB==5,∵△AOB的面积=AB·OD=OA·OB,∴OD===半径,∴直线AB与☉O相切.(2)图中所示的阴影局部的面积=△AOB的面积-扇形OMN的面积=×3×4-π×=6-π.2.解:(1)∵A的坐标为(0,6),N的坐标为(0,2),∴AN=4,∵∠ABN=30°,∠ANB=90°,∴AB=2AN=8,∴由勾股定理可知:NB=4,∴B(4,2).(2)证明:连接MC,NC.∵AN是☉M的直径,∴∠ACN=90°,∴∠NCB=90°,在Rt△NCB中,D为NB的中点,∴CD=NB=ND,∴∠CND=∠NCD,∵MC=MN,∴∠MCN=∠MNC.∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是☉M的切线.3.解:(1)证明:∵CD是☉O的切线,∴OC⊥CD.∵AD⊥CD,∴OC∥AD.∴∠DAC=∠ACO.∵OA=OC,∴∠OAC=∠ACO.∴∠DAC=∠OAC.∴AC平分∠DAO.(2)①∵OC∥AD,∴∠EOC=∠DAO=105°.∴∠OCE=180°-∠EOC-∠E=180°―105°―30°=45°.②如图,过点O作OG⊥CE于G,可得FG=CG.在Rt△OGC中,OC=2,∠OCE=45°,∴OG=CG=2×=2.∴FG=CG=2.在Rt△OGE中,OG=2,∠E=30°,∴EG===2.∴EF=EG-FG=2-2.4.解:(1)证明:连接OD,CD.∵BC是直径,∴∠BDC=90°.∵△ABC是等边三角形,∴点D是AB的中点.∵点O是BC的中点,∴OD∥AC.∵DF⊥AC,∴OD⊥DF.∵OD是半径,∴DF是☉O的切线.(2)连接OD,OE,DE.∵同(1)可知点E是AC的中点,∴DE是△ABC的中位线,△ADE是等边三角形.∵等边三角形ABC的边长为8,∴等边三角形ADE的边长为4.∵DF⊥AC,∴EF=2,DF=2.∴△DEF的面积=·EF·DF=×2×2=2.△ADE的面积=△ODE的面积=4.扇形ODE的面积==.∴阴影局部的面积=△DEF的面积+△ODE的面积-扇形ODE的面积=2+4-π=6-.5.解:(1)DE与半圆O相切.理由如下:∵CD⊥AB,∴∠D=90°.∵四边形ABCO是平行四边形,∴OC∥AD,∴∠OCE=∠D=90°,∴OC⊥DE.又∵OC是半圆O的半径,∴DE与半圆O相切.(2)①证明:连接AC,∵四边形ABCO是平行四边形,∴AB=OC,BC∥AF,∴∠BCA=∠FAC,∴=,∴BA=CF,∴CF=OC.②∵CF=OC=OF,∴△OCF为等边三角形,∴∠COF=60°,∴在Rt△OCE中,CE=OC=12,OE=2OC=24,∴EF=12,==4π,∴C阴影局部=EF+CE+=12+12+4π.6.[解析] (1)直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,进而得出答案;(2)直接利用正方形的性质得出的度数是90°,进而得出DG=DF,那么BE=DG.证明:(1)∵正方形ABCD内接于☉O,∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,又∵DF∥BE,∴∠EDF+∠BED=180°,∴∠EDF=90°,∴四边形EBFD是矩形.(2)∵正方形ABCD内接于☉O,∴的度数是90°,∴∠AFD=45°,又∵∠GDF=90°,∴∠DGF=∠DFG=45°,∴DG=DF,又∵在矩形EBFD中,BE=DF,∴BE=DG.7.[解析] (1)连接OB,由圆的半径相等和条件证明∠OBD=90°,即可证明BD是☉O的切线;(2)过点D作DG⊥BE于G,根据等腰三角形的性质得到EG=BE=5,由两角相等的三角形相似,得△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sin A=,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.解:(1)BD与☉O相切.理由如下:连接OB,∵OB=OA,DE=DB,∴∠A=∠OBA,∠DEB=∠ABD,又∵CD⊥OA,∴∠A+∠AEC=∠A+∠DEB=90°,∴∠OBA+∠ABD=90°,∴OB⊥BD,∴BD是☉O的切线.(2)如图,过点D作DG⊥BE于G,∵DE=DB,∴EG=BE=5,∵∠ACE=∠DGE=90°,∠AEC=∠GED,∴△ACE∽△DGE,∴∠GDE=∠A,∵tan A=,∴sin A=,∴sin∠EDG=sin A==,∴DE=13,在Rt△EDG中,DG==12,∵CD=15,DE=13,∴CE=2,∵△ACE∽△DGE,∴=,∴AC=·DG=, ∴☉O的直径=2OA=4AC=.8.证明:(1)∵OM=OE,∴∠OME=∠OEM.∵ME平分∠DMN,∴∠OME=∠DME.∴∠OEM=∠DME.∵MD⊥DE,∴∠MDE=90°.∴在△MDE中,∠DEM+∠DME=90°.∴∠DEM+∠OEM=90°.即∠OED=90°,∴OE⊥DE.又∵OE为☉O的半径,∴DE是☉O的切线.(2)如图,连接NE.∵MN为☉O的直径,∴∠MEN=90°.∴∠MEN=∠MDE=90°.又由(1)可知,∠NME=∠DME.∴△DME∽△EMN.∴=,∴ME2=MD·MN.。
1 / 2江苏省徐州市第34中学九年级数学《圆》单元检测 人教新课标版一、选择题(每题3分,合计24分)(每小题有四个选项,只有一个正确答案)1. 如图1,在⊙O 中,∠ABC =50°,则∠AOC 等于┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ) A .50° B .80° C .90° D .100°2. 如图2,AB 是⊙O 的弦,OC ⊥AB ,垂足为C ,若⊙O 的半径为5,OC=3,则弦AB 的长为( ) A .4 B . 6 C .8 D .423. 已知⊙O 与⊙Q 的半径分别为3cm 和7cm ,两圆的圆心距O 1 O 2 =10cm ,则两圆的位置关系是( ) A .外切 B .内切 C .相交 D .相离4. 如图3,在Rt △ABC 中∠ACB =90°,AC =6,AB =10,CD 是斜边AB 上的中线,以AC 为直径作⊙O ,设线段CD的中点为P ,则点P 与⊙O 的位置关系是┈┈┈┈┈┈┈┈┈┈┈( )。
A 、点P 在⊙O 内B 、点P 在⊙O 上C 、点P 在⊙O 外D 、无法确定(图1) (图2) (图3) (图4)5.如图4,⊙B 的半径为4cm , 60=∠MBN ,点A 、C 分别是射线BM 、BN 上的动点,且直线BN AC ⊥.当AC 平移到与⊙B 相切时,AB 的长度是┈┈┈┈┈┈┈┈┈┈ ( ) A.cm 8 B.cm 6 C.cm 4 D.cm 26. 有下列四个命题中,其中正确的有┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( )①圆的对称轴是直径; ②经过三个点一定可以作圆; ③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧. A .4个 B.3个 C.2个 D.1个7. 圆锥的底面圆的周长是4πcm,母线长是6cm ,则该圆锥的侧面展开图的圆心角的度数( ) A .40° B 。