卓越联盟自主招生数学试题及答案
- 格式:doc
- 大小:1.18 MB
- 文档页数:7

卓越联盟自主招生数学试题一、选择题:(本大题共4小题,每小题5分.在每小题给出的4个结论中,只有一项是符合题目要求的.)(1)已知()f x 是定义在实数集上的偶函数,且在(0,)+∞上递增,则(A )0.72(2)(log 5)(3)f f f <-<- (B) 0.72(3)(2)(log 5)f f f -<<-(C) 0.72(3)(log 5)(2)f f f -<-< (D) 0.72(2)(3)(log 5)f f f <-<-(2)已知函数()sin()(0,0)2f x x πωϕωϕ=+><<的图象经过点(,0)6B π-,且()f x 的相邻两个零点的距离为2π,为得到()y f x =的图象,可将sin y x =图象上所有点 (A )先向右平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变 (B) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变 (C) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 (D) 先向右平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 (3)如图,在,,,,A B C D E 五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为(A )21 (B)24 (C)30 ( D)48(4)设函数()f x 在R 上存在导数()f x ',对任意的x R ∈,有2()()f x f x x -+=,且在(0,)+∞上()f x x '>.若(2)()22f a f a a --≥-,则实数a 的取值范围为(A )[1,)+∞ (B) (,1]-∞ (C) (,2]-∞ (D) [2,)+∞二、填空题:(本大题共4小题,每小题6分,共24分)(5)已知抛物线22(0)y px p =>的焦点是双曲线2218x y p -=的一个焦点,则双曲线的渐 近线方程为 .(6)设点O 在ABC ∆的内部,点D ,E 分别为边AC ,BC 的中点,且21OD DE +=, 则23OA OB OC ++= .(7)设曲线y 与x 轴所围成的区域为D ,向区域D 内随机投一点,则该点落 入区域22{(,)2}x y D x y ∈+<内的概率为 .(8)如图,AE 是圆O 的切线,A 是切点,AD 与OE垂直,垂足是D ,割线EC 交圆O 于,B C ,且,ODC DBC αβ∠=∠=,则OEC ∠= (用,αβ表示).三、解答题(本大题共4小题,共56分.解答应写出文字说明,证明过程或演算步骤)(9)(本小题满分13分)在ABC ∆中,三个内角A 、B 、C 所对边分别为a 、b 、c .已知()(sin sin )()sin a c A C a b B -+=-.(1)求角C 的大小; (2)求sin sin A B ⋅的最大值.(10)(本题满分13分) 设椭圆2221(2)4x y a a +=>的离心率为,斜率为k 的直线l 过点(0,1)E 且与椭圆交于,C D 两点.(1)求椭圆方程;(2)若直线l 与x 轴相交于点G ,且GC DE =,求k 的值; (3)设A 为椭圆的下顶点,AC k 、AD k 分别为直线AC 、AD 的斜率,证明对任意的k 恒 有2AC AD k k ⋅=-.(11)(本题满分15分)设0x >,(1)证明:2112x e x x >++; (2)若2112x y e x x e =++,证明:0y x <<. (12)(本题满分15分)已知数列{}n a 中,13a =,2*1,,n n n a a na n N R αα+=-+∈∈.(1)若2n a n ≥对*n N ∀∈都成立,求α的取值范围;(2)当2α=-时,证明*121112()222n n N a a a +++<∈---.答案:(1)A ; (2)B ; (3)C ; (4)B .(5)y x =±; (6)2; (7)11π-; (8)βα-.。


2023学年第一学期金华卓越联盟12月阶段联考高一数学试题(答案在最后)考生须知:1.本卷共6页满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写班级、学号和姓名;考场号、座位号写在指定位置;3.所有答案必须写在答题纸上,写在试卷上无效;4.考试结束后,只需上交答题纸.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}{}1,3,5,7,2,3,5,6A B ==,则A B ⋃=()A.{}3,5 B.{}3,5,6 C.{}1,2,3,5,6,7 D.{}1,2,3,4,5,6,7【答案】C 【解析】【分析】根据集合并集的定义进行求解即可.【详解】因为{}{}1,3,5,7,2,3,5,6A B ==,所以A B ⋃={}1,2,3,5,6,7,故选:C2.在0360 的范围内,与520- 终边相同的角是()A.310B.200C.140D.20【答案】B 【解析】【分析】根据终边相同角的性质进行求解即可.【详解】与520- 终边相同的角可以表示为()523600Z k k ︒-∈,由题意可知1322036036052990k k ︒︒︒<<⇒<<-,因为Z k ∈,所以2k =,于是有5203602200︒︒⨯=- ,故选:B3.命题“22,40x x ∀≥-<”的否定是()A.22,40x x ∃≥-≥B.22,40x x ∃<-≥C.22,40x x ∀<-≥D.22,40x x ∀<-<【答案】A 【解析】【分析】根据含有一个量词的命题的否定,即可判断出答案.【详解】命题“22,40x x ∀≥-<”为全称量词命题,它的否定为22,40x x ∃≥-≥,故选:A4.设,a b 都是不等于1的正数,则“444a b >>”是“44log log a b <”成立的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【答案】D 【解析】【分析】根据题意,由指数函数以及对数函数的单调性将不等式化简,再由充分条件,必要条件的定义,即可得到结果.【详解】因为,a b 都是不等于1的正数,由444a b >>可得1a b >>,由44log log a b <可得0a b <<,则1a b >>是0a b <<的既不充分也不必要条件,即“444a b >>”是“44log log a b <”成立的既不充分也不必要条件.故选:D5.直线:l x a =与二次函数()y f x =交点个数为()A.0个 B.1个C.2个D.以上都有可能【答案】B 【解析】【分析】数形结合判断即可.【详解】直线:l x a =为的纵坐标为R ,图像为一条与y 轴平行的直线,设二次函数为2,0y Ax Bx C A =++≠,当0A >时,1,2,1A B C ===;开口向上,图像与直线一定有一个交点,如图:当0A <时,如1,2,1A B C =-==如;开口向下,图像与直线一定有一个交点,如图:故选:B6.设函数()348f x x x =+-,用二分法求方程3480x x +-=近似解的过程中,计算得到()()10,30f f <>,则方程的近似解落在区间()A.31,2⎛⎫ ⎪⎝⎭B.3,22⎛⎫⎪⎝⎭C.52,2⎛⎫ ⎪⎝⎭D.5,32⎛⎫⎪⎝⎭【答案】A 【解析】【分析】根据题意,求得3()0,(2)02f f >>,得到3(1)(02f f ⋅<,结合零点的存在性定理,即可求解.【详解】由函数()348f x x x =+-,且()()10,30f f <>,可得3(70,(2)2602f f =>=>,所以3(1)(02f f ⋅<,根据零点的存在性定理,可得方程3480x x +-=的近似解落在区间为31,2⎛⎫⎪⎝⎭.故选:A.7.2022年第19届亚运会于2023年9月23日至10月8日在杭州举行,秉持“绿色、智能、节俭、文明”的办赛理念,其中“绿色低碳”被摆在首位,比如所有场馆实现100%绿色供电、所有亚运会官方指定用车均为新能源汽车.Peukert 于1898年提出蓄电池的容量C (单位:A h ⋅),放电时间t (单位:h )与放电电流I (单位:A )之间关系的经验公式n C I t =⋅,其中32log 2n =为Peukert 常数.在电池容量不变的条件下,当放电电流10A I =时,放电时间56h t =,则当放电电流15A I =时,放电时间为()A.28h B.28.5hC.29hD.29.5h【答案】A 【解析】【分析】将10A I=时,56h t =代入公式n C I t =⋅,结合32log 2n =即可计算15A I =时的放电时间.【详解】由题意得:561015n nC t =⨯=,则1025656153nn n t ⎛⎫=⨯=⨯ ⎪⎝⎭,由32log 2n =,故32log 22565656283232nt ⎛⎫=⨯=== ⎪⎝⎭⎛⎫ ⎪⎝⎭,故放电时间为28h .故选:A.8.已知定义在R 上的函数()(),f x g x ,其中函数()f x 满足()()f x f x -=且在[)0,∞+上单调递减,函数()g x 满足()()22g x g x -=+且在()2,+∞上单调递减,设函数()()()()()12F x f x g x f x g x ⎡⎤=++-⎣⎦,则对任意x ∈R ,均有()A.()()22F x F x -≥+B.()()22F x F x -≤+C.()()2222F x F x -≥+ D.()()2222F xF x -≤+【答案】C 【解析】【分析】判断函数()f x 以及()g x 的性质,化简()()()()()12F x f x g x f x g x ⎡⎤=++-⎣⎦的表达式,讨论()()f x g x ≤恒成立以及()()f x g x ≤恒成立和()()f x g x ≥,()()f x g x ≤均存在,结合函数性质,即可判断选项的正误,即得答案.【详解】因为()()f x f x -=,则()f x 为偶函数,()f x 在[)0,∞+上单调递减,则在(,0]-∞上单调递增,函数()g x 满足()()22g x g x -=+且在()2,+∞上单调递减,则()g x 图象关于2x =对称,在(,2]-∞上单调递增,当()()f x g x ≥时,()()()()()1()2F x f x g x f x g x f x =++-=⎡⎤⎣⎦,当()()f x g x ≤时,()()()()()1()2F x f x g x g x f x g x =++-=⎡⎤⎣⎦;①当()()f x g x ≤恒成立时,()()F x g x =,图象关于2x =对称,此时()()22F x F x -=+,()()2222F xF x -=+;②当()()f x g x ≥恒成立时,()()F x f x =,图象关于y 轴对称,当|2||2|x x -+≥时,()()22F x F x -≤+;当|2||2|x x -≤+时,()()22F x F x -≥+;即说明A ,B 错误;当220x -≥,即202x ≤≤时,22022x x ≤-≤+,则()()2222F x F x -≥+,当220x -≤,即22x ≥时,()()()222222F x F xF x -=-≥+,故若()()F x f x =,则()()2222F xF x -≥+,则说明D 错误;③若()()f x g x ≥,()()f x g x ≤均存在,则不妨作()F x 示意图如图:222,2x x -+关于直线2x =对称,且2222x x -≤+,则()()2222F x F x -≥+,综合上述,可知C 正确,故选:C二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列命题是真命题的是()A.1R,1x x x∃∈+=- B.20,2x x x ∃>=C.2R,1x x x ∀∈-≥- D.0,ln 0x x ∀>>【答案】BC 【解析】【分析】根据基本不等式,求得1x x+的取值范围,可判定A 不正确;根据当2x =时,得到22x x =,可判定B 正确;结合配方法,可判定C 正确;结合对数函数的性质,可判定D 不正确.【详解】对于A 中,当0x >时,则12x x +≥=,当且仅当1x =时,等号成立;当0x <时,则11[()2x x x x +=--+≤-=--,当且仅当=1x -时,等号成立,所以1x x+的取值范围为(,2][2,)-∞-+∞ ,所以A 不正确;对于B 中,当2x =时,可得22x x =,所以命题20,2x x x ∃>=为真命题,所以B 正确;对于C 中,由221331(244x x x -+=-+≥,所以命题2R,1x x x ∀∈-≥-为真命题,所以C 正确;对于D 中,当01x <<时,ln 0x <,所以命题0,ln 0x x ∀>>为假命题,所以D 不正确.故选:BC.10.已知幂函数()f x 的图象经过点()4,2,则()A.函数()f x 为增函数B.函数()f x 为偶函数C.当4x ≥时,()2f x ≥D.当120x x >>时,1212()()()22f x f x x x f ++<【答案】ACD 【解析】【分析】根据题意,求得幂函数为()12f x x =,利用奇偶性的定义,以及幂函数的图象与性质,结合指数幂的运算性质,逐项判定,即可求解.【详解】设幂函数的解析式为()(R)f x x αα=∈,因为幂函数()f x 的图象过点()4,2,可得42α=,解得12α=,即()12f x x =,所以函数()f x 的定义域为[0,)+∞,不关于原点对称,所以函数()f x 为非奇非偶函数,且()f x 在[0,)+∞上单调递增,所以A 正确,B 不正确;当4x ≥时,可得()()42f x f ≥=,所以C 正确;当120x x >>时,22121212()()[][(222f x f x x x x x f +++-=-0==<,因为()0f x ≥,所以1212()()()22f x f x x x f ++<,所以D 正确.故选:ACD.11.已知()2f x x bx c =++在()0,1上有两实根,则()()01f f ⋅的值可能为()A.14B.18C.116 D.132【答案】CD 【解析】【分析】根据给定条件,设出方程的两个实根,并表示,b c 及()()01f f ⋅,再用基本不等式求出范围即可.【详解】设方程()0f x =的两个实根为12,x x ,则12,(0,1)x x ∈,显然1212(),b x x c x x =-+=,此时2221212124()4()0b c x x x x x x ∆=-=+-=-≥,即方程()0f x =有两个实根,因此1212121122(0)(1)(1)(1)(1)(1)f f c b c x x x x x x x x x x ⋅=++=--+=-⋅-221122111()(2216x x x x +-+-≤⋅=,当且仅当1212x x ==时取等号,显然()()0·10f f >,即()()10·10,16f f ⎛⎤∈ ⎥⎝⎦,所以()()01f f ⋅的值可能为116,132,即AB 错误,CD 正确.故选:CD12.一般地,若函数()f x 的定义域为[,]a b ,值域为[,]ka kb ,则称[,]a b 为()f x 的“k 倍美好区间”.特别地,若函数的定义域为[,]a b ,值域也为[,]a b ,则称[,]a b 为()f x 的“完美区间”.下列结论正确的是()A.若[2,]b 为2(6)4f x x x =-+的“完美区间”,则6b =B.函数1()f x x=存在“完美区间”C.二次函数2113()22f x x =-+存在“2倍美好区间”D.函数||1()||m x f x x -=存在“完美区间”,则实数m 的取值范围为(2,){0}+∞⋃【答案】BCD 【解析】【分析】分析每个函数的定义域及其在相应区间的单调性,按“k 倍美好区间”,“完美区间”的定义,列出相应方程,再根据方程解的情况,判断正误.【详解】对于A ,因为函数2(6)4f x x x =-+的对称轴为2x =,故函数()f x 在[2,]b 上单增,所以其值域为2[2,46]b b -+,又因为[2,]b 为2(6)4f x x x =-+的完美区间,所以246b b b -+=,解得2b =或3b =,因为2b >,所以3b =,A 错误;对于B ,函数1()f x x =在(),0∞-和()0,∞+都单调递减,假设函数1()f x x=存在完美区间[,]a b ,则11a bb a ⎧=⎪⎪⎨⎪=⎪⎩,即a ,b 互为倒数且a b <,故函数1()f x x =存在完美区间,B 正确;对于C ,若2113()22f x x =-+存在“2倍美好区间”,则设定义域为[,]a b ,值域为[2,2].a b 当0a b <<时,易得2113()22f x x =-+在区间上单调递减,22113222113222a b b a ⎧-+=⎪⎪⎨⎪-+=⎪⎩,两式相减,得4a b +=,代入方程组解得1a =,3b =,C 正确.对于D ,()f x 的定义域为{}0x x ≠,假设函数1,01()1,0m x m x xf x x m x x ⎧+<⎪-⎪==⎨⎪->⎪⎩存在“完美区间”[,]a b ,若0b <,由函数()f x 在(,0)-∞内单调递减,则11m b am a b ⎧+=⎪⎪⎨⎪+=⎪⎩,解得0m =;若0a >,由函数()f x 在(0,)+∞内单调递增,则11m a am bb ⎧-=⎪⎪⎨⎪-=⎪⎩,即1x m x =-在(0,)+∞有两解a ,b ,得2m>,故实数m 的取值范围为(2,){0}+∞⋃,D 正确.故选:BCD.【点睛】抓住“k 倍美好区间”,“完美区间”的定义,在已知单调性的前提下,即可通过分析函数在区间端点处a ,b 的取值,列出方程组.三、填空题:本题共4小题,每小题5分,共20分.13.已知函数()7538f x ax bx cx dx =+++-,且()25f -=,则()2f =__________.【答案】21-【解析】【分析】利用代入法,整体法进行求解即可.【详解】因为()7538f x ax bx cx dx =+++-,所以()()()()()7532222285f a b c d -=-+-+-+--=即753222213a b c d ⋅+⋅+⋅+⋅=-,所以()75322222813821f a b c d =⋅+⋅+⋅+⋅-=--=-,故答案为:21-14.如图所示的时钟显示的时刻为4:30,此时时针与分针的夹角为()0ααπ<≤.若一个半径为1的扇形的圆心角为α,则该扇形的面积为______.【答案】8π【解析】【分析】先求出圆心角为α,再根据扇形的面积公式即可求解.【详解】解:由题意4πα=,所以该扇形的面积2812S r πα==.故答案为:8π.15.秋冬季是流感的高发季节,为了预防流感,某学校决定用药熏消毒法对所有教室进行消毒.如图所示,已知药物释放过程中,室内空气中的含药量()3mg /my 与时间()1h 02t t ⎛⎫≤< ⎪⎝⎭成正比;药物释放完毕后,y 与t 的函数关系式为116t ay -⎛⎫= ⎪⎝⎭(a 为常数,12t ≥),据测定,当空气中每立方米的含药量降低到()30.25mg /m 以下时,学生方可进教室,则学校应安排工作人员至少提前__________小时进行消毒工作.【答案】1【解析】【分析】根据题意,求得参数a 的值,得到含药量()3mg /m y 与时间()h t 的函数关系式,令0.25y ≤,结合指数幂的运算性质,即可求解.【详解】由图中的一次函数的图象得,图象中线段所在的直线方程为12(0)2y t t =≤≤,又由点1(,1)2在曲线116t a y -⎛⎫= ⎪⎝⎭上,可得121116a -⎛⎫= ⎪⎝⎭,解得12a =,所以含药量()3mg /m y 与时间()h t 的函数关系式为1212,0211,162t t t y t -⎧≤≤⎪⎪=⎨⎛⎫⎪> ⎪⎪⎝⎭⎩,当12t >时,令10.254y ≤=,即1211164t -⎛⎫≤ ⎪⎝⎭,可得1122t -≥,解得1t ≥,所以学校应安排工作人员至少提前1小时进行消毒工作.故答案为:1.16.设函数()2461f x ax bx a =+-+,当[]4,4x ∈-时,恒有()0f x ≥成立,则10a b +的最小值为__________.【答案】13-【解析】【分析】将()2461f x ax bx a =+-+化为()216)(4f x x a bx -=++,和10a b +比较系数,求得x 的值,结合()0f x ≥恒成立,即可求得答案.【详解】由题意得()216)(4f x x a bx -=++,令246101x x -=,解得3x =或12x =-,当3x =时,()033031f a b =++≥,即1103a b +≥-,当12x =-时,1012152f a b ⎛⎫=--+≥ ⎪⎝-⎭,则102a b +≤,验证:3x =时,38b a -=,1103a b +=-,即112,4221a b ==-时,10a b +取到最小值13-,故答案为:13-四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(1)01430.25337(0.064)(2)2568---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭(2)3121log 24lg539--⎛⎫-- ⎪⎝⎭【答案】(1)2916;(2)0【解析】【分析】(1)根据指数幂的运算法则,即可求得答案;(2)根据指数幂的运算性质以及对数的运算法则,即可求得答案.【详解】(1)01430.25337(0.064)(2)2568---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭13()44(0.25)3(0.4)1(2)4⨯--⨯-=-+-+511292164161+=-+=;(2)3121log 24lg539--⎛⎫-- ⎪⎝⎭312log 3lg5332=-+⨯33lg51lg21(lg 5lg 2)022=-+--=-+=.18.已知集合{}(){}|234,|812A x a x a a B x x =+≤≤-∈=≤≤R .(1)若集合B 是集合A 的充分条件,求a 的取值范围;(2)若A B ⋂=∅,求a 的取值范围.【答案】(1)16,63⎡⎤⎢⎥⎣⎦(2)()(),410,-∞+∞ 【解析】【分析】(1)将原问题等价转换为由包含关系求参数,根据包含关系列出不等式组求解即可.(2)由题意分集合A 是否为空集进行讨论即可,讨论时,根据题意列出相应的不等式组求解即可.【小问1详解】由题意若集合B 是集合A 的充分条件,则当且仅当B A ⊆,即当且仅当283412a a +≤⎧⎨-≥⎩,解得1663a ≤≤,即a 的取值范围为16,63⎡⎤⎢⎥⎣⎦.【小问2详解】当A =∅时,满足题意,即满足A B ⋂=∅,此时234a a +>-,解得3a <;当A ≠∅且A B ⋂=∅时,当且仅当3348a a ≥⎧⎨-<⎩或3212a a ≥⎧⎨+>⎩,解得34a ≤<或10a >;综上所述,若A B ⋂=∅,则a 的取值范围为()(),410,-∞+∞ .19.已知函数()221x f x a =-+.(1)求()0f ;(2)探究()f x 的单调性,并证明你的结论;(3)若()f x 为奇函数,求满足()()22f ax f <的x 的取值范围.【答案】(1)1a -(2)单调递增,证明见解析(3)(,1)-∞【解析】【分析】(1)根据函数解析式,将0x =代入,即得答案;(2)判断函数单调递增,根据函数单调性的定义即可证明该结论;(3)根据函数为奇函数求出a ,则根据函数的单调性解不等式,即可求得答案.【小问1详解】由于()221x f x a =-+,故()012102f a a =-=-+;【小问2详解】探究:()f x 在R 上单调递增,证明如下:()f x 的定义域为R ,任取1212,R,x x x x ∈<,则()()()()()121212122222221211212x x x x x x f x f x a a ⋅--=--+=++++,因为1212,22x x x x ∴<<,12120,120x x +>+>,故()()()121222201212x x x x ⋅-<++,即()()12f x f x <,所以()f x 在R 上单调递增;【小问3详解】因为()f x 为奇函数,故()()f x f x -=-,即222121x x a a --=-+++,即222222*********x x x x x a -⋅=+=+=++++,所以1a =,则()()22f ax f <,即()()22f x f <,而()f x 在R 上单调递增,故22,1x x <∴<,即x 的取值范围为(,1)-∞.20.已知函数sin cos sin cos y αααα=++⋅当sin cos t αα=+时,t ⎡∈⎣(1)若t =,求tan α的值;(2)求函数sin cos sin cos y αααα=++⋅的值域.【答案】(1)1(2)11,2⎡-+⎢⎣【解析】【分析】(1)利用辅助角公式及特殊角的三角函数值即可求解.(2)先利用换元法由(1)可得21122y t t =+-;再利用二次函数的单调性求出最值即可得出答案.【小问1详解】πsin cos4t ααα⎛⎫=+=+ ⎪⎝⎭,t =.∴π4α⎛⎫+= ⎪⎝⎭,解得:π2π,Z 4k k α=+∈.∴ππtan tan 2πtan 144k α⎛⎫=+== ⎪⎝⎭.【小问2详解】sin cos t αα=+,22sin cos 1αα+=.∴()22sin cos 12sin cos t αααα=+=+,∴21sin cos 2t αα-=.则22111sin cos sin cos 222t y t t t αααα-=++⋅=+=+-,t ⎡∈⎣.函数21122y t t =+-在区间1⎡⎤-⎣⎦上单调递减,在区间⎡-⎣上单调递增.∴当1t =-时,()2min 1111122y =⨯---=-.又 当t =(2111222y =⨯=当t =时,211112222y =⨯+=>-.∴当t =时,max 12y =.故函数sin cos sin cos y αααα=++⋅的值域为11,2⎡-+⎢⎣.21.若正数,a b 满足24a b +=.(1)求ab 的最大值;(2)求511a b++的最小值.【答案】(1)2(2)72105+【解析】【分析】(1)直接运用基本不等式进行求解即可;(2)根据已知等式,进行常值代换、结合基本不等式进行求解即可.【小问1详解】因为正数,a b 满足24a b +=,所以有422a b ab =+≥⇒≤,当且仅当2a b =时取等号,即当2,1a b ==时,ab 有最大值【小问2详解】因为正数,a b 满足24a b +=,所以有125a b ++=,于是有()151111017212772515155a b a b a b b a ⎛++⎛⎫⎛⎫+++=++≥+= ⎪ ⎪ ++⎝⎭⎝⎭⎝,当且仅当1101a b b a +=+时取等号,即当且仅当2210,36a b --==时,511a b ++有最小值75+.22.已知函数()()ln 11,20,ln ,0.x x f x x x ⎧--+-<<⎪=⎨>⎪⎩.(1)求函数()f x 的单调递增区间;(2)若关于x 的方程(21)f x m -=有4个不同的解,记为()12341234,,,,x x x x x x x x <<<,且312415x x x x λ⋅->恒成立,求λ的取值范围.【答案】(1)(1,0),(1,)-+∞(2)5510λ->.【解析】【分析】(1)将函数化为分段函数,根据对数函数的单调性及复合函数的单调性直接得解;(2)根据题意可得出31323431,1,21x x x x x x x =-=-=-,分离参数可得233342521x x x λ-+->-,令321t x =-,换元后利用均值不等式求解.【小问1详解】(1)()()()ln 2,21ln ,10ln ,01ln ,1x x x x f x x x x x ⎧-+-<≤-⎪---<<⎪=⎨-<≤⎪⎪>⎩.根据复合函数单调性的知识得()f x 的单调递增区间有(1,0),(1,)-+∞.【小问2详解】由(1)可知1234221121021121x x x x -<-<-<-<<-<<-化简可得:1234110122x x x x -<<<<<<<∵()()()()123421212121f x f x f x f x m-=-=-=-=∴()()()()1234ln 212ln 21ln 21ln 21x x x x --+=---=--=-⎡⎤⎡⎤⎣⎦⎣⎦∴()()12341212212121x x x x -+=--=-=-∴31323431,1,21x x x x x x x =-=-=-∵312415x x x x λ⋅->恒成立∴()()()333121115x x x λ⋅---->∴233342521x x x λ-+->-对任意31,12x ⎛⎫∈ ⎪⎝⎭恒成立即:2333max42521x x x λ⎛⎫-+-⎪> ⎪- ⎪⎝⎭令321t x =-,则31(0,1),2t t x +∈=∴223331441211152552114202210t t x x t x t +⎛⎫-++--+- ⎪-⎝⎭==--+≤-+=-(当且仅当55t =时,等号成立)∴5510λ->.【点睛】关键点点睛:根据题意中方程有四个解可转化出124,,x x x 三者与3x 的关系,进而将不等式转化为关于3x 的不等式,为分离参数创造条件,分离参数后,整体换元是第二个关键点,由321t x =-换元,化简变形成为能够使用均值不等式的结构,求出函数最值,得到参数的取值范围,对能力要求较高,属于难题.。

2011年卓越联盟自主招生数学试题(1)向量a ,b 均为非零向量,(a -2b )⊥a ,(b -2a )⊥b ,则a ,b 的夹角为(A )6π (B )3π (C )23π (D )56π(2)已知sin2(?+?)=n sin2?,则tan()tan()αβγαβγ++-+22等于(A )11n n -+ (B )1n n +(C )1n n - (D )11n n +-(3)在正方体ABCD —A 1B 1C 1D 1中,E 为棱AA 1的中点,F 是棱A 1B 1上的点,且A 1F :FB 1=1:3,则异面直线EF 与BC 1所成角的正弦值为(A )153(B )155(C )53(D )55(4)i 为虚数单位,设复数z 满足|z |=1,则2221z z z i -+-+的最大值为(A )2-1(B )2-2(C )2+1 (D )2+2(5)已知抛物线的顶点在原点,焦点在x 轴上,△ABC 三个顶点都在抛物线上,且△ABC 的重心为抛物线的焦点,若BC 边所在直线的方程为4x +y -20=0,则抛物线方程为(A )y 2=16x(B )y 2=8x(C )y 2=-16x (D )y 2=-8x(6)在三棱锥ABC —A 1B 1C 1中,底面边长与侧棱长均等于2,且E 为CC 1的中点,则点C 1到平面AB 1E 的距离为 (A )3(B )2(C )3 (D )2 (7)若关于x 的方程||4x x +=kx 2有四个不同的实数解,则k 的取值范围为( ) (A )(0,1)(B )(14,1)(C )(14,+∞)(D )(1,+∞)(8)如图,△ABC 内接于⊙O ,过BC 中点D 作平行于AC 的直线l ,l 交AB 于E ,交⊙O 于G 、F ,交⊙O 在A 点的切线于P ,若PE =3,ED =2,EF =3,则PA 的长为 (A )5(B )6 (C )7(D )22(9)数列{a n }共有11项,a 1=0,a 11=4,且|a k +1-a k |=1,k =1,2,…,10.满足这种条件的不同数列的个数为( )(A )100(B )120(C )140 (D )160(10)设?是坐标平面按顺时针方向绕原点做角度为27π的旋转,?表示坐标平面关于y 轴的镜面反射.用??表示变换的复合,先做?,再做?,用?k 表示连续k 次的变换,则???2??3??4是( ) (A )?4(B )?5(C )?2? (D )??2(11)设数列{a n }满足a 1=a ,a 2=b ,2a n +2=a n +1+a n . (Ⅰ)设b n =a n +1-a n ,证明:若a ≠b ,则{b n }是等比数列; (Ⅱ)若lim n →∞(a 1+a 2+…+a n )=4,求a ,b 的值.(12)在△ABC 中,AB =2AC ,AD 是A 的角平分线,且AD =kAC . (Ⅰ)求k 的取值范围;(Ⅱ)若S △ABC =1,问k 为何值时,BC 最短(13)已知椭圆的两个焦点为F 1(-1,0),F 2(1,0),且椭圆与直线y =x (Ⅰ)求椭圆的方程;(Ⅱ)过F 1作两条互相垂直的直线l 1,l 2,与椭圆分别交于P ,Q 及M ,N ,求四边形PMQN 面积的最大值与最小值.(14)一袋中有a 个白球和b 个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在重复n 次这样的操作后,记袋中白球的个数为X n . (Ⅰ)求EX 1;(Ⅱ)设P (X n =a +k )=p k ,求P (X n +1=a +k ),k =0,1,…,b ;(Ⅲ)证明:EX n +1=(1-1a b +)EX n +1. (15)(Ⅰ)设f (x )=x ln x ,求f ′(x );(Ⅱ)设0<a <b ,求常数C ,使得1|ln |ba x C dxb a --⎰取得最小值; (Ⅲ)记(Ⅱ)中的最小值为m a ,b ,证明:m a ,b <ln2.2012年卓越联盟自主招生数学试题 2013年卓越联盟自主招生数学试题一、选择题:(本大题共4小题,每小题5分.在每小题给出的4个结论中,只有一项是符合题目要求的.) (1)已知()f x 是定义在实数集上的偶函数,且在(0,)+∞上递增,则 (A )0.72(2)(log 5)(3)f f f <-<- (B) 0.72(3)(2)(log 5)f f f -<<- (C) 0.72(3)(log 5)(2)f f f -<-< (D) 0.72(2)(3)(log 5)f f f <-<- (2)已知函数()sin()(0,0)2f x x πωϕωϕ=+><<的图象经过点(,0)6B π-,且()f x 的相邻两个零点的距离为2π,为得到()y f x =的图象,可将sin y x =图象上所有点 (A )先向右平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变(B) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变(C) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变(D) 先向右平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变(3)如图,在,,,,A B C D E 五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为 (A )21 (B)24 (C)30 ( D)48 (4)设函数()f x 在R 上存在导数()f x ',对任意的x R ∈,有2()()f x f x x -+=,且在(0,)+∞上()f x x '>.若(2)()22f a f a a --≥-,则实数a 的取值范围为(A )[1,)+∞ (B) (,1]-∞ (C) (,2]-∞ (D) [2,)+∞ 二、填空题:(本大题共4小题,每小题6分,共24分)(5)已知抛物线22(0)y px p =>的焦点是双曲线2218x y p-=的一个焦点,则双曲线的渐 近线方程为 .(6)设点O 在ABC ∆的内部,点D ,E 分别为边AC ,BC 的中点,且21OD DE +=u u u r u u u r, 则23OA OB OC ++=u u u r u u u r u u u r.(7)设曲线22y x x -与x 轴所围成的区域为D ,向区域D 内随机投一点,则该点落 入区域22{(,)2}x y D x y ∈+<内的概率为 .(8)如图,AE 是圆O 的切线,A 是切点,AD 与OE 垂直,垂足是D ,割线EC 交圆O 于,B C ,且,ODC DBC αβ∠=∠=,则OEC ∠= (用,αβ表示).三、解答题(本大题共4小题,共56分.解答应写出文字说明,证明过程或演算步骤) (9)(本小题满分13分)在ABC ∆中,三个内角A 、B 、C 所对边分别为a 、b 、c . 已知()(sin sin )()sin a c A C a b B -+=-.(1)求角C 的大小; (2)求sin sin A B ⋅的最大值. (10)(本题满分13分)设椭圆2221(2)4x y a a +=>斜率为k 的直线l 过点(0,1)E 且与椭圆交于,C D 两点.(1)求椭圆方程;(2)若直线l 与x 轴相交于点G ,且GC DE =u u u r u u u r,求k 的值;(3)设A 为椭圆的下顶点,AC k 、AD k 分别为直线AC 、AD 的斜率,证明对任意的k 恒 有2AC AD k k ⋅=-. (11)(本题满分15分)设0x >,(1)证明:2112x e x x >++; (2)若2112x y e x x e =++,证明:0y x <<.(12)(本题满分15分)已知数列{}n a 中,13a =,2*1,,n n n a a na n N R αα+=-+∈∈. (1)若2n a n ≥对*n N ∀∈都成立,求α的取值范围; (2)当2α=-时,证明*121112()222n n N a a a +++<∈---L . 2013大学自主招生模拟试题一一.选择题1. 把圆x 2+(y -1)2=1与椭圆9x 2+(y +1)2=9的公共点,用线段连接起来所得到的图形为( ) (A )线段 (B )不等边三角形 (C )等边三角形 (D )四边形2. 等比数列{a n }的首项a 1=1536,公比q=-12,用πn 表示它的前n 项之积。


参照机密级管理★启用前贵州学校卓越联盟发展计划项目2023-2024学年高一下学期期中考试数学注意事项:1.答卷前,考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.在中,若,则是( )A.B.或C.或D.2.已知复数则( )B.1D.23.若直线不平行于平面,且直线,则下列说法正确的是( )A.内存在与平行的直线B.内所有直线都与异面C.与有公共交点D.内所有直线都与相交4.已知向量满足,且,则与的夹角为( )A.B. C. D.5.若一圆柱的侧面展开图是一个面积为的正方形,则该圆柱的体积为()A. B. C. D.ABC V π,6B b a ===A π6π65π6π32π3π31i z i+=1z =l βl β⊄βl βl l ββl ,a b 6a b ⋅=- 3,4a b == a b π6π32π35π624π2π2π42π322π6.如图,在中,已知,则为( )7.已知是边长为6的等边三角形,点分别是上的点,满足,连接交于点,求( )A. B. C. D.8.已知在钝角中,,点是边上一点,且,则的最小值为( )A.B. C. D.二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知,则下列说法正确的是()A..B..C.在复平面内对应的点位于实轴上,则.D.在复平面内的点在直线上.10.在中,,点是线段的中点,线段交于,则下列说法正确的是()ABC V π,223BAC AB AD BD ∠====sin C ABC V ,D E ,AB AC ,2AD DB AE EC == ,CD BE G GA AC ⋅=725-365725365-ABC V B 2sin ,1b A a c =+=D AC 2AC CD =BD 12131418()12i 43i z +=+3z z ⋅=23i z ++=()()i ,a b z a b R +∈20a b -=2i z -15y x =+ABC V 2AE EC =D BC BE AD FA.B.C.D.与的面积之比为11.如图,在棱长为2的正方体中,分别是,的中点,是线段上的动点,则()A.不存在点,使四点共面B.存在点,使平面C.三棱锥的体积是定值D.经过四点的球的表面积为三、填空题:本题共3小题,每小题5分,共15分.12.已知复数,且,则__________.13.贵州中天201大厦是贵阳标志性建筑之一,又名为“芦笙楼”.它是以贵州少数民族芦笙为原型设计,外形造型看上去就像是用很多微型大楼“拼接”起来的一样,而这一部分其实具有相当先进的建筑工艺,采用的是筒式悬挂结构,目前是世界上最高的筒式悬挂建筑.某数学兴趣小组成员为测量中天201大厦的高度,在与楼底位于同一水平面上的两处进行测量,已知在处测得塔顶的仰角为,在处测得塔顶的仰角为米,则中天201大厦的高度为__________米.12AD BC BA=- 1233BE BA BC=+ 43AD AF=BFD V BFA V 1:41111ABCD A B C D -,,M N P 11,AA CC 11C D Q 11D A Q ,,,B N P Q Q PQ ∥MBN M BCN -,,,C M B N 10π122i,z 3i z a b =+=-()12z i,,z b a b R +=∈20232024a b +=O ,A B A P 60 B P 45,30,116AOB AB ∠==14.在梯形中,,梯形外接圆圆心为,圆上有一个动点,求的取值范围__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)已知复数的共轭复数为在复平面上对应的点在第一象限,且满足,(1)求复数;(2)求复数的模长.16.(本小题满分15分)已知向量是平面内的一组基底,且与的夹角为锐角,(1)求证三点共线.(2)设,若的最小值是,求锐角的值.17.(本小题满分15分)如图,在四棱锥中,,底面为矩形,对角线与相交于点,点到平面的距离为为的中点.(1)求证:平面.ABCD AB ∥1,2C 4,2DADC CD AB D DADC==⋅=- ABCD O P AO AP ⋅z z z 6i,25z z z z -=⋅=z 1izz +-,a b1,a b a == b α,35,3OA a b OB a b OC a b=+=+=--,,A B C c a b =+ ,c ta t R +∈ 32αP ABCD -PD CD ⊥ABCD BD AC ,2O PD DC ==B PCD 1,E PC PA ∥BDE(2)求三棱锥的体积.18.(本小题满分17分)在①;②;③;这三个条件中任选一个,补充在下面的问题中,并解答问题(其中为的面积).问题:在中,角的对边分别为,满足:__________.(1)求角的大小;(2)若与角的内角平分线相交于点,求面积的取值范围.19.(本小题满分17分)“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小."意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:(1)若是边长为4的等边三角形,求该三角形的费马点到各顶点的距离之和;(2)的内角所对的边分别为,且,点为的费马点(i )若,求;(ii)求的最小值.P ADE -20S BC ⋅= cos sin 0b A A a c +--=sin sin sin sin C B aA C b c+=--S ABC V ABC V ,,A B C ,,a b c B b =A B D ACD V ABC V 120 120AOB BOC COA ∠∠∠=== O ABC V 120 ABC V O ABC V ,,A B C ,,a b c sin a b A =P ABC V ac =PA PB PB PC PC PA ⋅+⋅+⋅2||||||PA PC PB ⋅贵州学校卓越联盟发展计划项目2023-2024学年高一下学期期中考试数学参考答案1.C 在中,由正弦定理得,又,则或.所以选C.2.A由,所以,则A.3.C 因为直线不平行于平面,且直线,所以直线与平面相交,则与有公共交点,C 正确;根据题意知内所有直线都与异面或相交,故错误;内不存在与平行的直线,错误.4.C 设与的夹角为,则,因为,所以.故选:C.5.D 如图,圆柱的侧面展开图是一个面积为的正方形,则该圆柱的高,底面圆的周长为,解得,故圆柱的体积为:.故选D.6.B 在中,由余弦定理:,由为锐角,所以ABC V πsinA sinB sin 6a b ===π5π66A <<π3A =2π3()1i i 1i z 1i i i1+⋅-+===-⋅-()()()1i 111i 1i 1i 1i 2z++===--+1z =l βl β⊄l βl ββl B,D βl A a b θ61cos 122a b a b θ⋅-===-[]0,πθ∈2π3θ=24π2πh =2π2πr =1r =22π2πV sh r h ===ABD V 2222222121cos 22214BA BD AD B BA BD +-+-===⋅⨯⨯B7.方法一(基底法)应为共线,设即所以解得所以方法二(投影法)过点连接的中点如图所示,过点分别做边的垂线,垂足分别是,易得,所以在边上的投影是方法三(坐标法)以边的中点为坐标原点,以边为轴建立如图所示直角坐标系,,设由共线可得解得,数量积转换为坐标运算即可.8.C在,得,又,得所以,又所以sin B==()ππsin sin sin cos cos sin33C A B B B=+=+=,,,,D G C B G E、()()11AG xAD x AC y AE y AB=+-=+-()()1123x yAG AB x AC AC y AB=+-=+-()1213xyyx⎧=-⎪⎪⎨⎪-=⎪⎩43,55x y==212127255555 GA AC AG AC AC AB AC AC AB AC⎛⎫⎛⎫⋅=-⋅=-+⋅=-+⋅=-⎪ ⎪⎝⎭⎝⎭D AC F,D G AC,M N1319M AF,22510A MN MC====AGAC972,655AN GA AC AG AC AN AC⋅=-⋅=-⋅=-⨯=BC O AC x(()()(3,3,0,3,0,,1,2A B C D E⎛--⎝(),G x y,,,,D G C B G E、))4309302y xy x⎧-+=⎪⎨--=⎪⎩35xy⎧=-⎪⎪⎨⎪=⎪⎩ABCV2sin sinA B A=sinB=ππ2B<<2π3B=1,2a c AC CD+==222211111,()222442BD BA BC BD BA BC c a ac⎡⎤⎛⎫=+=+=++⨯- ⎪⎢⎥⎝⎭⎣⎦,因为,又即,当且仅当时等号成立,选C.9.BCD对于由.得.,故A 错;对于,故正确;对于C.,因为点在实轴上,所以,故C 正确;对于,对应复平面内的点的坐标为,且故D 正确.10.ABD对于:根据,又因为点是线段的中点,,故故A正确;对于:因为,所以,故正确;对于,因为点是线段的中点,所以,设,则,,又,则,又因为、BD =221,21a c a c ac +=++=BD =22222a c a c ++⎛⎫≥ ⎪⎝⎭2212a c +≥12a c ==14BD ≥A ()12i 43i z +=+()()()()43i 12i 43i 2i 12i 12i 12i z +-+===-++-()()2i 2i 53z z ⋅=-+=≠B,z 23i 2i 23i 42i ++=-++=+==B ()()()()i 2i 22i a b a b b a +-=++-()2,2a b b a +-20b a -=()()22i (2i)34i D,2i 2i 2i 2i 5z +++===---+34,55⎛⎫ ⎪⎝⎭431555=+A AD BD BA =-D BC 12BD BC = 12AD BC BA =- B 2AE EC =23AE AC = ()22213333BE BA AE BA AC BA BC BA BC BA =+=+=+-=+B C D BC 1122AD AB AC =+ AD k AF =1122k AF AB AC =+1122AF AB AC k k =+ 2AE EC = 313,224AC AE AF AB AE k k==+ F B 、三点共线,所以,解得,故错误;对于D :由于,故,故D 正确;故选:ABD.11.BC 对选项,当与重合时,易知,从而可得四点共面,选项错误;对选项,当为的中点时,易知,从而可得平面选项正确;对选项,点到面的距离为2,而,所以是定值选项正确;对选项,根据分割补形法易知:经过四点的球即为长宽高分别为2,2,1的长方体的外接球,所求球的直径满足:,经过四点的球的表面积为选项错误.故选:.12.2 由则,所以解得所以.13. 设则在中,由余弦定理:解得14.由可知,在结合圆内接四边形对角互补可得,所以梯形是等腰梯形.取边的中点连接,可得E 13124k k +=54k =C 54k =5,::1:44BFD BEA AD AF S S FD AF =∴==V V A Q 1A PN ∥1A B ,,,B N P Q A ∴B Q 11A D PQ ∥MN PQ ∥,MBN B ∴C M BCN 1BCN S =V 23M BCN V -=C ∴D ,,,C M B N ∴2R 2222(2)2219R =++=∴,,,C M B N 24π9π,R D =∴BC 122i,3i z a z b =+=-()()()122i 3i i i z z a b a b b +=++-=+-=01a b b +=⎧⎨=-⎩1,1a b ==-20232024202320241(1)2a b +=+-=OP h =OB h =ABC V 2221162h h =+-h =12DA DC DA DC⋅=-120ADC ∠= 60,120DAB DCB ∠∠== ABCD AB O OD 2OD OA OB AD ====方法一(极化恒等式)连接,过中点连接如图所示,由极化恒等式可得,点在圆上运动过程中,点与点重合取得最小值点与点重合取得最大值3,所以方法二(坐标法)建系如图,设是角的终边,又因为点在圆上,所以易得.15.解:(1)设,则由题有解得又在复平面上对应的点在第一象限,故.所以(2)由(1)知则整理得所以16.(1)解:应为,所以即OP OP G AG 222114AO AP AG OP AG ⋅=-=-P 13,P AG ≤≤A 1,PB 08AO AP ≤⋅≤ (),,P x y OP θP O 2cos ,2sin x y θθ==()()2cos 2,2sin ,2,0AP AO θθ=+=4cos 4AP AO θ⋅=+ 08AO AP ≤⋅≤i z a b =+iz a b =-()()()()i i 6ii i 25a b a b a b a b ⎧+--=⎪⎨+-=⎪⎩3,4b a ==±z 4a =43iz =+43i z =+()43i 43i 1i 1i z z ++=++--913i 22=+1i z z +=-==,35,3OA a b OB a b OC a b =+=+=--2424AB OA OB a b AC OC OC a b=-=+=-=-- AC AB=-又因为有公共点所以三点共线(2)方法一转换为二次函数的最值由题意知记,易得是开口向上的二次函数在对称轴处取得最小值,即当,.所以化简得方法二几何法找最值由向量加法的三角形法则可知:的终点落在直线上,当向量与垂直时,取得最小值设与的夹角为,由题意知.,AC AB A ,,A B C c ta+====()()224f t t t αα=++++()f t ()1t α=-+()94f t =()()29(1)2144αααα--++++=2933cos 344α=-=1πcos 23αα=⇒=,t R c ta ∈+ BC c ta + BC c ta + 32c ta + aθθα<3sin 2c θ= 3sin cos 2c θθ=⇒= c ==由数量积定义可知:.化简得即17.(1)证明:如图,连接.点为的中点,且点为的中点为的中位线,即.又平面平面平面(2)为矩形又平面平面点到平面的距离为1,即棱锥的高为1.又为的中点,且.18.(1)选①:由已知得:,所以,cos a c a c θ⋅== =2α+=()()2413cos 449ααα++=+-211cos cos 42αα=⇒=π3α=EO E PC O AC EO ∴APC V EO ∥PA EO ⊂ ,BDE PA ⊄BDEPA ∴∥BDEABCDAB ∴∥CDCD ⊂ PCD AB ∴∥PCDB PCD A PDE -E PC 2PD DC==111221222PDE PDC S S ∴==⨯⨯⨯=V V 11111333P ADE A PDE V V AD S PDE --∴==⋅=⨯⨯=V ()12sinB cos π02ac a B ⨯+⋅-=()sin 0ac B B -=所以,,又所以,,即:.选②:由正弦定理得:,所以,所以,,又因为.所以,.即:.选③由正弦定理得:,即:.得:.由余弦定理得:又因为,所以.(2)由题可得:,则.令,在中由正弦定理得:所以,,sin0B B =cos 0B ≠tan B =π3B =sin cos sin sin sin B A B A AC =+()sin cos sin sin sin B A B A A A B +=++sin cos sin sin sin cos sin cos B A B A A A B B A+=++sin sin sin cos B A A A B =+sin 0B ≠1cos B B=+π2sin 16B ⎛⎫-= ⎪⎝⎭π3B =c b a a c b c +=--222b c a ac -=-222a c b ac +-=2221cos 222a cb ac B ac ac +-===0πB <<π3B =2π3BAC ACB ∠∠+=π3ACD CAD ∠∠+=ACD ∠θ=ACD V 4πsin sin sin 3AD CD AC D θθ====⎛⎫- ⎪⎝⎭π4sin ,4sin 3AD CD θθ⎛⎫==- ⎪⎝⎭所以,.又因为,所以,,所以,.即:.(1)因为为等边三角形,三个内角均小于,故费马点在三角形内,使得,且,如图:过作于,则,故该三角形的费马点到各顶点的距离之和为(2)(i )因为,由正弦定理,故得,所以所以三角形的三个角都小于,则由费马点定义可知:,设,由得:,整理得,则12πππS sin sin 02333ACD AD CD θθθ⎛⎫=⋅⋅=-<< ⎪⎝⎭V π26θ⎛⎫=+ ⎪⎝⎭ππ5π2666θ<+<1πsin 2126θ⎛⎫<+≤ ⎪⎝⎭0S ACD <≤V (S ACD ∈V ABC V 120 O 120AOB BOC COA ∠∠∠=== OB OC OA ==O OD AC ⊥D 2,30CD OCD ∠== cos30CD OC == O OB OC OA ++=sin a b A =sin sin a b A B =sin ,sin 1sin sin b A b B A B ==π2B =ABC 120 120APB BPC APC ∠∠∠=== ,,PA x PB y PC z === ∣APB BPC APC ABC S S S S ++=V V V V 11112222xy yz xz ++=-⨯4xy yz xz ++=PA PB PB PC PA PC ⋅+⋅+⋅.(ii )点为的费马点,则,设,由余弦定理得,,,故由得,即即,而,即时,等号成立.设,解得或(舍去),由.最小值为.1111422222xy yz xz ⎛⎫⎛⎫⎛⎫=⋅-+⋅-+⋅-=-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭P ABC V 2π3APB BPC CPA ∠∠∠===,,,0,0,0PB x PA m PB mx PC n Pb nx m n x =====>>>()22222222π||2cos 13AB x m x mx m m x =+-=++()22222222π||2cos 13BC x n x nx n n x =+-=++()2222222222π||2cos3AC m x n x mnx m n mn x =+-=++22||BC AB AC +=∣()()()222222211n n x m m x m n mn x +++++=++()()2222222m n m n x m n mn x ++++=++2m n mn ++=0,0,2,2m n m n mn mn m n >>++=-=+≥m n =1m n ==t =2220t t --≥1t ≥1t ≤21(14t mn =≥+≥+=+22||||||PA PC mx nx mn PB x ⋅⋅==4+。

2011年同济等九校(卓越联盟)自主招生数学试题(1)向量a ,b 均为非零向量,(a -2b )⊥a ,(b -2a )⊥b ,则a ,b 的夹角为(A )6π(B )3π(C )23π (D )56π (2)已知sin2(α+γ)=n sin2β,则tan()tan()αβγαβγ++-+22等于 (A )11n n -+ (B )1n n + (C )1n n - (D )11n n +- (3)在正方体ABCD —A 1B 1C 1D 1中,E 为棱AA 1的中点,F 是棱A 1B 1上的点,且A 1F :FB 1=1:3,则异面直线EF 与BC 1所成角的正弦值为 (A )153 (B )155 (C )53 (D )55(4)i 为虚数单位,设复数z 满足|z |=1,则2221z z z i-+-+的最大值为 (A )2-1 (B )2-2 (C )2+1 (D )2+2(5)已知抛物线的顶点在原点,焦点在x 轴上,△ABC 三个顶点都在抛物线上,且△ABC 的重心为抛物线的焦点,若BC 边所在直线的方程为4x +y -20=0,则抛物线方程为(A )y 2=16x (B )y 2=8x (C )y 2=-16x (D )y 2=-8x(6)在三棱锥ABC —A 1B 1C 1中,底面边长与侧棱长均等于2,且E 为CC 1的中点,则点C 1到平面AB 1E 的距离为(A )3 (B )2 (C )32 (D )22(7)若关于x 的方程||4x x +=kx 2有四个不同的实数解,则k 的取值范围为( ) (A )(0,1) (B )(14,1) (C )(14,+∞) (D )(1,+∞) (8)如图,△ABC 内接于⊙O ,过BC 中点D 作平行于AC 的直线l ,l 交AB 于E ,交⊙O 于G 、F ,交⊙O 在A 点的切线于P ,若PE =3,ED =2,EF =3,则PA 的长为(A )5 (B )6(C )7(D )22 (9)数列{a n }共有11项,a 1=0,a 11=4,且|a k +1-a k |=1,k =1,2,…,10.满足这种条件的不同数列的个数为( )(A )100 (B )120 (C )140 (D )160(10)设σ是坐标平面按顺时针方向绕原点做角度为27π的旋转,τ表示坐标平面关于y 轴的镜面反射.用τσ表示变换的复合,先做τ,再做σ,用σk 表示连续k 次的变换,则στσ2τσ3τσ4是( ) (A )σ4 (B )σ5 (C )σ2τ(D )τσ2 (11)设数列{a n }满足a 1=a ,a 2=b ,2a n +2=a n +1+a n .(Ⅰ)设b n=a n+1-a n,证明:若a≠b,则{b n}是等比数列;(a1+a2+…+a n)=4,求a,b的值.(Ⅱ)若limn1)考察数列定义2)a1+a2+a3+...+a n=a n-a n-1+2(a n-1-a n-2)+3(a n-2-a n-3)+...+(n-1)(a2-a1)+na1=b n+2b n-1+3b n-3+...+b1+na(错位相减,可得a,b的值)(12)在△ABC中,AB=2AC,AD是A的角平分线,且AD=kAC.(Ⅰ)求k的取值范围;(Ⅱ)若S△ABC=1,问k为何值时,BC最短?(13)已知椭圆的两个焦点为F1(-1,0),F2(1,0),且椭圆与直线y=x-3相切.(Ⅰ)求椭圆的方程;(Ⅱ)过F1作两条互相垂直的直线l1,l2,与椭圆分别交于P,Q及M,N,求四边形PMQN面积的最大值与最小值.(14)一袋中有a个白球和b个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在重复n次这样的操作后,记袋中白球的个数为X n.(Ⅰ)求EX1;(Ⅱ)设P(X n=a+k)=p k,求P(X n+1=a+k),k=0,1,…,b;(Ⅲ)证明:EX n+1=(1-1a b+)EX n+1.(15)(Ⅰ)设f(x)=x ln x,求f′(x);(Ⅱ)设0<a<b,求常数C,使得1|ln|bax C dxb a--⎰取得最小值;(Ⅲ)记(Ⅱ)中的最小值为m a,b,证明:m a,b<ln2.。

清北学长精心打造——卓越自主招生数学模拟试题及参考答案(一)一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中只有一项是符合题目要求的。
1.已知△ABC 的三边a ,b ,c 成等比数列,a ,b ,c 所对的角依次为A ,B ,C.则sinB+cosB 的取值范围是( ) A .(1,1+]23 B .[21,1+]23 C .(1,]2 D .[21,]2 2.一个口袋里有5个大小一样的小球,其中两个是红色的,两个是白色的,一个是黑色的,依次从中摸出5个小球,相邻两个小球的颜色均不相同的概率是( ) A 1/2 B 2/5 C 3/5 D 4/73.正四棱锥ABCD S -中,侧棱与底面所成的角为α,侧面与底面所成的角为β,侧面等腰三角形的底角为γ,相邻两侧面所成的二面角为θ,则α、β、γ、θ的大小关系( ) (A )θγβα<<<(B )γθβα<<<(C )βγαθ<<<(D )θβγα<<< 4. 已知f (x )=|x +1|+|x +2|+…+|x +2007|+|x -1|+|x -2|+…+|x -2007|(x ∈R ),且f (a 2-3a +2)=f (a -1).则a 的值有( ).(A )2个 (B )3个 (C )4个 (D )无数个5.平面上满足约束条件⎪⎩⎪⎨⎧≤--≤+≥01002y x y x x 的点(x ,y )形成的区域为D ,区域D 关于直线y=2x对称的区域为E ,则区域D 和区域E 中距离最近的两面三刀点的距离为( )A .556 B .5512 C .538 D .53166. 若m 、n ∈{x |x =a 2×102+a 1×10+a 0},其中a i ∈{1,2,3,4,5,6,7},i =0,1,2,并且m +n =636,则实数对(m ,n )表示平面上不同点的个数为( ).(A )60个 (B )70个 (C )90个 (D )120个 7.数列{}n a 定义如下:()1221211,2,2+++===-++n n n na a a a n n 201122012>+m a ,则正整数m 的最小值为( ). A 4025 B 4250 C 3650 D 4425 8. 用红、黄、蓝三种颜色之一去涂途中标号为9,,2,1的9个小正方形(如图),使得任意相邻(有公共边的)小正方形所涂颜色都不相同,且“3、5、7”号数字涂相同的颜色,则符合条件的所有涂法共有( )A 96B 108C 112 D120 9.设a n =2n ,b n =n ,(n=1,2,3,。

河北省卓越联盟2023-2024学年高一上学期10月月考数学试
题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
..
..
.已知集合(){}1,0M =,则下列与相等的集合个数为(
)
二、多选题
..
..
11.对于给定的实数a ,关于实数x 的不等式()()0a x a ax a -+≥的解集不可能为(
)
A .∅
B .{}1x
a x ≤≤-∣C .{x
x a ≤∣或}1x ³-D .R 12.已知全集{}0,1,2,3,4,5,U A =是U 的子集,当x A ∈时,1x A -∉且1x A +∉,则称x 为A 的一个“孤立元素”,则下列说法正确的是(
)
A .若A 中元素均为孤立元素,则A 中最多有3个元素
B .若A 中不含孤立元素,则A 中最少有2个元素
C .若A 中元素均为孤立元素,且仅有2个元素,则这样的集合A 共有9个
D .若A 中不含孤立元素,且仅有4个元素,则这样的集合A 共有6个
三、填空题
15.若{}{}2
,0,1,,0a a b -=16.若220,0,x y x y >>+=四、解答题。

2023学年第二学期金华市卓越联盟5月阶段性模拟考高一年级数学学科参考答案命题:浦江三中吴保林审稿:东阳二中郭扬文一.选择题(本题共8小题,每小题5分,共40分,每小题给出的四个选项中只有一个是符合题目要求的)题目12345678选项A C D B C A D B二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得部分分,有选错的得0分)题号91011选项AC BCD ABD三.填空题(本题共3小题,每小题5分,共15分))12.;13.200;14.54π四.解答题(本题共5题,共77分.解答应写出文字说明、证明过程或演算步骤)15.(1)由题意1cos3122a b a b a b π⋅⋅===⨯,∴1a b ⋅= ······································2分()222222444444a b a ba ab b -=-=-⋅+=-+= ∴22a b -== ···································6分(2)由题意得)220a b a b λ+⋅+=······································8分所以()222420a a b b λλ++⋅+= ,即有()8420λλ+++=∴4λ=-··································13分16.(1)令12,,22x t t ⎡⎤=∈⎢⎥⎣⎦()214222,22x x f x t t t ⎡⎤=-⋅=-∈⎢⎥⎣⎦,···································2分所以当1,0t x ==时,()f x 有最小值1-····································4分当2,1t x ==时,()f x 有最大值0····································6分(2)∵()()()()()2442222222xxx x x x x x g x a a ----=+-+=+-+-[)22,2,x x μμ-+=∈+∞,∴()22g x a μμ=--··································10分当对称轴22a ≤即4a ≤时:()min 2211g x a =-=-,解得132a =(舍)······················12分当对称轴22a≥即4a ≥时:()2min 2114a g x =--=-,解得6a =···························14分综上:6a =····································15分3x17.(1)∵在ABC ∆中,有()sin sin C A B =+∴()()sin sin 2sin B A B A A -++=,2sin cos 2sin B A A =······························4分当2A π=时,等式显然不成立,所以2A π≠······························5分∴sin tan B A=·····························6分(2)∵由正弦定理推出2sin sin sin B A C=································8分且(1)得sin cos sin B A A =,∴2sin sin cos sin B B A C =即sin cos sin B A C=所以sin cos cos sin cos sin A C A C A C +=,∴2C π=····························12分∴2sin sin cos 2B B B π⎛⎫=-=⎪⎝⎭即21cos cos B B -=,2cos cos 10B B +-=,∴51cos 2B -=····························15分18.(1)∵面PBD ⊥面ABCD ,面PBD 面ABCD BD =,PB BD ⊥,PB ⊂面PBD ∴PB ⊥面ABCD又∵AB ⊂面ABCD ,∴PB AB⊥·······························3分(2)∵PA 面BDN ,PA ⊂面PAC ,面PAC 面BDN NO =,∴PA NO ,可知N 为PC 中点······························6分1111332222326N PAD C PAD P ACD V V V ---===⨯⨯⨯=·······························9分(3)由题意知PB ⊥面ABCD ,过点N 作PB 平行线交BC 于点H ∴NH ⊥面ABCD ,再作HK BD ⊥(K 为垂足)∴NKH ∠为二面角N BD C --的平面角,4NKH π∠=······························13分不妨设NH x KH ==,NC =,2BH x =-且2BH KH =,∴23x NH ==∴2PN NC ==······························17分19.(1)(ⅰ)2tan1524DQ ︒===-···································2分(ⅱ) 57sin 60sin CPCR CPR =∆中,有在,3311-=-=PB CP 又,解得622-=CR 26-=-=∴CR AC AR ··············7分(2))4tan(21tan 2111θπθ---=--=∆∆ADQ ABP S S S ··································9分)(θθθθπθπθπθθθπθπθθπθπθθsin cos cos 211)4cos(cos 4sin211)4cos(cos cos )4sin()4cos(sin 211)4cos()4sin(cos sin 2112+-=--=--+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+-=)(42sin 21112sin 2cos 111πθθθ++-=++-=································14分2212118max -=+-==∴S 时,当且仅当πθ································17分。
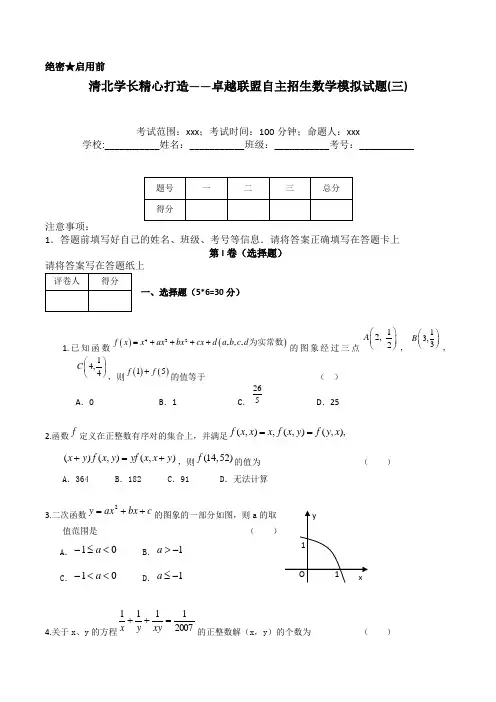
绝密★启用前清北学长精心打造——卓越联盟自主招生数学模拟试题(三)考试范围:xxx ;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(5*6=30分)1.已知函数()()432,,,f x x a x b x c x d a b c d =++++为实常数的图象经过三点12,2A ⎛⎫ ⎪⎝⎭,13,3B ⎛⎫ ⎪⎝⎭,14,4C ⎛⎫ ⎪⎝⎭,则()()15f f +的值等于( ) A .0 B .1C .265D .252.函数f 定义在正整数有序对的集合上,并满足(,),(,)(,),f x x x f x y f y x ==()(,)(,)x y f x y yf x x y +=+,则(14,52)f 的值为( )A .364B .182C .91D .无法计算3.二次函数c bx ax y ++=2的图象的一部分如图,则a 的取 值范围是 ( )A .01<≤-aB .1->aC .01<<-aD .1-≤a4.关于x 、y 的方程20071111=++xy y x 的正整数解(x ,y )的个数为( )A .16B .24C .32D .48第II 卷(非选择题)二、填空题(6*6=36分)5.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x =的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.6. 平面上给定ΔA 1A 2A 3及点p 0,定义A s =A s-3,s ≥4,构造点列p 0,p 1,p 2,…,使得p k+1为绕中心A k+1顺时针旋转1200时p k 所到达的位置,k=0,1,2,…,若p 1986=p 0.则ΔA 1A 2A 3为 三角形。
2023学年第二学期金华卓越联盟5月阶段联考高二年级数学试题考生须知:1、本卷共6页,满分150分,考试时间120分钟.2、答题前,在答题纸指定的区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3、所有试题必须写在答题纸上,写在试卷上无效.4、考试结束后,只需上交答题纸.选择题部分一、单选题:本题共8小题,每题5分,共40分,在每题给出的4个选项中,只有一个选项符合要求.1.若集合,则( )A .或B .C .D .2.已知复数,则( )A .-2B .2C .D .3.若,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.下列说法错误的个数为( )①已知,若,则②已知,则③投掷一枚均匀的硬币5次,已知正面向上不少于3次,则出现5次正面向上的概率为A .0B .1C .2D .35.科学家从由实际生活得出的大量统计数据中发现以1开头的数出现的频率较高,以1开头的数出现的频数约为总数的三成,并提出定律:在大量进制随机数据中,以开头的数出现的概率为,如裴波那契数、阶乘数、素数等都比较符合该定律.后来常有数学爱好者用此定律来检验某些经济数据、选举{ln 0}01xM x x N xx ⎧⎫=>=>⎨⎬+⎩⎭,M N = {1x x <-0}x >{}101x x x -<<>或{}01x x <<{}1x x >2iz i-=z z -=4i-4i 0a b >,a b >3ln 3ln abb a ->-()210X N σ~,()809P X ≥=.()81208P X ≤≤=.153X B ⎛⎫~ ⎪⎝⎭,()()5093E X D X ==,.116b n ()1log b bn P n n+=数据等大数据的真实性.若,则的值为()A .14B .15C .24D .256.袋中装有5个大小相同的球,其中有2个白球,2个黑球,1个红球,现从袋中每次取出1球,取出后不放回,取得白球得1分,取得黑球得2分,取得红球得3分,直到取到的球的总分大于或等于4分时终止,用表示终止取球时所需的取球次数,则( )A .B .C .D .7.体积为1的正三棱雉的外接球的半径与底面正三角形的边长比的最小值为( )A BCD8.已知函数,当时,记的最大值为,有,则实数的最大值为( )A .2B .1C .D .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.9.下列选项中正确的有()A .已知在上的投影向量长度为,且,则B .C .若非零向量满足,则D .已知,且与夹角为锐角,则的取值范围是10.下列命题错误的是()A .线性相关模型中,决定系数越大相关性越强,相关系数越大相关性也越强B .回归直线至少会经过其中一个样本点C .已知一系列样本点的经验回归方程为,若样本点与的残差相等,则D .以模型去拟合某组数据时,为了求出回归方程,设,将其变换后得到()()*165ln6ln2ln2ln8kn p n k N =-=∈+∑()*4k N k ∈>,k X ()3P X ==25123545()()322111432f x x x a x b a b ⎛⎫=-+-+≥∈ ⎪⎝⎭R ,02]x ∈[,()f x M M k ≥k 2312a b12b 5b = 252a b ⋅=()a b c a b c⋅≤ a b , 1a b a b ==-= 2a b +=()()1223a b ==,,, a a b λ+ λ58∞⎛⎫-+ ⎪⎝⎭,2R r ()i i x y ,()()i 123i i x y =⋯,,,ˆ2ˆy x a =+()2m ,()3n ,28m n +=e bxy a =ln z y =线性方程,则的值分别为3,411.如图,已知圆台的下底面直径,母线,且,是下底面圆周上一动点,则()A .圆台的侧面积为B .圆台C .当点是弧中点时,三棱雉的内切球半径D .的最大值为非选择题部分三、填空题:本题共3小题每题5分,共15分.12.的展开式中的常数项为______.13.在锐角三角形中,边长为1,且,则边的长度取值范围是______.14.某学校举办校庆,安排3名男老师和2名女老师进行3天值班,值班分为上午和下午,每班次一人,其中女老师不在下午值班,且每个人至少要值班一次,则不同的安排方法共有______种(用数字作答).四、解答题:本题共5小题,共77分.解答题应写出文字说明、证明过程和演算步骤.15.(本题满分13分)设函数,其中,已知.(1)求的解析式;(2)已知,求的单调递增区间及值域.16.(本题满分15分)在如图所示的直三棱柱中,分别是线段上的动点.4ln3z x =+a b ,OO '4AB =2BC =AC BC ⊥P OO '6πOO 'πP AB A BCP -23r >2PA PC +922x x ⎛⎫- ⎪⎝⎭ABC BC 2B A =AC ()cos f x x x ωω=-()03ω∈,π26f ⎛⎫-=- ⎪⎝⎭()f x π02x ⎡⎤∈⎢⎥⎣⎦,()f x 111ABC A B C -122AB BC AA D E ===,,,11BC A B ,(1)若平面,求的值;(2)若三棱柱是正三棱柱,是的中点,求二面角余弦值的最小值.17.(本题满分15分)已知函数,.(1)求曲线在点处的切线方程;(2)讨论的单调性;(3)证明:当时,.18.(本题满分17分)某超市为促进消费推出优惠活动,为预估活动期间客户投入的消费金额,采用随机抽样统计了200名客户的消费金额,分组如下:(单位:元),得到如图所示频率分布直方图:活跃客户非活跃客户总计男20女60总计(1)利用抽样的数据计算本次活动的人均消费金额(同一组中的数据用该组的中点值表示)(2)若把消费金额不低于800元的客户,称为“活跃客户”,经数据处理,现在列联表中得到一定的相关数据,求列联表中的值,并根据列联表判断是否有的把握认为“活跃客户”与性别有关?(3)为感谢客户,该超市推出免单福利,方案如下:从“活跃客户”中按分层抽样的方法抽取12人,从中抽取2人进行免单,试写出总单金额的分布列及其期望.(每一组消费金额按该组中点值估计,期望结果保留至整数.)附:0.1500.1000.0500.0100.005DE ∥111132ACC A B E EA =,::CD BD :D BC D BE A --()()212ln 22f x x x a x =+++a ∈R ()y f x =()()11f --,()f x 2a <-()234af x a a ae ++>-[)[)[)[]020020040040060010001200,,,,,,,, xyx y ,95%Y ()2P kχ≥0.1500.1000.0500.0100.005k2.0722.7063.8416.6357.87919.(本题满分17分)已知①设函数的值域是,对于中的每个,若函数在每一处都等于它对应的,这样的函数叫做函数的反函数,记作,我们习惯记自变量为,因此可改成即为原函数的反函数.易知与互为反函数,且.如的反函数是可改写成即为的反函数,与互为反函数.②是定义在且取值于的一个函数,定义,则称是函数在上的次迭代.例如,则.对于一些相对复杂的函数,为求出其次迭代函数,我们引入如下一种关系:对于给定的函数和,若函数的反函数存在,且有,称与关于相似,记作,其中称为桥函数,桥函数满足以下性质:(1)若,则(2)若为的一个不动点,即,则为的一个不动点.(1)若函数,求(写出结果即可)(2)证明:若,则.(3)若函数,求(桥函数可选取),若,试选取恰当桥函数,计算.2023学年第二学期金华卓越联盟5月阶段联考()2P kχ≥()()()()()22n ad bc a b c d a c b d χ-=++++()()y f x x A =∈C C y ()g y ()g y x ()()x g y y C =∈()()y f x x A =∈()()1x f y y C -=∈x ()()1x f y y C -=∈()()1y f x x C -=∈()()1y fx x C -=∈()()y f x x A =∈()()1f f x x -=2x y =2log x y =2log y x =2xy =2log y x =2xy =()f x D D ()()()()()()()()()012f x x f x f x f x f f f f x ===-⋯,,, ()()()n f x f f f ff f x == ()()n f x ()f x D n ()f x x a =+()()n f x x na =+n ()f x ()g x ()x ϕ()1x ϕ-()()1f x g x ϕϕ-= ()f x ()g x ()x ϕf g ϕ~()x ϕf g ϕ~1g fϕ-~0x ()f x ()00f x x =()0x ϕ()g x ()22f x x =()()n fx f g ϕ~()()n n fg ϕ~()22f x x x =+()()n f x ()1x x ϕ=+()2612c x x x =-+()()n cx高二年级数学学科参考答案一、单选题:本题共8小题,每题5分,共40分,在每题给出的4个选项中,只有一个选项符合要求.1.D2.C3.C4.B5.A6.B7.D8.C二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.9.BC10.AB11.ABD三、填空题:本题共三小题每题5分,共15分.12.537613.14.252四、解答题:本题共5小题,共77分.解答题应写出文字说明、证明过程和演算步骤.15.解(1)可化为,所以所以又所以所以(2)令解得又所以故的单调递增区间为所以所以16.方法1.(1)过点作,交于,连接,如图,()f x ()π2sin 6f x x ω⎛⎫=-⎪⎝⎭2ππsin 2666πf ω⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭πππ2k π662ω--=-+212k k Z ω=-∈,()03ω∈,02k ω==,()π2sin 26f x x ⎛⎫=- ⎪⎝⎭()111πππ2π22π262k x k k -≤-≤+∈Z ()111ππππ63k x k k -≤≤+∈Z π02x ⎡⎤∈⎢⎥⎣⎦,10k =()f x π03x ⎡⎤∈⎢⎥⎣⎦,π02x ⎡⎤∈⎢⎥⎣⎦,ππ5π2666x ⎡⎤-∈-⎢⎥⎣⎦,()[]12f x ∈-,E 1EM A A ∥AB M DM由平面,平面,则平面且又平面,,且平面,故平面平面又平面平面,平面平面,所以从而.故方法2过点作,可得,所以四点共面四边形是平行四边形所以所以(2)过作,垂足为,正三棱雉可得平面,再过作,垂足为,连接,1AA ⊂11AA C C ME ⊄11AA C C EM ∥11ACC A 1132B E BM EA AM ==DE ∥11ACC A DE EM E = ,DE EM ⊂DEM DEM ∥11ACC A DEM ABC DM =11A ACC ABC AC =DM AC∥32BM BD AM CD ==23CD BD =D MD AB ∥MD AE ∥1MDEA 11111111A A ED AA C C AA C C E MD A M ED A M ED E MD⎧⎪=∴⎨⎪⊂⎩∥平面平面平面∥,平面 ∴1EA MD 1A E MD∴=11125A E DM CD AB AB CB ===23CD BD =D DG AB ⊥G DG ⊥11A ABB G GN BE ⊥N DN则即为二面角的平面角.当位于时此时故二面角方法2:取的中点由正三棱锥得平面如图建立空间直角坐标系设平面的法向量令得平面法向量,EB NG EB DGEBDGN EB ND NG DG G ⊥⊥⎧⇒⊥⇒⊥⎨=⎩平面 DNG ∠B AE D --cos GNDNG DN ∠===E 1A min DG =min cos DNG ∠==B AE D --BA O OC ⊥11AA B B ()()[]1200100112E t B D t ⎛--∈-⎝,,,,,,,,()121002BE t BD ⎛=+= ⎝,,,,DEB ()n x y z =,,()102210BD n y z BE n x t y ⎧⋅=+=⎪⎨⎪⋅=++=⎩y =)11n t ⎛⎫=+- ⎪ ⎪⎝⎭ 11AA B B ()001m =,,cos cos m n θ==,当时取到17.(1)令又过点直线方程为可化为(2)当在上恒成立,故在上单调递增;当时,令得;令得,故在上单调递增,在上单调递减综上所述:时增区间为当时单调递增区间为,单调递减区间为(3)证明:不等式可化为恒成立由(2)知,当时,,令,则.令则.因为,所以所以在上单调递增.1t=min cos θ=()()()222222x a af x x x x x '++=++=>-++()111x k f a ='=--=+,312⎛⎫- ⎪⎝⎭,-()()3112y a x +=++()112y a x a =++-()()()2222x af x x x ++=+'>- ()00a f x '≥>,()2x ∞∈-+,()f x ()2∞-+,0a <()0f x '>2x >-+()0f x '<22x -<<-()fx ()2∞-++(22--+,0a ≥()2∞-+,0a<()2∞-+(22--,()2340af x a a ae ++-+>2a <-()(()min 112ln 222f x f a a a =-=-+--()()()222min 154343ln 222a a a f x a ae a f x a ae a a a a ae a ++-+≥++-+=-+-++()()215ln 222a g a a a a ae a =-+-++()()12ln 32a ag a a a e ae =+---+'()()12ln 32a ah a a a e ae =+---+()()1222a h a e a a=+-+'2a <-()0h a '>()h a ()2∞--,所以,所以,所以在上单调递减.因为,所以,所以,即当时,.18.(1)(2)列联表如下活跃客户非活跃客户总计男2080100女4060100总计60140200因此有的把握与性别有关.(3)可视作抽出消费900元8人,消费1100元4人Y 180020002200P19.(1)(2)因为,有,即所以有,即由数学归纳法或递推法可知成立(3)根据相似函数不动点也相似,桥函数选取时可令不动点为一解,当,可选取桥函数()()2121ln202h a h e -<-=-++<()0g a '<()g a ()2∞--,()22ln2210g e--=-++>()()20g a g >->()()()22min 43430aaf x a ae a f x a ae ag a ++-+≥++-+=>2a <-()234af x a a ae ++>-100013000155000270002590002110001620X =⨯+⨯+⨯+⨯+⨯+⨯=......8040x y ==,()2220012003200952410010060140χ⨯-==⨯⨯⨯.23841χ>.95%14331633111()141611800200022001933333311E Y =⨯+⨯+⨯≈()()2122n nn fx x -=⋅f g ϕ~1f g ϕϕ-= f g ϕϕ= 1f fg f g g g g ϕϕϕϕϕϕ-=== ()()22fg ϕ~()()n n fg ϕ~()22f x x x =+11(不唯一),易得由(2)可知,即有.当,选取桥函数,.易得由(2)可知,,即有()1x x ϕ=+()()()211121,11211x x g f f x x x ϕϕϕϕ---=-==+=-+-+= ()2nn g x =()()n n fg ϕ~()()()()2n 1111n n n f gg x ϕϕϕ-==-=+- ()2612c x x x =-+()3x x ϕ=-()1123x x g f x ϕϕϕ--=+==, ()2n n g x =()()n n f g ϕ~()()()2133nn n f g x ϕϕ-==-+。
绝密★考试结束前2023学年第二学期金华市卓越联盟5月阶段性模拟考高一年级数学学科试题(答案在最后)命题:考生须知:1.本卷共4页满分150分,考试时间120分钟。
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3.所有答案必须写在答题纸上,写在试卷上无效。
4.考试结束后,只需上交答题纸。
选择题部分一.选择题(本题共8小题,每小题5分,共40分,每小题给出的四个选项中只有一个是符合题目要求的)1.已知复数z 满足(1i)1z -=,则z 的虚部为()A .12B .1C .1i 2D .-i2.数据1,2,3,4,5,6,7,8,9,10的第75百分位数为()A .7B .7.5C .8D .8.53.已知向量(1,2)a =- ,(,4)b m = ,且a b,则2a b -= ()A .(4,0)B .(0,4)C .(-4,8)D .(4,-8)4.已知圆锥的侧面积为12π,它的侧面展开图是圆心角为2π3的扇形,则此圆锥的体积为()A .B .162π3C .D .163π35.如图,A B C '''△为水平放置的ABC △的直观图,其中2A B ''=,A C B C ''''==形ABC △中AC 的长为()A B .3C .D .26.在ABC △中,点D 是线段AC 上靠近A 的一个三等分点,点E 是线段AB 的中点,则DE =()A .1163BA BC--B .5163BA BC-+C .5163BA BC--D .16BA BC-7.在正方体1111ABCD A B C D -中,M ,N ,P ,Q 分别是棱11C D ,1A A ,AB ,11A D 的中点,则()A .PN 与QM 为异面直线B .1A B 与MN 所成的角为45°C .平面PMN 截该正方体所得截面形状为等腰梯形D .点1C ,1D 到平面PMN 的距离相等8.为庆祝五四青年节,某校举行了师生游园活动,其中有一游戏项目是夹弹珠.如图,四个半径都是1cm 的玻璃弹珠放在一个半球面形状的容器中,每个弹珠的顶端恰好与容器的上沿处于同一水平面,则这个容器的容积是()A .32(5cm 3+B .34(5cm 3+C .32(5+D .38(5cm 3+二.选择题(本题共3小题,每小题6分,共18分,每小题给出的四个选项中,有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)9.某市举办了普法知识竞赛,从参赛者中随机抽取1000人,统计成绩后,画出频率分布直方图如图所示,则()A .直方图中x 的值为0.030B .估计该市普法知识竞赛成绩的平均数为85分C .估计该市普法知识竞赛成绩的众数为95分D .估计该市普法知识竞赛成绩的中位数为88分10.已知函数2()sin 22sin f x x x =+,则()A .函数()f x 的图象关于点π(,0)8对称B .函数()f x 在区间π(0,)4上单调递增C .函数()f x 的图象向左平移3π8个单位长度所得到的图象所对应的函数为偶函数D .函数()f x 在区间(π,π)-上恰有3个零点11.如图1,在等腰梯形ABCD 中,AB CD ,12DA AB BC ===,E 为CD 中点,将DAE △沿AE 折起,使D 点到达P 的位置(点P 不在平面ABCE 内),连接PB ,PC (如图2),则在翻折过程中,下列说法正确的是()A .BC 平面PAEB .PB AE⊥C .存在某个位置,使PC ⊥平面PAED .PB 与平面ABCE 所成角的取值范围为π(0,2非选择题部分三.填空题(本题共3小题,每小题5分,共15分)12.函数log (1)8a y x =-+(0a >且1a ≠)的图象恒过定点A ,且点A 在幂函数()f x 的图象上,则()f x ________.13.如图,某山的高度300m BC =,一架无人机在Q 处观测到山顶C 的仰角为15°,地面上A 处的俯角为45°,若60BAC ∠=︒,则此无人机距离地面的高度PQ 为________m .14.已知三棱锥S ABC -的四个顶点在球O 的球面上,SA SB SC ==,ABC △是边长为6的正三角形,E 为SA 的中点,直线CE ,SB 所成角为90°,则球O 的表面积为________.四.解答题(本题共5题,共77分.解答应写出文字说明、证明过程或演算步骤)15.(13分)已知平面向量a ,b ,a = ,||1b = ,且a 与b 的夹角为π3.(1)求|2|a b -;(2)若2a b + 与2()a b λλ+∈R垂直,求λ的值.16.(15分)已知函数()42xxf x a =-⋅.(1)当2a =时,求()f x 在[-1,1]上的最值;(2)设函数()()()g x f x f x =+-,若()g x 存在最小值为-11,求实数a .17.(15分)在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足2b ac =,sin()sin 2sin B A C A -+=(1)求证:sin tan B A =;(2)求cos B 的值.18.(17分)如图,在四棱锥P-ABCD 中,底面ABCD 为平行四边形,120ABC ∠=︒,1AB =,PA =,PD CD ⊥,PB BD ⊥,点N 在棱PC 上,PBD ABCD ⊥平面平面.(1)证明:AB PB ⊥;(2)若PA BDN 平面 ,求三棱锥N-PAD 的体积;(3)若二面角N-BD-C 的平面角为π4,求PNNC.19.(17分)五一假期,杭州吴山广场的鸽子吸引了众多游客.热爱摄影的小华计划在广场一角架设一台可转动镜头的相机,希望可以捕捉到鸽子的展翅瞬间.小华设计了一个草图,为简化模型,假设广场形状为正方形,边长为1,已知相机架设于A 点处,其可捕捉到图像的角度为45°,即45PAQ ∠=︒,其中P ,Q 分别在边BC ,CD 上,记(045)BAP θθ∠=︒︒ .(1)设AC 与PQ 相交于点R ,当30θ=︒时,(ⅰ)求线段DQ 的长;(ⅱ)求线段AR 的长;(2)为节省能源,小华计划在广场上人员较多的时段关闭相机镜头的自动转动功能,为使相机能够捕捉到的面积(即四边形APCQ 的面积,记为S )最大,θ应取何值?S 的最大值为多少?2023学年第二学期金华市卓越联盟5月阶段性模拟考高一年级数学学科参考答案一.选择题(本题共8小题,每小题5分,共40分,每小题给出的四个选项中只有一个是符合题目要求的)题目12345678选项ACDBCADB二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求。