2004中国数学奥林匹克

2004年小学数学奥林匹克预赛试卷2004年3月21日上午8：30-9：301. 计算：13 +34 +25 +57 +78 +920 +1021 +1124 +1935 =____________。

2. 计算：2002÷200220022003 +12004 =____________。

3. 已知右面的除法算式，那么被除数应是____________。

4. 甲车以每小时60千米的速度前进，乙车以每小时100千米的速度追赶，则在乙车追上甲车的前9秒钟，两车相距____________米。

5. B 是自然数，A 是一个数字，如果B444 =0.3A7,那么B=____________。

6. 在等式A ×（B+C ）=110+C 中，A 、B 、C 是互不相等的质数，那么A+B+C=____________。

7. 小明在计算34 ，45 ，79 ，911 这四个分数的平均数时，不小心把其中一个分数的分子、分母颠倒了，这样他算出的平均值与正确的平均值的差最小是____________。

8. 如图，阴影部分的面积（π取3）为____________。

9. 120名少先队员选举大队长，有甲、乙、丙三个候选人，每个少先队员只能选他们之中一个人，不能弃权，若前100票中，甲得了45票，乙得了35票，甲要当选至少还需要____________张选票。

10. 小华每分钟吹一次肥皂泡，每次恰好吹出100个，肥皂泡吹出后，经过一分钟有一半破了，经过两分钟还有二十分之一没有破，经过两分半钟肥皂泡全破了。

小华在第20次吹出100个新的肥皂泡的时候，没有破的肥皂泡有____________个。

11. 甲乙两种商品成本共200元，甲商品按30%的利润定价，乙商品按20%的利润定价，两种商品都按定价的90%出售，结果获得利润27.7元，那么甲种商品的成本是____________元。

12.甲、乙、丙、丁四个人共同生产一批零件，甲生产的占其他三人生产总数的213，乙生产的占其他三人生产总数的14，丙生产的占其他三人生产总数的411，已知丁生产了60个，那么甲、乙、丙三人共生产零件____________个。

首届中国东南地区数学奥林匹克竞赛试题第一天（2004年7月10日 8：00 — 12：00 温州）一、设实数a 、b 、c 满足2223232a b c ++=，求证：39271a b c---++≥ 二、设D 是ABC ∆的边BC 上的一点，点P 在线段AD 上，过点D 作一直线分别与线段AB 、PB 交于点M 、E ，与线段AC 、PC 的延长线交于点F 、N 。

如果DE=DF ， 求证：DM=DN三、（1）是否存在正整数的无穷数列{}n a ，使得对任意的正整数n 都有2122n n n a a a ++≥。

（2）是否存在正无理数的无穷数列{}n a ，使得对任意的正整数n 都有2122n n n a a a ++≥。

四、给定大于2004的正整数n ，将1、2、3、…、2n 分别填入n ×n 棋盘（由n 行n 列方格构成）的方格中，使每个方格恰有一个数。

如果一个方格中填的数大于它所在行至少2004个方格内所填的数，且大于它所在列至少2004个方格内所填的数，则称这个方格为“优格”。

求棋盘中“优格”个数的最大值。

第二天（2004年7月11日 8：00 — 12：00 温州）五、已知不等式63)cos()2sin 2364sin cos a a πθθθθ+-+-<++对于0,2πθ⎡⎤∈⎢⎥⎣⎦恒成立，求a 的取值范围。

六、设点D 为等腰ABC ∆的底边BC 上一点，F 为过A 、D 、C 三点的圆在ABC ∆内的弧上一点，过B 、D 、F 三点的圆与边AB 交于点E 。

求证：CD EF DF AE BD AF ⋅+⋅=⋅七、n 支球队要举行主客场双循环比赛（每两支球队比赛两场，各有一场主场比赛），每支球队在一周（从周日到周六的七天）内可以进行多场客场比赛。

但如果某周内该球队有主场比赛，在这一周内不能安排该球队的客场比赛。

如果4周内能够完成全部比赛，球n 的最大值。

注：A 、B 两队在A 方场地举行的比赛，称为A 的主场比赛，B 的客场比赛。

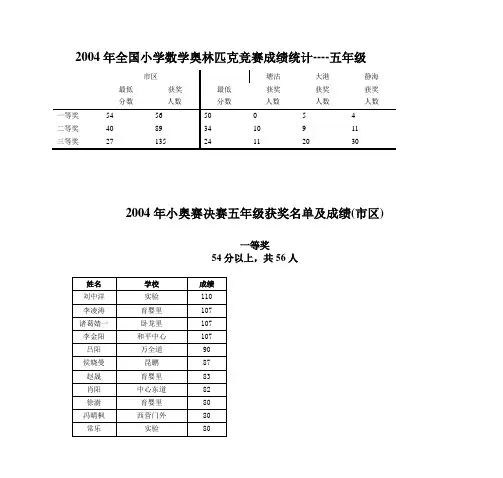
2004年全国小学数学奥林匹克预赛试卷
无
【期刊名称】《小学生课程辅导：数学辅导版》
【年(卷),期】2004(000)007
【总页数】2页(P89-90)
【作者】无
【作者单位】无
【正文语种】中文
【中图分类】G623.5
【相关文献】
1.2004年全国小学数学奥林匹克决赛题解析 [J], 罗克元
2.2005年小学数学奥林匹克预赛题解析 [J], 宫正升
3.2004年全国初中应用物理知识竞赛河南赛区预赛试卷 [J], 姚良炬
4.2004年全国初中应用物理知识竞赛河南赛区预赛试卷 [J], 姚良炬
5.2003年小学数学奥林匹克预赛试题 [J], 肖玲
因版权原因，仅展示原文概要，查看原文内容请购买。

30
蒋东吴
上海道
30
孙思齐
二中心
30
吕宏宁
桂林路
30
李响
浙江路小学
27
赵大地
泰达一小
27
王点
泰达一小
25
实验
70
范斯腾
河东实验
69
李鑫
二十中附小
67
赵天辰
上海道
67
李舜
实验
67
薛伊冰
南大附小
67
纪昂
盘山道
64
余明
鞍山道
64
安禹丞
五马路
64
李鑫悦
中心东道
64
金晓
求真
64
黄凯
六纬路
60
程鹏
昆一
60
孙思颖
河东实验
60
李天玉
河东实验
60
田文君
鞍山道
60
于浩成
中营
60
樊征征
万全道
60
郑君倜
万全道
60
赵旭
万全道
60
新村小学
27
黄家盛
鞍山道
27
蔺吉军
鞍山道
27
李思竹
岳阳道
27
任轶
岳阳道
27
赵瑞
和平中心
27
马一翔
逸阳
27
翟津铭
实验
27
2004年小学数学奥林匹克竞赛五年级大港区获奖名单及成绩
一等奖（50以上，5人）
姓名
学校
成绩
王振宇
大港一小
70
赵宸宇
大港石化一小
60
许昕
大港一小

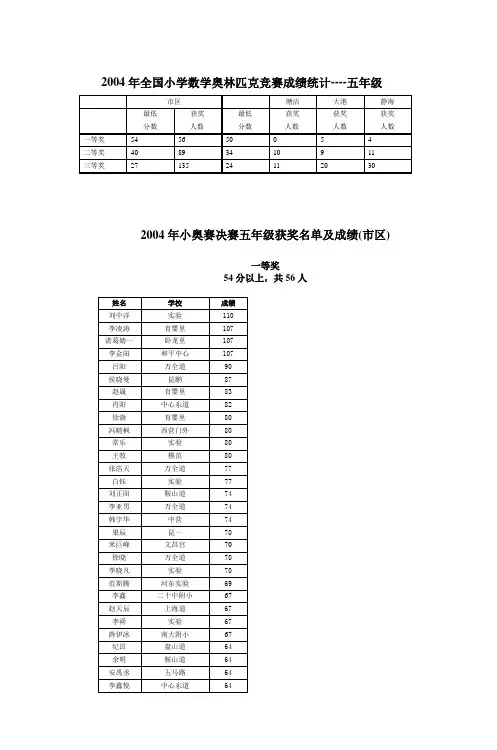
2004年小学数学奥林匹克预赛试卷(吉林地区)1．计算：2．计算：3．在下面的数之间适当填上+、一、×、÷运算符号及括号，使算式的结果等于20042 2 2 2 2 2 2 2 2 24．自然数N是一个两位数，它是一个质数，而且N的个位数字与十位数字都是质数，这样的自然数有__________个5．在算式A×(B+C)=110+C中，A、B、C是三个互不相等的质数，那么B=_______6．在12、22、32、42、……中，1、4、9、16、……叫做"完全平方数"。

从1到500这500个整数中，去掉所有的"完全平方数"，剩下的整数的和是__________。

7．下面各数的和是______________。

8．有一次考试中，甲、乙两人考试结果如下：甲答错了全部试题的，乙答错了7题，甲、乙答错的试题占全部试题的，那么甲、乙都答对的试题至少有___________题。

9．如图，设。

如果三角形DEF的面积是19平方厘米，那么三角形ABC的面积是_________。

10．张先生以标价的95%买下一套房子，经过一段时间后，他又以超出原标价的40%的价格将房子卖出。

这段时间物价的总涨幅为20%，张先生买进和卖出这套房子所得的利润为_____%11．某人到商店买红蓝两种笔，红笔定价5元，蓝笔定价9元，由于购买量较多，商店给予优惠：红笔85折，蓝笔8折，结果此人付的钱比原来节省了18%，已知他买了蓝笔30支，那么红笔买了___________支。

12．一位富豪有350万元遗产，在临终前，他对怀孕的妻子写下这样的一份遗嘱：如果生下来是个男孩，就把遗产的三分之二给儿子，母亲拿三分之一；如果生下来是个女孩，就把遗产的三分之一给女儿，三分之二给母亲。

结果他的妻子生了双胞胎(一男一女)，按遗嘱的要求，母亲可以得到_________万元。

第一届小学"希望杯"全国数学邀请赛四年级第2试一、填空题(每小题4分，共60分)1．计算：3×2÷2－2×6÷3÷3+5－3=________ 。

·版权所有·转载必究·1
2004年第45届国际数学奥林匹克试题
1．△ABC 为锐角三角形，AB ≠ AC；以BC为直径的圆分别交AB和AC于M 和N ．记BC中点为O．∠BAC和∠MON的角平分线交于R．求证△BMR的外接圆和△CNR的外接圆有一个公共点在BC边上．
2．求所有的实系数多项式f，使得对所有满足ab + bc + ca = 0的实数a，b，c 有
f(a–b) + f(b–c) + f(c–a) = 2f(a + b + c)．
3．定义一个由6个单位正方形构成的“钩”（图传不上：3 X 3 的去掉中心块和一边上连
续的两块，包括由此图经旋转、反射得到的图形）．定出所有的能被钩覆盖的m×n的矩形．
4．设n ≥3．t_1，t_2，…，t_n > 0 满足
n^2 + 1 > (t_1 + t_2 + …+ t_n)(1/t_1 + 1/t_2 + …+ 1/t_n)
证明t_1，t_2，…，t_n中随便取3个数都能构成一个三角形．
5．凸四边形ABCD的对角线BD 不平分∠ABC和∠CDA．ABCD内一点P满足∠PBC = ∠DBA和∠PDC = ∠BDA．求证：ABCD是圆的内接四边形当且仅当AP = CP．
6．称一个正整数为“交替的”，如果它的十进表示的任两个连续数位的奇偶性不同．求所有的正整数n，n的某个倍数是交替的．。

图1
之和为 n 的牌组的个数 ,则 an 等于函数
f ( x) = 1 + x
n
得 ∠BOE = 45° ,且与
0 2
2
半圆相交于点 E. 过点 E 作半圆的切线 ,分别交 AB 的延长线和 AT 于点 D 和点 F. 则等腰直角 △ADF 覆 盖 △ABC ,且
AD = AO + OD =
1+ x
≥- 17 + 2 8 + 2
32 = - 17 + 12 2.
①
上式中的等号可以成立 . 事实上 ,由上述推导过程知 ,等号成立当且仅当 平均不等式中的等号成立 ,而这等价于
2
2 2 y =2x , y = 2x , 即 2 即 2 z y z =2y , z =2x , 4 =8 ,
个单位正方形所得到的图形称为 “十字形” . 在一个
5. 设 u 、 v、 w 为正实数 , 满足条件 u
v wu + w vw +
其中用到了轮换 (1 ,3 ,6 ,10 ,15) . (5) 19 是 “好 数” , 因 为 如 下 的 排 列 中 , k + ak
( k = 1 ,2 , …,19) 都是完全平方数 :
k : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ak : 8 7 6 5 4 3 2 1 16 15 14 13 12 11 10 9 19 18 17
2
+
v +w
2
2
1
+
w + u
2
2
2
+ 2 uv + 2 vw + 2 wu

张尧
成都七中
苏勇
华东师范大学附属第二中学
章尧
人大附中
王国桢
兰州一中
杜松沛
河南师大附中
张娜
太原五中
李舟
武钢三中
张凌人
上海中学
刘扬阳
长沙市一中
甄一村
成都七中
王晟
杭州外国语学校
陈世腾
海南中学
赵琳博
北大附中
郑志诚
莆田一中
左力
陕西省西安中学
支持
镇海中学
胡 劲
华师一附中
祖鹏鹤
河南师大附中
李杨佳
长沙市一中
傅列
华东师大二附中
王枫
安师大附中
毛智超
西北工大附中
杨健慧
河师大附中
荣 膺
福州一中
曹楠
东北师大附中
万时凯
景德镇市一中
陈子娟
长沙市一中
魏崟泷
蚌埠二中
李思其
金陵中学
赵 沨
石家庄二中
林 嵩
深圳中学
张辉
利津一中
吴昊
北京二十二中
戴莽原
新疆实验中学
雷慧天
武钢三中
赵煦
北京二中
龙忠慧
湖南师大附中
周桐
山西大学附属中学
王一壘
绍兴一中
孙毅然
北京四中
陈宗文
上海中学
邢硕博
清华附中
茅越
江苏省启东中学
俞能昆
马鞍山二中
田 伟
石家庄二中
三等奖(31名)
杨磊
长沙市雅礼中学
藏经涛
哈师大附中
李邱华
江苏省启东中学
曹志敏
江苏省华罗庚中学

中华数学竞赛网

2004 年第 4 届中国西部数学奥林匹克竞赛
1圣.求所才有的学整数习n网，使w得wnw4 +.61n30+01lxn2u+e3第nx+一i3.1天是c完o全m平方学数.习网 圣才 2 .四边形 ABCD 为一凸四边形， I1 、 I2 分别为 ΔABC 、 ΔDBC 的内心，过点 I1 、 I2 的直线分别交
3 . 求 所 有 的 实 数 k ， 使 得 不 等 式 a3 + b3 + c3 + d 3 +1 ≥ k (a + b + c + d ) 对 任 意 a 、 b 、 c 、
d ∈[−1，+ ∞] 都成立.
圣才学习网 学习网 4 .设n∈ N+ ，用d (n) 表示n的所有正约数的个数，φ (n) 表示1，2 ，"，n中与n 互质的数的个
圣
中华数学竞赛网

中华数学竞赛网

3 .已知锐角 ΔABC 的三边长不全相等，周长为 l ， P 是其内部一动点，点 P 在边 B D 、 E 、 F .求证： 2( AF + BD + CE ) = l 的充分必要条件是：点 P 在 ΔABC 的内心与外
才
圣
中华数学竞赛网

AB 、 DC 于点 E 、 F ，分别延长 AB 、 DC ，它们相交于点 P ，且 PE = PF .求证： A 、 B 、C 、 D
圣才学习网 学习网 四点共圆. 才
圣
中华数学竞赛网

中华数学竞赛网

圣才 数.求所有的非负整数 c ，使得存在正整数 n ，满足 d (n) + φ (n) = n + c ，且对这样的每一个 c ，求出所有

2004 年第 2 期
23
竞赛之窗
2004 中国数学奥林匹克
第 一 天 ( 2004 - 01 - 08)
一、 凸四边形 EFGH 的顶点 E 、 F、 G、 H 分别在 凸四 边 形 ABCD 的 边 AB 、 BC 、 CD 、 DA 上 , 且 满 足
A E B F CG DH ・ ・ ・ = 1. 而点 A 、 B、 C、 D 分别在凸四边 EB FC GD HA
∑a
n i =1
2
n
2
i
≤
.
i =1
∑a
1
i
n
i =1
∑( a
ai
i
2
2 2 + x )
3
3
≤∑
( a2i + x2 ) 2
( 2 ) 如图 2 ,
F1 C E1 A = = λ. CG1 AH1
若 EF 与 AC 不 平 行 . 设 FE 的 延长线与 CA 的 延长线相交于点
T. 由梅涅劳斯定
边形的 5 个顶点 ,则此凸五边形内部至少含有 M 中 的一个点 . 求 n 的最小值 .
( 冷岗松 供题)
第 二 天 ( 2004 - 01 - 09)
(1) 存在性 . 由 x i + 1 = 2 x i + 2 x i - 2 a - x i - 1 , 四、
i = 1 ,2 , … 及 x0 = 0 知每一 x i 是 x1 的 3
n i- 1
因此 ,| x i | ≤ | a| , i = 0 ,1 ,2 , …, n + 1.
n
五、 当 x2 ≥a1 ( a1 - 1) 时 ,由
假设存在一个整点凸五边形 ,其内部不含整点 . 因整点多边形的面积均可表示为

正华
30
郑思远
红星
30
闫玮
红星
30
张绍琛
求真
30
张正
求真
30
郝苓淇
求真
30
夏岩
红桥实验
30
张月
佳园里
30
赵晓璐
咸阳北路
30
温馨
六一
30
陈睿
跃升里
30
田楚杰
鞍山道
30
芦钰
鞍山道
30
于梦薇
鞍山道
30
胡钧瀚
鞍山道
30
温元正
鞍山道
30
周明华
鞍山道
30
邢琨
昆鹏
30
孙宇
昆鹏
30
周翰驰
昆鹏
30
刘晓瑶
三水道
30
陈天用
大邱庄万全小学
30
郑秋臣
大邱庄津海小学
30
田洁
大邱庄津海小学
30
王竞颜
大邱庄尧舜实验
30
袁红超
陈官屯镇小集小学
25
张兴鹏
刘上道
25
孙中涵
实验小学
25
史凤强
蔡公庄惠丰小学
25
刘靓
静海镇孙家场
25
曲畅
大邱庄尧舜实验
25
高翠
团泊镇
24
曹月
静海镇三小
24
汤玉笑
静海镇四小
24
尚义嘉
大邱庄尧舜实验
24
五年级塘沽考点成绩汇总
团泊镇
34
三等奖
24分以上30人
张启文
沿庄镇
30
田祎伟

首届中国东南地区数学奥林匹克第一天（2004年7月10日 8：00 — 12：00 温州）一、 设实数a 、b 、c 满足2223232a b c ++=，求证：39271a b c ---++≥二、 设D 是ABC ∆的边BC 上的一点，点P 在线段AD 上，过点D 作一直线分别与线段AB 、PB 交于点M 、E ，与线段AC 、PC 的延长线交于点F 、N 。

如果DE=DF ，求证：DM=DN 三、 （1）是否存在正整数的无穷数列{}n a ，使得对任意的正整数n 都有2122n n n a a a ++≥。

（2）是否存在正无理数的无穷数列{}n a ，使得对任意的正整数n 都有2122n n n a a a ++≥。

四、 给定大于2004的正整数n ，将1、2、3、…、2n 分别填入n ×n 棋盘（由n 行n 列方格构成）的方格中，使每个方格恰有一个数。

如果一个方格中填的数大于它所在行至少2004个方格内所填的数，且大于它所在列至少2004个方格内所填的数，则称这个方格为“优格”。

求棋盘中“优格”个数的最大值。

第二天（2004年7月11日 8：00 — 12：00 温州）五、63)cos()2sin 2364sin cos a a πθθθθ+-+-<++对于0,2πθ⎡⎤∈⎢⎥⎣⎦恒成立，求a 的取值范围。

六、 设点D 为等腰ABC ∆的底边BC 上一点，F 为过A 、D 、C 三点的圆在ABC∆内的弧上一点，过B 、D 、F 三点的圆与边AB 交于点E 。

求证：CD EF DF AE BD AF ⋅+⋅=⋅ 七、 n 支球队要举行主客场双循环比赛（每两支球队比赛两场，各有一场主场比赛），每支球队在一周（从周日到周六的七天）内可以进行多场客场比赛。

但如果某周内该球队有主场比赛，在这一周内不能安排该球队的客场比赛。

如果4周内能够完成全部比赛，求n 的最大值。

注：A 、B 两队在A 方场地举行的比赛，称为A 的主场比赛，B 的客场比赛。

目录2005年北方数学奥林匹克 (2)2006年北方数学奥林匹克 (4)2007年北方数学奥林匹克 (6)2008年北方数学奥林匹克 (7)2009年北方数学奥林匹克 (10)2010年北方数学奥林匹克 (13)2011年北方数学奥林匹克 (15)2012年北方数学奥林匹克 (17)2005年北方数学奥林匹克1.AB是⊙O的一条弦，它的中点为M，过点M作一条非直径的弦CD，过点C和D作⊙O的两条切线，分别与直线AB相交于P、Q两点.求证：P A=QB.（裘宗沪供题）2.定义在R上的函数f(x)满足：（1）f(0)=0;（2）对任意xx∈(−∞,−1)∪(1,+∞)，都有f�1x�+f�1y�=f(x+y1+xy)；（3）当x∈(−1,0)时，都有f(x)>0.求证：f�119�+f�129�+⋯+ f�1n2+7n+11�>f(12)，其中n∈N+. （刘贵谭祖春供题）3.在公差为d(d>0)的整数等差数列a1,a2,⋯,a3n(n≥2)中，任取n+2个数.证明：其中必存在两个数a i、a j(i≠j)，满足不等式1<�a i−a j�nn<2. （刘康宁安振平供题）4.已知n位数的各位数字只能取集合{1,2,3,4,5}中的元素，设含有数字5且在5的前面不含3的n位数的个数为f(n).求f(n).（蒋西明供题）5.如果三个正实数x、y、z满足x2+xx+x2=254，x2+xy+y2=36，y2+yx+x2=1694.求xx+xy+yx的值. （张同君供题）6.设0≤α、β、γ≤π2，ccc2α+ccc2β+ccc2γ=1.求证：2≤（1+ccc2α）2cin4α+（1+ccc2β）2cin4β+（1+ccc2γ）2cin4γ≤(1+ccc2α)(1+ccc2β)(1+ccc2γ)（谭祖春供题）2006年北方数学奥林匹克1. 如图1，AB 为⊙O 的直径，非直径的弦CC ⊥AA ，E 是OC 的中点，连结AE 并延长交⊙O 于点P ，连结DP 交BC 于点F .求证：F 是BC 的中点.图12. 设p 是大于2的质数，数列{a n }满足na n+1=(n +1)a n −(p 2)4.求证：当a 1=5时，16|a 81. 3. 已知AD 是△ABC 的边BC 上的高，且AC +AC =AA +AC .求∠A 的取值范围.4. 设函数f (x )=x 2+ax +b (a 、b ∈R ).若存在实数m ，使得|f (m )|≤14，且|f (m +1)|≤14，求Δ=a 2−4b 的最大值和最小值.5. 已知正数a 、b 、c 满足a +b +c =3.求证：a 2+92a +(b+c )+b 2+92b +(c+a )+c 2+92c 2+(a+b )2≤5. 6. 组委会说明试题有误.7. 是否可以将正整数1,2,⋯,64分别填入8×8的64个方格 ，使得凡具备“”形的四个方格（方向课以任意转置）内的数之和都能被5整除？8. 已知数列{a n }满足a k+1=a k +12006a k 2，a 0=12，k ∈N .求证：A1−12008<a2006<1.1.在锐角△ABC中，BD、CE分别是AC、AB边上的高.以AB为直径作圆交CE于M，在BD上取点N是AN=AM.证明：AN⊥CN.2.设△ABC三边长分别为a、b、c，且a+b+c=3.求f(a,b,c)=a2+ b2+c2+43abc的最小值.3.在数列{a n}中，a n+1=a n2a n+1(n∈N).求证：当0≤n≤1004时，有[a n]=2007−n（其中[x]表示不超过x的最大整数）.4.平面上每个点被染为n中颜色之一，同时满足：（1）每种颜色的点都有无穷多个，且不全在同一条直线上；（2）至少有一条直线上所有的点恰为两种颜色.求n的最小值，使得存在互不同色的4个点共圆.5.设α,β∈(0,π2)，求A=(1−�tanα2tanβ2)2cctα+cctβ的最大值.6.已知f(x)=ll(x+1)−12lcl3x.（1）解方程f(x)=0；（2）求集合M={n|f(n2−214n−1998)≥0,n∈Z}.7.设n是正整数，a=�√n�（其中[x]表示不超过x的最大整数），求同时满足下列条件的n的最大值：（1）n不是完全平方数；（2）a3|n28.设△ABC的内切圆半径为1，三边长AC=a，CA=b，AA=c.若a、b、c都是整数，求证：△AAC为直角三角形.1. 如图1，⊙O 是梯形ABCD 的内切圆，切点分别为E 、F 、G 、H ，AB ∥CD .作BP ∥AD 交DC 的延长线于点P ，AO 的延长线交CP 于点Q .若AD =AD ，求证：∠CAQ =∠PAQ .图1 （张利民 供题）2. 已知∠A 、∠A 、∠C 是△AAC 的三个内角.证明：tan A 2+tan B 2+tan C 2√3≥�tan 2A 2+tan 2A 2+tan 2C 26 （张 雷 供题）3. 给定三角形数表如图2：1 2 3 4 ⋯ 97 98 99 100 3 5 7 ⋯ 195 197 199 8 12 ⋯ 392 396 20 ⋯ 788 ⋱ ⋯ ⋰ ⋱ ⋰ M图2其中，第一行各数依次是1,2,⋯,100，从第二行起，每个数分别等于它上面一行左、右两数的和.求M 的值.（焦和平 供题）4.证明：（1）存在无穷个正整数n，使n2+1的最大质因子小于n；（2）存在无穷个正整数n，使n2+1|n!. （张雷供题）5.如图3，已知□ABCD，过A、B、C三点的⊙O1分别交AD、BD 于点E、F，过C、D、F三点的⊙O2交AD于点G，设⊙O1、⊙O2R222.的半径分别为R1、R2.求证：AG图3（吕建恒刘康宁供题）6.设a、b、c为直角三角形的三边长，其中，c为斜边长.求使得a3+b3+c3abc≥k成立的k的最大值.（李铁汉供题）7.设n是正整数，整数a是方程x4+3ax2+2ax−2×3n=0的根.求所有满足条件的数对(n,a).（李铁汉供题）8.给定由n(n+1)2个点组成的正三角形点阵（如图4），记以点阵中三个点为顶点的所有正三角形的个数为f(n)，求f(n)的表达式.图4（张利民供题）2009年北方数学奥林匹克1. 设数列{x n }满足x 1=1，x n =�x n−12+x n−1+x n−1(n ≥2).求数列{x n }的通项公式. （张 雷 供题）2. 如图1，在锐角△ABC 中，已知AA >AC ，cccA +cccC =1，E 、F 分别是AB 、AC 延长线上的点，且满足∠AAF =∠ACD =90°.（1） 求证：AD +CF =DF ；（2） 设∠DAC 的平分线与EF 交于点P ，求证：CP 平分∠ACF .图1（刘康宁 吕建恒 徐庆金 供题）3. 已知有26个互不相等的正整数，其中任意六个数中都至少有两个数，一个数整除另一个数.证明：一定存在六个数，其中一个数能被另外五个数整除.（张同君 供题）4. 船长和三位水手共得到2009枚面值相同的金币.四人商定按照如下规则对金币进行分配：水手1、水手2、水手3每人写下一个正整E数分别为b 1、b 2、b 3，满足b 1≥b 2≥b 3，且b 1+b 2+b 3=2009；船长在不知道水手写的数的情况下，将2009枚金币分成3堆，各堆数量分别为a 1、a 2、a 3，且a 1≥a 2≥a 3.对于水手k (k =1,2,3)，当b k <a k 时，可以从第k 堆拿走b k 枚金币，否则不能拿.最后所有余下的金币归船长所有.若无论三位水手怎样写数，船长总可以确保自己拿到n 枚金币.试确定n 的最大值，并证明你的结论. （张 利 供题）5. 如图2，在给定的扇形AOB 中，圆心角为锐角.在弧AB 上取异于A 、B 的一点C ，在线段OC 上取一点P ，连结AP ，过点B 作直线BQ ∥AP 交射线OC 于点Q .证明：封闭图形OAQPBO 的面积与点C 、P 的选取无关.图2 （徐庆金 供题）6. 设x 、y 、z >0，且x 2+x 2+y 2=3，求证：∑x 2009−2008(x−1)y+z ≥12(x +x +y ). （杨海滨 贾应红 供题）7. 记[m ]为不超过实数m 的最大整数.设x 、y 均为正实数，且对所有的正整数n ，都有[x [nx ]]=n −1成立.证明xy =1，且y 是大于1的无O理数.（刘康宁供题）8.求能被209整除且各位数字之和等于209的最小正整数.（张雷供题）2010年北方数学奥林匹克1.已知数列{a n}满足a1=2，a n=22n a n−1+2n2n(n=2,3,⋯).求通项a n(n=1,2,⋯). （吴树勋供题）2.已知PA、PB是⊙O的切线，切点分别是A、B，PCD是⊙O的一条割线，过点C作PA的平行线，分别交弦AB、AD于点E、F.求证：CD=DF.（李新焕供题）3.求所有的正整数(x,x,y)，使得1+2x×3y=5z成立.（张雷供题）4.在7×7的方格表的64个网格线交点（称为“结点”）处放棋子，每点至多放1枚，一共放了k枚棋子.若无论怎样放，总存在4枚棋子，它们所在的结点构成一个矩形（矩形的边平行于棋盘网格线）的四个顶点.试求k的最小值.（张利民供题）5.设正实数a、b、c满足(a+2b)(b+2c)=9.求证：�a2+b22+2�b3+c323≥3.（张雷供题）6.已知⊙O是△ABC的内切圆，D、E、N是切点，连结NO并延长交DE于点K，连结AK并延长交BC于点M.求证：M是BD的中点.（康春波供题）7.求[x,x,y]=(x,x)+(x,y)+(y,x)满足x≤x≤y,(x,x,y)=1的所以正整数解，其中，[m,n]和(m,n)分别表示正整数m、n的最小公倍数和最大公约数.（王全供题）8.设x、x、y∈[0,1]，且|x−x|≤12，|x−y|≤12，|y−x|≤12.试求W=x+x+y−xx−xy−yx的最小值和最大值.（刘康宁安振平供题）2011年北方数学奥林匹克1.已知数列{a n}的通项a n=(√3+√2)2n(n∈N+)，设b n=a n+1a n. （1）试求b n+2、b n+1、b n之间的递推关系；（2）求a2011整数部分的个位数字.（刘洪柱供题）2.如图1，△ABC的内切圆分别切BC、CA、AB、于点D、E、F，P 为内切圆内一点，线段PA、PB、PC分别于内切圆交于点X、Y、Z.证明：XD、YE、ZF三线共点.图1（徐庆金供题）3.求不定方程1+2x×7y=y2的全部正整数解(x,x,y). （翁世有供题）4.设n个集合A1,A2,⋯,A n是集合A={1,2,⋯,29}的一个分划，且A i(i=1,2,⋯,n)中任意个元素之和都不等于30.求n的最小可能值. 【注】若集合A的非空子集A1,A2,⋯,A n(n∈N+,n≥2)满足A i∩A j=∅(i≠j)，A1∪A2∪⋯∪A n=A，则称A1,A2,⋯,A n是集合A的一个分划.（张雷供题）5. 若正整数a 、b 、c 满足a 2+b 2=c 2，则称(a ,b ,c )为勾股数组.求含有30的所有勾股数组. （杨春宏 供题）6. 如图2，过点P 引的切线P A 和割线PBC ，AC ⊥PP ，垂足为D .证明：AC 是△ABD 外接圆的切线.图2（吕建恒 供题） 7. 在△ABC 中，证明：11+ccs 2A+ccs 2A +11+ccs 2A+ccs 2C +11+ccs 2C+ccs 2A ≤2.（安振平 供题） 8. 已知n 是正整数，实数x 满足�1−|2−⋯|(n −1)−|n −x ||⋯|�=x .求x 的值. （张利民供题）P2012年北方数学奥林匹克1.如图1，在△ABC中，∠C=90°，I是内心.直线BI交AC于D，作DE平行于AI交BC于E，直线EI交AB于F.证明：DF垂直于AI.图12.正整数x1,x2,⋯,x n(n∈ℕ+)，满足x12+x22+⋯+x n2=111，求S=x1+x2+⋯+x n n的最大可能值.3.设S={x|x=a2+ab+b2,a,b∈ℤ}.求证：(1)若m∈S,3|m，则3m∈S；(2)若m,n∈S，则m⋅n∈S.4.平面上有n(n≥4)条直线，对于直线a，b，在余下的n-2条直线中，如果至少存在两条直线与直线a，b都相交，则称直线a，b是相合的直线对，否则称其是相离的直线对.若n条直线中相合直线对的个数比相离直线对的个数多2012.求n的最小可能值（直线对中的两条直线不计顺序）.5.已知数列{a n}:a0=0,a n=1a n−1−2,n∈ℕ+，在数列{a n}中任意取定一项a k，构造数列{b n}:b0=a k,b n=2b n−1+1b n−1,n∈ℕ+.试判断数列{b n}是有限数列还是无穷数列？并给出证明.6.设n是正整数，证明�1+13��1+13�⋯�1+13�<2.7.如图2在五边形ABCDE中，BC=DE，CD平行于BE，AB>AE，AA AA，求证：AC平分线段BE.若∠AAC=∠CAD，且图28.设p是奇素数，如果存在正整数a使p!|a p+1，证明：(1)�a+1,a p+1a+1�=p.(2)a p+1a+1没有小于ｐ的素因子.p!|a+1.。

过P2 作 平 行 于BC 的 直 线
EP2 P3 . ABC .证毕.
DP2 P3 ,也就不大于S
5.能否把1,1,2,2,. . . ,1986,1986这些数排成一行, 使得两个1之间夹着1个数,两个2之间夹着2个数,. . . , 两 个1986之间夹着1986个数.请证明你的结论. 解:不能.假设可以做出这样的排列,将已排好的数按顺序编号为1,2,. . . ,3972. 当n为奇数时,两个n的编号奇偶性相同;当n为偶数时,两个n的编号奇偶性不同. 而1到1986之间有993个 偶数,所以一共有2k + 993个编号为偶数的数.(k ∈ N∗ ) 但是1到3972之间有1986个偶数,k = 496.5.矛 盾.所以不能按要求排成这样一行. √ 6.用任意的方式,给平面上的每一点染上黑色或白色. 求证:一定存在一个边长为1或 3的正三角形,它的
3
第二届中国数学奥林匹克(1987年)
北京 北京大学
1.设n为自然数,求证方程z n+1 − z n − 1 = 0有模为1的复根的充分必要条件是 n + 2可被6整除. 证明:当6|n + 2时,令z = ei 3 = ∴ z n+1 − z n − 1 = e ∴z
n+1 n −i π 3
π
1 2
2 2 a1 x2 1 + a2 x2 + · · · + an xn ; 2 2 a1 x2 1 + a2 x2 + · · · + an xn
0(i = 1, 2, . . . , n),则显然有a1 x1 + a2 x2 + · · · + an xn 0, ai −a1 > 0(i = 2, 3, . . . , n). ∴

任意１点．设ＡＥＤ＝！ｘ，＇ＡＣＦ．二，，＇ＤＥＦ二：．证明：
（１）Ｓ｝ ，（１一、）ｎｓａ－ ，
Ｓ，｝ 二ｘ（ｔ一ｒ）（１一：）Ｓｎｓｃ
（２） 了 Ｓｅ ｅ＋了Ｓｖｚｒ｝了Ｓｐｎｅｃ． ２某 班 有 ４７个学生，所用教室有６排，每排有 ８ 个座位，用（ｉ，１）表示位于第 ‘排第Ｊ列的座位．新学
２３
２００４中国数学奥林匹克 压
第 一 天（２００４－０ －０ｓ）
一 、凸 四 边形 ＥＦＧＨ的顶点Ｅ，Ｆ ，Ｇ ，Ｈ 分别在 凸四边形 ＡＢｃｎ的边 ＡＢ，Ｂ Ｃ，Ｃ Ｄ，Ｄ Ａ上，且满足
ＥＡＢＥ· ＦＢＣＦ · ＧＣＤＧ · １ＤｆＡＨ －１ ．而 点，、。、。、。分别在凸四边
（李 胜 宏 供题 ） 六 、证 明 ：除了有限个正整数外，其他的正整数
设 、二 ｎ ，．＝１，２，＂…由于当。３２时，
三、 先 证 ｎ３１１．
｛ｆ ｎ＋ ２· Ｙ．，」二ｆ（ｎ＋ ２） ２（ｎ－ １）１
二！ｎ ＋卜号」二。２二，。，
设顶 点 在 Ｍ中的一个凸七边形为Ａபைடு நூலகம்Ａ２ － Ａ 连结Ａ，Ａ， ．由条件（２）知，在凸五边形Ａ，Ａ， Ａ， Ａ， Ａ， 中至少有Ｍ中一个点，记为Ｐ，．连结 Ｐ，Ａ，，Ｐ．Ａ，，
的交点为Ｅ，Ｆ 在ＤＡ的延长线上．连结 ＢＦ＇，Ｇ 在 ＢＡ 的延长线上，使得 ＤＧ／／Ｂ Ｆ，Ｈ 在 ＧＦ的延长线上， ＣＨ土ＧＦ．证明：Ｂ，Ｅ，Ｆ，Ｈ四点共圆．
４．（ １） 证 明：存在和为 １的五个非负实数 ａ，ｂ ， 。、么。，使得将它们任意放置在 一个圆周上，总有两
个相邻数的乘积不刁、于９１＇
ｎ均可表示为２０１”个正整数之和：，二ａ 十ａ：十
…＋ａ：、，且满足 １＿。＜ａ２＜…＜处，，ａ；｝久 ，，

第3届女子数学奥林匹克试题第3届女子数学奥林匹克于2004年8月11日至15日在江西省南昌市举行，共有45个代表队的179名选手参加了此次竞赛，他们分别来自北京，上海等数十个城市以及美国，俄罗斯，菲律宾，香港，澳门等国家和地区。

竞赛共安排两天考试，每天四个小时，各考四道题。

通过竞赛，有18名选手获得金牌，39名选手获得银牌，58名选手获得铜牌。

试 题1．如果存在1,2,……n 的一个排列a （1）,a （2）……a （n ），使得k+a k （k=1,2,……n ）都是完全平方数，就称n 为好数。

试问：在集合{11，13，15，17，19}中哪些为好数，那些不是，说明理由。

2．设为a,b,c 正实数，求cb a cc b a b c b a c a 382423++-++++++最小值。

3．已知钝角三角形ABC 的外接圆半径为1，证明：存在一个斜边为12+的等腰直角三角形覆盖三角形ABC4．一副3色牌，共有32张，其中红黄蓝各10张，编号为1，2，，，，10；另有大小王各1张。

从中任取几张，然后按如下规则算分：每张编号为K 的牌记2k 分。

大小王编号为0。

若分值之和为2004，就称这些牌为一个好牌组。

求好牌组的组数。

5．设为u ，v ，w 正实数，满足条件1≥++uv w wu v vw u ，试求u +v +w 的最小值．6．给定锐角三角形ABC ，O 为外心，直线AO 交边BC 于D ，动点E ，F 在AB ，AC 上，使得A ，E ，D ，F 四点共圆。

求证：线段EF 在BC 上的投影长度为定值。

7．设n∈N,且正整数p,q满足（p,q）=1．问有多少个不同的整数可表为ip+jq （其中i,j∈N, i+j≤n）?8．记"十字型"为一个3×3的方格去掉4个角上的1×1方格所形成的图形．问10×11的方格中至多能放入多少个互不重叠的十字形．解：答案：15个首先证明最多可放15个“十字形”。

育才教育—初中数学竞赛试题一、选择题（共5小题，每小题6分，满分30分. 以下每道小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填得零分）1. 已知实数b a ≠，且满足)1(33)1(2+-=+a a ，2)1(3)1(3+-=+b b .则ba a ab b+的值为（ ）. （A ）23 （B ）23- （C ）2- （D ）13-答：选（B ）∵ a 、b 是关于x 的方程()03)1(312=-+++x x的两个根，整理此方程，得0152=++x x ，∵ 0425>-=∆， ∴ 5-=+b a ，1=ab . 故a 、b 均为负数. 因此()232222-=-+-=+-=--=+abab b a ab abb a ab b a ab a b b a a a b b .2. 若直角三角形的两条直角边长为a 、b ，斜边长为c ，斜边上的高为h ，则有 （ ）.（A ）2h ab = （B ）h b a 111=+ （C ）222111hb a =+ （D ）2222h b a =+ 答：选（C ）∵ 0>>h a ，0>>h b ，∴ 2h ab >，222222h h h b a =+>+；因此，结论（A ）、（D ）显然不正确.设斜边为c ，则有c b a >+，ab ch h b a 2121)(21=>+，即有h b a 111>+， 因此，结论（B ）也不正确. 由ab h b a 212122=+化简整理后，得222111hb a =+，因此结论（C ）是正确的.3．一条抛物线c bx ax y ++=2的顶点为（4，11-），且与x 轴的两个交点的横坐标为一正一负，则a 、b 、c 中为正数的（ ）.（A ）只有a （B ）只有b （C ）只有c （D ）只有a 和b 答：选（A ）由顶点为（4，11-），抛物线交x 轴于两点，知a >0. 设抛物线与x 轴的两个交点的横坐标为1x ，2x ，即为方程02=++c bx ax的两个根.由题设021<x x ，知0<ac，所以0<c . 根据对称轴x =4，即有02>-ab，知b <0.故知结论（A ）是正确的.4．如图所示，在△ABC 中，DE ∥AB ∥FG ，且FG 到DE 、AB 的距离之比为1:2. 若△ABC 的面积为32，△CDE 的面积为2，则△CFG的面积S等于（ ）.)（A ）6 （B ）8 （C ）10 （D ）12 答：选（B ）由DE ∥AB ∥FG 知，△CDE ∽△CAB ，△CDE ∽△CFG ，所以41322===∆∆CAB CDE S S CACD， 又由题设知21=FA FD ，所以 31=AD FD ， AC AC AD FD 41433131=⨯==，故DC FD =，于是（第4题图）41212=⎪⎭⎫ ⎝⎛=∆∆CFG CDE S S ，8=∆CFG S . 因此，结论（B ）是正确的.5．如果x 和y 是非零实数，使得3=+y x 和03=+x y x ，那么x +y 等于（ ）.（A ）3 （B ）13 （C ）2131- （D ）134-答：选（D ）将x y -=3代入03=+x y x ，得0323=+-x x x .（1）当x >0时，0323=+-x x x ，方程032=+-x x 无实根； （2）当x <0时，0323=--x x x ，得方程032=--x x 解得2131±=x ，正根舍去，从而2131-=x . 于是2137213133-=-+=-=x y . 故134-=+y x .因此，结论（D ）是在正确的.二、填空题（共5小题，每小题6分，满分30分） 6． 如图所示，在△ABC 中，AB =AC ，AD =AE ，︒=∠60BAD ，则=∠EDC （度）.答：30°解：设α2=∠CAD ，由AB =AC 知αα-︒=-︒-︒=∠60)260180(21B ，α+︒=︒-∠-︒=∠6060180B ADB ， 由AD =AE 知，α-︒=∠90ADE ， 所以︒=∠-∠-︒=∠30180ADB ADE EDC .（第6题图）7．据有关资料统计，两个城市之间每天的电话通话次数T 与这两个城市的人口数m 、n （单位：万人）以及两城市间的距离d （单位：km ）有2dkmnT =的关系(k 为常数) . 现测得A 、B 、C 三个城市的人口及它们之间的距离如图所示，且已知A 、B 两个城市间每天的电话通话次数为t ，那么B 、C 两个城市间每天的电话通话次数为 次（用t 表示）.答：2t解：据题意，有k t 21608050⨯=， ∴t k 532=. 因此，B 、C 两个城市间每天的电话通话次数为2645532320100802tt k T BC =⨯=⨯⨯=. 8．已知实数a 、b 、x 、y 满足2=+=+y x b a ，5=+by ax ，则=+++)()(2222y x ab xy b a .答：5-解：由2=+=+y x b a ，得4))((=+++=++bx ay by ax y x b a ， ∵ 5=+by ax ， ∴ 1-=+bx ay .因而，5))(()()(2222-=++=+++by ax bx ay y x ab xy b a . 9． 如图所示，在梯形ABCD 中，AD ∥BC (BC >AD )，︒=∠90D ，BC =CD =12, ︒=∠45ABE ，若AE =10，则CE 的长为 .答：4或6解：延长DA 至M ，使BM ⊥BE . 过B 作BG ⊥AM ，G 为垂足.易知四边形BCDG 为正方形， 所以BC =BG . 又GBM CBE ∠=∠，∴ Rt △BEC ≌Rt △BMG .（第9题图）（第7题图）∴ BM =BE ，︒=∠=∠45ABM ABE ， ∴△ABE ≌△ABM ，AM =AE =10.设CE =x ，则AG =x -10，AD =x x -=--2)10(12，DE =x -12. 在Rt △ADE 中，222DE AD AE +=， ∴ 22)12()2(100x x -++=， 即024102=+-x x ，解之，得41=x ，62=x . 故CE 的长为4或6.10．实数x 、y 、z 满足x+y +z =5，xy +yz +zx =3，则z 的最大值是 .答：313 解：∵ z y x -=+5，35)5(3)(32+-=--=+-=z z z z y x z xy ， ∴ x 、y 是关于t 的一元二次方程035)5(22=+-+--z z t z t的两实根.∵ 0)35(4)5(22≥+---=∆z z z ，即0131032≤--z z ，0)1)(133(≤+-z z .∴ 313≤z ，当31==y x 时，313=z . 故z 的最大值为313.三、解答题（共4题，每小题15分，满分60分）11．通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散. 学生注意力指标数y 随时间x （分钟）变化的函数图象如图所示（y 越大表示学生注意力越集中）. 当100≤≤x 时，图象是抛物线的一部分，当2010≤≤x 和4020≤≤x 时，图象是线段.（1）当100≤≤x 时，求注意力指标数y 与时间x 的函数关系式；（2）一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排，使学生在听这道题时，注意力的指标数都不低于36.解：（1）当100≤≤x 时，设抛物线的函数关系式为c bx ax y ++=2，由于它的图象经过点（0，20），（5，39），（10，48），所以⎪⎩⎪⎨⎧=++=++=.4810100,39525,20c b a c b a c 解得，51-=a ，524=b ，20=c .所以20524512++-=x x y ，100≤≤x . …………………（5分）（2）当4020≤≤x 时，7657+-=x y .所以，当100≤≤x 时，令y =36，得2052451362++-=x x ，解得x =4，20=x （舍去）；当4020≤≤x 时，令 y =36，得765736+-=x ，解得74287200==x . ……………………（10分）因为24742447428>=-，所以，老师可以经过适当的安排，在学生注意力指标数不低于36时，讲授完这道竞赛题. ……………………（15分）12．已知a ，b 是实数，关于x ，y 的方程组⎩⎨⎧+=--=b ax y bx ax x y ,23 有整数解),(y x ，求a ，b 满足的关系式.解：将b ax y +=代入bx ax x y --=23，消去a 、b ，得xy x y -=3， ………………………（5分）3)1(x y x =+.若x +1=0，即1-=x ，则上式左边为0，右边为1-不可能. 所以x +1≠0，于是111123+-+-=+=x x x x x y .因为x 、y 都是整数，所以11±=+x ，即2-=x 或=x 0，进而y =8或=y 0. 故⎩⎨⎧=-=82y x 或⎩⎨⎧==00y x ………………………（10分）当⎩⎨⎧=-=82y x 时，代入b ax y +=得，082=+-b a ； 当⎩⎨⎧==00y x 时，代入b ax y +=得，0=b . 综上所述，a 、b 满足关系式是082=+-b a ，或者0=b ，a 是任意实数.………………………（15分）13．D 是△ABC 的边AB 上的一点，使得AB =3AD ，P 是△ABC 外接圆上一点，使得ACB ADP ∠=∠，求PDPB的值.解：连结AP ，则ADP ACB APB ∠=∠=∠，所以，△APB ∽△ADP ， …………………………（5分） ∴AD AP AP AB =， 所以223AD AD AB AP =•=，∴AD AP 3=， …………………………（10分） 所以3==ADAPPD PB . …………………………（15分） D 试卷试题①②③④414．已知0<a ，0≤b ，0>c ，且ac b ac b 242-=-，求ac b 42-的最小值. 解：令c bx ax y ++=2，由0<a ，0≤b ，0>c ，判别式042>-=∆ac b ，所以这个二次函数的图象是一条开口向下的抛物线，且与x 轴有两个不同的交点)0,(1x A ，)0,(2x B ，（第13（A ）题图）因为021<=a c x x ，不妨设21x x <，则210x x <<，对称轴02≤-=ab x ，于是c a acb b a ac b b x =--=-+-=2424221， ………………（5分）所以aac b a ac b b c a b ac 242444222--≥--=≥-， …………………（10分） 故442≥-ac b ，当1-=a ，b =0，c =1时，等号成立.所以，ac b 42-的最小值为4. ………………………（15分）育才教育初中数学竞赛试题参考答案一、选择题（共5小题，每小题6分，满分30分. 以下每道小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填得零分）1. 已知实数b a ≠，且满足)1(33)1(2+-=+a a ，2)1(3)1(3+-=+b b .则ba a ab b+的值为（ ）. （A ）23 （B ）23- （C ）2- （D ）13-2. 若直角三角形的两条直角边长为a 、b ，斜边长为c ，斜边上的高为h ，则有 （ ）.（A ）2h ab = （B ）h b a 111=+ （C ）222111h b a =+ （D ）2222h b a =+3．一条抛物线c bx ax y ++=2的顶点为（4，11-），且与x 轴的两个交点的横坐标为一正一负，则a 、b 、c 中为正数的（ ）.（A ）只有a （B ）只有b （C ）只有c （D ）只有a 和b4．如图所示，在△ABC 中，DE ∥AB ∥FG ，且FG 到DE 、AB 的距离之比为1:2. 若△ABC 的面积为32，△CDE 的面积为2，则△CFG的面积S等于（ ）.（A ）6 （B ）8 （C ）10 （D ）125．如果x 和y 是非零实数，使得3=+y x 和03=+x y x ， 那么x +y 等于（ ）.（A ）3 （B ）13 （C ）2131- （D ）134-A二、填空题（共5小题，每小题6分，满分30分） 6． 如图所示，在△ABC 中，AB =AC ，AD =AE ，︒=∠60BAD ，则=∠EDC （度）.7．据有关资料统计，两个城市之间每天的电话通话次数T 与这两个城市的人口数m 、n （单位：万人）以及两城市间的距离d （单位：km ）有2dkmnT =的关系(k为常数) . 现测得A 、B 、C 三个城市的人口及它们之间的距离如图所示，且已知A 、B 两个城市间每天的电话通话次数为t ，那么B 、C 两个城市间每天的电话通话次数为 次（用t 表示）.8．已知实数a 、b 、x 、y 满足2=+=+y x b a ，5=+by ax ，则=+++)()(2222y x ab xy b a .9． 如图所示，在梯形ABCD 中，AD ∥BC (BC >AD )，︒=∠90D ，BC =CD =12, ︒=∠45ABE ，若AE =10，则CE 的长为 .10．实数x 、y 、z 满足x+y +z =5，xy +yz +zx =3，则z 的最大值是 .三、解答题（共4题，每小题15分，满分60分）11．通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散. 学生注意力指标数y 随时间x （分钟）变化的函数图象如图所示（y 越大表示学生注意力越集中）. 当100≤≤x 时，图象是抛物线的一部分，当2010≤≤x 和4020≤≤x 时，图象是线段.1112．已知a ，b 是实数，关于x ，y 的方程组⎩⎨⎧+=--=bax y bx ax x y ,23 有整数解),(y x ，求a ，b 满足的关系式.13．D 是△ABC 的边AB 上的一点，使得AB =3AD ，P 是△ABC 外接圆上一点，使得ACB ADP ∠=∠，求PD PB 的值.14．已知0<a ，0≤b ，0>c ，且ac b ac b 242-=-，求ac b 42-的最小值.。