车身曲线曲面数学模型基础

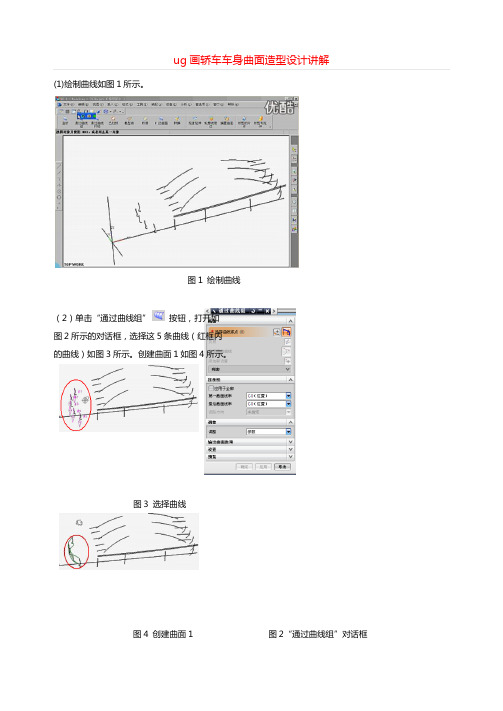
ug画轿车车身曲面造型设计讲解(1)绘制曲线如图1所示。

图1 绘制曲线（2）单击“通过曲线组”按钮，打开如图2所示的对话框，选择这5条曲线（红框内的曲线）如图3所示。

创建曲面1如图4所示。

图3 选择曲线图4 创建曲面1 图2“通过曲线组”对话框（3）选择下面的3条曲线，创建曲线组曲面如图5所示。

图5 创建曲面2 （4）选择上面的5条曲线，创建曲面3如图6所示。

图6 创建曲面3 （5）选择车尾上面的5条曲线，创建曲面4如图7所示。

图7 创建曲面4（6）选择车尾部的5条曲线，创建曲面5如图8所示。

曲面3 曲面4曲面1 曲面5曲面2图8 创建曲面5（7）单击“桥接”按钮，打开“桥接”对话框如图9所示。

先单击（侧面）按钮，去选择“曲面1”的右侧面，再单“第一侧面线串”按钮，再去选择“曲面2”，创建两曲面的连接，如图10所示。

侧面第一侧面线串图9 “桥接”对话框桥接曲面1（8）用同样的方法，创建的桥接曲面2，如图11所示。

图11 创建桥接曲面2（9）单击“截型体”按钮，打开如图12所示的“截型体”对话框。

在对话框中单击“圆角-hro”按钮，打开“截面”对话框如图13所示。

选择“曲面3”的左边线，弹出如图14所示的对话框。

特别提醒：在UG4、UG5中为“截型体”，但是在UG6以后的版本则称之为“剖切曲面”按钮，当使用该功能时，弹出的“剖切曲面”对话框如下图所示。

图12 “截型体”对话框图13“截面”面对话框图14 对话框“剖切曲面”对话框然后，在视窗单击右键，分别选择右键菜单中的“渲染样式”|“着色”命令，显示如图15所示。

图15 着色显示（10）选择车顶上的面，将其删除，结果如图16所示。

图16 删除车顶上的面（11）恢复原状，如图17所示。

图17 线框显示（12）单击“通过曲线组”按钮，打开如图18所示的“通过曲线组”对话框，选择图19中的3条线创建曲线组曲面。

选择这3条线生成曲面图19 创建曲线组曲面图18 “通过曲线组”对话框（13）同理，创建曲线组曲面如图20所示。

车身A级(Class A)曲面模型的构造Class A曲面是由CATIA软件开发商Dassault System公司提出的新概念，主要是指车身零件中对外观和形状要求极高的曲面。

本文从车身开发的角度，通过大量实例描述了车身Class A曲面模型的定义及创建方法，而车身曲面模型的光顺是车身开发人员一直追求的目标，本文提出了一个切实可行的设计思路。

一、前言车身设计方法从无到有，以及现在千姿百态的车身样式，都应当归功于现代科学技术的飞速进展。

从设计理念上而言，车身开发的基本思路并未发生根本性变化，依然是“概念设计→总布置设计→详细结构设计→试验验证→产品”这样一个流程。

然而由于现代技术的介入，使车身的开发周期大大缩短，车身的设计质量大大提高。

车身外形的变化也经历了由简单到复杂的演化过程，即箱式→船形→楔形→光滑曲面过渡的外凸形，这一过程也得益于各种先进技术的大量应用，如三维图形技术以及空气动力学仿真技术等。

现代车身设计，尤其是外观零件的设计，已经完全摈弃了由二维转三维的阶段，而是直接由虚拟三维到实际三维。

正是借助于先进的设计方法和工具，车身开发周期才能由原来的4到5年缩短至目前的2到3年，甚至更短的时间。

Class A曲面设计，即完全在计算机三维虚拟环境下构造合格的车身曲面的一种方法，是数学与计算机图形学相结合的典型应用，它不同于图板工作模式，使设计更加灵活，编辑起来更加方便快捷。

随着逆向设计、稳健设计、基于分析的设计以及面向制造的设计等新方法涌入车身设计过程，基于三维的车身曲面模型设计越来越重要，在整个产品链中的地位也日益提高。

二、Class A曲面的定义Class A一词最初是由法国Dassault System公司在开发大型CAD/CAM 软件包CATIA时提出并付诸应用的，常译作A级曲面，专指车身模型中对曲面质量有较高要求或特殊要求的一类曲面，如外形曲面、仪表板和内饰件的表面等。

从CATIA V5版本开始，软件中新增加了ACA(Automotive Class A)模块，专门用于Class A曲面的设计。

曲线、曲面造型过程的可视化设计作者：王哲王知行 | 阅读次数：438 转自：CAD世界网时间：2004年12月6日15:55摘要:由于NURBS曲面、曲线构造的复杂性,描述NURBS曲线、曲面必然采用复杂的数据结构,这样给人—机交互带来很大的困难。

本文利用VC＋＋编写的NURBS曲线、曲面造型系统可以实时观察曲线、曲面的控制点、节点信息,可以实时对控制点、节点进行诸如添加、修改、删除等操作,这对NURBS曲线曲面造型无疑会带来极大的方便。

关键词:NURBS，造型。

1 NURBS曲线、曲面造型方法1．1 NURBS曲线方程一条p阶NURBS曲线被定义作:式中:｛P i｝——控制点(形成控制多边形);｛ωi｝——权因子;｛N i，p（u）｝——p阶B样条基函数,其节点矢量为:U＝｛a，…，a，u，…，u m－p－1，b，…，b｝p＋1除非另述,一般假定a＝0，b＝1及对于所有的i都有ωi＞0。

令:则NURBS曲线方程还可写作:1．2 NURBS曲面方程u向p阶、v向q阶的NURBS曲面定义为:式中:｛P i，j｝——构成曲面控制点网;｛ωi，j｝——权因子;｛N i，p（u）｝、｛N j，q（v）｝——p阶、q阶B样条基函数,其节点矢量为:U＝｛0，…，0，u，...，u r－p－1，1， (1)p＋1V＝｛0，...，0，v q＋1，...，v s－q－1，1， (1)这里,r＝n＋p＋1，s＝m＋q＋1。

令:NURBS曲面方程还可写作:2 NURBS曲线、曲面的数据结构NURBS曲线的属性信息有:次数k，控制点d，权因子w和节点矢量U。

NURBS曲面的属性信息有:次数k、l,控制点d i,j，权因子w i,j和节点矢量U，V。

能否管理好NURBS 曲线、曲面,取决于能否对这些属性信息进行有效的组织和管理。

而要对曲线、曲面进行方便、有效的管理和计算,良好的数据结构是必不可少的。

NURBS曲线、曲面数据结构图如下:Nurbs数据结构图Nurbs曲面数据结构图这种数据结构形式具有如下几个优点:(1)运算灵活,便于修改;(2)易于检索、提高运算速度;(3)结构简单、便于维护。

自由曲线曲面造型技术自由曲线曲面造型技术是一种用于制作3D图形的先进技术。

它可以让设计师轻松地将自己的想法转化成真实的3D模型。

该技术旨在为设计师提供更高的创作自由度，使其能够以更自然、更流畅的方式来表现自己的创意。

下面我们来详细了解一下自由曲线曲面造型技术。

一、基础知识1. 什么是自由曲线曲面造型技术？自由曲线曲面造型技术是一种用于编辑多边形网格模型的技术。

它允许设计师自由地绘制曲线和曲面，以创建具有复杂形状和曲率变化的物体。

2. 自由曲线曲面造型技术的应用范围自由曲线曲面造型技术广泛应用于艺术设计领域、工业设计领域、建筑设计领域和汽车设计领域等。

它可以用于设计和制造车身、雕塑、建筑立面和自然景观等。

二、自由曲线曲面造型技术的基本原理自由曲线曲面造型技术的基本原理是“控制点—曲线/曲面—几何体”的过程。

它的主要思想是通过控制点操纵曲线/曲面的形状，最终得到所需的几何体。

三、自由曲线曲面造型技术的工具和实现方式1. 曲线工具曲线工具允许设计师创建用于控制曲面形状的曲线。

这些曲线可以是贝塞尔曲线、NURBS曲线等，设计师可以自由选择。

2. 曲面工具曲面工具是将曲线连接起来形成的曲面。

设计师可以通过调整控制点、曲线和曲面的参数，来控制曲面的形状。

3. 几何体工具几何体工具是将曲面转换成带有体积的3D模型，如球体、立方体、圆柱体等。

设计师可以通过这些工具来创建真实的3D模型。

四、自由曲线曲面造型技术的优点1. 创意自由度高自由曲线曲面造型技术可以允许设计师非常灵活地表达自己的想法。

它可以让设计师轻松创建复杂形状和曲率变化的物体。

2. 精度高自由曲线曲面造型技术具有非常高的精度，可以帮助设计师创建精细的3D模型，并且不会出现几何失真的问题。

3. 可控性强自由曲线曲面造型技术基于控制点和曲线，具有非常强的可控性。

这意味着设计师可以精确地控制曲线和曲面的形状，从而创造出高质量的3D模型。

五、自由曲线曲面造型技术的应用案例自由曲线曲面造型技术已经被应用于许多领域，以下是一些典型的应用案例：1. 工业设计中的3D模型制作自由曲线曲面造型技术广泛应用于工业设计领域，例如汽车、飞机、手机等产品。

曲面加工的数学原理及应用1. 引言曲面加工是一种重要的制造工艺，广泛应用于航空航天、汽车制造、机械加工等领域。

本文将介绍曲面加工的数学原理和应用，包括曲线与曲面的表示方法、曲面加工的数学模型、以及常见的曲面加工方法。

2. 曲线与曲面的表示方法在曲面加工中，曲线和曲面的表示方法是一项基础工作。

以下是常见的曲线与曲面的表示方法：•参数方程表示：曲线或曲面上的点的坐标可以用参数表示。

例如，对于二维曲线，可以使用参数方程x=f(t), y=g(t)来表示，其中t是参数，f(t)和g(t)是关于t的函数。

对于三维曲面，可以使用参数方程x=f(u,v), y= g(u,v), z=ℎ(u,v)来表示，其中u和v分别是两个参数，f(u,v)、g(u,v)和ℎ(u,v)是关于u和v的函数。

•隐式方程表示：曲线或曲面上的点的坐标满足一个方程。

例如，对于二维曲线，可以使用方程y=f(x)来表示，其中f(x)是关于x的函数。

对于三维曲面，可以使用方程F(x,y,z)=0来表示，其中F(x,y,z)是关于x、y和z的函数。

•参数化曲线表示：曲线上的点可以通过参数化表示。

例如，对于二维曲线，可以使用一个参数t表示曲线上的点的位置，并通过t的变化得到曲线上不同点的坐标。

对于三维曲线，可以使用两个参数t和s表示曲线上的点的位置。

3. 曲面加工的数学模型曲面加工的数学模型是描述曲面加工过程中曲线和曲面变化的一种数学模型。

常见的曲面加工数学模型有以下几种：•曲线插值：在曲面加工中，经常需要在给定的点之间插值出曲线。

常用的曲线插值方法包括线性插值、样条插值、贝塞尔曲线等，通过这些方法可以产生平滑的曲线。

•曲线拟合：曲面加工通常需要将给定的数据拟合成曲线。

拟合曲线的方法有最小二乘法、最小二乘多项式拟合、最小二乘样条拟合等，通过这些方法可以得到最接近给定数据的曲线。

•曲面拟合：曲面加工中，经常需要将给定的数据拟合成曲面。

常用的曲面拟合方法有最小二乘法、最小二乘多项式拟合、最小二乘样条拟合等，通过这些方法可以得到最接近给定数据的曲面。

曲面模型知识点归纳总结曲面模型是计算机图形学中的一个重要概念，其在计算机辅助设计、动画制作、虚拟现实等领域都有广泛的应用。

曲面模型是一种由曲面构成的三维模型，可以用来描述自然界中的曲面形状，也可以用来构建艺术、工程、医学等领域中需要的复杂的曲面模型。

学习曲面模型知识，能够帮助我们更好地理解三维模型的构建和运用，下面对曲面模型的知识点进行归纳总结。

一、曲面模型的基本概念1. 曲面模型是什么？曲面模型是由曲面定义的三维模型，通常是通过一系列曲面片或曲线来描述一个物体的形状和结构。

曲面模型可以用来描述复杂的物体，比如人体、汽车、飞机等。

2. 曲面模型的优点与多边形或其它类型的模型相比，曲面模型有许多优点。

它可以更加准确地描述复杂的曲面形状，同时对于建模的复杂度也能够有着更好的控制。

此外，曲面模型还可以更好地进行光照和纹理的处理，使得渲染效果更加真实。

3. 曲面模型的应用曲面模型广泛应用于计算机辅助设计、动画制作、虚拟现实、医学成像、工程设计等领域。

比如在游戏开发中，曲面模型可以用来制作角色、场景、道具等；在医学成像中，可以用来重建人体器官的形状；在工程设计中，可以用来进行汽车、飞机、船舶的设计。

二、曲面的表示方法1. 参数曲面参数曲面是通过参数方程来表示的曲面，通常是由两个参数u、v来描述曲面上的点。

这种表示方法可以很好地描述复杂的曲面形状，如球面、圆柱面、双曲面等。

2. B样条曲面B样条曲面是由B样条曲线推广而来的曲面表示方法，它通过一系列的控制点和权重来定义曲面的形状。

B样条曲面具有良好的局部控制性和平滑性，因此在实际应用中被广泛使用。

3. NURBS曲面NURBS曲面是一种更加通用的曲面表示方法，它是由有理B样条曲线推广而来的，可以用更少的控制点和权重来定义复杂的曲面形状。

NURBS曲面是目前最为常用的曲面表示方法之一。

4. 曲面的渲染曲面的渲染是指将曲面模型转化为图像的过程，通常包括光照、纹理、阴影等处理。

奥斯古德的逆向曲面模型（Osgood's Reverse Curve Surface Model）是一种用于描述和分析曲面形状的数学模型。

它由美国数学家威廉·奥斯古德（William F. Osgood）于20世纪初提出。

逆向曲面模型可以被用来表示各种复杂的曲面形状，如汽车车身、船体、工业设计等。

该模型的基本思想是将曲面划分为无数小块，并通过控制每个小块的形状来实现整体的曲面形状控制。

奥斯古德的逆向曲面模型主要包含以下几个要素：
1. 控制点：曲面模型的形状是通过控制点的位置和权重来确定的。

每个控制点都对应着曲面上的一个局部区域，并影响该区域的形状。

2. 权重函数：权重函数决定了每个控制点对整体曲面形状的影响程度。

通常使用插值函数或调和函数来定义权重函数。

3. 插值方法：通过插值方法将控制点之间的形状衔接起来，从而形成光滑的曲面。

常用的插值方法有贝塞尔插值、B样条插值等。

4. 曲面参数化：为了方便对曲面进行计算和操作，通常将曲面参数化为二维平面上的参数域。

常用的参数化方法有参数方程、三角网格等。

奥斯古德的逆向曲面模型在曲面设计和计算机图形学领域有广泛的应用。

它提供了一种灵活而有效的方法来控制曲面形状，并且可以通过调整控制点和权重来实现对曲面的局部调整和全局变形。

这使得设计人员能够更好地实现他们的设计意图，并满足实际应用的需求。

汽车车身A级曲面的表示与次数选择作为一种新颖的设计展示形式，汽车车身曲面已经在汽车设计领域中具有了重要的地位。

其中，A级曲面是一种被广泛使用的汽车设计曲面之一。

本文将介绍A级曲面的表示方法以及相应的次数选择问题。

A级曲面是一种最基础的汽车设计曲面，通常用于车身表面的主要曲线、连续曲面联通和型式线的设计。

A级曲面的特点在于其表面的连续性和光滑度，设计人员需要通过合理的曲面构建和优化来达到这一点。

表示A级曲面的方法和次数选择会影响到车身设计的效果和质量。

曲面表示方法目前，常见汽车车身曲面的表示方法包括：1. Bézier曲线Bézier曲线是基于多项式函数的一种数学方法，它能够通过少量控制点来构建连续光滑的曲线。

它被广泛应用于汽车车身曲面设计中，可以通过调整控制点的位置来实现曲线的精细调整和优化。

2. NURBS曲线NURBS曲线是非均匀有理B样条曲线的缩写，是一种比Bézier曲线更高级的曲线构造方法。

同样可以通过少量控制点来构建光滑的曲线，但相比于Bézier曲线，NURBS曲线更具有精确性和自由度，能够更好地实现曲面的优化和参数化管理。

3. 曲面拟合曲面拟合是通过对一组离散点进行曲面近似求解的方式，可以通过调整离散点的位置和权重来实现曲面的优化和精细调整。

曲面拟合的优势在于可以快速处理不规则曲面和复杂形式的汽车设计。

曲面表示次数选择表示A级曲面的次数通常会影响到车身曲面的精细度和流畅感。

通常的选择方法有以下几种：1. 3次曲面3次曲面是指由三次多项式函数组成的曲面，通常用于大致的曲面布局和分块设计。

具有计算速度快和精度较低的特点，但不适用于精细和低误差的曲面设计。

2. 4次曲面4次曲面由四次多项式函数组成的曲面，可以更好地达到曲面的精细度和光滑性，适用于大多数的汽车车身设计。

3. 高次曲面高次曲面拥有更高的曲面精度和更流畅的曲线特点，通常可以满足更为精细的曲面设计需求。