正定矩阵概念及例题22页PPT

f

x2 1

x2 2

5
x2 3
2t x1x2
2x1x3 4x2 x3
为正定二次型?
解
二次型的矩阵为
A


1 t 1
t 1 2
251 ,
要使二次型为正定二次型 , 则A的各阶顺序 主子式均为正 , 即
高等代数课件--天津科技大学理学院高等代数精品课程教研小组
1＞0
（1） xTAx ＞0 ，则称 f 为正定二次型，
相应地矩阵A称为正定矩阵；
（2） xTAx ＜0 ，则称 f 为负定二次型，相应
地矩阵A称为负定矩阵；
高等代数课件--天津科技大学理学院高等代数精品课程教研小组
（3）xTAx≥ 0 ，则称 f 为半正定二次型，相应
地矩阵A称为半正定矩阵；
（4）xTAx ≤0 ，则称 f 为半负定二次型，相应
0 1 2
2

5 2

2 6
2 0
2 0 4
高等代数课件--天津科技大学理学院高等代数精品课程教研小组
解 (1) 2＞0,
2 2
1 2
5＞0,
2 1 0
1 2 1 4＞0, ∴该矩阵为正定矩阵.
0 1 2
解 (2)∵-5＞0, 5 2 26 ＞0, 2 6
, 1t
t 1
1 t 2＞0,
1t t1
1
2 5t 2 4t ＞0,
1 2 5
1 t 2＞0
因此

5t
2

4t ＜0
解之得 4＜t＜0 5
故当 4 ＜t＜0 时,该二次型为正定二次型. 5

1 4 为半正定矩阵 6 0
2 2 ( 3) f x1 , x 2 x1 3 x 2 为负定二次型
1 为负定矩阵。 3 2 2 (4) f x1 , x2 , x3 x1 3 x2 为半负定二次型
交矩阵P，使得P T AP , 其中 diag(1 , 2 , , n )
对于任意非零向量 x x T Ax x T ( P 1 )T P 1 x ( P 1 x )T ( P 1 x )
T 设y P 1 x （y1 , y2 ,, yn） , 则y为非零向量
1
1
2
1
E n
设C PQ, 则C T AC E , 所以A与单位阵合同。
若A与单位阵合同，则存在可逆矩阵C,使A=
CTEC= CTC，则对于非零向量x xT Ax xT C T Cx (Cx )T (Cx )
C可逆，x 0, 故Cx 0，则(Cx )T (Cx ) 0 所以f正定。
1 3 为半负定矩阵。 0 2 2 (5) f x1 , x 2 x1 3 x2 为不定二次型
1 为不定矩阵。 3
二、正(负)定二次型的判别
准则1 对称矩阵A为正定的充分必要条件是： A的 特征值全为正． 证明 必要性 假设i ( i 1,2 , n)为A的特征值， i 为对应于i的
第六章
二次型
中南财经政法大学信息系
一、正(负)定二次型的概念
定义6.6 具有实对称矩阵A的n元二次型为
f X X AX
T
x1 x 1) 如果对于任意的非零向量 X＝ 2 ，都有 xn

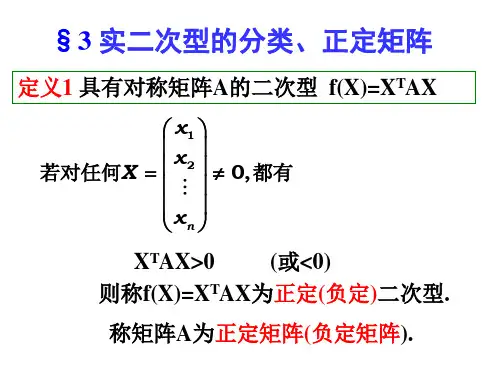
5.4 正定矩阵 5.4.1 正定矩阵[1] 二次型的分类n 个变数的二次型∑===nj i Tji ij n x A x x x a x x q 1,1),,( ，其实就是定义在n R 的一个二次齐次函数，对n R 的每个特定向量q x ,0对应一个函数值)(0x q ，依据)(x q 值的符号，在教材184页上给出了二次型的分类定义：1．正定二次型。

若对一切nR x ∈，当0)(0>=⇒≠Ax x x q x T称二次型)(x q 正定。

显然，正定二次型也就是函数值定正的二次型（当然有唯一的例外，0=x 时，0=q ）。

2．正半定（或半正定）二次型。

若对一切nR x ∈，皆有0)(≥=Ax x x q T，且至少有一 00≠x 能使0)(0=x q .3．负定。

对二次型Ax x x q T=)(，当(-q )为正定时，称q 为负定二次型。

4．负半定（或半负定）。

对二次型Ax x x q T=)(，当(-q )为正半定时，称q 为负半定二次型。

5．不定二次型。

若二次型Ax x q T=既能取正值，又能取负值，称为不定二次型。

容易明白，对标准形的二次型（以下给出的均为充要条件）。

若系数全正为正定二次型；若系数全为非负，且至少有一为0，则为正半定二次型； 若系数全负为负定二次型；若系数全为非正，且至少有一为0，则为负半定二次型； 若系数有正、有负，则为不定二次型。

对于不是标准形的二次型，为确定其类型，可通过化成标准形，并依据惯性律而作出判断。

例19 设n a a a ,,,21 是n 个实数，问它们满足什么条件时，二次型212322221121)()()(),,,(x a x x a x x a x x x x q n n n ++++++=是正定二次型。

解 乍一看，这是n 个带正系数1的平方项之和，应明显是正定的。

但与定义一对照，发现这并非是二次型的标准形，每一项都是线性型而非单独变换的平方。

xA j x j A x i i j，同理， ( xA (x 由于 x j x i 是数量， j x i) i x jx i ) xx j xA j，则 i i x 而A对称，故 xAx 0 ( xx i j) i j
由于 i j ，则 xix j 0
第四章
二次型和正定矩阵
• 在本章中，我们将介绍特征值和特征向量， 然后介绍由特征向量组成的矩阵，并且运 用这些知识来判断二次型的正定性，与此 同时，我们也介绍特征值与行列式、秩、 迹的关系，最后我们介绍用行列式来判断 二次型正定性的方法，作为特征值方法的 补充。
第一节 引言
• 二次型 完整形式：
• 定理 如果 A 为对称矩阵，那么其所有特征值都为实数。 例
2 A 2 2 1
2 2 2 A I ( 2 ) ( 1 ) 2 3 21
则 A I 0为二次方程
其两个特征值为 1 0 和 2 3
定理 如果A为对称矩阵，那么对应着不同特征值的特征向量正 交。
• 证明 令 i 和 j 是两个不同特征值，分别对应于特征向量 x i 和 x 。 j 那么有 Axj j xj Axi i xi 分别左乘 x j 和 x i ，有 j xA x x i x j xx i j jA i ix jx i
已知A的两特征值为 1 0 和 2 3
1 0
I)x0得到 Ax 0 由(A 1
即
2 2
2 x1 0 1 x2
由方程可得 x2 2x1，那么 作为特征向量我们取
1 2 2 2 x x 1 3 x 1 x 1 2 1 1 3

求得 A 的特征值为 2, 2 3 ，
全为正， 因此二次型正定.
7
n 阶实对称矩阵 A 正定的充分必要条件是 A 的 准则2 顺序主子式全大于零. 证略.
其中 A (aij )nn 的 k 阶顺序主子式是指行列式
a11 | Ak | a 21 ak 1
a12 a 22
a1k a2k ,
i 1 j 1
T 取 X i (0, ,1, ,0) ，则有
n
n
f ( X i ) aii 0, (i 0,1,.n) .
4.若 A 和 B 为正定矩阵，则 A+B 也为正定矩阵. 证 对任意非零向量X ，
X T ( A B) X X T AX X T BX 0 .
设 B T AB 为正定阵, 必要性：
这就是说,齐次线性方程组Bx 0 只有零解,
因此 B 列满秩,即 r ( B) n ；
T T T T T 充分性: 因为 ( B AB ) B A B B AB ,
可见 B AB 为实对称阵.
T
将上述过程逆推,即可得证.
23
T
证
因为 ( A A) A A , 故 A A 是 n 阶对称矩阵.
T T
T
T
又 r( A) n ，可知齐次线性方程组AX o 仅有零解，
于是 所以对任意 X o ，必有AX o ，
X T ( AT A) X ( AX )T ( AX ) 0 ,
即二次型 X T ( AT A) X 为正定二次型，
即矩阵 A A 为正定， A 的秩 r ( A) n ， A A 为 且 则 正定矩阵.
T
类似结论有：

X
T i
O)A
Xi O
0.
即Ai为正定矩阵,故其行列式 Ai 0.
, xi ),
14
充分必要性.设矩阵A的所有顺序主子式>0.要证 明A是正定矩阵.用数学归纳法证明.n=1时显然:
a11 0, x1 0,a11 x12 0.
设对于n－1结论成立.An-1正定,存在n-1阶非退化矩
阵G,使得
2 5 0 2 5 0 2 0 7 2 0 7
5
( 6)( 5)( 7) 4( 5) 4( 7) ( 6)( 5)( 7) 8 48 ( 6)( 2 12 35) 8( 6) ( 6)( 2 12 27) =( 3)( 6)( 9).
定义 如果实二次型f=XTAX对于某些向量X为 正数,并且对于对于某些向量X为负数,则称二 次型是不定的.
2
二、正定矩阵的充分必要条件
定理 实对称矩阵A正定的充分必要条件是其 特征值都是正数.
证明 设实对称矩阵A的特征值 1, ,n 都是正数. 存在正交矩阵Q,使得 QTAQ= , 为对角矩阵, 其对角线元素为1, ,n , 对于X O, 令Y Q1X ,
X T P T PX (PX )T PX PX 2 0.
设A正定,则A合同于单位矩阵,即存在可逆矩 阵,使得A=PTEP=PTP.
10
例 A正定,B实对称,则存在可逆矩阵R, 使得 RTAR和RTBR同时为对角形. 证明存在P,使得PTAP=E,PTBP实对称,存在正交 矩阵Q,使得 QTPTBPQ=D为对角形,令R=PQ,则
C2TC1T AC1C2
En1
TG
O 1
En1
TG
G T
ann
En1 O
GT

北京航空航天大学 数学与系统科学学院
答疑时间：星期二晚上18:00－20:30 星期四晚上18:00－20:30
答疑地点：J4-102 Email: liyongzhu@
朱立永
线性代数
第六章 二次型
§6.1 二次型及其矩阵表示 §6.2 化二次型为标准形 §6.3 惯性定理 §6.4 正定二次型和正定矩阵
线性代数
§6.4 正定二次型和正定矩阵
定义6.4.1 设 f (x1, x2 ,, xn ) X T AX 为n元
实二次型. 若对于任意非零实向量 X
(x1, x2, , xn )T 0 ,都有
f (x1, x2 , , xn ) X T AX＞0 则称实二次型 f 为正定二次型;相应的实对 称矩阵 A称为正定矩阵.
件是 A的特征值全大于0,从而正定矩阵的
行列式大于0. 证 由定理5.3.5,必有正交矩阵 Q ,使
线性代数
1
QT AQ Q1AQ B
2 ,
n
其中,1, 2, , n 是 A 的全部特征值.因为
，
A正定的充要条件是B 正定.而 B对应的
二次型为
，
Y T BY
1 y12
2
y
2 2
n
y
2 n
由定理6.4.1可知,该二次型正定的充分必
要条件是 i 0(i 1, 2, , n).
线性代数
由于 A B 12 n＞ 0 ,即正定矩阵 的行列式大于0.证毕.
例6.4.1 判断实二次型 f (x1, x2, x3)
3x12 3x22 x32 4x1x2 的正定性.
，
解 二次型 f 的矩阵为
A3 A t
1

正定矩阵
正定矩阵式⾃共轭矩阵的⼀种。

正定矩阵类似复数中的正实数。

定义：对于对称矩阵M，当且仅当存在任意向量x，都有
若上式⼤于等于零，则称M为半正定矩阵。

正定矩阵记为M>0。

也被称为正定⼆次型
正定矩阵的判定
1、所有特征值为正数（根据谱定理，若条件成⽴，必然可以找到对⾓矩阵呢D和正定矩阵P，使M=P^-1DP）；
2、所有的顺序主⼦式为正定；
3、Cholesky分解得到的矩阵，其主对⾓线上的元素全为正数；
4、矩阵有半双线性映射形式。

⾸先解释双线性映射。

假设三个向量空间X, Y和Z，有Z = B(X, Y)。

对于X或Y中的任意向量都有到Z的唯⼀映射。

如果把X固定，Y中的元素就存在到Z的线性映射，反过来也⼀样。

所谓半双线性映射，就是它的两个参数⼀个是线性的，另⼀个是半线性的（或共轭线性）。

如：
复数空间的内积都是半双线性的。

正定矩阵的性质
1、正定矩阵均可逆，且逆矩阵也为正定矩阵；
2、正定矩阵与正实数的乘积也为正定；
3、迹Tr(M)>0；
4、存在唯⼀的平⽅根矩阵B，使得：。

【解析】要注意首先要说明 AT A 是实对称矩阵.
【法一】由A可逆, 则有 AT A AT EA , 则AT A与单位阵合
同, 所以 AT A正定.
【法二】由A可逆, 则对任意n维实列向量X≠O, 有 AX≠O, X T AT AX ( AX )T AX 0, 所以 AT A 正定.
矩阵之间的关系
A的特征值均大于0 A与单位阵E合同 存在可逆阵P, 使得 A PT P A的各阶顺序主子式 > 0
例3 设A为n阶正定矩阵, E为n阶单位阵, 证明 A E 1
例4 A为n阶实对称矩阵, 且满足 A3 2A2 4A 3E O,
证明A为正定矩阵. 例5 证明
（1）若 An 正定，有实数域上矩阵 Pnm ，r(P) m n ，
2 4 5
例2 若二次型 f ( x1 , x2 , x3 ) 2 x12 x22 x32 2 x1 x2 tx2 x3 是正定的, 则 t 的取值范围?
【解析】已知二次型正定,反求其中未知参数的取值范围一般用
顺序主子式求解.
2 1 0
二次型矩阵为
A2 1
21 0
——负定
2 2 2
(4)
XT
2
5
4
X
判断是否正定？
2 4 5
二、正定矩阵的充分必要条件
准则1 n阶实对称矩阵A正定 A的特征值全为正数.
2 2 2
例1
判断矩阵
A
2 2
5 4
4 5
是否为正定矩阵？
【解析】可求得A的全部特征值为1(二重)和10, 则该实对称矩阵A
的特征值全大于0, 故A为正定矩阵.
对于负定矩阵有类似的结论
A正定 -A负定 二次型 f 为正定 二次型 -f 为负定

正定二次型
★正定二次型和正定矩阵的概念 ★判别二次型或矩阵正定的方法
正定二次型是二次型中讨论最多的类型，本节 结合二次型的标准型中系数给出正定二次型的概念， 并给出了判定二次型正定及实对称矩阵的几种方法。
下页
关闭
正定二次型和正定矩阵的概念
二次型的标准形不是唯一的。 标准形中所含项数是确定的( 即是二次型的秩 )。 限定变换为实变换时，标准形中正系数的个数是 不变的。
上页 下页 返回
第五章主要方法
一) 方阵的特征值与特征向量的求法
(1).计算A的特征多项式 f ( ) | A E |;
(2).求出f ( ) 0的全部根 ,即A的全部特征值 ;
( 3).把A的 特 征 值 逐 个 代 入 齐 线 次性 方 程 组 ( A E ) x 0, 并 求 出 这 个 方 程 组 的 个 一基 础 解 系, 则 这 个 基 础 解 系 的 非 线 零性 组 合 就 是 A的 属 于特征值 的 全 部 特 征 向 量 .
上页 下页
返回
3 1 0 例16 判定对称矩阵 A 1 3 0 正定性。 0 0 3 解 方法一 因为a11 3 0,
a11 a12 a21 a22
3 1 0 3 1 8 0, | A | 1 3 0 24 0, 1 3 0 0 3
1.定义法： 2. 用霍尔维兹定理： A 的各阶主子式都为正， 则A 是正定的; 3. 用A的特征值： A 的特征值全为正，则A 是正定的; 4. 化A所对应的二次型为标准形,根据标准形 中的正平方项个数判断;
上页 返回
由实二次型的矩阵表示及对称矩阵的正定性判 别法知，判断二次型的正定性也有两种方法。 一是利用对称矩阵A 的正定性。若二次型 f 的 对称矩阵A 是正定的，则f 是正定二次型；若A 是 负定的，则 f 也是负定二次型。 二是将 f 化为标准形。若其标准形的 n 个系数 全为正，则 f 是正定的；若 f 的标准形的 n 个系数 全为负，则 f 是负定的。 由于将 f 化为标准形非常复杂，因此第二种方 法一般不用。

定理1 设A为正定矩阵,若A与B合同,则B也是 正定矩阵.
类似可以证明:
与负定矩阵合同的矩阵是负定矩阵.与半正定 (半负定)矩阵合同的矩阵是半正定(半负定)矩阵.
任一对称阵合同于对角阵,而对角阵的有定性
较易判别.
d1
定理2 对角阵D
d2
dn
为正定矩阵的充分必要条件是di 0, (i 1, 2,...,n)
定义2 具有对称阵A的二次型 f(X)=XTAX
x1
若对任何X
x
2
,
都有
XTAX≥0
(或≤0)
xn
且有X 0
x10
x
0 2
0,
使得X
T 0
AX
0
0
xn 0
则称二次型f(x)=xTAx为半正定(半负定)二次型
矩阵A称为半正定(半负定)矩阵.
例2 二次型f (x1, x2, x3) x12 2x1x2 4x1x3 x22 4x2x3 4x32
例3
f
(x1, x2 )
x12
2x
2 2
由 f(1,1)=-1 <0 f(2,1)=2 >0
故它是不定二次型.
若A与B合同,存在可逆阵C,使CTAC=B 若A是正定的,对任意Y≠0, 令X=CY,则X≠0, YTBY=YTCTACY=(CY)TACY=XTAX>0 故B也是正定的.即有合同关系保持正定型.
可写成 f(x1,x2,x3)=-(x1+x2-2x3)2 ≤0
而当 x1+x2-2x3=0时, f(x1,x2,x3)= 故 f(x1,x2,x3)是半负定0二次型.
1 1 2
对应矩阵
1

正定二次型 例 如果二次型 对任意 都有则称 f 为 ，对应的矩阵 A 称为 正定二次型 正定矩阵负定二次型不定二次型例 解 化二次型 为标准形 .有f 在正交变换下的标准形为令 1二次型矩阵 的特征值为2定理设有实二次型 秩为 r，有两个实的可逆变换 和 使及则 中正 (负) 数的个数与 中正 (负) 数的个数相等 .分别记作例二次型 可以化为负系数个数称为 ，标准形中正系数的个数称为 ，正惯性指数负惯性指数符号差它们的差 称为 .正惯性指数 + 负惯性指数 = 二次型矩阵的秩.1正惯性指数 + 负惯性指数 + 零的个数 = 二次型矩阵的阶数.2正定的判别 定理 实二次型 正定的充要条件为正惯性指数等于变量个数 . 正定 特征值全正实二次型 正定的充要条件为 A 的特征值全正 .推论例 解 判断二次型 是否正定 .二次型的矩阵为 令 求出特征值为A 的特征值都大于零，所以二次型是正定二次型 .正定 特征值全正例判断矩阵 是否正定 .解说明矩阵的特征值一正一负，不正定 .例判断矩阵 是否正定 .解说明矩阵的特征值必为两个正数，正定 .霍尔维茨定理 对称矩阵 A 正定 各阶顺序主子式都大于零 .定理顺序主子式称对角线元是A 的前 k 个对角线元的 k 阶子式是 A 的 k 阶例解判断二次型 是否正定.二次型的矩阵为顺序主子式都大于零，所以二次型是正定二次型 .正定 顺序主子式值全正例解若二次型 正定，求参数 t 应满足的条件 .二次型的矩阵为即正定 顺序主子式值全正解为正定二次型.二次型矩阵为所以特征值是解 为正定二次型 .所以 A 的特征值是正定 特征值全正正定矩阵的性质 A 正定，则其对角线元素都大于零 . A 正定， 所以对于任意 ，都有取 则性质 证明（A）（B）（C）（D）解（A）（B）对角线不正 不正定（A）（B）（C）（D）解（D）（C）二次型例正定的充要条件是解没有非零解 .正定矩阵的性质若 A, B 都正定，则2可能不正定.若 A 正定，则 均正定 .1正定 特征值全正必然正定，例 （ ） C 则上述描述中正确的个数为 若同阶实对称矩阵 A, B 均正定，有如下一些描述解 （A ） （B ） （C ） （D ） 1234(I) 未必正定(II) 未必正定 (III) 未必正定(IV) 未必正定若 A 正定，则 均正定 .定理证明 如果 其中 P 是可逆矩阵，从而且对于任意 ，都有 A 正定 存在可逆矩阵 P ， 使 充分性 : 显然 A 对称， 必要性 : 正定阵必可正交相似于对角阵， 即其中 且 令则 即 记 定理得证 .A 正定 A 合同于单位阵例解化二次型 为标准形 .令二次型的矩阵为则取则规范形称形如 的标准形为二次型的 规范形它的系数分别为在这个顺序下，二次型的规范形是唯一的 .例设二次型的矩阵为 则二次型的规范形为 解容易算出(II) 若二次型的规范形为 求 的值.设二次型(I) 求二次型的矩阵的所有特征值； 例 解 <<霍尔维茨定理例矩阵 负定，对称矩阵 A 负定奇数阶顺序主子式偶数阶顺序主子式 推论若二次型 负定，例解则 k 满足由题意 正定，正定 顺序主子式值全正正定 特征值全正设 则在实数域上，与 A 合同矩阵为例（A）（B）（C）（D）（）D 解 合同 特征值符号全相同例 （ ）D 矩阵 在等价、相似、合同三种关系中满足几个？ A 的三个特征值是 0，0，9 .解 （A ）（B ） （C ） （D ） 0123 矩阵等价 同维且同秩对称阵相似 特征值全相同合同 特征值符号全相同（ ）解 （A ） （B ） （C ） （D ） 0123对调，得矩阵 B ，则 A 与 B 在等价、相似、合同三种关系中满足几个？乘积化相似合同等价（ ）解（A ） （B ） （C ） （D ） 0123对调，得矩阵 B ，则 A 与 B 在等价、相似、合同三种关系中满足几个？D 具体化合同。