理想气体的等温过程和绝热过程

理想气体中的等温过程与绝热过程在研究理想气体的性质和行为时，等温过程和绝热过程是两个重要的概念。

它们描述了气体在外界条件改变下的变化规律，是热力学和物理学中的基础概念之一。

本文将详细介绍等温过程和绝热过程的定义、特点和数学表达，以及它们在实际应用中的意义和重要性。

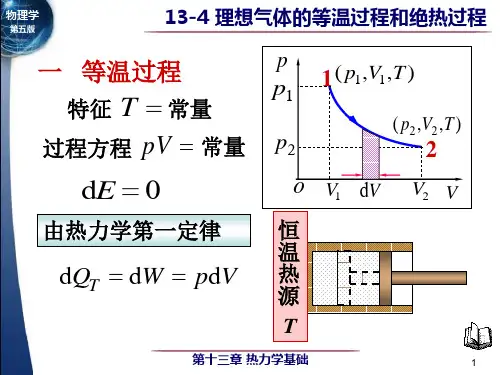
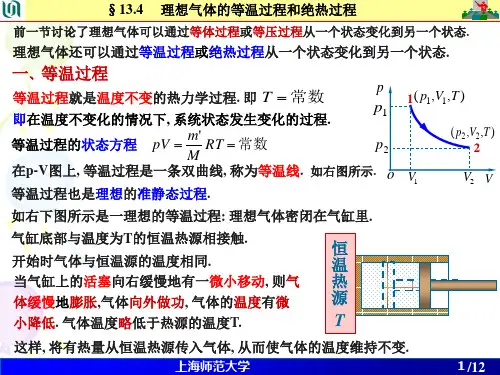
一、等温过程等温过程是指在气体与外界保持恒定温度的条件下，体积和压力发生变化的过程。

根据理想气体状态方程PV=nRT，当温度保持不变时，压力和体积成反比关系。

也就是说，当压力增加时，体积减小；压力减小时，体积增加，以保持气体的温度不变。

以一定量的理想气体为例，假设其体积从V₁变化到V₂，对应的压力由P₁变化到P₂。

根据等温过程的特点，我们可以得到以下数学表达式：P₁V₁ = P₂V₂这个表达式被称为爱德华·博伯定律，也是描述等温过程中气体性质的重要公式之一。

从公式中可以看出，当气体的温度不变时，压力和体积之间存在一个不变的乘积关系。

等温过程在实际应用中有着重要的意义。

在工程领域中，等温过程常常用于设计和优化热机、制冷设备等。

在化学实验中，等温过程也是调整反应条件和控制反应速率的基础。

二、绝热过程绝热过程是指在理想气体与外界没有热量交换的条件下，体积和温度发生变化的过程。

在绝热过程中，气体与外界之间没有能量的转移，因此其内能保持不变。

根据内能守恒定律，绝热过程中气体的温度变化与体积变化呈反比关系。

同样以一定量的理想气体为例，假设其体积从V₁变化到V₂，对应的温度由T₁变化到T₂。

根据绝热过程的特点，我们可以得到以下数学表达式：T₁V₁^(γ－1) = T₂V₂^(γ－1)其中，γ为气体的绝热指数，表示气体热容比。

对于单原子分子气体，γ约等于5/3；对于双原子分子气体，γ约等于7/5。

从上述公式中可以看出，当气体的体积增加时，温度会降低，反之亦然。

绝热过程的应用也非常广泛。

例如，在内燃机中，汽缸中的气体在燃烧过程中发生绝热膨胀，从而驱动活塞运动，产生功。

热学练习题理想气体的等温过程与绝热过程的比较在热学中，理想气体的等温过程和绝热过程是两个重要的概念。

虽然它们都涉及气体的热力学性质，但是两者之间存在着明显的区别。

本文将就理想气体的等温过程和绝热过程展开比较和分析。

一、理想气体的等温过程理想气体的等温过程是指在恒温条件下进行的过程。

在这个过程中，系统的温度保持不变，而气体的压力和体积会相应地发生变化。

根据理想气体的状态方程PV=nRT（式中P为气体的压力，V为体积，n为物质的量，R为气体常数，T为温度），我们可以得到等温过程的数学表达式为PV=常数。

在等温过程中，当气体的体积减小时，压力会增加，反之亦然。

这符合气体的玻意耳定律，即在恒温条件下，气体的压力和体积成反比。

在理想气体的等温过程中，工作与热量的转化也是平衡的，即所吸收的热量等于所做的功。

二、理想气体的绝热过程理想气体的绝热过程是指在没有热量交换的情况下进行的过程。

在这个过程中，气体的内能发生改变，但是温度保持不变。

根据绝热条件下的理想气体状态方程，我们可以得到绝热过程的数学表达式为PV^γ=常数。

在绝热过程中，当气体的体积减小时，压力会增加，但是由于没有热量交换，所以气体的温度也不会发生变化。

这符合绝热条件下的理想气体的关系，即压力和体积不再成反比，而是与体积的幂指数γ有关。

这个指数γ被称为绝热指数，对于单原子理想气体，γ=5/3；对于双原子理想气体，γ=7/5。

在绝热过程中，工作与热量的转化是不平衡的，即所吸收的热量不等于所做的功。

三、等温过程与绝热过程的比较1. 温度变化：等温过程中，气体的温度保持不变；绝热过程中，气体的温度也保持不变。

2. 压力变化：等温过程中，气体的压力和体积成反比；绝热过程中，气体的压力和体积不再成反比，而与体积的幂指数γ有关。

3. 热量交换：等温过程中，热量和功的转化是平衡的；绝热过程中，热量和功的转化是不平衡的。

4. 内能变化：等温过程中，气体的内能不变；绝热过程中，气体的内能发生改变。

热学试题理想气体的等温过程与绝热过程的深入比较热学试题：理想气体的等温过程与绝热过程的深入比较理想气体的等温过程和绝热过程是热学中常见的两种过程。

它们在气体物理性质、能量转化以及热力学循环中都占据重要地位。

本文将对等温过程和绝热过程进行深入比较，探讨其相似与差异，并分析其应用。

一、理想气体的等温过程等温过程指的是在恒温条件下，气体的温度保持不变的过程。

在理想气体的等温过程中，压强和体积成反比，即当体积增大时，压强减小；当体积减小时，压强增大。

这种关系可用以下方程表示：P1 * V1 = P2 * V2其中，P1和P2分别为过程开始和结束时的压强，V1和V2分别为过程开始和结束时的体积。

等温过程的特点是温度保持不变，因此，理想气体所受的压强和体积的乘积在任何时刻都相等。

二、理想气体的绝热过程绝热过程指的是在没有热量交换的情况下进行的气体过程。

在理想气体的绝热过程中，气体的内能保持不变，即Q=0，其中Q表示传递给气体或由气体吸收的热量。

绝热过程中，气体的压强与体积之间存在以下关系：P1 * V1^(γ) = P2 * V2^(γ)其中，γ为绝热指数，取决于气体分子数和自由度。

对于单原子分子的理想气体，γ=5/3；对于双原子分子的理想气体，γ=7/5。

绝热过程的特点是内能保持不变，因此，理想气体所受的压强和体积的乘积的幂次在任何时刻都相等。

三、等温过程与绝热过程的比较1. 物理性质比较：等温过程和绝热过程在物理性质上存在一定的差异。

等温过程中，气体的温度保持不变，因此分子之间的平均碰撞频率相对较高，分子间的相互作用较强。

而在绝热过程中，气体的温度变化较大，分子之间的平均碰撞频率较低，分子间的相互作用较弱。

2. 能量转化比较：等温过程中，气体与周围环境之间发生热量交换，但总的内能保持不变。

这意味着等温过程中，气体吸热量与放热量相等，热量转化效率较低。

而在绝热过程中，气体与周围环境之间没有热量交换，内能保持不变。

理想气体的等温过程与绝热过程理想气体是指在一定温度下，气体分子之间完全没有相互作用的气体模型。

在理想气体的热力学过程中，等温过程和绝热过程是两个重要的概念。

本文将分别介绍理想气体的等温过程和绝热过程，并探讨它们的特点和应用。

一、理想气体的等温过程等温过程是指在气体发生变化的过程中，温度保持不变。

对于理想气体而言，等温过程可以用以下方程来描述：PV = 常数（1）式中，P表示气体的压强，V表示气体的体积。

根据理想气体状态方程，PV = nRT，式中，n表示气体的物质的量，R是气体常数，T是气体的绝对温度。

结合方程（1）和PV = nRT，我们可以得到：nRT = 常数（2）由方程（2）可知，在等温过程中，气体的物质的量n和体积V是成反比的关系。

也就是说，在体积增大的同时，物质的量会减少，反之亦然。

这说明了在等温过程中，气体分子会随着体积的改变而发生数量的变化。

等温过程还有一个重要的特点是气体对外做功。

根据热力学的能量守恒定律，气体所做的功等于外界对气体做的功。

在等温过程中，气体扩大或收缩的功可以通过以下公式计算：W = - nRT * ln(V2/V1) （3）式中，W表示气体所做的功，V1和V2分别表示气体的初始体积和最终体积。

二、理想气体的绝热过程绝热过程是指在气体发生变化的过程中，没有热量的交换。

绝热过程的特点是温度和压强同时变化。

对于理想气体而言，绝热过程可以用以下方程来描述：PV^γ = 常数（4）式中，γ表示气体的绝热指数，对于大多数单原子理想气体而言，γ约等于5/3。

根据理想气体状态方程，PV = nRT，我们可以推导出绝热过程中，温度和压强的关系：T = (Pv^(γ-1))/(nR) （5）式中，Tv表示绝热过程中气体的温度。

由方程（5）可知，在绝热过程中，随着气体体积的减小，气体的温度也会随之降低。

反之，体积的增大会导致温度的升高。

这与等温过程中温度保持不变的特点形成了鲜明的对比。

气体主要热力过程的基本公式气体主要的热力过程包括等温过程、绝热过程、等容过程和等压过程。

这些过程有着各自独特的特点和基本公式。

1.等温过程：在等温过程中，气体的温度保持恒定，因此温度对于等温过程是一个常数。

根据理想气体状态方程PV=nRT，可以推导得到等温过程下的基本公式：a.等温压强与体积的关系：PV=常数。

在等温过程中，气体的温度保持不变，所以根据状态方程，压强P与体积V呈反比关系。

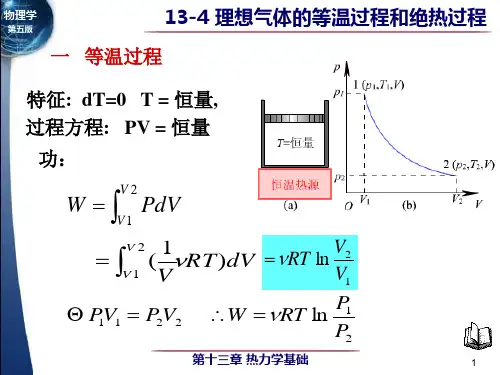
b.等温过程下物体做功：W = nRT ln(V₂/V₁)。

根据热力学第一定律，等温过程中气体所做的功等于气体的内能的减少，也等于热量的增加。

根据理想气体状态方程，可以推导得到等温过程下气体所做的功的公式。

2.绝热过程：在绝热过程中，气体与外界没有热量交换，因此绝热过程中不发生传热。

根据绝热过程中的基本公式：a.绝热条件下PV^γ=常数，其中γ为气体的绝热指数（也为比热容比）。

b.绝热过程下物体做功：W=(P₁V₁-P₂V₂)/(γ-1)。

根据热力学第一定律，绝热过程中气体所做的功等于气体的内能的减少，也等于热量的增加。

根据绝热条件下的基本公式，可以推导得到绝热过程下气体所做的功的公式。

3.等容过程：在等容过程中，气体的体积保持恒定，因此体积对于等容过程是一个常数。

根据理想气体状态方程，可以推导得到等容过程下的基本公式：a.等容压强与温度的关系：PαT。

在等容过程中，气体的体积保持不变，所以根据状态方程，压强P与温度T呈正比关系。

b.等容过程下物体做功：W=0。

在等容过程中，气体的体积保持不变，不进行体积的变化，故不做功。

4.等压过程：在等压过程中，气体的压强保持恒定，因此压强对于等压过程是一个常数。

根据理想气体状态方程，可以推导得到等压过程下的基本公式：a.等压体积与温度的关系：VαT。

在等压过程中，气体的压强保持不变，所以根据状态方程，体积V与温度T呈正比关系。

b.等压过程下物体做功：W=P(V₂-V₁)。

在等压过程中，气体的压强保持不变，所以根据热力学第一定律，气体所做的功等于气体的内能的减少，也等于热量的增加。

热学中理想气体的等温过程与绝热过程的研究在热学中，理想气体是一种非常重要的概念。

理解理想气体的行为对于研究物质的热力学性质至关重要。

在本文中，我们将研究理想气体的等温过程和绝热过程。

一、等温过程等温过程是指在温度不变的情况下改变气体的容积，从而改变气体的压强和密度的过程。

对于理想气体而言，等温过程是一个非常特殊的过程，因为理想气体的等温过程满足泊松定律。

泊松定律指出，在等温过程中，理想气体的压强与密度成反比。

即P∝1/V，其中P表示气体的压强，V表示气体的体积。

如果我们将温度和物质的物态方程考虑在内，可以得到PV=nRT，其中n表示气体的摩尔数，R为气体常数，T表示气体的温度。

根据泊松定律，可以推导出，对于理想气体，在等温过程中PV=constant。

二、绝热过程绝热过程是指在没有热量交换的情况下改变气体的容积，从而改变气体的压强和密度的过程。

在绝热过程中，理想气体的内能不会发生改变，因为没有热量传递。

因此，绝热过程也称为内能守恒过程。

绝热过程的一个重要特点是，理想气体的压强和密度的变化满足玻意耳定律。

玻意耳定律指出，在绝热过程中，理想气体的压强与密度成正比。

即P∝ργ，其中γ是热容比，表示气体在绝热过程中的热容与气体在等压过程中的热容之比。

对于单原子分子气体而言，γ=5/3；对于双原子分子气体而言，γ=7/5。

绝热过程可以用绝热指数k来描述，k=cp/cv，其中cp表示气体在等压过程中的比热容，cv表示气体在等容过程中的比热容。

对于理想气体而言，k=γ。

三、等温过程与绝热过程的区别从上述内容可以看出，等温过程和绝热过程有着明显的不同点。

等温过程中，理想气体的压强与密度成反比；绝热过程中，理想气体的压强与密度成正比。

这意味着，在等温过程中，气体的温度保持不变，而在绝热过程中，气体的温度会随着容积的改变而发生变化。

此外，等温过程和绝热过程的热容比也不同。

在等温过程中，热容比始终为1；在绝热过程中，热容比取决于气体的分子结构。

理想气体的等温过程与绝热过程计算理想气体的等温过程和绝热过程是热力学中常见的两种过程。

在本文中，我们将着重讨论这两种过程的计算方法和相关概念。

等温过程是指气体在保持恒定温度的条件下发生的过程。

在等温过程中，气体与外界交换热量，但由于温度不变，气体内部能量的平均值也保持不变。

根据理想气体状态方程PV=nRT，等温过程中气体的体积和压力成反比。

换句话说，当气体的体积增大时，压力会下降，反之亦然。

为了计算等温过程中气体的状态变化，我们可以使用维尔纳二次定律，即P1V1=P2V2，其中P1和V1是初始状态下的压力和体积，P2和V2是终态下的压力和体积。

这个方程的推导基于理想气体状态方程和等温过程的定义。

接下来，让我们进一步探讨绝热过程。

绝热过程是指气体在没有与外界交换热量的条件下发生的过程。

在绝热过程中，气体的内部能量发生变化，但没有热量的进出。

根据理想气体状态方程，绝热过程中气体的压力和体积满足PV^γ=常数，其中γ是气体的绝热指数。

对于单原子理想气体（如氦气），γ=5/3；而对于双原子理想气体（如氮气），γ=7/5。

与等温过程类似，为了计算绝热过程中气体的状态变化，我们可以使用维尔纳二次定律。

然而，在绝热过程中，由于没有热量交换，我们需要使用绝热指数γ来代替温度，在方程中的体积和压力关系为P1V1^γ=P2V2^γ。

通过上述的计算方法，我们可以得到等温过程和绝热过程中气体状态变化的结果。

这些结果对于热力学系统的分析和工程应用具有重要意义。

除了等温过程和绝热过程，理想气体还有其他类型的过程，如等容过程和等压过程。

每种过程在计算上都具有一定的特点和方法。

总结起来，理想气体的等温过程和绝热过程是热力学中重要的概念。

通过合适的计算方法，我们可以得到气体在这两种过程中的状态变化。

这些计算结果对于热力学系统的研究和实际应用非常有价值。

在实际工程中，我们可以利用这些计算结果来设计和优化热力学系统，提高能源利用效率。