绝热过程、多方过程
- 格式:ppt
- 大小:350.50 KB
- 文档页数:13





热力学第一定律一、基本概念1、体系和环境(1)、体系和环境体系:作为研究对象的物质及其所在的空间称为体系;环境:体系以外且与体系密切相关的物质及其所在空间称为环境;界面:体系和环境之间存在有界面,界面可以是容器的器壁,也可以是假想的界面,本质上,界面是认为设想的几何面,其中不包含物质,不具备物理和化学性质。
(2)、体系的分类体系和环境之间可以有物质和能量的交换,依据此,可将体系分为敞开体系、封闭体系、隔离体系。
①、敞开体系:体系与环境之间既有能量交换又有物质交换;②、封闭体系:体系与环境之间只有能量交换而无物质交换;③、隔离体系:体系与环境之间既无能量交换也无物质交换。
2、状态和状态函数(1)、状态和状态函数的定义状态:状态是指体系所有性质的总体表现;状态函数:体系的热力学性质称为状态函数。
(2)、状态函数的性质:①、体系的状态一定,状态函数就有定值。
②、状态函数的变化值只取决于始、末状态,与变化的经历无关。
③、状态函数的微分为全微分。
(3)、状态函数的分类。
①、广度性质:体系的广度量与物质的数量成正比,如V,U等,它具有加和性②、强度性质:体系的强度量与物质的数量无关,如T,p等,它不具有加和性。
(4)、热力学平衡态一定条件下,体系中各个相的宏观性质不随时间变化,将体系与环境隔离体系的性质仍不改变的状态。
热力学平衡态应满足如下条件:①、热平衡:体系中的各个部分温度相等,即体系内部处于热平衡,有单一的温度;②、力学平衡:体系内部处于力平衡,有单一的压力;③、相平衡:体系内部各相之间的分布达到平衡,宏观上没有任何一种物质从一个相转移到另一个相;④、化学平衡:体系内部处于化学平衡,宏观上表现为体系的组成不随时间变化。
(5)、状态函数的数学性质若状态函数①、单值性:环形积分等于零,,或可写作全微分性质:③、归一化关系④、复合函数的偏微分,则⑤、偏微商的分离⑥、完全微分3、过程与途径在一定环境条件下,体系发生由始态到终态的变化,则称体系发生了一个热力学过程,(1)、变化过程①、等温过程:体系始态与终态温度相同,且变化过程中温度始终等于环境温度、等于;②、等压过程:体系始态与终态压力相同,且变化过程中压力始终等于环境压力、等于;④、体系由变化到,程,计算其热力学函数,如热力学能、熵变等要设计过程。




理想气体多方过程的概念理想气体多方过程是热力学中用来描述理想气体状态变化的一种过程。
在理想气体多方过程中,气体的体积、压强和温度会同时发生变化,且遵循一定的数学关系。
其特点是气体分子之间没有相互作用、无摩擦且无内能损失。
在理想气体多方过程中,可以通过改变气体的体积、压强或温度来实现不同的多方过程,包括等体过程、等压过程、等温过程、绝热过程和绝热指数过程等。
下面将对这些多方过程进行详细介绍。
1. 等体过程(Isochoric Process):在等体过程中,气体的体积保持不变,即气体分子在容器中自由运动,但体积不发生改变。
在等体过程中,由于体积不变,所以系统对外不做功。
根据理想气体状态方程PV=nRT可知,当体积不变时,温度和压强呈正比关系。
2. 等压过程(Isobaric Process):在等压过程中,气体的压强保持不变,即气体在容器中扩张或收缩,但压强不发生改变。
在等压过程中,气体对外做功的大小等于压强乘以体积的变化量。
根据理想气体状态方程PV=nRT可知,在等压过程中温度和体积呈正比关系。
3. 等温过程(Isothermal Process):在等温过程中,气体的温度保持不变,即气体在容器中的温度始终为常数。
在等温过程中,根据理想气体状态方程PV=nRT可知,温度不变意味着压强和体积的乘积也保持不变。
在等温过程中,气体对外做功与体积的改变量和压强的大小有关。
4. 绝热过程(Adiabatic Process):在绝热过程中,气体与外界没有热量交换,即没有热量进入或离开气体系统。
由于没有热量交换,绝热过程中的气体内能保持不变。
在绝热过程中,气体分子之间发生弹性碰撞,从而使得气体的温度、体积和压强发生变化。
5. 绝热指数过程(Adiabatic Index Process):绝热指数过程是绝热过程的一种特例,指气体绝热过程中绝热指数(多方反应的比例系数)保持不变。
绝热指数过程常用于描述气体在容器中的膨胀或压缩过程。

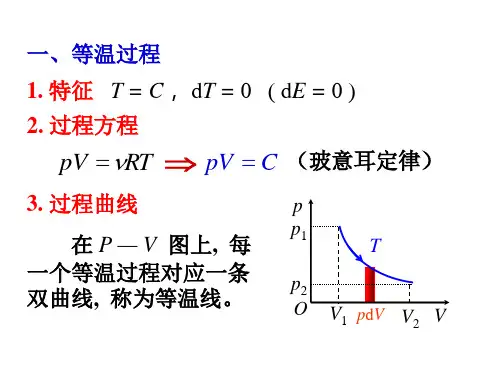
§6-5 理想气体的等温过程和绝热过程一、等温过程(Isothermal Process )1.特点:理想气体的温度保持不变,T =const 。
2.过程曲线:在PV 图上是一条双曲线,叫等温线。
3.过程方程:P 1V 1= P 2V 24.内能、功和热量的变化系统经过等温过程,从状态()T V P ,,11变成()T V P ,,22内能 012=-=∆E E E功 ⎰=21V V T PdV W由气体状态方程 RT M m PV =得 VRT M m P 1= 12ln 121V V RT M m dV V RT M m W V V T ==⎰——用体积表示。
用压强表示为21ln P P RT M m W T = 热量:由热力学第一定律得 1221ln ln V V RT M m P P RT M m Q T ==5.特征:在等压过程中,系统从外界吸收的热量,全部用来对外作功。
注意:对于等温过程,不能定义摩尔热容;如果要定义,则∞=C 。
二、绝热过程(Adiabatic Process )1.特点:系统与外界没有热量交换的过程,Q =0。
2.内能、功和热量的变化系统经过绝热过程,从状态()11T V P ,,变成()22T V P ,,内能 ()12,12T T C Mm E E E m V -=-=∆ 热量 Q =0由热力学第一定律 0=+∆=W E Q ,得功 ()12,T T C Mm W m V -=- 用状态参量P ,V 表示,根据状态方程R PV T M m =,可知()1 22112211,-=-γV P V P V P V P R C W mV --= 证明:由定义可知,m V m V m V m V mP C R C R C C C ,,,,,1+=+==γ 因而1,-=γm V C R 故 11,-=γR C m V 因而 12211-γV P V P W -= 3.特征:在绝热过程中,系统对外界所作的功是由于系统内能的减少来完成的。
理想气体的多方过程方程推导理想气体的多方过程方程推导理想气体是一个非常重要的物理模型,而多方过程是其中的一个重要概念。
本文将为大家介绍理想气体的多方过程方程推导。
1.多方过程的定义多方过程是指在系统中,压强、体积、温度这三个物理量不断变化的过程。
在实际应用中,多方过程通常以绝热过程为典型代表。
2.多方过程的方程根据热力学理论,理想气体的多方过程可以表示为以下方程:pV^n=C其中,p表示气体的压强,V表示气体的体积,n表示多方过程中的指数,C为常数(在多方过程中,C的值不断变化)。
3.多方过程方程的推导根据热力学第一定律以及绝热过程的定义,有如下公式:dU=-pdV其中,dU表示气体内能的微小变化。
当气体发生绝热过程时,系统内没有热量的输入和输出,因此dU=0。
代入上式,得到:0=-pdV由于多方过程中三个物理量的变化不止一个,因此我们需要对该方程进行变形。
根据气体状态方程pV=RT,其中R为气体常数,将其代入0=-pdV 式子中,可得:0=-\frac{RT}{V}dV整理后,得到:V^n dV +C=0同时,将多方过程方程式子中的pV^n=C带入上式中,得到:V^n dV+pV^n dV=0因此,可以将上式整理成如下形式:(dV/V)+(n/(1-n))(dp/p)=0将上式积分,得到多方过程方程。
具体地,积分过程如下:∫(dV/V)+(n/(1-n))dp/p=-∫(n/(1-n))即:ln(V)+\frac{n}{1-n}ln(p)=const整理,可得到多方过程方程:pV^n=C4.总结本文介绍了理想气体的多方过程方程推导过程,让大家了解了其数学上的基础。
对于理解理想气体在物理学、化学等科学领域的应用,也有一定的帮助。