17
作用
③ 换底公式
换底
log a
b
log c log c
b a
(a 0且a 1 , c 0且c 1, b 0)
18
2.对数函数
① 对数函数定义： y=loga x (a>0, 且a≠1)
19
②对数函数图象和性质：
0<a<1
y
图象 定义域
(1,0)
x
0
x=1
y=logax (0<a<1)
R
(0,+∞)
a>1
y 1 y=1
0
x
R
(0,+∞)
性质
1)在R上是减函数; 2)过定点(0,1) 3)当x>0时, 0<y<1;
当x<0时, y>1.
1)在R上是增函数; 2)过定点(0,1) 3)当x>0时, y>1;
当x<0时, 0<y<1.
15
对数函数模块
1.对数
① 对数定义：
转化
当a 0,且a 1时，a x N x loga N
若g[ f ( x)] x2 x 1,求a的值。
23
例2.求下列问题的定义域：
(1) y
11 2 x 3 ; 例2.求下列问题的定义域：
2 x x ① y 2x 3 1 1 2 x x
(2)若f ( x)的定义域为[0，2]，求f ( x x) ②若f (x)的定义域为[0，2]，求f (x2 x)
当0<x<1时, y<0. 20
幂函数模块
1.幂函数的定义：
一般地，函数 y=xa( 为常数)叫
做幂函数.
21
2.幂函数的一般研究方法：
1）借助函数模块分析； 2）利用图像法分析。
3.幂函数的一个重要特点：
0 幂函数在第一象限为增函数； 0 幂函数在第一象限为减函数。
22
例1.已知f ( x) 2x a, g( x) 1 ( x2 3), 4
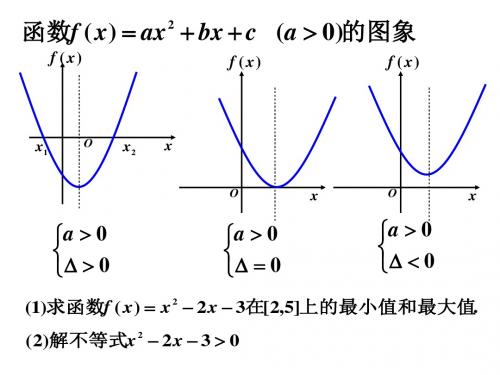
5).应用 : 利用二次函数的图象可 以来解一元二次不等式 , 讨论一元二次方程的实 根的分布情况.
9
指数函数、对数函数 与幂函数
10
乘方(指数)、开方、对数三者间的联系
开方
b N (b为奇数）
已知指数、幂,
a b N (b为偶数） 求底数
乘方(指数幂) ab N
对数 b loga N
已知底数、指 数,求幂
已知底数、真 数,求指数
11
指数函数模块
1.指数幂的运算性质：
(ar )s ars (a 0, r、s Q) an( aaramrr )sssamnaa(rarrss((0aa, m、00,n,rr、、Nss*,n QQ1))) aaaaaaarrrsrsrsassaaarrarsrrss(((assaa(a000,,,0rrr,、、、r、ssss QQQQ))) )
几个重要结论： loga a 1，loga 1 0 , aloga N N
16
② 对数运算: (a>0, a≠1, N>0)
loga M n n loga M
log a
n
M
1 n loga
M
loga (M N ) loga M loga N
M loga N loga M loga N
x
7
4).单调性 : ①当a 0时,在(, b ]上是减函数, 2a
在( b ,)上是增函数. 2a
②当a 0时,在(, b ]上是增函数, 2a
在( b ,)上是减函数.
Hale Waihona Puke 2ayy x
b
2a
O
x
x b 2a
O
x
8
4).奇偶性 : 二次函数y ax2 bx c (a 0), ①当b 0时,函数是偶函数; ②当b 0时,函数是非奇非偶函数;
2.二次函数的三种表示形 式 : (1)一般式 : f ( x) ax2 bx c (a 0) (2)顶点式 : f ( x) a( x h)2 k (a 0) (3)两根式 : f ( x) a( x x1 )( x x2 ) (a 0)
6
3.二次函数的内容 :
1).定义域 : R
12
2.负分数指数幂的意义：
m
an
1
m
an
n
1 am
(a 0, m、n N * , n 1)
3.零指数幂的意义：
a0 1(a 0)
13
4.指数函数的定义：
一般地，函数 y=ax(a>0且a≠1) 叫做指数函数.
14
5.指数函数的图象和性质：
图象
定义域 值域
0<a<1 y
1 y=1
0
x
函数模块
1
1. 函数的三要素 2. 函数的表示法
1)定义域; 2)对应关系; 3)值域.
1)解析法; 2)图象法 (数形结合，以点为主)；
3)列表法
2
3. 离散型函数 连续型函数
定义域是否连续
函 数
模
4. 分段函数 （整体部分思想）
块
3
5. 函数的单调性 6. 函数的奇偶性
1)定义法;
2)图象法;
2).值域 : ①当a 0时, 值域为[4ac b2 ,) 4a
②当a 0时, 值域为(, 4ac b2 ] 4a
3).图象是抛物线, 对称轴是x b , 2a
顶点坐标(,
b
4ac b2
,
)
y
2a 4a
①当a 0时,开口向上; ②当a 0时,开口向下;
O
x
x b 2a
y x
b
2a
O
3)复合函数： 函
同增异减
数
1)定义法;
模
2)图象法.
块
4
7.反函数 1)抓住“反”
2)求反函数的步骤
①确定定义域 ②反求 ③互换 x、y
3)互为反函 数的特点
1. 互为反函数的图象关于 y = x对称；
2. 点(a, b)在一个函数上, 则 (b, a)必在其反函数上。
5
二次函数
1.一元二次函数的定义 : 形如f ( x) ax2 bx c (a 0)的函数.
2
的定义域。
的定义域.
24
例3.求下列各函数的值域： 1)函数f ( x) 1 在[2，0）（0，3）上的值域
x 是 ____________ . 2)函数y 3x 值域是 _________ .
3x 4
25
例4.已知函数f ( x) x (a, b为常数， ax b
且a 0)满足f (2) 1,方程f ( x) x有唯一解， 求： 1)函数f ( x)的解析式; 2) f [ f (3)]的值.
(0,+∞)
值域 性质
R
(1)过定点(1, 0) (2)在(0,+∞)上是减
函数; (3)当x>1时, y<0;
当0<x<1时, y>0.
a>1
y x=1 y=logax
(a>1)
0 (1,0) x
(0,+∞)
R
(1)过定点(1, 0) (2)在(0,+∞)上是增
函数; (3)当x>1时, y>0;
