材料力学扭转

材料力学扭转材料力学是研究材料在外力作用下的变形和破坏规律的一门学科，而扭转则是材料力学中非常重要的一种变形形式。

在工程实践中，我们经常会遇到各种扭转现象，比如轴承、螺纹、螺栓等零部件的扭转变形。

因此，了解材料力学中的扭转现象对于工程设计和实际应用具有重要意义。

首先，我们来看一下什么是扭转。

扭转是指材料在外力作用下沿着一定轴线发生的旋转变形。

在扭转过程中，材料内部会受到剪切应力的作用，从而导致材料发生扭转变形。

扭转变形不仅会影响材料的外观和尺寸，还会对材料的力学性能产生影响。

在材料力学中，我们通常用剪切模量来描述材料的扭转性能。

剪切模量是指材料在扭转过程中所表现出的抗扭转能力。

剪切模量越大，材料的抗扭转能力就越强，反之则越弱。

因此，在工程设计中，我们需要根据材料的剪切模量来选择合适的材料，以满足工程的扭转性能要求。

除了剪切模量，材料的断裂韧性也是影响材料扭转性能的重要因素。

断裂韧性是指材料在扭转过程中抵抗断裂的能力。

材料的断裂韧性越大，其扭转性能就越好，能够更好地抵抗扭转变形和破坏。

因此，在工程设计中，我们还需要考虑材料的断裂韧性，以确保材料在扭转过程中不会发生过早的断裂。

此外，材料的微观结构也会对其扭转性能产生影响。

晶粒的大小、形状以及晶界的性质都会影响材料的扭转性能。

一般来说，晶粒越细小，晶界越强化，材料的扭转性能就会越好。

因此，在材料的制备过程中，我们需要通过控制材料的微观结构来提高其扭转性能。

总的来说，材料力学中的扭转现象是工程设计中不可忽视的重要问题。

了解材料的扭转性能，选择合适的材料，并通过控制材料的微观结构来提高其扭转性能，对于保证工程零部件的稳定性和可靠性具有重要意义。

希望本文能够对大家对材料力学中的扭转问题有所帮助。

材料力学扭转知识点总结1. 概述材料力学是研究材料的力学性能和行为的一门学科，而扭转则是指在材料中施加扭矩力的作用。

材料力学扭转是材料力学中重要的一个分支，涉及到材料的变形、强度、破坏等方面的内容。

本文将对材料力学扭转的主要知识点进行总结。

2. 扭转应力扭转应力是材料在扭转加载下产生的应力。

与拉伸、压缩应力相比，扭转应力呈圆柱对称分布，沿着截面的半径方向逐渐减小，最大应力出现在材料的表面。

扭转应力的大小与施加的扭矩、材料断面的形状和尺寸有关。

3. 扭转变形扭转加载下，材料会产生扭转变形。

扭转变形主要表现为材料的轴线在垂直截面上的位移，称为扭转角。

扭转角的大小与施加的扭矩、材料的几何形状和材料的性质有关。

当材料的弹性变形超过一定范围时，会发生塑性变形，导致材料的破坏。

4. 扭转刚度扭转刚度是指材料对扭转加载的抵抗能力。

扭转刚度可以由杨氏模量计算得出，与材料的剪切模量相关。

较高的扭转刚度意味着材料在扭转加载下能够保持较小的变形，具有较好的强度和刚度。

5. 扭转强度扭转强度是指材料在扭转加载下破坏的能力。

与拉伸强度、压缩强度类似，扭转强度也是一个材料的重要指标，用来评估材料在扭转加载下的耐用性能。

6. 扭转应力-应变关系材料在扭转加载下的应力-应变关系可以描述材料在扭转过程中的力学行为。

对于线弹性材料而言，扭转应力与扭转角之间呈线性关系，称为胜肽方程。

扭转应力-应变关系可用来预测材料的扭转刚度、扭转变形等力学性能。

7. 扭转实验扭转实验是研究材料力学扭转性能的重要手段。

通过在材料上施加一定的扭矩载荷，并测量相应的应变和变形，可以获取材料的扭转应力-应变关系、扭转刚度等信息。

扭转实验可以通过机械试验机、扭转试验机等设备进行。

8. 扭转设计与应用在工程实践中，材料力学扭转的理论和实验成果被广泛应用于各种设计和制造中。

例如，扭杆、螺旋弹簧、传动轴等都是在扭转加载下工作的零件，需要考虑材料的扭转强度、刚度等特性。

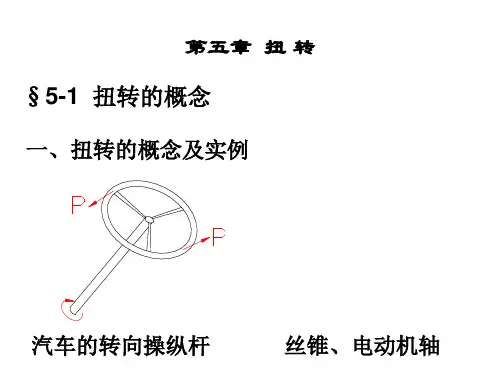
第3章 扭转1、扭转的概念：杆件的两端个作用一个力偶，其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线，致使杆件的任意两个横截面都发生绕轴线的相对转动，即为扭转变形。

2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中，e M 为外力偶矩。

又由截面法：e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。

规定：若按右手螺旋法则把T 表示为矢量，当矢量方向与研究部分中截面的外法线的方向一致时，T 为正；反之为负。

3、纯剪切（1）薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=（2）切应力互等定理：在单元体相互垂直的两个平面上，切应力必然成对存在，且数值相等；两者都垂直于平面的交线，方向则共同指向或背离这一交线。

（3）切应变 剪切胡克定律：当切应力不超过材料的剪切比例极限时，切应变γ与切应力τ成正比。

γτG = G 为比例常数，称为材料的切变模量。

弹性模量E 、泊松比μ和切变模量G 存在关系：)1(2μ+=EG 4、圆轴扭转时的应力（1）变形几何关系：距圆心为ρ处的切应变为dxd ϕργρ=（2）物理关系：ρτ为横截面上距圆心为ρ处的切应力。

dxd G G ϕρτγτρρρ=⇒= （3）静力关系：内力系对圆心的力矩就是横截面的扭矩：dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式：dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩（截面二次极矩）横截面上距圆心为ρ的任意点的切应力：pI T ρτρ=ρ最大时为R ，得最大切应力：pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。

则tW T =max τp I 和t W 的计算（1）实心轴：3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===（2）空心轴：)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角，l 为两横截面间的距离。

材料力学扭转材料力学中的扭转是指在材料上施加一个力矩，使其绕一个轴进行转动的现象。

扭转在工程领域中广泛应用，例如在机械设计、结构设计以及材料测试等方面。

材料力学中的扭转主要涉及到弹性力学和塑性力学两个方面。

在弹性力学中，当材料受到扭矩时，它会发生弯曲变形以及剪切变形。

而在塑性力学中，材料会发生塑性流动，产生塑性变形。

在材料力学中，对于扭转的研究主要关注以下几个方面：1. 扭转角度：扭转角度是指材料在扭转过程中绕轴旋转的角度。

扭转角度通常以弧度为单位进行计量。

2. 扭转力矩：扭转力矩是作用在材料上的力矩，它使材料发生扭转。

扭转力矩的大小与施加的力及材料的形状及性质有关。

3. 扭转应变：材料在扭转过程中会发生弯曲变形和剪切变形，从而导致产生应变。

扭转应变是指材料在扭转过程中产生的应变。

4. 扭转刚度：扭转刚度是指材料抵抗扭转变形的能力。

材料的扭转刚度与其形状、尺寸以及材料的性质密切相关。

对于材料力学中的扭转现象，研究者可以通过实验和数值模拟来进行研究。

实验可以通过应用一定的扭转力矩使试样产生扭转，然后测量扭转角度和应变等参数来分析材料的扭转性能。

数值模拟可以通过建立数学模型和使用计算机进行仿真来研究材料的扭转行为。

在工程实际应用中，对于扭转现象的研究对于设计和优化机械结构以及预测和评估材料的强度和可靠性有重要意义。

通过研究材料的扭转行为，工程师可以合理设计和选择材料，从而确保结构的稳定性和安全性。

综上所述，材料力学中的扭转是指在材料上施加一个力矩，使其绕一个轴进行转动的现象。

材料的扭转行为涉及到弹性力学和塑性力学方面的研究，对于工程实践中的结构设计和材料选择具有重要意义。