表面硬度过程能力分析表spc-100及CPK

SPC Process Capability (Cpk) and Statistical Process Control (SPC)Continuous Process Improvement乙选手甲选手谁的成绩好呢?谁较有潜力呢?你会选谁当选手呢?您的工厂/服务品质/供应商若有问题,您希望是甲状况还是乙状况呢?品质的一致性过程能力分析●何谓过程能力？制造程序潜在精度的测定，以衡量加工的一致性过程加工品质在一定因素与正常管制状态下满足技术标准的程度●基本精神将过程能力计量化将测得的制程能力与品质要求作比较过程能力与生产能力有本质的区别，过程能力是指质量上所能达到的程度，而生产能力是指数量上所能达到的程度，一个指质量，一个指数量。

过程能力靶心图Cp > 1.67Cpk >1.67Cpk >1.33正态分布正态分布基础知识34.13%13.595%2.14%0.135%+3σ5统计基础知识正态分布基础知识μ±kσ在内的概率在外的概率μ±0.67σ50.00%50.00%μ±1σ68.26%31.74%μ±1.96σ95.00% 5.00%μ±2σ95.45% 4.55%μ±2.58σ99.00% 1.00%μ±3σ99.73%0.27%6CPK 的计算公式-易于理解为单侧下限过程能力指数为单侧上限过程能力指数CPK=Min {CPL ，CPU} USL---表示规范限的上限值(上公差)LSL---表示规范限的下限值(下公差)T ---表示规范限的宽度,通常指公差---表示样本的平均值µ---规格中心值σ---标准差,反映数据的离散程度Cpk 等于对上公差的Cp 和对下公差的Cp 中二者较小的CPK 的计算公式样本的标准差σ按下面的公式计算而得：σ=()121−−∑=n x x ni i 计算CPK 时，我们一般选用100的样本数。

spc中cp\cpk\ppk等等级标准作者: sea_kang(站内联系TA)收录: 2009-07-17 发布: 2009-07-17Cp、Cpk、Pp、Ppk过程能力计算及评价方法：1．稳定过程的能力指数Cp、Cpk计算及评价方法：（1）计算公式：K=2︱M-μ︱/T注：T=规格上限USL-规格下限LSL，规范中心M= （USL+LSL）/2，μ为过程输出中心。

（A. Cp = T / 6σ（当产品和/或过程特性为双边规格时）或Cpu（上稳定过程的能力指数）=（USL-μ）/3σ（当产品和/或过程特性为单边规时）Cpl（上稳定过程的能力指数）=（μ-LSL）/3σ（当产品和/或过程特性为单边规时）注：σ=R / d2 （ R 为全距之平均值，d2为系数，与抽样的样本大小n有关，当n = 4时，d2 = 2.059；当n = 5时，d2 = 2.3267）B. Cpk=min{ USL-μ, μ-LSL}/3σ=(1-K)*Cp当产品特性为单边规格时，Cpk值即以Cpu值或Cpl值计算，但需取绝对值；Cpk 值取Cpu值和Cpl值中的最小值。

(2) 等级评价及处理方法：等级 Cp值判断处理方法等级说明特级CP≥1.67过程能力过剩为提高质量，对关键项目再次缩小公差范围：为提高效率降低成本放宽波动幅度，减低设备等级。

Cp值当T与3σ的比越大，Cp值也越大，也就是说过程越稳定。

1级 1.67＞CP≥1.33过程能力充分不是关键项目时可：1.放宽波动幅度。

2.降低对材料的要求。

3.减少检验的频次。

2级 1.33＞CP≥1过程能力尚可必须用控制图或其他方法进行控制和监督：对产品按常规进行检验。

3级 1＞CP≥0.67过程能力不足分析散步大的原因，全数检查或增加检验频次。

4级 0.67＞ CP 过程能力严重不足停止继续加工，找出原因。

否则全数检查挑选出不合格品。

Cpk等级评价等级 Cpk值改进措施处理方法等级说明A Cpk≥1.67继续保持制程非常稳定，继续保持，当Cpk大于2倍时，可以考虑缩小规格。

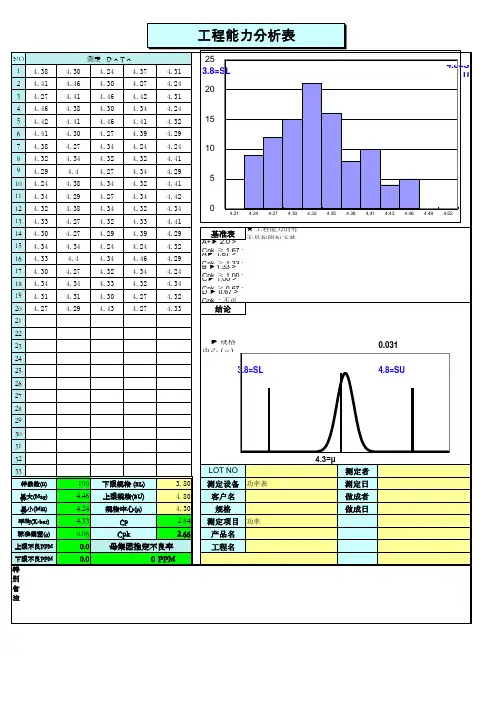
NO测定 D A T A 14.38 4.30 4.24 4.37 4.31 3.8=SL 4.8=SU 24.41 4.46 4.30 4.27 4.2434.27 4.41 4.46 4.42 4.3144.46 4.38 4.30 4.34 4.2454.42 4.41 4.46 4.41 4.3264.41 4.30 4.27 4.39 4.2974.38 4.27 4.34 4.24 4.2484.32 4.34 4.32 4.32 4.4194.29 4.4 4.27 4.34 4.29104.24 4.38 4.34 4.32 4.41114.34 4.29 4.27 4.34 4.42124.32 4.38 4.34 4.32 4.34134.33 4.27 4.32 4.33 4.41144.30 4.27 4.29 4.39 4.29基准表★ 工程能力的有无是按照如下基准来判断154.34 4.34 4.24 4.24 4.32A+▶ 2.0 > Cpk ≥ 1.67 : 优,应当保持164.33 4.4 4.34 4.46 4.29A ▶ 1.67 > Cpk ≥ 1.33 : 能力良好，状态稳定，但应尽力提升为A ＋级174.30 4.27 4.32 4.34 4.24 B ▶1.33 > Cpk ≥ 1.00 : 状态一般，应利用各种资源及方法将其提升为 A 级184.34 4.34 4.33 4.32 4.34C ▶ 1.00 > Cpk ≥ 0.67 : 差 制程不良较多，必须提升其能力194.31 4.31 4.30 4.27 4.32 D ▶ 0.67 > Cpk : 不可接受,其能力太差，应考虑重新整改设计制程204.27 4.29 4.43 4.27 4.33结论212223▶ 规格中心 (μ) 与 测定 平均值的差异 :0.03124253.8=SL4.8=SU 262728293031324.3=μ33LOT NO 测定者样品数(n)100下限规格 (SL) 3.80测定设备功率表测定日最大(Max)4.46上限规格(SU) 4.80客户名做成者最小(Min)4.24规格中心(μ) 4.30规格做成日平均(X-bar)4.33Cp 2.84测定项目功率标准偏差(σ)0.06Cpk 2.66产品名上限不良PPM0.0母集团推定不良率工程名下限不良PPM 0.00PPM 特别备注工程能力分析表0 5 10 15 20 25 4.21 4.24 4.27 4.30 4.32 4.35 4.38 4.41 4.43 4.46 4.49 4.52。

CPK与PPK两者在SPC品质分析中的应用摘要:在进行过程质量统计分析的时候,工序能力指数Cpk(Index of Process Capability与过程能力指数Ppk(Index of Process Performance是评价过程及改进方向和目标的两个重要指标。

质量管理中数理统计的理论和方法非常重要。

由于每天生产产品的质量,如工件的厚度、表面粗糙度等不断变动的缘故,为了加工出厚度均匀、粗糙度一致的工件,即使对加工环境的温度、湿度,对切削时的进刀量等操作条件做出严格的规定,实际生产出来的产品质量仍然存在波动。

而且上面所列出的加工条件固定不变也是难以办到的事,这些加工条件也存在着一定程度的波动,因此工序质量在各种影响因素制约下,呈现波动特性。

统计方法能够对这些波动的状况及其相互关系进行定量分析,是监控、改进产品质量非常有用的工具。

工序与过程能力指数在质量控制中越来越频繁地使用。

近来随着生产力的高度发展,对产品质量和服务质量的要求不断提高,不合格品率越来越低,而与其对应的过程能力指数要求越来越大。

这反映了生产能力的进步、不合格品率下降、经济效益的提高。

Cpk主要用于周期性的过程评价,而Ppk 则用于实时过程性能研究和初始过程能力评估。

Cpk 反映的是在稳定状态下的实际加工能力,有助于过程管理水平的提高。

Ppk 因其具有不同于Cpk 的特点,反映了实时过程的性能,可对当前的过程性能有更多的了解。

总而言之,将过程能力指数和过程性能指数联合起来进行研究,有助于为企业提供一套准确的过程管理与过程控制方法。

CPK与PPK的区别1cpk 主要是子组间的变差产生,所以数据要分组,也就是说,采值是进行分组,涉及到子组,子组容量,采值频次等。

它针对的是一个长期的过程。

做cpk时,过程要求受控。

2Ppk是整体变差的影响,它不考虑采值的过程,可以连续采值也可以间断采值。

3PK的评价过程是稳定过程,PPK可以不是稳定的过程;CPK的样本容量是30~50,PPK的样本容量是大于或等于100;CPK评价的是单批(几小时或几天,PPK评价的是多批(几周或几个月。

日期
地点工厂:部门:
质检部
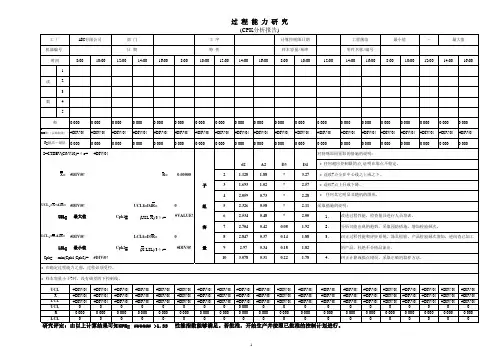
过 程 信 息
统 计值 描
值零件
零件号:零件名称重要趋势的数据点
X 图
R 图
读数125图纸号工程更改上升
连续点数44下公差限21.4176模具模具号:型腔号
数量
22标准值0.0000尺寸
质量特性描述单位
下降
连续点数43上公差限21.4876标准值21.4376
上公差0.05
下公差lower -0.02数量
12总和2,680.8450下限
21.4176
标准值
上限
21.4876
超差点数
总平均值 ( X )21.4468最大值
21.4690
最小值
21.4270
超出下控制限的点数0
超出上控制限的点数
极差均值 (R)
0.0124
D 2 值(n=4) 2.0590
上限能力指数(CPU)
2.2605
过 程 能 力 指 数 统 计
1.4852
1.4832
1.484
1.485
1.486
平均值
21.430
21.440
21.450
21.460
21.470
21.480
21.490
21.500
平均值平均值(X 图)
上下公差(bilateral)单边下公差(MIN)
单边上公差(MAX)。