2019-2020年中考数学试卷解析分类汇编：矩形菱形与正方形(最新整理)

矩形菱形与正方形一、选择题1. （2019·云南省昆明市·4分）如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若=，则3S△EDH=13S△DHC，其中结论正确的有（）A．1个 B．2个 C．3个 D．4个【考点】正方形的性质；全等三角形的判定与性质．【分析】①根据题意可知∠ACD=45°，则GF=FC，则EG=EF﹣GF=CD﹣FC=DF；②由SAS证明△EHF≌△DHC，得到∠HEF=∠HDC，从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=180°；③同②证明△EHF≌△DHC即可；④若=，则AE=2BE，可以证明△EGH≌△DFH，则∠EHG=∠DHF且EH=DH，则∠DHE=90°，△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2．【解答】解：①∵四边形ABCD为正方形，EF∥AD，∴EF=AD=CD，∠ACD=45°，∠GFC=90°，∴△CFG为等腰直角三角形，∴GF=FC，∵EG=EF﹣GF，DF=CD﹣FC，∴EG=DF，故①正确；②∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF≌△DHC（SAS），∴∠HEF=∠HDC，∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°，故②正确；③∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF≌△DHC（SAS），故③正确；④∵=，∴AE=2BE，∵△CFG为等腰直角三角形，H为CG的中点，∴FH=GH，∠FHG=90°，∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，在△EGH和△DFH中，，∴△EGH≌△DFH（SAS），∴∠EHG=∠DHF，EH=DH，∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°，∴△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，如图所示：设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC=×HM×CD=3x2，S△EDH=×DH2=13x2，∴3S△EDH=13S△DHC，故④正确；故选：D．2．（2019·山东省东营市·3分）如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为点F ，连接DF ，分析下列四个结论：①△AEF ∽△CAB ；②CF ＝2AF ；③DF ＝DC ；④tan ∠CAD ＝2．其中正确的结论有( )A.4个 B ．3个 C ．2个 D ．1个第10题图DA【知识点】特殊平行四边形——矩形的性质、相似三角形——相似三角形的判定与性质、锐角三角函数——锐角三角函数值的求法【答案】B.【解析】∵矩形ABCD 中，∴AD ∥BC .∴△AEF ∽△CAB ….......................①正确；∵△AEF ∽△CAB ，∴AF CF ＝AE BC ＝12，∴CF ＝2AF ……………………………②正确； 过点D 作DH ⊥AC 于点H .易证△ABF ≌△CDH (AAS ).∴AF ＝CH . ∵EF ∥DH ,∴AF FH ＝AE ED＝1.∴AF ＝FH .∴FH ＝CH . ∴DH 垂直平分CF .∴DF ＝DC . ……………………………………………③正确；第10题答案图DA设EF ＝1，则BF ＝2.∵△ABF ∽△EAF .∴AF EF ＝BF AF .∴AF ＝EF •BF ＝1×2＝ 2. ∴tan ∠ABF ＝AF BF ＝22.∵∠CAD ＝∠ABF ，∴tan ∠CAD ＝tan ∠ABF ＝22.…………④错误. 故选择B. 【点拨】本题考查了矩形的性质、相似三角形的判定和性质，图形面积的计算，锐角三角函数值的求法，正确的作出辅助线是解本题的关键．3．（2019·山东省菏泽市·3分）在▱ABCD 中，AB=3，BC=4，当▱ABCD 的面积最大时，下列结论正确的有（ ）①AC=5；②∠A+∠C=180°；③AC ⊥BD ；④AC=BD ．A ．①②③B ．①②④C ．②③④D ．①③④【考点】平行四边形的性质．【分析】当▱ABCD 的面积最大时，四边形ABCD 为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD ，根据勾股定理求出AC ，即可得出结论．【解答】解：根据题意得：当▱ABCD 的面积最大时，四边形ABCD 为矩形，∴∠A=∠B=∠C=∠D=90°，AC=BD ，∴AC==5，①正确，②正确，④正确；③不正确；故选：B ．【点评】本题考查了平行四边形的性质、矩形的性质以及勾股定理；得出▱ABCD 的面积最大时，四边形ABCD 为矩形是解决问题的关键．4．（2019贵州毕节3分）如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC=2：1，则线段CH 的长是（ ）A ．3B ．4C ．5D ．6【考点】正方形的性质；翻折变换（折叠问题）．【分析】根据折叠的性质可得DH=EH ，在直角△CEH 中，若设CH=x ，则DH=EH=9﹣x ，CE=3cm ，可以根据勾股定理列出方程，从而解出CH 的长．【解答】解：由题意设CH=xcm，则DH=EH=（9﹣x）cm，∵BE：EC=2：1，∴CE=BC=3cm∴在Rt△ECH中，EH2=EC2+CH2，即（9﹣x）2=32+x2，解得：x=4，即CH=4cm．故选（B）5．（2019海南3分）如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）A．30° B．45° C．60° D．75°【考点】矩形的性质；平行线的性质．【分析】首先过点D作DE∥a，由∠1=60°，可求得∠3的度数，易得∠ADC=∠2+∠3，继而求得答案．【解答】解：过点D作DE∥a，∵四边形ABCD是矩形，∴∠BAD=∠ADC=90°，∴∠3=90°﹣∠1=90°﹣60°=30°，∵a∥b，∴DE∥a∥b，∴∠4=∠3=30°，∠2=∠5，∴∠2=90°﹣30°=60°．故选C．【点评】此题考查了矩形的性质以及平行线的性质．注意准确作出辅助线是解此题的关键．6.(2019河北3分）关于ABCD的叙述，正确的是（）A．若AB⊥BC，则是菱形B．若AC⊥BD，则ABCD是正方形C．若AC=BD，则ABCD是矩形D．若AB=AD，则ABCD是正方形答案：B解析：A项应是矩形；B项应是菱形；D项应是菱形。

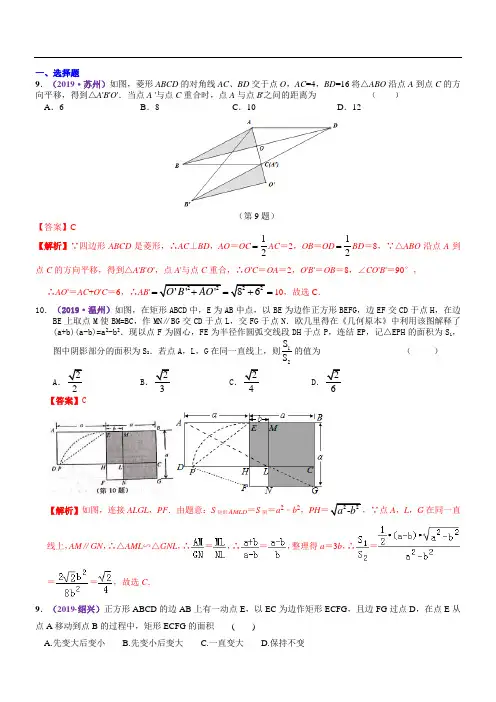
一、选择题9．（2019·苏州）如图，菱形ABCD 的对角线AC 、BD 交于点O ，AC =4，BD =16将△ABO 沿点A 到点C 的方向平移，得到△A 'B 'O '．当点A '与点C 重合时，点A 与点B '之问的距离为 （ ） A ．6 B ．8 C ．10 D ．12（第9题）【答案】C【解析】∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝OC 12=AC ＝2，OB ＝OD 12=BD ＝8，∵△ABO 沿点A 到点C 的方向平移，得到△A 'B 'O '，点A '与点C 重合，∴O 'C ＝OA ＝2，O 'B '＝OB ＝8，∠CO 'B '＝90°， ∴AO '＝AC +O 'C ＝6，∴AB'=10，故选C ．10．（2019·温州）如图，在矩形ABCD 中，E 为AB 中点，以BE 为边作正方形BEFG ，边EF 交CD 于点H ，在边BE 上取点M 使BM=BC ，作MN ∥BG 交CD 于点L ，交FG 于点N ．欧几里得在《几何原本》中利用该图解释了(a+b)(a-b)=a 2-b 2．现以点F 为圆心，FE 为半径作圆弧交线段DH 于点P ，连结EP ，记△EPH 的面积为S 1，图中阴影部分的面积为S 2．若点A ，L ，G 在同一直线上，则12S S 的值为 （ ）A．2 B．3 C．4 D．6【答案】C【解析】如图，连接ALGL ，PF ．由题意：S 矩形AMLD ＝S 阴＝a 2﹣b 2，PH＝22-a b ，∵点A ，L ，G 在同一直线上，AM ∥GN ，∴△AML ∽△GNL ，∴＝，∴＝，整理得a ＝3b ，∴＝＝＝，故选C ．9．（2019·绍兴）正方形ABCD 的边AB 上有一动点E ，以EC 为边作矩形ECFG ，且边FG 过点D ，在点E 从点A 移动到点B 的过程中，矩形ECFG 的面积 ( )A.先变大后变小B.先变小后变大C.一直变大D.保持不变10． （2019·烟台）如图，面积为24的ABCD 中，对角线BD 平分，过点D 作交BC 的延长线于点E ，6DE =，则sin DCE ∠的值为（ ）．A ．2425B ．45C ．34D ．1225【答案】A【解析】连接AC ，交BD 于点F ，过点D 作DM CE ⊥，垂足为M因为四边形ABCD 是平行四边形， 所以F 是BD 的中点，AD//BC ， 所以DBC ADB ∠=∠，因为BD 是 ABC ∠的平分线， 所以ABD DBC ∠=∠， 所以ABD ADB ∠=∠， 所以AB AD =，所以□ABCD 是菱形， 所以AC BD ⊥， 又因为DE BD ⊥， 所以AC//DE ，因为AC//DE ，F 是BD 的中点， 所以C 是BE 的中点，所以132CF DE ==， 因为四边形ABCD 是菱形， 所以26AC FC ==，2ABCD AC BDS ⨯=菱形， FAB所以222486ABCDS BD AC⨯===菱形， 所以142BF BD ==， 在Rt △BFD 中，由勾股定理得5BC ==，因为四边形ABCD 是菱形， 所以5DC BC ==，因为ABCD S BC DM =⨯菱形 所以245ABCDS DM BC==菱形， 在Rt △DCM 中，24sin 25DM DCE DC ∠==． 6．（2019·江西）如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有（ ）A.3种B.4种C.5种D.6种【答案】B【解题过程】具体拼法有4种，如图所示：4．（2019·株洲）对于任意的矩形，下列说法一定正确的是（） A ．对角线垂直且相等B ．四边都互相垂直C ．四个角都相等D ．是轴对称图形，但不是中心对称图形 【答案】C 【解析】根据矩形的性质可知，矩形的对角线相等但不一定垂直，所以选项A 是错误的；矩形相邻的边互相垂直，对边互相平行，所以选项B 是错误的；矩形的四个角都是直角，所以四个角都相等是正确的；矩形既是轴对称图形，又是中心对称图形，所以选项D 是错误的；故选C.3． （2019·娄底）顺次连接菱形四边中点得到的四边形是（ ）A 平行四边形B ． 菱形C ． 矩形D ． 正方形 【答案】C【解析】如图：菱形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点，∴EH ∥FG ∥BD ，EH ＝FG ＝ 12 BD ；EF ∥HG ∥AC ，EF ＝HG ＝12AC ，故四边形EFGH 是平行四边形， 又∵AC ⊥BD ，∴EH ⊥EF ，∠HEF ＝90° ∴四边形EFGH 是矩形． 故选C ．10．（2019·安徽）如图，在正方形ABCD 中，点E 、F 将对角线AC 三等分，且AC=12.点P 在正方形的边上，则满足PE+PF=9的点P 的个数是A. 0B. 4C. 6D. 8【答案】D【解题过程】如图，作点F 关于CD 的对称点F /，连接PF /、PF ，则PE ＋PF ＝EF /，根据两点之间线段最知可知此时PE ＋PF 的值最小.过点E 作EH ⊥FF /，垂足为点H ，FF’交CD 于点G ，易知△EHF 、△CFG 是等腰直角三角形，∴EH ＝FH ＝FG ＝F’G＝2EF ＝，∴EF’＝9.根据正方形的对称性可知正方形ABCD 的每条边上都有一点P 使得PE ＋PF 最小值.连接DE 、DF ，易求得DE ＋DF ＝＞9，CE ＋CF ＝12＞0，故点P 位于点B 、D 时，PE ＋PF ＞9，点P 位于点A 、C 时，PE ＋PF ＞9，∴该正方形每条边上都有2处点使得PE ＋PF ＝9，共计点P 有8处.1.（2019·无锡）下列结论中，矩形具有而菱形不一定具有的性质是（） A.内角和为360° B.对角线互相平分 C.对角线相等 D.对角线互相垂直 【答案】C【解析】本题考查了矩形的性质、菱形的性质，矩形的对角线相等且平分，菱形的对角线垂直且平分，所以矩形具有而菱形不具有的为对角线相等，故选C ．2. (2019·泰安)如图,矩形ABCD 中,AB ＝4,AD ＝2,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点,连接PB,则PB的最小值是A.2B.4C.2D.B【答案】D【解析】∵F为EC上一动点,P为DF中点,∴点P的运动轨迹为△DEC的中位线MN,∴MN∥EC,连接ME,则四边形EBCM为正方形,连接BM,则BM⊥CE,易证BM⊥MN,故此时点P与点M重合,点F与点C重合,BP取到最小值,在Rt△BCP中,BP＝22BC CP＝22.3.（2019·眉山）如图，在矩形ABCD中AB=6，BC=8，过对角线交点O作EF⊥AC交AD于点E，交BC于点F，则DE的长是A．1 B．74C．2 D．125【答案】B【解析】连接CE，∵四边形ABCD是矩形，∴∠ADC=90°，OC=OA，AD=BC=8，DC=AB=6，∵EF⊥AC，OA=OC，∴AE=CE，在Rt△DEC中，DE2+DC2=CE2，即DE2+36=（8-DE）2，解得：x=74，故选B.4.（2019·攀枝花）下列说法错误的是（）A．平行四边形的对边相等B．对角线相等的四边形是矩形C．对角线互相垂直的平行四边形是菱形D．正方形既是轴对称图形、又是中心对称图形【答案】B【解析】对角线相等的四边形不一定是矩形，如等腰梯形.故选B．5.（2019·攀枝花）如图，在正方形ABCD中，E是BC边上的一点，BE＝4，EC＝8，将正方形边AB沿AE折叠到AF，延长EF交DC于G。

矩形菱形与正方形.选择题1. （2019?贵阳?3分）如图，菱形ABCD的周长是4cm, / ABC= 60 °那么这个菱形的对角线AC的长是（A . 1cmB . 2 cm C. 3cm D. 4cm【分析】由于四边形ABCD是菱形，AC是对角线，根据/ ABC = 60°而AB = BC,易证△ BAC是等边三角形，从而可求AC的长.【解答】解：•••四边形ABCD是菱形，AC是对角线，AB= BC = CD = AD,•••/ ABC= 60°•••△ ABC是等边三角形，AB = BC = AC,•••菱形ABCD的周长是4cm,• • AB = BC = AC = 1 cm.故选：A.【点评】本题考查了菱形的性质、等边三角形的判定和性质.菱形的对角线平分对角,解题的关键是证明△ ABC是等边三角形.2. （2019?铜仁?4分）如图为矩形ABCD，一条直线将该矩形分割成两个多边形，若这两个多边形的内角和分别为a和b,贝U a+b不可能是（）A. 360°B. 540°C. 630°D. 720°【解答】解：一条直线将该矩形ABCD分割成两个多边形，每一个多边形的内角和都是180°的倍数，都能被180整除，分析四个答案，只有630不能被180整除，所以a+b不可能是630故选：C.3. （2019?铜仁?4分）如图，四边形ABCD为菱形，AB = 2,/ DAB = 60。

，点A. 30°B. 25°C. 20°D. 15【解答】解：•/四边形ABCD是菱形，/ D = 150°• AB// CD , / BAD = 2/ 1 ,•/ BAD+ / D = 180°•/ BAD = 180° - 150°= 30°,•/ 1 = 15°故选：D.5. （2019?江苏无锡?3分）下列结论中，矩形具有而菱形不一定具有的性质是（E、F分别且CE = ；CD , CF = ；CB，贝U S“EF =( 3 3V3 【解答】解：•••四边形ABCD 为菱形，AB= 2, / DAB = 60°AB= BC = CD = 2,/ DCB = 60°•/ CE= 1CD, CF = 1CB3 32• • CE= CF = 一3•••△ CEF为等边三角形.=_故选：D.4. .( 2019?可北?3 分)如图，菱形ABCD 中，/ D = 150 °,则/ 1=(在边DC、BC 上,A _BA .内角和为360°B •对角线互相平分C .对角线相等D .对角线互相垂直【分析】分别根据矩形和菱形的性质可得出其对角线性质的不同，可得到答案. 【解答】解：矩形和菱形的内角和都为 360° ,矩形的对角线互相平分且相等， 菱形的对角线垂直且平分，•••矩形具有而菱形不具有的性质为对角线相等， 故选：C .【点评】本题考查了矩形的性质，菱形的性质，熟记两图形的性质是解题的关键.6. （2019?江苏宿迁?3分）如图，在平面直角坐标系 xOy 中，菱形ABCD 的顶点A 与原点O 对角线 AC 、BD 交于点M ，点D 、M 恰好都在反比C . 2【分析】设D (m , ' ) , B(t, 0),利用菱形的性质得到 M 点为BD 的中点，贝U M C 匚,D2~~),把 M (:—,')代入 y =「得 t = 3m ,利用 OD = AB = t 得到 m 2+ (' ) 2= (3m ) 2IB 2 2D x io2,解得k = 2 _m 2，所以M (2m , _m )，根据正切定义得到tan / MAB =：=-亠 = AM We'从而得到“=". 【解答】解：设D (m ,), B (t , 0),ID••• M 点为菱形对角线的交点,••• BD 丄 AC , AM = CM , BM = DM , JL ）代入y =上得时！丄=k2 '加）代入y 芷得2 •加k ,•-1= 3m ,mH k•M (—：)， , nri-t 把M (重合，顶点B 落在x 轴的正半轴上,B.A .匚AC三一的值为（•••四边形ABCD为菱形,OD = AB = t,「•m2+（二）2=（3m）2,解得k= 2 _ m2,D ••• M （2m, '：m）,在Rt△ ABM 中,tan / MAB =—AM【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数的图象是双曲线，图象上的点（X，y）的横纵坐标的积是定值的性质.7. （2019?江西分）如图，由10根完全相同的小棒拼接而成,相同的小棒，拼接后的图形恰好有3个菱形的方法共有（A . 3种B . 4种C. 5种y=「（k为常数，心0）xk，即xy= k.也考查了菱形请你再添2根与前面完全）D. 6种【解析】D共有如下6种拼接方法: -= "•【答案】C【解析】由勾股定理可得 .「，由菱形性质可得」 ，所以周长等于 ■.故选C.9. （2019?广东省广州市?3分）如图，矩形 ABCD 中，对角线AC 的垂直平分线BE = 3, AF = 5,贝U AC 的长为( )A . 4 三B . 4 二C . 10D . 8【分析】连接AE ,由线段垂直平分线的性质得出 OA = OC, AE = CE ，证明△ AOFCOE得出 AF = CE = 5,得出 AE = CE = 5, BC = BE+CE = 8,由勾股定8. （2019?天津？3分）如图，四边形ABC 为菱形，A 、B 两点的坐标分别是 （2, 0） 点C 、D 在坐标轴上，则菱形ABC 的周长等于(0,1),4.3 C. 4 5D. 20EF 分别交①④理求出AB = </ A=4，再由勾股定理求出AC即可.【解答】解：连接AE，如图：•/ EF是AC的垂直平分线，••• OA= OC, AE = CE,•••四边形ABCD是矩形，•••/ B= 90° AD // BC,•••/ OAF = / OCE,f ZA0F=ZC0E在厶AOF和厶COE中，，OARC ,ZOAF=ZOCEL•••△ AOF ◎△ COE (ASA),• AF = CE = 5,• AE= CE = 5, BC = BE+CE = 3+5 = 8,•AB= |,|J = ◎£-'-"= 4,• AC= 匚'.|；「=凳―==4【点评】本题考查矩形的性质、线段的垂直平分线的性质、全等三角形的判定与性质、勾股定理等知识，熟练掌握矩形的性质和勾股定理，证明三角形全等是解题的关键.10. （2019?甘肃省庆阳市?3分）如图①，在矩形ABCD中，AB V AD，对角线AC , BD相交于点O,动点P由点A出发，沿AB T BCf CD向点D运动.设点P的运动路程为、△ AOP 的面积为y, y与X的函数关系图象如图②所示，则AD边的长为（）△ AOP 面积逐渐增大，当 P 点到达B 点时，结合图象 可得△ AOP 面积最大为3，得到AB 与BC 的积为12;当P 点在BC 上运动时，△ AOP 面积逐渐减小，当 P 点到达C 点时，△ AOP 面积为0,此时结合图象可知 P 点运动路径 长为7,得到AB 与BC 的和为7,构造关于AB 的一元二方程可求解.【解答】解：当P 点在AB 上运动时，△ AOP 面积逐渐增大，当P 点到达B 点时，△ AOP 面积最大为3.••• 1 AB?丄BC = 3,即卩 AB?BC = 12. 2 2 ，当P 点在BC 上运动时，△ AOP 面积逐渐减小，当 P 点到达C 点时，△ AOP 面积为0, 此时结合图象可知 P 点运动路径长为7, • - AB+BC = 7.贝U BC = 7- AB ，代入 AB?BC = 12,得 AB 2 - 7AB+12= 0,解得 AB = 4 或 3, 因为AB v AD ,即卩AB v BC ,所以 AB = 3, BC = 4. 故选：B .【点评】本题主要考查动点问题的函数图象，解题的关键是分析三角形面积随动点运动 的变化过程，找到分界点极值，结合图象得到相关线段的具体数值.11. （2019?贵州省安顺市?3分）如图，在菱形 ABCD 中，按以下步骤作图：1①分别以点C 和点D 为圆心，大于 CD 的长为半径作弧，两弧相交于M 、N 两点;②作直线 MN ，且MN 恰好经过点 A ，与CD 交于点E ,连接BE . 则下列说法错误的是（ ）A . 3B . 4C .5【分析】当P 点在AB 上运动时,D = 60•••/ABC = 60。

Powered by 矩形菱形与正方形
一、选择题
1．（2016·黑龙江大庆）下列说法正确的是（ ）
A ．对角线互相垂直的四边形是菱形
B ．矩形的对角线互相垂直
C ．一组对边平行的四边形是平行四边形
D ．四边相等的四边形是菱形
【考点】矩形的性质；平行四边形的判定；菱形的判定．
【分析】直接利用菱形的判定定理、矩形的性质与平行四边形的判定定理求解即可求得答案．
【解答】解：A 、对角线互相垂直且平分的四边形是菱形；故本选项错误；
B 、矩形的对角线相等，菱形的对角线互相垂直；故本选项错误；
C 、两组组对边分别平行的四边形是平行四边形；故本选项错误；
D 、四边相等的四边形是菱形；故本选项正确．
故选D ．
【点评】此题考查了矩形的性质、菱形的判定以及平行四边形的判定．注意掌握各特殊平行四边形对角线的性质是解此题的关键．
2. （2016·湖北鄂州）如图，菱形ABCD 的边AB=8，∠B=60°，P 是AB 上一点，BP=3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点为A ′，当CA ′的长度最小时，CQ 的长为（ ） A. 5 B. 7 C. 8 D. 213
【考点】菱形的性质，梯形，轴对称（折叠），等边三角形的判定和性质，最值问题．
【分析】如下图所示，由题意可知，△ABC 为等边三角形；过C 作CH ⊥AB ，则AH=HB ；连接DH ；要使CA ′的长度最小，则梯形APQD 沿直线PQ
折叠后A 的对应点。

A．48 cm B．36 cm
C．2ห้องสมุดไป่ตู้ cm D．18 cm
【解析】 由已知得S菱形EFGH＝S四边形ABCD＋(S①＋S②＋S③＋S④)＝18.设菱形EFGH的边长为x，∵∠F＝30°，∴菱形EFGH的高为，∴＝18，解得x＝6.
∵四个平行四边形的周长和为菱形周长的2倍，
∴周长和为48 cm.
(第5题)
【解析】 (1)∵四边形ABCD是平行四边形，
C．对角线相等的四边形
D．对角线互相垂直的四边形
【解析】 如解图．根据题意，得四边形EFGH是菱形，E，F，G，H分别是边AD，AB，BC，CD的中点，
(第4题解)
∴EF＝FG＝GH＝EH，BD＝2EF，AC＝2FG，
∴BD＝AC.
∴原四边形一定是对角线相等的四边形．故选C.
5．如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠，无缝隙)．若①②③④四个平行四边形面积的和为14 cm2，四边形ABCD的面积是11 cm2，则①②③④四个平行四边形周长的和为(A)
——教学资料参考参考范本——
2019-2020学年度最新中考数学总复习全程考点训练20矩形菱形和正方形含解析
______年______月______日
____________________部门
一、选择题
1．下列关于矩形的说法中，正确的是(D)
A．对角线相等的四边形是矩形
B．对角线互相平分的四边形是矩形
∵EF∥BC，∴∠DBF＝∠EFB.
∴∠EBF＝∠EFB，∴BE＝EF.∴BD＝BE＝EF.
又∵EF∥BD，∴四边形BDFE为菱形．
(第13题)
13．如图，在▱ABCD中，O是CD的中点，连结AO并延长，交BC的延长线于点E.

A ． 52 B． 48 C． 40 D． 20 【分析】 由勾股定理即可求得 AB 的长，继而求得菱形 ABCD 的周长． 【解答】 解：∵菱形 ABCD 中， BD=24 ， AC=10 ，
2
∴OB=12 ， OA=5 ， 在 Rt△ABO 中， AB=
=13 ，
∴菱形 ABCD 的周长 =4AB=52 ， 故选： A ．
∵
，
∴△ APH ≌△ FGH （ASA ），
∴AP=GF=1 ， GH=PH= PG，
∴PD=AD ﹣ AP=1 ， ∵CG=2 、 CD=1 ， ∴DG=1 ，
则 GH= PG= ×
=，
4
故选： C．
A．1 B．
C．
D．
【分析】根据轴对称图形的性质，解决问题即可； 【解答】解：∵四边形 ABCD 是正方形， ∴直线 AC 是正方形 ABCD 的对称轴， ∵EG⊥ AB ． EI⊥ AD ， FH ⊥ AB ， FJ⊥ AD ，垂足分别为 G， I，H ， J． ∴根据对称性可知：四边形 EFHG 的面积与四边形 EFJI 的面积相等，
A．1 B．
C．
D．
【分析】延长 GH 交 AD 于点 P，先证 △APH ≌△ FGH 得 AP=GF=1 ， GH=PH= PG，再利用勾股定理求得 PG= ，
从而得出答案． 【解答】解：如图，延长
GH 交 AD 于点 P，
∵四边形 ABCD 和四边形 CEFG 都是矩形， ∴∠ ADC= ∠ ADG= ∠ CGF=9°0 ， AD=BC=2 、 GF=CE=1 ， ∴AD ∥ GF， ∴∠ GFH= ∠PAH ， 又∵ H 是 AF 的中点， ∴AH=FH ， 在△APH 和 △FGH 中，

矩形菱形与正方形一.选择题1. ( 2019甘肃省兰州市)如图，边长为2的正方形ABCD 的对角线AC 与BD 交于点O ，将正方形ABCD 沿直线DF 折叠，点C 落在对角线BD 上的点E 处，折痕DF 交AC 于点M ，则DM ＝（ ）A.21B. 22C.3－1 D. 2－1【答案】D ．【考点】正方形的性质，折叠的性质，相似三角形的性质与判定，角平分线的性质. 【考察能力】空间想象能力，推理论证能力，运算求解能力. 【难度】较难【解析】过点M 作MP ⊥CD 垂足为P ，过点O 作OQ ⊥CD 垂足为Q ，∵ 正方形的边长为2， ∴OD ＝1， OC ＝1， OQ ＝DQ ＝22，由折叠可知，∠EDF ＝∠CDF. 又∵AC ⊥BD ， ∴OM ＝PM ， 设OM ＝PM ＝x ∵OQ ⊥CD ，MP ⊥CD∴∠OQC ＝∠MPC ＝900， ∠PCM ＝∠QCO ， ∴△CMP ∽△COQ∴OQ MP ＝COCM， 即1122x x -=， 解得x ＝2－1 ∴OM ＝PM ＝2－1. 故选D.2.（2019▪贵州毕节▪3分）平行四边形ABCD 中，AC.BD 是两条对角线，现从以下四个关系①AB ＝BC ；②AC ＝BD ；③AC ⊥BD ；④AB ⊥BC 中随机取出一个作为条件，即可推出平行四边形ABCD 是菱形的概率为（ ） A ．B ．C ．D ．1【分析】菱形的判定：①菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）；②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．【解答】解：根据平行四边形的判定定理，可推出平行四边形ABCD是菱形的有①或③，概率为．故选：B．【点评】本题考查了菱形及概率，熟练掌握菱形的判定定理是解题的关键．3.（2019▪广西池河▪3分）如图，在正方形ABCD中，点E，F分别在BC，CD上，BE＝CF，则图中与∠AEB相等的角的个数是（）A．1 B．2 C．3 D．4【分析】根据正方形的性质，利用SAS即可证明△ABE≌△BCF，再根据全等三角形的性质可得∠BFC＝∠AEB，进一步得到∠BFC＝∠ABF，从而求解．【解答】证明：∵四边形ABCD是正方形，∴AB∥BC，AB＝BC，∠ABE＝∠BCF＝90°，在△ABE和△BCF中，，∴△ABE≌△BCF（SAS），∴∠BFC＝∠AEB，∴∠BFC＝∠ABF，故图中与∠AEB相等的角的个数是2．故选：B．【点评】本题考查正方形的性质、全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．4. （2019•南京•2分）面积为4的正方形的边长是（）A．4的平方根B．4的算术平方根C．4开平方的结果D．4的立方根【分析】已知正方形面积求边长就是求面积的算术平方根；【解答】解：面积为4的正方形的边长是，即为4的算术平方根；故选：B．【点评】本题考查算术平方根；熟练掌握正方形面积与边长的关系，算术平方根的意义是解题的关键．5. （2019•湖南岳阳•3分）下列命题是假命题的是（）A．平行四边形既是轴对称图形，又是中心对称图形B．同角（或等角）的余角相等C．线段垂直平分线上的点到线段两端的距离相等D．正方形的对角线相等，且互相垂直平分【分析】由平行四边形的性质得出A是假命题；由同角（或等角）的余角相等，得出B是真命题；由线段垂直平分线的性质和正方形的性质得出C.D是真命题，即可得出答案．【解答】解：A．平行四边形既是轴对称图形，又是中心对称图形；假命题；B．同角（或等角）的余角相等；真命题；C．线段垂直平分线上的点到线段两端的距离相等；真命题；D．正方形的对角线相等，且互相垂直平分；真命题；故选：A．【点评】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．6（2019，山东枣庄，3分）如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A 顺时针旋转90°到△ABF的位置．若四边形AECF的面积为20，DE＝2，则AE的长为（）A．4 B．2C．6 D．2【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积，进而可求出正方形的边长，再利用勾股定理得出答案．【解答】解：∵△ADE绕点A顺时针旋转90°到△ABF的位置．∴四边形AECF的面积等于正方形ABCD的面积等于20，∴AD＝DC＝2，∵DE＝2，∴Rt△ADE中，AE＝＝2故选：D．【点评】本题主要考查了旋转的性质以及正方形的性质，正确利用旋转的性质得出对应边关系是解题关键．7. （2019•湖北十堰•3分）矩形具有而平行四边形不一定具有的性质是（）A．对边相等B．对角相等C．对角线相等D．对角线互相平分【分析】矩形的对角线互相平分且相等，而平行四边形的对角线互相平分，不一定相等．【解答】解：矩形的对角线相等，而平行四边形的对角线不一定相等．故选：C．【点评】本题考查矩形的性质，矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质．如，矩形的对角线相等．8. （2019•湖北孝感•3分）如图，正方形ABCD中，点E.F分别在边CD，AD上，BE与CF交于点G．若BC＝4，DE＝AF＝1，则GF的长为（）A．B．C．D．【分析】证明△BCE≌△CDF（SAS），得∠CBE＝∠DCF，所以∠CGE＝90°，根据等角的余弦可得CG的长，可得结论．【解答】解：正方形ABCD中，∵BC＝4，∴BC＝CD＝AD＝4，∠BCE＝∠CDF＝90°，∵AF＝DE＝1，∴DF＝CE＝3，∴BE＝CF＝5，在△BCE和△CDF中，，∴△BCE≌△CDF（SAS），∴∠CBE＝∠DCF，∵∠CBE+∠CEB＝∠ECG+∠CEB＝90°＝∠CGE，cos∠CBE＝cos∠ECG＝，∴，CG＝，∴GF＝CF﹣CG＝5﹣＝，故选：A．【点评】此题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，锐角三角函数，证明△BCE≌△CDF是解本题的关键．9. （2019•湖南衡阳•3分）如图，在直角三角形ABC中，∠C＝90°，AC＝BC，E是AB的中点，过点E作AC和BC的垂线，垂足分别为点D和点F，四边形CDEF沿着CA方向匀速运动，点C与点A重合时停止运动，设运动时间为t，运动过程中四边形CDEF与△ABC的重叠部分面积为S．则S关于t的函数图象大致为（）A．B．C．D．【分析】根据已知条件得到△ABC是等腰直角三角形，推出四边形EFCD是正方形，设正方形的边长为a，当移动的距离＜a时，如图1S＝正方形的面积﹣△EE′H的面积＝a2﹣t2；当移动的距离＞a时，如图2，S＝S△AC′H＝（2a﹣t）2＝t2﹣2at+2a2，根据函数关系式即可得到结论；【解答】解：∵在直角三角形ABC中，∠C＝90°，AC＝BC，∴△ABC是等腰直角三角形，∵EF⊥BC，ED⊥AC，∴四边形EFCD是矩形，∵E是AB的中点，∴EF＝AC，DE＝BC，∴EF＝ED，∴四边形EFCD是正方形，设正方形的边长为a，如图1当移动的距离＜a时，S＝正方形的面积﹣△EE′H的面积＝a2﹣t2；当移动的距离＞a时，如图2，S＝S△AC′H＝（2a﹣t）2＝t2﹣2at+2a2，∴S关于t的函数图象大致为C选项，故选：C．【点评】本题考查动点问题的函数图象，正方形的性质、勾股定理等知识，解题的关键是读懂题意，学会分类讨论的思想，属于中考常考题型．10. (2019•广东•3分）如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB.AM 交于点N 、K ．则下列结论：①△ANH ≌△GNF ；②∠AFN=∠HFG ；③FN=2NK ；④S △AFN : S △ADM =1 : 4．其中正确的结论有A ．1个B ．2个C ．3个D ．4个【答案】C【解析】AH=GF=2，∠ANH=∠GNF ，∠AHN=∠GFN ，△ANH ≌△GNF （AAS ），①正确；由①得AN=GN=1，∵NG ⊥FG ，NA 不垂直于AF ，∴FN 不是∠AFG 的角平分线，∴∠AFN≠∠HFG ，②错误；由△AKH ∽△MKF ，且AH:MF=1:3，∴KH:KF=1:3，又∵FN=HN ，∴K 为NH 的中点，即FN=2NK ，③正确；S △AFN =21AN·FG=1，S △ADM =21DM·AD=4，∴S △AFN : S △ADM =1 : 4，④正确. 【考点】正方形的性质，平行线的应用，角平分线的性质，全等三角形，相似三角形，三角形的面积11. （2019•广东深圳•3分）已知菱形ABCD ，E ，F 是动点，边长为4，BE=AF ，∠BAD=120°，则下列结论正确的有几个（ ）①△BEC ≌△AFC ； ②△ECF 为等边三角形 ③∠AGE=∠AFC ④若AF=1，则31GE GF A. 1 B. 2 C. 3 D. 4【答案】D【解析】在四边形ABCD 是菱形，因为∠BAD=120°，则∠B=∠DAC=60°，则AC=BC ，且BE=AF ，故可得△BEC ≌△AFC ；因为△BEC ≌△AFC ，所以FC=EC ，∠FCA=∠ECB ，所以△ECF 为等边三角形；因为∠AGE=180°-∠BAC-∠AEG ；∠AFC=180°-∠FAC-∠ACF ，则根据等式性质可得∠AGE=∠AFC ；因为AF=1，则AE=3，所以根据相似可得31GE GF .12 （2019•广西贵港•3分）如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为S 1，S 2，则下列结论错误的是（ ）A ．S 1+S 2＝CP 2B ．4F ＝2FDC ．CD ＝4PD D ．cos ∠HCD ＝【分析】根据勾股定理可判断A ；连接CF ，作FG ⊥EC ，易证得△FGC 是等腰直角三角形，设EG ＝x ，则FG ＝2x ，利用三角形相似的性质以及勾股定理得到CG ＝2x ，CF ＝2x ，EC ＝3x ，BC ＝x ，FD ＝x ，即可证得3FD ＝AD ，可判断B ；根据平行线分线段成比例定理可判断C ；求得cos ∠HCD 可判断D ．【解答】解：∵正方形ABCD ，DPMN 的面积分别为S 1，S 2， ∴S 1＝CD 2，S 2＝PD 2，在Rt △PCD 中，PC 2＝CD 2+PD 2， ∴S 1+S 2＝CP 2，故A 结论正确；连接CF，∵点H与B关于CE对称，∴CH＝CB，∠BCE＝∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE＝EH，∠EHC＝∠B＝90°，∠BEC＝∠HEC，∴CH＝CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH＝∠FCD，FH＝FD，∴∠ECH+∠ECH＝∠BCD＝45°，即∠ECF＝45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG＝CG，∵∠BEC＝∠HEC，∠B＝∠FGE＝90°，∴△FEG∽△CEB，∴＝＝，∴FG＝2EG，设EG＝x，则FG＝2x，∴CG＝2x，CF＝2x，∴EC＝3x，∵EB2+BC2＝EC2，∴BC2＝9x2，∴BC2＝x2，∴BC＝x，在Rt△FDC中，FD＝＝＝x，∴3FD＝AD，∴AF＝2FD，故B结论正确；∵AB∥CN，∴＝，∵PD＝ND，AE＝CD，∴CD＝4PD，故C结论正确；∵EG＝x，FG＝2x，∴EF＝x，∵FH＝FD＝x，∵BC＝x，∴AE＝x，作HQ⊥AD于Q，∴HQ∥AB，∴＝，即＝，∴HQ＝x，∴CD﹣HQ＝x﹣x＝x，∴cos∠HCD＝＝＝，故结论D错误，故选：D．【点评】本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13. （2019•江苏苏州•3分）如图，菱形ABCD 的对角线AC ，BD 交于点O ，416AC BD ==，，将ABO V 沿点A 到点C 的方向平移，得到A B C '''V ，当点A '与点C 重合时，点A 与点B '之间的距离为（）A ．6B ．C ．10D ．12B【分析】考察菱形的性质，勾股定理，中等偏易题型【解答】由菱形的性质得28AO OC CO BO OD B O '''======，90AOB AO B ''∠=∠=oAO B ''∴V 为直角三角形10AB '∴===故选C14. （2019•湖南株洲•3分）对于任意的矩形，下列说法一定正确的是（ ）A ．对角线垂直且相等B ．四边都互相垂直C ．四个角都相等D ．是轴对称图形，但不是中心对称图形【分析】直接利用矩形的性质分析得出答案．【解答】解：A.矩形的对角线相等，但不垂直，故此选项错误；B.矩形的邻边都互相垂直，对边互相平行，故此选项错误；C.矩形的四个角都相等，正确；D.矩形是轴对称图形，也是中心对称图形，故此选项错误．故选：C．【点评】此题主要考查了矩形的性质，正确把握矩形的性质是解题关键．15. （2019•山东省德州市•4分）如图，正方形ABCD，点F在边AB上，且AF：FB＝1：2，CE⊥DF，垂足为M，且交AD于点E，AC与DF交于点N，延长CB至G，使BG＝BC，连接CM．有如下结论：①DE＝AF；②AN＝AB；③∠ADF＝∠GMF；④S△ANF：S四边形CNFB＝1：8．上述结论中，所有正确结论的序号是（）A．①②B．①③C．①②③D．②③④【考点】正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质【分析】①正确．证明△ADF≌△DCE（ASA），即可判断．②正确．利用平行线分线段成比例定理，等腰直角三角形的性质解决问题即可．③正确．作GH⊥CE于H，设AF＝DE＝a，BF＝2a，则AB＝CD＝BC＝3a，EC＝a，通过计算证明MH＝CH即可解决问题．④错误．设△ANF的面积为m，由AF∥CD，推出＝＝，△AFN∽△CDN，推出△ADN的面积为3m，△DCN的面积为9m，推出△ADC的面积＝△ABC的面积＝12m，由此即可判断．【解答】解：∵四边形ABCD是正方形，∴AD＝AB＝CD＝BC，∠CDE＝∠DAF＝90°，∵CE⊥DF，∴∠DCE+∠CDF＝∠ADF+∠CDF＝90°，∴∠ADF＝∠DCE，在△ADF与△DCE中，，∴△ADF≌△DCE（ASA），∴DE＝AF；故①正确；∵AB∥CD，∴＝，∵AF：FB＝1：2，∴AF：AB＝AF：CD＝1：3，∴＝，∴＝，∵AC＝AB，∴＝，∴AN＝AB；故②正确；作GH⊥CE于H，设AF＝DE＝a，BF＝2a，则AB＝CD＝BC＝3a，EC＝a，由△CMD∽△CDE，可得CM＝a，由△GHC∽△CDE，可得CH＝a，∴CH＝MH＝CM，∵GH⊥CM，∴GM＝GC，∴∠GMH＝∠GCH，∵∠FMG+∠GMH＝90°，∠DCE+∠GCM＝90°，∴∠FEG＝∠DCE，∵∠ADF＝∠DCE，∴∠ADF＝∠GMF；故③正确，设△ANF的面积为m，∵AF∥CD，∴＝＝，△AFN∽△CDN，∴△ADN的面积为3m，△DCN的面积为9m，∴△ADC的面积＝△ABC的面积＝12m，∴S△ANF：S四边形CNFB＝1：11，故④错误，故选：C．【点评】本题考查正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会利用参数解决问题，属于中考选择题中的压轴题．二.填空题1. (2019安徽)（4分）如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12，点P在正方形的边上，则满足PE+PF＝9的点P的个数是（）A．0 B．4 C．6 D．8【分析】作点F关于BC的对称点M，连接FM交BC于点N，连接EM，可得点N到点E和点F的距离之和最小，可求最小值，即可求解．【解答】解：如图，作点F关于BC的对称点M，连接FM交BC于点N，连接EM，∵点E，F将对角线AC三等分，且AC＝12，∴EC＝8，FC＝4，∵点M与点F关于BC对称∴CF＝CM＝4，∠ACB＝∠BCM＝45°∴∠ACM＝90°∴EM＝＝4则在线段BC存在点N到点E和点F的距离之和最小为4＜9∴在线段BC上点N的左右两边各有一个点P使PE+PF＝9，同理在线段AB，AD，CD上都存在两个点使PE+PF＝9．即共有8个点P满足PE+PF＝9，故选：D．【点评】本题考查了正方形的性质，最短路径问题，在BC上找到点N使点N到点E和点F的距离之和最小是本题的关键．2.（2019•浙江金华•3分）如图，矩形ABCD的对角线交于点O，已知AB=m，∠BAC=∠α，则下列结论错误的是（）A. ∠BDC=∠αB. BC=m·tanαC. AO=D. BD=【答案】C【考点】锐角三角函数的定义【解析】【解答】解：A.∵矩形ABCD，∴AB=DC，∠ABC=∠DCB=90°，又∵BC=CB，∴△ABC≌△DCB（SAS），∴∠BDC=∠BAC=α，故正确，A不符合题意；B.∵矩形ABCD，∴∠ABC=90°，在Rt△ABC中，∵∠BAC=α，AB=m，∴tanα= ，∴BC=AB·tanα=mtanα，故正确，B不符合题意；C.∵矩形ABCD，∴∠ABC=90°，在Rt△ABC中，∵∠BAC=α，AB=m，∴cosα= ，∴AC= = ，∴AO= AC=故错误，C符合题意；D.∵矩形ABCD，∴AC=BD，由C知AC= = ，∴BD=AC= ，故正确，D不符合题意；故答案为：C.【分析】A.由矩形性质和全等三角形判定SAS可得△ABC≌△DCB，根据全等三角形性质可得∠BDC=∠BAC=α，故A正确；B.由矩形性质得∠ABC=90°，在Rt△ABC中，根据正切函数定义可得BC=AB·tanα=mtanα，故正确；C.由矩形性质得∠ABC=90°，在Rt△ABC中，根据余弦函数定义可得AC= =，再由AO= AC即可求得AO长，故错误；D.由矩形性质得AC=BD，由C知AC= = ，从而可得BD长，故正确；3．（2019•浙江绍兴•4分）正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D．在点E从点A移动到点B的过程中，矩形ECFG的面积（）A．先变大后变小B．先变小后变大C．一直变大D．保持不变【分析】由△BCE∽△FCD，根据相似三角形的对应边成比例，可得CF•CE＝CD•BC，即可得矩形ECFG与正方形ABCD的面积相等．【解答】解：∵正方形ABCD和矩形ECFG中，∠DCB＝∠FCE＝90°，∠F＝∠B＝90°，∴∠DCF＝∠ECB，∴△BCE∽△FCD，∴，∴CF•CE＝CB•CD，∴矩形ECFG与正方形ABCD的面积相等．故选：D．【点评】此题考查了正方形的性质、矩形的性质、相似三角形的判定与性质，由相似三角形得出比例线段是解题的关键．4．（2019•浙江绍兴•4分）如图1，长、宽均为3，高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，则图2中水面高度为（）A．B．C．D．【分析】设DE＝x，则AD＝8﹣x，由长方体容器内水的体积得出方程，解方程求出DE，再由勾股定理求出CD，过点C作CF⊥BG于F，由△CDE∽△BCF的比例线段求得结果即可．【解答】解：过点C作CF⊥BG于F，如图所示：设DE＝x，则AD＝8﹣x，根据题意得：（8﹣x+8）×3×3＝3×3×6，解得：x＝4，∴DE＝4，∵∠E＝90°，由勾股定理得：CD＝，∵∠BCE＝∠DCF＝90°，∴∠DCE＝∠BCF，∵∠DEC＝∠BFC＝90°，∴△CDE∽△BCF，∴，即，∴CF＝．故选：A．【点评】本题考查了勾股定理的应用、长方体的体积、梯形的面积的计算方法；熟练掌握勾股定理，由长方体容器内水的体积得出方程是解决问题的关键．5.（2019•浙江衢州•3分）如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E 出发，沿E→A→D→C移动至终点C，设P点经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是（）A B C D【答案】C【考点】动点问题的函数图象【解析】【解答】解：①当点P在AE上时，∵正方形边长为4，E为AB中点，∴AE=2，∵P点经过的路径长为x，∴PE=x，∴y=S△CPE= ·PE·BC= ×x×4=2x，②当点P在AD上时，∵正方形边长为4，E为AB中点，∴AE=2，∵P点经过的路径长为x，∴AP=x-2，DP=6-x，∴y=S△CPE=S正方形ABCD-S△BEC-S△APE-S△PDC，=4×4- ×2×4- ×2×（x-2）- ×4×（6-x），=16-4-x+2-12+2x，=x+2，③当点P在DC上时，∵正方形边长为4，E为AB中点，∴AE=2，∵P点经过的路径长为x，∴PD=x-6，PC=10-x，∴y=S△CPE= ·PC·BC= ×（10-x）×4=-2x+20，综上所述：y与x的函数表达式为：y= .故答案为：C.【分析】结合题意分情况讨论：①当点P在AE上时，②当点P在AD上时，③当点P在DC上时，根据三角形面积公式即可得出每段的y与x的函数表达式.6. （2019•甘肃•3分）如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为．【分析】设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，所以AF＝8，BF＝AB﹣AF＝10﹣8＝2，在Rt△BEF中，BE2+BF2＝EF2，即（6﹣x）2+22＝x2，解得x＝．【解答】解：设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，在Rt△DAF中，AD＝6，DF＝10，∴AF＝8，∴BF＝AB﹣AF＝10﹣8＝2，在Rt△BEF中，BE2+BF2＝EF2，即（6﹣x）2+22＝x2，解得x＝，故答案为．【点评】本题考查了矩形，熟练掌握矩形的性质以及勾股定理是解题的关键．7．（2019•浙江绍兴•5分）如图，在直线AP上方有一个正方形ABCD，∠P AD＝30°，以点B 为圆心，AB长为半径作弧，与AP交于点A，M，分别以点A，M为圆心，AM长为半径作弧，两弧交于点E，连结ED，则∠ADE的度数为15°或45°．【分析】分点E与正方形ABCD的直线AP的同侧、点E与正方形ABCD的直线AP的两侧两种情况，根据正方形的性质、等腰三角形的性质解答．【解答】解：∵四边形ABCD是正方形，∴AD＝AE，∠DAE＝90°，∴∠BAM＝180°﹣90°﹣30°＝60°，AD＝AB，当点E与正方形ABCD的直线AP的同侧时，由题意得，点E与点B重合，∴∠ADE＝45°，当点E与正方形ABCD的直线AP的两侧时，由题意得，E′A＝E′M，∴△AE′M为等边三角形，∴∠E′AM＝60°，∴∠DAE′＝360°﹣120°﹣90°＝150°，∵AD＝AE′，∴∠ADE′＝15°，故答案为：15°或45°．【点评】本题考查的是正方形的性质、等边三角形的判定和性质，掌握正方形的性质、灵活运用分情况讨论思想是解题的关键．8.（2019•浙江绍兴•5分）把边长为2的正方形纸片ABCD分割成如图的四块，其中点O为正方形的中心，点E，F分别为AB，AD的中点．用这四块纸片拼成与此正方形不全等的四边形MNPQ（要求这四块纸片不重叠无缝隙），则四边形MNPQ的周长是6+2或10或8+2．【分析】先根据题意画出图形，再根据周长的定义即可求解．【解答】解：如图所示：图1的周长为1+2+3+2＝6+2；图2的周长为1+4+1+4＝10；图3的周长为3+5++＝8+2．故四边形MNPQ的周长是6+2或10或8+2．故答案为：6+2或10或8+2．【点评】考查了平面镶嵌（密铺），关键是得到与此正方形不全等的四边形MNPQ（要求这四块纸片不重叠无缝隙）的各种情况．9. （2019•湖北十堰•3分）如图，已知菱形ABCD的对角线AC，BD交于点O，E为BC的中点，若OE＝3，则菱形的周长为24．【分析】根据菱形的对角线互相平分可得BO＝DO，然后求出OE是△BCD的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半求出CD，然后根据菱形的周长公式计算即可得解．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，BO＝DO，∵点E是BC的中点，∴OE是△BCD的中位线，∴CD＝2OE＝2×3＝6，∴菱形ABCD的周长＝4×6＝24；故答案为：24．【点评】本题考查了菱形的性质以及三角形中位线定理；熟记菱形性质与三角形中位线定理是解题的关键．10. （2019•湖北十堰•3分）如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝6．【分析】作DH⊥AE于H，如图，由于AF＝4，则△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，当BF为此圆的切线时，∠ABF最大，即BF⊥AF，利用勾股定理计算出BF＝3，接着证明△ADH≌△ABF得到DH＝BF＝3，然后根据三角形面积公式求解．【解答】解：作DH⊥AE于H，如图，∵AF＝4，当△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，在Rt△ABF中，BF＝＝3，∵∠EAF＝90°，∴∠BAF+∠BAH＝90°，∵∠DAH+∠BAH＝90°，∴∠DAH＝∠BAF，在△ADH和△ABF中，∴△ADH≌△ABF（AAS），∴DH＝BF＝3，∴S△ADE＝AE•DH＝×3×4＝6．故答案为6．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．11. （2019•湖北天门•3分）如图，为测量旗杆AB的高度，在教学楼一楼点C处测得旗杆顶部的仰角为60°，在四楼点D处测得旗杆顶部的仰角为30°，点C与点B在同一水平线上．已知CD＝9.6m，则旗杆AB的高度为14.4m．【分析】作DE⊥AB于E，则∠AED＝90°，四边形BCDE是矩形，得出BE＝CD＝9.6m，∠CDE＝∠DEA＝90°，求出∠ADC＝120°，证出∠CAD＝30°＝∠ACD，得出AD＝CD＝9.6m，在Rt△ADE中，由直角三角形的性质得出AE＝AD＝4.8m，即可得出答案．【解答】解：作DE⊥AB于E，如图所示：则∠AED＝90°，四边形BCDE是矩形，∴BE＝CD＝9.6m，∠CDE＝∠DEA＝90°，∴∠ADC＝90°+30°＝120°，∵∠ACB＝60°，∴∠ACD＝30°，∴∠CAD＝30°＝∠ACD，∴AD＝CD＝9.6m，在Rt△ADE中，∠ADE＝30°，∴AE＝AD＝4.8m，∴AB＝AE+BE＝4.8m+9.6m＝14.4m；故答案为：14.4．【点评】本题考查了解直角三角形的应用﹣仰角俯角问题、矩形的判定与性质、等腰三角形的判定；正确作出辅助线是解题的关键．12. （2019•湖北天门•3分）如图，在平面直角坐标系中，四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，点A1，A2，A3，…都在x轴上，点C1，C2，C3，…都在直线y ＝x+上，且∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，OA1＝1，则点C6的坐标是（97，32）．【分析】根据菱形的边长求得A1.A2.A3…的坐标然后分别表示出C1.C2.C3…的坐标找出规律进而求得C6的坐标．【解答】解：∵OA1＝1，∴OC1＝1，∴∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，∴C1的纵坐标为：sin60°•OC1＝，横坐标为cos60°•OC1＝，∴C1（，），∵四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，∴A1C2＝2，A2C3＝4，A3C4＝8，…，∴C2的纵坐标为：sin60°•A1C2＝，代入y＝x+求得横坐标为2，∴C2（，2，），C3的纵坐标为：sin60°•A2C3＝4，代入y＝x+求得横坐标为11，∴C3（11，4），∴C4（23，8），C5（47，16），∴C6（97，32）；故答案为（97，32）．【点评】本题是对点的坐标变化规律的考查，主要利用了菱形的性质，解直角三角形，根据已知点的变化规律求出菱形的边长，得出系列C点的坐标，找出规律是解题的关键．13. （2019•广东深圳•3分）如图在正方形ABCD中，BE=1，将BC沿CE翻折，使点B对应点刚好落在对角线AC上，将AD沿AF翻折，使点D对应点落在对角线AC上，求EF= .【答案】6【解析】14. (2019甘肃省天水市)如图，在矩形ABCD中，AB=3，AD=5，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，那么sin∠EFC的值为______．.【答案】错误！未找到引用源。

矩形菱形与正方形一、选择题1. （2019•安徽省,第10题4分）如图，正方形ABCD的对角线BD长为2，若直线l满足：①点D到直线l的距离为；②A、C两点到直线l的距离相等．则符合题意的直线l的条数为（）A． 1 B． 2 C． 3 D． 4考点：正方形的性质．分析：连接AC与BD相交于O，根据正方形的性质求出OD=，然后根据点到直线的距离和平行线间的距离相等解答．解答：解：如图，连接AC与BD相交于O，∵正方形ABCD的对角线BD长为2，∴OD=，∴直线l∥AC并且到D的距离为，同理，在点D的另一侧还有一条直线满足条件，故共有2条直线l．故选B．点评：本题考查了正方形的性质，主要利用了正方形的对角线互相垂直平分，点D到O 的距离小于是本题的关键．2. （2019•福建泉州，第5题3分）正方形的对称轴的条数为（）3. （2019•珠海，第2题3分）边长为3cm的菱形的周长是（）4.（2019•广西玉林市、防城港市，第6题3分）下列命题是假命题的是（）5.（2019•毕节地区，第8题3分）如图，菱形ABCD中，对角线AC、BC相交于点O，H 为AD边中点，菱形ABCD的周长为28，则OH的长等于（）AAB6.（2019•襄阳，第12题3分）如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（）PEAB（（7.（2019•孝感，第9题3分）如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（）8．（2019·台湾，第12题3分）如图，D 为△ABC 内部一点，E 、F 两点分别在AB 、BC 上，且四边形DEBF 为矩形，直线CD 交AB 于G 点．若CF ＝6，BF ＝9，AG ＝8，则△ADC 的面积为何？( )A ．16B ．24C ．36D ．54分析：由于△ADC ＝△AGC ﹣△ADG ，根据矩形的性质和三角形的面积公式计算即可求解． 解：△ADC ＝△AGC ﹣△ADG ＝12×AG ×BC ﹣12×AG ×BF＝12×8×(6＋9)﹣12×8×9＝60﹣36＝24． 故选：B ．点评：考查了三角形的面积和矩形的性质，本题关键是活用三角形面积公式进行计算． 9．（2019·台湾，第27题3分）如图，矩形ABCD 中，AD ＝3AB ，O 为AD 中点，是半圆．甲、乙两人想在上取一点P ，使得△PBC 的面积等于矩形ABCD 的面积其作法如下： (甲) 延长BO 交于P 点，则P 即为所求；(乙) 以A 为圆心，AB 长为半径画弧，交于P 点，则P 即为所求． 对于甲、乙两人的作法，下列判断何者正确？( )A ．两人皆正确B ．两人皆错误C ．甲正确，乙错误D ．甲错误，乙正确分析：利用三角形的面积公式进而得出需P甲H＝P乙K＝2AB，即可得出答案．解：要使得△PBC的面积等于矩形ABCD的面积，需P甲H＝P乙K＝2A B．故两人皆错误．故选：B．点评：此题主要考查了三角形面积求法以及矩形的性质，利用四边形与三角形面积关系得出是解题关键．10．（2019•浙江宁波，第6题4分）菱形的两条对角线长分别是6和8，则此菱形的边长是（）===511．（2019•浙江宁波，第11题4分）如图，正方形ABCD和正方形CEFG中，点D在CG 上，BC=1，CE=3，H是AF的中点，那么CH的长是（）．．=，=3，===2，=AF=×2=．11.（2019•呼和浩特，第9题3分）已知矩形ABCD的周长为20cm，两条对角线AC，BD 相交于点O，过点O作AC的垂线EF，分别交两边AD，BC于E，F（不与顶点重合），则以下关于△CDE与△ABF判断完全正确的一项为（）=12. （2019•湘潭，第7题，3分）以下四个命题正确的是（）13. （2019•株洲，第7题，3分）已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）14. （2019年江苏南京，第6题，2分）如图，在矩形AOBC中，点A的坐标是（﹣2，1），点C的纵坐标是4，则B、C两点的坐标分别是（）（第3题图）A．（，3）、（﹣，4）B．（，3）、（﹣，4）C．（，）、（﹣，4）D．（，）、（﹣，4）考点：矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质。

矩形菱形与正方形一、选择题1. （2018•上海，第6题4分）如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）A．△ABD与△ABC的周长相等B．△ABD与△ABC的面积相等C．菱形的周长等于两条对角线之和的两倍D．菱形的面积等于两条对角线之积的两倍考点：菱形的性质．分析：分别利用菱形的性质结合各选项进而求出即可．解答：解：A、∵四边形ABCD是菱形，∴AB=BC=AD，∵AC＜BD，∴△ABD与△ABC的周长不相等，故此选项错误；B、∵S△ABD=S平行四边形ABCD，S△ABC=S平行四边形ABCD，∴△ABD与△ABC的面积相等，故此选项正确；C、菱形的周长与两条对角线之和不存在固定的数量关系，故此选项错误；D、菱形的面积等于两条对角线之积的，故此选项错误；故选：B．点评：此题主要考查了菱形的性质应用，正确把握菱形的性质是解题关键．和AD的延长线于点E、F，AE=3，则四边形AECF的周长为（）A．22 B．18 C．14 D．11考点：菱形的性质分析：根据菱形的对角线平分一组对角可得∠BAC=∠BCA，再根据等角的余角相等求出∠BAE=∠E，根据等角对等边可得BE=AB，然后求出EC，同理可得AF，然后判断出四边形AECF是平行四边形，再根据周长的定义列式计算即可得解．解答：解：在菱形ABCD中，∠BAC=∠BCA，∵AE⊥AC，∴∠BAC+∠BAE=∠BCA+∠E=90°，∴∠BAE=∠E，∴BE=AB=4，∴EC=BE+BC=4+4=8，同理可得AF=8，∵AD∥BC，∴四边形AECF是平行四边形，∴四边形AECF的周长=2（AE+EC）=2（3+8）=22．故选A．点评：本题考查了菱形的对角线平分一组对角的性质，等角的余角相等的性质，平行四边形的判定与性质，熟记性质并求出EC的长度是解题的关键．AM=CN，MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC的度数为（）A．28°B．52°C．62°D．72°考点：菱形的性质，全等三角形．分析：根据菱形的性质以及AM=CN，利用ASA可得△AMO≌△CNO，可得AO=CO，然后可得BO⊥AC，继而可求得∠OBC的度数．解答：∵四边形ABCD为菱形，∴AB∥CD，AB=BC，∴∠MAO=∠NCO，∠AMO=∠CNO，在△AMO和△CNO中，∵，∴△AMO≌△CNO（ASA），∴AO=CO，∵AB=BC，∴BO⊥AC，∴∠BOC=90°，∵∠DAC=28°，∴∠BCA=∠DAC=28°，∴∠OBC=90°﹣28°=62°．故选C．点评：本题考查了菱形的性质和全等三角形的判定和性质，注意掌握菱形对边平行以及对角线相互垂直的性质．4.（2018•山东聊城，第9题，3分）如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（）BE=，BF=BE=2CF=AE=BC=BF+CF=3A重合，则折痕EF的长为（）A． 6 B．12 C．2 D． 4考点：翻折变换（折叠问题）．分析：设BE=x，表示出CE=16﹣x，根据翻折的性质可得AE=CE，然后在Rt△ABE中，利用勾股定理列出方程求出x，再根据翻折的性质可得∠AEF=∠CEF，根据两直线平行，内错角相等可得∠AFE=∠CEF，然后求出∠AEF=∠AFE，根据等角对等边可得AE=AF，过点E作EH⊥AD于H，可得四边形ABEH是矩形，根据矩形的性质求出EH、AH，然后求出FH，再利用勾股定理列式计算即可得解．解答：解：设BE=x，则CE=BC﹣BE=16﹣x，∵沿EF翻折后点C与点A重合，∴AE=CE=16﹣x，在Rt△ABE中，AB2+BE2=AE2，即82+x2=（16﹣x）2，解得x=6，∴AE=16﹣6=10，由翻折的性质得，∠AEF=∠CEF，∵矩形ABCD的对边AD∥BC，∴∠AFE=∠CEF，∴∠AEF=∠AFE，∴AE=AF=10，过点E作EH⊥AD于H，则四边形ABEH是矩形，∴EH=AB=8，AH=BE=6，∴FH=AF﹣AH=10﹣6=4，在Rt△EFH中，EF===4．故选D．点评：本题考查了翻折变换的性质，矩形的判定与性质，勾股定理，熟记各性质并作利用勾股定理列方程求出BE的长度是解题的关键，也是本题的突破口．7.（2018•遵义9．（3分））如图，边长为2的正方形ABCD中，P是CD的中点，连接AP并延长交BC的延长线于点F，作△CPF的外接圆⊙O，连接BP并延长交⊙O于点E，连接EF，则EF的长为（）==BP===，=，EF=8.（2018•十堰9．（3分））如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G 为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为（）DE=．A．矩形B．等腰梯形C．对角线相等的四边形D．对角线互相垂直的四边形考点：中点四边形．分析：首先根据题意画出图形，由四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，利用三角形中位线的性质与菱形的性质，即可判定原四边形一定是对角线相等的四边形．解答：解：如图，根据题意得：四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，∴EF=FG=CH=EH，BD=2EF，AC=2FG，∴BD=AC．∴原四边形一定是对角线相等的四边形．故选C．点评：此题考查了菱形的性质与三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．10. （2018•山东淄博,第9题4分）如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A﹣B﹣F﹣C的路径行走至C，乙沿着A﹣F﹣E﹣C﹣D的路径行走至D，丙沿着A﹣F﹣C﹣D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（）A．甲乙丙B．甲丙乙C．乙丙甲D．丙甲乙考点：正方形的性质；线段的性质：两点之间线段最短；比较线段的长短．分析：根据正方形的性质得出AB=BC=CD=AD，∠B=∠ECF，根据直角三角形得出AF＞AB，EF＞CF，分别求出甲、乙、丙行走的距离，再比较即可．解答：解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=90°，甲行走的距离是AB+BF+CF=AB+BC=2AB；乙行走的距离是AF+EF+EC+CD；丙行走的距离是AF+FC+CD，∵∠B=∠ECF=90°，∴AF＞AB，EF＞CF，∴AF+FC+CD＞2AB，AF+FC+CD＜AF+EF+EC+CD，∴甲比丙先到，丙比乙先到，即顺序是甲丙乙，故选B．点评：本题考查了正方形的性质，直角三角形的性质的应用，题目比较典型，难度适中．11．（2018•福建福州,第9题4分）如图，在正方形ABCD的外侧，作等边三角形ADE. AC，BE相交于点F，则∠BFC为【】A．45° B．55° C．60° D．75°12．（2018•甘肃兰分）将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，（）．（A）（B）2 （C）（D）图2-① 图2-②【考点】正方形、有内角的菱形的对角线与边长的关系【分析】由正方形的对角线长为2可知正方形和菱形的边长为，当=60°时，菱形较短的对角线等于边长，故答案为．【答案】A14．（2018•广州,第10题3分）如图3，四边形、都是正方形，点在线段上，连接，和相交于点．设，（）．下列结论：①；②；③；④．其中结论正确的个数是（）．（A）4个（B）3个（C）2个（D）1个【考点】三角形全等、相似三角形【分析】①由可证，故①正确；②延长BG交DE于点H，由①可得，（对顶角）∴=90°，故②正确；③由可得，故③不正确；④，等于相似比的平方，即，∴，故④正确．【答案】B7.8.二、填空题1. （2018•上海，第18题4分）如图，已知在矩形ABCD中，点E在边BC上，BE=2CE，将矩形沿着过点E的直线翻折后，点C、D分别落在边BC下方的点C′、D′处，且点C′、D′、B在同一条直线上，折痕与边AD交于点F，D′F与BE交于点G．设AB=t，那么△EFG的周长为2t （用含t的代数式表示）．∴EF=t÷的周长=3×t则长AD与宽AB的比值是．AF=kk k=k=，即，∴CF=3∴AD=BC=CF=3的比值是故答案为AC=，则正方形的周长为 4 ．根据正方形的对角线等于边长的AC=÷本题考查了正方形的性质，比较简单，熟记正方形的对角线等于边长的4. （2018•江苏苏州,第17题3分）如图，在矩形ABCD中，=，以点B为圆心，BC长为半径画弧，交边AD 于点E．若AE•ED=，则矩形ABCD的面积为 5 ．AB=3x=BC=5x=×5. （2018•山东淄博,第15题4分）已知▱ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD 成为一个菱形，你添加的条件是AD=DC ．考点：菱形的判定；平行四边形的性质．专题：开放型．分析：根据菱形的定义得出答案即可．解答：解：∵邻边相等的平行四边形是菱形，∴平行四边形ABCD的对角线AC、BD相交于点O，试添加一个条件：可以为：AD=DC；故答案为：AD=DC．点评：此题主要考查了菱形的判定以及平行四边形的性质，根据菱形的定义得出是解题关键．6．（2018•四川宜宾，第12题，3分）菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线长度是 5 cm．，BO=AB•cos∠ABO=5×∴BD=2BO=7．（2018•四川凉山州，第14题，4分）顺次连接矩形四边中点所形成的四边形是菱形．学校的一块菱形花园两对角线的长分别是6m和8m，则这个花园的面积为 24m2．O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为．么菱形的面积等于．6.7.8.三、解答题1. （2018•四川巴中，第28题10分）如图，在四边形ABCD中，点H是BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连结BE，CF．（1）请你添加一个条件，使得△BEH≌△CFH，你添加的条件是，并证明．（2）在问题（1）中，当BH与EH满足什么关系时，四边形BFCE是矩形，请说明理由．考点：矩形的判定．分析：（1）根据全等三角形的判定方法，可得出当EH=FH，BE∥CF，∠EBH=∠FCH时，都可以证明△BEH≌△CFH，（2）由（1）可得出四边形BFCE是平行四边形，再根据对角线相等的平行四边形为矩形可得出BH=EH时，四边形BFCE是矩形．解答：（1）答：添加：EH=FH，证明：∵点H是BC的中点，∴BH=CH，在△△BEH和△CFH中，，∴△BEH≌△CFH（SAS）；（2）解：∵BH=CH，EH=FH，∴四边形BFCE是平行四边形（对角线互相平分的四边形为平行四边形），∵当BH=EH时，则BC=EF，∴平行四边形BFCE为矩形（对角线相等的平行四边形为矩形）．点评：本题考查了全等三角形的判定和性质以及平行四边形的判定，是基础题，难度不大．2. （2018•山东威海，第24题11分）猜想与证明：如图1摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM、ME，试猜想DM与ME的关系，并证明你的结论．拓展与延伸：（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为 DM=DE ．（2）如图2摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明（1）中的结论仍然成立．AE、BF，交点为G ．(1)求证：AE⊥BF；(2)将△BCF 沿BF 对折，得到△BPF（如图2），延长FP 交BA 的延长线于点Q ，求sin∠BQP 的值；(3)将△ABE 绕点A 逆时针方向旋转，使边AB 正好落在AE 上，得到△AHM（如图3），若AM 和BF 相交于点N ，当正方形ABCD 的面积为4时，求四边形GHMN 的面积．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；解直角三角形．分析：（1）由四边形ABCD 是正方形，可得∠ABE=∠BCF=90°，AB=BC ，又由BE=CF ，即可证得△ABE≌△BCF,可得∠BAE=∠CBF，由∠ABF+∠CBF=900可得∠ABF+∠BAE=900，即AE⊥BF；（2）由△BCF≌△BPF, 可得CF=PF,BC=BP,∠BFE=∠BFP，由CD∥AB 得∠BFC=∠ABF,从而QB=QF ，设PF 为x,则BP 为2x,在Rt△QBF 中可求 QB 为25x ，即可求得答案； （3）由2)(AMAN AHM AGN =∆∆可求出△AG N 的面积，进一步可求出四边形GHMN 的面积． 解答：(1)证明：∵E、F 分别是正方形ABCD 边BC 、CD 的中点，∴CF=BE，∴Rt△ABE≌Rt△BCF ∴∠BAE=∠CBF 又∵∠BAE+∠BEA=900，∴∠CBF+∠BEA=900，∴∠BGE=900， ∴AE⊥BF(2)根据题意得：FP=FC ，∠PFB=∠BFC，∠FPB=900，∵CD∥AB, ∴∠CFB=∠ABF，∴∠ABF=∠PFB．∴QF=QB令PF=k （k>O ），则PB=2k ，在Rt△BPQ 中，设QB=x ， ∴x 2=(x －k)2+4k 2, ∴x=25k ，∴sin∠BQP=54252==k k QP BP (3)由题意得：∠BAE=∠EAM,又AE⊥BF, ∴AN=AB=2,∵ ∠AHM=900, ∴GN//HM, ∴2)(AM AN AHM AGN =∆∆ ∴54)52(12==ΛAGN ∴ 四边形GHMN=S ΔAHM － S ΔAGN=1一54= 54 答：四边形GHMN 的面积是54. 点评：此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质以及三角函数等知识．此题综合性较强，难度较大，注意掌握旋转前后图形的对应关系，注意数形结合思想的应用．4. （2018•山东烟台，第25题10分）在正方形ABCD 中，动点E ，F 分别从D ，C 两点同时出发，以相同的速度在直线DC ，CB 上移动．（1）如图①，当点E 自D 向C ，点F 自C 向B 移动时，连接AE 和DF 交于点P ，请你写出AE 与DF 的位置关系，并说明理由；（2）如图②，当E ，F 分别移动到边DC ，CB 的延长线上时，连接AE 和DF ，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）（3）如图③，当E ，F 分别在边CD ，BC 的延长线上移动时，连接AE ，DF ，（1）中的结论还成立吗？请说明理由；（4）如图④，当E ，F 分别在边DC ，CB 上移动时，连接AE 和DF 交于点P ，由于点E ，F 的移动，使得点P 也随之运动，请你画出点P 运动路径的草图．若AD=2，试求出线段CP 的最小值．考点：全等三角形，正方形的性质，勾股定理，运动与变化的思想.分析：（1）AE=DF，AE⊥DF．先证得△ADE≌△DCF．由全等三角形的性质得AE=DF，∠DAE=∠CDF，再由等角的余角相等可得AE⊥DF；（2）是．四边形ABCD是正方形，所以AD=DC，∠ADE=∠DCF=90°，DE=CF，所以△ADE≌△DCF，于是AE=DF，∠DAE=∠CDF，因为∠CDF+∠ADF=90°，∠DAE+∠ADF=90°，所以AE⊥DF；（3）成立．由（1）同理可证AE=DF，∠DAE=∠CDF，延长FD交AE于点G，再由等角的余角相等可得AE⊥DF；（4）由于点P在运动中保持∠APD=90°，所以点P的路径是一段以AD为直径的弧，设AD的中点为O，连接OC交弧于点P，此时CP的长度最小，再由勾股定理可得OC的长，再求CP即可．解答：（1）AE=DF，AE⊥DF．理由：∵四边形ABCD是正方形，∴AD=DC，∠ADC=∠C=90°．∵DE=C F，∴△ADE≌△DCF．∴AE=DF，∠DAE=∠CDF，由于∠CDF+∠ADF=90°，∴∠DAE+∠ADF=90°．∴AE⊥DF；（2）是；（3）成立．理由：由（1）同理可证AE=DF，∠DAE=∠CDF延长FD交AE于点G，则∠CDF+∠ADG=90°，∴∠ADG+∠DAE=90°．∴AE⊥DF；（4）如图：由于点P在运动中保持∠APD=90°，∴点P的路径是一段以AD为直径的弧，设AD的中点为O，连接OC交弧于点P，此时CP的长度最小，在Rt△ODC中，OC=，∴CP=OC﹣OP=．点评：本题主要考查了四边形的综合知识．综合性较强，特别是第（4）题要认真分析．5. （2018•浙江杭州，第22题，12分）菱形ABCD的对角线AC，BD相交于点O，AC=4，BD=4，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．（1）用含x的代数式分别表示S1，S2；（2）若S1=S2，求x的值．可以求出．然后在两种情况下分别建立关于，AO=AC=2=BD•AC=8∴tan∠ABO==．==sin60°=FP==4××﹣=tan30°=．FM=﹣）•（（（﹣﹣=﹣=8（=，．=4＞2，．（．8+226.（2018•十堰14．（3分））如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是①（只填写序号）．是矩形，则应添加的条件是∠ABC=90°或AC=BD（不唯一）（添加一个条件即可）．8. (2019年湖北咸宁24．（12分）)如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．（1）∠PBD的度数为45°，点D的坐标为（t，t）（用t表示）；（2）当t为何值时，△PBE为等腰三角形？（3）探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值．考点：四边形综合题；解一元一次方程；全等三角形的判定与性质；等腰三角形的性质；勾股定理；正方形的性质．专题：压轴题；探究型．分析：（1）易证△BAP≌△PQD，从而得到DQ=AP=t，从而可以求出∠PBD的度数和点D的坐标．（2）由于∠EBP=45°，故图1是以正方形为背景的一个基本图形，容易得到EP=AP+CE．由于△PBE底边不定，故分三种情况讨论，借助于三角形全等及勾股定理进行求解，然后结合条件进行取舍，最终确定符合要求的t 值．（3）由（2）已证的结论EP=AP+CE很容易得到△POE周长等于AO+CO=8，从而解决问题．解答：解：（1）如图1，由题可得：AP=OQ=1×t=t（秒）∴AO=PQ．∵四边形OABC是正方形，∴AO=AB=BC=OC，∠BAO=∠AOC=∠OCB=∠ABC=90°．∵DP⊥BP，∴∠BPD=90°．∴∠BPA=90°﹣∠DPQ=∠PDQ．∵AO=PQ，AO=AB，∴AB=PQ．在△BAP和△PQD中，∴△BAP≌△PQD．∴AP=DQ，BP=PD．∵∠BPD=90°，BP=PD，∴∠PBD=∠PDB=45°．∵AP=t，∴DQ=t．∴点D坐标为（t，t）．故答案为：45°，（t，t）．（2）①若PB=PE，则∠PBE=∠PEB=45°．∴∠BPE=90°．∵∠BPD=90°，∴∠BPE=∠BPD．∴点E与点D重合．∴点Q与点O重合．与条件“DQ∥y轴”矛盾，∴这种情况应舍去．②若EB=EP，则∠PBE=∠BPE=45°．∴∠BEP=90°．∴∠PEO=90°﹣∠BEC=∠EBC．在△POE和△ECB中，∴△POE≌△ECB．∴OE=B C，OP=EC．∴OE=OC．∴点E与点C重合（EC=0）．∴点P与点O重合（PO=0）．∵点B（﹣4，4），∴AO=CO=4．此时t=AP=AO=4．③若BP=BE，在Rt△BAP和Rt△BCE中，∴Rt△BAP≌Rt△BCE（HL）．∴AP=CE．∵AP=t，∴CE=t．∴PO=EO=4﹣t．∵∠POE=90°，∴PE==（4﹣t）．延长OA到点F，使得AF=CE，连接BF，如图2所示．在△FAB和△ECB中，∴△FAB≌△ECB．∴FB=EB，∠FBA=∠EBC．∵∠EBP=45°，∠ABC=90°，∴∠ABP+∠EBC=45°．∴∠FBP=∠FBA+∠ABP=∠EBC+∠ABP=45°．∴∠FBP=∠EBP．在△FBP和△EBP中，∴△FBP≌△EBP．∴FP=EP．∴EP=FP=FA+AP=CE+AP．∴EP=t+t=2t．∴（4﹣t）=2t．解得：t=4﹣4∴当t为4秒或（4﹣4）秒时，△PBE为等腰三角形．（3）∵EP=CE+AP，∴OP+PE+OE=OP+AP+CE+OE=AO+CO=4+4=8．∴△POE周长是定值，该定值为8．点评：本题考查了正方形的性质、等腰三角形的性质、全等三角形的性质与判定、勾股定理等知识，考查了分类讨论的思想，考查了利用基本活动经验解决问题的能力，综合性非常强．熟悉正方形与一个度数为45°的角组成的基本图形（其中角的顶点与正方形的一个顶点重合，角的两边与正方形的两边分别相交）是解决本题的关键．9.( 2019年河南14.)如图，在菱形ABCD中,AB =1,∠DAB=600,把菱形ABCD绕点A顺时针旋转300得到菱形AB/C/D/，其中点C的运动能路径为/CC，则图中阴影部分的面积为 .答案：33 42+π.解析：由旋转可知，阴影部分面积=扇形ACC/面积－2个三角形D/FC的面积。

2019年中考数学真题分类汇编矩形菱形与正方形一.选择题1. （2019·湖北江汉油田、潜江市、天门市、仙桃市·3分）如图，正方形ABCD中，AB=6，G是BC的中点．将△ABG沿AG对折至△AFG，延长GF交DC于点E，则DE的长是（）A．1 B．1.5 C．2 D．2.5【分析】根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE；在直角△ECG中，根据勾股定理即可求出DE的长．【解答】解：∵AB=AD=AF，∠D=∠AFE=90°，在Rt△ABG和Rt△AFG中，∵，∴Rt△AFE≌Rt△ADE，∴EF=DE，设DE=FE=x，则EC=6﹣x．∵G为BC中点，BC=6，∴CG=3，在Rt△ECG中，根据勾股定理，得：（6﹣x）2+9=（x+3）2，解得x=2．则DE=2．故选：C．【点评】本题考查了翻折变换，解题的关键是掌握翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理．2.（2019•江苏宿迁•3分）如图，菱形ABCD的对角线AC.BD相交于点O，点E为边CD的中点，若菱形ABCD 的周长为16，∠BAD＝60°,则△OCE的面积是（）A. B. 2 C. D. 4【答案】A【分析】根据菱形的性质得菱形边长为4，AC⊥BD，由一个角是60度的等腰三角形是等边三角形得△ABD是等边三角形；在Rt△AOD中，根据勾股定理得AO=2，AC=2AO=4，根据三角形面积公式得S△ACD=OD·AC=4，根据中位线定理得OE∥AD，根据相似三角形的面积比等于相似比继而可求出△OCE的面积.【详解】∵菱形ABCD的周长为16，∴菱形ABCD的边长为4，∵∠BAD＝60°，∴△ABD是等边三角形，又∵O是菱形对角线AC.BD的交点，∴AC⊥BD，在Rt△AOD中，∴AO=，∴AC=2AO=4，∴S△ACD=OD·AC= ×2×4=4，又∵O、E分别是中点，∴OE∥AD，∴△COE∽△CAD，∴，∴，∴S△COE=S△CAD=×4=，故选A.【点睛】本题考查了相似三角形的判定与性质，等边三角形的判定与性质，勾股定理，菱形的性质，结合图形熟练应用相关性质是解题的关键.3.（2019•江苏无锡•3分）如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H 都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）A．等于B．等于C．等于D．随点E位置的变化而变化【分析】根据题意推知EF∥AD，由该平行线的性质推知△AEH∽△ACD，结合该相似三角形的对应边成比例和锐角三角函数的定义解答．【解答】解：∵EF∥AD，∴∠AFE=∠FAG，∴△AEH∽△ACD，∴==．设EH=3x，AH=4x，∴HG=GF=3x，∴tan∠AFE=tan∠FAG===．故选：A．【点评】考查了正方形的性质，矩形的性质以及解直角三角形，此题将求∠AFE的正切值转化为求∠FAG的正切值来解答的．4.（2019•江苏淮安•3分）如图，菱形ABCD的对角线AC.BD的长分别为6和8，则这个菱形的周长是（）A．20 B．24 C．40 D．48【分析】由菱形对角线的性质，相互垂直平分即可得出菱形的边长，菱形四边相等即可得出周长．【解答】解：由菱形对角线性质知，AO=AC=3，BO=BD=4，且AO⊥BO，则AB==5，故这个菱形的周长L=4AB=20．故选：A．【点评】本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键，难度一般．5.（2019•江苏淮安•3分）如图，在平面直角坐标系中，直线l为正比例函数y=x的图象，点A1的坐标为（1，0），过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x轴的垂线，垂足为A3，交直线l于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形A n B n C n D n的面积是（）n﹣1．【分析】根据正比例函数的性质得到∠D1OA1=45°，分别求出正方形A1B1C1D1的面积、正方形A2B2C2D2的面积，总结规律解答．【解答】解：∵直线l为正比例函数y=x的图象，∴∠D1OA1=45°，∴D1A1=OA1=1，∴正方形A1B1C1D1的面积=1=（）1﹣1，由勾股定理得，OD1=，D1A2=，∴A2B2=A2O=，∴正方形A2B2C2D2的面积==（）2﹣1，同理，A3D3=OA3=，∴正方形A3B3C3D3的面积==（）3﹣1，…由规律可知，正方形A n B n C n D n的面积=（）n﹣1，故答案为：（）n﹣1．【点评】本题考查的是正方形的性质、一次函数图象上点的坐标特征，根据一次函数解析式得到∠D1OA1=45°，正确找出规律是解题的关键．6.（2019•山东烟台市•3分）对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O 折叠菱形，使B，B′两点重合，MN是折痕．若B'M=1，则CN的长为（）A．7 B．6 C．5 D．4【分析】连接AC.BD，如图，利用菱形的性质得OC=AC=3，OD=BD=4，∠COD=90°，再利用勾股定理计算出CD=5，接着证明△OBM≌△ODN得到DN=BM，然后根据折叠的性质得BM=B'M=1，从而有DN=1，于是计算CD ﹣DN即可．【解答】解：连接AC.BD，如图，∵点O为菱形ABCD的对角线的交点，∴OC=AC=3，OD=BD=4，∠COD=90°，在Rt△COD中，CD==5，∵AB∥CD，∴∠MBO=∠NDO，在△OBM和△ODN中，∴△OBM≌△ODN，∴DN=BM，∵过点O折叠菱形，使B，B′两点重合，MN是折痕，∴BM=B'M=1，∴DN=1，∴CN=CD﹣DN=5﹣1=4．故选：D．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了菱形的性质．7.（2019•山东聊城市•3分）如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA=5，OC=3．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为（）A．（﹣，） B．（﹣，） C．（﹣，）D．（﹣，）【分析】直接利用相似三角形的判定与性质得出△ONC1三边关系，再利用勾股定理得出答案．【解答】解：过点C1作C1N⊥x轴于点N，过点A1作A1M⊥x轴于点M，由题意可得：∠C1NO=∠A1MO=90°，∠1=∠2=∠3，则△A1OM∽△OC1N，∵OA=5，OC=3，∴OA1=5，A1M=3，∴OM=4，∴设NO=3x，则NC1=4x，OC1=3，则（3x）2+（4x）2=9，解得：x=±（负数舍去），则NO=，NC1=，故点C的对应点C1的坐标为：（﹣，）．故选：A．【点评】此题主要考查了矩形的性质以及勾股定理等知识，正确得出△A1OM∽△OC1N是解题关键．8.（2019•上海•4分）已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）A．∠A=∠B B．∠A=∠C C．AC=BD D．AB⊥BC【分析】由矩形的判定方法即可得出答案．【解答】解：A.∠A=∠B，∠A+∠B=180°，所以∠A=∠B=90°，可以判定这个平行四边形为矩形，正确；B.∠A=∠C不能判定这个平行四边形为矩形，错误；C.AC=BD，对角线相等，可推出平行四边形ABCD是矩形，故正确；D.AB⊥BC，所以∠B=90°，可以判定这个平行四边形为矩形，正确；故选：B．【点评】本题主要考查的是矩形的判定定理．但需要注意的是本题的知识点是关于各个图形的性质以及判定．9. （2019•遂宁•4分）下列说法正确的是（）A．有两条边和一个角对应相等的两个三角形全等B．正方形既是轴对称图形又是中心对称图形C．矩形的对角线互相垂直平分D．六边形的内角和是540°【分析】直接利用全等三角形的判定以及矩形、菱形的性质和多边形内角和定理．【解答】解：A.有两条边和一个角对应相等的两个三角形全等，错误，必须是两边及其夹角分别对应相等的两个三角形全等；B.正方形既是轴对称图形又是中心对称图形，正确；C.矩形的对角线相等且互相平分，故此选项错误；D.六边形的内角和是720°，故此选项错误．故选：B．【点评】此题主要考查了全等三角形的判定以及矩形、菱形的性质和多边形内角和定理，正确把握相关性质是解题关键．10. （2019•资阳•3分）如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=12厘米，EF=16厘米，则边AD的长是（）A．12厘米B．16厘米C．20厘米D．28厘米【分析】利用三个角是直角的四边形是矩形易证四边形EFGH为矩形，那么由折叠可得HF的长即为边AD的长．【解答】解：∵∠HEM=∠AEH，∠BEF=∠FEM，∴∠HEF=∠HEM+∠FEM=×180°=90°，同理可得：∠EHG=∠HGF=∠EFG=90°，∴四边形EFGH为矩形，AD=AH+HD=HM+MF=HF，HF===20，∴AD=20厘米．故选：C．【点评】此题主要考查了翻折变换的性质以及勾股定理等知识，得出四边形EFGH为矩形是解题关键．11. （2019•杭州•3分）如图，已知点P矩形ABCD内一点（不含边界），设，，，，若，，则（）A. B.C. D.【答案】A【考点】三角形内角和定理，矩形的性质【解析】【解答】解：∵矩形ABCD∴∠PAB+∠PAD=90°即∠PAB=90°-∠PAB∵∠PAB=80°∴∠PAB+∠PBA=180°-80°=100°∴90°-∠PAB+∠PBA=100°即∠PBA-∠PAB=10°①同理可得：∠PDC-∠PCB=180°-50°-90°=40°②由②-①得：∠PDC-∠PCB-（∠PBA-∠PAB）=30°∴故答案为：A【分析】根据矩形的性质，可得出∠PAB=90°-∠PAB，再根据三角形内角和定理可得出∠PAB+∠PBA=100°，从而可得出∠PBA-∠PAB=10°①；同理可证得∠PDC-∠PCB=40°②，再将②-①，可得出答案。

一、选择题1.（2019江苏省无锡市，7，3）下列结论中，矩形具有而菱形不一定具有的性质是（）A.内角和为360°B.对角线互相平分C.对角线相等D.对角线互相垂直【答案】C【解析】本题考查了矩形的性质、菱形的性质，矩形的对角线相等且平分，菱形的对角线垂直且平分，所以矩形具有而菱形不具有的为对角线相等，故选C．【知识点】矩形的性质；菱形的性质2. (2019山东泰安,12,4分)如图,矩形ABCD中,AB＝4,AD＝2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是（）A.2B.4C.2D.第12题图【答案】D【思路分析】首先分析点P的运动轨迹,得到点P在△DEC的中位线上运动,点B到线段MN距离最短,即垂线段最短,过点B作MN的垂线,垂足为M,根据勾股定理可求出BM的长度.【解题过程】∵F为EC上一动点,P为DF中点,∴点P的运动轨迹为△DEC的中位线MN,∴MN∥EC,连接ME,则四边形EBCM为正方形,连接BM,则BM⊥CE,易证BM⊥MN,故此时点P与点M重合,点F与点C重合,BP取到最小值,在Rt△BCP中,BP【知识点】三角形中位线,正方形的性质,勾股定理3.（2019四川眉山，11，3分）如图，在矩形ABCD中AB=6，BC=8，过对角线交点O作EF⊥AC交AD于点E，交BC于点F，则DE的长是（）A．1 B．74C．2 D．125【答案】B【思路分析】连接CE，利用EO垂直平分AC，可得AE=CE，在Rt△CDE中，利用勾股定理求出DE的长即可.【解题过程】解：连接CE，∵四边形ABCD是矩形，∴∠ADC=90°，OC=OA，AD=BC=8，DC=AB=6，∵EF⊥AC，OA=OC，∴AE=CE，在Rt△DEC中，DE2+DC2=CE2，即DE2+36=（8-DE）2，解得：x=74，故选B.【知识点】矩形的性质，垂直平分线的性质，勾股定理4.（2019四川攀枝花，6，3分）下列说法错误的是（）A．平行四边形的对边相等B．对角线相等的四边形是矩形C．对角线互相垂直的平行四边形是菱形D．正方形既是轴对称图形、又是中心对称图形【答案】B【解析】对角线相等的四边形不一定是矩形，如等腰梯形.故选B．【知识点】平行四边形的性质；矩形的性质；菱形的判定；轴对称图形；中心对称图形5.（2019四川攀枝花，10，3分）如图，在正方形ABCD中，E是BC边上的一点，BE＝4，EC＝8，将正方形边AB沿AE折叠到AF，延长EF交DC于G。

一、选择题1.（ 2019 广东深圳， 12， 3 分）已知菱形ABCD的边长为4，∠BAD=120°，E、F分别为AB，AD上的点，且BE=AF ，则以下结论正确的有（）个．①△ BEC ≌△ AFC ；②△ ECF 为等边三角形；③∠ AGE=∠AFC；④若GF 1 AF=1，则= ．EG 3A ． 1B ．2 C．3D．4【答案】 D【思路剖析】【解题过程】在四边形ABCD是菱形，∵∠ BAD=120°，∴∠ B=∠BAC=60°，∴ AC=BC，且 BE=AF，∴△ BEC≌△AFC，故①正确；∵△ BEC≌△ AFC，∴ FC=EC，∠ FCA=∠ ECB，∴∠ ECF=∠ ACB=60°，∴△ ECF为等边三角形，故②正确；∵∠ AGE=180°－∠ BAC－∠ AEG；∠ AFC=180°－∠ FAC－∠ ACF，∴∠ AGE=∠ AFC，故③正确；∵ AF=1，则 AE=3，易得△ CFG∽△ CBE，∴GF CF，△ CEG∽△ CAE ，∴EGCE，∵ CE=CF，AC=BC ，BE BC AE AC∴ GF =EG，∴ GF BE 1 ，故④正确．应选 D．BE AEEG AE 3【知识点】四边形多结论题；菱形的性质；全等三角形的判断；等边三角形的判断；2.（ 2019 广西省贵港市，题号 12，分值 3 分）如图，E是正方形ABCD的边AB的中点，点H与B对于CE对称， EH 的延伸线与AD 交于点 F ，与CD的延伸线交于点N ，点P在AD的延伸线上，作正方形DPMN ，连结CP ，记正方形ABCD ，DPMN 的面积分别为S1， S2，则以下结论错误的选项是( )1 2 2 2FD C．CD 4PD 3A ． S S CP B．4F D． cos HCD5【答案】 D ．【思路剖析】依据勾股定理可判断 A ；连结CF，作FG EC ，易证得FGC 是等腰直角三角形，设EG x ，则 FG 2x ，利用三角形相像的性质以及勾股定理获得CG 2x ， CF 2 2x ， EC 3x ， BC 6 5x ， FD2 5x ，即可证5 5得 3FD AD ，可判断B；依据平行线分线段成比率定理可判断 C ；求得 cos HCD 可判断D．【解题过程】解：正方形 ABCD ， DPMN 的面积分别为S1 ，S2，S1 CD2， S2 PD2，在 Rt PCD 中， PC 2 CD 2 PD2，S1 S2 CP 2，故 A 结论正确；连结CF，点 H与B对于CE对称，CH CB ，BCE ECH ，CH CB在 BCE 和 HCE 中，ECH BCE ，BCEHCE (SAS) ，CE CEBE EH ，EHC B 90 ，BEC HEC ，CH CD ，在 Rt FCH 和 Rt FCD 中CH CD ，Rt FCH Rt FCD(HL) ，FCH FCD ，FH FD ，CF CFECH ECH 145 ，即ECF 45 ，BCD2作 FG EC于G，CFG 是等腰直角三角形，FG CG ，BEC HEC ， B FGE 90 ，FEG∽ CEB ，EG EB 1FG 2EG ，FG BC，2设 EG x ，则 FG 2 x ，CG 2 x ， CF 2 2x ，EC 3x ，EB 2 BC 2 EC2，5 BC2 9 x2， BC 2 36x2， BC 6 5 x，4 5 5在 Rt FDC 中， FD CF 2 CD 2 (2 2x)2 36 x22 5 x ，5 53FD AD ，AF 2FD ，故 B 结论正确；AB//CN，ND FD 1 ，AE AF 2PD1，ND，AE CD2CD 4PD ，故 C 结论正确；EG x ， FG 2 x ，EF 5x ，FH FD 2 5 x，56 5x ，BC53 5x ，AE5作 HQ AD于Q，HQ//AB，HQ HF HQ，即AE EF 3 5 x5 2 5x 6 5 6 5 6 5 24 55 ， HQ5 xx ， CD HQ x x25x ，25 5 2524 5xcos HCD CD HQCF 25 6 10，故结论 D 错误，应选： D ．2 2 x25【知识点】正方形的性质；全等三角形的判断与性质；轴对称的性质；解直角三角形3. （2019 广西河池， T9，F3 分）如图，在正方形ABCD 中，点E，F分别在 BC ， CD 上， BE CF ，则图中与AEB 相等的角的个数是()A ．1B． 2C．3D．4【答案】 B ．【分析】证明：四边形ABCD是正方形，AB//BC，AB BC，ABE BCF 90 ，AB BC在ABE 和BCF 中，ABE BCF ，ABE BCF (SAS) ，BFC AEB ，BFC ABF ，BE CF故图中与AEB 相等的角的个数是2．应选：B．【知识点】正方形的性质；全等三角形的判断与性质4.（ 2019 贵州遵义， 10，4 分）我们把按序连结随意一个四边形各边中点所得四边形叫做中点四边形，已知四边形 ABCD 的中点四边形是正方形，对角线AC 与 BD 的关系，以下说法正确的选项是（ A)AC,BD相等且相互均分(B) AC,BD 垂直且相互均分(C) AC,BD 相等且相互垂直(D)AC,BD 垂直且均分对角【答案】 C【分析】因为中点四边形是正方形，正方形的对角线相等且垂直均分，边形都是平行四边形，所以原四边形的对角线 AC,BD 相等且相互垂直【知识点】三角形中位线定理，正方形的性质依据中位线定理可证随意四边形的中点四，应选 C5.(2019 黑龙江绥化 ,10 题 ,3 分 )如图,正方形ABCD中,E,F是对角线AC上的两个动点,P是正方形四边上的随意一点 ,且 AB ＝ 4,EF＝ 2,设 AE ＝ x,当△ PEF 是等腰三角形时,以下对于①当 x＝ 0(即 E,A 两点重合 )时 ,P 点有 6 个;P 点个数的说法中,必定正确的选项是()②当0<x< 4 2 2 时 ,P 点最多有9 个;③当P 点有8 个时 ,x＝ 2 2 2 ;④当△PEF 是等边三角形时,P 点有 4 个 .A. ①③B. ①④C.②④D.②③第 10题图【答案】 B【思路剖析】依据三角形的边的关系求出角度,在圆中求出扇形圆心角,暗影部分就是△ABC的面积减去△AOD 的面积和扇形BOD 的面积 ,分别算出各图形的面积,即可获得结果.【解题过程】①以点 A, 点 F 为圆心 ,EF 长为半径作弧 ,与 AB,AD 共有 4 个交点 ,作 EF 的垂直均分线 ,与 AB,AD 有2 个交点 ,共 6 个交点 ,故点 P 有 6 个 ,正确 ;②线段 EF 在线段 AC 上运动时 ,当点 E 或点 F 为 AC 的中点时 ,存在 8 个点 ,使△ PEF 为等腰三角形 ,不行能存在 9 个点 ,故错误 ;③由②知 ,点 E 为 AC 的中点时 ,x＝ 2 2 ,点 F 为 AC 的中点时 ,x＝ 2 2 2,故错误 ;④作 AC 的平行线 ,与 AC 的距离为 3 ,其与正方形有 4 个交点 ,故正确 .应选 B.【知识点】等腰三角形 ,正方形 ,等边三角形6.（2019湖北孝感，10，3分）如图，正方形BC＝ 4， DE ＝AF＝1，则 GF 的长为（ABCD）中，点E、F 分别在边CD ，AD 上，BE 与CF 交于点G．若A．B．C．D．【答案】 A【分析】解：正方形ABCD 中，∵ BC＝ 4，∴BC＝ CD＝ AD＝ 4，∠ BCE＝∠ CDF ＝90°，∵AF ＝DE＝1，∴DF ＝CE＝3，∴ BE ＝CF＝ 5，在△ BCE 和△ CDF 中，，∴△ BCE ≌△ CDF （ SAS），∴∠ CBE ＝∠ DCF ，∵∠ CBE +∠CEB ＝∠ ECG+∠ CEB＝90°＝∠ CGE，cos∠ CBE＝ cos∠ ECG ∴，CG，∴GF ＝ CF﹣ CG＝ 5应选： A．，，【知识点】正方形的性质；全等三角形的判断与性质；勾股定理；锐角三角函数7. （2019湖北十堰，5，3分）矩形拥有而平行四边形不必定拥有的性质是（）A．对边相等 B ．对角相等C．对角线相等 D ．对角线相互均分【答案】 C【分析】解：矩形的对角线相等，而平行四边形的对角线不必定相等．应选：C．【知识点】平行四边形的性质；矩形的性质8.（ 2019 湖南郴州， 8， 3 分）我国古代数学家刘徽将勾股形（先人称直角三角形为勾股形）切割成一个正方形和两对全等的三角形，以下图，已知∠A＝ 90°， BD＝ 4， CF＝ 6，则正方形ADOF 的边长是（）A．B． 2C．D．4【答案】 B【分析】解：设正方形ADOF 的边长为x，由题意得： BE＝BD ＝ 4，CE＝CF ＝6，∴BC＝ BE+CE＝ BD+CF＝ 10，2 2 2在 Rt △ ABC 中， AC +AB＝BC ，222即（ 6+ x ） +（ x+4 ） ＝10 ，整理得， x 2+10x ﹣ 24＝0，解得： x ＝ 2，或 x ＝﹣ 12（舍去）， ∴ x ＝ 2，即正方形 ADOF 的边长是 2；应选： B ．【知识点】 数学知识；勾股定理；正方形的性质9.(2019 内蒙古包头市， 11 题，3 分 )如图 5，在正方形 ABCD 中，AB=1，点 E 、F 分别在边 BC 和 CD 上，AE =AF ，∠ EAF =600，则 CF 的长是（）A.B.C.D.【答案】 C. 【思路剖析】连结 AC ，过 F 作 FG ⊥ AC 于 G ，先依据 AB=1 求出 AC 的长；设 FG=k ，用 k 表示出 AC 的长，列出对于 k 的【解题过程】解：连结 AC ，∵四边形 ABCD 是正方形，∴ AB=AD =1，∠ B=∠ D=900， AC 均分∠ BAD ，又∵ AE =AF ，∴ Rt △ ABE ≌ Rt △ ADF (HL ).∴∠ BAE =∠FAD ，∵ AC 均分∠ BAD ， ∴∠BAC =∠DAC =450，同理，∠ ACD=∠ ACB=450.∴∠ CAF =∠CAE = ∠ EAF =300,过F作FG⊥AC于G，在 Rt△ ABC 中， AC=设 GF =k，在 Rt△ AFG 中， AG=在 Rt△ CGF 中，∠ ACD=450，∴ CG=FG =k,∴CF=.∴ AC=AG+CG= k+ = . k.∴ k=.∴CF==.应选 C.【知识点】正方形的性质，全等三角形的判断，解直角三角形，勾股定理.10. （2019宁夏，6，3分）如图，四边形ABCD 的两条对角线订交于点O，且相互均分．增添以下条件，仍不能判断四边形ABCD 为菱形的是（）．A ．AC BD B．AB AD C．AC BD D．ABD CBD【答案】 C【分析】因为四边形ABCD 的两条对角线相互均分，所以四边形ABCD 为平行四边形，因为对角线相互垂直的平行四边形是菱形，所以选项 A 能够判断四边形ABCD 为菱形，因为有一组临边相等的平行四边形是菱形，所以选项 B 能够判断四边形ABCD 为菱形，因为对角线相等的平行四边形为矩形，所需选项C不可以判断四边形ABCD为菱形，选项 D ，因为四边形ABCD为平行四边形，所以AD / /BC ，所以ADB CBD ，又因为ABD CBD，所以ABD ADB ,所以 AD AB ，所以平行四边形ABCD 为菱形，应选项 D 也能够判定四边形ABCD 为菱形，故此题正确选项为C．【知识点】菱形的判断．11. （2019年陕西省，6，3分）如图，在Rt△ ABC 中，ACB 90 ， A 65 ，CD AB ，垂足为D，E是 BC 的中点，连结ED，则EDC 的度数是（）．A．25B．30C．50D．65第6题图【答案】 D【分析】因为CD AB ，所以ADC BDC 90 ，所以ACD 90 A 25 ，因为ACB 90 ，所以DCE 90ACD 65 ，因为在Rt △ CDB中，E是BC的中点，所以EC ED ，所以EDC DCE 65 ．【知识点】直角三角形斜边上的中线等于斜边的一半、直角三角形的性质．12. （ 2019 年陕西省， 8，3 分）如图，在正方形ABCD 中，AB 4 ．若以 CD 为底边向其形外作等腰直角△DCE ，连结 BE，则 BE 的长为（）．A．4 5 B．2 2 C．2 10 D．2 3A DEB C第 8 题图第 8题答图【答案】 C【分析】如图，连结BD，因为四边形ABCD 为正方形，所以BDC 45 ，AD AB 4， A 90 ，在Rt△ ABD 中，由勾股定理得，BD AB 2 BD 2 4 2 ，因为所△DCE是等腰直角三角形，所以CDE 45 ，所以 BDE BDC CDE 90 ， DE EC DC 22 ，在Rt△BDE 中，由勾股定理得，2 2BE BD2 DE 2 2 10．【知识点】正方形的性质、等腰直角三角形的性质，勾股定理．13. （ 2019 贵州省安顺市，9，3分）如图，在菱形ABCD 中，按以下步骤作图：①分别以点 C 和点 D 为圆心，大于1CD 为半径作弧，两弧交于点M，N 两点；2②作直线 MN ，且 MN 恰巧经过点 A，与 CD 交于点 E，连结 BE ，则以下说法错误的选项是（）A．∠ ABC＝ 60° B ． S△ABE＝2S△ADEC．若 AB＝ 4，则 BE＝4 721D ． sin∠ CBE＝14【答案】 C第9题图【思路剖析】由作法得 AE 垂直均分 CD ，则∠ AED ＝ 90°， CE＝ DE，于是可判断∠ DAE ＝ 30°，∠ D＝ 60°，从而获得∠ ABC＝ 60°；利用 AB＝ 2DE 获得 S△ABE＝ 2S△ADE；作 EH ⊥ BC 于 H，如图，若 AB＝ 4，则可计算出CH ＝1 CE ＝1，EH ＝ 3 CH＝ 3 ，利用勾股定理可计算出BE＝ 2 7 ；利用正弦的定义得sin∠ CBE＝EH＝2 BE 21．14【解题过程】解：由作法得AE 垂直均分CD，∴∠ AED ＝ 90°， CE＝ DE ，第9题答图∵四边形 ABCD 为菱形，∴AD＝ 2DE ，∴∠ DAE ＝ 30°，∠ D＝ 60°，∴∠ ABC＝ 60°，所以 A 选项的说法正确；∵AB＝ 2DE，∴S△ABE＝ 2S△ADE，所以 B 选项的说法正确；作 EH ⊥BC 于 H ，如图，若 AB＝4，在 Rt△ECH 中，∵∠ ECH ＝ 60°，∴ CH＝CE＝ 1， EH＝ 3 CH＝ 3 ，在 Rt△BEH 中， BE ＝＝ 2 7 ，所以C选项的说法错误；sin∠ CBE＝EH＝ 3 ＝21，所以 D 选项的说法正确．BE 2 7 14应选： C．【知识点】三角形的面积；线段垂直均分线的性质；菱形的性质；基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直均分线；作已知角的角均分线；过一点作已知直线的垂线）；解直角三角形．14. (2019 黑龙江大庆 ,6 题 ,3 分 )以下说法中不正确的选项是()A. 四边相等的四边形是菱形C.菱形的对角线相互垂直且相等B. 对角线垂直的平行四边形是菱形D.菱形的邻边相等【答案】 C【分析】菱形的对角线相互垂直且相互均分,不必定相等,应选 C.【知识点】菱形的判断和性质15. （2019 广西桂林，11，3 分）将矩形ABCD 按以下图的方式折叠，BE ，EG，FG 为折痕，若极点A，C，D 都落在点O 处，且点B，O，G 在同一条直线上，同时点E，O，F 在另一条直线上，则AD的值为( ) ABA．6B． 2 C．3D． 3 5 2【答案】 B【分析】解：由折叠可得， AE OE DE，CG OG DG ，E ，G分别为 AD，CD的中点，设 CD 2a ， AD 2b ，则 AB 2a OB ， DG OG CG a ， BG 3a ， BC AD 2b ，C 90 ，Rt BCG 中， CG 2 BC 2 BG2，即 a 2 (2b) 2 (3a)2，b 2 2a 2，即 b 2 a ，b2 ，aAD 的值为2 ，AB应选： B．【知识点】翻折变换（折叠问题）；矩形的性质16.（2019湖北荆州，5，3分）如图，矩形ABCD 的极点 A， B， C 分别落在∠ MON 的边 OM， ON 上，若 OA＝OC，要求只用无刻度的直尺作∠MON 的均分线．小明的作法以下：连结AC，BD 交于点E，作射线OE，则射线 OE 均分∠ MON ．有以下几条几何性质：① 矩形的四个角都是直角，② 矩形的对角线相互均分，③ 等腰三角形的“三线合一” ．小明的作法依照是（）A．①②B．①③C．②③D．①②③【答案】 C【分析】解：∵四边形ABCD 为矩形，∴AE ＝CE，而 OA＝OC，∴OE 为∠ AOC 的均分线．应选： C．【知识点】等腰三角形的性质；矩形的性质；作图—基本作图17. （2019湖南邵阳，9，3分）如图，在Rt ABC中，BAC 90 ， B 36 ，AD是斜边 BC 上的中线，将 ACD 沿 AD 对折，使点C落在点 F 处，线段 DF 与 AB 订交于点 E ，则BED等于()A． 120 B． 108 C． 72 D． 36【答案】 B【分析】解：在 Rt ABC 中， BAC 90， B 36 ，C 90 B 54 ．AD 是斜边BC上的中线，AD BD CD，BAD B 36 ，DAC C 54 ，ADC 180 DAC C 72 ．将 ACD 沿AD对折，使点 C 落在点F处，ADF ADC 72 ，BED BAD ADF 3672 108 ．应选： B．【知识点】直角三角形斜边上的中线；翻折变换（折叠问题）18.（ 2019 内蒙古赤峰， 8，3 分）如图，菱形 ABCD 周长为 20，对角线 AC、BD 订交于点 O，E 是 CD 的中点，则 OE 的长是（）A．B． 3 C． 4 D． 5【答案】 A【分析】解：∵四边形ABCD 为菱形，∴CD＝BC 5，且 O 为 BD 的中点，∵E 为 CD 的中点，∴OE 为△ BCD 的中位线，∴OE CB＝，应选： A．【知识点】直角三角形斜边上的中线；三角形中位线定理；菱形的性质19.（2019四川泸州，10，3分）一个菱形的边长为6，面积为A． 8B． 12C．16【答案】【分析】解：以下图：28，则该菱形的两条对角线的长度之和为（D． 32）∵四边形ABCD 是菱形，∴AO＝ CO AC ，DO ＝ BO BD ， AC⊥ BD ，∵面积为 28，∴AC?BD＝ 2OD ?AO＝ 28 ①∵菱形的边长为6，2 2② ，∴OD +OA ＝362 2 2＝ 36+28＝ 64．由①②两式可得：（ OD +AO）＝ OD +OA +2OD?AO∴OD +AO＝ 8，∴2（ OD +AO）＝ 16，即该菱形的两条对角线的长度之和为 16．应选： C．【知识点】菱形的性质；勾股定理；菱形面积公式20. （ 2019 四川省雅安市，10， 3 分）如图，在四边形ABCD 中， AB=CD ， AC 、BD 是对角线，E、F、G、H分别是 AD 、 BD 、 BC、 AC 的中点，连结EF、 FG、 GH、HE ，则四边形EFGH 的形状是（）A ．平行四边形B．矩形C．菱形D．正方形AE DFHB G C【答案】 C【思路剖析】由点E、F、G、H分别是随意四边形ABCD 中 AD 、BD、 BC、CA 的中点，依据三角形中位线的性质，可得EF ＝ GH＝AB ， EH ＝ FG＝CD ，又由 AB=CD ，得 EF ＝ FG ＝ GH ＝ EH 时，四边形EFGH 是菱形．【解题过程】∵点 E、F 、G、H 分别是随意四边形ABCD 中 AD 、BD、 BC、CA 的中点，∴ EF ＝GH ＝AB，EH＝FG ＝ CD ，∵ AB=CD 【知识点】中点四边形；，∴ EF＝ FG＝GH ＝ EH 时，四边形EFGH 是菱形，应选 C．菱形的判断；三角形中位线二、填空题1.（ 2019 广东深圳， 15， 3 分）如图，在正方形ABCD中，BE=1，将BC沿CE翻折，点B的对应点恰巧落在对角线 AC 上；将 AD 沿 AF 翻折，点 D 的对应点恰巧落在对角线AC 上，连结 EF ，则 EF=____________ ．【答案】 6【分析】设点 B 的对应点是点G，点 D 的对应点是点H ，作 FM ⊥ AB 于点 M ，由折叠可知， EG=EB=AG=1 ，∴2 2 AE= 2 ；AM=DF=FH=1 ，∴ AB=FM= 2 +1，EM= 2 －1，∴EF= EM 2 + FM 2 =(2－1)+( 2+ 1) = 6 ．【知识点】正方形折叠；正方形的性质；勾股定理2. （ 2019 广西北部湾， 16， 3 分）如图，在菱形ABCD 中，对角线 AC ， BD 交与点 O，过点 A 作 AH ⊥ BC 于点 H，已知 BO=4 ， S 菱形ABCD =24，则 AH= .【答案】24. 5【思路剖析】此题考察了菱形的性质、勾股定理以及菱形面积公式，依据菱形面积=对角线积的一半可求AC ，再依据勾股定理求出 BC，而后由菱形的面积即可得出结果．【解题过程】解：∵四边形 ABCD 是菱形，∴BO=DO=4 ， AO=CO ， AC ⊥ BD ，∴BD=8.∵S 菱形ABCD= 1AC×BD=24 ，2∴AC=6 ，∴OC= 1AC=3 ，2∴BC= OB2OC2=5，∵S 菱形ABCD =BC×AH=24 ，24∴AH=.5故答案为24．5【知识点】菱形的性质；勾股定理；菱形面积公式.3.（ 2019 贵州黔西南州， 16，3 分）如图，点 E 在正方形 ABCD 的边 AB 上，若 EB＝ 1， EC＝ 2，那么正方形ABCD 的面积为．【答案】 3【分析】解：由勾股定理得， BC ，∴正方形 ABCD 的面积＝ BC 2＝ 3，故答案为： 3．【知识点】勾股定理4. （2019贵州遵义，个角向内对折后，点极点分别在平行四边形15， 4 分）如图，平行四边形纸片B 与点C 重合于点C’，点 A 与点ABCD 的四条边上，则EF=DABCD 的边 AB,BC 的长分别是 10cm 和重合于点 A’，四条折痕围成一个信封四边形 cm.7.5cm,将其四EHFG ，其【答案】 10【分析】∵折叠，∴∠ BEH= ∠FEH ，同理∠ AEG= ∠ FEG,∵∠ BEH+ ∠ FEH+ ∠ AEG+ ∠ FEG=180°，所以∠HEG=90°，同理∠ FGE=∠ HFG=90°，所以四边形 EHFG 是矩形，∴EF=GH. ∵对折后，点 B 与点 C 重合于点 C’，∴CH=C’H=BH, ∴ H 是 BC 的中点，同理 G 是 AD 的中点，∴ GH=AB=10cm, ∴ EF=10cm【知识点】折叠的性质，矩形的性质，矩形的判断5.（ 2019 湖北十堰， 16，3 分）如图，正方形 ABCD 和 Rt△AEF ，AB＝ 5，AE＝ AF＝ 4，连结 BF，DE．若△ AEF绕点 A 旋转，当∠ ABF 最大时， S△ADE＝．【答案】 6【分析】解：作 DH ⊥AE 于 H ，如图，∵AF ＝4，当△ AEF 绕点 A 旋转时，点 F 在以 A 为圆心， 4 为半径的圆上，∴当 BF 为此圆的切线时，∠ ABF 最大，即 BF⊥ AF，在 Rt△ ABF 中， BF 3，∵∠ EAF ＝ 90°，∴∠ BAF +∠ BAH ＝ 90°，∵∠ DAH +∠ BAH ＝90°，∴∠ DAH ＝∠ BAF ，在△ ADH 和△ ABF 中∠∠，∴△ ADH ≌△ ABF （AAS），∴DH ＝ BF＝ 3，∴ S△ADE AE?DH3× 4＝ 6．故答案为6．【知识点】等腰直角三角形；正方形的性质；旋转的性质6.（2019湖北十堰，12，3分）如图，已知菱形ABCD的对角线AC，BD 交于点 O，E 为 BC 的中点，若 OE＝ 3，则菱形的周长为．【答案】 24【分析】解：∵四边形ABCD 是菱形，∴AB ＝BC＝ CD ＝ AD ， BO＝ DO，∵点 E 是 BC 的中点，∴OE 是△ BCD 的中位线，∴CD ＝ 2OE＝ 2× 3＝ 6，∴菱形 ABCD 的周长＝ 4×6＝ 24；故答案为： 24．【知识点】直角三角形斜边上的中线；三角形中位线定理；菱形的性质7. （2019 湖北咸宁，16，3 分）如图，先有一张矩形纸片ABCD ，AB ＝4，BC＝ 8，点M，N 分别在矩形的边AD ，BC 上，将矩形纸片沿直线MN 折叠，使点 C 落在矩形的边AD 上，记为点P，点 D 落在G 处，连结PC ，交MN 于点 Q，连结 CM．以下结论：① CQ＝CD；②四边形 CMPN③ P，A 重合时，是菱形；MN＝2；④ △ PQM 的面积 S 的取值范围是3≤ S≤ 5．此中正确的选项是（把正确结论的序号都填上）．【答案】②③【分析】解：如图1，∵PM ∥ CN，∴∠ PMN ＝∠ MNC ，∵∠ MNC ＝∠ PNM ，∴∠ PMN ＝∠ PNM ，∴PM ＝ PN，∵ NC＝ NP，∴PM ＝CN，∵MP∥CN，∴四边形 CNPM 是平行四边形，∵ CN＝ NP，∴四边形 CNPM 是菱形，故②正确；∴CP⊥ MN ，∠ BCP＝∠ MCP ，∴∠ MQC ＝∠ D＝90°，∵ CP＝ CP，若 CQ＝ CD ，则 Rt △ CMQ ≌△ CMD ，∴∠ DCM ＝∠ QCM ＝∠ BCP＝30°，这个不必定建立，故① 错误；点 P 与点 A 重合时，如图 2，设 BN＝ x，则 AN＝NC＝ 8﹣ x，22 2＝AN，在 Rt△ ABN 中， AB +BN即 42+x2＝（ 8﹣ x）2，解得 x＝ 3，∴ CN＝ 8﹣ 3＝ 5， AC ，∴，∴，∴MN＝2QN＝2 ．故③ 正确；当 MN 过点 D 时，如图 3，此时， CN 最短，四边形CMPN 的面积最小，则 S 最小为 S 菱形当 P 点与 A 点重合时， CN 最长，四边形CMPN 的面积最大，则S 最大为∴4≤S≤5，故④ 错误．故答案为：②③ ．【知识点】菱形的判断与性质；矩形的性质；翻折变换（折叠问题）8.（ 2019 北京市， 16 题， 2 分）在矩形ABCD中，M，N，P，Q分别为边点重合）．对于随意矩形 ABCD ，下边四个结论中，①存在无数个四边形 MNPQ 是平行四边形；②存在无数个四边形 MNPQ 是矩形；③存在无数个四边形 MNPQ 是菱形；④起码存在一个四边形 MNPQ 是正方形．全部正确结论的序号是_______．【答案】①②③，S，AB ， BC， CD ，DA 上的点（不与端【思路剖析】如图16-1，经矩形ABCD 对角线交点O，① 任画两条和矩形对边分别订交的直线，按序连结交点获得的四边形为平行四边形，明显有无数个四边形；②任画两条和矩形对边分别订交且相等的直线，按序连结交点获得的四边形为矩形，明显有无数个四边形；③任画两条和矩形对边分别订交且垂直的直线，按序连结交点获得的四边形为菱形，明显有无数个四边形；④画两条和矩形对边分别订交，而且垂直且相等的直线，按序连结交点获得的四边形为正方形，明显只有一个四边形 .【解题过程】如图16-1，O为矩形ABCD对角线的交点，①图中任过点O 的两条线段 PM，QN ，则四边形 MNPQ 是平行四边形；明显有无数个.本结论正确 .②图中任过点O 的两条相等的线段PM ， QN，则四边形 MNPQ 是矩形；明显有无数个.本结论正确 .③图中任过点O 的两条垂直的线段PM ， QN，则四边形 MNPQ 是菱形；明显有无数个.本结论正确 .④图中过点O 的两条相等且垂直的线段PM ， QN ，则四边形MNPQ 是正方形；明显有一个.本结论错误 .故填：①②③ .【知识点】三角形全等的性质和判断、矩形的性质和判断、平行四边形和菱形、正方形的判断.9.（ 2019 北京市， 14 题， 2 分）把图1中的菱形沿对角线分红四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图 3 所示的正方形，则图 1 中菱形的面积为_______．51图 1 图 2 图 3【答案】 12【分析】设图 1 中小直角三角形的两直角边长分别为a，b （ a>b）；则由图a b 52 和图3 列得方程组b，由加a 1a 3 1 1减消元法得，∴菱形的面积 S 4 ab 4 3 2 12 .故填 12.b 2 2 2【知识点】菱形的性质、二元一次方程组的解法.10.（ 2019 贵州省安顺市， 17， 4 分）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点D为斜边BC上的一个动点，过 D 分别作 DM ⊥ AB 于点 M，作 DN⊥ AC 于点 N，连结 MN ，则线段MN 的最小值为.AMNB第17题图DC【答案】12 5【思路剖析】连结AD，即可证明四边形AMDN 是矩形；由矩形AMDN 得出 MN ＝ AD，再由三角形的面积关系求出 AD 的最小值，即可得出结果．【解题过程】连结AD，以下图：AMNB第17题答图DC∵DM⊥ AB， DN ⊥ AC，∴∠ AMD ＝∠ AND ＝90°，又∵∠ BAC＝ 90°，∴四边形 AMDN 是矩形；∴ MN ＝ AD ，∵∠ BAC ＝ 90°， AB ＝3， AC ＝ 4，∴ BC ＝ 5，当 AD ⊥BC 时， AD 最短，此时△ ABC 的面积＝1BC?AD ＝ 1 AB?AC ，22 ∴ AD 的最小值＝AB AC12 ， BC5∴线段 MN 的最小值为12 ；5【知识点】 垂线段最短、矩形的判断与性质、勾股定理、直角三角形面积的计算方法11. （ 2019 黑龙江省龙东地域， 10， 3）如图，四边形OAA 1B 1 是边长为 1 的正方形，以对角线 OA 1 为边作第二个正方形 OA 1A 2B 2，连结 AA 2，获得 △AA 1A 2；再以对角线 OA 2 为边作第三个正方形 OA 2A 3B 3，连结 A 1A 3，得 到 △A 1A 2A 3，再以对角线 OA 3 为边作第三个正方形 OA 3A 4B 4，连结 A 2A 4，获得 △A 2 A 3A 4， ，记△AA 1A 2，△A 1A 2A 3， △A 2A 3A 4 的面积分别为 S 1， S 2， S 3 ，这样下去，则 S 2019＝ ________．A 3A 2A 1B 2B 1A 4O AB 3【答案】 22017.【思路剖析】读懂条件，理清题意，先从简单的情况下手，逐渐过渡到复杂状况，从中找到计算规律即可 .【解题过程】 △AA 1A 2 中， AA 1=1 ，AA 1 边上的高是 1，它的面积 S 1=1×1×1；2△A 1A 2A 3 中， A 1A 2=1× 2 ，A 1A 2 边上的高是 1× 2 ，它的面积 S 2=1×1× 2 ×1× 2 ；2△A 2A 3A 4 中， A 2A 3=1× 2 × 2 ， A 2A 3 边上的高是1× 2 × 2 ，它的面积 S 3= 1×1× 2 × 2×1× 2× 2 ；22) 2018这样下去， △A 2018 2019 2020 中， A 2018 2019= 2 222 = (， A 2018A 2019 边上的高是 (2) 2018，它 A AA2018个 2相乘的面积 S 2019 1 ( 2) 2018 ( 2) 2018 =2 2017. = 2 × ×【知识点】正方形的性质；勾股定理；三角形的面积12. （ 2019 黑龙江省龙东地域， 8， 3）如图，矩形 ABCD 中， AB ＝ 4，BC ＝6，点 P 是矩形 ABCD 内一动点，且S △PAB ＝ 1S △PCD ，则 PC ＋PD 的最小值是 ________．2A DPB C 【答案】 4 5.【思路剖析】联合已知条件，依据S△PAB＝1S△PCD可判断出点 P 在平行于AB，与 AB 的距离为2、与 CD 的距2离为 4 的直线上，再依据“将军饮马问题”的解法解之即可.【解题过程】过点P 作直线 l∥ AB，作点 D 对于直线 l 的对称点D1，连结 CD 1，∵矩形 ABCD 中， AB＝ 4，BC ＝ 6，∴ CD=4,DD 1=8,在Rt△CDD中，由勾股定理得CD= 4 5 ，∴PC＋PD的最小值是 4 5 .1 1D1 Al DPB C【知识点】矩形的性质；勾股定理；最短路径问题13. （ 2019 吉林长春， 13，3 分）如图，有一张矩形纸片ABCD ，AB=8 ，AD=6 ，先将矩形纸片ABCD 折叠，使边 AD 落在边 AB 上，点 D 落在点 E 处，折痕为 AF ；再将△ AEF 沿 EF 翻折， AF 与 BC 订交于点 G，则△GCF 的周长为【答案】 4+2 2【思路剖析】此题主要考察翻折变换以及等腰直角三角形的性质，依据折叠的性质可得CE=2 ，∠ A= ∠ AFC=45°，从而得出FG 的长，从而得出答案.【解题过程】解：由折叠的性质可知∠A=45°， AD=DF ，∴ FC=2 ，∠ AFC=45°，∴ CG=2 ，∴FG=2 2 ，∴△ GCF 的周长为4+2 2 .故答案为4+2 2 .【知识点】翻折变换（折叠问题）；等腰直角三角形的性质.14. （2019·江苏镇江，10，2）将边长为 1 的正方形ABCD 绕点 C 按顺时针方向旋转到FECG 的地点（如图），使得点 D 落在对角线CF 上， EF 与 AD 订交于点H，则 HD ＝．（结果保存根号）FAHDEGB C第 10题图【答案】 2 －1．【分析】此题考察了正方形的性质、旋转、等腰三角形的判断与性质、勾股定理．由正方形的对角线与相邻的边夹角为 45°，得∠ CFE＝∠ ECF ＝ 45°，而在Rt△ CEF 中，由勾股定理，得CF＝ 2 ，从而DF＝ 2 －1，易知△ DHF 是等腰直角三角形，于是DH ＝DF＝ 2 －1．所以此题答案为2－1．【知识点】正方形的性质；旋转；等腰三角形的判断与性质；勾股定理15.（ 2019 辽宁本溪， 15，3 分）如图，BD是矩形ABCD的对角线，在BA和BD上分别截取BE，BF，使BE=BF；分别以 E， F 为圆心，以大于 1 EF 的长为半径作弧，两弧在∠ABD 内交于点 G，作射线 BG 交 AD 于点 P，若2AP=3 ，则点 P 到 BD 的距离为.【答案】 3.【分析】解：过点P 作 PQ⊥ BD ，垂足为Q，依据题意可得BP 均分∠ ABD.∵四边形ABCD 为矩形，∴∠ A=90°，∴PA=PQ.∵PA=3 ，∴PQ=3，故答案为 3.【知识点】角均分线的性质.16. （2019 广西贺州，18，6 分）如图，正方形ABCD 的边长为4，点E是CD 的中点，AF 均分BAE 交BC 于点 F ，将ADE 绕点 A 顺时针旋转90 得ABG ，则CF 的长为．【答案】 6 2 5【分析】解：作 FM AD于M，FN AG 于 N ，如图，易得四边形CFMD 为矩形，则FM 4，正方形 ABCD 的边长为4，点E是 CD 的中点，DE 2 ，AE2 22 5 ，4 2ADE 绕点 A 顺时针旋转90 得ABG ，AG AE 2 5，BG DE 2 ， 3 4， GAE 90 ， ABG D 90，而 ABC 90，点 G 在 CB 的延伸线上，AF均分BAE交BC于点 F，12，2413，即FA均分GAD，FN FM 4 ，1 1FN AG，AB GF224 2 52 5 ，GF4CFCGGF4225625．故答案为 6 2 5 ．【知识点】旋转的性质；正方形的性质17. （2019广西梧州，18，6分）如图，在菱形ABCD 中，AB 2 ，BAD 60 ，将菱形ABCD 绕点A逆时针方向旋转，对应获得菱形AEFG ，点E在 AC 上，EF与CD 交于点P，则DP的长是．【答案】3 1【分析】解：连结 BD 交AC于O，以下图：四边形 ABCD 是菱形，CD AB 2 ，BCD BAD 60 ，ACD BAC 1， OA OC，AC BD ，BAD 302OB 11 ，AB2OA 3OB 3 ，AC 2 3 ，由旋转的性质得：AE AB 2，EAG BAD 60 ，CE AC AE 2 3 2 ，四边形 AEFG 是菱形，EF //AG，CEP EAG 60 ，CEP ACD 90 ，CPE 90 ，PE 1CE 3 1，PC 3PE 3 3 ，2DP CD PC 2 (33) 3 1 ；故答案为： 3 1 ．【知识点】等边三角形的判断与性质；旋转的性质；菱形的性质；含30 角的直角三角形的性质；平行线的性质18. （2019 江苏镇江，10，2 分）将边长为 1 的正方形ABCD 绕点C 按顺时针方向旋转到FECG 的地点（如图），使得点 D 落在对角线CF 上，EF 与AD 订交于点H ，则HD ．（结果保存根号）【答案】 2 1【分析】解：四边形 ABCD 为正方形，CD 1 ，CDA 90 ，边长为 1 的正方形 ABCD 绕点 C 按顺时针方向旋转到FECG 的地点，使得点 D 落在对角线CF上，CF 2 ，CFDE 45 ，DFH 为等腰直角三角形，DH DF CF CD 2 1 ．故答案为2 1 ．【知识点】旋转的性质；正方形的性质19.（2019江苏徐州，13，3分）【答案】 16【分析】此题解答时要运用矩形的性质和三角形中位线的性质.解：∵四边形ABCD 是矩形，∴ OA=OB=OC=OD，∵M，N 分别为 BC，OC 的中点，∴OB=2MN =2×4=8 ，∴AC=2OB=16.【知识点】矩形的性质；三角形中位线三、解答题1. (2019 海南 ,21 题 ,13 分 )如图,在边长为1 的正方形 ABCD 中 ,E 是边 CD 的中点 ,点 P 是边 AD 上一点 (与点 A,D 不重合 ),射线 PE 与 BC 的延伸线交于点Q.(1) 求证 :△PDE≌△ QCE;(2) 过点 E 作 EF ∥BC 交 PB 于点 F,连结 AF,当 PB＝ PQ 时,①求证 :四边形 AFEP 是平行四边形;②请判断四边形AFEP 能否为菱形 ,并说明原因 .第 21题图【思路剖析】 (1)由正方形性质获得边角关系 ,从而证明全等 ;(2) ①经过证明全等获得 AP ＝ EF,由平行线的传达性获得平行 ,故四边形 AFEP 是平行四边形 ;②列出方程获得 AP 的长 ,与 PE 比较 ,不可以判断四边形 AFEP 是菱形 .【解题过程】 (1) 证明 :∵四边形ABCD 是正方形 ,∴∠ D ＝∠ BCD ＝90° ,∴∠ ECQ＝ 90°＝∠ D.∵ E 是 CD 的中点 , ∴DE ＝ CE,又∵∠ DEP＝∠ CEQ,∴△ PDE ≌△ QCE;(2) ①证明 :如图 ,由 (1) 得△ PDE≌△ QCE, ∴PE＝ QE＝1 1PQ,又∵ EF∥ BC, ∴ PF＝ FB＝PB,∵ PB＝ PQ,∴ PF＝ PE, 2 2∴∠ 1＝∠ 2,∵四边形 ABCD 是正方形 ,∴∠ BAD ＝ 90° ,在 Rt△ABP 中 ,F 是 PB 的中点 ,∴ AF ＝1BP＝ FP,∴∠ 3 2＝∠ 4,∵ AD ∥ BC,EF ∥ BC, ∴ AD ∥ EF,∴∠ 1＝∠ 4,∴∠ 2＝∠ 3,又∵ PF＝ FP,∴△ APF ≌△ EFP,∴ AP＝ EF,又∵ AP ∥ EF,∴四边形 AFEP 是平行四边形 .②四边形AFEP 不是菱形 ,原因以下 :设 PD＝ x,则 AP ＝ 1－ x,由 (1) 可知△ PDE ≌△ QCE,∴ CQ＝ PD ＝ x,∴ BQ ＝1 1+xBC+CQ ＝ 1+x, ∵点 E,F 分别是 PQ,PB 的中点 ,∴ EF 是△ PBQ 的中位线 ,∴ EF＝ BQ ＝.由①可知 AP ＝EF,即 12 2－ x＝1+x,解得 x＝ 1 ,∴PD＝ 1 ,AP ＝2 ,在 Rt△PDE 中 ,DE＝1 ,∴PE＝PD2+DE2＝13 ,∴AP ≠PE,∴四2 3 3 3 2 6边形 AFEP 不是菱形 .第 21 题答图【知识点】三角形的心里 ,圆的对称性 ,等角平等边2.（ 2019 黑龙江哈尔滨， 24，8 分）已知 :在矩形 ABCD 中 ,BD 是对角线 ,AE ⊥ BD 于点 E,CF⊥ BD 于点 F；(1)如图 1,求证 :AE=CF ；(2) 如图 2,当∠ ADB=30°时 ,连结 AF 、 CE,在不增添任何协助线的状况下,请直接写出图 2 中四个三角形，使写出的每个三角形的面积都等于矩形ABCD 面积的1．8【思路剖析】（ 1）由 AAS 证明△ ABE≌△ CDF ，即可得出结论；（ 2）由平行线的性质得出∠ CBD＝∠ ADB ＝30°，由直角三角形的性质得出BE＝1AB， AE＝1AD，得出△2 2ABE 的面积＝1AB×AD＝1矩形 ABCD 的面积，由全等三角形的性质得出△ CDF 的面积═1矩形 ABCD 的面8 8 8积；作 EG⊥ BC 于 G，由直角三角形的性质得出EG＝1 1 1 1 1矩形2BE＝× AB＝AB ，得出△ BCE 的面积＝82 2 4ABCD 的面积，同理：△ ADF 的面积＝1矩形 ABCD 的面积．8【解题过程】解：1）证明：∵四边形 ABCD 是矩形，∴AB＝ CD ，AB∥ CD， AD ∥ BC，∴∠ ABE＝∠ DF ，∵AE⊥ BD 于点 E， CF⊥BD 于点 F，∴∠ AEB＝∠ CFD ＝ 90°，ABE CDF在△ABE 和△ CDF 中，AEB CFD ，AB CD∴△ ABE≌△ CDF （ AAS），∴AE＝ CF ；（ 2）解：△ ABE 的面积＝△CDF 的面积＝△ BCE 的面积＝△ ADF 的面积＝矩形ABCD 面积的1．原因以下：8∵AD∥ BC，。

2019年中考数学专题复习第二十一讲矩形菱形正方形【基础知识回顾】一、矩形：1、定义：有一个角是角的平行四边形叫做矩形2、矩形的性质：⑴矩形的四个角都⑵矩形的对角线3、矩形的判定：⑴用定义判定⑵有三个角是直角的是矩形⑶对角线相等的是矩形【名师提醒:1、矩形是对称图形，对称中心是，矩形又是对称图形，对称轴有条2、矩形被它的对角线分成四个全等的三角形和两对全等的三角形 3、矩形中常见题目是对角线相交成600或1200角时，利用直角三角形、等边三角形等图形的性质解决问题】二、菱形：1、定义：有一组邻边的平行四边形叫做菱形2、菱形的性质：⑴菱形的四条边都⑵菱形的对角线且每条对角线3、菱形的判定：⑴用定义判定⑵对角线互相垂直的是菱形⑶四条边都相等的是菱形【名师提醒:1、菱形既是对称图形,也是对称图形，它有条对称轴,分别是2、菱形被对角线分成四个全等的三角形和两对全等的三角形3、菱形的面积可以用平行四边形面积公式计算，也可以用两对角线积的来计算4、菱形常见题目是内角为1200或600时，利用等边三角形或直角三角形的相关知识解决的题目】三、正方形：1、定义：有一组邻边相等的是正方形，或有一个角是直角的是正方形2、性质：⑴正方形四个角都都是角，⑵正方形四边条都⑶正方形两对角线、且每条对角线平分一组内角3、判定:⑴先证是矩形,再证⑵先证是菱形，再证【名师提醒：1、菱形、正方形具有平行四边形的所有性质，正方形具有以上特殊四边形的所有性质。

这四者之间的关系可表示为：2、正方形也既是对称图形，又是对称图形，有条对称轴3、几种特殊四边形的性质和判定都是从、、三个方面来看的，要注意它们的区别和联系】【重点考点例析】考点一：矩形的性质例1 （2018•杭州）如图,已知点P是矩形ABCD内一点（不含边界）,设∠PAD=θ1，∠PBA=θ2，∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°，则( ）A．(θ1+θ4)-（θ2+θ3）=30°B．（θ2+θ4）—（θ1+θ3）=40°C．（θ1+θ2）-（θ3+θ4）=70°D．（θ1+θ2）+（θ3+θ4）=180°【思路分析】依据矩形的性质以及三角形内角和定理,可得∠ABC=θ2+80°-θ1，∠BCD=θ3+130°—θ4，再根据矩形ABCD中，∠ABC+∠BCD=180°,即可得到（θ1+θ4）-（θ2+θ3)=30°．【解答】解:如图,∵AD∥BC,∠APB=80°，∴∠CBP=∠APB—∠DAP=80°—θ1,∴∠ABC=θ2+80°—θ1，又∵△CDP中,∠DCP=180°-∠CPD-∠CDP=130°—θ4，∴∠BCD=θ3+130°—θ4,又∵矩形ABCD中，∠ABC+∠BCD=180°，∴θ2+80°-θ1+θ3+130°—θ4=180°，即（θ1+θ4）—（θ2+θ3）=30°，故选：A．【点评】本题主要考查了矩形的性质以及三角形内角和定理的运用,解决问题的关键是掌握:矩形的四个角都是直角．考点二:和菱形有关的对角线、周长、面积的计算问题例2 （2018•淮安)如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（）A．20 B．24C．40 D．48【思路分析】由菱形对角线的性质，相互垂直平分即可得出菱形的边长，菱形四边相等即可得出周长．【解答】解:由菱形对角线性质知，AO=12AC=3，BO=12BD=4,且AO⊥BO，则225AB AO BO=+=，故这个菱形的周长L=4AB=20．故选：A．【点评】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键,难度一般．考点三：和正方形有关的证明题例3 （2018•北京)如图,在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE 交DG的延长线于点H，连接BH．（1)求证:GF=GC；（2）用等式表示线段BH与AE的数量关系,并证明．【思路分析】（1）如图1，连接DF，根据对称得：△ADE≌△FDE，再由HL证明Rt△DFG≌Rt△DCG，可得结论;（2)证法一：如图2，作辅助线，构建AM=AE，先证明∠EDG=45°，得DE=EH,证明△DME≌△EBH，则EM=BH,根据等腰直角△AEM得：EM=2AE,得结论；证法二：如图3，作辅助线，构建全等三角形,证明△DAE≌△ENH，得AE=HN，AD=EN，再说明△BNH 是等腰直角三角形，可得结论．【解答】证明：（1）如图1,连接DF,∵四边形ABCD是正方形，∴DA=DC,∠A=∠C=90°，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA=DF=DC,∠DFE=∠A=90°，∴∠DFG=90°，在Rt△DFG和Rt△DCG中,∵DF DC DG DG⎧⎨⎩＝＝，∴Rt△DFG≌Rt△DCG(HL），∴GF=GC；（2）BH=2AE，理由是:证法一：如图2,在线段AD上截取AM，使AM=AE，∵AD=AB，∴DM=BE，由（1)知：∠1=∠2，∠3=∠4,∵∠ADC=90°，∴∠1+∠2+∠3+∠4=90°，∴2∠2+2∠3=90°，∴∠2+∠3=45°，即∠EDG=45°,∵EH⊥DE，∴∠DEH=90°，△DEH是等腰直角三角形，∴∠AED+∠BEH=∠AED+∠1=90°，DE=EH，∴∠1=∠BEH,在△DME和△EBH中，∵1DM BE BEH DE EH ⎧∠⎪∠⎪⎨⎩＝＝＝ ， ∴△DME ≌△EBH, ∴EM=BH ，Rt△AEM 中，∠A=90°，AM=AE ， ∴EM=2AE ， ∴BH=2AE;证法二:如图3，过点H 作HN ⊥AB 于N ，∴∠ENH=90°，由方法一可知：DE=EH ，∠1=∠NEH ， 在△DAE 和△ENH 中，∵1A ENH NEH DE EH ∠∠∠∠⎧⎪⎨⎪⎩＝＝＝ ， ∴△DAE ≌△ENH ， ∴AE=HN ，AD=EN ， ∵AD=AB ，∴AB=EN=AE+BE=BE+BN, ∴AE=BN=HN ，∴△BNH 是等腰直角三角形， ∴BH=2HN=2AE ．【点评】本题考查了正方形的性质,全等三角形的判定定理和性质定理，对称的性质，等腰直角三角形的性质等知识，解决本题的关键是利用正方形的性质得到相等的边和相等的角，证明三角形全等，作出辅助线也是解决本题的关键．【备考真题过关】一、选择题1．（2018•十堰）菱形不具备的性质是（)A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形，2. （2018•哈尔滨）如图，在菱形ABCD中，对角线AC、BD相交于点O，BD=8，tan∠ABD=34则线段AB的长为（）A．7B．27C．5 D．103。

2020年中考数学二轮专题——矩形、菱形、正方形基础过关1. (2019无锡)下列结论中，矩形具有而菱形不一定具有的性质是()A. 内角和为360°B. 对角线相互平分C. 对角线相等D. 对角线互相垂直2. (2019娄底)顺次连接菱形四边中点得到的四边形是()A. 平行四边形B. 菱形C. 矩形D. 正方形3. (2019重庆A卷)下列命题正确的是()A．有一个角是直角的平行四边形是矩形B．四条边相等的四边形是矩形C．有一组邻边相等的平行四边形是矩形D．对角线相等的四边形是矩形4. (2019青羊区二诊)在菱形ABCD中，对角线AC、BD交于点O，下列说法错误的是()A．AB∥DC B．OC＝OBC．AC⊥BD D．OA＝OC5. (2019毕节)如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为()A. 3B. 3C. 5D. 5第5题图6. (2019天津)如图，四边形ABCD为菱形，A，B两点的坐标分别是(2，0)，(0，1)，点C，D在坐标轴上，则菱形ABCD的周长等于()A. 5B. 4 3C. 4 5D. 20第6题图7. (2019呼和浩特)已知菱形的边长为3，较短的一条对角线的长为2，则该菱形较长的一条对角线的长为()A. 2 2B. 2 5C. 4 2D. 2108. (2019临沂)如图，在▱ABCD中，M，N是BD上的两点，BM＝DN，连接AM，MC，CN，N A.添加一个条件，使四边形AMCN 是矩形，这个条件是( )A. OM ＝12ACB. MB ＝MOC. BD ⊥ACD. ∠AMB ＝∠CND第8题图9. 如图，在正方形ABCD 外侧，作等边△ADE ，AC ，BE 相交于点F ，则∠BFC 为( ) A. 75°B. 60°C. 55°D. 45°第9题图10. 如图，在矩形ABCD 中，点E 在BC 上，AE ＝AD ，DF ⊥AE ，垂足为F ，若∠FDC ＝30°，且AB ＝3，则AD 的长为( )A ．3B ．4C ．5D ．6第10题图11. (2019贵阳)如图，菱形ABCD 的周长是4 cm ，∠ABC ＝60°，那么这个菱形的对角线AC 的长是( ) A. 1 cmB. 2 cmC. 3 cmD. 4 cm第11题图12. (2019德阳)已知▱ABCD 的对角线AC 、BD 相交于点O ，△AOD 是等边三角形，且AD ＝4，则AB 等于( )A. 2B. 4C. 2 3D. 4 313. (2019河池)如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，BE ＝CF ，则图中与∠AEB 相等的角的个数是( )A. 1B. 2C. 3D. 4第13题图14. 如图，在矩形ABCD 中，AB ＝12，BC ＝16，点E 是BC 的中点，点F 是边CD 上的任意一点，则AF ＋EF 的最小值为( )A ．12B ．14C ．12 5D ．14 5第14题图15. (2019兰州)如图，边长为2的正方形ABCD 的对角线AC 与BD 交于点O ，将正方形ABCD 沿直线DF 折叠，点C 落在对角线BD 上的点E 处，折痕DF 交AC 于点M ，则OM ＝( )A.12B.22C.3－1D.2－1第15题图16. (2019金华)如图，矩形ABCD 的对角线交于点O ，已知AB ＝m ，∠BAC ＝∠α，则下列结论错误．．的是( )A. ∠BDC ＝∠αB. BC ＝m ·tan αC. AO ＝m 2sin αD. BD ＝m cos α第16题图17. (2019台州)如图，有两张矩形纸片ABCD 和EFGH ，AB ＝EF ＝2 cm ，BC ＝FG ＝8 cm.把纸片ABCD 交叉叠放在纸片EFGH 上，使重叠部分为平行四边形，且点D 与点G 重合，当两张纸片交叉所成的角α最小时，tan α等于( )A. 14B. 12C. 817D. 815第17题图18.(2019绍兴)正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积()A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变第18题图19. (2019双流区一诊)一个菱形的周长为20 cm，一条对角线长为6 cm，则这个菱形的面积是______cm2.20. (2019扬州)如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN.若AB＝7，BE＝5，则MN＝________．第20题图21.(2019徐州)如图，矩形ABCD中，AC、BD交于点O、M、N分别为BC、OC的中点．若MN＝4，则AC的长为________．第21题图22. (2019菏泽)如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是________．第22题图23.如图，在矩形ABCD中，AB＝6，BC＝8，过对角线交点O作EF⊥AC交AD于点E，交BC于点F，则DE 的长是________．第23题图24. (2019北京)如图，在菱形ABCD 中，AC 为对角线，点E ，F 分别在AB ，AD 上，BE ＝DF ，连接EF . (1)求证：AC ⊥EF ；(2)延长EF 交CD 的延长线于点G ，连接BD 交AC 于点O .若BD ＝4，tan G ＝12，求AO 的长．第24题图25. (2019云南)如图，四边形ABCD 中，对角线AC 、BD 相交于点O ，AO ＝OC ，BO ＝OD ，且∠AOB ＝2∠OA D.(1)求证：四边形ABCD 是矩形；(2)若∠AOB ∶∠ODC ＝4∶3，求∠ADO 的度数．第25题图能力提升1. (2019烟台)如图，面积为24的▱ABCD中，对角线BD平分∠ABC，过点D作DE⊥BD交BC的延长线于点E，DE＝6，则sin∠DCE的值为()A. 2425 B.45 C.34 D.1225第1题图2. (2019安徽)如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12.点P在正方形的边上，则满足PE＋PF＝9的点P的个数是()A. 0B. 4C. 6D. 8第2题图3. (2019黄石)如图，矩形ABCD中，AC与BD相交于点E，AD∶AB＝3∶1，将△ABD沿BD折叠，点A的对应点为F，连接AF交BC于点G，且BG＝2，在AD边上有一点H，使得BH＋EH的值最小，此时BHCF＝()A.32 B.233 C.62 D.32第3题图4.(2019遵义)如图，平行四边形纸片ABCD的边AB，BC的长分别是10 cm和7.5 cm，将其四个角向内对折后，点B与点C重合于点C′，点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG，其顶点分别在平行四边形ABCD的四条边上，则EF＝________cm.第4题图5. (2019海南)如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点(与点A、D不重合)，射线PE与BC的延长线交于点Q.(1)求证：△PDE≌△QCE；(2)过点E作EF∥BC交PB于点F，连接AF，当PB＝PQ时．①求证：四边形AFEP是平行四边形；②请判断四边形AFEP是否为菱形，并说明理由．第5题图6. (2019双流区一诊)如图①，菱形ABCD中，点P是CD的中点，∠BCD＝60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点．(1)求证：△ADP≌△ECP;(2)若BP＝n·PK，试求出n的值；(3)作BM⊥AE于点M，作KN⊥AE于点N，连接MO、NO，如图②，请证明△MON是等腰三角形，并求出∠MON的度数．第6题图满分冲关1. (2019新都区一诊)如图，直线l 经过正方形ABCD 的顶点A ，先分别过此正方形的顶点B 、D 作BE ⊥l 于点E 、DF ⊥l 于点F ，然后再以正方形的对角线的交点O 为端点，引两条相互垂直的射线分别与AD 、CD 交于点G 、H 两点．若EF ＝25，S △ABE ＝2，则线段GH 长度的最小值是______．第1题图2. (2018本溪)在菱形ABCD 中，∠BAD ＝120°，点O 为射线CA 上的动点，作射线OM 与直线BC 相交于点E ，将射线OM 绕点O 逆时针旋转60°，得到射线ON ，射线ON 与直线CD 相交于点F .(1)如图①，点O 与点A 重合时，点E ，F 分别在线段BC ，CD 上，请直接写出CE ，CF ，CA 三条线段之间的数量关系；(2)如图②，点O 在CA 的延长线上，且OA ＝13AC ，E ，F 分别在线段BC 的延长线和线段CD 的延长线上，请写出CE ，CF ，CA 三条线段之间的数量关系，并说明理由；(3)点O 在线段AC 上，若AB ＝6，BO ＝27，当CF ＝1时，请直接写出BE 的长．参考答案基础过关1. C2. C 【解析】顺次连接任意四边形的四边中点，得到四边形一定是平行四边形，如果原四边形的对角线相等，则可得中点四边形的邻边相等，即是菱形；如果原四边形的对角线互相垂直，则可得中点四边形的邻边垂直，即是矩形．因为菱形的对角线互相垂直，所以它的中点四边形是矩形．3．A 【解析】根据矩形的判定定理可知，有一个角是直角的平行四边形是矩形，故A 正确；四条边相等的四边形是菱形，不是矩形，故B 错误；有一组邻边相等的平行四边形是菱形，不是矩形，故C 错误；对角线相等的平行四边形是矩形，故D 错误．4. B 【解析】∵四边形ABCD 是菱形，∴AB ∥CD ，AC ⊥BD ，OA ＝OC ，故A ，C ，D 正确．5. B 【解析】在Rt △BCE 中，BC ＝22－12＝3，∴正方形ABCD 的面积为(3)2＝3.6. C 【解析】∵A (2，0)，B (0，1)，∴OA ＝2，OB ＝1，在Rt △AOB 中，由勾股定理得AB ＝22＋12＝5，∵四边形ABCD 为菱形，∴菱形ABCD 的周长为4AB ＝4 5.7. C 【解析】菱形对角线相互垂直且平分，因此另一条对角线长为2×32－1＝4 2.8. A 【解析】∵四边形ABCD 是平行四边形，∴OB ＝OD ，OA ＝OC .∵BM ＝DN ，∴OM ＝ON ，∴四边形AMCN 是平行四边形．当OM ＝12AC 时，MN ＝AC ，∴四边形AMCN 是矩形．9. B 【解析】∵四边形ABCD 是正方形，∴∠BAD ＝90°，AB ＝AD ，∠BAF ＝45°，∵△ADE 是等边三角形，∴∠DAE ＝60°，AD ＝AE ，∴∠BAE ＝90°＋60°＝150°，AB ＝AE ，∴∠ABE ＝∠AEB ＝12(180°－150°)＝15°，∴∠BFC ＝∠BAF ＋∠ABE ＝45°＋15°＝60°，故选B .10. D 【解析】∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠AEB ＝∠DAF ，又∵DF ⊥AE ，∴∠DF A ＝∠B ，又∵AE ＝AD ，∴△ADF ≌△EAB ，∴DF ＝AB .∵∠ADF ＋∠FDC ＝90°，∠DAF ＋∠ADF ＝90°，∴∠FDC ＝∠DAF ＝30°，∴AD ＝2DF ＝2AB ＝6.11. A 【解析】∵菱形ABCD 的周长是4 cm ，∴AB ＝BC ＝CD ＝DA ＝1 cm ，又∵∠ABC ＝60°，∴△ABC 是等边三角形，∴AC ＝AB ＝BC ＝1 cm .12．D 【解析】在平行四边形ABCD 中，∵△AOD 为等边三角形，即OA ＝OD ＝AD ＝4，∴AC ＝BD ＝8，∴平行四边形ABCD 是矩形，∴由勾股定理得AB ＝4 3.13. C 【解析】四边形ABCD 是正方形，∴AD ∥BC ，∴∠DAE ＝∠AEB .∵BE ＝CF ，∠ABE ＝∠BCF ，AB ＝BC ∴△ABE ≌△BCF (SAS)，∴∠BFC ＝∠AEB .∵AB ∥CD ，∴∠ABF ＝∠BFC ＝∠AEB .∴与∠AEB 相等的角有3个．14．C 【解析】如解图，作点E 关于直线CD 的对称点E ′，连接AE ′交CD 于点F ，此时AF ＋EF 的最小值为AE ′的长．∵在矩形ABCD 中，AB ＝12，BC ＝16，E 是BC 的中点，∴BE ＝CE ＝CE ′＝8，∴BE ′＝24，∴AE ′＝AB 2＋BE ′2＝122＋242＝12 5.第14题解图15. D 【解析】∵四边形ABCD 是正方形，∴∠CBE ＝∠DCM ＝45°，BC ＝CD ＝ 2.∴AC ＝BD ＝2.∴OC ＝1.由折叠的性质知，DE ＝CD ＝2，CF ＝EF ，∴BE ＝2－2，∠DFC ＝90°.∴∠CDM ＋∠DCE ＝90°.又∠BCE ＋∠DCE ＝90°，∴∠BCE ＝∠CDM . ∴△BCE ≌△CDM .∴CM ＝BE ＝2－ 2.∴OM ＝OC －CM ＝1－(2－2)＝2－1.16. C 【解析】∵四边形ABCD 是矩形，∴AC ＝BD ，且OD ＝OC ，∠ABC ＝90°，∴∠BDC ＝∠OCD ＝∠BAO ＝∠α，tan α＝BC AB ＝BC m ，sin α＝BC AC ＝BC 2AO ，cos α＝AB AC ＝m AC ，∴BC ＝m ·tan α，AO ＝BC 2sin α，AC ＝m cos α，而BD ＝AC ，BC ≠m ，∴BD ＝m cos α，AO ≠m2sin α∴A 、B 、D 正确，C 错误．17．D 【解析】如解图，当B 、E 重合时， α最小，∵在△BMF 和△DMC 中，⎩⎪⎨⎪⎧∠BMF ＝∠DMC ∠F ＝∠C BF ＝DC ，∴△BMF ≌△DMC (AAS)，∴BM ＝DM ，设FM ＝x ，则DM ＝BM ＝8－x ，在Rt △BFM 中，由勾股定理得22＋x 2＝(8－x )2，解得x ＝154，∴tan α＝BF FM ＝2154＝815.第17题解图18. D 【解析】如解图，连接DE ，∵在正方形ABCD 中，S △DEC ＝12AD ·CD ＝12S 正方形ABCD ，在长方形ECFG 中，S △DEC ＝12×EC ·GE ＝12S 矩形ECFG ，而点E 从点A 移动到点B 的过程中，三角形DEC 的面积保持不变，∴矩形ECFG 的面积保持不变．第18题解图19. 24 【解析】如解图，在菱形ABCD 中，BD ＝6.∵菱形的周长为20，BD ＝6，∴AB ＝5，BO ＝3，∴AO ＝52－32＝4，AC ＝8.∴S 菱形ABCD ＝12×6×8＝24.第19题解图20.132 【解析】 如解图，连接FC ，则MN ＝12CF ，在Rt △CFG 中，FG ＝5，CG ＝5＋7＝12，∴FC ＝52＋122＝13，∴MN ＝132.第20题解图21. 16 【解析】在△OBC 中，根据三角形中位线等于它所对的第三边的一半，得到OB ＝2MN ＝8，又根据矩形的性质：对角线相等且互相平分，得到AC ＝BD ＝2OB ＝16.22. 85 【解析】如解图，连接BD 交AC 于点O ，∵四边形ABCD 是正方形，AC 是对角线，∴CD ＝AD ，∠DAE ＝∠DCF ＝45°，BD ⊥AC . ∵AE ＝CF , ∴△DAE ≌△DCF (SAS), ∴DE ＝DF ，同理可证：DE ＝BE ，BE ＝BF ，∴四边形BEDF 是菱形，∵AC ＝8，AO ＝OD ，AE ＝2，∴OE ＝2，OD ＝4，∴DE ＝OD 2＋OE 2＝42＋22＝2 5.∴四边形BEDF 的周长为4DE ＝8 5.第22题解图23. 74 【解析】如解图，连接EC ，∵OA ＝OC ，EF ⊥AC ，∴EC ＝AE ，设DE ＝x ，则EC ＝AE ＝8－x ，根据勾股定理可得(8－x )2＝x 2＋62，解得x ＝74.∴DE 的长为74.第23题解图24. (1)证明：∵四边形ABCD 是菱形， ∴AB ＝AD ，∴∠BAC ＝∠DAC . ∵AB ＝AD ，BE ＝DF ，∴AB －BE ＝AD －DF ，即AE ＝AF . ∴△AEF 是等腰三角形． 又∵∠BAC ＝∠DAC ， ∴AC ⊥EF ；(2)解：由题意作解图如下， ∵四边形ABCD 是菱形，∴AC ⊥BD ，AB ∥CD ，OB ＝12BD ＝12×4＝2.∴∠G ＝∠AEG .由(1)知EF ⊥AC .又∵BD ⊥AC . ∴EF ∥BD .∴∠AEG ＝∠ABO . ∴∠G ＝∠ABO .∵tan G ＝12，∴tan ∠ABO ＝AO OB ＝12.∴AO ＝OB ·tan ∠ABO ＝2×12＝1.第24题解图25. (1)证明：∵AO ＝OC ，BO ＝OD ， ∴四边形ABCD 是平行四边形．又∵∠AOB ＝2∠OAD ，∠AOB 是△AOD 的外角， ∴∠AOB ＝∠OAD ＋∠ADO . ∴∠OAD ＝∠ADO . ∴AO ＝OD .又∵AC ＝AO ＋OC ＝2AO ，BD ＝BO ＋OD ＝2OD ， ∴AC ＝BD .∴四边形ABCD 是矩形；(2)解：设∠AOB ＝∠DOC ＝4x ，∠ODC ＝3x ，则∠ODC ＝∠OCD ＝3x . 在△ODC 中，∠DOC ＋∠OCD ＋∠CDO ＝180°， ∴4x ＋3x ＋3x ＝180°， 解得x ＝18°.∴∠ODC ＝3×18°＝54°.∴∠ADO ＝90°－∠ODC ＝90°－54°＝36°.能力提升1. A 【解析】如解图，连接AC 交BD 于点O ，过点D 作DF ⊥BE 于点F .∵BD 平分∠ABC ，∴∠ABD ＝∠CBD .∵四边形ABCD 是平行四边形，∴BC ∥AD . ∴∠ADB ＝∠CBD .∴∠ABD ＝∠ADB .∴AB ＝AD . ∴▱ABCD 是菱形. ∴AO 垂直平分BD . ∵DE ⊥BD ，∴OC ∥DE .∴OC ＝12DE ＝12×6＝3.∵菱形ABCD 的面积为24，∴BD ＝8. ∴BO ＝4. ∴BC ＝DC ＝5.∵DF ·BC ＝24，∴DF ＝245. ∴sin ∠DCE ＝DF DC ＝2425.第1题解图2. D 【解析】如解图，∵点E ，F 将对角线AC 三等分，且AC ＝12，∴AE ＝EF ＝FC ＝4，当P 点在AD 上时，作E 点关于AD 的对称点E ′，连接E ′F ，则AE ′＝AE ＝4，当P 点运动至E ′F 和AD 交点时，PE ＋PF 具有最小值，由对称性可知∠E ′AF ＝90°，此时E ′F ＝（AE ′）2＋AF 2＝42＋82＝45<9，当P 点和A 点重合时，过点E 作EG ⊥AD ，垂足为G ，PE ＋PF ＝AE ＋AF ＝12，当P 点和D 点重合时，连接DF ，∵AD ＝CD ，∠DAE ＝∠DCF ，AE ＝CF ，∴△AED ≌△CFD (SAS)，∴DE ＝DF ，∴PE ＋PF ＝2DE ＝2EG 2＋DG 2＝2×（22）2＋（42）2＝410.∵45<9<12，45<9<410，∴在AD 上有两个位置存在PE ＋PF ＝9，同理在其余三边上各有两种情况，故正方形四条边上共存在8个位置使得PE ＋PF ＝9，∴满足条件的P 点有8个．第2题解图3. B 【解析】∵矩形ABCD 中，AD ∶AB ＝3∶1，∴∠ADB ＝30°，又△ABD 沿BD 折叠，点A 的对应点为F ，∴∠ADB ＝∠BDF ＝30°，∠ABD ＝∠DBF ＝60°，AD ＝FD ，AB ＝BF ，∴∠CDF ＝30°，△ADF 为等边三角形，DF ＝AF ，∴∠BAF ＝12(180°－∠ABD －∠DBF )＝30°＝∠CDF ，又DC ＝AB ，∴△ABF ≌△DCF ，∴CF ＝BF ，在Rt △ABG 中，ABG ＝90°，∠BAG ＝30°，BG ＝2，∴AB ＝23，∴CF ＝23，如解图，延长BA 到B ′使AB ′＝AB ，连接EB ′交AD 于H ，根据对称性可知此时点H 即为满足BH ＋EH 的值最小的H 点．∵∠ADB ＝30°，∴AB ＝BE ＝ED ，又∵AB ′＝AB ＝BE ＝AE ，∴△BB ′E 为直角三角形，在Rt △BEH 和Rt △BAH 中，BH ＝BH ，BE ＝BA ，∴Rt △BEH ≌Rt △BAH ，∴∠ABH ＝30°，∴BH ＝AB cos ∠ABH＝4，∴BH CF ＝423＝233.第3题解图4. 10 【解析】根据折叠的性质可得△CFH ≌△C ′FH ，△DFG ≌△A ′FG ，△AEG ≌△A ′EG ，△HBE ≌△HC ′E ，∵四边形HFGE 是矩形，∴HF ＝EG ，FG ＝HE ，∴△CFH ≌△C ′FH ≌△AEG ≌△A ′EG ，△DFG ≌△A ′FG ≌△HBE ≌△HC ′E ，∴EF ＝A ′F ＋ A ′E ＝FD ＋AE ＝ FD ＋CF ＝CD ＝AB ＝10 cm .5. (1)证明：∵四边形ABCD 是正方形， ∴∠D ＝∠BCD ＝90°. ∴∠ECQ ＝90°＝∠D . ∵E 是CD 的中点， ∴DE ＝CE .又∵∠DEP ＝∠CEQ ， ∴△PDE ≌△QCE (ASA)；(2)①证明：如解图，由(1)可知△PDE ≌△QCE ， ∴PE ＝QE ＝12PQ .又∵EF ∥BC ， ∴PF ＝FB ＝12PB .∵PB ＝PQ ， ∴PF ＝PE . ∴∠1＝∠2.∵四边形ABCD 是正方形， ∴∠BAD ＝90°.在Rt △ABP 中，∵F 是PB 的中点， ∴AF ＝12BP ＝FP .∴∠3＝∠4.又∵AD ∥BC ，EF ∥BC ， ∴AD ∥EF . ∴∠1＝∠4.∴∠2＝∠3. 又∵PF ＝FP ，∴△APF ≌△EFP (AAS)． ∴AP ＝EF . 又∵AP ∥EF ，∴四边形AFEP 是平行四边形；第5题解图②解：四边形AFEP 不是菱形，理由如下： 设PD ＝x ，则AP ＝1－x . 由(1)可知△PDE ≌△QCE . ∴CQ ＝PD ＝x . ∴BQ ＝BC ＋CQ ＝1＋x .∵点E ，F 分别是PQ ，PB 的中点， ∵EF 是△PBQ 的中位线． ∴EF ＝12BQ ＝1＋x 2.由①可知AP ＝EF . 即1－x ＝1＋x 2，解得x ＝13.∴PD ＝13，AP ＝23.在Rt △PDE 中，∵DE ＝12，∴PE ＝PD 2＋DE 2＝136. ∵AP ≠PE .∴四边形AFEP 不是菱形．6. (1)证明：∵四边形ABCD 为菱形， ∴AD ∥BC ，∴∠DAP ＝∠CEP ，∠ADP ＝∠ECP ， 在△ADP 和△ECP 中，⎩⎪⎨⎪⎧∠DAP ＝∠CEP ∠ADP ＝∠ECP DP ＝CP， ∴△ADP ≌△ECP (AAS)；(2)解：如解图①，过点P 作PI ∥CE 交DE 于点I ， 则PI CE ＝DPDC ，又点P 是CD 的中点， ∴PI CE ＝12， ∵△ADP ≌△ECP ， ∴AD ＝CE ， ∴KP KB ＝PI BE ＝14， ∴BP ＝3PK ， ∴n ＝3；第6题解图①(3)解：如解图②，过点O 作OG ⊥AE 于点G ， ∵BM ⊥AE 于点M ，KN ⊥AE 于点N ， ∴BM ∥OG ∥KN ， ∵点O 是线段BK 的中点， ∴MG ＝NG ，又∵OG ⊥MN ， ∴OM ＝ON ，即△MON 是等腰三角形，由题意得，△BPC ，△AMB ，△ABP 为直角三角形， 设BC ＝2，则CP ＝1，由勾股定理得，BP ＝3， 则AP ＝7，根据三角形面积公式，BM ＝2217， ∴MP ＝377.易得PB ＝3PO ，∴OG ＝13BM ＝22121，MG ＝23MP ＝277，tan ∠MOG ＝MGOG ＝3，∴∠MOG ＝60°，∴∠MON 的度数为120°.第6题解图②满分冲关1. 6 【解析】由题易证△ABE ≌△DAF .∵GO ⊥HO ，易得△AGO ≌△DHO ，∴GO ＝HO .∴△GHO 为等腰直角三角形．∴当GO 最小时，GH 取得最小值．令AF ＝a ，AE ＝b ，则BE ＝a ，DF ＝b ，∴a ＋b ＝25，12a ·b ＝2，∴AB 2＝a 2＋b 2＝12.∴AB ＝23.∴当GO ⊥AD 时，GO 有最小值，此时OG ∥AB ，∵O 为BD 中点，∴OG 为△ABD 的中位线，∴GO ＝12AB ＝3，∴GO 的最小值为3，∴GH 最小值为 6.2. 解：(1)CA ＝CE ＋CF ；【解法提示】∵在菱形ABCD 中，∠BAD ＝120°， ∴∠DAC ＝∠ACB ＝∠D ＝60°. 又∵∠EAF ＝60°， ∴∠DAF ＝∠CAE . ∵AD ＝CD 且∠D ＝60°，∴△ACD 是等边三角形，AD ＝AC ， ∴△ADF ≌△ACE ， ∴DF ＝CE .又∵CA ＝CD ＝DF ＋CF ， ∴CA ＝CE ＋CF . (2)CF －CE ＝43CA ，理由：如解图①，过点O 作OG ∥AD ，交CF 于点G ， ∵四边形ABCD 是菱形， ∴AB ＝BC ＝CD ＝DA . ∵∠BAD ＝120°， ∴∠B ＝∠ADC ＝60°，∴△ABC 和△ADC 都为等边三角形． ∵OG ∥AD ，∴∠OGC ＝∠ADC ＝∠ACD ＝60°， ∴△OGC 为等边三角形，∴OC ＝OG ，∠OCE ＝∠OGF ＝180°－60°＝120°. ∵∠COE ＝∠GOF ＝60°－∠EOG ，∴△OCE ≌△OFG ， ∴FG ＝CE . ∵CF ＝GF ＋CG ， ∴CF －CE ＝CO . ∵AO ＝13CA ，∴OC ＝43CA ，∴CF －CE ＝43CA ；第2题解图①(3)BE 的长为1或3或5.【解法提示】连接BD 交AC 于点I ,①如解图②，当点O 在AI 上时，过点O 作OP ⊥BC 于点P ，作OQ ⊥CD 于点Q ， 又∵菱形ABCD 中，AC 平分∠BCD ， ∴OP ＝OQ .∵∠POQ ＝360°－120°－90°×2＝60°， ∴∠EOF ＝∠POQ ， ∴∠EOP ＝∠FOQ . 又∵∠OPE ＝OQF ＝90°， ∴△EOP ≌△FOQ ， ∴EP ＝FQ .在Rt △AIB 中，AB ＝6，∠BAI ＝60°， ∴BI ＝AB ·sin60°＝3 3. 在Rt △BIO 中， BO ＝27，BI ＝33， ∴OI ＝OB 2－BI 2＝1. 又∵CI ＝12AC ＝3，∴OC ＝3＋1＝4， ∴CP ＝CQ ＝12OC ＝2.又∵CF ＝1，∴EP ＝FQ ＝1，∴BE ＝BC －CP －EP ＝6－2－1＝3;第2题解图②②如解图③，当点O 在AI 上，点F 在线段DC 的延长线上时，过点O 作OP ⊥BC 于点P ，过点O 作OQ ⊥CD 于点Q ，同理可得EP ＝QF ，OC ＝4，CQ ＝CP ＝2， ∵CF ＝1，∴QF ＝CQ ＋CF ＝3，∴BE ＝CB －CP －PE ＝6－2－3＝1;第2题解图③③如解图④，当点O 在IC 上时，由①知OC ＝3－1＝2， 又∵CF ＝1，∠ACD ＝60°， ∴OF ⊥CD ，∴∠OEC ＝360°－60°－120°－90°＝90°， ∴EC ＝12OC ＝1，∴BE ＝6－1＝5；第2题解图④④如解图⑤，当点O 在IC 上，点F 在线段DC 的延长线上时，过点O 作OP ⊥BC 于点P ，过点O 作OQ ⊥CD 于点Q ，同理可得QF ＝PE ，OC ＝2，CP ＝CQ ＝1，QF ＝CQ ＋CF ＝2，∴BE ＝BC －EP －CP ＝6－2－1＝3; 综上所述，BE 的长为1或3或5.第2题解图⑤。

2019-2020年中考数学试题分类解析汇编 专题36矩形、菱形、正方形一、选择题1.（浙江舟山、嘉兴3分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为 （A ）48cm（B ）36cm （C ）24cm（D ）18cm【答案】A 。

【考点】菱形的性质，平行四边形的性质。

【分析】根据①②③④四个平行四边形面积的和为14cm2，四边形ABCD 面积是11cm2，从图可求出⑤的面积： 2ABCD 1S S S 2cm ⑤四边形①+②+③+④=-=11-7=4。

从而可求出菱形的面积： 2EFGH S S 14418cm ==+=①+②+③+④+⑤菱形。

又∵∠EFG=30°，∴菱形的边长为6cm 。

从而根据菱形四边都相等的性质得：①②③④四个平行四边形周长的总和=2（AE+AH+HD+DG+GC+CF+FB+BE ） =2（EF+FG+GH+HE ）=48cm 。

故选A 。

2.（浙江温州4分）如图，在矩形ABCD 中，对角线AC ，BD 交与点O ．已知∠AOB=60°，AC=16，则图中长度为8的线段有A 、2条B 、4条C 、5条D 、6条【答案】D 。

【考点】矩形的性质。

等边三角形的判定和性质。

【分析】因为矩形的对角线相等且互相平分，AC=16，所以AO=BO=CO=DO=8；又由∠AOB=60°，所以三角形AOB 是等边三角形，所以AB=AO=8；又根据矩形的对边相等得，CD=AB=AO=8．从而可求出线段为8的线段有6条。

故选D 。

3.（辽宁大连3分）如图，矩形ABCD 中，AB ＝4，BC ＝5，AF 平分∠DAE，EF⊥AE，则CF 等于A ．23B ．1C ．32D ．2【答案】C 。

4.（黑龙江哈尔滨3分）如图，矩形ABCD 中，对角线AC 、BD 相交于点O ，∠AOB=600，AB=5，则AD 的长是．（A)53 （B ）52 （C ）5 (D)10 【答案】A 。

与五边形 MCNGF 面积相等，∴（OF＋FM）2＝GF＋ 1 GF＝ 5 GF2，∴ 2 GF＋FM＝ 5 GF，∴
4
4
2
2
FM＝ 5 GF－ 2 GF，∴ FM ＝ 5 2 .故选 A．
2
2
GF
2
. (2019·台州)如图,有两张矩形纸片 ABCD 和 EFGH,AB＝EF＝2cm,BC＝FG＝8cm,把纸片 ABCD
【解析】连接 AC，交 BD 于点 F，过点 D 作 DM CE ，垂足为 M，
因为四边形 ABCD 是平行四边形，
所以 F 是 BD 的中点，AD//BC，
所以 DBC ADB ，
因为 BD 是 ABC 的平分线，
所以 ABD DBC ，
所以 ABD ADB ，
所以 AB AD ，
AD 于点 E，交 BC 于点 F，则 DE 的长是
A．1
B． 7
4
C．2
D． 12
5
【答案】B 【解析】连接 CE，∵四边形 ABCD 是矩形，∴∠ADC=90°，OC=OA，AD=BC=8，DC=AB=6， ∵EF⊥AC，OA=OC，∴AE=CE，在 Rt△DEC 中，DE2+DC2=CE2，即 DE2+36=（8-DE）2，解得： x= 7 ，故选 B.
积
EC CD
相等，故选 D.
． （2019·烟台）如图，面积为 24 的□ABCD 中，对角线 BD 平分 ABC ，过点 D 作 DE BD
交 BC 的延长线于点 E， DE 6 ，则 sin DCE 的值为（ ）．
A． 24 25
B． 4 5
C． 3 4
D． 12 25

2019年全国各地100份中考数学试卷分类汇编第26章 矩形、菱形与正方形一、选择题1. （2019浙江省舟山，10，3分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ） （A ）48cm （B ）36cm （C ）24cm（D ）18cm【答案】A2. （2019山东德州8,3分）图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是（A ）2n（B ）4n（C ）12n + （D ）22n +【答案】C3. （2019山东泰安，17 ，3分）如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为A.17B.17C.18D.19 【答案】B4. （2019山东泰安，19 ，3分）如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC =3，则折痕CE 的长为 A.23 B.332C. 3D.6图1图2图3……（第10题）FAB CDH EG①②③④⑤【答案】A5. （2019浙江杭州，10，3）在矩形ABCD 中，有一个菱形B F D E (点E ，F 分别在线段AB ，CD 上)，记它们的面积分别 为ABCD BFDE S S 和．现给出下列命题：（ ） ①若232ABCD BFDE S S +=，则3tan 3EDF ∠=．②若2,DE BD EF =•则2DF AD =． 则:A ．①是真命题，②是真命题B ．①是真命题，②是假命题[来源:学.科.网Z.X.X.K]C ．①是假命题，②是真命题D ，①是假命题，②是假命题 【答案】A6. （2019浙江衢州，1,3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF AG 、分别架在墙体的点B 、点C 处，且AB AC =,侧面四边形BDEC 为矩形，若测得100FAG ∠=︒，则FBD ∠=( )[来源:Zxxk]A. 35°B. 40°C. 55°D. 70°【答案】C7. （2019浙江温州，6，4分）如图，在矩形ABCD 中，对角线AC ，BD 交于点O ．已知∠AOB = 60°，AC ＝16，则图中长度为8的线段有( ) A ．2条 B ．4条 C ．5条 D ．6条 【答案】D8. 2019四川重庆，10，4分）如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( )[来源:ZXXK]EAB CD FG（第5题）A ．1B ．2C ．3D ．4 【答案】C9. （2019浙江省嘉兴，10，4分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ） （A ）48cm （B ）36cm （C ）24cm（D ）18cm[来源:Z#xx#k]【答案】A10．（2019台湾台北，29）如图(十二)，长方形ABCD 中，E 为BC 中点，作AEC 的角平分线交AD 于F 点。