下载文档原格式
Lecture5 答案作业一：写出上下文无关文法，其终止符集V T={a,b}能生成语言L(G)={ab,ba,aba,bab,abab,baba,…}答案：上下文无关文法：G=(V,T,S,P)，V={S,A,B},T={a,b},P如下：S->aAb|aAba|bBa|bBabA->baA|∈B->abB|∈作业二：求一有限态自动机，它只能接受由“偶数个a”与/或“偶数个b”组成的任意字符串，例如：aa, bb, abab, abba, baba等。
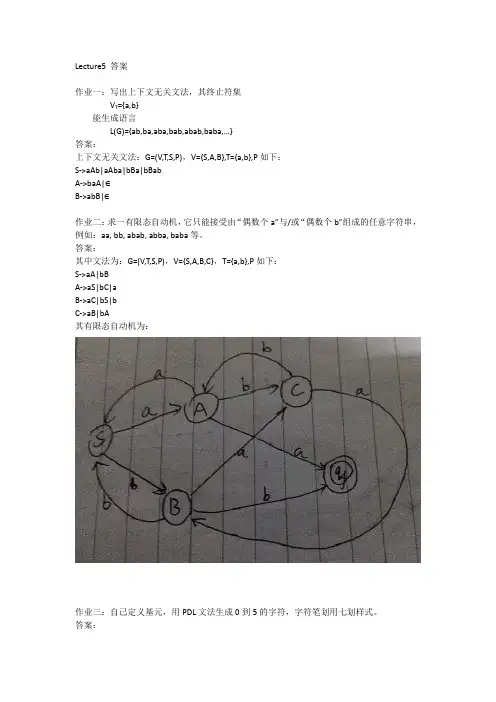
答案：其中文法为：G=(V,T,S,P)，V={S,A,B,C}，T={a,b},P如下：S->aA|bBA->aS|bC|aB->aC|bS|bC->aB|bA其有限态自动机为：作业三：自己定义基元，用PDL文法生成0到5的字符，字符笔划用七划样式。
答案：文法G = (V N, V T, P, S)，其中V N={S,S0,S1,S2,S3,S4,S5,A,B,C,D}，V T={ a↓, b→, (, ),+,*,~,-}，P：S->S0|S1|S2|S3|S4|S5，A->((~a+b)+a)，B->((a+b)+~a)，C->(b+a)，D->((~b+a)+b) S0->A*B，S1->(a+a)，S2->C+D，S3->((C-b)+a)-b，S4->((a+b)-a)+a，S5->D+a+(~b)作业四：试用树文法生成单位边长的立方体，定义三个基元为立方体的三种方向的边。
答案：对于该树状结构。
可以对应有一个上下文无关文法G=({S, A}, {$, a, b, c}, P, S)P: S->$AAA，A->aAA，A->bA，A->c,A->cAA,A->aA,A->b,A->bAA,A->cA,A->a则G T’=({S, A}, {$, a, b, c, (, )}, P’, S)P’: S->($AAA)，A->(aAA)，A->(bA)，A->(c),A->(cAA),A->(aA),A->(b),A->(bAA), A->(cA),A->(a)由G生成：S=>$AAA=>$aAAAA=>$abAAAA=>$abcAAA=>$abccAA=>$abcccAAA=>$abcccaAAA =>$abcccabAA=>$abcccabbA=>$abcccabbbAA=>$abcccabbbcAA=>$abcccabbbcaA=>$abcc cabbbcaa由G T’生成：S=>($AAA)=>($(aAA)AA)=>($(a(bA)A)AA)=>($(a(b(c))A)AA)=>($(a(b(c))(c))AA)=>( $(a(b(c))(c))(cAA)A)=>($(a(b(c))(c))(c(aA)A)A)=>($(a(b(c))(c))(c(a(b))A)A)=>($( a(b(c))(c))(c(a(b))(b))A)=>($(a(b(c))(c))(c(a(b))(b))(bAA))=>($(a(b(c))(c))(c(a (b))(b))(b(cA)A))=>($(a(b(c))(c))(c(a(b))(b))(b(c(a))A))=>($(a(b(c))(c))(c(a(b) )(b))(b(c(a))(a)))作业五：给出字符串样本集为{aaacc, aaacb, aacc, bacb, aaa, abc, bb, cc}推断一个有限态文法。
第5章：线性判别函数第一部分：计算与证明1． 有四个来自于两个类别的二维空间中的样本，其中第一类的两个样本为(1,4)T 和(2,3)T ，第二类的两个样本为(4,1)T 和(3,2)T 。
这里，上标T 表示向量转置。
假设初始的权向量a=(0,1)T ，且梯度更新步长ηk 固定为1。
试利用批处理感知器算法求解线性判别函数g(y)=a T y 的权向量。
解：首先对样本进行规范化处理。
将第二类样本更改为(4,1)T 和(3,2)T . 然后计算错分样本集：g(y 1) = (0,1)(1,4)T = 4 > 0 (正确) g(y 2) = (0,1)(2,3)T = 3 > 0 (正确) g(y 3) = (0,1)(-4,-1)T = -1 < 0 (错分) g(y 4) = (0,1)(-3,-2)T = -2 < 0 (错分) 所以错分样本集为Y={(-4,-1)T , (-3,-2)T }.接着，对错分样本集求和：(-4,-1)T +(-3,-2)T = (-7,-3)T第一次修正权向量a ，以完成一次梯度下降更新：a=(0,1)T + (-7,-3)T =(-7,-2)T 再次计算错分样本集：g(y 1) = (-7,-2)(1,4)T = -15 < 0 (错分) g(y 2) = (-7,-2)(2,3)T = -20 < 0 (错分) g(y 3) = (-7,-2)(-4,-1)T = 30 > 0 (正确) g(y 4) = (-7,-2)(-3,-2)T = 25 > 0 (正确) 所以错分样本集为Y={(1,4)T , (2,3)T }.接着，对错分样本集求和：(1,4)T +(2,3)T = (3,7)T第二次修正权向量a ，以完成二次梯度下降更新：a=(-7,-2)T + (3,7)T =(-4,5)T 再次计算错分样本集：g(y 1) = (-4,5)(1,4)T = 16 > 0 (正确) g(y 2) = (-4,5)(2,3)T = 7 > 0 (正确) g(y 3) = (-4,5)(-4,-1)T = 11 > 0 (正确) g(y 4) = (-4,5)(-3,-2)T = 2 > 0 (正确)此时，全部样本均被正确分类，算法结束，所得权向量a=(-4,5)T 。
模式识别大作业引言：转眼之间，研一就结束了。
这学期的模式识别课也接近了尾声。
我本科是机械专业，编程和算法的理解能力比较薄弱。
所以虽然这学期老师上课上的很精彩，但是这学期的模式识别课上的感觉还是有点吃力。
不过这学期也加强了编程的练习。
这次的作业花了很久的时间，因为平时自己的方向是主要是图像降噪，自己在看这一块图像降噪论文的时候感觉和模式识别的方向结合的比较少。
我看了这方面的模式识别和图像降噪结合的论文，发现也比较少。
在思考的过程中，我想到了聚类的方法。
包括K均值和C均值等等。
因为之前学过K均值，于是就选择了K均值的聚类方法。
然后用到了均值滤波和自适应滤波进行处理。
正文：k-means聚类算法的工作过程说明如下：首先从n个数据对象任意选择 k 个对象作为初始聚类中心；而对于所剩下其它对象，则根据它们与这些聚类中心的相似度（距离），分别将它们分配给与其最相似的（聚类中心所代表的）聚类；然后再计算每个所获新聚类的聚类中心（该聚类中所有对象的均值）；不断重复这一过程直到标准测度函数开始收敛为止。
一般都采用均方差作为标准测度函数。
k-means 算法接受输入量k ；然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。
聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的。
k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。
均值滤波是常用的非线性滤波方法 ,也是图像处理技术中最常用的预处理技术。
它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘。
均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标象素为中心的周围8个象素，构成一个滤波模板，即去掉目标象素本身）。
再用模板中的全体像素的平均值来代替原来像素值。
即对待处理的当前像素点（x，y），选择一个模板，该模板由其近邻的若干像素组成，求模板中所有像素的均值，再把该均值赋予当前像素点（x，y），作为处理后图像在该点上的灰度个g（x，y），即个g（x，y）=1/m ∑f（x，y）m为该模板中包含当前像素在内的像素总个数。
中科院模式识别大作业——人脸识别人脸识别是一种广泛应用于安全领域的技术，它通过对图像或视频中的人脸进行特征提取和比对，实现对个体身份的自动识别。
中科院模式识别大作业中的人脸识别任务主要包括了人脸检测、人脸对齐、特征提取和人脸比对等步骤。
下面将详细介绍这些步骤。
首先，人脸检测是人脸识别的第一步。
它的目的是在图像或视频中准确地定位人脸区域，去除背景和其他干扰信息。
传统的人脸检测算法主要基于特征匹配、分类器或神经网络等方法，而近年来深度学习技术的兴起也为人脸检测带来了重大突破。
深度学习方法通过构建卷积神经网络，在大规模数据上进行训练，可以准确地检测出各种姿态、光照和遮挡条件下的人脸区域。
接下来是人脸对齐，它的目的是将检测到的人脸区域进行准确的对齐，使得不同人脸之间的几何特征保持一致。
人脸对齐算法通常包括了关键点检测和对齐变换操作。
关键点检测通过在人脸中标注一些特定点(如眼睛、鼻子和嘴巴)来标定人脸的几何结构。
对齐变换操作则根据标定的关键点信息，对人脸进行旋转、尺度调整和平移等变换操作，使得不同人脸之间具有一致的几何结构。
人脸对齐可以提高后续特征提取的准确性，从而提高整个人脸识别系统的性能。
特征提取是人脸识别的核心步骤之一，它将对齐后的人脸图像转化为能够表示个体身份信息的特征向量。
传统的特征提取方法主要基于手工设计的特征描述子，如LBP、HOG等。
这些方法需要针对不同任务进行特征设计，且往往存在一定的局限性。
相比之下，深度学习方法可以通过网络自动地学习出适用于不同任务的特征表示。
常用的深度学习模型有卷积神经网络和人工神经网络等，它们通过在大规模数据上进行监督学习，可以提取出能够表达人脸细节和结构的高层次特征。
最后是人脸比对，它根据提取的特征向量进行个体身份的匹配。
人脸比对算法通常需要计算两个特征向量之间的相似度，常用的计算方法有欧氏距离、余弦相似度等。
在实际应用中，为了提高匹配的准确性，通常会结合分数归一化、阈值设定等技术来进行优化。
模式识别miniproject实验报告一、算法介绍：本实验采用了SVM（ Support Vector Machines）分类模型。
由于实际问题中很少线性可分，故本实验采用非线性SVM方法。
即通过一个适当的非线性映射ϕ(x) ，将数据由原始特征空间映射到一个新特征空间，然后在新空间中寻求最优（线性）判定面。
本实验选取的的核函数为RBF（径向基函数）中的高斯核函数，即k(x,y) = exp(-0.5*(norm(x-y)/s)^2)。
关于支持向量机的类型，本实验选取为二类分类算法，即svc_c。
算法方面，由于同时求解n个拉格朗日乘子涉及很多次迭代，计算开销太大，所以实验采用Sequential Minimal Optimization（SMO）算法，即每次只更新两个乘子，迭代获得最终解。
计算时，首先根据预先设定的规则，从所有样本中选出两个拉格朗日因子，然后保持其他拉格朗日乘子不变，更新所选样本对应的拉格朗日乘子，循环N次直到满足要求。
二、实验1、评价标准本实验采用正确率来作为评价指标，即。
2、整体试验方法及步骤（1）定义核函数的类型及相关参数；（2）构建两类训练样本：（考虑到实验程序运行时间问题，本实验只选用了testdata的第200至1200项共1000个作为训练样本）（3）训练支持向量机；（4）寻找支持向量；（5）测试输出；（6）计算评价指标，即正确率3、分类器训练算法的参数调整步骤（1）随机生成多个参数向量（解）（2）在目标函数上验证解的质量（3）根据解的质量由好到坏进行排序。
取出其中较好的一部分（例如一半）解，在这些解的每一个元素上加上一个随机数，从而得到一些新解（4）把新解和老解比较，取出最好的一部分，作为下一次迭代的初始解4、实验结果经实验，得到测试输出，将其第十一列，即样本类别与testdata 中的第十三列相比，即可得到正确率。
本实验将以上结果取于EXECL 中进行统计，部分结果截图如下。
模式识别大作业对sonar数据进行分类，用Fisher线性判别法和最近邻算法对其进行分类，并用MATLAB写程序对其进行模拟。
Fisher线性判别法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock');Mine=xlsread('C:\Users\Administrator\Documents\data\mine');%²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%¼ÆËã¾ùÖµÏòÁ¿mrock=mean(trainrock,2);mmine=mean(trainmine,2);%¼ÆËãÀàÄÚÀëÉ¢¶È¾ØÕófor j=1:48s1=(trainrock(:,j)-mrock);sr=s1*s1';srock=zeros(60);srock=sr+srock;endfor j=1:56s2=(trainmine(:,j)-mmine);sm=s2*s2';smine=zeros(60);smine=sm+smine;endSw=srock+smine;%¼ÆËãÀà¼äÀëÉ¢¶È¾ØÕóSb=(mrock-mmine)*(mrock-mmine)';%¼ÆËã×î¼ÑͶӰ·½ÏòW=inv(Sw)*(mrock-mmine);%¶ÔѵÁ·Ñù±¾½øÐÐͶӰintestrock=W'*testrock;intestmine=W'*testmine;%¼ÆËãÅбðãÐÖµµãintrainrock=W'*trainrock;intrainmine=W'*trainmine;w0=(mean(intrainrock,2)*48+mean(intrainmine,2)*56)/104;%·ÖÀಢ¼ÆËã׼ȷÂÊ%¶Ô´ý²âÑù±¾½øÐзÖÀàj1=1;k1=1;RocksortRock1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýRocksortMine1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýRocksortRocknumber1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅRocksortMinenumber1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:49if(intestrock(1,i)>w0)RocksortRock1(1,j1)=intestrock(1,i);RocksortRocknumber1(1,j1)=i;j1=j1+1;elseRocksortMine1(1,k1)=intestrock(1,i);RocksortMinenumber1(1,k1)=i;k1=k1+1;endendj2=1;k2=1;MinesortMine2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýMinesortRock2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýMinesortMinenumber2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅMinesortRocknumber2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:55if(intestmine(1,i)<=w0)MinesortMine2(1,j2)=intestmine(1,i);MinesortMinenumber2(1,j2)=i;j2=j2+1;elseMinesortRock2(1,k2)=intestmine(1,i);MinesortRocknumber2(1,k2)=i;k2=k2+1;endend%¼ÆËã·ÖÀà½á¹ûµÄÕýÈ·ÂÊright=(j1+j2-2)/(j1+j2+k1+k2-4);disp(right);最近邻算法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock'); Mine=xlsread('C:\Users\Administrator\Documents\data\mine'); %²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%×î½üÁÚ·ÖÀàrocklast=zeros(size(Rock'));minelast=zeros(size(Mine'));rgr=0;rwm=0;mgm=0;mwr=0;for i=1:49for j=1:48Ar(j,1)=(testrock(:,i)-trainrock(:,j))'*(testrock(:,i)-trainrock(:,j)) ;endfor k=1:56Br(k,1)=(testrock(:,i)-trainmine(:,k))'*(testrock(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Ar)<=min(Br))rocklast(:,i)=testrock(:,i);rgr=rgr+1;Ar=zeros(48,1);Br=zeros(56,1);elseminelast(:,i)=testrock(:,i);rwm=rwm+1;Ar=zeros(48,1);Br=zeros(56,1);endendfor i=1:55for j=1:48Am(j,1)=(testmine(:,i)-trainrock(:,j))'*(testmine(:,i)-trainrock(:,j)) ;endfor k=1:56Bm(k,1)=(testmine(:,i)-trainmine(:,k))'*(testmine(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Am)<min(Bm))rocklast(:,i)=testmine(:,i);mwr=mwr+1;Am=zeros(48,1);Bm=zeros(56,1);elseminelast(:,i)=testmine(:,i);mgm=mgm+1;Am=zeros(48,1);Bm=zeros(56,1);endendright=(rgr+mgm)/(rgr+mgm+rwm+mwr);disp(right);以上为两种算法在MATLAB里的源代码。
模式识别大作业共同空间模式及其几种改进方法的研究1 综述脑-机接口（brain -computer interface，BCI）系统通过记录大脑活动提供一种不依赖肌肉的大脑直接控制外部设备的方法，这为那些具有严重神经肌肉损伤（如肌肉萎缩性侧索硬化、脑瘫、脑干中风等）患者提供了与外界交流、控制外界设备的新方式。
在各种监控大脑活动的方法中，脑电图（electroencephalogram, EEG）以其较高的时间分辨率、简单的设备及信号采样要求，优于脑磁图（magnetoencephalogram, EMG）、功能核磁共振成像（ functional magnetic resonance imaging, fMRI），而作为一种理想的 BCI 控制信号被广泛研究[1]。
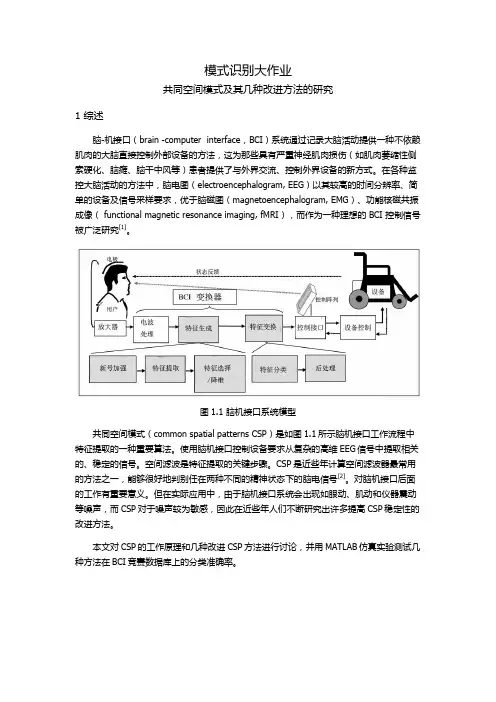
图1.1 脑机接口系统模型共同空间模式（common spatial patterns CSP）是如图1.1所示脑机接口工作流程中特征提取的一种重要算法。
使用脑机接口控制设备要求从复杂的高维EEG信号中提取相关的、稳定的信号。
空间滤波是特征提取的关键步骤。
CSP是近些年计算空间滤波器最常用的方法之一，能够很好地判别任在两种不同的精神状态下的脑电信号[2]。
对脑机接口后面的工作有重要意义。
但在实际应用中，由于脑机接口系统会出现如眼动、肌动和仪器震动等噪声，而CSP对于噪声较为敏感，因此在近些年人们不断研究出许多提高CSP稳定性的改进方法。
本文对CSP的工作原理和几种改进CSP方法进行讨论，并用MATLAB仿真实验测试几种方法在BCI竞赛数据库上的分类准确率。
2 经典共同空间模式CSP 算法的目标是创建公共空间滤波器，最大化第一类方差，最小化另一类方差，采用同时对角化两类任务协方差矩阵的方式，区别出两种任务的最大化公共空间特征[3]。
定义一个N x T的矩阵E来表示原始EEG信号数据段，其中N表示电极数目即空间导联数目，T表示每个通道的采样点数目。
模式识别大作业一．K均值聚类（必做，40分）1.K均值聚类的基本思想以及K均值聚类过程的流程图；2.利用K均值聚类对Iris数据进行分类，已知类别总数为3。
给出具体的C语言代码，并加注释。
例如，对于每一个子函数，标注其主要作用，及其所用参数的意义，对程序中定义的一些主要变量，标注其意义；3.给出函数调用关系图，并分析算法的时间复杂度；4.给出程序运行结果，包括分类结果（只要给出相对应的数据的编号即可）以及循环迭代的次数；5.分析K均值聚类的优缺点。
二．贝叶斯分类（必做，40分）1.什么是贝叶斯分类器，其分类的基本思想是什么；2.两类情况下，贝叶斯分类器的判别函数是什么，如何计算得到其判别函数；3.在Matlab下，利用mvnrnd()函数随机生成60个二维样本，分别属于两个类别（一类30个样本点），将这些样本描绘在二维坐标系下，注意特征值取值控制在（-5，5）范围以内；4.用样本的第一个特征作为分类依据将这60个样本进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志（正确分类的样本点用“O”，错误分类的样本点用“X”）画出来；5.用样本的第二个特征作为分类依据将这60个样本再进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来；6.用样本的两个特征作为分类依据将这60个样本进行分类，统计正确分类的百分比，并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来；7.分析上述实验的结果。
8.60个随即样本是如何产生的的；给出上述三种情况下的两类均值、方差、协方差矩阵以及判别函数；三．特征选择（选作，15分）1.经过K均值聚类后，Iris数据被分作3类。
从这三类中各选择10个样本点；2.通过特征选择将选出的30个样本点从4维降低为3维，并将它们在三维的坐标系中画出（用Excell）；3.在三维的特征空间下，利用这30个样本点设计贝叶斯分类器，然后对这30个样本点利用贝叶斯分类器进行判别分类，给出分类的正确率，分析实验结果，并说明特征选择的依据；。
模式识别miniproject
实验报告
报告人：李南云
学号：SA16173027
日期：2016.12.23
数据分析
在此简要的说明一下数据情况，给定数据集分为train和test 两个data文件，
train.data是11列8285行，意味着有8285个样本，矩阵的最后一列是该列所对应的样本类别。
根据统计，train数据前466个样本均为1类，而后7819个样本均为-1类，所以该分类器为二分类问题。
MATLAB中用importdata（）读取数据，并将样本和其所属类别分开来，样本为trnset，所属类别为trnclass，train数据用于训练分类器。
Test.data是11列2072行，同样也意味着有2072个样本，最后一列为该列所对应样本类别，test数据前117为1类，后1955个数据为-1类。
同样读取数据后，分为tstset和tstclass两个矩阵，前者代表2072个样本，后者代表所对应样本的类别，我们需要将train所训练好的分类器应用在tstset样本上，输出分类结果tstclass1，将其与tstclass相比较，计算每个类别的正确率和总的正确率。
算法介绍
本次实验采用了SVM（support vector machines）分类模型，由于数据线性不可分而且在实际问题中数据也大都线性不可分，所以本次试验采取的线性不可分SVM方法，即将数据向高维空间映射，使其变得线性可分。
本实验选取的二分类算法，SVC_C。
下面先以线性分类器为例，来引入SVM算法的一些概念和处理流程，如图1所示，假设C1和C2是需要区分的类别，而在二维平面中它们的样本如图，中间的一条直线就是一个线性分类函数，由图中可以看出，这个线性分类函数可以完全的将两类样本区分开来，我们就称这样的数据是线性可分的，否则则为线性不可分，本实验中所采用的数据在二维空间里分布如图2和图3所示（红色标注分类为1的样本，蓝色标注为分类为-1的样本），明显线性不可分。
图1
图2
图3
设图1中线性函数为g(x)=wx+b（x是样本的向量表示），那么当有一个样本x i需要判别的时候，就可以看g(x i)的值，若g(x i)>0就判别为C1类，若g(x i)<0就判别为C2类（等于的时候就拒绝判断）。
此时也等价与给函数g(x)附加一个符号函数sgn()，即f(x)=sgn[g(x)]是我们真正的判别函数，中间那条线的表达式是
g(x)=0,即wx+b=0，我们也把这个函数叫做分类面。
在此我们就不对几何间隔、二次规划问题、支持向量等做详细的介绍了。
SVM在线性分类器上做了重大改进，即为——核函数！
线性分类器只能对线性可分的样本进行处理，但是实际中很多样本都是线性不可分的，那么这种线性可分的分类器就不适用了，是否有某种办法，让线性不可分的数据变得线性可分呢？
实际上是有的！我们可以用一个二维平面中的分类问题作为例子，如图4
图4
横轴短点a和b之间红色的部分里的所有点为正类，两边的黑色点为负类，我们明显找不到符合要求的线性函数将两类数据区分开来，但是可以找到一条曲线例如图5中的曲线来判断所属类别，它的函数表达式可以写为g(x)=c0+ c1x+ c2x2。
图5
明显它不是一个线性函数，但是我们可以新建一个向量a 和y 1
y =[y 1y 2y 3]=[1x x 2] , a =[a 1a 2a 3]=[c 0c 1c 2
] 这样g(x)就可以转化为f(y)=<a,y>，即：g(x)=f(y)=a*y
在任意维度的空间中，这种形式的函数都是一个线性函数，因为自变量y 的次数不大于1.这样原来在二维空间中线性不可分的问题映射到四维空间中，就变成了线性可分的，这也就形成了我们最初想解决
线性不可分问题的基本思路——向高维空间转化，使其变得线性可分。
而转化的最关键部分就是找打x 对于y 的映射方法，遗憾的是假
设x ’是由x 变换得到的高维变量，在此维度下，问题线性可分，那么只需要计算f(x ’)=<w ’,x ’>+b 的值来进行分类，即只关心高维空间里内积<w ’,x ’>的值。
而从理论上来说x ’是由x 变换得来的，因此广义上可以吧它叫做x 的函数，而w ’是常量，它是一个低维空间向量里的常量w 经过x 与x ’之间相同的变换得到的，所以给定了一个w 和w ’的值，我们就可以有一个确定的f(x ’)的值与其对应。
那么是否能有这样一种的函数K(w,x)，它接受低维空间的输入值，却能够计算出高维空间的内积<w ’,x ’>？如果真的有这种函数，那么当给定了一个低维空间的输入x 之后，使g(x)=K(w,x)+b
和
f(x’)=<w’,x’>+b这两个函数的计算结果就完全一样，我们就不用费力的去找映射关系了。
而上述的K(w,x)却是存在，它被称为核函数（核，kernel），而且只要是满足了Mercer条件的函数，就可以作为核函数。
核函数的基本作用就是接受两个低维空间里的向量，能够计算出经过某个变换后在高维空间里的向量内积值。
那么就有两个问题：
1．既然有很多核函数，针对具体问题我们应该怎么选择呢？2．如果使用核函数向高维空间映射后，问题仍然是线性不可分的，那怎么办呢？
对于第一个问题——核函数的选择我不太了解它选择中所需要的指导原则
通常而言，径向基核函数（RBF）是比较合理的选择，本次实验也是采用的径向基核函数，这个核函数将样本非线性地映射到一个更高维的空间，与线性核不同，它能够处理分类标注和属性的非线性关系，并且，线性核是RBF的一个特例，同时，sigmoid核的表现很想一定参数的RBF核。
第二个原因，超参数的数量会影响到模型选择的复杂度，而多项式核比RBF核具有更多的超参数。
最后，RBF核有更少的数值复杂度。
当然也存在一些情形RBF核是不适用的。
特别的，当特征维数非常大的时候，很可能只能适用线性核。
本实验采用RBF作为核函数，并使用了‘boxconstraint’参数，这是SVM的惩罚系数，一般是按[···，0.1,1,10，···]这样的规律调
节尝试。
实验
1．评价标准
当然是使用正确率作为评价标准啦！我们统计了对于正类即1
的误判率和对于负类-1的误判率，因为所给数据中，正类较少，负类较多，我们尝试对读取的数据多少进行调节，并计算时间，
后续分析结果，总结问题。
2. 整体实验方法和步骤
①将train和test数据读取，并分别将其分成set和class；
②训练并得到分类器；
③测试输出；
④计算评价指标；
⑤减少读取的train数据的负类，并重复上述过程；
⑥总结；
3. 分类器训练算法的参数调整步骤：
①随机生成多个参数（解）；
②在目标函数上验证解的质量；
③根据解的质量由好到坏进行排序，取出其中较好的一部分，
在这些解的每个元素上加上一个随机数，从而得到一些新的
解；
④把新解和老解比较，取出最好的一部分，作为下一次迭代的
初始解；
实验结果
得到测试输出后，将其与test数据的第11列进行比较，相同即为判断正确，并计算正确率。
Excel中我用test数据的第11列减去输出结果，即结果为0即为正确，结果不为0 ，即为错误。
下图6为正类和负类部分excel数据截图
图6
经统计总的正确率为74.81%，对于正类数据的判别正确率为61.54%，负类数据的判别率为75.60%，负类数据的正确判别率明显更高一些，这可能是由于训练数据中负类数据占大多数的原因，所以负类的判别正确率明显的更好一些。
整个训练外加测试时间为24.8980秒。
下面我们只读取的train数据的前932个，即训练数据中正类和负类的数目相同，这时我们可以看到结果，总的正确率有所降低为69.16%，其中分类器判别正类的正确率为70.94%，负类为69.05%。
两相差减小，此时负类的判别率比起全部读取数据时降低了大约5%，而正类的却增加了近10%！此时明显对正类比较敏感，当然总体还是降低了····
当我再次把读取train的负类的数据量增加到正类的2倍时，即正类样本为466个，副类样本为932个，此时总的正确率为74.47%，test正类数据判断的正确率为62.39%，负类数据为75.19%，可以看到此时已经与将8285个训练样本全部放进去的结果大抵相同。
后来我又尝试了读取的train与test数据量相等，此时的总的正确率为72.78%，正类为63.25%，负类为73.35%。
没有提升，反而降低了，不过并没有太大的改变。
下面表格整理了一下结果：
本来想测一下所有的数据，给出一个曲线图，跑一个要20多秒，跑完的话时间太长了，所以没有测······。
