传热的基本原理和规律

图4-3 温度梯度与傅里叶定律 第二节 热传导热传导是由物质内部分子、原子和自由电子等微观粒子的热运动而产生的热量传递现象。

热传导的机理非常复杂，简而言之，非金属固体内部的热传导是通过相邻分子在碰撞时传递振动能实现的；金属固体的导热主要通过自由电子的迁移传递热量；在流体特别是气体中，热传导则是由于分子不规则的热运动引起的。

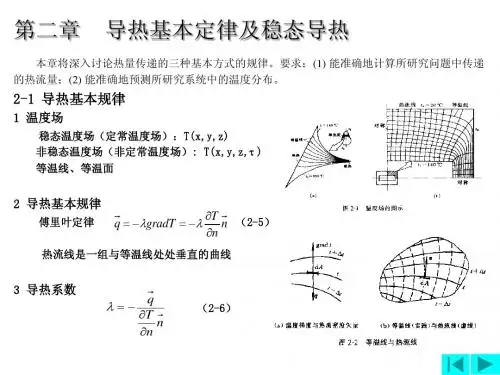
4-2-1 傅里叶定律一、温度场和等温面任一瞬间物体或系统内各点温度分布的空间，称为温度场。

在同一瞬间，具有相同温度的各点组成的面称为等温面。

因为空间内任一点不可能同时具有一个以上的不同温度，所以温度不同的等温面不能相交。

二、温度梯度从任一点开始，沿等温面移动，如图4-3所示，因为在等温面上无温度变化，所以无热量传递；而沿和等温面相交的任何方向移动，都有温度变化，在与等温面垂直的方向上温度变化率最大。

将相邻两等温面之间的温度差△t 与两等温面之间的垂直距离△n 之比的极限称为温度梯度，其数学定义式为：n t n t gradt ∂∂=∆∆=lim(4-1) 温度梯度nt ∂∂为向量，它的正方向指向温度增加的方向，如图4-3所示。

对稳定的一维温度场，温度梯度可表示为：xt gradt d d = （4-2） 三、傅里叶定律导热的机理相当复杂，但其宏观规律可用傅里叶定律来描述，其数学表达式为：nt SQ ∂∂∝d d 或 n t S Q ∂∂-=d d λ （4-3） 式中 nt ∂∂——温度梯度，是向量，其方向指向温度增加方向，℃/m ； Q ——导热速率，W ；S ——等温面的面积，m 2；λ——比例系数，称为导热系数，W/（m ·℃）。

式4-3中的负号表示热流方向总是和温度梯度的方向相反，如图4-3所示。

傅里叶定律表明：在热传导时，其传热速率与温度梯度及传热面积成正比。

必须注意，λ作为导热系数是表示材料导热性能的一个参数，λ越大，表明该材料导热越快。

和粘度μ一样，导热系数λ也是分子微观运动的一种宏观表现。

热传导的基本原理与计算方法热传导是指热量从高温区向低温区传递的过程。

它是热力学的一种基本现象，广泛应用于物理学、化学、材料科学等领域。

热传导研究的是物质中热量的传导机制、热传导的速率和规律以及如何控制和改变热传导过程。

一、热传导的基本原理在物理学中，热量的传导可以用热传导定律来描述，即热传导的速率与热差成正比，与导热系数和传热面积成反比。

物质温度较高的区域传递给相邻温度较低的区域，热量的传导是靠原子、分子、电子等的热运动完成的。

这些粒子在物质内做无规则的振动、流动，高温区的热粒子向低温区运动，直到它们的热平衡达到。

热传导的基本原理可以用一维热传导方程来描述：$$\frac{\partial T}{\partial t}=\alpha\frac{\partial^2 T}{\partialx^2}.$$其中，T代表温度，x代表长度，t代表时间，α代表物质的导热系数。

方程的右侧表示温度梯度，表示热量的传递速度。

二、计算热传导的基本方法由于热传导过程的复杂性，通过简单的数学方程来计算热传导的速率是不可能的。

因此，人们开发了许多传热学模型和计算方法。

这些方法主要可以分为两种：一种是基于传热学原理和模型计算的解析解，另一种是基于数值方法求解的计算机模拟。

1. 解析解法解析解法是指根据物理模型和数学方程分析热传导的过程，得到解析解的方法。

这种方法的优点是计算结果精确，适用于简单的热传导问题，如一维热传导、恒定温差热传导等。

解析解法的缺点是只能用于特定情况下的计算，不适用于复杂的三维热传导问题。

2. 数值模拟法数值模拟法是指利用数字计算机来模拟热传导过程，在计算机上求解热传导方程。

这种方法的优点是可以模拟任意形状复杂的热传导问题，适用范围广，计算结果较为准确。

数值模拟法的缺点是需要高性能计算机进行计算，耗费时间和资源较多。

三、热传导应用范围热传导的应用范围非常广泛，涉及物理、化学、材料等多个领域。

在工程领域，热传导的应用与产品的保温、散热、冷却、加热等相关。

传热学手册下册1987引言概述传热学是热力学的一个重要分支，研究热量如何在物质之间传递的规律。

《传热学手册下册1987》是一部经典的教材，深入剖析了传热学的各个方面，为学习者提供了丰富的知识和深刻的理解。

本文将对该手册进行全面介绍，以帮助读者更好地理解其中的关键内容。

一、基本概念与原理1.1 传热学基础热传递机制：介绍传热的基本机制，包括传导、传热与对流，并深入解析不同物质中的热传递规律。

传热方程：探讨传热方程的推导和应用，阐释不同传热问题中的数学模型。

传热原理：阐述传热的基本原理，如热平衡、热传递速率等，为读者奠定坚实的理论基础。

1.2 传热材料与性质导热材料：对导热材料的分类、选择和性质进行详细介绍，探讨不同材料在传热中的应用。

相变材料：分析相变材料在传热中的独特性质，包括潜热的利用和相变对传热的影响。

传热流体：讨论传热流体的特性，研究不同流体在热交换中的效果和应用。

1.3 传热设备与应用传热设备分类：对传热设备进行分类，包括换热器、冷却塔等，介绍其结构和工作原理。

传热设备选型：分析传热设备的选型依据，包括流体特性、传热效率等因素。

实际应用案例：通过实际案例，展示传热学在工程领域的应用，使读者更好地理解理论知识的实际运用。

二、深度解读与案例分析2.1 传热实验技术实验仪器与方法：详细介绍进行传热实验所需的仪器设备和实验方法，确保读者能够独立进行相关实验。

数据分析与处理：强调实验数据的采集、整理和分析方法，培养读者实际应用传热学知识的能力。

实验案例：提供一些典型的传热实验案例，通过案例分析，帮助读者更好地理解实验技术的应用。

2.2 传热系统优化优化理论：探讨传热系统的优化理论，包括传热表面增大、传热介质选择等方面的优化方法。

能源效率：分析传热系统在提高能源效率方面的策略，减少能源浪费，实现可持续发展。

案例研究：通过一些实际案例，展示传热系统优化在工程实践中的成功经验。

2.3 新兴技术与未来发展新材料应用：探讨新型材料在传热领域的应用前景，如纳米材料、复合材料等。

热传导与传热的基本规律与计算热传导是热量从高温区域传递到低温区域的过程，是热能传播的一种方式。

传热则是指热能从一个物体传递到另一个物体的过程。

在这篇文章中，我们将探讨热传导和传热的基本规律以及相关的计算方法。

一、热传导的基本规律在固体中，热传导是通过原子、分子的相互碰撞传递热能的过程。

基于这一过程，热传导满足以下基本规律：1. 热传导方向：热传导的方向是从高温区域到低温区域，即热量总是沿着温度梯度的方向传递。

2. 热传导速率：热传导速率与物体的热导率成正比，与物体的截面积成反比，与温度梯度成正比。

具体计算公式如下：Q = k * A * ΔT / d其中，Q表示传导热量，k表示物体的热导率，A表示传热截面积，ΔT表示温度差，d表示传热距离。

该公式表明，热传导速率正比于传热截面积和温度梯度，反比于传热距离。

二、导热物质的热导率热导率是导热物质的一个重要物理参数，它表示单位时间内，单位面积上的热量传递量。

不同物质的热导率不同，常见物质的热导率如下：- 金属材料：金属具有较高的热导率，如铜的热导率约为401W/(m·K)，铝的热导率约为237 W/(m·K)，铁的热导率约为80 W/(m·K)。

- 非金属材料：非金属材料的热导率较低，如水的热导率约为0.6W/(m·K)，木材的热导率约为0.1 W/(m·K)。

三、传热的计算方法在进行传热计算时，我们常用以下几种方法：1. 热传导计算：利用热传导速率公式，可以计算出物体的传导热量。

通过测量温度差、传热截面积和传热距离等参数，我们可以计算出传导热量的数值。

2. 对流传热计算：对流传热是指通过流体的传热过程。

常见的对流传热计算方法有冷却方式、自然对流、强制对流等。

其中，冷却方式是通过调整传热流体的流速、温度等参数，计算出传热量的大小。

3. 辐射传热计算：辐射传热是指通过热辐射的方式传递热量。

辐射传热计算需要考虑物体的表面温度、辐射率等参数，通过辐射传热公式计算出传热量的数值。

傅里叶导热定律：单位时间、单位面积上的传热量（热流密度）与温度梯度成正比。

1.引言1.1 概述傅里叶导热定律是热传导领域中的基本定律之一，它描述了物质内部传热的规律。

根据傅里叶导热定律，单位时间内通过一个单位面积的物质的传热量（热流密度）与温度梯度成正比关系。

也就是说，当一个物体内部存在温度差时，热量会以固定比例从高温区域传导到低温区域。

傅里叶导热定律是以法国数学家和物理学家傅里叶的名字命名的，在19世纪初他提出了这一理论。

这个定律对于热传导问题的研究有着重要的意义，不仅在物理学中具有广泛应用，而且在工程领域、地球科学、材料科学等方面也得到了广泛的应用和发展。

通过研究傅里叶导热定律，我们可以了解热传导过程中的热量分布规律，掌握不同物质导热性能的特点，为热工系统的设计和优化提供基础理论依据。

同时，这个定律的应用也使得我们可以解释一些实际问题，比如热传导导致的温度分布不均匀、能量损失问题等。

本文将介绍傅里叶导热定律的概念和原理，并深入探讨传热量与温度梯度之间的关系。

通过实验和理论分析，我们将进一步验证这一定律，并探讨其在实际应用中的意义和局限性。

最后，我们将给出结论，确认单位时间、单位面积上的传热量与温度梯度成正比的观点，并讨论傅里叶导热定律在热传导问题中的应用前景。

下一部分将介绍傅里叶导热定律的概念和原理。

1.2文章结构1.2 文章结构本文将从以下几个方面探讨傅里叶导热定律与传热量与温度梯度之间的关系。

文章结构如下：2. 正文2.1 傅里叶导热定律的概念和原理- 介绍傅里叶导热定律的基本概念以及其背后的物理原理- 着重解释热传导过程中的热流以及导热系数的概念2.2 传热量与温度梯度的关系- 分析传热量与温度梯度之间的关系，深入探讨它们的数学表达式- 解释为什么传热量与温度梯度成正比3. 结论3.1 结论1: 单位时间、单位面积上的传热量与温度梯度成正比- 总结并确认傅里叶导热定律的核心观点：单位时间、单位面积上的传热量与温度梯度成正比- 进一步解释这一结论的重要性和实际应用3.2 结论2: 傅里叶导热定律的应用与意义- 探讨傅里叶导热定律在不同领域中的应用，如工程热学、材料科学等- 讨论傅里叶导热定律对于能源利用、环境保护等方面的意义通过以上结构，我们将全面展示傅里叶导热定律的概念和原理，以及传热量与温度梯度的关系。

热传导和传热方程热传导是指物体内部或不同物体之间热能的传递过程。

在研究热传导过程中，我们通常会使用传热方程来描述热传导的行为和规律。

本文将探讨热传导的基本原理，以及传热方程的应用和推导。

一、热传导的基本原理热传导是一种通过分子间碰撞而传递热能的方式。

当物体的温度不均匀分布时，高温区域的分子会具有较高的动能，它们与周围分子发生碰撞，将热能传递给周围的低温区域，从而实现热量的传导。

这种通过分子碰撞传递热能的方式称为热传导。

热传导的速率与物体的温度梯度有关。

温度梯度越大，热传导的速率就越快。

热传导的速率还与物体的导热性质有关，导热性能越好，热传导的速率越快。

二、传热方程的基本形式传热方程是描述热传导过程的数学表达式，它可以用来计算热传导的速率和温度分布。

传热方程的基本形式如下：q = -kA(dT/dx)在这个方程中，q表示单位时间内的热量传递速率，k表示物体的导热系数，A表示传热截面的面积，dT/dx表示温度梯度。

根据传热方程，我们可以计算出热量传递的速率。

当温度梯度增大时，热量传递速率也会增大。

物体的导热系数越大，热量传递速率越大。

三、传热方程的应用传热方程在工程和科学研究中有着广泛的应用。

通过传热方程，我们可以计算热传导过程中的温度分布和热量传递速率，从而帮助我们设计和改进热传导设备和系统。

以散热器为例，散热器通过增大传热截面的面积和优化导热材料的选择，可以提高热量的传递速率，从而更有效地散热。

传热方程可以帮助我们计算散热器所需的散热面积和导热材料的选择。

传热方程还可以应用于热工学和热力学等领域的研究。

通过传热方程，我们可以分析和预测不同材料的导热性能，评估热传导过程中的能量损失，并优化热传导系统的设计。

四、传热方程的推导传热方程的推导是基于热传导的基本原理和数学方法进行的。

推导的具体过程根据实际情况和所研究的问题而略有不同。

下面以一维热传导问题为例，简要介绍传热方程的推导过程。

假设热传导过程发生在一维材料中，材料的长度为L。

热的传递方式和传热规律热是一种能量形式，能够由高温物体传递给低温物体。

热的传递方式有三种：传导、传热和辐射。

这些传递方式遵循着一些传热规律，对于研究热传递现象和设计高效的热交换设备具有重要意义。

一、传导的基本原理和规律传导是热能在物质内部传递的过程，它是通过分子间的碰撞和振动实现的。

热的传导按照傅里叶定律，可以用下式来表示：q = -kA(dt/dx)其中，q是传导热流密度，k是导热系数，A是传热的横截面积，(dt/dx)是温度梯度。

根据上式可知，传导的热流密度与导热系数成正比，与横截面积和温度梯度成正比。

此外，不同物质的导热性质也不同，这取决于物质的结构和组成。

例如，金属的导热性能较好，而木材的导热性能较差。

在传导过程中，热量会沿着温度梯度从高温区域向低温区域传递，直到达到热平衡。

传导的热流方向是从高温到低温，因为温度梯度的存在会产生熵增，使系统向热平衡的状态演化。

二、对流的基本原理和规律对流是热通过流体传递的过程，它包括了流体的传热和传质。

传热的对流可以分为自然对流和强制对流两种。

自然对流是由于密度差异造成的。

当热源使流体受热膨胀，密度减小时，流体会上升，形成对流循环。

相反，当流体受冷缩小，密度增大时，流体会下降。

自然对流的传热特点是流动缓慢，对流热流的强度与温差呈非线性关系。

强制对流是通过外力（如泵、扇等）使流体产生流动，从而加强传热效果。

当流体流动时，传热与流体的速度变化、流体的导热性质和流体的黏滞特性有关。

对流传热的规律可以由牛顿冷却定律描述：q = αA(ΔT)其中，q是传热速率，α是对流传热系数，A是传热面积，ΔT是温差。

传热速率与传热系数成正比，与传热面积和温差成正比。

传热系数反映了流体流动的特性，不同流动状态下的传热系数也不同。

三、辐射的基本原理和规律辐射是指热能以无需传质介质的方式传递的过程，一般通过光波、红外线或其他电磁波传递。

辐射的传热速率由斯特藩-玻尔兹曼定律描述：q = εσA(T^4 - T_0^4)其中，q是传热速率，ε是发射率，σ是斯特藩-玻尔兹曼常数，A是辐射面积，T和T_0分别是辐射物体和周围环境的绝对温度。

第四章传热本章介绍了三种基本传热方式，即导热、对流传热、辐射传热的基本概念和定律；详细分析了对流传热过程机理，建立了对流传热速率方程以及表面传热系数的经验关联式；由总传热速率方程出发，对传热过程进行设计计算和操作分析、诊断；介绍了换热设备的类型和列管式换热器的设计和选用。

本章重点要求掌握：①对流传热过程的基本概念、定律、传热速率方程；②管内强制湍流流动时表面传热系数的经验关联及影响因素；③总传热速率方程以及传热过程的计算。

4.1 概述4.1.1 传热在化工生产中的应用传热，即热量的传递，是自然界中普遍存在的物理现象。

由热力学第二定律可知，凡是有温度差存在的物系之间，就会导致热量从高温处向低温处的传递，故在科学技术、工业生产以及日常生活中都涉及许多的传热过程。

化工生产过程与传热关系十分密切。

这是因为化工生产中的很多过程都需要进行加热和冷却。

例如，为保证化学反应在一定的温度下进行，就需要向反应器输入或移出热量；化工生产设备的保温或保冷；生产过程中的热量的合理使用以及废热的回收利用，换热器网络的综合利用；蒸发、精馏、吸收、萃取、干燥等单元操作都与传热过程有关。

化工生产过程中需要解决的传热问题大致分为两类：(1)传热过程的计算，包括设计型计算和操作型计算；(2)传热过程的改进与强化。

这两类问题的解决，都需要从总的传热速率方程出发，即：（4.1.1）式中：Q—冷流体吸收或热流体放出的热流量，W；K—传热系数，W/(m2·℃)；A—传热面积，m2；Δtm—平均传热温差，℃。

4.1.2 传热的基本方式根据热量传递机理的不同，传热基本方式有三种，即热传导、对流和辐射。

热传导：热传导又称导热。

是指热量从物体的高温部分向同一物体的低温部分、或者从一个高温物体向一个与它直接接触的低温物体传热的过程。

对流传热：对流传热是依靠流体的宏观位移，将热量由一处带到另一处的传递现象。

在化工生产中的对流传热，往往是指流体与固体壁面直接接触时的热量传递。

第一节传热的基本概念一、传热在食品工程中的应用传热：是不同温度的两个物体之间或同一物体的两个不同温度部位之间所进行的热的转移。

传热在食品工程中的应用：(1)一般的加热、冷却、冷凝过程；(2)食品的杀菌和保藏；(3)蒸发浓缩、干燥、结晶(通过加热去除水分)；(4)蒸煮、焙烤(通过加热使食品完成一定的生化反应)。

食品生产过程对传热的要求：强化传热(加热或冷却物料)削弱传热(设备和管道的保温)二、传热的基本方式热的传递是由于系统内或物体内温度不同而引起的，根据传热机理不同，传热的基本方式有三种：热传导(conduction)；对流(convection)；辐射(radiation)。

1.热传导（又称导热）：物体各部分之间不发生相对位移，仅借分子、原子和自由电子等微观粒子的热运动而引起的热量传递称为热传导。

2.热对流：流体各部分之间发生相对位移所引起的热传递过程称为热对流。

热对流仅发生在流体中。

通常把流体与固体壁面之间的传热称为对流传热。

热对流的两种方式：强制对流：因泵（或风机）或搅拌等外力所导致的对流称为强制对流。

自然对流：由于流体各处的温度不同而引起的密度差异，致使流体产生相对位移，这种对流称为自然对流。

流动的原因不同，对流传热的规律也不同。

在同一流体中有可能同时发生自然对流和强制对流。

3、热辐射：因热的原因而产生的电磁波在空间的传递，称为热辐射。

所有物体都能将热以电磁波的形式发射出去，而不需要任何介质。

任何物体只要在绝对零度以上都能发射辐射能，但是只有在物体温度较高的时候，热辐射才能成为主要的传热形式。

实际上，上述三种传热方式很少单独出现，而往往是相互伴随着出现的。

只有固体中有纯热传导。

四、传热过程中基本问题与传热机理传热过程中的基本问题可以归结为：①载热体用量计算②传热面积计算③换热器的结构设计④提高换热器生产能力的途径。

解决这些问题，主要依靠两个基本关系。

⑴热量衡算根据能量守恒的概念，若忽略操作过程中的热量损失，则Q热=Q冷，称为热量衡算式。

热传导热传导规律及其在实际中的应用热传导是指热量从高温区域向低温区域传递的过程。

在物质中，热量一般通过三种方式传导：热传导、对流传导和辐射传导。

本文重点介绍热传导的规律以及在实际应用中的相关情况。

一、热传导规律热传导的规律可以通过热传导定律来描述。

热传导定律表明，在热传导过程中，热流密度（单位时间内通过单位面积的热量）与温度梯度（单位长度内温度的变化率）成正比。

设热流密度为q，温度梯度为∇T，热传导定律可以表示为以下公式：q = -k∇T其中，k为热导率，表示物质导热性能的一个参数。

热导率越大，说明物质的导热性能越好。

二、热传导的影响因素热传导的强弱取决于多种因素，以下是一些常见的影响因素：1. 导热性能：物质的导热性能决定了其传导热量的能力。

金属等导热性能较好的物质会比绝缘体等导热性能较差的物质更容易传导热量。

2. 温度差：温度差指的是两个接触表面之间的温度差异。

温度差越大，热传导强度越大。

3. 距离：热量的传导是通过物质内部的分子或电子碰撞引起的，因此物体之间的距离会影响热传导。

三、热传导的应用热传导在日常生活和工业生产中有广泛的应用，以下是一些常见的应用场景：1. 绝缘材料：根据热传导的规律，选择导热性能较差的绝缘材料可以在一定程度上减少热量的传导，起到隔热的作用。

这在建筑领域中用于保温材料的选择非常重要。

2. 传热设备：热传导在传热设备（如散热器、换热器等）中得到广泛应用。

通过设计合适的材料和结构，可以实现高效的传热，提高设备的散热或加热效果。

3. 热工加工：在一些加工过程中，需要控制材料的温度分布，以实现理想的加工效果。

通过掌握材料的热传导规律，可以有效控制热处理过程中的温度变化，提高产品质量。

4. 热障涂层：热障涂层是一种在工程结构表面喷涂的材料，能够减少热量的传导，提高结构的耐热性能。

这种涂层可以在航空航天、汽车等领域中发挥重要作用。

5. 散热设计：在电子设备等产品的设计中，合理的散热设计是非常重要的。

第三节传热学基本原理食物制熟过程中的传热学，涉及热量传递的方法和承担传热任务的介质两个方面的知识。

一、经典的热量传递方式只要有温度差存在的地方，就会有热量自发地从高温物体或区域传向低温物体或区域。

烹调的传热方式有传导、对流和辐射三种。

●温度差即温差----即食物有生到熟是食物吸收了一定的热量，而事物能吸收热量一定有种“推动力”，这种推动力就是温差。

●热传递---由于温差的存在，热量才会从高到底地传递下去，这种传递过程就是热传递。

●热阻---由于在热量传递中遇到阻力，这种阻力称热阻。

I=UR●热传递的方式--传导、对流和辐射（一）热传导热传导—指导热物体各部分没有相对位移，或不同物体直接接触时，因组成该物体的各物质的分子、原子和自由电子等微观粒子的额外运动而发生的热量传递现象。

从理论上讲，热传导可以在固体、液体和气体中进行，但是在地球引力场内，单纯的热传导只能在结构紧密的固体中进行。

因在液体和气体中，只要有温度差存在，液体分子的移动和气体分子的扩散就不可避免，从而产生对流现象。

也就是说，在液体中，热量的传递是以传导和对流两种方式同时进行。

Q=λA△t/δ（二）热对流对流—在液体（包括液体和气体）的运动中，热量从高温区域移向低温区域的现象。

在烹调中，单纯在流体之间进行的的热交换即纯对流现象并不是主要的，通常都是温度高的固体把热量传递到与之接触的流体中去，这样就出现了对流和传导同时存在的热交换现象。

典型的现象如：电水壶烧开水，电热元件产热后，传递到水中，使一部分水分子受热温度升高而流向低温区，同时低温区的水分子又立刻补充到高温区继续受热，于是对流现象产生。

单纯的对流现象：将一壶开水到入冷水桶中，此时所产生的热传递方式是典型的对流过程。

Q=аA△t（三）热辐射热辐射——是物质在高温状态（包括燃烧和其他激烈化学反应和核反应）下以光子的形式（电磁波）发射能量的过程。

Q=σ₀АТ⁴根据爱因斯坦质能关系式：E=mc² E表示能量，m表示物质质量，c表示光速（30万km/s）。

热传导的规律和计算方法【热传导的规律和计算方法】热传导是物质中热量从高温区传递到低温区的过程。

了解热传导的规律和计算方法，不仅可以帮助我们更好地理解热传导的机制，还可以在实际应用中进行热传导问题的计算和分析。

本文将介绍热传导的规律以及常用的计算方法。

一、热传导的规律热传导的规律可以用热传导定律来描述，即傅里叶热传导定律。

该定律可以表示为：q = -kA(dT/dx)式中，q表示热量传导速率，单位为瓦特（W）；k表示导热系数，单位为瓦特/米·摄氏度（W/m·°C）；A表示传热的截面积，单位为平方米（m^2）；dT/dx表示温度梯度，即温度随空间位置x的变化率，单位为摄氏度/米（°C/m）。

根据傅里叶热传导定律，热量传导速率正比于截面积和温度梯度的乘积，并与导热系数成反比。

这意味着截面积越大、温度梯度越大以及导热系数越小，热量传导速率就越大。

热传导的规律可以总结为以下几点：1. 热传导是由高温区到低温区的热量传递过程；2. 热传导速率与截面积和温度梯度的乘积成正比；3. 热传导速率与导热系数成反比。

二、热传导的计算方法热传导的计算方法主要包括两种情况：稳态热传导和非稳态热传导。

1. 稳态热传导计算方法稳态热传导是指热传导过程中温度分布保持不变的情况。

在这种情况下，我们可以根据物体两端的温度差和导热系数来计算热量传导速率。

热量传导速率的计算公式为：q = -kA(T2-T1)/L式中，q表示热量传导速率，单位为瓦特（W）；k表示导热系数，单位为瓦特/米·摄氏度（W/m·°C）；A表示传热的截面积，单位为平方米（m^2）；T2和T1分别表示物体的两端温度，单位为摄氏度（°C）；L表示物体的长度，单位为米（m）。

2. 非稳态热传导计算方法非稳态热传导是指热传导过程中温度分布会随时间变化的情况。

在这种情况下，我们需要根据物体的初始温度分布、导热系数和边界条件来求解热传导的温度分布和热量传导速率。