第六章-习题答案

第6章思考题与习题1．写出下列各酸的共轭碱：H 2O ，H 2C 2O 4，H 2PO 4-，HCO 3-，C 6H 5OH ，C 6H 5NH 3+，HS -。

答：H 2O 的共轭碱为OH -；；H 2C 2O 4的共轭碱为HC 2O 4-；H 2PO 4-的共轭碱为HPO 42-；HCO 3-的共轭碱为CO 32-；；C 6H 5OH 的共轭碱为C 6H 5O -；C 6H 5NH 3+的共轭碱为C 6H 5NH 3；HS -的共轭碱为S 2-；2. 写出下列各碱的共轭酸：H 2O,NO 3-，HSO 4-，S 2-，C 6H 5O -。

答：H 2O 的共轭酸为H +；NO 3-的共轭酸为HNO 3；HSO 4-的共轭酸为H 2SO 4；S 2的共轭酸为HS -；C 6H 5O -的共轭酸为C 2H 5OH3．为什么一般都用强酸（碱）溶液作酸（碱）标准溶液？为什么酸（碱）标准溶液的浓度不宜太浓或太稀？答：用强酸或强碱作滴定剂时，其滴定反应为：H ++OH -=H 2OK c =]][[1OH H =WK 1=1.0×1014(25℃)此类滴定反应的平衡常数K t 相当大，反应进行的十分完全。

但酸（碱）标准溶液的浓度太浓时，滴定终点时过量的体积一定，因而误差增大；若太稀，终点时指示剂变色不明显，故滴定的体积也会增大，致使误差增大。

故酸（碱）标准溶液的浓度均不宜太浓或太稀。

4．HCl 与HAc 的混合溶液（浓度均为0.10 mol ·L -1），能否以甲基橙为指示剂，用0.1000 mol ·L -1NaOH 溶液直接滴定其中的HCl ？此时有多少HAc 参与了反应？解：C 1=0.10mol ?L -1，K a2=1.8×10-5，所以（1）不能以甲基橙为指示剂准确滴定HCl（2）因为甲基橙的变色范围为 3.1～4.4所以当pH=4.0时为变色转折点pH=pKa+lgHA A 4.0=4.74+lg%1.0%x x x%=15%5．判断下列情况对测定结果的影响：（1）用混有少量的邻苯二甲酸的邻苯二甲酸氢钾标定NaOH 溶液的浓度；（2）用吸收了CO 2的NaOH 标准溶液滴定H 3PO 4至第一计量点；继续滴定至第二计量点时，对测定结果各如何影响？答：（1）使测定值偏小。

习题解答一、单项选择题1.若定义了int n=2, *p=&n, *q=p;则下面【】的赋值是非法的。

A.p=qB. *p=*qC. n=*qD. p=n【答案】D2.若定义了double *p, a;则能通过scanf函数给输入项读入数据的程序段是【】。

A.p=&a; scanf(“%1e”,p);B. *p=&a; scanf(“%1f”,p);C. p=&a; scanf(“%f”,p);D. p=&a; scanf(“%1f”,a);【答案】C3.若定义了int a[10], i=3, *p; p=&a[5];下面不能表示为a数组元素的是【】。

A.p[-5]B. a[i+5]C. *p++D. a[i-5]【答案】D4.若有如下定义：int n[5]={1,2,3,4,5},*p=n;则值为５的表达式是【】。

A.*+5B. *（p+5）C. *p+=4D. p+4【答案】C5.设变量b的地址已赋给指针变量ps，下面为“真”的表达式是【】。

A.b==&psB. b==psC. b==*psD. &b==&ps【答案】C6.设有以下定义和语句：int a[3][2]={1,2,3,4,5,6},*p[3];p[0]=a[1];则*(p[0]+1)所代表的数组元素是【】。

A.a[0][1]B. a[1][0]C. a[1][1]D. a[1][2]【答案】C7.若定义了char *str=”Hello!”;下面程序段中正确的是【】。

A.char c[ ], *p=c; strcpy(p,str);B.char c[5], *p; strcpy(p=&c[1],&str[3]);C.char c[5]; strcpy(c,str);D.char c[5]; strcpy(p=c+2,str+3);【答案】B8.若有下面的程序段，则不正确的fxy函数的首部是【】。

第6章 常微分方程数值解法 讨论一阶常微分方程初值问题(,),,()dyf x y a x bdx y a η⎧=≤≤⎪⎪⎨⎪=⎪⎩ (6.1.1)的数值解法.数值解法可区分为两大类：(1) 单步法：此类方法在计算1n x + 上的近似值1y n + 时只用到了前一点n x 上的信息.如Euler 法，Runge-Kutta 法，Taylor 级数法就是这类方法的典型代表.(2) 多步法：此类方法在计算1yn +时，除了需要n x 点的信息外，还需要12,,n n x x -- ，等前面若干个点上的信息.线性多步法是这类方法的典型代表.离散化方法1. Taylor(台劳)展开方法2. 化导数为差商的方法3. 数值积分方法一、线性多步法基本思想：是利用前面若干个节点上()y x 及其一阶导数的近似值的线性组合来逼近下一个节点上()y x 的值. 1．一般公式的形式101',,1,,ppn in ii n i i i y a yh b y n p p +--==-=+=+∑∑其中i a ,i b 为待定常数，p 为非负整数.说明：(1)在某些特殊情形中允许任何i a 或i b 为零，但恒假设p a 和p b 不能同时全为零，此时称为1p +步法，它需要1p +个初始值01,,,.p y y y 当0p =时，定义了一类1步法，即称单步法.(2) 若10b -=，此时公式的右端都是已知的，能够直接计算出1n y +，故此时称为显式方法；若10b -≠，则公式的右端含有未知项111'(,),n n n y f x y +++=此时称其为隐式方法.2．逼近准则 准确成立：101()()'(),,1,.ppn in ii n i i i y x a y xh b y x n p p +--==-=+=+∑∑【定义 6.1】 如果对任意()r y x M =，某一线性多步法准确成立，而当()y x 为某一个1r +次多项式时，线性多步法不准确成立，则称此线性多步法是r 阶的. 注：（1）方法的阶越高，逼近效果越好. （2）1p +步法的最高阶可达 22r p =+. 3．线性多步法阶与系数的关系 局部截断误差101()()'(),,1,.ppn n in ii n i i i T y x a y xh b y x n p p +--==-=--=+∑∑()01()'()(),qq n n n q n T c y x c hy x c h y x =++++其中001011011,1[()],1{1[()()2,3,.!pi i p pi i i i p pq q q i i i i c a c i a b c i a i b q q ===--==-⎧=-⎪⎪⎪=--+⎪⎨⎪⎪⎪=--+-=⎪⎩∑∑∑∑∑【定理6.1】 线性多步法是r 阶的充分必要条件是0110,0r r C C C C +====≠称1r C +为误差常数.线性多步法是相容的：满足条件010C C ==,即0011,()1pi i ppiii i a i a b===-⎧=⎪⎪⎨⎪-+=⎪⎩∑∑∑4．线性多步法的构造方法 待定系数法：r 阶方法的系数,iia b 确定，可令010,r CC C ==== 即解下面方程得到1,0()1011()(),2,3,,01p a ii p pi a b i i i i p pq q i a q i q r i i i ⎧=∑⎪⎪=⎪⎪-+=∑∑⎪⎨==-⎪⎪⎪-⎪-+-=∑∑⎪==-⎩二、线性多步法的收敛性 记1(),pp p iii r ra rρ+-==-∑1().pi p ii r b rσ-=-=∑分别称为线性多步法的第一、第二特征多项式.()r ρ以及相应的线性多步法满足根条件：若()r ρ的所有根的模均不大于1，且模为1的根是单根。

六、补充练习题（一）单项选择题1．在使用收款凭证、付款凭证、转账凭证的单位，与货币资金无关的业务，填制的凭证是（）A．收款凭证B．付款凭证C．转账凭证D．通用凭证2．下列凭证属于外来原始凭证的是（）A．领料单B．发料汇总表C．上缴税金的收据D．产品交库单3．下列凭证中属于自制原始凭证的是（）A．银行收款通知B．付款凭证C．从购买方获得的销售发票D．销售商品所开具的销售发票4．按填制程序和功能不同，会计凭证分为（）A．收款凭证、付款凭证和转账凭证B．一次凭证和累计凭证C．原始凭证和记账凭证D．外来凭证和自制凭证5．（）是用来编制会计分录的依据，（）是用来作为登记账户的依据。

A．原始凭证B．一次凭证C．记账凭证D．累计凭证6．下列有关记账凭证的说法不正确的有（）A．记账凭证的填制与审核的作用主要在于：一方面防止不该登入账簿的业务进入会计账簿，另一方面确保该登入的都正确地进入会计账簿B．在课堂上讲的会计分录在我国会计实际工作中是没有的，其对应的是记账凭证C．在会计电算化的情况下，记账凭证分为收款凭证、付款凭证和转账凭证的意义已经不大了D．记账凭证登记的依据全部是原始凭证7．付款凭证表头列示的会计科目是（）A．借方科目B．贷方科目C．有时为借方科目，有时为贷方科目D．不能肯定8．下列费用中，直接抵减当期损益的有（）A．生产工人工资B．广告费C．生产车间机器设备的折旧费D．生产产品所耗的材料费9．下列费用中，不应计入产品成本的有（）A．直接材料费B．直接人工费C．期间费用D．制造费用10．月末，如果某种产品一部分完工一部分未完工，归集在产品成本明细账中的费用总额，还要采用适当的分配方法，在（）之间进行分配，然后才能计算完工产品成本。

A．产品品种B．产品批别C．产品生产步骤D．完工产品和在产品11．“累计折旧”账户属于（）类账户。

A．资产B．负债C．费用D．成本12．下列项目属于管理费用的有（）A．银行借款利息B．厂部管理人员工资C．车间管理人员工资D．车间水电费13．“利润分配”账户年末贷方余额表示（）A．已分配的利润额B．未分配的利润额C．未弥补的亏损额D．已实现的净利润14．下列账户中不可能与“制造费用”账户发生对应关系的账户是（）A．原材料B．累计折旧C．应付职工薪酬D．库存商品15．下列不计入当期损益的是（）A．管理费用B．财务费用C．所得税费用D．制造费用16．产品生产间接耗用的费用，先归入（）然后计入有关产品成本中去。

第六章对映异构1、说明下列各名词的意义：⑴旋光性：⑵比旋光度：⑶对应异构体：⑷非对应异构体：⑸外消旋体：⑹内消旋体：答案：（1）旋光性：能使偏光振动平面的性质，称为物质的旋光性。

（2）比旋光度：通常规定1mol含1 g旋光性物质的溶液，放在1 dm (10cm)长的成液管中测得的旋光度，称为该物质的比旋光度。

（3）对应异构体：构造式相同的两个分子由于原子在空间的排列不同，彼此互为镜象，不能重合的分子，互称对应异构体。

（4）非对应异构体：构造式相同，构型不同，但不是实物与镜象关系的化合物互称非对映体。

（5）外消旋体：一对对映体右旋体和左旋体的等量混合物叫外消旋体。

（6）内消旋体：分子内，含有构造相同的手性碳原子，但存在对称面的分子，称为内消旋体，用meso表示。

2、下列化合物中有无手性C（用*表示手性C）（1）（2）（3）（4）答案：（1）*（2）无手性碳原子（3）**（4）3、分子式为C3H6DCl所有构造异构体的结构式，在这些化合物中那些具有手性？用投影式表示它们的对应异构体。

答案：解：分子式为C3H6DCl的化合物共有5个构造异构体，其中3个有对应异构体。

（手性）：（无手性）Cl CH 2CH 3HD DH ClCH 2CH 3CH 2Cl CH 3HDDHCH 2ClCH 3CH 2D CH 3HClClHCH 2DCH 34、 ⑴丙烷氯化已分离出二氯化合物C 3H 6Cl 2的四种构造异构体，写出它们的构造式：⑵ 从各个二氯化物进一步氯化后，可得的三氯化物（C 3H 5C l3）的数目已由气相色谱法确定。

从A 得出一个三氯化物，B 给出两个， C 和D 各给出三个，试推出A ，B 的结构。

⑶通过另一合成方法得到有旋光性的化合物C ，那么C 的构造式是什么？D 的构造式是怎样的？⑷有旋光的C 氯化时，所得到的三氯丙烷化合物中有一个E 是有旋光性的，另两个无旋光性，它们的构造式怎样？ 答案：(1)Cl 2CHCH 2CH 3(1) CH 3CCl 2CH 3(2) ClCH 2CHClCH 3(3) ClCH 2CH 2CH 2Cl (4)(2) 解：A 的构造式：CH 3CCl 2CH 3 B 的构造式：ClCH 2CH 2CH 2Cl (3)(4)另两个无旋光性的为：CH 2ClCCl 2CH 3ClCH 2ClCHCH 2Cl5、指出下列构型式是R 或S 。

第六章会计凭证习题一、应掌握的名词会计凭证原始凭证外来原始凭证自制原始凭证记账凭证一次凭证累计凭证汇总原始凭证会计凭证的传递收款凭证付款凭证转账凭证二、填空题１．会计凭证是具有一定格式用以记录经济业务的发生和完成情况明确经济责任，作为记账依据的书面证明。

２．填制和审核会计凭证是整个会计核算工作的起点和基础。

３．将现金送存银行，一般只填制现金付款凭证。

４．原始凭证按其来源不同，分为外来原始凭证自制原始凭证；按其填制方法不同，分为为一次凭证累计凭证汇总凭证５．记账凭证按其用途可分为专用凭证通用凭证；按其对经济业务反映方式的不同，可分为单式记账凭证复式记账凭证。

６．收款凭证是用来记录现金银行存款收入业务的记账凭证。

７．汇总转账凭证是根据转账凭证按账户的贷方设置并按对应的借方账户归类汇总的记账凭证。

三、判断题１．会计凭证按其经济业务的内容不同，可分为原始凭证和记账凭证两大类。

（B）２．凡不能证明经济业务发生或完成的各种单证，不能作为原始凭证据以记账。

（A）３．实际工作中，也有企业单位不分收款、付款、转账凭证，统一使用一种凭证，这种记账凭证称为通用记账凭证。

（A）４．按收款、付款、转账业务分别填制的记账凭证，称为专用记账凭证。

（A）５．每项经济业务的发生都必须从外部取得原始凭证。

（B）６．为了便于记账和查账需要编制原始凭证。

（B）７．原始凭证必要时可以涂改、挖补。

（B）８．只要是真实的原始凭证，就可以作为填制记账凭证的依据。

（？）９．复式记账凭证是指将多笔经济业务所涉及的全部会计科目及其内容在同一张记账凭证中反映的记账凭证。

（B）１０．记账凭证是具有法律效力的证明。

（B）１１．记账凭证只能根据审核无误的原始凭证填制。

（B）１２．除结账和更正错误的记账凭证可以不附原始凭证外，其他记账凭证必须附有原始凭证，并注明所附原始凭证的张数。

（ A ）１３．收款凭证是银行存款收入业务使用的凭证。

（ B ）１４．记账凭证按其对经济业务反映方式的不同，分为收款凭证、付款凭证、转账凭证。

第六章维生素一、单项选择题1. 维生素B1在体内的辅酶形式是A.NAD+B. TPPC. FMND. FADE. CoA2. 叶酸在体内的辅酶形式是A.TPPB. FH2C. FH4D. FADE. NAD+3. 维生素D的活性形式是A. Vit D3B. 25-OH-Vit D3C. 1,25-(OH) 2- Vit D3D. 24,25-(OH) 2- Vit D3E. 25,26-(OH)2- Vit D34.下列哪种辅酶或辅基参与酰基转移反应A. TPPB. FADC. FH4D. HSCoAE. 磷酸吡哆醛5.下列哪种物质可参与构成视紫红质A. 核黄素B. 11－顺视黄醛C. 生育酚D. Vit KE. 硫辛酸6.下列有关维生素C生理功能的叙述，哪一项是错误的A. 保护含-SH的酶为还原状态B. 保护谷胱甘肽为氧化型C. 维生素C参与体内氧化还原反应D. 参与某些物质的羟化反应E. 促进肠道对铁的吸收7.在下列化合物中不含B族维生素的是A. NAD+B. FMNC. HSCoAD. CoQE. FAD8.参与胶原蛋白中羟脯氨酸及羟赖氨酸合成的是A. Vit KB. Vit DC. Vit CD. Vit EE. Vit A9.NAD+在酶促反应中参与转移A. 氨基B. 氢原子C. 氧原子D. 羧基E. 酰基10.下列关于维生素的叙述哪一个是正确的A. 维生素都是含氮的有机化合物B. 维生素不经修饰即可作为辅酶或辅基C. 所有的辅酶（辅基）都是维生素D. 前列腺素由脂溶性维生素生成E. B族维生素主要参与构成辅酶或辅基11.日光或紫外线照射可使B. 生成胆固醇A. 7-脱氢胆固醇转变成维生素D3C. 7-脱氢胆固醇转变成维生素DD. 生成视黄醇2E. 维生素E活化12.长期大量食用生鸡蛋清，可造成下列哪种维生素的缺乏A. 叶酸B. 维生素B2C. 维生素B1D. 生物素E. 维生素C13.有些人长期不吃猪肝等动物性食物，但很喜欢吃蔬菜，这些人也不一定会患夜盲症。

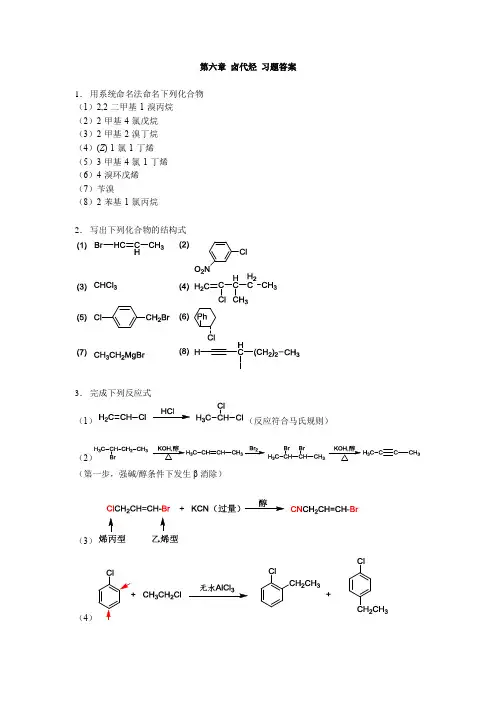
第六章卤代烃习题答案1．用系统命名法命名下列化合物（1）2,2-二甲基-1-溴丙烷（2）2-甲基-4-氯戊烷（3）2-甲基-2-溴丁烷（4）(Z)-1-氯-1-丁烯（5）3-甲基-4-氯-1-丁烯（6）4-溴环戊烯（7）苄溴（8）2-苯基-1-氯丙烷2．写出下列化合物的结构式3．完成下列反应式（1）（反应符合马氏规则）（2（第一步，强碱/醇条件下发生β消除）（3）（4（5（Cl离去生成稳定的苄基碳正离子）（6（优先生成π-π共轭产物）（7）（由于乙醇钠写在反应式左侧，应该为反应原料，因此发生威廉姆森反应生成醚；如果写在箭头上方表示为碱，加热条件下发生消除反应）（8（注意硝酰氧基的正确写法，不能写成-NO3）4．用化学方法鉴别下列化合物（1）（2）（3）5．按要求将下列各组化合物排序（1）C6H5CHBrC6H5>CH3CHBrCH3>CH3CH2CH2Br （依据碳正离子稳定性）（2）1-溴丁烷>2-溴丁烷>2-甲基-2-溴丙烷（根据位阻大小来判断）（3）（前面两个都是烯丙型，后面两个都是乙烯型，活性肯定是烯丙型最高因为烯丙型碳正离子更稳定，乙烯型活性最差。

作为离去基团，溴的离去活性相对于氯更高，因此可以得出以上活性排序）6．试判断在下列各种情况下卤代烷水解是属于S N1机理还是S N2机理（1）S N2 （2）S N1 （3）S N2 （4）S N17．完成下列转化。

（1）（2）（利用格氏试剂与二氧化碳的反应来增加一个碳原子）8．推断题9．推断题。

一、单项选择题（每小题1分）1. 中央金属固定,下列离子或化合物作为配体时,场强最强的是：（）a. NH3b. CN-c. H2Od. SCN-答案：b2. 具有理想正八面体的电子组态(高自旋时)是（）a. (t2g)3b. (t2g)1c. (t2g)4(e g)2d. 以上都不对答案：a3. 平面正方形场中,d轨道的最高简并度是（）a. 1b. 2c. 3d. 4答案：b4. 导致Ni2+水合能在第一系列过渡金属元素中最大的主要原因是( )a. 原子序数最大b.电子成对能最大c. CFSE最大d. H2O是弱场答案：c5.下列原子作为电子给予体时,哪个原子引起的分裂能最大（）a. Nb.Fc. Od. C答案：d6. 决定成对能P的主要因素是( )a. 分裂能b. 库仑能c. 交换能d. 配位场强度答案：c7．下列配位化合物高自旋的是（）a. [Co(NH3)6]3+b. [Co(NH3)6]2+c. [Co(NO2)6]3-d. [Co(CN)6]4-答案：b8.下列配位化合物磁矩最大的是（）a. [FeF6]3-b. [Mn(CN)6]3-c. [Ni(H2O)6]2+d. [Co(NH3)6]3+答案：a9. 判断下列配位化合物的稳定化能大小的次序是（）(1) [CoF6]4-(2)[NiF6]4- (3)[FeF6]3-a. (1)> (2)>(3)b. (1)=(2)<(3)c. (1)<(2)<(3)d. (2)>(1)>(3)答案：d10. Ni和CO可形成羰基配合物N i(CO)n,其中n是( )a. 6b. 3c. 4d. 5答案：c11．[Cu(H2O)4·2H2O]2+溶液出现蓝色的原因是（）a. 自旋相关效应b. d-d跃迁c. σ-π跃迁d. 姜-泰勒效应答案：b12．配位化合物d-d跃迁光谱一般出现在什么区域（）a. 红外b.微波c. 远紫外d. 可见—紫外答案：d13. 关于[FeF6]3-络离子，下列哪个叙述是错误的（）a. 是高自旋络离子b. CFSE为0c. 中心离子的电子排布与Fe3＋相同d. CFSE不为014. 下列哪个轨道上的电子在XY平面上出现的几率密度为零（）a. 3Pzb. 3dx2-y2c. 3sd. 3dz2答案：a15.下列配合物中磁矩最小的是( )a. [Cr(H2O)6]2+b. [Fe(CN)6]3-c. [Co(H2O)6]2+d. [Co(NH3)6]3+答案：d16．下列分子和离子中具有顺磁性的是（）a. NO+b. [Fe(CN)6]4-c. B2d. CO答案：c17. 下列配合物中分裂能Δ0最大的是( )a. [FeF6]4-b. [Os(CN)6]4-c. [Ru(CN)6]4-d. [Fe(CN)6]4-答案：b18.下列配合物中磁矩约为2.8μB的是( )a. K3[CoF6]b. K3[Fe(CN)6]c. Ba[TiF6]d. [V(H2O)6]3+答案：d19. CO与过渡金属形成羰基配位化合物时，C－O键会产生什么变化（）a. 削弱b. 加强c. 不变d. 变短答案：a20. 下列四种络合物中，d-d跃迁能量最低的是( )a. [Fe(H2O)6] 2+b. [Fe(H2O)6] 3+c. [FeF6] 4-d. [FeF6] 3-答案：c21. 某一晶体场的△>P，则( )a. 该场为强场b. 电子按高自旋排布c. 络合物的磁矩为零d. 晶体场稳定化能大于零答案：a22. 在平面正方形络合物中，四个配体分别位于±x和±y上，下列d轨道中能量最高的是( )a. d xyb. d x2-y2c. d yzd. d z2答案：b23. CuSO4水溶液呈蓝色的原因是( )a. d—d跃迁b. σ—π跃迁c. 姜—泰勒效应d. σ—π配键答案：a24. 四种配位化合物(1) CoF63- (2) Co(CN) 63- (3) Co(NH3) 63+ (4) CoCl63-的d-d跃迁光谱，波数从大到小顺序为（）a. (2)>(3)>(1)>(4)b.(4)>(1)>(3)>(2)c. (3)>(2)>(1)>(4)d. (2)>(3)>(4)>(1)答案：a25.下列分子中，不存在σ—π配键的是( )a. [Co (NH3)6]Cl3b. Ni(CO)4c. HCo(CO)4d. K[PtCl3(C2H4)]·H2O答案：a26. 下列哪个络合物的磁矩最大( )a. 六氰合钴(Ⅲ)离子b. 六氰合铁(Ⅲ)离子c. 六氨合钴(Ⅲ)离子d. 六水合锰(Ⅱ)离子答案：d27．推测下列三种络合物的d-d跃迁频率大小顺序( )(1)六水合铁(Ⅲ) (2)六水合铁(Ⅱ) (3)六氟合铁(Ⅱ)a. ν1>ν2>ν3b. ν1>ν3>ν2c. ν3>ν2>ν1d. ν3>ν1>ν2答案：a二、多项选择题（每小题2分）1. 正八面体场中，d轨道能级分裂为两组，其中能量较低的一组称为t2g，包括下列哪些轨道（）a. d xyb. d x2-y2c. d yzd. d z2e. d xz答案：a,c,e2. 具有理想正八面体的电子组态(高自旋时)是（）a. (t2g)3b.(t2g)1c. (t2g)4(e g)2d. d0e. d10答案：a,d,e3. 下列配位化合物低自旋的是( )a. [Co(NH3)6]3+b. [Co(NH3)6]2+c. [Co(NO2)6]3-d. [Co(CN)6]4-e. [Co(H2O)6]2+答案：a,c,d4. 下列分子和离子中，具有顺磁性的是（）a. [Co(NO2)6]3-b. [Fe(CN)6]4-c. B2d. COe. [Cu(H2O)6]2+答案：c,e5．下列分子(或离子)中，哪些是反磁性的( )a. [Fe(CN)6]3－(△> P)b. O2－c. COd. N2e. [Fe(CN)6]4－(△> P)答案：c,d,e6. 与H2O相比，下列哪些配位体对Δ值影响较大（）a. CN-b. NH3c. F-d. SCN-e. OH-答案：a,b7. 关于 [Fe(CN)6]4-络离子，下列哪些叙述是错误的( )a. 是高自旋络离子b.CFSE为0c. 中心离子的电子排布与Fe3＋相同d. CFSE不为0e. 是顺磁性的答案：a,b,c,e8. 络合物的化学键理论主要有哪些（）a. 价键理论b. 晶体场理论c. 分子轨道理论d. 配位场理论e. 点阵理论答案：a,b,c,d三、填空题（每小题1分）1. 成对能(P)是由库仑能和_ 贡献的。

2
)
d
3
3
6
1 4
sin
2
3 0
9
12
1 4
sin
2
2
3
3
3 6
3 8
9
12
3 8
5 4
.
6.5 求正弦曲线 y sin x (0 x )绕 x 轴旋转所得旋转体的体积．
解 所求旋转体的体积为
Vx
sin2 x dx 2
0
2 sin2
x dx 2
1
,
3
,
由于图形关于极轴的对称性，如习题 6.4 图，则所围图形的面积为
3
A 2[
3
1
(1
cos
)2
d
02
2 3
1 2
(3 cos
)2
d
]
3 (1 2 cos
0
cos2 )d
9
2
cos
2
d
3
2sin 3
3
0
3
(1
cos
2
)
d
9
0
2
2 3
(1
cos 2
的直线为 x 轴，过圆心 o 且垂直于 x 轴的直线为 y 轴，建立直角坐标系，如习题 6.11
图. 则底圆方程 x2 y2 R2 . 立体中过 x 轴上的点 x 作垂直于 x 轴的平面，截正劈
锥体得等腰三角形。该等腰三角形的底和高分别为 2 R2 x2 和 h. 因此截面面积 为 A(x) 1 2 R2 x2 h h R2 x2 .
图形的面积．
解 如习题 6.3 图，所求面积为
A
2

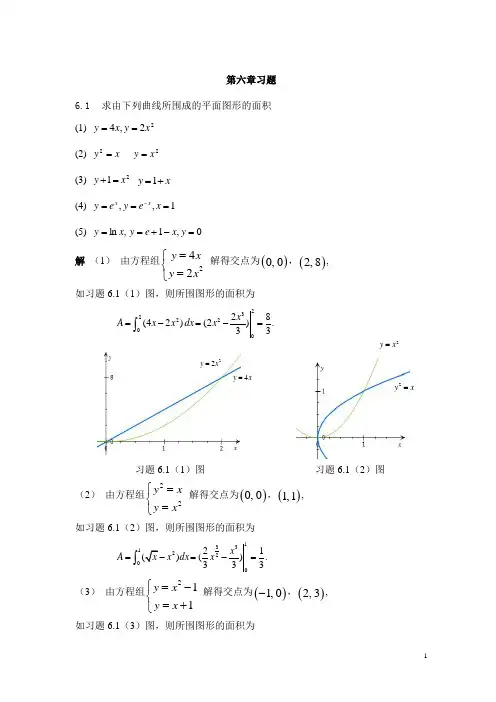
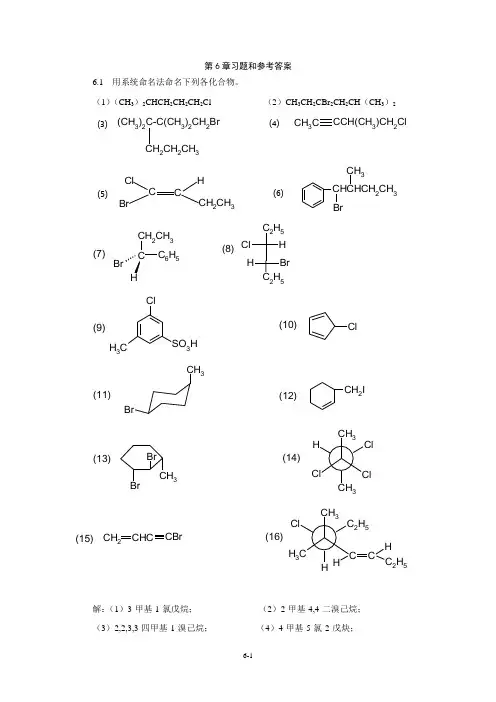
第6章习题和参考答案6.1 用系统命名法命名下列各化合物。

（1）（CH 3）2CHCH 2CH 2CH 2Cl （2）CH 3CH 2CBr 2CH 2CH （CH 3）2(CH 3)2C-C(CH 3)2CH 2BrCH 2CH 2CH 3CH 3C CCH(CH 3)CH 2Cl⑶⑷CCH Cl BrCH 2CH 3CHCHCH 2CH 3BrCH 3⑸⑹C 2H 5C 2H 5H ClBr HCCH 2CH 3HC 6H 5Br(7)(8)ClClCH 3SO 3H(9)(10)CH 3BrCH 2I(11)(12)CH 3ClClCl CH 3HBrCH 3Br (13)(14)CH 3CH 3C 2H 5H ClCHH C 2H 5CCH 2CHCCBr(15)(16)解：（1）3-甲基-1-氯戊烷； （2）2-甲基-4,4-二溴己烷； （3）2,2,3,3-四甲基-1-溴己烷； （4）4-甲基-5-氯-2-戊炔；（5）（Z ）-1-氯-1-溴-1-丁烯； （6）2-甲基-1-苯基-1-溴丁烷； (7) (R )-1-苯基-1-溴丙烷； （8）（3R ，4R ）-3-氯-4-溴己烷； (9) 3-甲基-5-氯苯磺酸； （10）5-氯-1,3-环己二烯； (11) 顺-1-甲基-4-溴环己烷； (12) 3-碘甲基环己烯 (13) (1S ，2R ，3R )-1-甲基-2,3-二溴环己烷； （14） （S ）-2,2,3-三氯丁烷(15) 4-溴-1-丁烯-3-炔； (16) (3E )，(6R )-5,5-二甲基-6-溴-3-辛烯 6.2 写出下列化合物的结构式。

（1） 异丙基氯； （2） 烯丙基溴； （3） β-苯基乙基溴； （4） 对氯苄基溴； （5） 新戊基碘； （6） 叔丁基氯(7) (S)-2-碘辛烷 (8) 6，7-二甲基-5-氯二环[3.2.1]辛烷(9) 反-1-苯基-2-氯环己烷 (10) 1，2，3-三氯环己烷所有异构体的稳定构象 解：CH 3CH 2CH 2CHCH 3ClBrCH 2CH CH 2(1)(2)CH 2CH 2BrCH 2BrCl(3)(4)C CH 2CH 3CH 3CH 3I C Cl CH 3CH 3CH 3(5)(6)C 6H 13CH 3I HCH 3C H 3ClClPh(9)(8)(7)ClClClClClClClClCl(10)6.3 写出1-溴丁烷与下列试剂反应的主要产物。

习 题 6—11、在平行四边形ABCD 中, 设−→−AB =a , −→−AD =b . 试用a 和b 表示向量−→−MA 、−→−MB 、−→−MC 、−→−MD , 其中M 是平行四边形对角线的交点.解： 由于平行四边形的对角线互相平分, 所以a +b −→−−→−==AM AC 2, 即 -(a +b )−→−=MA 2, 于是 21-=−→−MA (a +b ).因为−→−−→−-=MA MC , 所以21=−→−MC (a +b ). 又因-a +b −→−−→−==MD BD 2, 所以21=−→−MD (b -a ). 由于−→−−→−-=MD MB , 所以21=−→−MB (a -b ).2、若四边形的对角线互相平分，用向量方法证明它是平行四边形.证： =,BM =，∴=+=+BM =与 平行且相等,结论得证.3、 求起点为)1,2,1(A ，终点为)1,18,19(--B 的向量→AB 与12AB −−→-的坐标表达式.解：→AB =j i k j i 2020)11()218()119(--=-+--+--={20,20,0}--, 12AB −−→-={10,10,0}4、 求平行于a ={1，1，1}的单位向量.解：与a 平行的单位向量为{}1,1,131±=±a a .5、在空间直角坐标系中，指出下列各点在哪个卦限？(1,1,1),A - (1,1,1),B -(1,1,1),C -- (1,1,1).D -- 解： A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ.6、 求点),,(z y x M 与x 轴，xOy 平面及原点的对称点坐标.解：),,(z y x M 关于x 轴的对称点为),,(1z y x M --，关于xOy 平面的对称点为),,(2z y x M -，关于原点的对称点为),,(3z y x M ---.7、已知点A(a, b, c), 求它在各坐标平面上及各坐标轴上的垂足的坐标（即投影点的坐标）. 解：分别为),0,0(),0,,0(),0,0,(),,0,(),,,0(),0,,(c b a c a c b b a .8、过点(,,)P a b c 分别作平行于z 轴的直线和平行于xOy 面的平面，问它们上面的点的坐标各有什么特点？解：平行于z 轴的直线上面的点的坐标：x a,y b,z R ==∈；平行于xOy 面的平面上的点的坐标为 z c,x,y R =∈.9、求点P (2,-5,4)到原点、各坐标轴和各坐标面的距离.解：到原点的距离为x y 轴的距离为到z10、 求证以)1,3,4(1M 、)2,1,7(2M 、)3,2,5(3M 三点为顶点的三角形是一个等腰三角形. 解：222212(74)(13)(21)14M M =-+-+-=,222223(57)(21)(32)6M M =-+-+-= 222213(45)(32)(13)6M M =-+-+-=，即1323M M M M =，因此结论成立.11、 在yoz 坐标面上，求与三个点A(3, 1, 2), B(4, -2, -2), C(0, 5, 1)等距离的点的坐标. 解：设yoz 坐标面所求点为),,0(z y M ，依题意有||||||MC MB MA ==，从而222)2()1()30(-+-+-z y 222)2()2()40(++++-=z y222)2()1()30(-+-+-z y联立解得2,1-==z y ，故所求点的坐标为)2,1,0(-.12、 z 轴上，求与点A(-4, 1, 7), 点B(3, 5,-2)等距离的点. 解：设所求z 轴上的点为),0,0(z ，依题意：222)7()10()40(-+-++z 222)2()50()30(++-+-=z ，两边平方得914=z ，故所求点为)914,0,0(.13、 求λ使向量}5,1,{λ=a 与向量}50,10,2{=b 平行. 解：由b a //得5051012==λ得51=λ.14、 求与y 轴反向，模为10的向量a 的坐标表达式. 解：a =j j 10)(10-=-⋅={0,10,0}-.15、求与向量a ={1，5，6}平行，模为10的向量b 的坐标表达式. 解：}6,5,1{6210==a a a ,故 {}6,5,16210100±=±=a b .16、 已知向量6410=-+a i j k ，349=+-b i j k ，试求： （1）2+a b ； （2）32-a b ．解：（1） 264102(349)1248i a b i j k i j k j k +=-+++-=+-; （2）323(6410)2(349)=122048a b =i j k i j k i j k --+-+--+.17、已知两点A 和(3,0,4)B ，求向量AB 的模、方向余弦和方向角．解： 因为(1,1)AB =-, 所以2AB =,11cos ,cos 22αβγ===-,从而π3α=,3π4β=,2π3γ=.18、设向量的方向角为α、β、γ．若已知其中的两个角为π3α=，2π3β=．求第三个角γ． 解： π3α=,2π3β=,由222cos cos cos 1αβγ++=得21cos 2γ=.故π4γ=或3π4.19、 已知三点(1,0,0)=A ，(3,1,1)B ，(2,0,1)C ，求：（1）BC 与CA 及其模；（2）BC 的方向余弦、方向角；（3）与BC 同向的单位向量.解：（1）由题意知{}{}23,01,111,1,0,BC =---=--{}{}12,00,011,0,1,CA =---=-- 故 2,2==BC CA .（2）因为{}1,1,0,=--BC 所以，由向量的方向余弦的坐标表示式得：cos 0αβγ===，方向角为：3,42ππαβγ===.（3）与BC 同向的单位向量为：oa =⎧⎫=⎨⎬⎩⎭BCBC .20、 设23,23,34,m i j k n i j k p i j k =++=+-=-+和23a m n p =+-求向量在x 轴上的投影和在y 轴上的分向量.解：2(23)3(23)(34)5114a i j k i j k i j k i j k =++++---+=+-.故向量a 在x 轴上的投影5=x a ，在y 轴上的投影分量为11y a j =.21、一向量的终点为点B(-2,1,-4),它在x 轴，y 轴和z 轴上的投影依次为3，-3和8，求这向量起点A 的坐标.解：设点A 为（x, y, z ）,依题意有：84,31,32=---=-=--z y x ， 故12,4,5-==-=z y x ，即所求的点A （-5， 4，-12）.22、 已知向量a 的两个方向余弦为cos α=72 ,cos β=73, 且a 与z 轴的方向角是钝角.求cos γ. 解：因222cos cos cos 1,αβγ++=22223366cos 1cos 77497γγ=-==±故（）—（），，又γ是钝角，所以76cos -=γ.23、设三力1232234F ,F ,F i j i j k j k =-=-+=+作用于同一质点，求合力的大小和方向角.解： 合力123(2)(234)()F F F F i k i j k j k =++=-+-+++323i j k =-+，因此，合力的大小为|F |=合力的方向余弦为,222cos ,cos 223cos -===βγα因此παγβ===-习 题 6—21、 {}0,0,1=a ，{}0,1,0=b ，)1,0,0(=c ，求⋅a b ，c a ⋅，c b ⋅，及a a ⨯，b a ⨯，c a ⨯，c b ⨯. 解：依题意，i a =，j b =，k c =，故0=⋅=⋅j i b a ，0=⋅=⋅k i c a ，0=⋅=⋅k j c b .0=⨯=⨯i i a a ，k j i b a =⨯=⨯，j k i c a -=⨯=⨯，i k j c b =⨯=⨯.2、 }}{{1,2,2,21,1==b a ,，求b a ⋅及b a ⨯ .a 与b的夹角余弦. 解：（1）121221⋅=⨯+⨯+⨯=a b 6, 112221⨯==i j ka b }{3,3,0-.(2)cos a b a b a b θ++==3、 已知 π5,2,,3∧⎛⎫=== ⎪⎝⎭a b a b ，求23a b -解：()()2232323-=-⋅-a b a b a b 22412976=-⋅+=a a b b ，∴ 23-=ab4、 证明下列问题：1）证明向量}{1,0,1=a 与向量}{1,1,1-=b 垂直. 2） 证明向量c 与向量()()a c b b c a ⋅-⋅垂直. 证：1）01110)1(1=⨯+⨯+-⨯=⋅b a ,^π(,)2a b ∴=，即a 与b 垂直. 2） [()()]⋅-⋅⋅a c b b c a c [()()]=⋅⋅-⋅⋅a c b c b c a c ()[]=⋅⋅-⋅c b a c a c 0=[()()]∴⋅-⋅⊥a c b b c a c .5、 求点)1,2,1(M 的向径OM 与坐标轴之间的夹角.解：设OM 与x 、y 、z 轴之间的夹角分别为γβα,,，则211)2(11cos 22=++==α,22cos ==β, 21cos ==γ. 3π=∴α, 4π=β, 3π=γ.6、 求与k j i a ++=平行且满足1=⋅x a 的向量x .解：因x a //, 故可设{}λλλλ,,==a x ，再由1=⋅x a 得1=++λλλ，即31=λ，从而⎭⎬⎫⎩⎨⎧=31,31,31x .7、求与向量324=-+a i j k ，2=+-b i j k 都垂直的单位向量.解：=⨯=xy z x y zij kc a b a a a b b b 324112=--i j k =105+j k，||10==c 0||∴=c c c=.⎫±+⎪⎭j8、 在顶点为)2,1,1(-A 、)2,6,5(-B 和)1,3,1(-C 的三角形中，求三角形ABC 的面积以及AC 边上的高BD .解：{0,4,3},{4,5,0}AC AB =-=-,三角形ABC 的面积为,22516121521||21222=++=⨯=AB C A S ||||21,5)3(4||22BD S ==-+= ||521225BD ⋅⋅= .5||=∴BD9、 已知向量≠0a ，≠0b ，证明2222||||||()⨯=-⋅a b a b a b .解 2222||||||sin ()∧⨯=⋅a b a b ab 222||||[1cos ()]∧=⋅-a b ab 22||||=⋅a b 222||||cos ()∧-⋅a b ab 22||||=⋅a b 2().-⋅a b10、 证明：如果++=0a b c ，那么⨯=⨯=⨯b c c a a b ，并说明它的几何意义.证： 由++=0a b c , 有()++⨯=⨯=00a b c c c , 但⨯=0c c ，于是⨯+⨯=0a c b c ,所以⨯=-⨯=⨯b c a c c a . 同理 由()++⨯=0a b c a , 有 ⨯=⨯c a a b ,从而 ⨯=⨯=⨯b c c a a b .其几何意义是以三角形的任二边为邻边构成的平行四边形的面积相等.11、 已知向量23,3=-+=-+a i j k b i j k 和2=-c i j ，计算下列各式：（1）()()⋅-⋅a b c a c b （2）()()+⨯+a b b c （3）()⨯⋅a b c （4）⨯⨯a b c 解： （1）()()8(2)8(3)⋅-⋅=---+=a b c a c b i j i j k 824--j k .(2) 344,233+=-++=-+a b i j k b c i j k ，故()()+⨯+a b b c 344233=-=-i jk--j k . （3）231()231(2)(85)(2)11311312-⨯⋅=-⋅-=--+⋅-=-=--i jk a b c i j i j k i j 2. （4）由（3）知85,()851120⨯=--+⨯⨯=--=-i jka b i j k a b c 221++i j k .习 题 6—31、已知)3,2,1(A ，)4,1,2(-B ，求线段AB 的垂直平分面的方程. 解：设),,(z y x M 是所求平面上任一点，据题意有|,|||MB MA =()()()222321-+-+-z y x ()()(),412222-+++-=z y x化简得所求方程26270x y z -+-=.这就是所求平面上的点的坐标所满足的方程, 而不在此平面上的点的坐标都不满足这个方程，所以这个方程就是所求平面的方程.2、 一动点移动时，与)0,0,4(A 及xOy 平面等距离，求该动点的轨迹方程.解：设在给定的坐标系下，动点),,(z y x M ，所求的轨迹为C ，则(,,)M x y z C MA z ∈⇔= 亦即z z y x =++-222)4( 0)4(22=+-∴y x 从而所求的轨迹方程为0)4(22=+-y x .3、 求下列各球面的方程：（1）圆心)3,1,2(-，半径为6=R ； （2）圆心在原点，且经过点)3,2,6(-；（3）一条直径的两端点是)3,1,4()5,32(--与；（4）通过原点与)4,0,0(),0,3,1(),0,0,4(- 解：（1）所求的球面方程为：36)3()1()2(222=-+++-z y x （2）由已知，半径73)2(6222=+-+=R ，所以球面方程为49222=++z y x（3）由已知，球面的球心坐标1235,1213,3242=-=-=+-==+=c b a ， 球的半径21)35()31()24(21222=++++-=R ，所以球面方程为： 21)1()1()3(222=-+++-z y x（4）设所求的球面方程为：0222222=++++++l kz hy gx z y x因该球面经过点)4,0,0(),0,3,1(),0,0,4(),0,0,0(-，所以⎪⎪⎩⎪⎪⎨⎧=-=++=+=08160621008160k h g g l 解之得⎪⎪⎩⎪⎪⎨⎧=-=-==2210k g h l∴所求的球面方程为0424222=+--++z y x z y x .4、将yOz 坐标面上的抛物线22y z =绕z 旋转一周，求所生成的旋转曲面的方程． 解：222x y z +=(旋转抛物面) .5、将zOx 坐标面上的双曲线12222=-c z a x 分别绕x 轴和z 轴旋转一周，求所生成的旋转曲面的方程．解： 绕x 轴旋转得122222=+-c z y a x 绕z 轴旋转得122222=-+cz a y x .6、指出下列曲面的名称，并作图：（1）22149x z +=；（2）22y z =；（3）221x z += ；（4）22220x y z x ++-=； （5）222y x z +=；（6）22441x y z -+=；（7）221916x y z ++=；（8）222149x y z -+=-；（9）1334222=++z y x ；（10）2223122z y x +=+.解： (1)椭圆柱面；(2) 抛物柱面；(3) 圆柱面；(4)球面；（5）圆锥面；（6）双曲抛物面；（7）椭圆抛物面；（8）双叶双曲面；（9）为旋转椭球面；（10）单叶双曲面.7、指出下列方程在平面解析几何和空间解析几何中分别表示什么图形？ （1）1+=x y ；（2）422=+yx ；（3）122=-y x ；（4）22x y =.解：（1）1+=x y 在平面解析几何中表示直线，在空间解析几何中表示平面； （2）422=+y x 在平面解析几何中表示圆周，在空间解析几何中表示圆柱面； （3）122=-y x 在平面解析几何中表示双曲线，在空间解析几何中表示双曲柱面；（4）y x22=在平面解析几何中表示抛物线，在空间解析几何中表示抛物柱面.8、 说明下列旋转曲面是怎样形成的？（1）1994222=++z y x ；（2）14222=+-z y x （3）1222=--z y x ；（4）222)(y x a z +=- 解：（1）xOy 平面上椭圆19422=+y x 绕x 轴旋转而成；或者 xOz 平面上椭圆22149+=x z 绕x 轴旋转而成（2）xOy 平面上的双曲线1422=-y x 绕y 轴旋转而成；或者 yOz 平面上的双曲线2214-=y z 绕y 轴旋转而成（3）xOy 平面上的双曲线122=-y x 绕x 轴旋转而成；或者 xOz 平面上的双曲线221x z -=绕x 轴旋转而成 （4）yOz 平面上的直线a y z +=绕z 轴旋转而成或者 xOz 平面上的直线z x a =+绕z 轴旋转而成.9、 画出下列各曲面所围立体的图形：（1）012243=-++z y x 与三个坐标平面所围成；（2）42,42=+-=y x x z 及三坐标平面所围成； （3）22=0,(0)=1z z =a a >,y =x,x +y 及0x =在第一卦限所围成；（4）2222,8z x y z x y =+=--所围. 解：（1）平面012243=-++z y x 与三个坐标平面围成一个在第一卦限的四面体； （2）抛物柱面24z x =-与平面24x y +=及三坐标平面所围成；（3）坐标面=0z 、0x =及平面(0)z =a a >、y=x 和圆柱面22=1x +y 在第一卦限所围成； （4）开口向上的旋转抛物面22z x y =+与开口向下的抛物面228z x y =--所围.作图略.习 题 6—41、画出下列曲线在第一卦限内的图形（1）⎩⎨⎧==21y x ；（2）⎪⎩⎪⎨⎧=---=0422y x y x z ；（3）⎪⎩⎪⎨⎧=+=+222222a z x ay x解：（1）是平面1x =与2y =相交所得的一条直线； （2）上半球面z 与平面0x y -=的交线为14圆弧； （3）圆柱面222x y a +=与222x z a +=的交线.图形略.2、分别求母线平行于x 轴及y 轴而且通过曲线⎪⎩⎪⎨⎧=-+=++0162222222y z x z y x 的柱面方程.解：消去x 坐标得16322=-z y ，为母线平行于x 轴的柱面；消去y 坐标得：162322=+z x ，为母线平行于y 轴的柱面.3、求在yOz 平面内以坐标原点为圆心的单位圆的方程（任写出三种不同形式的方程）.解：⎩⎨⎧==+0122x z y ；⎩⎨⎧==++01222x z y x ； ⎪⎩⎪⎨⎧=+=++1122222z y z y x .4、试求平面20x -=与椭球面222116124x y z ++=相交所得椭圆的半轴与顶点.解：将椭圆方程22211612420x y z x ⎧++=⎪⎨⎪-=⎩化简为：221932y z x ⎧+=⎪⎨⎪=⎩，可知其为平面2=x 上的椭圆，半轴分别为3,3，顶点分别为)3,0,2(),3,0,2(),0,3,2(),0,3,2(--.5 、将下面曲线的一般方程化为参数方程（1）2229x y z y x ⎧++=⎨=⎩； （2）⎩⎨⎧==+++-04)1()1(22z z y x解：（1）原曲线方程即：⎪⎩⎪⎨⎧=+=199222z x xy ，化为⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤≤==tz t t y t x sin 3)20(cos 23cos 23π；（2）)20(0sin 3cos 31πθθθ≤≤⎪⎪⎩⎪⎪⎨⎧==+=z y x .6、求螺旋线⎪⎩⎪⎨⎧===θθθb z a y a x sin cos 在三个坐标面上的投影曲线的直角坐标方程.解：⎩⎨⎧==+0222z a y x ；⎪⎩⎪⎨⎧==0sin x b z a y ；⎪⎩⎪⎨⎧==0cosy b z a x .7、指出下列方程所表示的曲线（1）222253⎧++=⎨=⎩x y z x （2）⎩⎨⎧==++13094222z z y x ；（3）⎩⎨⎧-==+-3254222x z y x ； （4）⎩⎨⎧==+-+408422y x z y ； （5）⎪⎩⎪⎨⎧=-=-0214922x z y . 解：（1）圆； （2）椭圆； （3）双曲线； （4）抛物线； （5）双曲线.8、 求曲线⎩⎨⎧==-+30222z x z y 在xOy 面上的投影曲线方程，并指出原曲线是何种曲线.解：原曲线即：⎩⎨⎧=-=3922z x y ，是位于平面3=z 上的抛物线，在xOy 面上的投影曲线为⎩⎨⎧=-=0922z x y9、 求曲线 ⎪⎩⎪⎨⎧==++211222z z y x 在坐标面上的投影. 解：（1）消去变量z 后得,4322=+y x 在xOy 面上的投影为,04322⎪⎩⎪⎨⎧==+z y x 它是中心在原点，半径为23的圆周.（2）因为曲线在平面21=z 上，所以在xOz 面上的投影为线段.;23||,021≤⎪⎩⎪⎨⎧==x y z （3）同理在yOz 面上的投影也为线段..23||,21≤⎪⎩⎪⎨⎧==y x z10、 求抛物面x z y =+22与平面 02=-+z y x 的交线在三个坐标面上的投影曲线方程.解： 交线方程为⎩⎨⎧=-+=+0222z y x x z y ，（1）消去z 得投影,004522⎩⎨⎧==-++z x xy y x（2）消去y 得投影2252400x z xz x y ⎧+--=⎨=⎩，（3）消去x 得投影22200y z y z x ⎧++-=⎨=⎩.习 题 6—51、写出过点()3,2,10M 且以{}1,2,2=n 为法向量的平面方程. 解：平面的点法式方程为()()()032212=-+-+-z y x .2、求过三点()()()01,0,0,1,0,0,0,1C B A 的平面方程.解：设所求平面方程为0=+++d cz by ax ,将C B A ,,的坐标代入方程，可得d c b a -===，故所求平面方程为1=++z y x .3、求过点()1,0,0且与平面1243=++z y x 平行的平面方程. 解：依题意可取所求平面的法向量为}2,4,3{=n ,从而其方程为()()()0120403=-+-+-z y x 即 2243=++z y x .4、求通过x 轴和点(4, -3, -1)的平面的方程.解：平面通过x 轴, 一方面表明它的法线向量垂直于x 轴, 即A =0; 另一方面表明它必通过原点, 即D =0. 因此可设这平面的方程为By +Cz =0.又因为这平面通过点(4, -3, -1), 所以有-3B -C =0, 或C =-3B . 将其代入所设方程并除以B (B 0), 便得所求的平面方程为y -3z =0.5、求过点)1,1,1(，且垂直于平面7=+-z y x 和051223=+-+z y x 的平面方程.解：},1,1,1{1-=n }12,2,3{2-=n 取法向量},5,15,10{21=⨯=n n n所求平面方程为化简得:.0632=-++z y x6、设平面过原点及点)1,1,1(，且与平面8x y z -+=垂直，求此平面方程.解： 设所求平面为,0=+++D Cz By Ax 由平面过点)1,1,1(知平0,A B C D +++=由平面过原点知0D =，{1,1,1},n ⊥- 0A B C ∴-+=,0A C B ⇒=-=，所求平面方程为0.x z -=7、写出下列平面方程：（1）xOy 平面；（2）过z 轴的平面；（3）平行于zOx 的平面；（4）在x ，y ，z 轴上的截距相等的平面.解：（1）0=z ,（2）0=+by ax （b a ,为不等于零的常数）, （3）c y = (c 为常数), （4） a z y x =++ (0)a ≠.8、 求平行于0566=+++z y x 而与三个坐标面所围成的四面体体积为1的平面方程.解: 设平面为,1=++c z b y a x ,1=V 111,32abc ∴⋅=由所求平面与已知平面平行得,611161c b a ==化简得,61161c b a ==令tc t b t a t c b a 61,1,6161161===⇒===代入体积式 11111666t t t ∴=⋅⋅⋅ 1,6t ⇒=±,1,6,1===∴c b a 或1,6,1,a b c =-=-=-所求平面方程为666x y z ++=或666x y z ++=-.9、分别在下列条件下确定n m l ,,的值：（1）使08)3()1()3(=+-+++-z n y m x l 和016)3()9()3(=--+-++z l y n x m 表示同一平面； （2）使0532=-++z my x 与0266=+--z y lx 表示二平行平面； （3）使013=+-+z y lx 与027=-+z y x 表示二互相垂直的平面.解：（1）欲使所给的二方程表示同一平面，则：168339133-=--=-+=+-l n n m m l 即： ⎪⎩⎪⎨⎧=-+=-+=-+092072032n l m n l m ，解之得 97=l ，913=m ，937=n . （2）欲使所给的二方程表示二平行平面，则：6362-=-=m l ，所以4-=l ，3=m . （3）欲使所给的二方程表示二垂直平面，则：7230l ++=所以： 57l=-.10、求平面011=-+y x 与083=+x 的夹角； 解：设011=-+y x 与083=+x 的夹角为θ，则cos θ ∴ 4πθ=.11、 求点(2,1,1)到平面2240x y z +-+=的距离. 解：利用点到平面的距离公式可得933d ===.习 题 6—61、求下列各直线的方程：（1）通过点)1,0,3(-A 和点)1,5,2(-B 的直线； （2） 过点()1,1,1且与直线433221-=-=-z y x 平行的直线. （3）通过点)3,51(-M 且与z y x ,,三轴分别成︒︒︒120,45,60的直线； （4）一直线过点(2,3,4)-A ，且和y 轴垂直相交，求其方程. （5）通过点)2,0,1(-M 且与两直线11111-+==-z y x 和01111+=--=z y x 垂直的直线； （6）通过点)5,3,2(--M 且与平面02536=+--z y x 垂直的直线.解：（1）所求的直线方程为：015323-=-=++z y x 即：01553-=-=+z y x ，亦即01113-=-=+z y x . （2）依题意，可取L 的方向向量为{}4,3,2=s ，则直线L 的方程为413121-=-=-z y x . （3）所求直线的方向向量为：{}⎭⎬⎫⎩⎨⎧-=︒︒︒21,22,21120cos ,45cos ,60cos ，故直线方程为： 132511--=+=-z y x . （4）因为直线和y 轴垂直相交,所以交点为),0,3,0(-B 取{2,0,4},BA s −−→==所求直线方程.440322-=+=-z y x （5）所求直线的方向向量为：{}{}{}2,1,10,1,11,1,1---=-⨯-，所以，直线方程为：22111+==-z y x . （6）所求直线的方向向量为：{}5,3,6--，所以直线方程为： 235635x y z -++==--.2、求直线1,234x y z x y z ++=-⎧⎨-+=-⎩的点向式方程与参数方程.解 在直线上任取一点),,(000z y x ,取10=x ,063020000⎩⎨⎧=--=++⇒z y z y 解2,000-==z y .所求点的坐标为)2,0,1(-,取直线的方向向量{}{}3,1,21,1,1-⨯=s k j i kji34312111--=-=,所以直线的点向式方程为：,321041-+=--=-z y x 令102,413x y z t --+===--则所求参数方程: .3241⎪⎩⎪⎨⎧--=-=+=tz ty tx3、判别下列各对直线的相互位置，如果是相交的或平行的直线求出它们所在的平面，如果相交时请求出夹角的余弦.（1）⎩⎨⎧=-+=+-0623022y x z y x 与⎩⎨⎧=-+=--+01420112z x z y x ；（2）⎪⎩⎪⎨⎧--=+==212t z t y tx 与142475x y z --+==-. 解：（1）将所给的直线方程化为标准式为：4343223z y x =-=--43227-=--=-z y x 234234-==-- ∴二直线平行.又点)0,43,23(与点（7，2，0）在二直线上，∴向量⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧--0,45,2110,432,237平行于二直线所确定的平面，该平面的法向量为：{}{}19,22,50,45,2114,3,2--=⎭⎬⎫⎩⎨⎧⨯-，从而平面方程为：0)0(19)2(22)7(5=-+---z y x ，即0919225=++-z y x .（2）因为121475-≠≠-，所以两直线不平行，又因为0574121031=--=∆，所以两直线相交，二直线所决定的平面的法向量为{}{}{}1,1,35,7,412,1--=-⨯-，∴二直线所决定的平面的方程为：330x y z -++=.设两直线的夹角为ϕ，则cos ϕ==4、判别下列直线与平面的相关位置： （1）37423z y x =-+=--与3224=--z y x ；（2）723zy x =-=与8723=+-z y x ； （3）⎩⎨⎧=---=-+-01205235z y x z y x 与07734=-+-z y x ；（4）⎪⎩⎪⎨⎧-=+-==4992t z t y t x 与010743=-+-z y x .解（1） 0)2(3)2()7(4)2(=-⨯+-⨯-+⨯-，而017302)4(234≠=-⨯--⨯-⨯，所以，直线与平面平行.（2） 0717)2(233≠⨯+-⨯-⨯,所以，直线与平面相交，且因为772233=--=，∴直线与平面垂直. （3）直线的方向向量为：{}{}{}1,9,51,1,22,3,5=--⨯-， 0179354=⨯+⨯-⨯，所以直线与平面平行或者直线在平面上；取直线上的点)0,5,2(--M ，显然点在)0,5,2(--M 也在平面上（因为4(2)3(5)70⨯--⨯--=），所以，直线在平面上.（4）直线的方向向量为{}9,2,1-， 097)2(413≠⨯+-⨯-⨯∴直线与平面相交但不垂直.5、验证直线l ：21111-=-=-z y x 与平面π：032=--+z y x 相交，并求出它的交点和交角. 解： 032111)1(2≠-=⨯-⨯+-⨯∴直线与平面相交.又直线的参数方程为：⎪⎩⎪⎨⎧+=+=-=t z t y tx 211设交点处对应的参数为0t ，∴03)21()1()(2000=-+-++-⨯t t t ∴10-=t ，从而交点为（1，0，-1）. 又设直线l 与平面π的交角为θ，则：21662111)1(2sin =⨯⨯-⨯+-⨯=θ，∴6πθ=.6、确定m l ,的值，使： （1）直线13241zy x =+=-与平面0153=+-+z y lx 平行； （2）直线⎪⎩⎪⎨⎧-=--=+=135422t z t y t x 与平面076=-++z my lx 垂直.解：（1）欲使所给直线与平面平行，则须：015334=⨯-⨯+l 即1l =-. （2）欲使所给直线与平面垂直，则须：3642=-=m l ，所以：8,4-==m l .7、求下列各平面的方程： （１）通过点)1,0,2(-p ，且又通过直线32121-=-=+z y x 的平面； （２）通过直线115312-+=-+=-z y x 且与直线⎩⎨⎧=--+=---052032z y x z y x 平行的平面； （３）通过直线223221-=-+=-z y x 且与平面0523=--+z y x 垂直的平面；（4）. 求过点(2,1,0)M 与直线2335x t y t z t =-⎧⎪=+⎨⎪=⎩垂直的平面方程.解：（１）因为所求的平面过点)1,0,2(-p 和)2,0,1(-'p ，且它平行于向量{}3,1,2-，所以要求的平面方程为：03331212=--+-z y x , 即015=-++z y x .（２）已知直线的方向向量为{}{}{}2,1,11,2,13,1,5--⨯-=，∴平面方程为：2311510315x y z -++--=,即3250x y z +--= （３）所求平面的法向量为{}{}{}13,8,11,2,32,3,2-=-⨯-，∴平面的方程为：0)2(13)2(8)1(=--+--z y x ，即09138=+--z y x .（4）.所求平面的法向量为{}2,3,1，则平面的方程为：2(2)3(1)(0)0x y z -+-+-=, 即 2370x y z ++-=.8、求点(4,1,2)M 在平面1x y z ++=上的投影.解： 过点(4,1,2)M 作已知平面的垂线，垂线的方向向量就是已知平面的法向量(1,1,1)，所以垂线方程为412111x y z ---==，此垂线与已知平面的交点即为所求投影.为了求投影，将垂线方程化为参数方程412x t y t z t =+⎧⎪=+⎨⎪=+⎩，代入平面方程求得2t =-，故投影为(2,1,0)-. 9、求点)1,3,2(-p 到直线⎩⎨⎧=++-=++-0172230322z y x z y x 的距离.解：直线的标准方程为：2251211-+==-z y x 所以p 到直线的距离 1534532025)2(1212392292421243222222===-++-+--+-=d .10、设0M 是直线L 外一点，M 是直线L 上一点，且直线的方向向量为s ，试证：点0M 到直线L 的距离为d =.证：设0M M 与L 的夹角为θ，一方面由于0sin d M M θ=；另一方面，00sin M M s M M s θ⨯=，所以d =.11、求通过平面0134=-+-z y x 和025=+-+z y x 的交线且满足下列条件之一的平面： （1）通过原点； （2）与y 轴平行；（3）与平面0352=-+-z y x 垂直. 解： （1）设所求的平面为：0)25()134(=+-++-+-z y x z y x λ 欲使平面通过原点，则须：021=+-λ，即21=λ，故所求的平面方程为 0)25()134(2=+-++-+-z y x z y x 即：0539=++z y x .（2）同（1）中所设，可求出51=λ.故所求的平面方程为 0)25()134(5=+-++-+-z y x z y x 即：031421=-+z x .（3）如（1）所设，欲使所求平面与平面0352=-+-z y x 垂直，则须：0)3(5)51()4(2=-++--+λλλ从而3=λ，所以所求平面方程为05147=++y x .12、求直线⎩⎨⎧=++-=--+0101z y x z y x 在平面0=++z y x 上的投影直线的方程．解：应用平面束的方法．设过直线⎩⎨⎧=++-=--+0101z y x z y x 的平面束方程为0)1()1(=++-+--+z y x z y x λ即01)1()1()1(=-++-+-++λλλλz y x这平面与已知平面0=++z y x 垂直的条件是01)1(1)1(1)1(=⋅+-+⋅-+⋅+λλλ,解之得1-=λ代入平面束方程中得投影平面方程为10y z --=，所以投影直线为⎩⎨⎧=++=--001z y x z y .13、请用异于本章第五节例7的方法来推导点到平面的距离公式.证：设),,(0000z y x P 是平面π：0+++=Ax By Cz D 外的一点，下面我们来求点0P 到平面π的距离. 过0P 作平面π的垂线L ：000x x y y z z A B C---==，设L 与平面π的交点为(,,)P x y z ，则P 与0P 之间的距离即为所求.因为点(,,)P x y z 在L 上，所以000x x Aty y Bt z z Ct-=-=-=⎧⎪⎨⎪⎩，而(,,)P x y z 在平面π上，则000()()()0A x At B y Bt C z Ct D ++++++=000222Ax By Cz A B t DC ⇒=-+++++，故000222Ax By Cz Dd t A B C+++===++=.习 题 6—7飞机的速度：假设空气以每小时32公里的速度沿平行y 轴正向的方向流动，一架飞机在xoy 平面沿与x 轴正向成π6的方向飞行，若飞机相对于空气的速度是每小时840公里，问飞机相对于地面的速度是多少？解：如下图所示，设OA 为飞机相对于空气的速度，AB 为空气的流动速度，那么OB 就是飞机相对于地面的速度.840cos 840sin 4203420,3266OA i j i j AB j ππ=⋅+⋅=+=所以, 24203452,(420856.45OB i j OB =+=≈千米／小时.复习题A一 、判断正误:1、 若c b b a ⋅=⋅且≠0b ，则c a =； ( ⨯ )解析 c b b a ⋅-⋅=)(c a b -⋅=0时，不能判定=b 0或c a =．例如i a =，j b =，k c =，有⋅=⋅=0a b b c ，但c a ≠．2、 若c b b a ⨯=⨯且≠0b ，则c a =； ( ⨯ )解析 此结论不一定成立．例如i a =，j b =，)(j i c +-=，则k j i b a =⨯=⨯，k j i j c b =+-⨯=⨯)]([，c b b a ⨯=⨯，但c a ≠．3 、若0=⋅c a ，则=0a 或=0c ； ( ⨯ ) 解析 两个相互垂直的非零向量点积也为零．4、 a b b a ⨯-=⨯． ( √ ) 解析 这是叉积运算规律中的反交换律．二、选择题:1 、 当a 与b 满足（ D ）时，有b a b a +=+；(A)⊥a b ； (B)λ=a b (λ为常数)； (C)a ∥b ； (D)⋅=a b a b ．解析 只有当a 与b 方向相同时，才有a +b =a +b ．(A)中a ，b 夹角不为0，(B)，(C)中a ，b 方向可以相同，也可以相反．2、下列平面方程中，方程( C )过y 轴；图6-1 空所流动与飞机飞行速度的关系(A) 1=++z y x ； (B) 0=++z y x ； (C) 0=+z x ； (D) 1=+z x ． 解析 平面方程0=+++D Cz By Ax 若过y 轴，则0==D B ，故选C ．3 、在空间直角坐标系中，方程2221y x z --=所表示的曲面是( B )；(A) 椭球面； (B) 椭圆抛物面； (C) 椭圆柱面； (D) 单叶双曲面．解析 对于曲面2221y x z --=，垂直于z 轴的平面截曲面是椭圆，垂直于x 轴或y 轴的平面截曲面是开口向下的抛物线，根据曲面的截痕法，可以判断曲面是椭圆抛物面．4、空间曲线⎩⎨⎧=-+=5,222z y x z 在xOy 面上的投影方程为( C )；(A)722=+y x ； (B)⎩⎨⎧==+5722z y x ； (C) ⎩⎨⎧==+0722z y x ；(D)⎩⎨⎧=-+=0222z y x z解析 曲线⎩⎨⎧==+5722z y x 与xOy 平面平行，在xOy 面上的投影方程为⎩⎨⎧==+0722z y x ．5 、直线11121-+==-z y x 与平面1=+-z y x 的位置关系是( B )． (A) 垂直； (B) 平行； (C) 夹角为π4； (D) 夹角为π4-．解析 直线的方向向量s ={2，1，-1}，平面的法向量n ={1，-1，1}，n s ⋅=2-1-1=0，所以，s ⊥n ，直线与平面平行．三、填空题:1、若2=b a ，π()2=a,b ，则=⨯b a 2 ，=⋅b a 0 ； 解 =⨯b a b a sin()a,b π22=2，=⋅b a b a cos()a,b π22=0．2、与平面062=-+-z y x 垂直的单位向量为 }2,1,1{66-±； 解 平面的法向量 n ={1，-1，2}与平面垂直，其单位向量为0n =411++=6，所以，与平面垂直的单位向量为}2,1,1{66-±．3、过点)2,1,3(--和)5,0,3(且平行于x 轴的平面方程为 057=-+z y ；解 已知平面平行于x 轴，则平面方程可设为 0=++D Cz By ，将点 (-3，1，-2)和(3，0，5)代入方程，有{20,50,B C D C D -+=+= ⇒ 7,51,5B D C D ⎧=-⎪⎨⎪=-⎩得 05157=+--D Dz Dy ，即 057=-+z y ．4、过原点且垂直于平面022=+-z y 的直线为z yx -==20； 解 直线与平面垂直，则与平面的法向量 n ={0，2，-1}平行，取直线方向向量s =n ={0，2，-1}，由于直线过原点，所以直线方程为z yx -==20 ．5、曲线⎩⎨⎧=+=1,222z y x z 在xOy 平面上的投影曲线方程为 ⎩⎨⎧==+.0,1222z y x解: 投影柱面为 1222=+y x ，故 ⎩⎨⎧==+0,1222z y x 为空间曲线在xOy 平面上的投影曲线方程．四、解答题:1、 已知}1,2,1{-=a ，}2,1,1{=b ，计算(a) b a ⨯； (b) ()()-⋅+2a b a b ； (c) 2b a -；解: (a) b a ⨯=211121-kj i 1,3}5,{--=. (b) {2,4,2}{1,1,2}{1,5,0}2a b -=--=-，1,3}{2,{1,1,2}2,1}{1,-=+-=+b a ， 所以()()-⋅+2a b a b 7}3,1,2{}0,5,1{=-⋅-=．(c) 1}3,{0,{1,1,2}2,1}{1,--=--=-b a ，所以2b a -10)19(2=+=．2、已知向量21P P 的始点为)5,2,2(1-P ，终点为)7,4,1(2-P ，试求：(1)向量21P P 的坐标表示； (2)向量21P P 的模；(3)向量21P P 的方向余弦； (4)与向量21P P 方向一致的单位向量．解: (1) }2,6,3{}57),2(4,21{21-=-----=P P ；74926)3(222==++-=；(3) 21P P 在z y x ,,三个坐标轴上的方向余弦分别为362cos ,cos ,cos 777αβγ=-==；(4)k j i k j i 7276737263)(21++-=++-==P P．3、设向量{}1,1,1=-a ，{}1,1,1=-b ，求与a 和b 都垂直的单位向量.解： 令{}1110,2,2111=⨯=-=-i j kc a b，01⎧==⎨⎩c c c ，故与a 、b都垂直的单位向量为0⎧±=±⎨⎩c .4、向量d垂直于向量]1,3,2[-=a和]3,2,1[-=b ，且与]1,1,2[-=c的数量积为6-，求向量d解： d垂直于a与b ，故d平行于b a⨯，存在数λ使()b a d⨯=λ⨯-=]1,3,2[λ]3,2,1[-]7,7,7[λλλ--=因6-=⋅c d，故6)7(1)7()1(72-=-⨯+-⨯-+⨯λλλ， 73-=λ]3,3,3[-=∴d.5、求满足下列条件的平面方程：(1)过三点)2,1,0(1P ，)1,2,1(2P 和)4,0,3(3P；(2)过x 轴且与平面025=++z y x 的夹角为π3． 解 (1)解1： 用三点式．所求平面的方程为0241003211201210=---------z y x ，即01345=+--z y x ． 解2：}1,1,1{-=}2,1,3{-=，由题设知，所求平面的法向量为k j i kj in 452131113121--=--=⨯=P P P P ， 又因为平面过点)2,1,0(1P ，所以所求平面方程为0)2(4)1(5)0(=-----z y x ，即01345=+--z y x ．解3： 用下面的方法求出所求平面的法向量},,{C B A =n ，再根据点法式公式写出平面方程也可． 因为3121,P P P P ⊥⊥n n ，所以{0,320,A B C A B C +-=-+=解得A C A B 4,5-=-=，于是所求平面方程为0)2(4)1(5)0(=-----z A y A x A ，即 01345=+--z y x ．（2）因所求平面过x 轴，故该平面的法向量},,{C B A =n 垂直于x 轴，n 在x 轴上的投影0=A ，又平面过原点，所以可设它的方程为0=+Cz By ，由题设可知0≠B （因为0=B 时，所求平面方程为0=Cz 又0≠C ，即0=z ．这样它与已知平面025=++z y x 所夹锐角的余弦为π1cos 32=≠=，所以0≠B ），令C B C'=，则有0='+z C y ，由题设得 22222212)5(10121503cos ++'++⨯'+⨯+⨯=πC C ， 解得3='C 或13C '=-，于是所求平面方程为03=+z y 或03=-z y ．6、 一平面过直线⎩⎨⎧=+-=++04,05z x z y x 且与平面01284=+--z y x 垂直，求该平面方程；解法1： 直线⎩⎨⎧=+-=++04,05z x z y x 在平面上，令x =0，得 54-=y ，z =4，则（0，-54，4）为平面上的点．设所求平面的法向量为n =},,{C B A ，相交得到直线的两平面方程的法向量分别为 1n ={1，5，1}，2n ={1，0，-1}，则直线的方向向量s =1n ⨯2n =101151-kj i ={-5，2，-5}，由于所求平面经过直线，故平面的法向量与直线的方向向量垂直，即⋅n s ={-5，2，-5}•},,{C B A =C B A 525-+-=0，因为所求平面与平面01284=+--z y x 垂直，则}8,4,1{},,{--⋅C B A =C B A 84--=0，解方程组{5250,480,A B C A B C -+=--= ⇒ 2,5,2A CBC =-⎧⎪⎨=-⎪⎩ 所求平面方程为 0)4()54(25)0(2=-++---z C y C x C ，即012254=+-+z y x ．解法2： 用平面束（略）7、求既与两平面1:43x z π-=和2:251x y z π--=的交线平行，又过点(3,2,5)-的直线方程.解法1：{}11,0,4=-n ，{}22,1,5=--n ，{}124,3,1s =⨯=---n n ，从而根据点向式方程，所求直线方程为325431x y z +--==---，即325431x y z +--==. 解法2：设{},,s m n p =，因为1⊥s n ，所以40m p -=；又2⊥s n ，则250m n p --=，可解4,3m p n p ==，从而0p ≠．根据点向式方程，所求直线方程为32543x y z p p p +--==，即325431x y z +--==. 解法3：设平面3π过点(3,2,5)-，且平行于平面1π，则{}311,0,4==-n n 为3π的法向量，从而3π的方程为1(3)0(2)4(5)0x y z ⋅++⋅--⋅-=，即4230x z -+=．同理，过已知点且平行于平面2π的平面4π的方程为25330x y z --+=．故所求直线的方程为423025330x z x y z -+=⎧⎨--+=⎩．8、 一直线通过点)1,2,1(A ，且垂直于直线11231:+==-z y x L ，又和直线z y x ==相交，求该直线方程；解： 设所求直线的方向向量为{,,}m n p =s ，因垂直于L ，所以320m n p ++=；又因为直线过点)1,2,1(A ，则所求直线方程为 p z n y m x 121-=-=-，联立121,①,②320,③x y z m n p x y z m n p ---⎧==⎪⎨==⎪++=⎩由①，令λ=-=-=-p z n y m x 121，则有⎪⎩⎪⎨⎧+=+=+=,1,2,1p z n y m x λλλ代入方程②有{12,11,m n m p λλλλ+=++=+ 可得p m =，代入③解得p n 2-=， 因此，所求直线方程为112211-=--=-z y x ．9、 指出下列方程表示的图形名称：(a) 14222=++z y x ；(b) z y x 222=+；(c) 22y x z +=；(d) 022=-y x ；(e) 122=-y x ； (f) ⎩⎨⎧=+=222z y x z ．解： (a) 绕y 轴旋转的旋转椭球面．(b) 绕z 轴旋转的旋转抛物面． (c) 绕z 轴旋转的锥面． (d) 母线平行于z 轴的两垂直平面：y x =，y x -=． (e) 母线平行于z 轴的双曲柱面． (f) 旋转抛物面被平行于XOY 面的平面所截得到的圆，半径为2，圆心在（0，0，2）处．10、求曲面22z x y =+与222()z x y =-+所围立体在xOy 平面上的投影并作其图形．解： 将所给曲面方程联立消去z ，就得到两曲面交线C 的投影柱面的方程122=+y x ，所以柱面与xOy 平面的交线⎩⎨⎧==+'01:22z y x C 所围成的区域221+≤x y 即为曲面22z x y =+与222()z x y =-+所围立体在xOy 平面上的投影(图略)．复习题B1、设4=a ，3=b ，()6π=a,b ，求以2+a b 和3-a b 为邻边的平行四边形的面积.解：(2)(3)326A =+⨯-=⨯-⨯+⨯-⨯a b a b a a a b b a b b325=-⨯-⨯=-⨯a b a b a b 15sin()543302=⋅=⨯⨯⨯=a b a,b .2、设(3)(75)+⊥-a b a b ，(4)(72)-⊥-a b a b ，求()a,b . 解： 由已知可得：(3)(75)0+⋅-=a b a b ，(4)(72)0-⋅-=a b a b 即 22715160-+⋅=a b a b ，2278300+-⋅=a b a b ．这可看成是含三个变量a 、b 及⋅a b 的方程组，可将a 、b 都用⋅a b 表示，即==a b 1cos()22⋅⋅===⋅a b a b a,b a b a b ，()3π=a,b .3、求与}3,2,1{-=a 共线，且28=⋅b a 的向量b ．解 由于b 与a 共线，所以可设}3,2,{λλλλ-==a b ，由28=⋅b a ，得28}3,2,{}3,2,1{=-⋅-λλλ， 即2894=++λλλ，所以2=λ，从而}6,4,2{-=b ．4、 已知}0,1,1{},2,0,1{=-=b a ，求c ，使b c a c ⊥⊥,且6=c ．解法1: 待定系数法．设},,{z y x =c ，则由题设知0,0=⋅=⋅b c a c 及6=c ，所以有①20②③6x z ⎧-=⎪=由①得2xz = ④，由②得x y -= ⑤，将④和⑤代入③得62)(222=⎪⎭⎫⎝⎛+-+x x x ，解得2,4,4±==±=z y x ，于是 }2,4,4{-=c 或}2,4,4{--=c ．解法2: 利用向量的垂直平行条件，因为b c a c ⊥⊥,，所以c ∥b a ⨯．设λ是不为零的常数，则k j i k j i b a c λλλλλ+-=-=⨯=22011201)(，因为6=c ，所以6]1)2(2[2222=+-+λ，解得2±=λ，所以}2,4,4{-=c 或{4,4,2}=--c ．解法3: 先求出与向量b a ⨯方向一致的单位向量，然后乘以6±．k j i kji b a +-=-=⨯22011201，31)2(2222=+-+=⨯b a ，故与b a ⨯方向一致的单位向量为}1,2,2{31-．于是}1,2,2{36-±=c ，即}2,4,4{-=c 或}2,4,4{--=c ．5、求曲线222x y R x y z ⎧+=⎨++=⎩的参数式方程.解： 曲线参数式方程是把曲线上任一点(,,)P x y z 的坐标,,x y z 都用同一变量即参数表示出来，故可令cos ,sin x R t y R t ==，则(cos sin )z R t t =-+．6、求曲线22:2z L x y x⎧⎪=⎨+=⎪⎩xOy 面上及在zOx 面上的投影曲线的方程．解： 求L 在xOy 面上的投影的方程，即由L 的两个方程将z 消去，即得L 关于xOy 面的投影柱面的方程222x y x +=则L 在xOy 面上的投影曲线的方程为2220x y xz ⎧+=⎨=⎩． 同理求L 在zOx 面上的投影的方程，即由L 的两个方程消去y ，得L 关于zOx 面的投影柱面的方程z =L 在zOx面上的投影曲线方程为0z y ⎧=⎪⎨=⎪⎩．7、已知平面π过点0(1,0,1)M -和直线1211:201x y z L ---==，求平面π的方程． 解法1： 设平面π的法向量为n ，直线1L 的方向向量1(2,0,1)=s ，由题意可知1⊥n s ，(2,1,1)M 是直线1L 上的一点,则0(1,1,2)M M =在π上，所以0MM ⊥n ,故可取10MM =⨯n s (1,3,2)=--．则所求平面的点法式方程为1(1)3(0)2(1)0x y z ⋅-+⋅--⋅+=，即3230x y z +--=为所求平面方程．解法2： 设平面π的一般方程为0Ax By Cz D +++=，由题意可知，π过点0(1,0,1)M -，故有0A C D -+=, （1）在直线1L 上任取两点12(2,1,1),(4,1,2)M M ，将其代入平面方程，得20A B C D +++=, （2）420A B C D +++=, （3）由式（1）、（2）、（3）解得3,2,3B A C A D A ==-=-,故平面π的方程为3230x y z +--=.解法3： 设(),,M x y z 为π上任一点．由题意知向量0M M 、01M M 和1s 共面，其中()12,1,1M 为直线1L 上的点，1(2,0,1)=s 为直线1L 的方向向量．因此0011()0M M M M ⨯⋅=s ，故平面π的方程为1012110110201x y z --+--+=，即3230x y z +--=为所求平面方程．8、求一过原点的平面π，使它与平面0:π4830x y z -+-=成4π角，且垂直于平面1:π730x z ++=． 解： 由题意可设π的方程为0Ax By Cz ++=，其法向量为(,,)A B C =n ，平面0π的法向量为0(1,4,8)=-n ，平面1π的法向量为1(7,0,1)=n ，由题意得00||cos 4||||π⋅=⋅n n n n ，即=（1） 由10⋅=n n ，得70A C +=，将7C A =-代入（12=,解得20,B A =或10049B A =-，则所求平面π的方程为2070x y z +-= 或 491003430x y z --=．9、求过直线1L ：0230x y z x y z ++=⎧⎨-+=⎩且平行于直线2L ：23x y z ==的平面π的方程．解法1： 直线1L 的方向向量为1=s 111(4,1,3)213==---i j k，直线2L 的对称式方程为632x y z==，方向向量为2(6,3,2)=s ，依题意所求平面π的法向量1⊥n s 且2⊥n s ，故可取12=⨯n s s ，则413(7,26,18)632=--=-i j kn ，又因为1L 过原点，且1L 在平面π上，从而π也过原点，故所求平面π的方程为726180x y z -+=．解法2： 设所求平面π为 (23)0x y z x y z λ+++-+=，即(12)(1)(13)0x y z λλλ++-++=， 其法向量为(12,1,13)λλλ=+-+n ，由题意知2⊥n s ，故26(12)3(1)2(13)0λλλ⋅=++-++=n s ，得1115λ=-，则所求平面π的方程为726180x y z -+=．另外，容易验证230x y z -+=不是所求的平面方程．10、求过直线L ：⎩⎨⎧=+-+=+-+0185017228z y x z y x 且与球面1222=++z y x 相切的平面方程解： 设所求平面为 ()018517228=+-+++-+z y x z y x λ，即 (15)(288)(2)170x y z λλλλ+++-+++=，由题意：球心)0,0,0(到它的距离为1，即1)2()828()51(17222=--+++++λλλλ解得：89250-=λ 或 2-=λ 所求平面为：42124164387=--z y x 或 543=-y x11、求直线L ：11111--==-z y x 在平面π：012=-+-z y x 上投影直线0L 的方程，并求直线0L 绕y 轴旋转一周而成的曲面方程.解： 将直线L ：11111--==-z y x 化为一般方程 ⎩⎨⎧=-+=--0101y z y x ，设过直线L 且与平面π垂直的平面方程为()011=-++--y z y x λ，则有02)1(1=+--λλ，即2λ=-，平面方程为0123=+--z y x ，这样直线0L 的方程⎩⎨⎧=-+-=+--0120123z y x z y x 把此方程化为：⎩⎨⎧--==)1(221y z yx ，因此直线0L 绕y 轴旋转一周而成的曲面方程为：22221(2)(1)2x z y y ⎛⎫+=+-- ⎪⎝⎭即 0124174222=-++-y z y x .12、求过点)1,0,3(-A 且平行于平面1π：3450x y z --+=，又与直线1:2x L =1111y z -+=-相交的直线L 的方程．解法1： 用点向式方程.因为直线L 平行于平面1π，故直线L 的方向向量},,{p n m =s 垂直于平面1π的法向量}1,4,3{--=n ，从而得043=--p n m ①，又直线1L 的方向向量为}1,1,2{-=s ，)1,1,0(-B 是直线1L 上一点，)1,0,3(-A 是直线L 上一点，根据题设：直线L 与直线1L 相交，所以1s,s 及AB 共面，因此1()2110312m n pAB ⨯⋅=-=-s s ，即0=-+-p n m ②，将①和②联立解得p n p m 4,5-=-=，由此得145p n m =-=-，于是所求直线方程为11453-=-=-+z y x ．。

第六章 方差分析一、单项选择题1、方差分析是对多个正态总体（ ）这一假设进行检验。

A 、方差相等B 、方差相异C 、均值相等D 、均值不等2、方差分析使用的统计量F （ ）A 、是正态分布B 、是正偏态的C 、是负偏态的D 、取值小于零 3、设单因素方差分析中误差项离差平方和为125.00，水平项离差平方和为375，那么总离差平方和为（ ）A 、250B 、125.00C 、375.00D 、500 4、因素A 共4个水平，每个水平下重复5次实验，数据的平方和为1250，数据总和为150，A 、125 B 、-125 C 、无法计算 D 、14005、在单因素方差分析中，已知总离差平方和的自由度为24，水平项离差平方和的自由度为7，那么误差项离差平方和的自由度为（ ）A 、17B 、24C 、7D 、31 6、在一个双因素方差分析中，F A =2.300,F B =4.55相应的P － value 依次为0.11和0.0018，那么结论是（ ）A 、A 的作用显著，B 的作用不显著 B 、A 的作用不显著，B 的作用显著C 、A 的作用不显著，B 的作用不显著D 、A 的作用显著，B 的作用显著7、已知,8,6,30,560,700,1440======B A T f f f SSB SSA SST 那么F A =( )A 、1440B 、700C 、116.67D 、10.37 8、如果,16,25.2,5,00.8,4,25.12======E B A f MSE f MSB f MSA 那么SST ( )A 、无法计算B 、22.5C 、25D 、125二、多项选择题1、方差分析假定的内容有（ ）A 、数据来自正态总体B 、数据来自二项总体C 、各总体相互独立D 、各总体不相关E 、各总体方差相等2、一个单因素方差分析中，因素的水平为5，每个水平下的样本容量是6，SST =120,SSA=75那么以下正确的是（ ） A 、n=30 B 、df A = 4 C 、MSE=1.8 D 、df T =29 E 、F=10.423、在一个单因素方差分析问题中，因素的水平为4，每个水平下的样本容量是5,那么下列说法正确的是（ ）A 、检验的原假设为43210:μμμμ===HB 、检验的临界值为)5,4(αFC 、检验的原假设为543210:μμμμμ====HD 、检验的临界值为)16,3(αFE 、检验的统计量为163SSE SSA F =4、一个因素A 有6水平，因素B 有4水平的双因素方差分析中，以下正确的有（ ）A 、数据共24个B 、误差平方和的自由度为15C 、SSA 的自由度为6D 、SST 的自由度为3E 、SST=SSA+SSB+SSE5、一个因素A 有7水平，因素B 有8水平的双因素方差分析中，SST=225,SSA=78,SSB=140以下正确的有（ ）A 、SSE=2B 、SSE=7C 、78=A FD 、MSE=0.1667E 、因素A 的作用显著三、填空题1、方差分析的英文缩写为：_____________________________________________________。

第六章完全竞争市场一、单项选择题1、在完全竞争市场上，厂商实现短期均衡的条件是（）A、P＝ARB、P＝MRC、P＝SMCD、P＝SAC2、在微观经济学中，对（）行业的长期均衡状态的分析通常被用来作为对消费者统治说法的一种证明。

A、完全垄断B、完全竞争C、垄断竞争D、寡头竞争3、短期内，一个完全竞争厂商所得到的价格若低于以下哪种成本就会停止营业（）。

A、平均总成本B、平均可变成本C、短期边际成本D、平均固定成本4、根据完全竞争市场的条件，下列（）行业最接近完全竞争行业。

A、自行车行业B、服装行业C、玉米行业D、烟草行业5、在一个完全竞争的市场上，厂商所面临的需求曲线与其长期平均成本曲线相切是（）。

A、厂商在长期内要得到超额利润的条件B、该行业内厂商的数目不再变化的条件C、厂商在长期内要得到最大利润的条件D、以上说法中B和C都是正确的6、在短期内，（）是完全竞争厂商的关闭点。

A、SAC曲线与SMC曲线的交点B、MR曲线与SMC曲线的交点C、AVC曲线与SMC曲线的交点D、AFC曲线与SMC曲线的交点7、假定一个完全竞争行业内某厂商在目前产量水平上的边际成本、平均总成本和平均收均等于1美元，则这家厂商（）。

A、肯定只得到正常利润B、肯定没得到最大利润C、是否得到了最大利润还不能确定D、肯定得到了最少利润8、在短期内，（）是完全竞争厂商的收支相抵点。

A、SAC曲线与SMC曲线的交点B、MR曲线与SMC曲线的交点C、AVC曲线与SMC曲线的交点D、MR曲线与SAC曲线的切点9、在完全竞争的条件下，如果厂商把产量调整到平均总成本曲线最低点所对应的水平（）。

A、他将获得最大利润B、他不能获得最大利润C、他是否获得最大利润仍无法确定D、他一定亏损10、如果某厂商的边际收益大于边际成本，那么为了取得最大利润（）。

A、他在完全竞争的条件下应该增加产量，在不完全竞争条件下则不一定B、他在不完全竞争条件下应该增加产量，在完全竞争条件则不一定C、任何条件下都应该增加产量D、任何条件下都应该减少产量11、在MR=MC的均衡产量上，企业（）。

第六章维生素、辅酶和激素一、是非题1.胡萝卜中含有的β-胡萝卜素是维生素A的前体。

2.维生素A预防夜盲症是因为它可转变为视黄醛。

3.泛酸中含有β-丙氨酸。

4.维生素E又称α-生育酚，所以它与人的生育能力有关。

5.维生素K的存在是维持人和动物凝血因子正常功能的必要条件。

6.TPP是许多种脱氢酶如琥珀酸脱氢酶、谷氨酸脱氢酶等的辅酶。

7.作为氢的载体NAD+可以接受两个氢质子和两个电子。

8.在传递氢的过程中，NAD+和NADP+有严格的立体专一性。

9.NAD+和NADP+脱下的氢都是通过呼吸链交给分子氧生成水。

10.尼克酸（烟酸）合成的主要原料是含组氨酸丰富的蛋白质。

11.维生素和激素对人和动物的作用都是一样的，因为它们在体内的含量都非常少。

12.严格地说硫辛酸不属于维生素，因为它可以在动物体内合成。

13.维生素C（即抗坏血酸）可以在动物体内合成，所以不能算做维生素。

14.缺乏维生素C会引起坏血病，维生素C可提高机体的抗病能力和解毒作用。

15.GPT在血液中的含量是检查肝功能的指标之一，GPT实际上是一种转氨酶。

16.甾醇类激素作用于靶细胞后必定会有某种蛋白质的量在细胞内升高。

17.高等动物体内的激素只能由内分泌腺体细胞生成和分泌。

18.催产素和加压素的空间结构是其行使功能的必要条件。

19.下丘脑有调节垂体前叶激素分泌的功能，它本身分泌的激素主要是促进或抑制其它激素的分泌。

20.肾上腺分泌的所有激素以及性激素都是甾醇类物质。

21.胰岛素是由β-胰岛的细胞分泌的胰岛素原转化来的。

22.对于富含葡萄糖的细胞来说，胰岛素的分泌可以看成是合成代谢的信号。

23.甲状腺肿大是由于缺少碘，生物体补偿发育的结果。

24.胰岛素受体含有酪氨酸激酶活性，与胰岛素结合后自动使受体磷酸化。

25.cAMP可以作为所有激素的第二信使。

二、填空题1.胡萝卜素有α，β和γ三种，其中转变为维生素A的效率最高。

2.维生素A的化学名称是，它的化学组成是聚合物。

第六章卤代烃1.回答下列问题(1).在CH3CH2Cl(I),CH2═CHCl(II),CH≡CCl(III),C6H5Cl(IV)四种一氯代烃中，按C-X键键长次序排列，并讨论其理由。

解: IV< II < III <I(2).将四种化合物(A) CH3CH2CH2F，(B) CH3CH2CH2I ，(C) CH3CH2CH2Br ，(D) CH3CH2CH2Cl的沸点从最高到低排列，并讨论其理由。

解: B> C> D> A(3).四种化合物(A) CH3CHClCH2OH，(B) CH3CHNH2CH2Br ，(C) HC≡CCH2Cl，(D) CH3CONHCH2CH2Cl 中，哪些能生成稳定的格氏试剂？为什么？解: D(4).比较(A) CH3CH2CH2CH2Cl，(B) (CH3)2CHCH2Cl，(C) CH3CH2CH(Cl)CH3，(D) (CH3)3CCl四个氯代烃，它们发生S N2反应情况如何。

解: A> B> C> D(5).将①苄溴，②溴苯，③1–苯基–1–溴乙烷，④1–溴–2–苯基乙烷四个化合物按 S N1 反应的反应活性顺序排列，并讨论其理由。

解: ③>①>④>②(6).不活泼的乙烯型卤代烃能否生成格氏试剂？为什么？解:由于卤原子与双键间的 p-π共轭效应,使C-X键之间的键能增加,难以断裂。

(7).化合物：(A)正溴戊烷，(B)叔溴戊烷，(C)新戊基溴，(D)异戊基溴分别与水反应生成相应的醇，讨论它们的反应速率的差异？解: A> D> C> B(8).用极性溶剂代替质子溶剂对(A) S N1，(B) S N2，(C) 烯的亲电加成， (D) 醇的失水反应有何影响?解: 极性溶剂有利于S N1反应和烯的亲电加成反应的进行,不利于S N2反应和醇的失水反应的发生。

(9). 2–氯环己醇的反式异构体可以跟碱反应转化成环氧化物, 但顺式异构体却不能, 为什么?解: 2–氯环己醇的反式异构体跟碱反应时,进行反式消除,热力学能量低,反应速率快, 顺式异构体则不能。

第六章相平衡练习题一、是非题，下列各题的叙述是否正确，对的画√错的画×1、纯物质两相达平衡时，两相的吉布斯函数值一定相等。

（）2、理想液态混合物与其蒸气达成气、液两相平衡时，气相总压力p与液相组成x呈线性关系。

（）B3、已知Cu-Ni 可以形成完全互溶固熔体，其相图如右图，理论上，通过精炼可以得到两个纯组分。

（）4、二组分的理想液态混合物的蒸气总压力介于二纯组分的蒸气压之间。

( )5、在一定温度下，稀溶液中挥发性溶质与其蒸气达到平衡时气相中的分压与该组分在液相中的组成成正比。

（）6、恒沸混合物的恒沸温度与恒沸组成不随压力而改变。

( )7、在一个给定的体系中，特种数可以分析问题的角度不同而不同，但独立组分数是一个确定的数。

（）8、自由度就是可以独立变化的变量。

（）9、单组分体系的相图中两相平衡线都可以用克拉贝龙方程定量描述。

（）10、在相图中总可以利用杠杆规则计算两相平衡时两相的相对量。

( )二、选择题1、在p下，用水蒸气蒸馏法提纯某不溶于水的有机物时，系统的沸点：（）。

（1）必低于 K；（2）必高于 K；（3）取决于水与有机物的相对数量；（4）取决于有机物相对分子质量的大小。

2、已知A(l)、B(l)可以组成其t-x(y)图具有最大恒沸点的液态完全互溶的系统，则将某一组成的系统精馏可以得到：( )。

（1）两个纯组分；（2）两个恒沸混合物；（3）一个纯组分和一个恒沸混合物。

3、已知A和B 可构成固溶体，在组分A 中，若加入组分B 可使固溶体的熔点提高，则组B 在此固溶体中的含量必________组分B 在组分液相中的含量。

（1）大于；（2）小于；（3）等于；（4）不能确定。

4、硫酸与水可形成H2SO4H2O(s)，H2SO42H2O(s)，H2SO44H2O(s)三种水合物，问在101325 Pa的压力下，能与硫酸水溶液及冰平衡共存的硫酸水合物最多可有多少种？( )(1) 3种； (2) 2种； (3) 1种； (4) 不可能有硫酸水合物与之平衡共存5、对恒沸混合物的描写，下列各种叙述中哪一种是不正确的？(1) 与化合物一样，具有确定的组成；(2) 恒沸混合物的组成随压力的改变而改变；(3) 平衡时，气相和液相的组成相同；(4) 其沸点随外压的改变而改变。