当前位置：文档之家 › 固体物理(第11课)金属电子论和索末菲模型

固体物理(第11课)金属电子论和索末菲模型

  • 格式：ppt
  • 大小：1.56 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

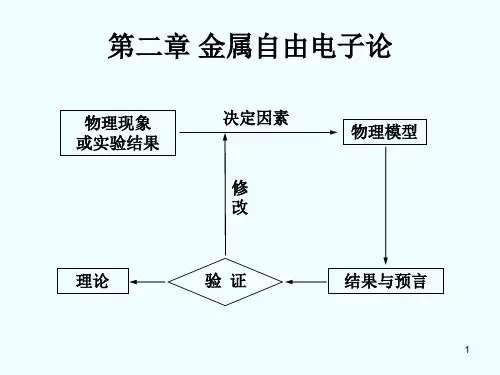
固体物理第二章金属自由电子论

固体物理第二章金属自由电子论
欧姆定律：20世纪以前，有关金属导电的一些经验规律 分子运动论：成功地处理了理想气体问题 电子的发现：1897年J. J汤姆生发现电子
原子核
价电子 芯电子
3
（3）弛豫时间近似 在dt时间内电子与离子实之间碰撞的几率应为 dt/τ 其中τ称为弛豫时间：电子在与离子实的相继两次碰撞之 间的平均自由时间。 不论碰撞前如何近似，认为与离子实碰撞后电子速度的统 计分布将恢复到平衡态——近似认为电子经历一个弛豫时 间τ后将恢复到平衡态。
1 ❖ 假设二： 电子按能量的分布遵从Fermi-Dirac统计； f(E)e(E)/kBT 1
❖ 假设三：电子在一有限深度的方势阱中运动，电子运动就是个一维方势井问题，
电子间的相互作用忽略不计；
能态问题，就是k的问题！
电子密度
波矢k密度
18
§2.2 Sommerfeld的自由电子论
思路回顾
1. 假设在E~E+dE的区间里有dN个电子，那么dU可以写成： 2. dN=dE内电子密度× dE
欧姆定律E=j ，其中E为外加电场强度、为电阻率、j 为电流密度。
电流的定义是什么?
9
特鲁德模型的成功之处 --成功地解释了欧姆定律
金属中取一垂直于电流线的面元S。从宏观的平均 效果来看，我们可以认为所有自由电子以同一速度u运动。
q neutS
ut
I q neuS
t
S
j I neu S
ne： 1202 /cm 3或 1203 /cm 3
即金属中传导电子的浓度比标准状况下经典理想气体的浓 度约大数千倍 。
由此可见，Drude 等人将金属中这种高浓度的传导 电子看成自由电子气体确实是一个极其大胆的简化。
2.特鲁德模型的成功之处 --成功地解释了欧姆定律

3.金属自由电子气的Sommerfeld模型

3.金属自由电子气的Sommerfeld模型
http://10.107.0.68/~jgche/ Sommerfeld模型
EF k BTF
k BT9
被激发电子数
电子经典能量
N U (T / TF )k BT 2
U c N (T / TF )k B T
el V
2
• 与严格的理论相比，只差一个因子 / 2 4.9 一般金属的TF~104-105K，因此，室温下，电子经 典比热被高估两个量级 注意，我们仅仅根据量子统计的规律，估计了参与 这个过程的电子数，其能量仍是经典的。这就抓住 了问题的本质！恰恰说明这是个量子问题。 • 思考：Drude模型中还有什么困难应该也只考 虑应用这个结论，即只有费米能级附近的电子 起作用，就会得到接近正确的结果？
L
k (r ) e
ik y L
ik r
边界条件导致k取值 的量子化，分立值
循环边界条件既保持 ik x L ik z L e e e 1 了固体的有限尺寸， 又易于操作。另一种 2 4 6 k x , k y , k z 0; ; ; ; 边界条件即驻波条 L LSommerfeld L 模型 件，作为习题。 14 http://10.107.0.68/~jgche/
8
3、比热的定性估计(半经典)
• 分析：电子从零度起被加热，不象经典粒子每 个电子都得到kBT的能量，而仅仅Fermi能级附 近的电子被激发 • Drude高估了对热容有贡献的电子数 • 估计：有 kBT /kBTF比例 的电子被激发，这部分 电子数目 N N ~ (k BT / k BTF ) (T / TF ) 2 2
V 4 3 N 2 k F 3 2 3
自旋 状态密度 体积
16
最高占据能级Fermi能级

索末菲模型的主要内容

索末菲模型的主要内容

索末菲模型的主要内容
哎呀呀，亲爱的朋友，你问我索末菲模型的主要内容？这可真是个有点难又特别有趣的问题呢！
我跟您说哈，索末菲模型就像是给原子世界搭的一个特别奇妙的舞台。

您想想，原子就像一个小小的宇宙，里面的电子可不是随便乱跑的哟！
在这个模型里呀，电子不再像以前人们想的那样，只是简单地绕着原子核转圈圈。

而是像一群调皮的小精灵，在不同的轨道上欢快地跳跃着。

比如说，电子的轨道不再是单一的圆形，还有椭圆形的呢！这就好比我们跑步，不只是沿着一个圆圆的操场跑，还能沿着椭圆形的跑道跑，是不是很神奇？
还有呢，索末菲提出了一些新的概念，像什么精细结构常数。

这东西可重要啦，就好像是给电子们的舞蹈定了一些特别的规则。

您可能会问，研究这个模型有啥用呀？那用处可大了去啦！它能帮助我们更好地理解原子的行为，就像我们了解好朋友的脾气一样，这样就能搞清楚很多物质的性质啦。

比如说，为啥有的材料能导电，有的就不能？这背后都有索末菲模型的功劳呢！
总之，索末菲模型给我们打开了一扇通往原子微观世界的神奇大门，让我们能更深入地探索其中的奥秘。

您说，这是不是超级厉害？。

固体物理(第11课)金属电子论和索末菲模型解读

固体物理(第11课)金属电子论和索末菲模型解读

V
2 3
k被限制在第一布里渊区
k
2
nx
I
2
V
ny
J
2
nz
K
L
L
L
2 a
2
Na
2 a
kz
2
Γ
a
kx
2
a
ky
2
Na
k
2
nx
I
2
ny
J
2
nz
K
L
L
L
L Na1 L Na2 L Na3
k空间 波矢空间 倒易点阵
b3 N3
b2 N2
b1 电子具有的波长 N1 k L L L 2 nx ny nz
独立电子：电子之间无相互作用 自由电子：近似于自由电子,即单电子近似。 忽略离子作用，不考虑碰撞，忽略晶格周期场。 引入了泡利不相容原理 服从费米－狄喇克统计分布 根据量子力学的波动现象，电子的波函数满足自由 电子的薛定谔方程。
平均势能为能量零点，电子处于无限深度的势阱内， 需作功才能逸出,电子的运动满足薛定谔方程。
波与晶面垂直。
➢可见金属晶体边长L是电子波长的l倍，这里采用了波恩
-卡门周期性边界条件。 ➢驻波一定要求格波在边界处为0，相比之下，波恩-卡门 周期性边界条件是一种行波，比驻波的要求更加宽松。
5.2 索末菲自由电子论
前提:1925年1月，物理学家泡利提出了不相容原理：一 切由自度等于半整数的粒子——费米子组成的系统中， 不能有两个或两个以上的粒子处于完全相同的状态。
晶格常数为a 的简立方
a
晶格常数b为2π/a
的倒易格点。
b对应面间距。
最大的 k，对应波
b V

第五章--金属电子论

第五章--金属电子论

——但是即使是在自由电子模型最为适用的碱金属中，传导 电子的电荷分布实际上也与离子实的强静电势密切相关。
尽管如此，在讨论那些主要依赖于传导电子动力学的相 关性质时，自由电子模型仍然获得了很大成功。
§5.1 特鲁德(Drude)经典自由电子气理论 特鲁德模型(1900年):
当金属原子聚集在一起形成金属时，原来金属原子的内层电子仍然紧 紧的被原子核束缚着，他们和原子核一起被称为原子实，在三维空间构成 长程周期性结构（金属晶体）。而金属原子的外层电子由于受到原子核的 束缚较弱，可以脱离原子，在金属体内自由的移动，称为传导电子。特鲁 德将这个由大量传导电子构成的系统称为自由电子气系统，并利用经典的 分子运动学进行处理，这就是特鲁德模型。Leabharlann va 83b
V L3
在k空间中，电子态的分布是均匀的，
分布密度只与金属的体积有关
每个波矢占据的体积为(2/L)3
3. 能态密度
在自由电子近似下，k空间的等能面是一个球面，即
2k 2 2 2 2 2 E k kx k y kz 2m 2m 在能量为E的球体中，波矢 k 的取值总数为 4 3 k k 3
电子气的浓度(1022～1023/cm3): Z m 23
n 6.02 10 A
Z 每个原子提供的传导电子 ρm 元素的密度 A 元素的原子量
电子的经典半径（1 ～ 2 Å）：
将电子视作带电的刚性小球
V 1 4 Vs rs3 N n 3
3 rs 4 n
——电子气系统和周围环境达到热平衡仅仅是通过碰撞实现的， 碰撞前后电子的速度毫无关联，且方向是随机的，其速度是和 碰撞发生处的温度相对应的。

金属,杜德,索末菲模型

金属,杜德,索末菲模型

m v 2 ~ k BT
has to change when going through regions with different T
1 2
1 2
Mechanics: Collision with ions, with other electrons, etc, where energy transfer can take place. Length scale to distinguish different v 2 :
忽略电子与电子之间的相互作用（独立电子近似）， 忽略电子与离子之间的相互作用（自由电子近似）， 电子只受到均匀外电场的作用；（Kinetic theory） 电子受到的碰撞是瞬时的，来自电子与离子实（杂质 原子）之间的散射； 电子在单位时间内散射的几率是1/τ，τ是电子驰豫 时间（relaxation time / life time）； 电子在各种散射下达到热力学平衡，即，电子在碰撞 之后的状态是随机的，由热力学平衡决定其分布。
| x1 x2 | l v
Thermal conductivity(3)
1D model:
j q ( x)
n n v (T ( x v )) v (T ( x v )) 2 2
n average left (right) going electron number per unit volume 2 v average velocity average energy carried by electrons If temperature varies slowly with x (on scale of mean free path l )
lቤተ መጻሕፍቲ ባይዱ

固体物理第二章金属自由电子论

固体物理第二章金属自由电子论

u为平均附加速度: v
v :电场附加给电子的平均速度(平均附加速度)。?? 10
考虑某一个电子，从上次碰撞发生起，有t时间的行 程。如果无外电场，其速度为v0。根据特鲁德模型德假 设，碰撞后电子出现的方向是随机的，因此v0将对总体 的电子平均速度毫无影响，即：
v0 0
但在外电场存在条件下，在上一次碰撞后立即附加
上一个速度：
eEt vt m
(E为外加电场，m为电子质量)。因此电子平均速度 只是由各电子的附加速度取平均获得。
vv0vt
eE
m
t2 t1
11
欧姆定律E=j ，其中E为外加电场强度、为电阻率、j 为电流密度。
成功用微观量解释了宏观量！
12
特鲁德模型的其他成功之处
Nat. Photon. 1, 641, 2007
EF0 ~ 几个eV
定义 Fermi 温度：
TF
E
0 F
kB
物理意义：设想将EF0转换成热振动能，相当于多高温度 下的振动能。
金属：TF： 104 ~ 105 K 36
一些金属元素费米能与费米温度的计算值
元素
Li Na K Rb Cs Cu Ag Au Be
EF0 (eV) 4.72 3.23 2.12 1.85 1.58 7.00 5.48 5.51 14.14
怎么求dN！ 接下来问题就来了！ dU EdN
Here comes the problem U EdN
16
§2.2 Sommerfeld的自由电子论
核心问题
怎么求dN！
对于理想气体貌似有某个方法 对于dV范围内的分子数为： dN=dV内分子密度×dV
对于dE范围内的：

5 金属电子论

5 金属电子论
A= 1 1 = ( )3 2 V L
2
2
1 sin( k x x ) sin( k y y ) sin( k z z ) V
π2 2 2 ( n x + n y + n z2 ) E= 2 mL2
ψ ( x, y , z ) =
2
1 sin( k x x ) sin( k y y ) sin( k z z ) V
其典型值为 1 ∼ 2 A
特鲁德将金属体内高浓度电子气视为理想气体, 运用 当时已经发展起来的解释理想气体性质的分子运动论来解 释金属的一些特性.
特鲁德模型的基本假设
(1) 独立电子假设 忽略电子-电子之间的相互作用(库仑斥力) (2) 自由电子假设 除了在碰撞瞬间, 忽略电子-原子实之间的相互作用
但是考虑所有正电荷所构成的平均势场， 电子各自独立地在平均势场中运动。
（2）索末菲电子气的能量状态
一维金属晶体中自由电子的能级
假设在长度为L的金属丝中有一个自由电子在运动. 金属晶体正电荷形成的势场是均匀的, 通常取其势能为能量零点. 由于电子不能逸出金属丝外, 在金属的边界处可取电 子的势能
U p (0) = U p ( L ) = ∞
需要考虑其行波解
波恩-卡门周期性边界条件
一维情况下
ψ (0) = ψ ( L)
ψ ( x ) = Ae ikx + Be − ikx
长L的金属线首尾相连
A + B = Ae ikL + Be − ikL
则
kx =
2π nx L
2π ⎧ kx = nx ⎪ L ⎪ 2π ⎪ ny ⎨k y = L ⎪ 2π ⎪ kz = nz ⎪ L ⎩
注:

《固体物理学》房晓勇主编教材课件-第五章 金属电子论基础

《固体物理学》房晓勇主编教材课件-第五章 金属电子论基础

海南大学
第
教学要求、重点
教学要求：
掌握金属自由电子气体模型。
海 掌握电子比热的量子理论。
大
了解逸出功和接触电势差。 纳 了解电场中的自由电子、光学性质、金属电子组率、霍耳效应 道
百
和金属热导率。
致
川
教学重点：
远
费密能、热容量、接触电势差、电子与声子的相互作
用、金属电导率
教学难点：
玻耳兹曼方程、弛豫时间的统计理论、纯金属电阻率
大
纳
经典自由电子气体理论的基础是自由电子气体模型，即 道
百 金属电子气体假定，它包括二层基本含意；
致
川
(1)忽略电子与离子实之间的相互作用，且因为存在表
面势垒，电子自由运动的范围仅限于样品内部。在金属中， 远
由于带正电的离子实均匀分布，施加在电子上的电场零．因
此对电子并没有作用。这一假定称为自由电子近似。
成自由电子气，称为金属电子气。是特鲁特(P.Drude)1900
这些自白电子可以同金属中离
海 年提出的，称为特鲁特模型。
大
海 子实碰幢，在一定温度下达到热
大
纳
道
纳 平衡状态。按照特鲁特模型，金 属中酌电子气体可以用具有确定
道
百
致
百 的平均速度和平均自由时间的电
致
川
远
川 子运动来描述。 例如，在外电
远
nx
( nx
=
0, ±1, ±2,⋅⋅⋅)
(1)
所以两个分立值之间的距离为2Л/L，因此单位长度允
许的状态数目为L/ 2Л 。
海南大学
4
第
而在dk范围内容纳的状态数为
dZ = L dk (2)

第5章金属电子理论

第5章金属电子理论

应用经典力学和电子气体服从经典麦克斯韦-玻尔兹曼统 计分布规律，对金属中的电子进行计算。得到了关于金属 的直流电导、金属电子的弛豫时间、平均自由程和金属电 子的热容的结果 经典电子论的成就： 解释金属的特征：电导、热导、温差电、电流磁输运等。 经典电子论的困难：关于固体热容量，按照经典统计法的 能量均分定理，N个价电子组成的电子气体，有3N个自由 度，对热容量的贡献为： — 对大多数金属，实验上测得的热容量值只有理论值的1％
在半径为k的球体积内电子的状态数为：
2V c 4 × πk 3 Z = ( 2 π) 3 3
= V c ⎛ 2 mE ⎞ ⎜ ⎟ 3π2 ⎝ h 2 ⎠
3 2
3 2
自由电子气的能态密度：
dZ ⎛ 2m ⎞ N ( E) = = 4 π VC ⎜ 2 ⎟ dE ⎝ h ⎠
⎛ 2m ⎞ 其中 C = 4 π V c ⎜ 2 ⎟ ⎝ h ⎠
⎡ π2 ⎛ k T ⎞2 ⎤ 2 3 ⎜ B ⎟ ⎥ = CE F 2 ⎢1 + 3 8 ⎜ EF ⎟ ⎥ ⎢ ⎝ ⎠ ⎦ ⎣ 2 0 N = C ( E F ) 3 2 ,因此有 由于系统的电子数 3
N =
∫
∞
0
∂f g (E )( − )d E ∂E
(−
∂f )函数的特点具有类似于δ函 ∂E
数的性质，仅在EF附近kBT的范围内才 有显著的值，且是E－EF的偶函数。
∂f )d E 因此一方面， N = ∫ g ( E )( − −∞ ∂E
∞
另一方面，将g(E)在EF附近展开为泰勒级数：
1 2 g( E ) = g( EF ) + g′( EF（E − EF） g′′( EF（E − EF） + ⋅ ⋅ ⋅ ) + ) 2

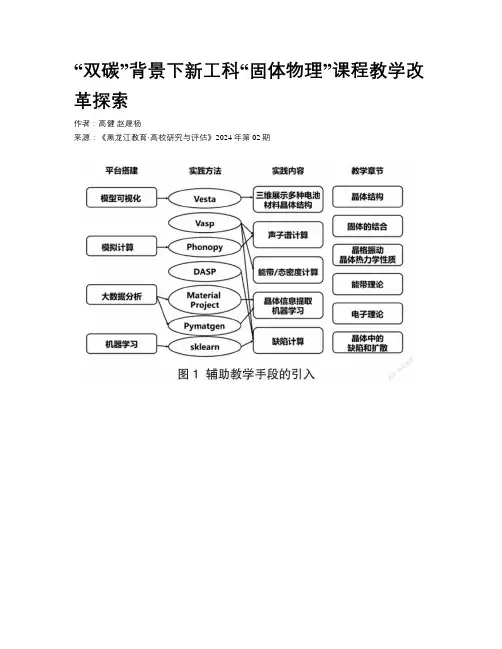
“双碳”背景下新工科“固体物理”课程教学改革探索

“双碳”背景下新工科“固体物理”课程教学改革探索

“双碳”背景下新工科“固体物理”课程教学改革探索作者：高健赵晟杨来源：《黑龙江教育·高校研究与评估》2024年第02期摘要：新能源材料的研发是实现“碳中和—碳达峰”的重要环节，“固体物理”是研究材料结构—性能关系、微观结构对宏观性能影响的物理专业基础课程，对加速新能源材料研发具有重要作用。

基于新工科发展要求，将“固体物理”课程引入工科本科生培养体系，首先需要解决“固体物理”理论性较强的难点。

在教学实践基础上，提出融入量子力学基本知识，利用可视化软件、计算软件和数据库等辅助教学手段，开展“翻转课堂”引入科技前沿，从而提高教与学的效率。

关键词：固体物理；教学模式；软件；实践；翻转课堂中图分类号：G642 文献标识码：A 文章编号：1002-4107（2024）02-0088-04“固体物理”是研究固体的物理性质、微观结构、固体中各种粒子运动形态和规律及它们相互关系的物理专业传统核心课，是各种材料科学的学科基础[1]。

“碳中和—碳达峰”和“中国制造2025”等国家计划对新能源材料的研发速度提出了新的挑战。

美国与中国先后开启“材料基因组计划”和“材料科学系统工程”[2-4]，将基于“固体物理”的理论计算模拟贯穿于新能源材料研发的各个步骤，通过数据挖掘探寻材料结构和性能之间的关系，显著提高了新材料的研发效率。

为了响应新一轮科技革命与产业变革，优化人才培养模式，构建跨学科、创新型和具有前瞻性的人才培养体系显得尤为重要。

为了实现这一目标，2017年以来，新工科建设迅速推进，在传统学科的基础上进行学科融合，对理工复合型课程建设提出了新的要求[5]。

对于新能源材料的研发而言，要求新型人才既具备宽厚的理论基础、前瞻的科技视野，又了解先进工业研发和生产技术，正是基于这一需求，在新工科人才培养体系中引入“固体物理”课程成为当务之急[6]。

然而，面向工科背景学生开设物理专业课程是一个挑战。

在教学实践中，传统的物理教学方法，即基于量子力学中的理论，进行严谨的数学和物理公式推导的这一过程，对于工科背景的学生来说过于抽象。

固体物理第二章金属自由电子论

固体物理第二章金属自由电子论

17
§2.2 Sommerfeld的自由电子论
核心问题
怎么求dN！
dN=dE内电子密度× dE
dN=dE内能量密度× dE
dN=f(E) × dE内能量密度× dE
先解解薛定谔方程，
E k 2k2 2m
看看k的密度再说吧！
❖ 假设一：电子的填充满足Pauli不相容原理； 有一个能态，就有一个电子
4
1. Drude 等人所做的简化近似可归纳为如下四个基本假设： （1）独立电子近似
忽略电子与电子之间的相互作用 ——近似认为电子的运动 是彼此独立的，就象孤立的单个电子一样，故又称为单电 子近似。
（2）自由电子近似
用经典粒子的碰撞图象来简化电子与离子实之间复杂的相
返 回
互作用 ——近似认为单个电子在与离子实的相继两次碰撞
固体物理第二章金属自由电子论
金属自由电子论
§ 2.1 经典电子论； § 2.2 Sommerfeld的自由电子论； § 2.3 Sommerfeld展开式及其应用； § 2.4 电子发射
2
§2.1 经典电子论——Drude模型
经典电子论诞生的背景
欧姆定律：20世纪以前，有关金属导电的一些经验规律 分子运动论：成功地处理了理想气体问题 电子的发现：1897年J. J汤姆生发现电子
子浓度(定义为单位体积中的平均电子数)。
由于在各种热力学过程中金属材料体积的变化通常很
微小，因此电子浓度这一状态参量的变化是甚微的。
若某一金属元素原子的原子量为A、价电子数为Z，
其所形成的晶体的质量密度为 m ，则该金属中的电子浓
度为
ne
ZNa
m
A
ห้องสมุดไป่ตู้

高二物理竞赛第四章金属电子论课件

高二物理竞赛第四章金属电子论课件

----电子的波函数(是电子位矢
r
的函数)
常用边界条件: 周期性边界条件
x, y, z x L, y, z x, y, z x, y L, z x, y, z x, y, z L
k
(r
)
Ae ikr
E
2k 2 2m
2 2m
(k
2 x
k
2 y
k
2 z
)
k
波矢，
2π k
为电子的德布罗意波长。
EF---费米能级(等于这个系统中电子的化学势)，它的意 义是在体积不变的条件下，系统增加一个电子所需的自由能。 它是温度T和晶体自由电子总数N的函数。
2. f (E) ~ (E EF) 图象
f
(E)
1 e( E EF ) kBT
1
a. kBT 0
b. kBT 1
c. kBT 2.5
f (E)
1
陡变
E EF E EF
0
E EF
1 E EF
f
(
E)
1 02
E EF E EF
1 E EF
f
(
E)
1 02
E EF E EF
随着T的增加，f(E)发生变化的能量范围变宽，但在任何情
况下，此能量范围约在EF附近kBT范围内。
3.费米面
E=EF的等能面称为费米面。
在绝对零度时，费米面以内 的状态都被电子占据，球外没有 电子。
T0时，费米球面的半径kF 比绝对零度时费米面半径小， 此时费米面以内能量离EF约kBT 范围的能级上的电子能被激发 到EF之上约kBT范围的能级。
费米能级
E
0 F
(a) T=0k

第六章金属电子论

第六章金属电子论

O
L
x
(2)势阱内的哈密顿算符Ĥ 2 d 2 2 d 2 ˆ H 2 V ( x) 2 2m dx 2m dx
(3)势阱中的薛定谔方程 Ĥψ(r)=Eψ(r) (4)自由电子的能量
P k E ，P k，k 波矢。 2m 2m
y A Ax A Az 1 L3 2 为归一化常数，
x, y, z
V
2
dxdydz 1

V
n y nz nx A sin x sin y sin zdxdydz 1 L L L
4.对结果的讨论 ψ(x,y,z)代表驻波，驻波的平均速度为零，平 均动量为零，意味着电子在晶体中不能运动。之 所以得到此种结果，是因为所采用的边界条件是 驻波条件。 5.采用周期性边界条件 (1)一维晶体周期性边界条件——无限多个线度都 是L的势阱连接起来。在各个势阱相应的位置上 电子的状态相同。
二、三维晶体中电子气的能量分布
1. 三维无限深势阱分布 0 x,y,z L, V x , y, z 0 x , y, z 0及x , y, z L。 V x , y, z
2.势阱内的薛定谔方程 2 2 E 2m E：粒子在势阱内的能量；
在E E dE的体积元中可 容纳的电子数为 :
2 mE 2m dE dZ 2 2 2 E 2m 4VC 2 h
32
kz
dk
VC
k
O
ky
E dE
12
kx
(3)能级密度
dZ 2m DE 4VC 2 dE h 2m C 4VC 2 h

金属的费米索末菲电子理论.ppt

金属的费米索末菲电子理论.ppt

1
Z(E) E 2
1.2.3 自由电子按能级分布
金属中大量的自由电子是怎样占 据这些能级的呢？
金属中自由电子的能量是量子化 的，构成准连续谱。
美国物理学家。生于意大利罗马。
1922年获比萨大学博士学位。
1923年前往德国。在玻恩的指导下从事研究 工作。
1925年一月至1926年秋季在佛罗伦萨大学 工作，开始研究费米-狄拉克统计问题。
作用: 成功地计算出金属电导率以及电导率和热导 率的关系。
缺陷：
➢解释不了霍尔系数“反常”现象； ➢实际测量的电子平均自由程比经典理论估计的大许多； ➢金属电子比热测量值只有经典自由电子理论估计值的百分 之一； ➢金属导体，绝缘体，半导体导电性的巨大差异。
1.2.1 金属中自由电子的能级
一维势阱模型（索末菲假设）
由于等能面为球面，所以，在k空间中，电子填充的 部分为球体，称为Fermi球（Fermi sphere）。Fermi 球的表面称为Fermi面（Fermi surface）；Fermi面所 对应的能量称为Fermi能（Fermi energy，EF0）。
EF0
2kF2 2m
—— 费米能 Fermi energy
假设在长度为L的金属丝中 有一个自由电子在运动，且金属 晶体内的电子与离子没有相互作 用，其势能不是位置的函数，即 电子势能在晶体内到处一样，取 U(x)＝0；由于电子不能逸出金 属丝外，则在边界处
➢金属中自由电子的能量是量子化的，其各分立能级 组成不连续的能谱，而且由于金属中自由电子数目 很大，相邻能级间波长差很小，所以能级间能量差 很小，又称为准连续的能谱。
1941年底，费米在哥伦比亚大学主持建造了世界上第一座原 子反应堆

11金属自由自由电子气体模型及基态性质

11金属自由自由电子气体模型及基态性质
二者的一致性，表明周期性边条件的合理性 由周期性边界条件：（讲解以下推导过程）
Where the quantity nx, ny, nz are any integer(整数）
路漫漫其修远兮, 吾将上下而求索
路漫漫其修远兮, 吾将上下而求索
nx, ny, nz取值为整数，意味着波矢k取值是量子化的。
三、基态和基态能量 1.N个电子的基态、费米球、费米面 电子的分布满足：能量最小原理 和 泡利不相容原理 我们已知在波矢空间状态密度：
考虑到每个波矢状态代表点可容纳自旋相反的两个电子， 则单位相体积可容纳的电子数为：
路漫漫其修远兮, 吾将上下而求索
N个电子的基态(T=0K)，可从能量最低的 k=0 态开始，从 低到高，依次填充而得到,每个k态两个电子。
路漫漫其修远兮, 吾将上下而求索
驻波边界条件 常用边界条件
周期性边界条件
人们广泛使用的是周期性边界条件（periodic boundary condition),又称为波恩-卡门（Born-von Karman)边条件
亦即：
对于一维
相当于首尾相接成环，从而既有有限尺寸，又消除了边界 的存在。
路漫漫其修远兮, 吾将上下而求索
每个点表示一个允许的单电子态。
路漫漫其修远兮, 吾将上下而求索
金属中自由电子波矢： nx, ny, nz取值为整数 所以，每个代表点（单电子态）在k空间是均匀分布的。 由此： (1)在波矢空间每个(波矢)状态代表点占有的体积为：
(2)波矢空间状态密度(单位体积中的状态代表点数): 注意量纲
路漫漫其修远兮, 吾将上下而求索
满足薛定谔方程：
路漫漫其修远兮, 吾将上下而求索
其中：V(r)为电子在金属中的势能，为电子的本征能量

第三章 金属电子论(09年10月)

第三章 金属电子论(09年10月)

u tΔΔS为平均附加速度:v0.23~2.4 nm电子在发生碰撞前可自由穿过10个晶格。

A. Sommerfeld下，电子的能量和动量不随时间或位置改变，此时可以用: ，其中的方向为平面波的方向，(E)和动量(P)由德布罗意关系表示n 2、n 3是整数。

从上述分析可见，在k 空间，电子的状态是分立的，只允许波矢k 具有确定的分立值。

这样k 可以被解释为量子数。

因此单电子的本征能量亦取分立值。

由于单电子的本征能量为：的区域所允许的k 点(许可态)的数目个电子对许可k 态的占据，简单地由泡利不相容原理态，电子自旋能够取两个可能值：k 空间的电子态密度自由电子气系统的基态T=0K ，N 个自由电子的基态，可从能量最态开始，按能量从低到态两个电子，依次填充个电子，它的空间具有最k F 为半费米球，其。

对于基态，费米球内所有状态都被电子占据，而费米球外的状态全部未被定义为费米球的表面，在基态它把占据态和未N 个自由电子的基态为电子浓度。

相对应的能量称为费米能量：所受到的外力为：由于自由电子的动量与波矢之间的关系：则由牛顿第二定律可知：从上式可以看出，波矢k将随时间变化。

时刻将电场施加到电子气的基态，则在后一时刻费米球中心将移到新的位置：如果不发生碰撞，恒定的外加电场将使k空间中的费米球匀速移动。

由于电子与离子实的碰撞将使电子失τ为迟豫时间，Δk决定电子的漂移速度(平均速度) 。

不同的是，在量子体系中，由于非平衡费米球中与E=0时费米球交叠部分，方向上分布的对称性，对电流没有贡献。

电流来源于原费米球面撞，费米球整体的位移Δk和外力F的关系可由下式给出：为电子的漂移速度。

项为自由电子加速度而项表示碰撞效应项(相当于电子遭受碰撞而引入的摩擦阻力。

作用在一个电子上的洛仑兹力为：数为零，于是：则运动方程为：轴平行于磁场，于是运动方程可写为：其中。

：固体的界面效应和表面效应在金属自由电子模型中，金属内部被假设为均匀势场，离子实提供一个正电背景。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

由上式可得 :
- 2 2 p 2 ( r, t ),即p与算符 i相当. p2 E 2m
利用能量动量关系式
2 2 得到 i t 2m 设粒子在力场中的势能 为U(r), 则粒子能量和动量关系 式为 p2 E U (r) 2m
上式两边同乘以波函数 ( r, t ),并以算符 i 和 i分别 t 代替E和p,得到下列方程 2 2 i U ( r ) t 2m 2 2 2 或 E U ( r ) [ 2 U ( r )] 2m 2m 上式称为薛定鄂方程 2 2 ˆ 表示 算符 [ U ( r )] 称为哈密顿算符 , 通常以 H 或H 2m 于是上式可写成 H E 这种方程称为本征值方 程, E称为算符 H的本征值, 称为 算符H的本征函数 .
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
19+ 18-
金属自由电子模型（钾）
1 电子气浓度 势垒限制电子逸出 N ZN Lna NA N A
同理有
2 t 2 px 2 ( r, t ) 2 2 p y ( r, t ) 2 2 t
2 ( r, t ) 2 t
2
p2 y
将以上三式相加得
2 2 2 2 p 2 同理有 2 ( r, t ) 2 2 2 x y z 其中是劈形算符, i j k x y z
未考虑波粒二象性，电子散射。
金属的比热
特鲁德模型认为金属中电子具有经典理想气体分子的 运动特征，它们遵循玻尔兹曼统计规律：每个电子有 三个自由度，每个自由度有kBT/2的平均能量，共有3 kBT/2内能，电子气比热CV=3kBn/2,在高温下相当于 晶格振动的比热,这与实验不相符。 从经典理论来看，只能说明电子没有热运动，直接动 摇了经典电子运动论。 量子力学和费米统计规律建立后，这一矛盾才解决。 并在此基础上建立了新的金属电子理论。
5.2 索末菲自由电子论
前提:1925年1月，物理学家泡利提出了不相容原理：一 切由自度等于半整数的粒子——费米子组成的系统中， 不能有两个或两个以上的粒子处于完全相同的状态。 这一原理解释了原子的电子壳层结构和元素周期律，推 动了电子自旋概念的确立。 费米和狄拉克分别在泡利不相容原理及玻尔兹曼统计基 础上，提出电子服从某一统计规律，后来称为费米－狄 喇克统计分布。电子、质子、中子（全同粒子）
如果U(r) 不含时间,自由粒子的薛定谔方程 的解 可以用分离变量法简化 考虑写成下列形式： (r, t) ( r ) f (t ) 将其代入薛定谔方程 ,并把方程两边用 ( r ) f (t )去除 i df 1 2 2 得到 [ U ( r ) ] f dt 2 m 上式左边只含 t ,而右边只含 r, t和r是互相独立的变量 , 所以只有两边都等于同 一常量时, 等式才被满足 , 以E表示这个常量.

b3 N3
b2 N2
说 明
电子以平面简谐波形式存在于金属晶体中，其波长由k
确定，而k又取决于倒易矢量b，每个倒易矢量b都与晶 格点阵中的一族晶面垂直，且代表这族晶面的面间距。 故k的取值为l×b/n，即l×2π/na时，意味着电子波长 为 na/l，即L/l， na代表了某方向的晶体的长度L，且该平面 波与晶面垂直。 可见金属晶体边长L是电子波长的l倍，这里采用了波恩 -卡门周期性边界条件。 驻波一定要求格波在边界处为0，相比之下，波恩-卡门 周期性边界条件是一种行波，比驻波的要求更加宽松。
作业1
1.
2.
特鲁德模型对金属晶体中的电子作了哪些假 设,试根据特鲁德模型推导金属晶体中电压与 电流的关系. 试说明特鲁德模型中金属中的电子对热容的 贡献.
补充
3. 自由粒子的能量 E ,动量P,波长 , 频率满足以下方程： E h P h n k

上述公式称为德布罗意 公式.由于自由粒子能量和动 量都 是常数 , 所以由德布罗意公式可 知,与自由粒子联系的波 , 它的频率和波矢 (或波长 )都不变,即它是 A cos[2 ( x t )]
补充资料：三维晶格情况下的波矢
k的分布密度（单位体积中k点的数目）： 3 2 V 2 nx 2 n y 2 nz k被限制在第一布里渊区 k I J K
L L L
1
V 2 3
2 a
2 Na
2 aΒιβλιοθήκη kzky2 a
kx
Γ
2 Na
金属电子的平均自由程
me 平均自由时间 测量ρ即可知 2 ne 如铜在T 273K时 1.56 cm 得到 2.7 1014 s 平均自由程 v 1 3 2 根据经典的能量均分定理，有 me v k BT 2 2 7 1 根据上述模型，室温下，v 的值约为10 cm s 算出金属中电子的平均自由程为 1 ~ 10 A ，特鲁德模型有较大误差 实验测试值为10 3 A
由等式左边得到
i df df E 即 i Ef f dt dt
2
由等式左边得到 2 U ( r ) E 2m 解出 则有 f(t) Ce
iE t iE t
( r, t ) ( r )Ce
薛定谔方程简介
1. 含时薛定谔方程： 2 2 2 2 ( 2 2 2 ) V x, y , z, t i 2m x y z t 式中Ψ Ψ(x,y, z, t)是粒子在势场V x,y,z,t 中运动 的波函数。
2 3 1 3 1 2 1 2 3 1 2 3
a
a1、a2、a3 b1、b2、b3 N N1 N 2 N 3 n N1、N 2、N 3 h1 h2 h3 1. k b1 b2 b3 , h1、h2、h3 Z N1 N2 N3 平均一个k点占据的体积： 示意图 3 3 b1 b2 b3 1 1 2 2 * N1 N 2 N 3 N N V
n 利用气体压强 P RT NA 金属中的电子气体压强非常大 电子不会逸出到金属晶体以外。
5条假设
1. 独立电子假设 ：忽略电子-电子之间的库仑排斥力 2. 自由电子假设：电子速度各向同性，电子和离子碰 撞，忽略电子-离子的库仑吸引力。 3. 碰撞假设：碰撞后电子方向随机，速度只与温度有 关，单个电子的平均能量为：
5.1 经典的金属自由电子论
5.1.1 特鲁德模型(示意图) 为了说明导电、导热等物理现象。 金属由正离子和电子组成，满壳层电子与原子核构 成原子实，外壳层电子即价电子数为-eZ，受到原子 核束缚较弱，称为传导电子，弥散于金属内部，构成 自由电子气体。 服从玻尔兹曼统计：e-hω/kT，在外电场作用下服从 牛顿运动定律。 每个电子对热容的贡献是3kBT/2。但与实验值相差 较大。
2. 定态薛定谔方程： 在恒定势场条件下，即V x, y , z, t V x, y , z 波函数应有以下形式： ( x, y , z, t ) e
E i t
其空间部分ψ ψ(x , y , z)应满足如下方程： 2 2 V x, y , z E , 定态薛定谔方程 2 2m x ( x, y , z ) 粒子的定态波函数
2 a
2 nx 2 n y 2 nz k I J K L L L
L Na1 L Na2 L Na3
k 空间 波矢空间 倒易点阵
b 1 N1
电子具有的波长 k L L L 2 n x n y nz Na Na Na nx ny nz
1 2 3 E mv k BT 2 2
4. 驰豫时间近似(relaxation time approximation) 电子与离子两次碰撞之间的平均时间间隔，1/ 为碰 撞概率，平均自由程(mean free path)：l=v。在无外 力作用时，电子的平均集体运动速度按照exp(-T/ )的 方式趋于0，弛豫时间与电子速度和位置无关。 5 . 隐含假设：电子是经典粒子（当时没有量子力学）
n V N La
3
Z
M
Z

M
其中NL为单胞数，na为单胞中 原子数，Z为价电子数，a3为单 胞体积，ρ为元素密度，NA为 阿伏加德罗常数，M为原子量， 典型值为1022~1023个/cm3 电子平均半径 rs
电子势垒模型
V 1 4 3 rs N n 3 3 13 3 13 rs ( ) ( ) a 典型值： 1 ~ 2A 4n 4na Z
i ( pr Et ) Ae
这种波称为德布罗意波
对自由粒子波函数 i E t 由上式可得 i E 即E与算符 i 相当 t t 对自由粒子波函数
2
i ( pr Et ) Ae 求偏微商,得到
i ( pr Et ) Ae 进行二次偏微商 ,得到 2 Ap x 2 i ( p x x p y y p z z Et ) e
平面波.
波长 , 频率 ,沿x方向传播的平面波可用 下式来表示 :

如果波沿单位矢量 n的方向传播 ,则 A cos[2 ( r n

t )] 其中k 2 n
A cos[k r t ] 将其改写成复数形式 :