结构力学 第9章矩阵位移法
- 格式:ppt
- 大小:717.50 KB
- 文档页数:17

第9章矩阵位移法习题解答习题9.1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
()(2)矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。
()(3)单元刚度矩阵都具有对称性和奇异性。
()(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
()(5)结构刚度矩阵与单元的编号方式有关。
()(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
()【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错误。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统一编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1)矩阵位移法分析包含三个基本环节,其一是结构的,其二是分析,其三是分析。
(2)已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。
(3)将非结点荷载转换为等效结点荷载,等效的原则是。
(4)矩阵位移法中,在求解结点位移之前,主要工作是形成矩阵和_________________ 列阵。
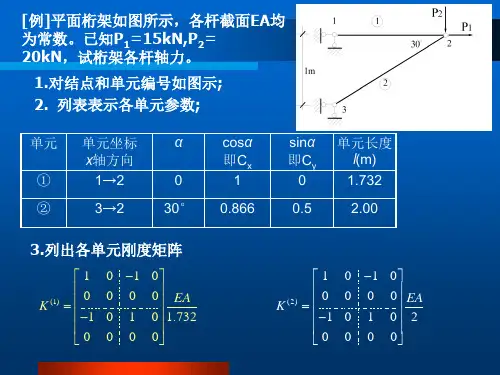
(5)用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸>=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买,则2 尹> =O(6 )用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。
【解】(1)离散化,单元,整体;(2)灯8;(3)结点位移相等;(4)结构刚度,综合结点荷载;(5)[0 0 0 0.3 -0.8 0.5]。
(6)-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。
【解】各刚度系数的物理意义如习题解9.3图所示。


第9章 矩阵位移法9.1 复习笔记一、矩阵位移法的基本思路矩阵位移法又称为杆件结构的有限元法。
分析的两个基本步骤:(1)单元分析;(2)整体分析。
单元分析:建立杆端力与杆端位移间的刚度方程,形成单元刚度矩阵。
整体分析:将单元合成整体,按照刚度集成规则形成整体刚度矩阵,建立位移基本方程。
二、单元刚度矩阵(局部坐标系)进行单元分析,推导单元刚度方程和单元刚度矩阵。
单元刚度方程是指由单元杆端位移求单元杆端力的一组方程,可以用“”表示,由位移求力称为“正问题”。
相应的由力求位移称为“反问题”。
正问题的解是唯一的确定的,但是反问题则可能无解,如果有解也非唯一解。
当外部荷载为不平衡力系时,反问题无解;当外荷载为平衡力系时,反问题有解但是因为杆件除本身变形外还可有任意刚体位移,此时反问题的解不唯一。
本书暂不考虑反问题的求解。
1.一般单元图9-1所示为平面刚架中的一个等截面直杆单元.单元的两个端点采用局部编码1和2,由端点1到端点2的方向规定为杆轴的正方向,在图中用箭头标明。
F →∆e图9-1图中采用坐标系,其中轴与杆轴重合。
这坐标系称为单元坐标系或者局部坐标系。
字母、的上面都画了一横,作为局部坐标系的标志。
推导单元刚度方程时,有以下几点需要注意:重新规定正负号规则、讨论杆件单元的一般情况、采用矩阵表示形式。
在局部坐标系中,图9-2所示的位移、力分量方向为正方向。
图9-2杆件性质:长度l ,截面面积A ,截面惯性矩I ,弹性模量E ;杆端位移u 、v 、θ。
根据杆端位移可以推导出下面两组刚度方程:(9-1)x y x x y(9-2)将上述六个刚度方程列成矩阵形式:(9-3)其中就是局部坐标系下单元刚度矩阵,即为(9-4)2.单元刚度矩阵的性质 (1)单元刚度系数的意义e e ek F∆=eK代表单元杆端第j 个位移分量等于1时所引起的第i 个杆端力分量。
(2)是对称矩阵,即。
(3)一般单元的是奇异矩阵,即,因此不存在逆矩阵。