传热过程计算..

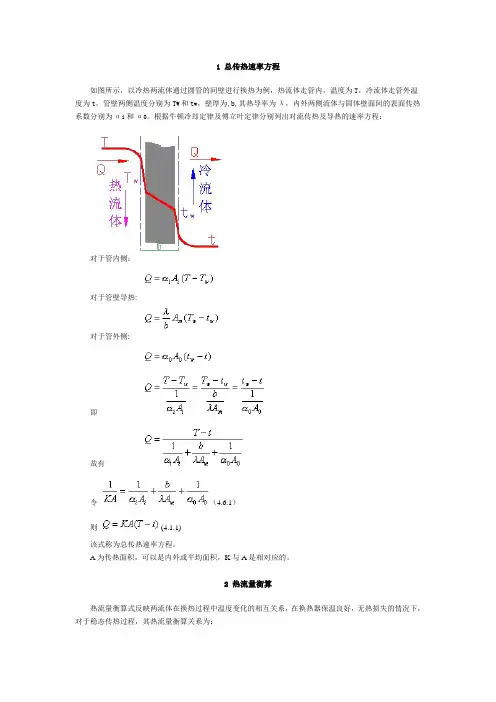
1 总传热速率方程如图所示，以冷热两流体通过圆管的间壁进行换热为例，热流体走管内，温度为T，冷流体走管外温度为t，管壁两侧温度分别为T W和t w，壁厚为,b,其热导率为λ，内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。

根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程：对于管内侧：对于管壁导热:对于管外侧:即故有令（4.6.1）则(4.1.1)该式称为总传热速率方程。

A为传热面积，可以是内外或平均面积，K与A是相对应的。

2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系，在换热器保温良好，无热损失的情况下，对于稳态传热过程，其热流量衡算关系为：（热流体放出的热流量）=（冷流体吸收的热流量）在进行热衡算时，对有、无相变化的传热过程其表达式又有所区别。

（1）无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量，W；m h,m c-----热、冷流体的质量流量，kg/s；C ph,C pc------热、冷流体的比定压热容，kJ/(kg·K)；T1,t1 ------热、冷流体的进口温度，K；T2,t2------热、冷流体的出口温度，K。

（2）有相变化传热过程两物流在换热过程中，其中一侧物流发生相变化，如蒸汽冷凝或液体沸腾，其热流量衡算式为：一侧有相变化两侧物流均发生相变化，如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热，J/kg；D,D1,D2--------相变物流量，kg/s。

对于过冷或过热物流发生相变时的热流量衡算，则应按以上方法分段进行加和计算。

3 传热系数和传热面积（1）传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数，是进行传热计算的依据。

K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等，K值通常可以由实验测定，或取生产实际的经验数据，也可以通过分析计算求得。

传热系数K可利用式（4.6.1）进行计算。

热传递热量计算公式
热传递是指热量从一个物体传递到另一个物体的过程。

热传递的计算可以通过多种公式来实现，具体取决于热传递的方式。

以下是一些常见的热传递计算公式：
1. 热传导（导热）的计算公式：
热传导是指热量通过物质内部传递的过程。

其计算公式可以用傅立叶定律来表示：
Q = -kAΔT/Δx.
其中，Q表示传导热量，k表示热导率，A表示传热面积，ΔT表示温度差，Δx表示传热距离。

2. 热对流的计算公式：
热对流是指热量通过流体（气体或液体）对流传递的过程。

其计算公式可以用牛顿冷却定律来表示：
Q = hAΔT.
其中，Q表示对流热量，h表示对流换热系数，A表示传热面积，ΔT表示温度差。

3. 热辐射的计算公式：
热辐射是指热量通过辐射传递的过程。

其计算公式可以用斯特藩-玻尔兹曼定律来表示：
Q = εσA(T₁^4 T₂^4)。

其中，Q表示辐射热量，ε表示发射率，σ表示斯特藩-玻尔兹曼常数，A表示辐射面积，T₁和T₂分别表示两个物体的绝对温度。

以上是一些常见的热传递计算公式，它们分别适用于不同的热传递方式。

在实际问题中，需要根据具体情况选择合适的公式进行计算。

第四节 传热过程计算化工原理中所涉及的传热过程计算主要有两类：一类是设计计算，即根据生产要求的热负荷，确定换热器的传热面积；另一类是校核计算，即计算给定换热器的传热量、流体的流量或温度等。

两者都是以换热器的热量衡算和传热速率方程为计算的基础。

应用前述的热传导速率方程和对流传热速率方程时，需要知道壁面的温度。

而实际上壁温常常是未知的，为了避开壁温，故引出间壁两侧流体间的总传热速率方程。

4—4—1 能量衡算对间壁式换热器做能量衡算，以小时为基准，因系统中无外功加入，且一般位能和动能项均可忽略，故实质上为焓衡算。

假设换热器绝热良好，热损失可以忽略时，则在单位时间内换热器中热流体放出的热量等于冷流体吸收的热量，即 ， .、)()(1221c c c h h h H H W H H W Q -=-= (4—30)式中 Q —换热器的热负荷，kj/h 或W ；W －流体的质量流量，kg ／h ；H －单位质量流体的焓，kJ ／kg 。

下标c 、h 分别表示冷流体和热流体，下标1和2表示换热器的进口和出口。

式4-30即为换热器的热量衡算式，它是传热计算的基本方程式，通常可由该式计算换热器的传热量(又称热负荷)。

.若换热器中两流体无相变化，且流体的比热容不随温度而变或可取平均温度下的比热容时，式4-30可表示为Q )()(1221t t c W T T c W pc c ph h -=-= （4-31）式中 c p －流体的平均比热容，kJ ／(kg ·℃)；t —冷流体的温度，℃；T －热流体的温度，℃。

若换热器中的热流体有相变化，例如饱和蒸气冷凝时，式4-30可表示为Q )(12t t c W r W pc c h -== (4-32)式中 W h —饱和蒸气(即热流体)的冷凝速率，k 2／h ；r —饱和蒸气的冷凝潜热，kJ ／kg 。

式4-32的应用条件是冷凝液在饱和温度下离开换热器。

若冷凝液的温度低于饱和温度时，则式4-32变为Q )()]([1221t t c W T T c r W pc c ph h -=-+= （4-33）式中 C ph －冷凝液的比热容，kJ ／(kg ·℃)；T s —冷凝液的饱和温度，℃。

6.6 传热过程的计算工业上大量存在传热过程（我们指间壁式传热过程），他包括了流体与固体表面间的给热和固体内部的导热。

前面我们已经学过了导热和各种情况下的给热所遵循的规律，本节讨论传热过程的计算问题。

6.6.1 传热过程的数学描述在连续化的工业生产中，换热器内进行的大都是定态传热过程。

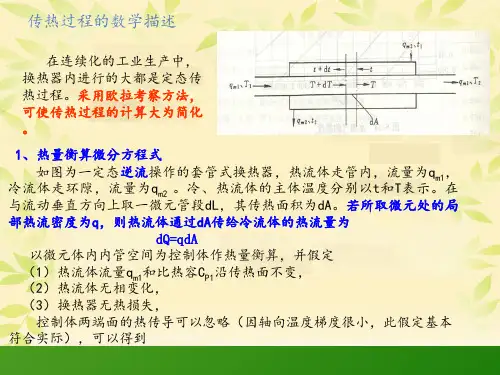
（1）热量衡算微分方程式如图为一套管式换热器，内管为传热管，传热管外径1d ，内径2d ，微元传热管外表面积d A 1，管外侧1α；内表面积d A 2，内侧2α，平均面积d A m ，壁面导热系数λ。

对微元体做热量衡算得 Q A q T c m p s d d d 11==-Q A q T c m p s d d d 22==-以上两式是在以下的假设前提下：① 热流体流量1s m 和比热1p c 沿传热面不变；② 热流体无相变化； ③ 换热器无热损失；④ 控制体两端面的热传导可以忽略。

（2）微元传热速率方程式如图所示套管换热器中，热量由热流体传给管壁内侧，再由管壁内侧传至外侧，最后由管壁外侧传给冷流体。

对上述微元，我们可以得到33211321d d d d d d d A q A q A q Q Q Q Q m =======阻力推动力=++-=-=-=-22m 1122w m w w 11w d 1d d 1d 1d d 1A A b A t T A t t A b t T A T T αλααλα 令 2211d 1d d 1d 1A A b A A K m αλα++= 则 )(d d 1d t T A K A K tT Q -=-=)(d d t T K AQ q -==式中 K ——总传热系数，W/m 2·K 。

因为沿着流体流动方向（套管换热器沿管长）流体的温度是变化的，所以α值也是变化的。

但若取一定性温度，则α与传热面无关，可以认为是一常数，这样K 也为一常数。

对上式进行积分，可以得到m t KA Q ∆= （3）传热系数和热阻 ① K 的计算由前面的分析可知，传热过程的总热阻1/K 由各串联环节的热阻叠加而成，原则上减小任何环节的热阻都可提高传热系数，增大传热过程的速率。

热传导三种方式公式热传导是指物体内部或不同物体之间因温度差异而产生热量传递的现象。

热传导过程可以通过三种方式进行：热对流、热辐射和热传导。

本文将分别介绍三种热传导方式及其公式。

1.热对流热对流是指流体（气体或液体）在物体表面或内部通过对流方式进行热传递。

在流体中，热量传递是通过流体分子间的碰撞实现的。

热对流的公式如下所示：Q=hAΔT其中，Q为热量，h为热传递系数，A为传热面积，ΔT为温度差异。

热传递系数h是由流体的性质、流速、传热面积等因素决定的，通过实验得到的。

例如，一个半径为10cm的球体，其表面与气体接触，气体温度为30℃，球体内部温度为100℃，求其表面每秒钟传递多少热量？解：首先计算出表面积，A=4πr²=4π某10²=1256.64cm²。

然后选择恰当的热传递系数，假设为h=10W/(m²·K)，将其转换为cm单位，得h=0.1W/(cm²·K)。

最后代入公式得到：Q=hAΔT=0.1某1256.64某(100-30)=940.98W。

2.热辐射热辐射是指物体通过辐射方式进行热传递，而不需要介质来传递热量。

所有物体都可以辐射热量，其公式如下所示：Q=σεA(T₁⁴-T₂⁴)其中，Q为热量，σ为斯特腾-玻尔兹曼常数，ε为辐射率，A为表面积，T₁和T₂分别为两侧物体的绝对温度。

斯特腾-玻尔兹曼常数σ是一个物理常数，其数值为5.67某10⁻⁸W/(m²·K⁴)，可以通过实验测定得到物体的辐射率ε。

例如，一个黑色矩形板，长50cm、宽30cm、温度为100℃，悬空悬浮在25℃的房间内，求每秒钟它向房间内传递多少热量？解：首先计算出表面积，A=2(50某30+30某100+50某100)cm²=27,000cm²。

然后计算出物体的辐射率，或参考已知黑色物体的典型值，假设为ε=1、最后代入公式得到：Q=σεA(T₁⁴-T₂⁴)=5.67某10⁻⁸某1某27,000某(373⁴-298⁴)=648.43W。