传热过程的计算
- 格式:doc
- 大小:259.00 KB
- 文档页数:11


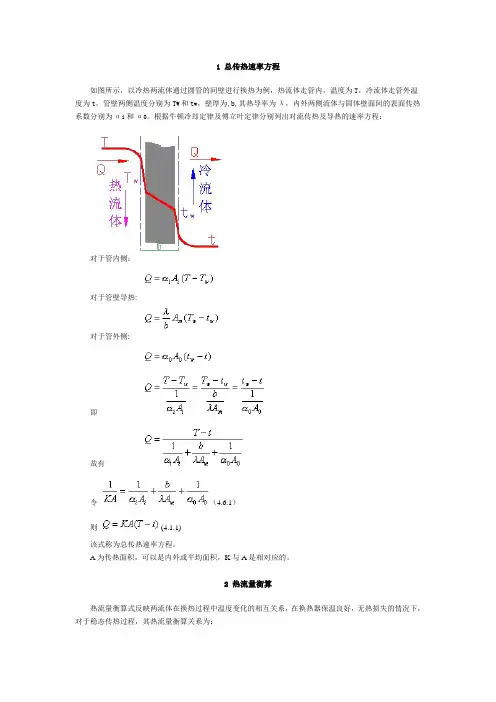
1 总传热速率方程如图所示,以冷热两流体通过圆管的间壁进行换热为例,热流体走管内,温度为T,冷流体走管外温度为t,管壁两侧温度分别为T W和t w,壁厚为,b,其热导率为λ,内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。
根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程:对于管内侧:对于管壁导热:对于管外侧:即故有令(4.6.1)则(4.1.1)该式称为总传热速率方程。
A为传热面积,可以是内外或平均面积,K与A是相对应的。
2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系,在换热器保温良好,无热损失的情况下,对于稳态传热过程,其热流量衡算关系为:(热流体放出的热流量)=(冷流体吸收的热流量)在进行热衡算时,对有、无相变化的传热过程其表达式又有所区别。
(1)无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量,W;m h,m c-----热、冷流体的质量流量,kg/s;C ph,C pc------热、冷流体的比定压热容,kJ/(kg·K);T1,t1 ------热、冷流体的进口温度,K;T2,t2------热、冷流体的出口温度,K。
(2)有相变化传热过程两物流在换热过程中,其中一侧物流发生相变化,如蒸汽冷凝或液体沸腾,其热流量衡算式为:一侧有相变化两侧物流均发生相变化,如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热,J/kg;D,D1,D2--------相变物流量,kg/s。
对于过冷或过热物流发生相变时的热流量衡算,则应按以上方法分段进行加和计算。
3 传热系数和传热面积(1)传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数,是进行传热计算的依据。
K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等,K值通常可以由实验测定,或取生产实际的经验数据,也可以通过分析计算求得。
传热系数K可利用式(4.6.1)进行计算。
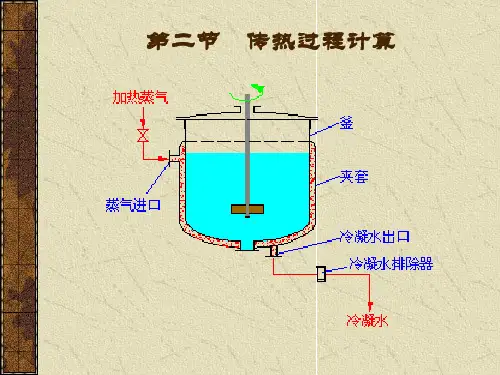


第五节 传热过程的计算化工生产中广泛采用间壁换热方法进行热量的传递。
间壁换热过程由固体壁的导热和壁两侧流体的对流传热组合而成,导热和对流传热的规律前面已讨论过,本节在此基础上进一步讨论传热的计算问题。
化工原理中所涉及的传热过程计算主要有两类:一类是设计计算,即根据生产要求的热负荷,确定换热器的传热面积;另一类是校核计算,即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算基础。
4-5-1 热量衡算流体在间壁两侧进行稳定传热时,在不考虑热损失的情况下,单位时间热流体放出的热量应等于冷流体吸收的热量,即:Q=Q c =Q h (4-59) 式中 Q ——换热器的热负荷,即单位时间热流体向冷流体传递的热量,W ; Q h ——单位时间热流体放出热量,W ; Q c ——单位时间冷流体吸收热量,W 。
若换热器间壁两侧流体无相变化,且流体的比热容不随温度而变或可取平均温度下的比热容时,式(4-59)可表示为()()1221t t c W T T c W Q pc c ph h -=-= (4-60) 式中 c p ——流体的平均比热容,kJ/(kg ·℃); t ——冷流体的温度,℃; T ——热流体的温度,℃; W ——流体的质量流量,kg/h 。
若换热器中的热流体有相变化,例如饱和蒸气冷凝,则()12t t c W r W Q pc c h -== (4-61) 式中 W h ——饱和蒸气(即热流体)的冷凝速率,kg/h ; r ——饱和蒸气的冷凝潜热,kJ/kg 。
式(4-61)的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时,则式(4-61)变为()[]()122t t c W T T c r W Q pc c s ph h -=-+= (4-62) 式中 c ph ——冷凝液的比热容,kJ/(kg ·℃); T s ——冷凝液的饱和温度,℃。

第四节 传热过程计算化工原理中所涉及的传热过程计算主要有两类:一类是设计计算,即根据生产要求的热负荷,确定换热器的传热面积;另一类是校核计算,即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算的基础。
应用前述的热传导速率方程和对流传热速率方程时,需要知道壁面的温度。
而实际上壁温常常是未知的,为了避开壁温,故引出间壁两侧流体间的总传热速率方程。
4—4—1 能量衡算对间壁式换热器做能量衡算,以小时为基准,因系统中无外功加入,且一般位能和动能项均可忽略,故实质上为焓衡算。
假设换热器绝热良好,热损失可以忽略时,则在单位时间内换热器中热流体放出的热量等于冷流体吸收的热量,即 , .、)()(1221c c c h h h H H W H H W Q -=-= (4—30)式中 Q —换热器的热负荷,kj/h 或W ;W -流体的质量流量,kg /h ;H -单位质量流体的焓,kJ /kg 。
下标c 、h 分别表示冷流体和热流体,下标1和2表示换热器的进口和出口。
式4-30即为换热器的热量衡算式,它是传热计算的基本方程式,通常可由该式计算换热器的传热量(又称热负荷)。
.若换热器中两流体无相变化,且流体的比热容不随温度而变或可取平均温度下的比热容时,式4-30可表示为Q )()(1221t t c W T T c W pc c ph h -=-= (4-31)式中 c p -流体的平均比热容,kJ /(kg ·℃);t —冷流体的温度,℃;T -热流体的温度,℃。
若换热器中的热流体有相变化,例如饱和蒸气冷凝时,式4-30可表示为Q )(12t t c W r W pc c h -== (4-32)式中 W h —饱和蒸气(即热流体)的冷凝速率,k 2/h ;r —饱和蒸气的冷凝潜热,kJ /kg 。
式4-32的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时,则式4-32变为Q )()]([1221t t c W T T c r W pc c ph h -=-+= (4-33)式中 C ph -冷凝液的比热容,kJ /(kg ·℃);T s —冷凝液的饱和温度,℃。



6.6 传热过程的计算工业上大量存在传热过程(我们指间壁式传热过程),他包括了流体与固体表面间的给热和固体内部的导热。
前面我们已经学过了导热和各种情况下的给热所遵循的规律,本节讨论传热过程的计算问题。
6.6.1 传热过程的数学描述在连续化的工业生产中,换热器内进行的大都是定态传热过程。
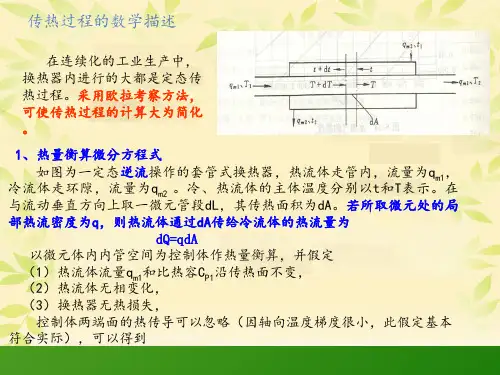
(1)热量衡算微分方程式如图为一套管式换热器,内管为传热管,传热管外径1d ,内径2d ,微元传热管外表面积d A 1,管外侧1α;内表面积d A 2,内侧2α,平均面积d A m ,壁面导热系数λ。
对微元体做热量衡算得 Q A q T c m p s d d d 11==-Q A q T c m p s d d d 22==-以上两式是在以下的假设前提下:① 热流体流量1s m 和比热1p c 沿传热面不变;② 热流体无相变化; ③ 换热器无热损失;④ 控制体两端面的热传导可以忽略。
(2)微元传热速率方程式如图所示套管换热器中,热量由热流体传给管壁内侧,再由管壁内侧传至外侧,最后由管壁外侧传给冷流体。
对上述微元,我们可以得到33211321d d d d d d d A q A q A q Q Q Q Q m =======阻力推动力=++-=-=-=-22m 1122w m w w 11w d 1d d 1d 1d d 1A A b A t T A t t A b t T A T T αλααλα 令 2211d 1d d 1d 1A A b A A K m αλα++= 则 )(d d 1d t T A K A K tT Q -=-=)(d d t T K AQ q -==式中 K ——总传热系数,W/m 2·K 。
因为沿着流体流动方向(套管换热器沿管长)流体的温度是变化的,所以α值也是变化的。
但若取一定性温度,则α与传热面无关,可以认为是一常数,这样K 也为一常数。
对上式进行积分,可以得到m t KA Q ∆= (3)传热系数和热阻 ① K 的计算由前面的分析可知,传热过程的总热阻1/K 由各串联环节的热阻叠加而成,原则上减小任何环节的热阻都可提高传热系数,增大传热过程的速率。
1 总传热速率方程如图所示,以冷热两流体通过圆管的间壁进行换热为例,热流体走管内,温度为T,冷流体走管外温度为t,管壁两侧温度分别为T W和t w,壁厚为,b,其热导率为λ,内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。
根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程:对于管内侧:对于管壁导热:对于管外侧:即故有令(4.6.1)则(4.1.1)该式称为总传热速率方程。
A为传热面积,可以是内外或平均面积,K与A是相对应的。
2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系,在换热器保温良好,无热损失的情况下,对于稳态传热过程,其热流量衡算关系为:(热流体放出的热流量)=(冷流体吸收的热流量)在进行热衡算时,对有、无相变化的传热过程其表达式又有所区别。
(1)无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量,W;m h,m c-----热、冷流体的质量流量,kg/s;C ph,C pc------热、冷流体的比定压热容,kJ/(kg·K);T1,t1 ------热、冷流体的进口温度,K;T2,t2------热、冷流体的出口温度,K。
(2)有相变化传热过程两物流在换热过程中,其中一侧物流发生相变化,如蒸汽冷凝或液体沸腾,其热流量衡算式为:一侧有相变化两侧物流均发生相变化,如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热,J/kg;D,D1,D2--------相变物流量,kg/s。
对于过冷或过热物流发生相变时的热流量衡算,则应按以上方法分段进行加和计算。
3 传热系数和传热面积(1)传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数,是进行传热计算的依据。
K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等,K值通常可以由实验测定,或取生产实际的经验数据,也可以通过分析计算求得。
传热系数K可利用式(4.6.1)进行计算。
但传热系数K应和所选的传热面积A相对应,假设和传热面积A i、A m和A0相对应的传热系数K分别为K i、K m和K0,则其相互关系为:在工程上,一般以圆管外表面积A0为基准计算总传热系数K0,除加以说明外,常将A0、K0分别以A、K表示,即:(4.6.2)该式又可以改写为:式中:d i,d0,d m------圆管的内径、外径、管壁的平均直径。
(2)污垢热阻换热器的传热表面在经过一段时间运行后,壁面往往积一层污垢,对传热形成附加的热阻,称为污垢热阻,这层污垢热阻在计算传热系数K时一般不容忽视。
由于污垢层的厚度及其热导率不易估计,通常根据经验确定污垢热阻。
若管壁内、外侧表面上的污垢热阻分别用R di和R d0表示,根据串联热阻叠加原则,式(4.6.2)变为:污垢热阻往往对换热器的操作有很大影响,需要采取措施防止或减少污垢的积累或定期清洗。
污垢热阻的大致范围在进行换热器的传热计算时,常需先估计传热系数K。
列管换热器中K值大致范围列管式换热器中K值大致范围热流体冷流体传热系数K/(W·m²·K-1)水轻油重油气体水蒸汽冷凝水蒸汽冷凝低沸点烃类蒸汽冷凝高沸点烃类蒸汽冷凝水蒸汽冷凝水蒸汽冷凝水蒸汽冷凝水水水水水气体水水水沸腾轻油沸腾重油沸腾850~1700340~91060~28017~2801420~425030~300455~114060~1702000~4250455~1020140~425(3)壁温的计算在计算自然对流、强制对流、冷凝和沸腾表面传热系数以及在选用换热器类型和管材时都需要知道壁温,由以下各式得:或壁温接近表面传热系数大的一侧流体温度。
例题4 平均温度差由于换热器中沿程流体的温度、物性是变化的,故式(4.1.1)中的传热温差(T-t)和传热系数K一般也就会变动,在工程计算中通常用平均传热温差代替,于是得到总的传热速率方程的表达式:Q=KAΔt m间壁两侧流体平均温度差的计算方法与换热器中两流体的相互流动方向有关,而两流体的温度变化情况,可分为恒温传热和变温传热。
(1)恒温传热时的平均温度差换热器的间壁两侧流体均有相变化时,例如在蒸发器中,间壁的一侧,液体保持在恒定的沸腾温度t 下蒸发,间壁的另一侧,加热用的饱和蒸气在一定的冷凝温度T下进行冷凝,属恒温传热,此时传热温度差(T-t)不变,即:Δt m=T-t(2)变温传热时的平均温度差变温传热时,两流体相互流动的方向不同,则对温度差的影响不同,分述如下。
◎逆流和并流时的平均温度差在换热器中,冷、热两流体平行而同向流动,称为并流;两者平行而反向的流动,称为逆流。
平均温度差的推导过程经推导得:为对数平均温差:逆流:并流:对于同样的进出口条件,逆并,并可以节省加热剂或冷却剂的用量,工业上一般采用逆流。
对于一侧有变化,另一侧恒温,逆并。
.4 平均温度差(续)◎错流和折流时的平均温度差在大多数的列管换热器中,两流体并非简单的逆流或并流,因为传热的好坏,除考虑温度差的大小外,还要考虑到影响传热系数的多种因素以及换热器的结构是否紧凑合理等。
所以实际上两流体的流向,是比较复杂的多程流动,或是相互垂直的交叉流动。
图中,(a)图两流体的流向互相垂直,称为错流,(b)图一流体只沿一个方向流动,而另一流体反复折流,称为简单折流。
若两股流体均作折流,或既有折流又有错流,则称为复杂折流。
对于错流和折流时的平均温度差,可采用安德伍德(Underwood)和鲍曼(Bowman)提出的图算法。
该法是先按纯逆流计算对数平均温度差△t m',然后再根据实际流动情况乘以校正系数ε△t,即:m'对数平均温度差的校正值动画校正系数ε△t与冷热两流体的温度变化有关,是R和P两参数的函数,即=热流体温降/冷流体温升=冷流体温升/流体最初温差校正系数ε△t可根据R和P两参数从相应的图中查得。
对数平均温差校正系数ε△t的查图对数平均温度差的校正系数值温差校正系数ε△t恒小于1,这是由于在列管换热器内增设了折流挡板及采用多管程,使得换热的冷、热流体在换热器内呈折流或错流,导致实际平均传热温差恒低于纯逆流时的平均传热温差。
当ε△t值小于0.8时,则传热效率低,经济上不合理,操作不稳定。
原因: 换热器内出现温度交叉或温度逼近现象。
避免措施: 采用多个换热器串联或采用多壳程结构,换热器个数或所需的壳程数,可用图解法确定。
5 传热效率和传热单元数法在传热计算中,传热速率方程和热流量衡算式将换热器和换热物流的各参数关联起来。
当已知工艺物流的流量、进、出温度时,可根据前面介绍的方法,计算平均传热温差△t m及热流量Q,从而求得所需的传热面积A,此类问题即前面提及的设计型计算问题。
然而,当给定两物流的流量、进口温度以及传热面积、传热系数K时,却难以采取解析方法直接确定两流体的出口温度。
往往需采用试差方法求解。
此类问题即前面所提及的操作型计算问题。
对此,若采用1955年由凯斯和伦敦导出的传热效率及传热单元数法,则能避免试差而方便地求得其解。
(1)传热效率假设冷、热两流体在一传热面为无穷大的间壁换热器内进行逆流换热,其结果必然会有一端达到平衡,或是热流体出口温度降到冷流体的入口温度;或是冷流体的出口温度升到热流体的入口温度,如图中(b)及(c)所示。
然而究竟哪一侧流体能获得最大的温度变化(T1-t1),这将取决于两流体热容量流率(mC p)的相对大小。
由热流量衡算式得:可见,只有热容量流率相对小的流体才有可能获得较大的温度变化,将该流体的热容量流率以(mC p)min 表示,而相对大的热容量流率表示为(mC p)max。
(b)冷流体C pc m c相对小的理论极限情况(c)热流体C pc m c相对小的理论极限情况将换热器实际热流量Q与其无限大传热面积时的最大可能传热量Qmax之比,称为换热器的传热效率ε。
◇ 逆流当较小时当较小时◇ 并流其温度变化最大的依然是热容量流率较小的流体,最大可能的传热温差仍为T1-t1。
故具有相同的传热效率定义式。
5 传热效率和传热单元数法(续)(2)传热单元数在换热器中,取微元传热面积,由热流量衡算和传热速率方程可得:◇对于热流体:为传热单元数取、为常数,则有◇ 对于冷流体:◎多个换热器串联◎传热单元数物理意义:全部温差变化相当于多少平均,NTU数值上表示单位传热推动力引起的温度变化;表明了换热器传热能力的强弱。
(3)传热效率与传热单元数的关系换热器中传热效率与传热单元数的关系可根据热流量衡算及传热速率方程导出。
推导过程热容量流率比整理不同流型,不同结构,则关系不同。
的具体关系图4.6.10 单程逆流换热器中ε与NTU和R间关系图4.6.11 单程并流换热器中ε与NTU和R间关系图4.6.10 折流换热器中ε与NTU和R间关系◎在传热单元数相同时,逆流时换热器的传热效率总是大于并流时。
(4)应用已知R和NTU,可求得,进而求和,可避免试差计算。
例题传热单元数NTU,热容量流率R与传热效率之间的关系动画11。