等量电荷两条线上的场强分布特点

一．等量异种同种电荷产生电场电场线场强关系1．等量异种点电荷形成的电场中电场线的分布特点(1)两点电荷连线上各点，电场线方向从正电荷指向负电荷．(2)两点电荷连线的中垂面(中垂线)上，电场线方向均相同，即场强方向均相同，且总与中垂面(线)垂直．在中垂面(线)上到O点等距离处各点的场强相等(O为两点电荷连线中点)．(3)在中垂面(线)上的电荷受到的静电力的方向总与中垂面(线)垂直，因此，在中垂面(线)上移动电荷时静电力不做功．(4) 等量异种点电荷连线上以中点O场强最小，中垂线上以中点O的场强为最大；(5)等量异种点电荷连线和中垂线上关于中点对称处的场强相同；2．等量同种点电荷形成的电场中电场线的分布特点(1)两点电荷连线中点O处场强为零，此处无电场线．(2)中点O附近的电场线非常稀疏，但场强并不为零．(3)两点电荷连线中垂面(中垂线)上，场强方向总沿面(线)远离O(等量正电荷)．(4)在中垂面(线)上从O点到无穷远，电场线先变密后变疏，即场强先变强后变弱．(5)等量同种点电荷连线上以中点电场强度最小，等于零．因无限远处场强E∞＝0，则沿中垂线从中点到无限远处，电场强度先增大后减小，之间某位置场强必有最大值．(6)等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.PS:等量异种电荷和等量同种电荷连线上以及中垂线上电场强度各有怎样的规律？(1)等量异种点电荷连线上以中点O场强最小，中垂线上以中点O的场强为最大；等量同种点电荷连线上以中点电场强度最小，等于零．因无限远处场强E∞＝0，则沿中垂线从中点到无限远处，电场强度先增大后减小，之间某位置场强必有最大值．(2)等量异种点电荷连线和中垂线上关于中点对称处的场强相同；等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.二．等量异种同种电荷产生电场电势等势面1.等量异种点电荷的电场：是两簇对称曲面，两点电荷连线的中垂面是一个等势面．如图1－4－6所示．在从正电荷到负电荷的连线上电势逐渐降低，φA>φA′；在中垂线上φB＝φB′.2.等量同种点电荷的电场：是两簇对称曲面，如图1－4－7所示，在AA′线上O点电势最低；在中垂线上O点电势最高，向两侧电势逐渐降低，A、A′和B、B′对称等势．-三、练习1．如图所示，在真空中有两个固定的等量异种点电荷+Q和-Q。

等量电荷场强和电势的分布规律电荷是电场的源头，产生电场的物理量是电荷。

在静电学中，由于电荷静止不动，电场在空间中呈现出一定的分布规律。

等量电荷场是一种最简单、最基本的电场分布形式，它在物理学教学和实验中有非常重要的应用。

一、等量电荷场的基本概念等量电荷场是指单位面积或单位体积内电荷量相等的场。

在静电场中，分布均匀的点电荷集合就构成了等量电荷场。

在等量电荷场中，每个点电荷的电场强度大小、方向和位置是固定的，即与其他电荷无关。

可以通过计算每个点电荷产生的电场强度，来确定等量电荷场的总电场强度分布。

通常，等量电荷场的分布形式是对称的，如球形等量电荷场、圆柱等量电荷场和平面点电荷场等。

二、球形等量电荷场E = k·Q/R²k 表示库仑常量，Q 表示电荷量，R 表示电荷与点 P 的距离。

利用叠加原理，可以得到球形等量电荷场的总电场强度，它的大小和方向与 P 点的距离 R 有关。

当 P 点在球面上时，球形等量电荷场的电场强度为：当 P 点在球心时，球形等量电荷场的电场强度为：在球心处，根据电势公式，有：当电荷等量分布于一个高度为 h、半径为 R 的圆柱体表面上时，它形成了一个圆柱形等量电荷场。

由于高度相同、面积分布均匀，因此认为整个圆柱体电荷密度为λ，即电荷分布的线密度满足：λ = Q/2πRh根据库仑定律，电荷线密度为λ 的圆柱体电荷在轴线上任意一点的电场强度为：ε 表示介电常数，r 表示电荷距离轴线的距离。

由于电荷在圆柱体表面上分布均匀，因此相对于中心轴线的任意一圆周，圆周上各点产生的电场强度大小和方向均相同。

与球形等量电荷场类似，圆柱形等量电荷场的电势跟电场强度成反比，电势沿轴线的变化规律为：V = λ/2πεln(r1/r2)r1 和 r2 分别表示轴线上距圆柱形等量电荷场两端点的距离。

四、平面点电荷场平面点电荷场是指电荷等量分布在一个无限大、厚度可忽略不记的导体板上。

根据库仑定律，假设平面板上分布的电荷是 Q，任意一点 P 离电荷所在板的距离为 r，可得到点 P 产生的电场强度为：由于点电荷具有球对称的特点，因此由点产生的电场强度大小与距离 r 的平方成反比。

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析1.等量同种电荷（1）两点电荷的连线上分析：在其连线上的中点，由于Q 相等，r相等，即E 大小相等，而两点电荷在的场强方向相反，故合场强为零，由||||212212r Q k r Q k E E E -=-=知，从中点往两边合场强增大，且关于中点对称。

（2）两点电荷的中垂线上分析：中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。

由于中垂线上的点到线两端的距离相等，由2rQ k E =知|E 1|=|E 2|，即大小相等，方向如图2所示：把E 1、E 2进行合成，故合场强E 如图所示。

所以从中垂线上中点往两边场强先是由零增大，但由2r Q k E =可知。

r 越大，E 减小，所以合场强又开始减小。

2.等量异种电荷（1）两点电荷的连线上分析：可根据电场线的疏密直接知中点最稀疏，故中点场强最小，往两边越密场强越大。

方向从正点荷指向负电荷。

（2）两点电荷的中垂线上分析：把正点荷、负点荷在中垂线上某点场强进行合成，合场强方向在连线上且由正电荷指向负电荷。

当A 点离中垂线中点越远，E 1、E 2大小越小，且夹角越大，所以合场强越小，又因为两边对称，可以中垂线上从中点经两边场强减小，方向与两点电荷的连线平行且由正电荷指向负电荷。

1.正电核电场线向外发散，负电荷电场线向内收缩，等势线总是和电场线垂直，在同一等势线上移动电荷，电场力不做功；2.电场力做正功，电势能减少，动能增加；电场力做负功，电势能增加，动能减少（不分正负电荷，通用）3.沿电场线方向，电势降落；沿电场线方向，电势降落最快。

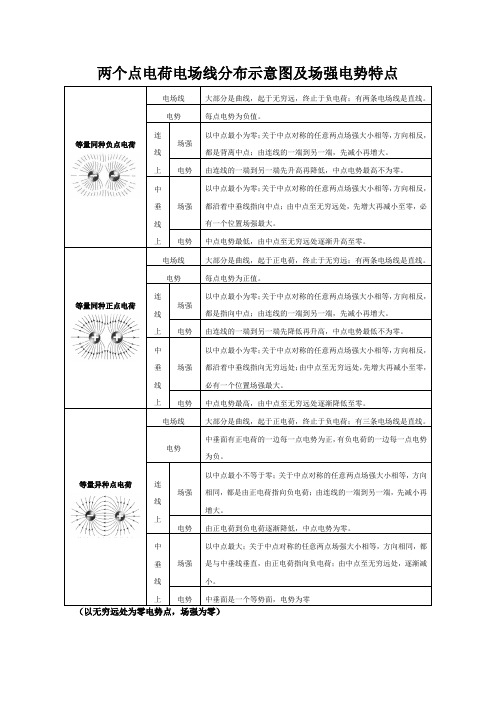
等量同种负点电荷电场线大部分是曲线，起于无穷远，终止于负电荷；有两条电场线是直线。

电势每点电势为负值。

连线上场强以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都是背离中点；由连线的一端到另一端，先减小再增大。

电势由连线的一端到另一端先升高再降低，中点电势最高不为零。

中垂线上场强以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都沿着中垂线指向中点；由中点至无穷远处，先增大再减小至零，必有一个位置场强最大。

电势中点电势最低，由中点至无穷远处逐渐升高至零。

等量同种正点电荷电场线大部分是曲线，起于正电荷，终止于无穷远；有两条电场线是直线。

电势每点电势为正值。

连线上场强以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都是指向中点；由连线的一端到另一端，先减小再增大。

电势由连线的一端到另一端先降低再升高，中点电势最低不为零。

中垂线上场强以中点最小为零；关于中点对称的任意两点场强大小相等，方向相反，都沿着中垂线指向无穷远处；由中点至无穷远处，先增大再减小至零，必有一个位置场强最大。

电势中点电势最高，由中点至无穷远处逐渐降低至零。

等量异种点电荷电场线大部分是曲线，起于正电荷，终止于负电荷；有三条电场线是直线。

电势中垂面有正电荷的一边每一点电势为正，有负电荷的一边每一点电势为负。

连线上场强以中点最小不等于零；关于中点对称的任意两点场强大小相等，方向相同，都是由正电荷指向负电荷；由连线的一端到另一端，先减小再增大。

电势由正电荷到负电荷逐渐降低，中点电势为零。

中垂线上场强以中点最大；关于中点对称的任意两点场强大小相等，方向相同，都是与中垂线垂直，由正电荷指向负电荷；由中点至无穷远处，逐渐减小。

电势中垂面是一个等势面，电势为零（以无穷远处为零电势点，场强为零）（以无穷远处为零电势点，场强为零）注意：电场线、等势面的特点和电场线与等势面间的关系：①电场线的方向为该点的场强方向，电场线的疏密表示场强的大小。

等量电荷两条线上的场强分布特点等量同种（异种）点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q，两电荷连线AB长度为L,中点为O.一、等量异种电荷1、两电荷连线上如图1所示，在两电荷连线上任取一点G，设AG长度为x，则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和，方向从A指向B（由正电荷指向负电荷一侧），由点电荷场强公式知：EG= EA+ EB=∵x+(L-x)等于定值L，∴当x=(L-x)，即x= 时，x与(L-x)乘积最大，EG有最小值，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称。

2、中垂线上如图2所示，在中垂线上，任取一点H，设OH=x，根据对称性知：EH沿水平方向向右，即在中垂线上各点场强水平向右（垂直于中垂线指向负电荷一侧），沿中垂线移动电荷，电场力不做功，由电势差定义知：中垂线为一等势线，与无限远处等势，即各点电势为零。

H点的场强EH=，∴在O点，即x=0处，EH最大，x越大，即距O点越远EH越小，两侧电场强度数值关于O 点对称。

二、等量同种电荷1、电荷连线上如图3所示，在两电荷连线上任取一点N，设AN长度为x，则N点场强EN为两点电荷在该点的场强EA、EB的矢量和，方向沿AB连线，O点左侧从A指向B，右侧从B指向A（沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之），N点电场强度大小知：EN = ，∴当x= 时，EN =0，，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称，方向相反。

2、中垂线上如图4所示，根据对称性知：在O点两侧，电场强度方向均沿中垂线方向从O点指向无限远（若两电荷为等量负电荷则反之），由极限分析法易得：在O点处，E =0；在距O点无限远处，E =0。

说明中间某位置有极大值，可见：合电场强度的大小随着距O点的距离增大，先从零增大到最大，然后逐渐减小。

关于等量点电荷周围场强和电势的分布特点作者：田军来源：《试题与研究·教学论坛》2017年第24期等量点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q，两电荷连线AB长度为L，中点为O。

一、等量的同种电荷形成的电场的特点1.场强特点①两点电荷连线上：任取一点P，设AP长度为x，则P点场强EP为两点电荷在该点的场强EA、EB的矢量和，方向沿AB连线，O点左侧从A指向B，右侧从B指向A（沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之）。

P点电场强度大小知：EP=，∴当x=时，EP=0，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称，方向相反。

②两点电荷连线的中垂线上：在O点两侧，电场强度方向均沿中垂线方向从O点指向无限远（若两电荷为等量负电荷则反之），由极限分析法易得：在O点处，E=0；在距O点无限远处，E=0。

说明中间某位置有极大值，可见：合电场强度的大小随着距O点的距离增大，先从零增大到最大，然后逐渐减小。

在中垂线上，任取一点P，设OP=x，由点电荷场强公式，P 点场强EP=2EAcosθ==运用数学方法，令y=，求导可得：y=令y′=0，则x2+2=3x2x2+2，即x2+2=3x2，∴当x=±L时，EP有最大值，∴从中点沿中垂线向两侧，电场强度的数值先增大后减小，两侧方向相反，关于O点对称的点数值相等。

2.电势特点①中点O点处的电势：φO=φA+φB=4>0②两点电荷连线上任意一点P处的电势：总结：在两个等量正电荷的连线上，由A点向B点方向，电势先减后增，在rA=R/2（即中点O处）电势最小，但电势总为正。

③两点电荷连线的中垂线上任意一点Q处的电势：总结：在两个等量正电荷的连线的中垂线上，由O点向N（M）点方向，电势一直减小且大于零，即O点最大，N（M）点为零。

二、等量的异种电荷形成的电场的特点1.场强特点①两电荷连线上任取一点G，设AG长度为x，则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和，方向从A指向B（由正电荷指向负电荷一侧），由点电荷场强公式知：∵x+（L-x）等于定值L，∴当x=（L-x），即x=时，x与（L-x）乘积最大，EG有最小值，即在两电荷连线中点O处场强最小，从O点向两侧逐渐增大，数值关于O点对称。

等量电荷电场的场强和电势分布的特点等量的点电荷形成的电场中的场强和电势特点一. 等量的同种电荷形成的电场的特点设两点电荷的带电量均为q，间距为R，向右为正方向1. 场强特点:在两个等量正电荷的连线上，由A点向B点方向，电场强度的大小先减后增，即中点O处, 场强最小为0；场强的方向先向右再向左, 除中点O外，场强方向指向中点O在两个等量正电荷连线的中垂线上，由O点向N（M）点方向，电场强度的大小先增后减；场强的方向由O点指向N（M）。

外推等量的两个负电荷形成的场结论：在两个等量负电荷的连线上，由A点向B点方向，电场强度的大小先减后增，中点O处, 场强最小为零；场强的方向先向左再向右（除中点O外）。

在等量负电荷的连线的中垂线上，由O点向N（M）点方向，电场强度的大小先增后减，场强的方向由N（M）指向O点2.电势特点:在两个等量正电荷的连线上，由A点向B点方向，电势先减后增，中点O处, 电势最小，但电势总为正。

在两个等量正电荷的连线的中垂线上，由O点向N（M）点方向，电势一直减小且大于零，即O点最大，N(M)点为零外推等量的两个负电荷形成的场在两个等量负电荷连线上，由A点向B点方向，电势先增后减，在中点O处, 电势最大但电势总为负；在两个等量负电荷连线的中垂线上，由O点向N（M）点方向，电势一直增大且小于零，即O点最小，N(M)点为零二：等量的异种电荷形成的电场的特点1. 场强特点在两个等量异种电荷的连线上，由A点向B点方向，电场强度的大小先减小后增大，中点O处场强最小；场强的方向指向负电荷在两个等量异种电荷的连线的中垂线上，由O点向N（M）点方向，电场强度的大小一直在减小；场强的方向平行于AB连线指向负电荷一端2.电势特点:在两个等量异种电荷的连线上，由A点向B点方向，电势一直在减小，中点O 处电势为零，正电荷一侧为正势，负电荷一侧为负势。

等量异种电荷连线的中垂线上任意一点电势均为零即等量异种电荷的连线的中垂线（面）是零势线（面）库仑定律内容表述：真空中两个静止点电荷之间的相互作用力的大小跟两个点电荷的电荷量的乘积成正比，跟它们的距离的二次方成反比．作用力的方向在两个点电荷的连线上公式：静电力常量：k = 9.0×109 N·m2/C2库仑定律适用条件：真空中，点电荷点电荷——理想化模型，实际上是不存在的．但只要带电体本身的大小跟它们之间的距离相比可以忽略，带电体就可以看作点电荷．并非是体积小就能当点电荷（理想化研究方法）启示与小结：可以看出，万有引力公式和库仑定律公式在表面上很相似，只有质量和电荷量的区别，体现了科学的一种对称美，它们的实质区别是：首先万有引力公式计算出的力只能是相互吸引的力，绝没有相排斥的力．其次，由计算结果看出，电子和质子间的万有引力比它们之间的静电引力小的很多，因此在研究微观带电粒子间的相互作用时，主要考虑静电力，万有引力虽然存在，但相比之下非常小，所以可忽略不计电场：是力的作用媒介：电荷之间的相互作用是通过特殊形式的物质——电场发生的，电荷的周围都存在电场，电场的物质性是客观存在的，具有物质的基本属性——质量和能量。

两等量同种（异种）电荷场强分布特点等量同种（异种）点电荷在空间的场强分布比较复杂，但在两条线（点电荷连线及其中垂线）上仍有其规律性，为研究方便，设它们带电量为Q ，两电荷连线AB 长度为L,中点为O.一、 等量异种电荷1、 两电荷连线上如图1所示，在两电荷连线上任取一点G ，设AG 长度为x ，则G 点场强E G 为两点电荷分别在该点的场强E A 、E B荷指向负电荷一侧），由点电荷场强公式知：E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ，∴当x=(L-x)，即x=2L时，x 与 (L-x)乘积最大， E G 有最小值，即在两电荷连线中点O 处场强最小，从O 点向两侧逐渐增大，数值关于O 点对称。

2、 中垂线上如图2所示，在中垂线上，任取一点H ，设OH=x ，根据对称性知：E H 沿水平方向向右，即在中垂线上各点场强水平向右（垂直于中垂线指向负电荷一侧），沿中垂线移动电荷，电场力不做功，由电势差定义知：中垂线为一等势线，与无限远处等势，即各点电势为零。

H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ，∴在O 点，即x=0处，E H 最大，x 越大，即距O 点越远E H 越小，两侧电场强度数值关于O 点对称。

图1G O B图2H二、 等量同种电荷1、 电荷连线上如图3所示，在两电荷连线上任取一点N ，设AN 长度为x ，则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和，方向沿AB 连线，O 点左侧从A 指向B ，右侧从B 指向A （沿两电荷连线指向较远一侧电荷，若两电荷为等量负电荷则反之），N 点电场强度大小知：E N =22)(x L kQx kQ --， ∴当x=2L时，E N =0，，即在两电荷连线中点O 处场强最小， 从O 点向两侧逐渐增大，数值关于O 点对称，方向相反。

等量同种正点电荷
注意：电场线、等势面的特点和电场线与等势面间的关系：
①电场线的方向为该点的场强方向，电场线的疏密表示场强的大小。

②电场线互不相交，等势面也互不相交。

③电场线和等势面在相交处互相垂直。

④电场线的方向是电势降低的方向，而且是降低最快的方向。

⑤电场线密的地方等差等势面密；等差等势面密的地方电场线也密。

电容器动态变化的两类典型问题讨论
平行板电容器充电后，继续保持电容器两极板与电池两极相连接，若电容器的d 、S 、ε变化，将引起电容器的C 、Q 、U 、E 怎样变化：由于电容器始终连接在电池上，因此两板间的电压保持不变，可根据下列几式讨论C 、Q 、E 的变化情况
d
d U E d S kd SU CU Q d S kd S C 144∝=∝==∝= επεεπε 平行板电容器充电后，切断与电池的连接，若电容器的d 、S 、ε变化，将引起电容器的C 、Q 、U 、E 怎样变化：由于电容器充电后，切断与电池的连接，使电容器的带电量保持不变，可根据下列几式讨论C 、U 、E 的变化情况
S Q S kQ d kd
S Q Cd Q d S d S kdQ d kd d S kd S C εεππεεεππεεπε∝=⋅==∝=∝=44,4,4ＵＥ＝　４ＳＱ　ＣＱＵ＝。