济南外国语学校2008—2013年面向全省招生考试数学试题及答案.doc

数 学 试 题(考试时间90分钟，满分100分) 请将全部答案写在答题纸上，否则不得分。

．．．．．．．．．．．．．．．．．．．真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！本试题共有17道题．其中1—6题为选择题，6-12题为填空题， 13-17题为解答题一、选择题：（本大题共6题，每题4分，满分24分）1．已知关于x 的方程01)2(=-+x b a 无解，那么b a 的值是（ ） A ．负数 B ．正数 C ．非负数 D ．非正数 2．如图，两个反比例函数y =x k 1和y=xk2 (其中k 1>k 2>0)在第一象限内的图象依次是C l 和C 2，设点P 在C 1上，PC ⊥x 轴于点C ，交C 1于点A ，PD 上y 轴于点D ，交C 2于点B ，则四边形PAOB 的面积为( )(A)k l +k 2 (B)k l -k 2 (C)k l ·k 2 (D)21k k3．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（ ） A ．第①块B ．第②块C ．第③块D ．第④块4．如图，在Rt △ABC 中，∠C=90°，AC=BC=6cm ，点P从点A 出发，沿AB 方向以每秒cm 的速度向终点B 运动；同时，动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动，将△PQC 沿QC 翻折，点P 的对应点为点P′．设点Q 运动的时间为t 秒，若四边形QPCP′为菱形，则t 的值为（ ） A ．2 B ．2 C ．22 D ．35．已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B 1在y 轴上，点C 1、E 1、E 2、C 2、E 3、E 4、C 3在x 轴上．若正方形A 1B 1C 1D 1的边长为1，∠B 1C 1O=60°，B 1C 1∥B 2C 2∥B 3C 3，则点A 3到x 轴的距离是（ ）6.若函数22(100196|100196|)2y x x x x =-++-+，则当自变量取1、2、3、…、100这100个自然数时，函数值的和是（ ）。

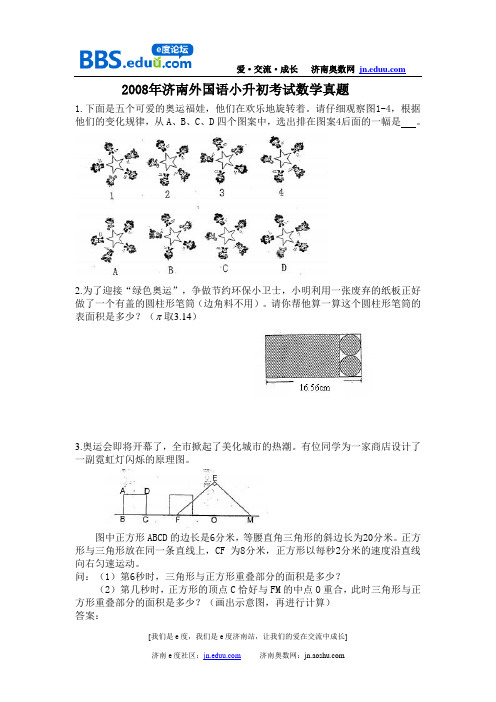
2008年济南外国语小升初考试数学真题1.下面是五个可爱的奥运福娃，他们在欢乐地旋转着。

请仔细观察图1-4，根据他们的变化规律，从A、B、C、D四个图案中，选出排在图案4后面的一幅是。

2.为了迎接“绿色奥运”，争做节约环保小卫士，小明利用一张废弃的纸板正好做了一个有盖的圆柱形笔筒（边角料不用）。

请你帮他算一算这个圆柱形笔筒的表面积是多少？（ 取3.14）3.奥运会即将开幕了，全市掀起了美化城市的热潮。

有位同学为一家商店设计了一副霓虹灯闪烁的原理图。

图中正方形ABCD的边长是6分米，等腰直角三角形的斜边长为20分米。

正方形与三角形放在同一条直线上，CF为8分米，正方形以每秒2分米的速度沿直线向右匀速运动。

问：（1）第6秒时，三角形与正方形重叠部分的面积是多少？（2）第几秒时，正方形的顶点C恰好与FM的中点O重合，此时三角形与正方形重叠部分的面积是多少？（画出示意图，再进行计算）答案：4.下面是一副象棋的棋盘，如果用（2,3）表示“马”的位置，用（5,6）表示“炮”的位置，那么“车”的位置用同样的办法应表示为。

5.请你仔细观察下面这张纸的折叠步骤，最后一个步骤是在折好的纸上穿孔，然后打开这张纸，应该是A、B、C、D四个图案中的哪一个：。

6.“书籍是人类进步的阶梯。

”在学校开展的读书月活动中，小强和小丽积极响应，踊跃读书并开展竞赛。

请你根据他们的对话，通过计算判断一下他俩谁读的书多？7.你做过用手指记数的游戏吗？一个小朋友按下图所示的规则练习记数，当他数到25是，对应的是指；数到107时，对应的是指。

根据你发现的规律，数到2008时，对应的是指。

（填出指头的名称，各指头的名称从上到下依次为大拇指、食指、中指、无名指、小指）8.小红、小亮的家与学校的位置如图所示。

请仔细读图获取信息，当已知小红去学校的速度为每分钟50米时，编一道应用题，并做出解答。

（提示：可以增加条件，根据所编题目的难易程度得分。

）。

济南外国语学校2012-2013学年度第一学期 高二期末模块考试数学（文）试题（2013.1）说明：本卷为发展卷，采用长卷出题、附加计分的方式。

第Ⅰ、Ⅱ卷为必做题，第Ⅲ卷为选做题，必做题满分为 120 分，选做题满分为30分。

第Ⅰ卷为第1题 页至第 10 题，第Ⅱ卷为第11 题至第18 题，第Ⅲ卷为第19 题至第22 题。

考试时间120 分钟。

温馨提示：生命的意义在于不断迎接挑战，做完必做题后再挑战一下发展题吧，你一定能够成功！第I 卷（选择题，共50分）一、选择题(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的)1. 已知在等差数列{}n a 中，若1a =4，45-=a ，则该数列的公差d 等于 A. 1 B.53C. - 2D. 32. 在ABC △中，已知4,6a b ==，60B =，则sin A 的值为A.3B.2C. 3D.23. 设a b >，c d >，则下列不等式成立的是 A. a c b d ->- B. ac bd > C.a dc b>D. b d a c +<+4. 在ABC △中，60,6,10A b c ===，则ABC △的面积为A.B. C. 15 D. 30 5. 在等差数列{}n a 中，有67812a a a ++=，则该数列的前13项之和为 A ．24B. 52C. 56D. 1046. 不等式组13y x x y y <⎧⎪+≤⎨⎪≥-⎩表示的区域为D ，点P (0，－2)，Q (0，0)，则A. P ∉D ，且Q ∉DB. P ∉D ，且Q ∈DC. P ∈D ，且Q ∉DD. P ∈D ，且Q ∈D7. 在ABC △中，::4:3:2a b c =，那么cos C 的值为 A.14B. 14-C. 78D.11168. 在各项都为正数的等比数列{}n a 中，首项31=a ，前三项和为321S =，则4a = A ．32B. 24C. 27D ．549．已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≤-≥-+≤-+01033032y y x y x ,若目标函数y x z +=2的最大值是A ．6B ．3C.23D ．110. 等比数列}{n a 的前n 项和n S ，若36,963==S S ，则=++987a a aA. 72B. 81C. 90D. 99提示：请将1—10题答案涂在答题卡上，11-22题写在答题纸上第Ⅱ卷（非选择题，共70 分）二、填空题(本大题共4小题，每小题5分，共20分)11. 在△ABC 中，角A,B,C 的对边分别是c b a ,,，若45,30,3===B A a ，则=b .12. 正数,x y 满足2x y +=，则x y ⋅的最大值为______ .13. 数列{}n a 的前n 项和n S 满足31nn S =-，则n a = .14. 在ABC ∆中，若cos cos a B b A =，则ABC ∆的形状一定是三、解答题(本大题共4小题，共50分.解答应写出文字说明，证明过程或演算步骤) 15. (本小题满分12分)解下列不等式（1） 2230x x +-< ; （2）203xx -≤+. 16. (本小题满分12分)已知在△ABC 中，角A,B,C 的对边分别是c b a ,,，若54cos ,5,6===C b a（1）求边长c 的大小;（2）求三角形ABC 的面积. 17. (本小题满分13分)已知等差数列{}n a 的前n 项和为n S ，365,36a S ==，（1）求数列{}n a 的通项公式；（2） 设2n an b =，求数列{}n b 的前n 项和n T .18 (本小题满分13分)云南省镇雄县高坡村发生山体滑坡，牵动了全国人民的心，为了安置广大灾民，救灾指挥部决定建造一批简易房,每间简易房是地面面积为1002m ，墙高为3m 的长方体样式，已知简易房屋顶每12m 的造价为500元，墙壁每12m 的造价为400元.问怎样设计一间简易房地面的长与宽，能使一间简易房的总造价最低？最低造价是多少？第Ⅲ卷（发展题，共 30 分）19 （3分）在下列函数中，最小值是A. )0(2≠+=x x x yB. )0(1>+=x xx y C. 2y =D. 2xxy e e-=+20 （3分）不等式2(2)2(2)40a x a x x R a -+--<∈对一切恒成立，则实数的 取值范围是 .21. (本小题满分12分) 设锐角三角形ABC 的内角A,B,C 的对边分别为a b c ，，,2sin a b A = （1）求B 的大小；（2）求C A sin cos +的取值范围. 22. (本小题满分12分)等差数列{}n a 中，11a =，前n 项和n S 满足条件)(1242*∈++=N n n n S S n n . (1)求数列{}n a 的通项公式； （2）记2n an n b a =，求数列{}n b 的前n 项和n T济南外国语学校2012-2013学年度第一学期高二期末模块考试数学试题（2013.1）文科答题纸二、填空题（每小题5分，共20分）11、12、13、14、三、解答题（共50分）15、（12分）16、（12分）17、（13分）18、（13分）发展卷19、20 、21、（12分）22、（12分）2013年1月高二期末模块考试数学试卷（文科）发展卷参考答案一、选择题（5*10=50）1.C2.A3.D4.B5.B6.C7.C8.B9.A 10.B 二、填空题（5*4=20）11.23 12 1 13.132-⋅=n n a 14 等腰三角形.三、解答题15.解：(1) (3)(1)0x x +-< {|31}x x ∴-<< - ----------------------------------------6分(2)203x x -≥+ {|23}x x x ∴≥<-或 ----------------------------------------12分16. 解：（1）由题知C ab b a c cos 2222-+=解得132=c ,13=c ----------------------------------------6分（2）53cos 1sin 2=-=C C 9sin 21=⋅=∆C ab S ABC----------------------------------------12分17解: （1）设{}n a 的公差为d , 则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩------3分 即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩,-----------------------------------------6分*12(1)21,()n a n n n N ∴=+-=-∈.-------------------------------8分 (2) 2122na n nb -==135212222n n T -∴=++++--------------------------------------10分2(14)2(41)143n n --==-------------------------------------------13分18．解：设地面的长为x m,宽为m x 100--------------------------------------2分 则总造价400)10066(500100⨯⨯++⨯=xx y --------------------------------------6分2400)100(50000⨯++=xx y ------------------------------------8分9800024002050000=⨯+≥所以，当且仅当xx 100=时，即x=10m 时，y 取得最小值.--------------------------------------11分答：设计地面长宽均为10m 时，造价最低，为98000元。

2008年济南市高中阶段学校招生考试数学试卷参考答案及评分标准一、选择题1．A2．B3．C4．B5．B6．C7．C8．A9．B10．D11．B12．C 二、填空题13．914．(3)(1)+-15．BD=CD，OE=OF，DE∥AC等16．417．15x x三、解答题18．（1）解：2210x-+=1分21x= ................................................................................... 2分1x=.................................................................................. 3分2（2）解：解①得x＞－2 ..................................................................................... 4分解②得x＜3 ........................................................................................ 5分∴此不等式组的解集是－2＜x＜3 .............................................................. 6分解集在数轴上表示正确............................................................................. 7分19．（1）证明：∵AB∥DE，∴∠B=∠DEF∵AC∥DF，∴∠F=∠ACB .............................................................................1分∵BE=CF，∴BE+EC= CF + EC即BC=EF ...................................................2分∴△ABC≌△DEF∴AB=DE................................................. 3分（2）解：过点O作OG⊥AP于点G连接OF ............................................... 4分∵ DB=10，∴ OD=5∴ AO=AD+OD=3+5=8∵∠PAC=30°∴ OG=12AO=1842⨯=cm ........................ 5分∵ OG⊥EF，∴ EG=GF∵3==∴ EF=6cm ............................................ 7分20．解：组成的所有坐标列树状图为：....................................5分或列表为：................................... 5分方法一：根据已知的数据，点(,)m n不在第二象限的概率为123 164=方法二：1－43164= ............................................................................................ 8分21．解：设康乃馨每支x元，水仙花每支y元................................................... 1分由题意得：3192218x yx y+=⎧⎨+=⎩........................................................................ 4分解得：54x y =⎧⎨=⎩ ............................................................................................. 6分第三束花的价格为353417x y +=+⨯= ........................................................ 7分 答：第三束花的价格是17元． .................................................................. 8分 22．解:（1）设CD 为x 千米，由题意得，∠CBD=30°，∠CAD=45° ∴AD=CD=x ..................................1分 在Rt △BCD 中，tan30°=x BD∴ BD= ...................................2分 AD+DB=AB=40∴ 40x += ............................ 3分 解得 x ≈14.7∴ 牧民区到公路的最短距离CD 为14.7千米． ............................................ 4分 （若用分母有理化得到CD=14.6千米，可得4分）（2）设汽车在草地上行驶的速度为v ，则在公路上行驶的速度为3v ，在Rt △ADC 中，∠CAD=45°，∴ AC=CD 方案I 用的时间134333AD CD AD CDCD t v vvv+=+==......................................... 5分方案II 用的时间2A C t vv==6分∴ 2143C D t t vv-=-3v.......................................................................................... 7分∵ 4＞0∴ 21t t -＞0 .............................................................................................. 8分 ∴方案I 用的时间少，方案I 比较合理 ....................................................... 9分23．解：（1）y y ⎧=+⎪⎨=⎪⎩ .......................................................................... 1分解得：2x y =⎧⎪⎨=⎪⎩ ....................................................................................... 2分∴点P 的坐标为（2，） ........................................................................ 3分（2）将0y =代入y =++=∴ 4x =，即OA=4 ........................................................................................ 4分做PD ⊥OA 于D ，则OD=2，∵ tan ∠2=∴ ∠POA=60° ............................................................................................ 5分∵4=∴△POA 是等边三角形． ..................... 6分 （3）① 当0<t≤4时，如图在Rt △EOF 中，∵∠EOF=60°，OE=t ∴EF=23t ，OF=21t∴S=21·OF·EF=283t ............................ 7分当4<t<8时，如图设EB 与OP 相交于点C 易知：CE=PE=t －4，AE=8－t∴AF=4－t 21，EF=23（8－t ）∴OF=OA －AF=4－（4－21t ）=21t∴S=21（CE+OF ）·EF=12（t －4+12t ）2（8－t ）=－3832t +43t －83.............................. 8分② 当0<t≤4时，82t ， t=4时，S最大=23当4<t<8时，S=－3832t +43t －83=－383（t －316）2+338t=316时，S最大=338∵338>23，∴当t=316时，S最大=338 ................................................. 9分24．解：（1）设抛物线的解析式为2(1)3y a x =-- ........................................... 1分 将A （－1，0）代入: 20(11)3a =--- ∴ 34a = ................................. 2分∴ 抛物线的解析式为23(1)34y x =--，即：2339424y x x =--.......................... 3分（2）是定值，1PM PN BEAD+= ........................................................................... 4分∵ AB 为直径，∴ ∠AEB=90°，∵ PM ⊥AE ，∴ PM ∥BE∴ △APM ∽△ABE ，∴ PM AP BEAB=①同理: PN PB AD AB = ② .................................................................................. 5分① + ②:1PM PN AP PB BEADABAB+=+=................................................................... 6分（3）∵ 直线EC 为抛物线对称轴，∴ EC 垂直平分AB∴ EA=EB ∵ ∠AEB=90°∴ △AEB 为等腰直角三角形．∴ ∠EAB=∠EBA=45° .................... 7分 如图，过点P 作PH ⊥BE 于H ，由已知及作法可知，四边形PHEM 是矩形， ∴PH=ME 且PH ∥ME 在△APM 和△PBH 中∵∠AMP=∠PHB=90°， ∠EAB=∠BPH=45° ∴ PH=BH 且△APM ∽△PBH ∴ PA PM PB BH =∴PA PM PM PBPHM E== ① ................... 8分在△MEP 和△EGF 中，∵ PE ⊥FG ， ∴ ∠FGE+∠SEG=90° ∵∠MEP+∠SEG=90° ∴ ∠FGE=∠MEP ∵ ∠PME=∠FEG=90° ∴△MEP ∽△EGF∴PM EF=②M E EG由①、②知：PA EF=................................................................................... 9分PB EG（本题若按分类证明，只要合理，可给满分）。

济南市外国语学校小升初数学试卷一.(共8题，共16分)1.以下的说法中错误的有（）个。

（1）分针的转速是时针转速的60倍。

（2）用0、1、2、3这四个数字能组成18个不同的四位数。

（3）一个三条边的长度都是整厘米的三角形，其中两条边长度是3厘米和5厘米，那么第三条边的长度有5种可能。

（4）-2℃与10℃相差12℃。

A.4B.3C.2D.12.已知点A和点B在同一条数轴上，点A表示数-2，点B与点A相距3.5个单位长度，那么点B表示的数是（）。

A.-1.5B.5.5C.1.5或-5.5D.-1.5或3.53.规定10米记作0米，11米记作+1米，则下列说法错误的是（）。

A.6米记作-6米。

B.15米记作+5米。

C.8米记作-2米。

D.+2米表示长度为12米。

4.平行四边形面积一定，底和高（）。

A.成正比例B.成反比例C.不成比例D.不成反比例5.如果规定从原点出发，向南走为正，那么-100米表示的意义是（）。

A.向东走100米B.向西走100米C.向北走100米 D.向南走100米6.把一个圆柱削成一个最大的圆锥，圆柱与削去部分的体积比是（）。

A.3：1B.2：1C.3：2D.2：37.以明明家为起点，向东走为正，向西走为负．如果明明从家出发，先走了+20米，又走了-30米，这时明明离家的距离是（）米。

A.20B.-30C.10D.-108.一个圆柱和一个圆锥，底面周长的比是2：3，体积比是5：6，那么这个圆柱和圆锥高的最简单的整数比是（）。

A.8：5B.5：8C.12：5D.5：12二.(共8题，共16分)1.甲数的20%等于乙数的，则甲数大于乙数，甲乙两数均不为零。

（）2.圆的直径一定，圆的周长与圆周率成正比例。

（）3.圆柱的底面直径是3 cm，高是9.42 cm，它的侧面沿高展开后是一个正方形。

（）4.正方体的体积与棱长不成比例。

（）5.圆柱体与圆锥体的体积比是3:1，则圆柱体与圆锥体一定等底等高。

山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题（文科）2012.11本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分，考试时间120分钟。

第I卷（选择题共60分）1、 选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的）1.设集合U={1,2,3,4,5}，A={1,3,5},B={2,5},则A∩(C U B)等于（ ）A.{2}B.{2,3}C.{3}D.{1,3}【答案】D【解析】,所以，选D.2.复数=( )A. B. C. D.【答案】C【解析】，选C.3.的（）A．充分不必要条件　Ｂ．必要不充分条件C．充分必要条件 D．既不充分又不必要条件【答案】A【解析】或，所以充分不必要条件，选A.4. 已知函数，则的值等于（ ）A. B. C. D.0【答案】C【解析】，所以，选C.5.下列函数中既是偶函数又在（0，+∞）上是增函数的是（ ）A. B. C. D.【答案】B【解析】函数为奇函数，排除A.当时，函数和为减函数，排除C,D,选B.6. 函数的零点为（ ）A.1,2B. ±1,-2C.1,-2D.±1, 2【答案】C【解析】由得，即，解得或，选C.7. 若点在函数的图象上，则tan的值为（ ）A.0B.C.1D.【答案】D【解析】因为点在函数的图象上，所以，解得，所以，选D.8. 已知向量a=（2,1），b=（-1，k），a·（2a-b）=0，则k=（）A. -12B. -6C. 6D. 12【答案】D【解析】因为，即，所以，即，选D.9.某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名。

现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为（）A. 6 B. 7 C. 8 D.9【答案】C【解析】设从高二应抽取人，则有，解得，选C.10.若a>0,b>0,且函数在x=1处有极值，则ab的最大值（）A.2B.3C.6D.9【答案】D【解析】函数的导数为，函数在处有极值，则有，即，所以，即，当且仅当时取等号，选D.11. 已知函数其中若的最小正周期为,且当时, 取得最大值,则( )A. 在区间上是增函数B. 在区间上是增函数C. 在区间上是减函数D. 在区间上是减函数【答案】A【解析】由，所以，所以函数，当时，函数取得最大值，即，所以，因为，所以，，由，得，函数的增区间为，当时，增区间为，所以在区间上是增函数，选A.12. 函数f(x)的定义域为R，f(-1)=2,对任意，,则的解集为( )A.(-1，1)B.(-1，+∞)C.(-∞，-l)D.(-∞,+∞)【答案】B【解析】设, 则，，对任意，有，即函数在R上单调递增，则的解集为，即的解集为，选B.注意事项：1．第Ⅱ卷必须用0．5毫米黑色签字笔在答题纸各题的答题区域内作答，不能写在试题卷上; 如需改动，先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸,修正带,不按以上要求作答的答案无效。

山东省济南市外国语学校小升初数学试卷一.(共8题，共16分)1.下面叙述中，有（）句话是正确的。

（1）分母是质数的最简分数，不能化成有限小数（2）任何长方体，只有相对的两个面才完全相等（3）爸爸跑100米用了13分钟（4）长方形的周长一定，长和宽不成比例（5）因为圆周长C=πd，所以，圆周长一定，π和d成反比例（6）圆锥体体积比与它等底等高的圆柱体体积少三分之二A.1B.2C.3D.42.一条裙子原价430元，现价打九折出售，比原价便宜（）元。

A.430×90%B.430×（1＋90%）C.430×（1－9%）D.430×（1－90%）3.一种饼干包装袋上标着：净重(150±5)克，表示这种饼干标准质量是150克，实际每袋最少不少于( )克。

A.145B.150C.155D.1604.一块试验田去年产水稻800千克，比前年增收二成，这块试验田前年产水稻多少千克？列式正确的是（）。

A.800×（1+20%）B.800×（1﹣20%）C.800÷（1+20%） D.800÷（1﹣20%）5.服装店老板买进500双袜子，每双进价3元，原定零售价是4元．因为太贵，没人买，老板决定按零售价八折出售，卖了60%，剩下的又按原零售价的七折售完．请你算一下，卖完着500双袜子时（）。

A.盈利20元B.亏本20元C.盈利25元D.亏本25元6.一件衣服先按获取利润40元销售，后将利润降低到25元出售，现在的利润是（）。

A.-25元B.+15元C.-40元D.+25元7.上学期，六年级某班共收到班费800元，购买图书、奖品、门锁等用去650元，班级活动开支220元，上学期结余（）元。

A.+370B.+30C.﹣70D.8708.一种精密的机器零件长4mm，在图纸上长8cm，图纸的比例尺是（）。

A.1∶2B.2∶1C.1∶20D.20∶1二.(共8题，共16分)1.除数一定，被除数和商正比例。

济南外国语学校2012-2013学年度第一学期 高二期末模块考试数学（理）试题（2013.1）说明：本卷为发展卷，采用长卷出题、附加计分的方式。

第Ⅰ、Ⅱ卷为必做题，第Ⅲ卷为选做题，必做题满分为 120 分，选做题满分为30分。

第Ⅰ卷为第1题 页至第 10 题，第Ⅱ卷为第11 题至第18 题，第Ⅲ卷为第19 题至第22 题。

考试时间120 分钟。

温馨提示：生命的意义在于不断迎接挑战，做完必做题后再挑战一下发展题吧，你一定能够成功！第I 卷（选择题，共50分）一、选择题(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的)1. 已知在等差数列{}n a 中，若1a =4，45-=a ，则该数列的公差d 等于 A.1 B.53C. - 2D. 3 2.在ABC △中，已知4,6a b ==，60B =，则sin A 的值为A.3B.2C.3D.23. 设a b >，c d >，则下列不等式成立的是 A. a c b d ->- B. ac bd > C.a dc b>D. b d a c +<+4.在ABC △中，60,6,10A b c ===，则ABC △的面积为A.B. C.15 D.30 5. 在等差数列{}n a 中，有67812a a a ++=，则该数列的前13项之和为 A ．24 B.52 C.56 D.1046. 不等式组13y x x y y <⎧⎪+≤⎨⎪≥-⎩表示的区域为D ，点P (0，－2)，Q (0，0)，则A. P ∉D ，且Q ∉DB. P ∉D ，且Q ∈DC. P ∈D ，且Q ∉DD. P ∈D ，且Q ∈D7.在ABC △中，::4:3:2a b c =，那么cos C 的值为A.14 B.14- C.78 D.11168. 在各项都为正数的等比数列{}n a 中，首项31=a ，前三项和为321S =，则4a = A ．32B.24C.27D ．549．已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≤-≥-+≤-+01033032y y x y x ,若目标函数y x z +=2的最大值是A ．6B ．3 C.23D ．1 10. 等比数列}{n a 的前n 项和n S ，若36,963==S S ，则=++987a a a A. 72 B. 81 C. 90 D. 99提示：请将1—10题答案涂在答题卡上，11-22题写在答题纸上第Ⅱ卷（非选择题，共70分）二、填空题(本大题共4小题，每小题5分，共20分) 11. 正数,x y 满足2x y +=，则x y ⋅的最大值为______ .12. 数列{}n a 的前n 项和n S 满足31nn S =-，则n a = .13. 若不等式220ax bx ++>的解集是11(,)23-，则a b +的值为 . 14. 在ABC ∆中，若cos cos a B b A =，则ABC ∆的形状一定是三、解答题(本大题共4小题，共50分.解答应写出文字说明，证明过程或演算步骤) 15. (本小题满分12分) 解下列不等式 （1）2230x x +-< ; （2）203xx -≤+. 16. (本小题满分12分)已知在△ABC 中，角A,B,C 的对边分别是c b a ,,，若46,5,cos 5a b A ===-（1）求角B 的大小;（2）求边c. 17. (本小题满分13分)已知等差数列{}n a 的前n 项和为n S ，365,36a S ==，（1）求数列{}n a 的通项公式；（2） 设2n an b =，求数列{}n b 的前n 项和n T . 18. (本小题满分13分)云南省镇雄县高坡村发生山体滑坡，牵动了全国人民的心，为了安置广大灾民，救灾指挥 部决定建造一批简易房,每间简易房是地面面积为1002m ，墙高为3m 的长方体样式，已知简易房屋顶每12m 的造价为500元，墙壁每12m 的造价为400元.问怎样设计一间简易房的地面的长与宽，能使一间简易房的总造价最低？最低造价是多少？第Ⅲ卷（发展题，共30分）19、（3分）在下列函数中，最小值是22的是 A.12lg (0)lg y x x x =+> B. 2sin sin y x x=+()0,x π∈ C. 2y =D.2xxy e e-=+20（3分）在锐角ABC ∆中，1,2,BC B A ==则AC 的取值范围为 . 21. (本小题满分12分)已知锐角三角形ABC 的内角A,B,C 的对边分别为a b c ，，,若2sin a b A = （1）求B 的大小；（2）求C A sin cos +的取值范围. 22. (本小题满分12分)已知各项均为正数的数列{}n a ，满足221120n n n n a a a a ++--= （*∈N n ），且21=a .（1）求数列{}n a 的通项公式；（2）设n n n a a b 21log ⋅=,若n b 的前n 项和为n S ，求n S ;（3）在（2）的条件下，求使5021>⋅++n n n S 成立的正整数n 的最小值.济南外国语学校2012-2013学年度第一学期高二期末模块考试数学试题（2013.1）理科答题纸二、填空题（每小题5分，共20分）11、12、13、14、三、解答题（共50分）15、（12分）16、（12分）17、（13分）18、（13分）发展卷19、20 、（每小题3分）21、（12分）22、（12分）2013年1月高二期末模块考试数学试卷（理科）参考答案一、选择题 1.C 2.A 3.D 4.B 5.B 6.C 7.C 8.B 9.A 10.B二、填空题 11. 1 12. 132-⋅=n n a 13.14- 14、等腰三角形三、解答题15.解：(1) (3)(1)0x x +-< {|31}x x ∴-<< -----------------------------------------6分(2)203x x -≥+ {|23}x x x ∴≥<-或 -----------------------------------------12分 16. 解：（1）由题知54cos -=A则53sin =A 且A 为钝角 -----------------------------------------4分由正弦定理得B b A a sin sin =，21sin =B 所以30=B -----------------------------------------8分（2）bca cb A 2cos 222-+=整理得01182=-+c c解得433-=c -----------------------------------------12分17解: （1）设{}n a 的公差为d , 则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩------------------3分 即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩,-----------------------------------------6分*12(1)21,()n a n n n N ∴=+-=-∈.-------------------------------8分 (2) 2122na n nb -==135212222n n T -∴=++++--------------------------------------10分2(14)2(41)143n n --==-------------------------------------------12分18. 解：设地面的长为x m,宽为m x100--------------------------------------2分 则总造价400)10066(500100⨯⨯++⨯=xx y --------------------------------------6分2400)100(50000⨯++=xx y9800024002050000=⨯+≥所以，当且仅当xx 100=时，即x=10m 时，y 取得最小值.--------------------------------------10分答：设计地面长宽均为10m 时，造价最低，为98000元。

济南外国语学校20XX 年面向全省招生考试数学试题（2008.4）一．选择题（本题共8小题，每小题4分，共32分）1．下列运算正确的是 ( A ）1262a a a ÷= （B ）222()a b a b +=+ （C ）22142x x x-=-+ （D2．如图所示的一块长方体木头，沿虚线所示位置截下去所得到的截面图形是（A ） （B ） （C ） （D ）3．正比例函数与反比例函数图象都经过点（1，4），在第一象限内正比例函数图象在反比例函数图象上方的自变量x 的取值范围是（A ）x ＞1 （B ）0＜x ＜1 （C ）x ＞4 （D ）0＜x ＜44．小宝和爸爸、妈妈三人在操场上玩跷跷板，爸爸体重为69千克，坐在跷跷板的一端，体重只有妈妈一半的小宝和妈妈同坐在跷跷板的一端，这时爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃，加在他和妈妈坐的一端，结果爸爸被跷起离地.小宝体重可能是(A ）23.3千克 (B) 23千克 ( C) 21.1千克 ( D) 19.9千克 5．二次函数221y ax x a =++-的图象可能是6．一物体及其正视图如图所示，则它的左视图与俯视图分别是右侧图形中的 ( A ）①、② （B ）③、② （C ）①、④ （D ）③、④③①② ④ 正视图 A B C D7、如图是一张简易活动餐桌,现测得OA=OB=30cm ， OC=OD=50cm ，现要求桌面离地面的高度为40cm ，那么 两条桌腿的张角∠COD 的大小应为（A ）100° （ B ）120° （C ）135° （D ）150°8．某兴趣小组决定去市场购买A ，B ，C 三种仪器，其单价分别为3元，5元，7元，购买这批仪器需花62元；经过讨价还价，最后以每种单价各下降1元成交，结果只花50元就买下了这批仪器.那么A 种仪器最多可买（A ）8件 （B ）7件 （C ）6件 （D ）5件 二．填空题（本题共6小题，每小题4分，共24分）9.若对任意实数x 不等式b ax >都成立，那么a 、b 的取值范围为10．如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪下,则右图展开后得到的图形的面积为11． 已知△ABC 是边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边， 画第三个等腰Rt △ADE ，…，依此类推， 第n 个等腰直角三角形的斜边长是12．如图，△ABC 是等腰直角三角形，BC 是斜边，点P 是 △ABC 内一定点，延长BP 至p '，将△ABP 绕点A 旋转后， 与△ACP /重合，如果AP =2，那么PP /= ．13．已知∠BAC =45°,一动点O 在射线AB 上运动（点O 与点A 不重合），设OA ＝x ,如果半径为1的⊙O 与射线AC 只有一个公共点，那么x 的取值范围是 .14．一青蛙在如图8×8的正方形（每个小正方形的边长为1）网格的格蛙从点A 开始连续跳六次正好跳回到点A ，则所构成的封闭图形的面积的最大值是______。

济南外国语2013数学部分试题1、计算题,（5-13/35*9）+（6-13/35*8）+（7-13/35*7）+（8-13/35*6）+（9-13/35 *5）=？2、应用题，银行9点开门，17点关门，9点存50万，若每小时的存/提量一定。

到14点的时候50万能够增长至60万。

若提款两扩大4被，存款量不变，扩大到50万到一个时间，若提款两扩大10倍，存量变成1/2，关门利润有50万，开门留款多少。

3、有一个圆，半径=3，圆上面有A、B2个点，和半径平行=3，延长半径，以A、B、及延长点作为三角形的三个顶点，求阴影面积是多少。

解题思路：等比等高的规律。

以及六分之一圆面体。

4、倒数第二道应用题：苹果和梨的比是1比2,苹果卖了20%,梨卖的和剩下的比是1比3,这时苹果卖了18千克,梨卖了12千克,剩下苹果是梨的4/15,问梨和苹果各多少千克？苹果梨的答案是37，745、 (36/5+44/7+52/9)/(11/7小+13/9+9/5)=？6. 数学：合唱团一共96人，其中女生占9/16，后来又有若干个女生加入，女生人数占总数的10/17，问后来有多少女生参加？7. 一个底面积72平方厘米的圆柱容器，水深2.5厘米。

现在放入一个棱长6厘米的正方形铁块，水未完全淹没铁块。

求现在水面的高度。

8.把半径为2分米的圆柱体去，切拼成近似长方体，表面积增加20平方分米，求圆柱体体积。

（8分）9.用若干个大小相同的小正方体，拼成一个图形，从侧面看和从正面看到如下图形。

问最少需要几块，最多需要几块？10.填空题：妈妈给孩子准备早餐，有7种早餐，每天选2个搭配，选到牛奶和鸡蛋可能性为（）。

11.一座楼四层，每层有3个窗户，每个窗户有4块玻璃分别是白色和灰色每个窗户分别代表一个数字，从左往右表示一个数字，四个楼所表示的数分别是791，275，362,612第三层代表那一个三位数？12.填空：6.17*23+6.17*45+617*0.32=_________.13.填空：写出50以内的两个质数，要乘积最大这两个质数的乘积是（）。