2 信号分析基础(频谱分析)
- 格式:pdf
- 大小:1.04 MB
- 文档页数:75




信号分析基础理论知识之频谱分析1. 从时域到频域实际的波形可视为由若干正弦波所合成,每一正弦分量各有其一定的频率和幅值。
(a) 波形;(b) 由三个正弦波组成;(c) 频谱2. 傅里叶变换(1) FT (连续傅里叶变换)正变换:逆变换:其中,ω=2πf,f(t)为时域数据序列,F(ω)为频域的谱函数序列。
(2) DFT(离散傅里叶变换)对N个样点的数字化的时域波形进行数值积分计算,计算某一频率点的幅值。
可在计算机上进行,但计算量巨大。
(3) FFT(快速傅里叶变换)离散变换的一种快速算法,计算速度快,适合工程应用,但具有如下限制:参与计算的数据点数(FFT分析点数)必须为2的幂次方,即2n。
频率分辨率问题,频率间隔Δf。
3. 频谱泄露误差泄漏产生:当实际信号的频率处于f(i)和f(i+1)之间时,则会产生频率泄漏现象,导致误差。
频率误差:FFT频率反映的频率为(i-1)Δf Hz或者iΔf Hz,最大频率误差为Δf/2。
幅值误差:谱峰的幅值减小,泄漏到附近的谱峰上,最大幅值误差为36.3%。
整周期采样:信号的频率正好处于f(i)的位置上,即信号频率等于Δf 的整数倍,则不会产生泄漏。
产生机理(边缘截断):常用校正方法:加窗处理:如hanning、平顶窗等,仅能校正幅值,不能校正频率;频率计校正:可以对若干个单个谱峰进行校正,特点为快速实时,既能校正幅值,又能校正频率;平滑处理:能有效校正最大谱峰处的幅值,不能校正频率。
4. 加窗和平滑加窗可消除或减轻信号截断和周期化带来的不连续问题。
平滑是将频谱任何一点的附近若干点进行相加,将泄露到两边的能量加回来。
(a) 整周期;(b) 严重泄露;(c) 加汉宁窗;(d) 平滑5. 窗函数基本特性相当于滤波器。
6. 常用窗(a) 指数窗形式;(b) hanning窗形式;(c)hamming窗形式(d) 平顶窗形式;(e) Kaiser窗形式;(f) 余弦矩形窗形式7. 平均和重叠平均:对较长的信号进行平均计算,用以消除随机噪声带来的误差。

频谱分析的理论基础及振动案例分析频谱分析是一种通过将信号中各频率成分分离出来,并定量描述其幅度、相位等特征的方法。
其理论基础主要涉及信号的傅里叶变换、功率谱密度以及频谱分析方法等方面。
振动案例分析是频谱分析的一个应用领域,用于研究物体的振动特性以及故障诊断等。
下面将分别对频谱分析的理论基础及振动案例分析进行更详细的讨论。
首先,频谱分析的理论基础涉及信号的傅里叶变换。
傅里叶变换是一种将信号从时域转换到频域的变换方法,用于分析信号的频率成分。
对于一个连续的实际信号x(t),其傅里叶变换可以表示为:X(f) = ∫[x(t) * exp(-2πift)]dt其中,X(f)为信号在频率为f时的复数幅度。
通过计算信号x(t)在不同频率上的傅里叶变换,就可以得到信号的频谱分布情况。
功率谱密度也是频谱分析的重要理论基础。
信号的功率谱密度描述了信号在不同频率上的功率分布情况。
对于一个随机平稳信号x(t),其功率谱密度可以通过自相关函数R(τ)进行计算,即:S(f) = Lim(T -> ∞) [1/(2T)] * ,F{∫[x(t) * exp(-2πift)]dt},²其中,F{}表示傅里叶变换,S(f)为信号在频率为f时的功率谱密度。
功率谱密度可以用来反映信号在不同频率上的能量分布情况,从而了解信号的频谱特性。
频谱分析方法包括离散傅里叶变换(DFT)、快速傅里叶变换(FFT)等。
DFT是将连续信号的傅里叶变换转化为离散信号的变换方法,通过对信号进行采样和截断来获得有限长度的离散信号,进而进行频谱分析。
FFT是DFT的一种高效实现方法,能够快速计算信号的频谱。
振动案例分析是频谱分析的一个重要应用领域,主要用于研究物体的振动特性以及故障诊断。
在实际工程中,振动往往是由于机械结构的不平衡、不稳定或者故障引起的。
频谱分析方法可以通过分析振动信号的频谱特性,进一步判断振动是否正常以及故障的类型和原因。


第二章 信号分析基础1、信号分析中常用函数包括:δ函数、sinc(t)函数、复指数函数e st① δ函数具有“抽样(乘积)、筛选(积分)、卷积”特性,其拉氏变换和傅氏变换的值均为1。
② 卷积特性的表达式为)()()()()(t f d t f t t f =-=*⎰+∞∞-ττδτδ,τ为两信号之间的时差。
③ sinc(t)函数又称为闸门函数、滤波函数或内插函数,分别对应其用处:闸门(或抽样)、低通滤波、采样信号复原时sinc(t)函数叠加构成非采样点波形。
④ 复指数函数e st 中出现的“负频率”是与负指数相关联的,是数学运算的结果,并无确切的物理含义。
2、一个信号不能够在时域或频域都是有限的。
3、信号的时域统计分析:均值x μ、均方值ψ2x 、方差σ2x 。
三者具有如下关系:2x2x 2x μσψ+= 式中,ψ2x (又称平均功率,平均能量的一种表达)表达了信号的强度; σ2x 描述了信号的波动量; μ2x 描述了信号的静态量。
4、各态历经过程:此过程中的任一个样本函数x(t)都经历了过程的各种状态,从它的一个样本函数x(t)中可以提取到整个过程统计特征的信息。
5、相关函数的性质:① 自相关函数R x (τ)是τ的偶函数,满足:)()(ττ-=x x R R 。
② 互相关函数R xy (τ)是τ的非奇非偶函数,满足:)()(ττ-=yx xy R R 。
③ 当τ=0时,自相关函数具有最大值。
对于功率信号,若均值μx =0,则在τ=0点处,有ψ2x =σ2x =R x (τ)。
④ 周期信号的R x (τ)仍然是与原信号同频率的周期信号,但不具有原信号的相位信息。
⑤ 两周期信号(同频)的R xy (τ)仍然是与原信号同频率的周期信号,但保留了原信号的相位信息。
⑥ 两个不同频的周期信号互不相关,其互相关函数R xy (τ)=0。
⑦ 随机信号的R x (τ)将随|τ|值增大而很快趋于0。
有限带宽白噪声信号的R x (τ)是一个sinc(τ)型函数,即可说明。

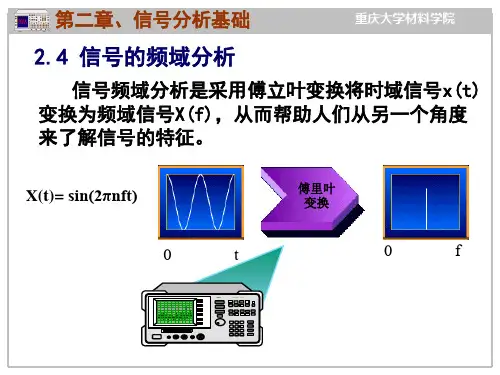


频谱分析:将时域信号变换至频域加以分析的方法称为频谱分析。
频谱分析的目的是把复杂的时间历程波形,经过傅里叶变换分解为若干单一的谐波分量来研究,以获得信号的频率结构以及各谐波和相位信息。
(傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。
从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。
从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。
)很多情况下的振动是周期的,任何关于时间的周期函数都能展开成傅立叶级数,即无限多个测试信号的频域分析是把信号的幅值、相位或能量变换以频率坐标轴表示,进而分析其频率特性的一种分析方法,又称为频谱分析。
对信号进行频谱分析可以获得更多有用信息,如求得动态信号中的各个频率成分和频率分布范围,求出各个频率成分的幅值分布和能量分布,从而得到主要幅度和能量分布的频率值。
由时间函数求频谱函数的傅里叶变换公式就是将该时间函数乘以以频率为系数的指数函数之后,在从负无限大到正无限大的整个区间内,对时间进行积分,这样就得到了与这个时间函数对应的,以频率为自变量的频谱函数。
频谱函数是信号的频域表示方式。
根据上述傅里叶变换公式,可以求出常数(直流信号)的频谱函数为频域中位于零频率处的一个冲激函数,表示直流信号就是一个频率等于零的信号。
与此相反,冲激函数的频谱函数等于常数,表示冲激函数含有无限多个、频率无限密集的正弦成分。
同样的,单个正弦波的频谱函数就是频域中位于该正弦波频率处的一对冲激函数。
利用傅里叶变换的方法对信号进行分解,并按频率展开,使其成为频率的函数,进而在频率域中对信号进行研究和处理的一种过程,称为频谱分析。
对信号进行频谱分析,是对其进行傅里叶变换,得到其振幅谱与相位谱。
分析软件主要为Matlab。
对于信号来说,分模拟信号与数字信号。
进行频谱分析时,对于模拟信号来说,首先对其进行抽样,使其离散化,然后利用离散傅里叶变换(DFT)或者快速傅里叶变换(FFT),然后对其幅度(ABS)和相位(ANGLE)的图像进行分析,而对于数字信号来说,则可直接进行离散傅里叶变换或快速傅里叶变换。