当前位置：文档之家 › 线性时不变系统因果和稳定性共41页

线性时不变系统因果和稳定性共41页

  • 格式：ppt
  • 大小：3.59 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

线性时不变系统的稳定性分析

线性时不变系统的稳定性分析

线性时不变系统的稳定性分析稳定性是控制系统理论中的重要概念，对于线性时不变系统来说尤其重要。

稳定性分析可以帮助我们确定系统的输出是否会在输入变化或干扰的情况下产生不受控制的波动或发散。

本文将探讨线性时不变系统的稳定性分析方法。

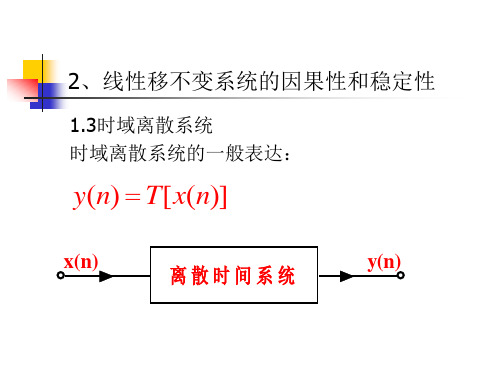
一、线性时不变系统的定义线性时不变系统（Linear Time-Invariant System，LTI系统）是指满足叠加性和时移不变性两个性质的系统。

叠加性指系统对输入的响应是可加的，时移不变性指系统对延时输入的响应是不变的。

线性时不变系统可以用微分方程或差分方程来描述。

二、稳定性的定义在系统稳定性分析中，我们关注的是系统的零输入响应或者零状态响应。

稳定性可以分为BIBO稳定性和渐近稳定性两种类型。

1. BIBO稳定性BIBO稳定性（Bounded-Input Bounded-Output Stability）是指当输入有界时，系统的输出也是有界的。

如果对于任意有界的输入信号，系统的输出都有界，则系统是BIBO稳定的。

2. 渐近稳定性渐近稳定性是指当输入信号趋于稳定时，系统的输出也趋于稳定。

如果对于任意渐近稳定的输入信号，系统的输出也渐近稳定，则系统是渐近稳定的。

三、稳定性分析方法稳定性分析的常用方法包括传输函数法、状态空间法和频域法。

下面将分别介绍这三种方法。

1. 传输函数法传输函数法是用传输函数来描述系统的稳定性。

传输函数是输入和输出的关系，它是Laplace变换或Z变换的比值。

对于连续时间系统，传输函数可以表示为H(s)；对于离散时间系统，传输函数可以表示为H(z)。

通过分析传输函数的极点（Pole）可以判断系统的稳定性。

对于连续时间系统，如果传输函数的极点都位于左半平面，则系统是BIBO稳定的；如果传输函数的极点有位于右半平面的，则系统是不稳定的。

对于离散时间系统，如果传输函数的极点都位于单位圆内部，则系统是BIBO稳定的；如果传输函数的极点有位于单位圆外部的，则系统是不稳定的。

线性移不变系统的因果性和稳定性

线性移不变系统的因果性和稳定性
方法一： T[x(n)]=nx(n)=y(n) T[x(n-m)]=nx(n-m)
而y(n-m)=(n-m)x(n-m)
显然：T[x(n-m)] y(n-m) 时变系统
线性移不变系统的因果性和稳定性
方法二：寻找一个反例
x1(n)=(n) y1(n)=n(n)=0
x2 (n)=x1(n-1)=δ(n-1)
探讨
y2 (n) n (n 1) (n 1)
该系统是有移变增量n的系统，若已知当前的输入是1，而不知
当前所在时刻，仍不能确定当前的输出是多少。
结论：系统有一个移变的增益，则系统一定是一个移变系统
线性移不变系统的因果性和稳定性
深入讨论
例：考虑y(n)=x(2n)是否为移不变系统？
x1(n)
5
4
4
3
3
2 1
2 1
-4
0
4n
线性移不变系统的因果性和稳定性
y1(n)
5
3
3
1
1
-2
02
n
x2(n)=x1(n-2)
5
4
4
3
3
2 1
21
-2 0
4 6n
线性移不变系统的因果性和稳定性
y2(n)
5
3
3
1
1
-2 0
3
n
y1(n)
5
3 1
3 1
-2 0 2
n
线性移不变系统的因果性和稳定性
LSI系统输入与输出的关系
x(n) *[h1(n) * h2 (n)] [x(n)* h2 (n)]* h1(n)
x(n) h1(n)
y(n) x(n)
h2(n)

线性时不变系统及其特性.ppt

线性时不变系统及其特性.ppt
叠加性：
e ( t ) rt ( ) 1 1 e ( t ) et ( ) rt ( ) rt ( ) 1 2 1 2 et ( ) rt ( ) 2 2
e1 (t)
H H
H
r1 ( t )
r2 ( t )
r1 (t) r2 (t)
e2 (t)
e1 (t) e2 (t)
d A r ( t ) 1 0 A r ( t )5 A e ( t ) d t 原方程两端乘A：
d r ( t ) A 1 0 r ( t )5 A e ( t ) d t
(1),(2)两式矛盾。故此系统不满足均匀性
t 0( 1 )
t 0( 2 )
t 0
r ( 0 ) e ( 0 ) e (2 )
现在的响应=现在的激励+以前的激励
所以该系统为因果系统。
例： 微分方程 r 所代表的系统是否是因果系统 ( t ) e ( t ) e ( t 2 ) 解：
t 0
r ( 0 ) e ( 0 ) e (2 )
e( t )
r (t )
O
T
t
O
t
e( t t 0 )
r (t t 0 )
O t0
t0 T
t
O
t0
t
二．时变系统与时不变系统
判断方法 先时移，再经系统＝先经系统，再时移
f (t )
H
H f (t )
DE
y (t )
f (t )

y (t )
f (t )
若 则
未来的激励
所以该系统为非因果系统。
定义 一个系统，在零初始条件下，其输出响应与输入信号施加于系 统的时间起点无关，称为非时变系统，否则称为时变系统。 分析： 电路分析上看：元件的参数值是否随时间而变 从方程看：系数是否随时间而变 从输入输出关系看：

线性时不变系统的因果和稳定性

线性时不变系统的因果和稳定性

线性移不变系统的因果性和稳定性
稳定系统
稳定系统是指有界输入产生有界输出（BIBO）的系统。 若： x(n) ≤ M < ∞
则： y(n) ≤ P < ∞
LSI系统是稳定系统的充分必要条件：
n =−∞
∑
∞
h( n) = P < ∞
结论：因果稳定的LSI系统的单位抽样响应是因果的（单边的） 且是绝对可和的。
则：T[ax1 (n)]=aT[x1 (n)]=ay1 (n)
线性移不变系统的因果性和稳定性
例：证明y(n)=ax(n)+b(a、b为常数）所代表的系统 不是线性系统。
证：设T[x1(n)]=ax1(n)+b T[x2(n)]=ax2(n)+b
则：T[x1(n)+x2(n)]=a[x1(n)+x2(n)]+b
N M
∑ a y (n − k ) = ∑ b
k =0 k m=0
m
x ( n − m)
阶差：为未知序列（指输出序列y(n)）变量序号的最高值 与最低值之差。
线性：各y(n-k)及各x(n-m)项都只有一次幂且不存在它们的 相乘项；否则时非线性的。
差分方程
线性常系数差分方程的求解
手工迭代 迭代法 序列域求解法 计算机软件（MATLAB） 经典解法 变换域求解法
∞ m=-∞
∞
m =−∞
⇐ 满足比例性和可加性 ⇐ 满足移不变性
＝ ∑ x(m)h(n-m)
线性移不变系统的因果性和稳定性 结论：
y ( n) = x ( n) * h( n)
x(n) LSI系 统 系 h(n) y(n)=x(n)*h(n)

第二章线性时不变系统详解演示文稿

第二章线性时不变系统详解演示文稿
othxe(rw)ishe(t )d
2.3
线
求: y(t) x(t) h(t)
x( )h(t )d
x(t )h( )d
性 时 不
解：这里利用卷积 x的(t积分)h微(分)d性质。
xt xt ut ut T
变
h( )
2T
系
统
的
0
性 x(t)
质
(1)
0
2T
y(t)
2T
T
y
t
t
y
注意：①上述结论都是针对LTI而 言的； ②卷积运算必须收敛。
24
第二十四页，总共四十页。
例① 对于由两个单元级联构成的非线性系统如下：
x(t) 平方
乘2 y(t) 2x2 (t)
交换两个级联单元的顺序后
2.3
x(t )
y(t) 4x2 (t)
线
乘2
平方
性
时
系统总的响应发生了变化，所以级联的无序性只适用于线性系统
23
第二十三页，总共四十页。
由于卷积满足交换律，因此，系统级联的先后次序可以调换。具
体的推导过程看课本P78页。
2.3
xn h1n h2n xn h2n h1n
线
性
时
不
变 系
x(t) h1(t)
h2 (t) y(t) 结论：
统
LTI系统总响应与系统
的
级联的次序无关。
性 质
x(t) h2 (t)
y (t ) h1 (t )
将x(t)用一系列的矩形脉冲近似。
x(t)
2.2
连
x(k)
续
x (t)
时
间

判断系统线性,时变,因果方法.ppt

判断系统线性,时变,因果方法.ppt

系统不满足均匀性
系统不具有叠加性 此系统为非线性系统。 请看下面证明过程
证明均匀性
设信号e(t)作用系统，响应为r(t) 当Ae(t)作用于系统时，若此系统具有线性，则
d Ar ( t ) 10 Ar ( t ) 5 Ae ( t ) d t t 0( 1 )
原方程两端乘A：
d r ( t ) A 10 r ( t ) 5 Ae ( t ) d t t 0( 2 )
t 0 t 0
( 3 ) ( 4 )
d t r t r t 10 r t r t 5 e t e t 0( 5 ) 1 2 1 2 1 2 d t
(3)+(4)得 (5)、(6)式矛盾，该系统为不具有叠加性
f t 1
C 2
C f t 2 2

C H f t 1 1 C 1
Hห้องสมุดไป่ตู้
H C f t C f t 1 1 2 2
H
H f t 1
f t 2
H
H f t 2
C H f t 2 2 C 2
是否为时不变系统？
f t
D t f t E H

t f t
f t
t D Ef H


t f t

可见, 时移、再经系统 经系统、再时移，, 所以此系统是时变系统。
三．线性时不变系统的微分特性
线性时不变系统满足微分特性、积分特性
e t
de t dt
系 统

系统的因果性和稳定性

若系统 n时刻的输出，只取决于n时刻以及n时刻以前 的输入序列，而与n时刻以后的输入无关，则称该系统为 因果系统。
LSI系统是因果系统的充要条件：
h(n) 0 n 0
满足上式的序列称为因果序列，因此因果系统的单位取样 响应必然是因果序列。因果性系统的条件从概念上也容易 理解，因为单位取样响应是输入为δ(n)的零状态响应，在 n=0时刻以前即n<0时，没有加入信号，输出只能等于零， 注：关于此条件的严格证明可参考程佩青《数字信号处理 教程〉
N4 N0 N2
N5 N1 N3
x(n) h(n)
0 N0 N1 h(n m)
n0
N1 N00
m
h(n m)
0 n N0 m h(n m)
n 0 N2 N3
n
h(n m)
n N0 N2
0 N2
m
h(n m) n N1 N3
m
0
n N1 m 0
N3
3. 判断以下系统是否是（1）线性（2） 移不变（3）因果（4）稳定的？
由于x2 (n) x1(n 1)，而y2 (n) y1(n 1) y(1) 1边界条件下的系统不是移不变系统
当输入x3(n) x1(n) x2 (n) (n) (n 1)时，输出 y3(n) (1 a) (n) (1 a a2 )an1u(n 1)
an1u(n 1) y1(n) y2 (n) 不满足可加性 y(1) 1边界条件下的系统不是线性系统
（1）若边界条件
y(1) 0
求其单位抽样响应。 （2）若边界条件
求y其(单1) 位1抽样响应，并判断是否为 线性时不变系统。
解：1)令输入x(n) (n)，则输出y(n) h(n)，
又已知y(1) 0

信号与系统 第二章 线性时不变系统 课件 优质课件

y(2) 1 0 2 1 y(3) y(4) y(5) y(6)
y(n) x(n) h(n) { 1, 2, 2,8,3,6,5,1, }
优点：计算非常简单。
缺点：①只适用于两个有限长序列的卷积和；
②一般情况下，无法写出 y(n)的封闭表达式。

x(n) h(n) x(k)h(n k) k


x( ) (t ) x( ) h(t )




x( ) (t )d x( )h(t )d


x(t) y(t)
y(t) x( )h(t )d
表明:连续LTI系统可以完全由它的单位冲激响应
h(t)
x(t)
h1(t)
y(t)
+
h2(t)
y t xth1 t xt h2 t xt h1 t h2 t
yt xtht
ht h1t h2 t
结论：两个LTI系统并联，其总的单位脉冲(冲激)响
一. 用单位冲激信号表示连续时间信号


x( ) (t )d x(t) (t )d



x(t) (t )d
x(t)

x(t) x( ) (t )d
x(t) lim x( ) (t ) 0
为积分变量 ； 2. 反转：将h()变为h(- )； 3. 平移：将h(- )平移t，变为h[-(-t)]； 4. 相乘： 将x()和h(t- )相乘； 5. 积分：求x()h(t- )乘积下的面积。
例: x(t) eatu(t) , a 0
h(t) u(t)

§1.6线性时不变系统

§1.6线性时不变系统•线性系统与非线性系统•时变系统与时不变系统•因果系统与非因果系统•稳定系统与不稳定系统通信与信息工程学院江帆一、系统的定义若干相互作用、相互联系的事物按一定规律组成具有特定功能的整体称为系统。

电子系统是电子元器件的集合体。

电路侧重于局部，系统侧重于全部。

电路、系统两词通用。

二、系统的分类及性质可以从多种角度来观察、分析研究系统的特征，提出对系统进行分类的方法。

下面讨论几种常用的分类法。

1. 连续系统与离散系统若系统的输入信号是连续信号，系统的输出信号也是连续信号，则称该系统为连续时间系统，简称为连续系统。

若系统的输入信号和输出信号均是离散信号，则称该系统为离散时间系统，简称为离散系统。

2. 动态系统与即时系统若系统在任一时刻的响应不仅与该时刻的激励有关，而且与它过去的历史状况有关，则称为动态系统或记忆系统。

含有记忆元件(电容、电感等)的系统是动态系统。

否则称即时系统或无记忆系统。

3. 线性系统与非线性系统满足线性性质的系统称为线性系统。

（1）线性性质系统的激励f (·)所引起的响应y(·) 可简记为y(·)= T[ f (·)]系统f (·)y (·)线性性质包括两方面：齐次性和可加性。

若系统的激励f (·)增大a倍时，其响应y(·)也增大a倍，即T[a f(·)] = a T[ f (·)]则称该系统是齐次的。

若系统对于激励f1(·)与f2(·)之和的响应等于各个激励所引起的响应之和，即T[f1(·)+ f2(·)] = T[ f1(·)]+T[ f2(·)] 则称该系统是可加的。

若系统既是齐次的又是可加的，则称该系统是线性的，即T[a f 1(·) + b f 2(·)] = a T[ f 1(·)] + bT[ f 2(·)]()()t e t e 2211αα+H()()t r t r 2211αα+)()()()(22112211t t t t r r e e αααα+→+H()t e 2()t r 2H)(1t e ()t r 1（2）动态系统是线性系统的条件动态系统不仅与激励{ f(·) }有关，而且与系统的初始状态{x(0)}有关。

线性系统理论系统的运动稳定性PPT课件

第16页/共57页
4.几种稳定性之间的关系
5. Lyapunov稳定性 与微分方程解关于 初值的连续性依赖性 在微分方程理论中,解的适定性,即解 的存在性,惟一性及它对初值的连续依 赖性,是一个非常重要的内容.
第17页/共57页
5.1.4 Lyapunov第二方法的主要定 理
Lyapunov把动力学系统稳定性的 方法归纳为本质不同的两种方法,分 别称为Lyapunov第一方法(间接法:通 过对线性化方程的稳定性分析给出原 非线性系统在小范围内稳定性的信息) 和第二方法(直接法:通过构造一类似 于“能量”函数,分析它及其一次导
内存在一个正定函数 V (x) ，它沿着系统
x f ( x, t ) , x(t0 ) x0 , t t0
的全导数 V( x) 在 内为半负定的，但在 内 V( x) 在系统
x f ( x, t ) , x(t0 ) x0 , t t0
的非零解上非零，则该系统的零平衡点 为渐近稳定。
第25页/共57页
定理5.1.5 如果在 R n 上存在一个具 有无穷大性质的正定函数 V (x) ，它 沿着系统
x f ( x, t ) , x(t0 ) x0 , t t0
的全导数 V( x) 在 Rn 内为负定的，则该 系统的零平衡点为全局渐近稳定 的。
第26页/共57页
定理5.1.6 如果在原点的某邻域
第8页/共57页
第9页/共57页
定义5.1.5 （Lyapunov意义下的大范围渐近
稳定性） 设 xe 为系统
x f ( x, t) , x(t0 ) x0 , t t0
的一个平衡状态，如果以状态空间中的任一
有限点 x0为初始状态的受扰运动 (t; x0 , t0 )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。